Using the Single-Constant Kubelka–Munk Model for Surface Color Prediction of Pre-Colored Fiber Blends
Abstract
1. Introduction
2. Methods
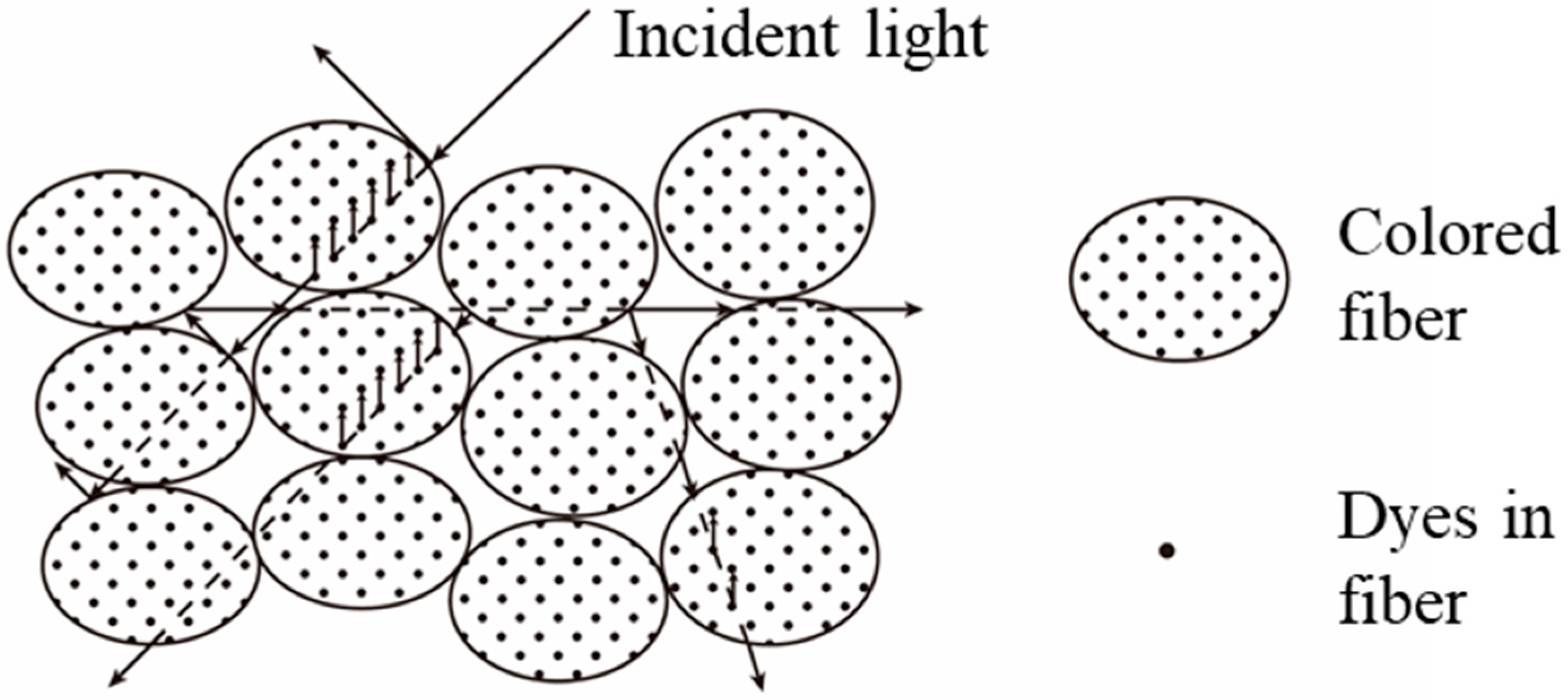
2.1. Light Scattering in the Medium of Pre-Colored Fiber Blending
2.2. Improved Single-Constant KM Model Based on Light Scattering Correction
3. Experimental
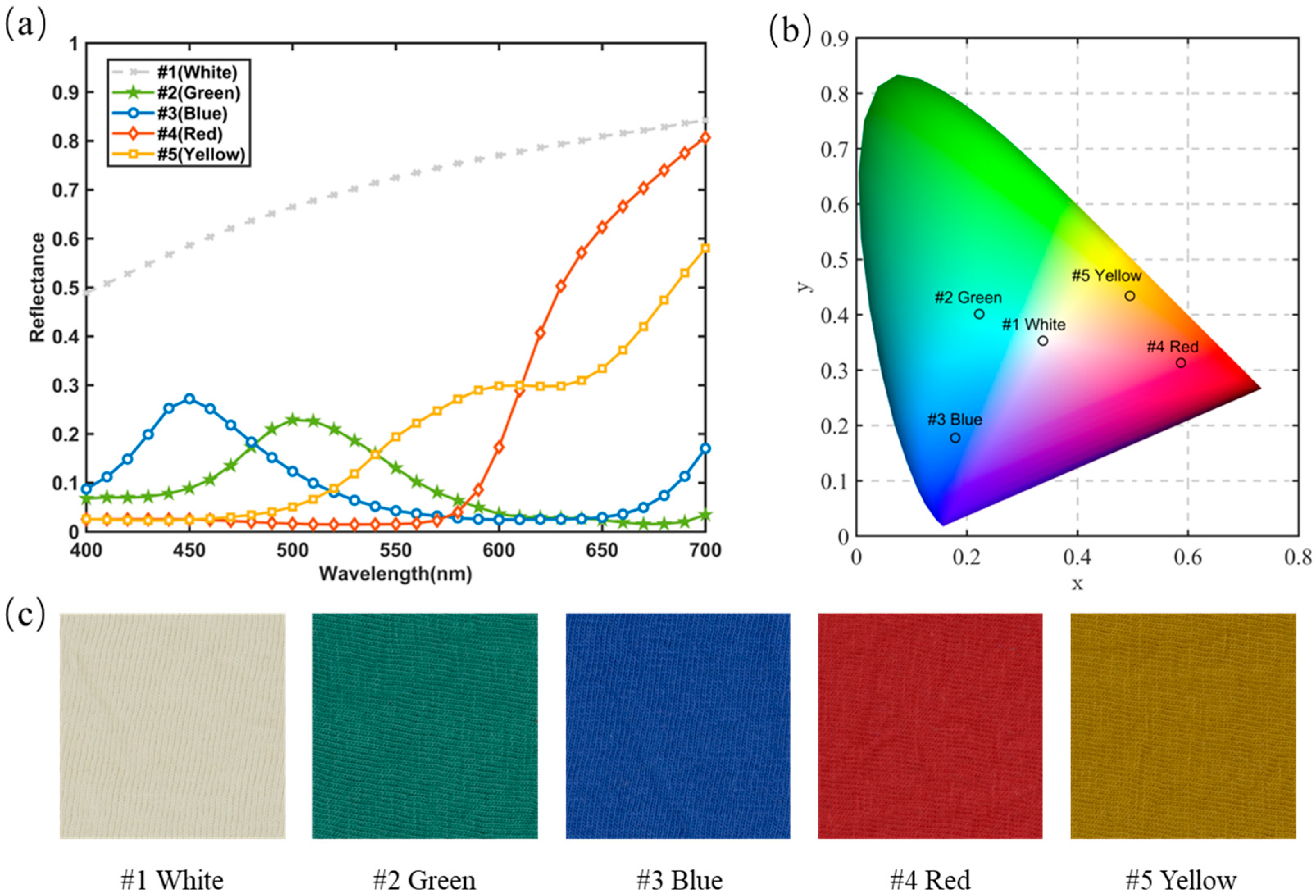
3.1. Sample Preparation
3.2. Sample Measurement
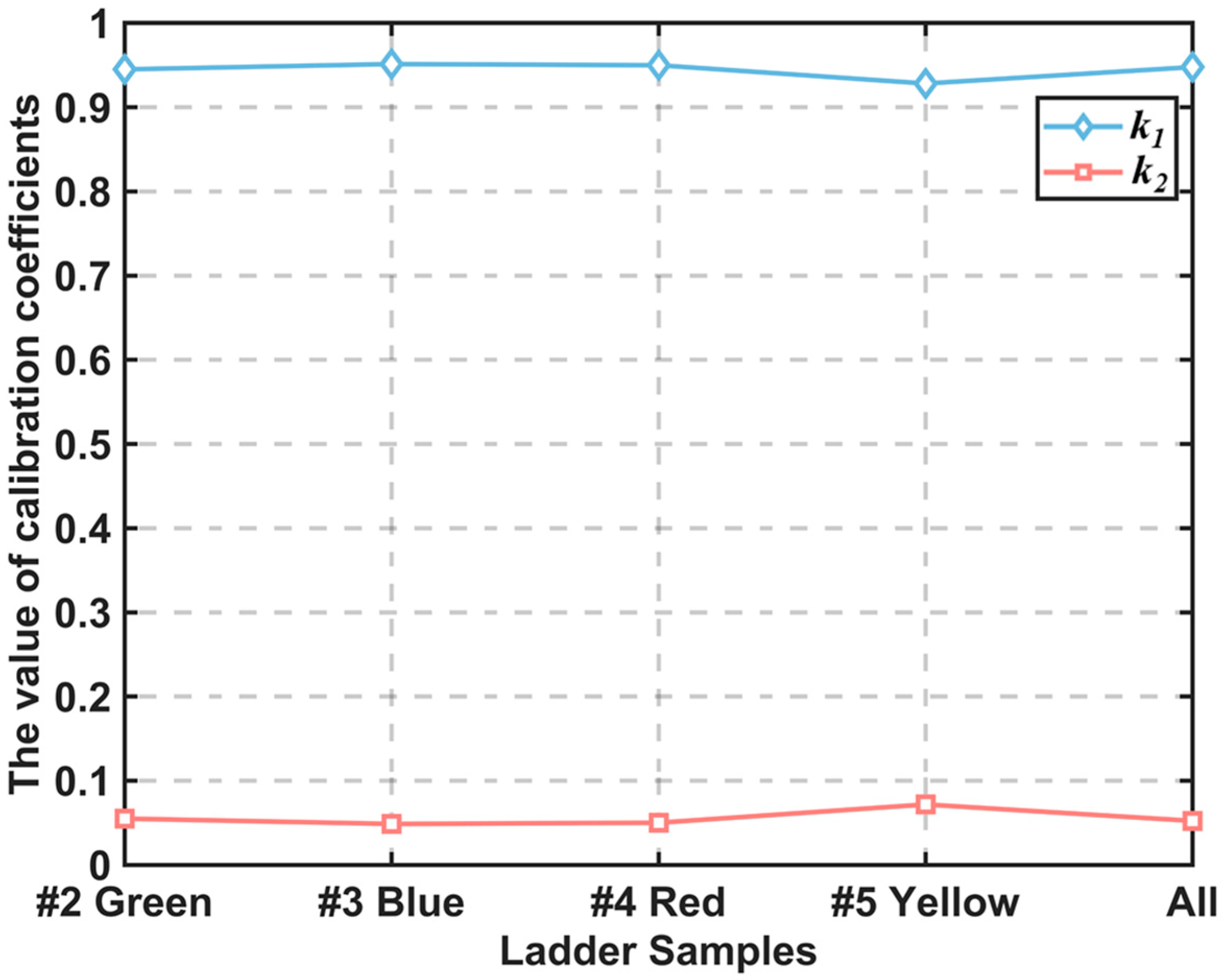
3.3. Determination of the Coefficients k1 and k2
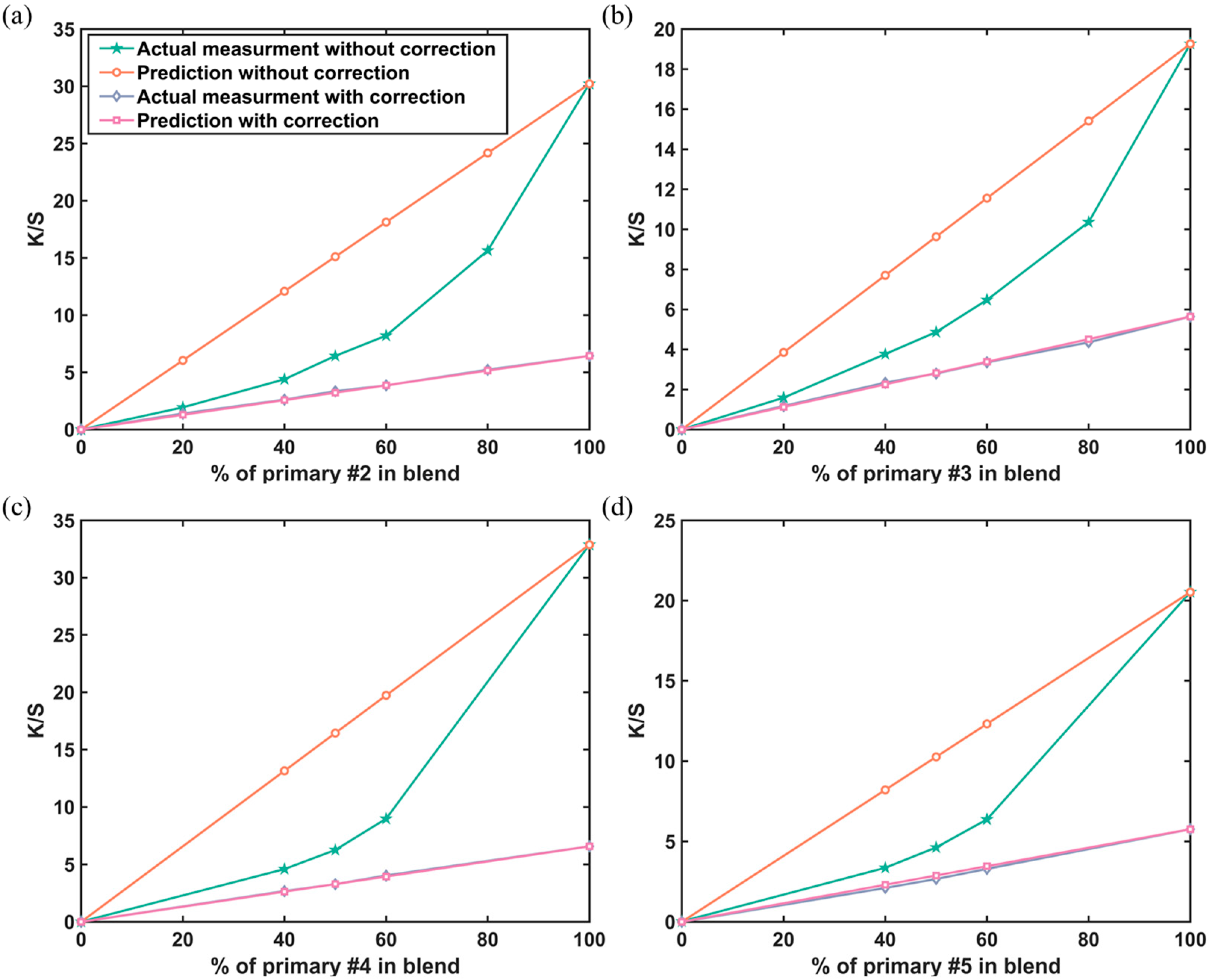
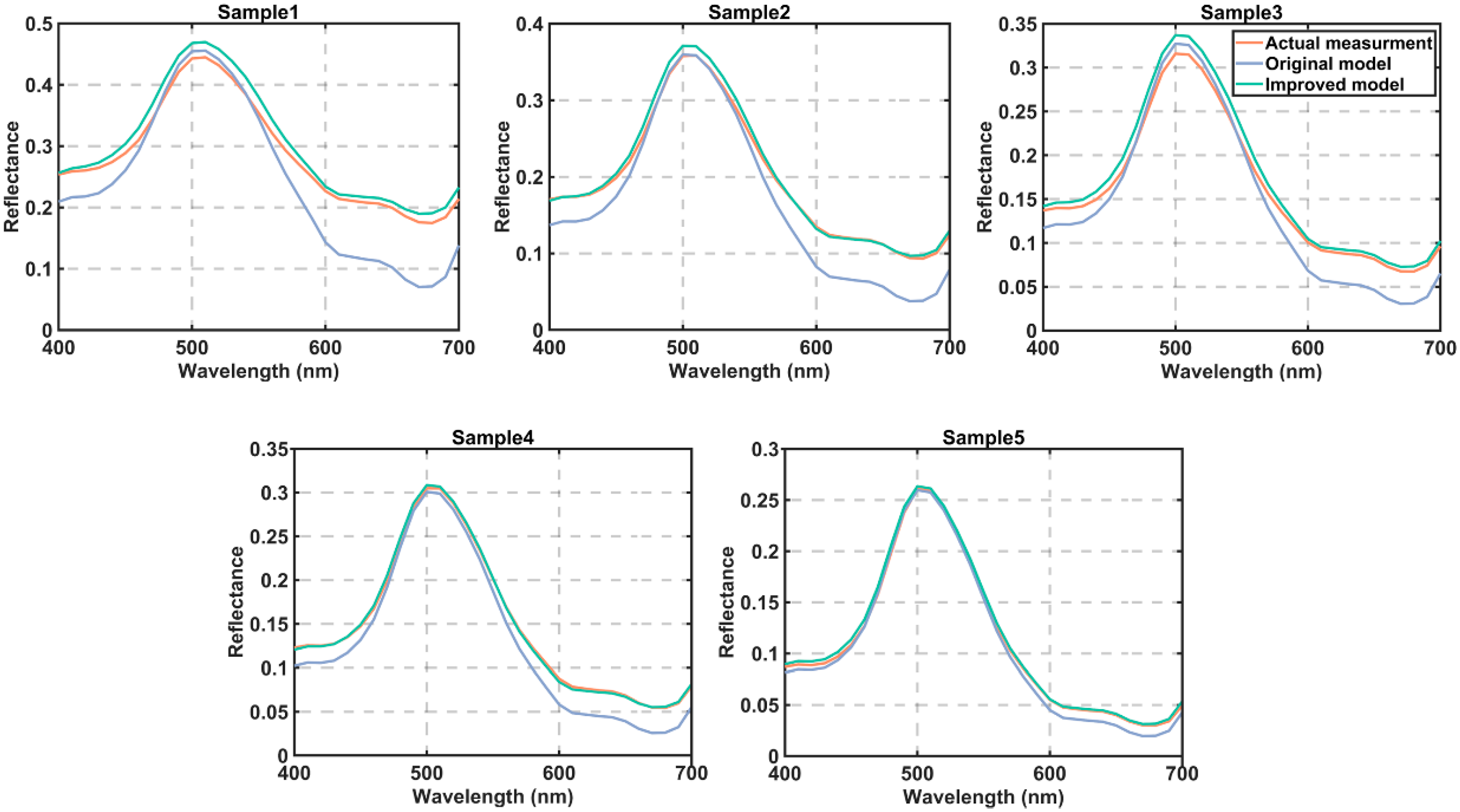
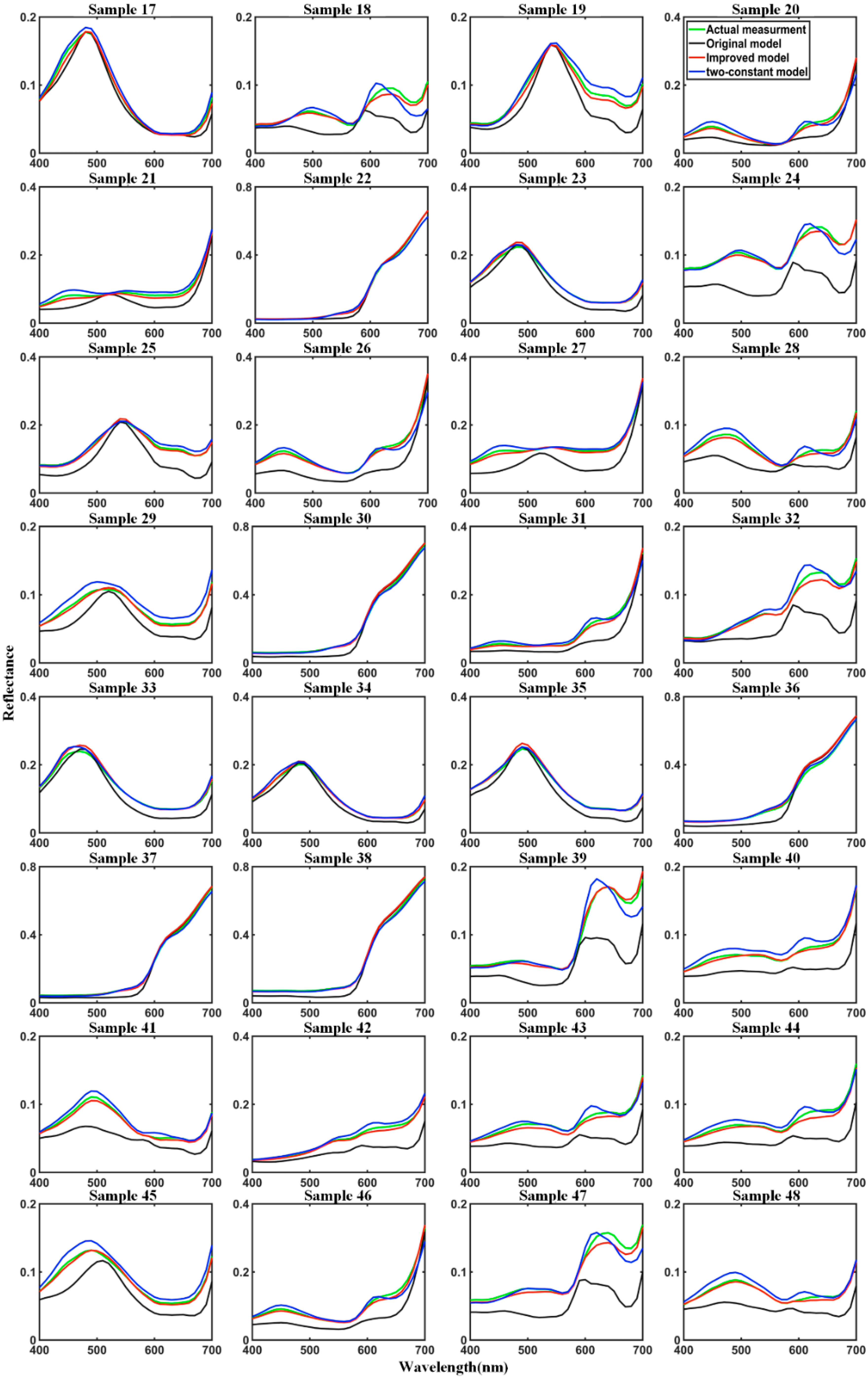
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sun, X.; Xue, Y.; Liu, Y.; Zhang, G.; Liu, L.; Wang, L. Research on full color gamut mixing model constructed by CNC spinning and Stearns-Noechel color prediction method. Text. Res. J. 2023, 93, 1358–1370. [Google Scholar] [CrossRef]
- Yang, R.; Xu, Y.; Xie, C.; Wang, H. Kubelka-Munk double constant theory of digital rotor spun color blended yarn. Dyes Pigment. 2019, 165, 151–156. [Google Scholar] [CrossRef]
- Philips-Invernizzi, B.; Dupont, D.; Jolly-Desodt, A.M.; Cazé, C. Color formulation by fiber blending using the Stearns-Noechel model. Color Res. Appl. 2002, 27, 100–107. [Google Scholar] [CrossRef]
- Zhang, G.; Pan, R.; Zhou, J.; Wang, L.; Gao, W. Spectrophotometric color matching for pre-colored fiber blends based on a hybrid of least squares and grid search method. Text. Res. J. 2022, 92, 2569–2579. [Google Scholar] [CrossRef]
- Burlone, D.A. Formulation of blends of pre-colored nylon fiber. Color Res. Appl. 1983, 8, 114–120. [Google Scholar] [CrossRef]
- Burlone, D.A. Theoretical and practical aspects of selected fiber-blend color-formulation functions. Color Res. Appl. 1984, 9, 213–219. [Google Scholar] [CrossRef]
- Furferi, R.; Governi, L.; Volpe, Y. Methods for predicting spectral response of fibers blends. In Proceedings of the New Trends in Image Analysis and Processing—ICIAP 2015 Workshops: ICIAP 2015 International Workshops, Genoa, Italy, 7–8 September 2015. [Google Scholar]
- Wei, C.-A.; Wan, X.; Li, J. A modified single-constant Kubelka–Munk model for color prediction of pre-colored fiber blends. Cellulose 2018, 25, 2091–2102. [Google Scholar] [CrossRef]
- Li, J.; Xie, D.; Li, M.; Liu, S.; Wei, C.-A. Optimal learning samples for two-constant Kubelka-Munk theory to match the color of pre-colored fiber blends. Front. Neurosci. 2022, 16, 945454. [Google Scholar] [CrossRef] [PubMed]
- Yang, R.; He, C.; Pan, B.; Wang, Z. Color-matching model of digital rotor spinning viscose mélange yarn based on the Kubelka–Munk theory. Text. Res. J. 2022, 92, 574–584. [Google Scholar] [CrossRef]
- Wu, M.; Sun, X.; Lu, Z.; Chen, Y.; Zhang, Y.; Zhang, Q. Optimized combined spectral calibration model based on single-constant Kubelka–Munk theory for color prediction of pre-colored cotton fiber blends. Text. Res. J. 2024, 94, 1083–1095. [Google Scholar] [CrossRef]
- Wei, C.-A.; Xie, D.; Wan, X.; Liu, S.; Li, J. A novel correction method of Kubelka–Munk model for color prediction of pre-colored fiber blends. Fibers Polym. 2024, 25, 2139–2148. [Google Scholar] [CrossRef]
- Shen, J.; Zhou, X.; Ma, H.; Chen, W. Spectrophotometric prediction of pre-colored fiber blends with a hybrid model based on artificial neural network and Stearns-Noechel model. Text. Res. J. 2017, 87, 296–304. [Google Scholar] [CrossRef]
- Yang, L.; Bai, J.; Zhang, R.; Yi, D. The optimization of color-prediction models for colored cotton fiber yarns. Text. Res. J. 2019, 89, 4007–4014. [Google Scholar] [CrossRef]
- Sun, X.; Xue, Y.; Xu, Q.; Shen, J.; Xu, Z. Research on colored yarns for a full color phase mixing model and the Stearns–Noechel color prediction approach. Text. Res. J. 2023, 93, 206–220. [Google Scholar] [CrossRef]
- Philips-Invernizzi, B.; Dupont, D.; Cazé, C. Formulation of colored fiber blends from Friele’s theoretical model. Color Res. Appl. 2002, 27, 191–198. [Google Scholar] [CrossRef]
- Yang, R.; Zhang, K.; Wang, Z. Friele color matching model of digital rotor spinning viscose mélange fabric. Fibers Polym. 2022, 23, 1018–1023. [Google Scholar] [CrossRef]
- Hemingray, C.; Westland, S. A novel approach to using neural networks to predict the colour of fibre blends. Color. Technol. 2016, 132, 297–303. [Google Scholar] [CrossRef]
- Kubelka, P.; Munk, F. An article on optics of paint layers. Z. Tech. Phys. 1931, 12, 259–274. [Google Scholar]
- Yang, H.; Zhu, S.; Pan, N. On the Kubelka-Munk single-constant/two-constant theories. Text. Res. J. 2010, 80, 263–270. [Google Scholar] [CrossRef]
- Imre, P.; Tamás, T. Interior point methods for nonlinear optimization. In Nonlinear Optimization; Di Pillo, G., Schoen, F., Eds.; Springer: Berlin, Germany, 2010; Volume 1989, pp. 215–276. [Google Scholar]
- Walowit, E.; McCarthy, C.J.; Berns, R.S. An algorithm for the optimization of kubelka-munk absorption and scattering coefficients. Color Res. Appl. 1987, 12, 340–343. [Google Scholar] [CrossRef]
- Luo, M.R.; Cui, G.; Rigg, B. The development of the CIE 2000 colour-difference formula: CIEDE2000. Color Res. Appl. 2001, 26, 340–350. [Google Scholar] [CrossRef]
- Aspland, R.; Shanbhag, P. Comparison of color-difference equations for textiles: CMC (2:1) and CIEDE2000. AATCC Rev. 2004, 4, 26. [Google Scholar]
- Nguyen, R.M.H.; Prasad, D.K.; Brown, M.S. Training-based spectral reconstruction from a single RGB Image. In Proceedings of the Computer Vision—ECCV 2014, Zurich, Switzerland, 6–12 September 2014. [Google Scholar]



| Sample No. | Recipe (%) | Sample No. | Recipe (%) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| #1 | #2 | #3 | #4 | #5 | #1 | #2 | #3 | #4 | #5 | ||||
| 1 |  | 80 | 20 | 0 | 0 | 0 | 25 |  | 33.3 | 33.3 | 0 | 0 | 33.3 |
| 2 |  | 60 | 40 | 0 | 0 | 0 | 26 |  | 33.3 | 0 | 33.3 | 33.3 | 0 |
| 3 |  | 50 | 50 | 0 | 0 | 0 | 27 |  | 33.3 | 0 | 33.3 | 0 | 33.3 |
| 4 |  | 40 | 60 | 0 | 0 | 0 | 28 |  | 0 | 33.3 | 33.3 | 33.3 | 0 |
| 5 |  | 20 | 80 | 0 | 0 | 0 | 29 |  | 0 | 33.3 | 33.3 | 0 | 33.3 |
| 6 |  | 80 | 0 | 20 | 0 | 0 | 30 |  | 33.3 | 0 | 0 | 33.3 | 33.3 |
| 7 |  | 60 | 0 | 40 | 0 | 0 | 31 |  | 0 | 0 | 33.3 | 33.3 | 33.3 |
| 8 |  | 50 | 0 | 50 | 0 | 0 | 32 |  | 0 | 33.3 | 0 | 33.3 | 33.3 |
| 9 |  | 40 | 0 | 60 | 0 | 0 | 33 |  | 40 | 20 | 40 | 0 | 0 |
| 10 |  | 20 | 0 | 80 | 0 | 0 | 34 |  | 20 | 40 | 40 | 0 | 0 |
| 11 |  | 60 | 0 | 0 | 40 | 0 | 35 |  | 40 | 40 | 20 | 0 | 0 |
| 12 |  | 50 | 0 | 0 | 50 | 0 | 36 |  | 40 | 0 | 0 | 20 | 40 |
| 13 |  | 40 | 0 | 0 | 60 | 0 | 37 |  | 20 | 0 | 0 | 40 | 40 |
| 14 |  | 60 | 0 | 0 | 0 | 40 | 38 |  | 40 | 0 | 0 | 40 | 20 |
| 15 |  | 50 | 0 | 0 | 0 | 50 | 39 |  | 20 | 25 | 0 | 55 | 0 |
| 16 |  | 40 | 0 | 0 | 0 | 60 | 40 |  | 0 | 20 | 30 | 20 | 30 |
| 17 |  | 0 | 50 | 50 | 0 | 0 | 41 |  | 0 | 50 | 25 | 15 | 10 |
| 18 |  | 0 | 50 | 0 | 50 | 0 | 42 |  | 0 | 15 | 15 | 15 | 55 |
| 19 |  | 0 | 50 | 0 | 0 | 50 | 43 |  | 0 | 30 | 20 | 30 | 20 |
| 20 |  | 0 | 0 | 50 | 50 | 44 |  | 0 | 25 | 25 | 25 | 25 | |
| 21 |  | 0 | 0 | 50 | 0 | 50 | 45 |  | 10 | 30 | 40 | 0 | 20 |
| 22 |  | 0 | 0 | 0 | 50 | 50 | 46 |  | 20 | 0 | 35 | 35 | 10 |
| 23 |  | 33.3 | 33.3 | 33.3 | 0 | 0 | 47 |  | 20 | 30 | 0 | 40 | 10 |
| 24 |  | 33.3 | 33.3 | 0 | 33.3 | 0 | 48 |  | 0 | 35 | 30 | 20 | 15 |
| Primary | #2 Green | #3 Blue | #4 Red | #5 Yellow | All |
|---|---|---|---|---|---|
| k1 | 0.9450 | 0.9513 | 0.9499 | 0.9282 | 0.9477 |
| k2 | 0.0550 | 0.0487 | 0.0501 | 0.0718 | 0.0523 |
| Models | Original KM Model | Our Proposed Model | Two-Constant KM Model | |
|---|---|---|---|---|
| Metrics | ||||
| ΔE2000 | Avg. | 6.37 | 1.20 | 1.58 |
| Max. | 13.00 | 2.47 | 3.57 | |
| Min. | 1.47 | 0.25 | 0.51 | |
| Std. | 2.32 | 0.54 | 0.67 | |
| ΔEcmc | Avg. | 6.53 | 1.35 | 1.80 |
| Max. | 15.75 | 2.58 | 3.81 | |
| Min. | 2.03 | 0.28 | 0.58 | |
| Std. | 2.97 | 0.62 | 0.83 | |
| RMSE (%) | Avg. | 3.0912 | 0.5704 | 0.8541 |
| Max. | 5.0598 | 2.0588 | 1.3589 | |
| Min. | 0.9702 | 0.2304 | 0.3581 | |
| Std. | 1.1001 | 0.3643 | 0.2582 | |
| GFC | Avg. | 0.9852 | 0.9995 | 0.9978 |
| Max. | 0.9991 | 1.0000 | 0.9999 | |
| Min. | 0.9637 | 0.9983 | 0.9843 | |
| Std. | 0.0098 | 0.0004 | 0.0033 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, C.-A.; Li, M.; Liu, S.; Xie, D.; Li, J. Using the Single-Constant Kubelka–Munk Model for Surface Color Prediction of Pre-Colored Fiber Blends. Coatings 2024, 14, 948. https://doi.org/10.3390/coatings14080948
Wei C-A, Li M, Liu S, Xie D, Li J. Using the Single-Constant Kubelka–Munk Model for Surface Color Prediction of Pre-Colored Fiber Blends. Coatings. 2024; 14(8):948. https://doi.org/10.3390/coatings14080948
Chicago/Turabian StyleWei, Chun-Ao, Miaoxin Li, Shiwei Liu, Dehong Xie, and Junfeng Li. 2024. "Using the Single-Constant Kubelka–Munk Model for Surface Color Prediction of Pre-Colored Fiber Blends" Coatings 14, no. 8: 948. https://doi.org/10.3390/coatings14080948
APA StyleWei, C.-A., Li, M., Liu, S., Xie, D., & Li, J. (2024). Using the Single-Constant Kubelka–Munk Model for Surface Color Prediction of Pre-Colored Fiber Blends. Coatings, 14(8), 948. https://doi.org/10.3390/coatings14080948






