A New Method for Evaluating Liquefaction by Energy-Based Pore Water Pressure Models
Abstract
:1. Introduction
2. Pore Water Pressure Modelling
2.1. Proposal of Pore Water Pressure Model
2.2. Numerical Model of Cyclic Triaxial Test
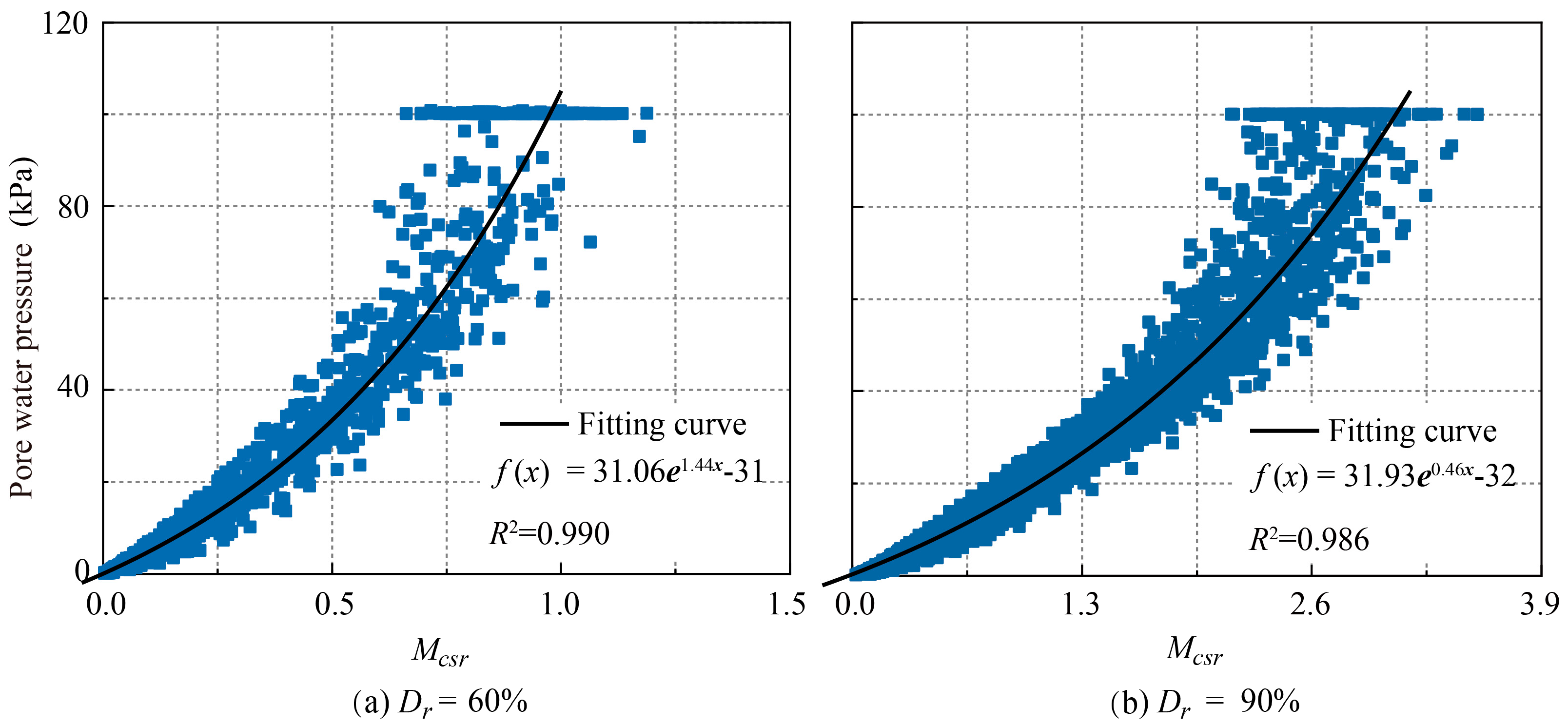
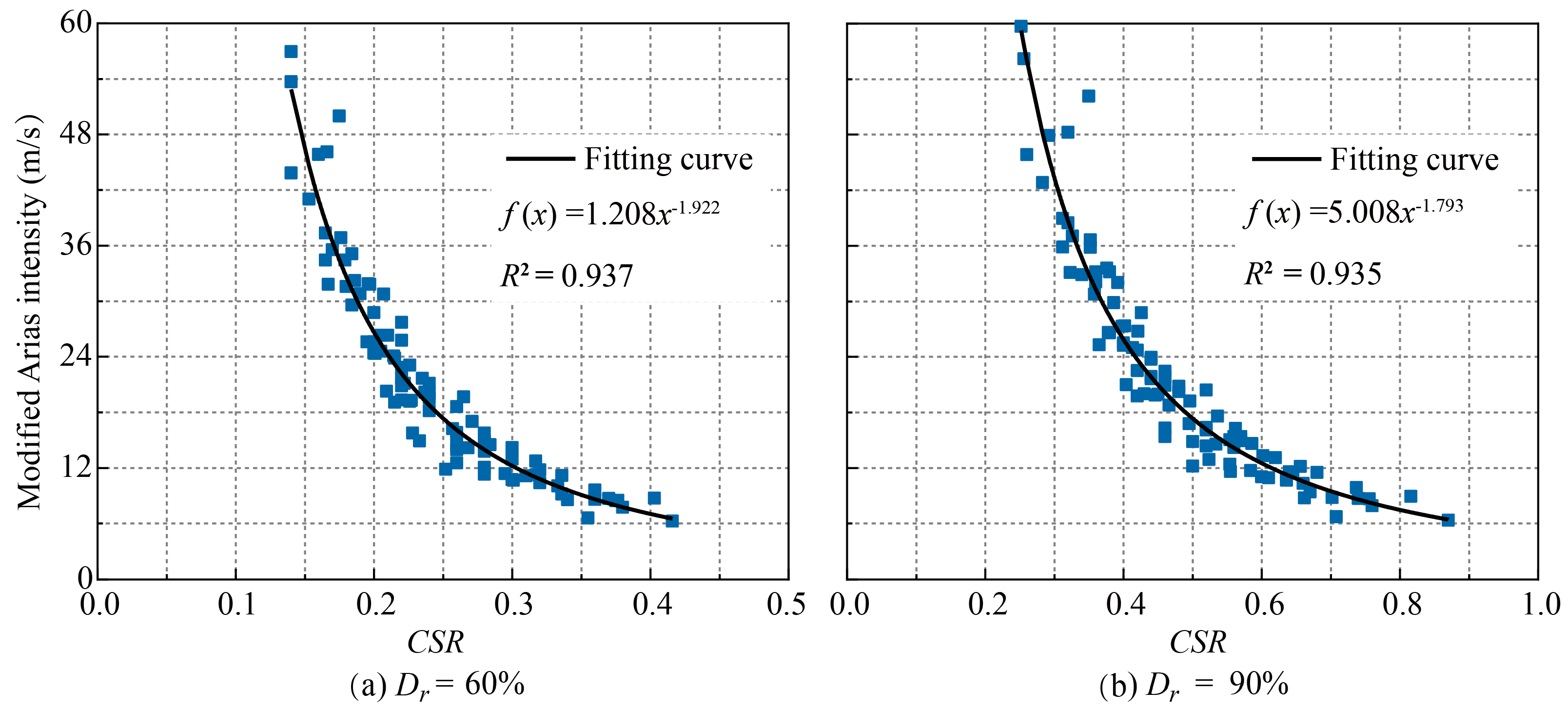
2.3. The Relationship Between Pore Water Pressure and Arias Intensity
- (1)
- For the Dr = 60%:
- (2)
- For the Dr = 90%:
2.4. Criteria for Liquefaction
- (1)
- For the Dr = 60%:
- (2)
- For the Dr = 90%:
- (1)
- For the Dr = 60%:
- (2)
- For the Dr = 90%:
2.5. Effect of Consolidation Pressure and Consolidation Ratio
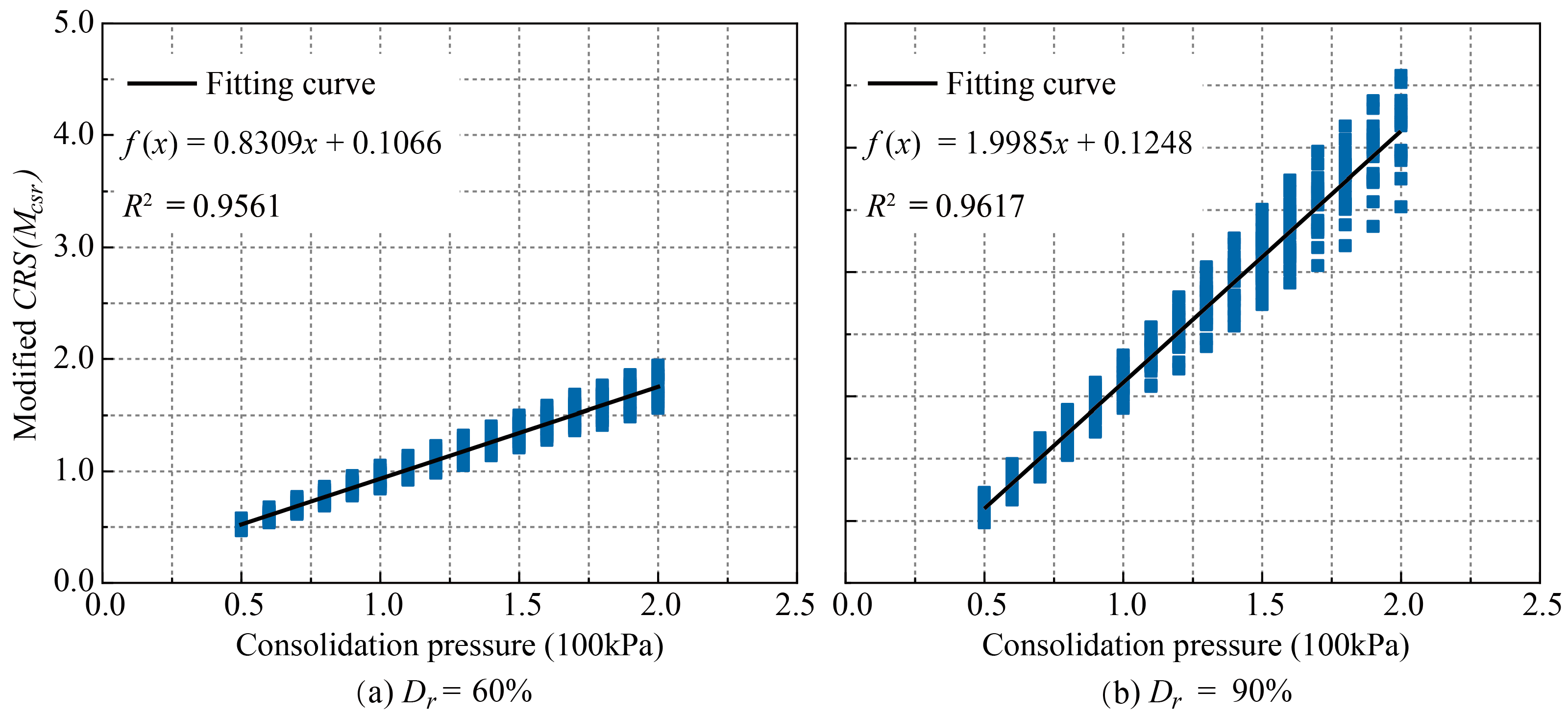
2.5.1. Effect of Consolidation Pressure on the Pore Water Pressure Model
- (1)
- For the Dr = 60%:
- (2)
- For the Dr = 90%:
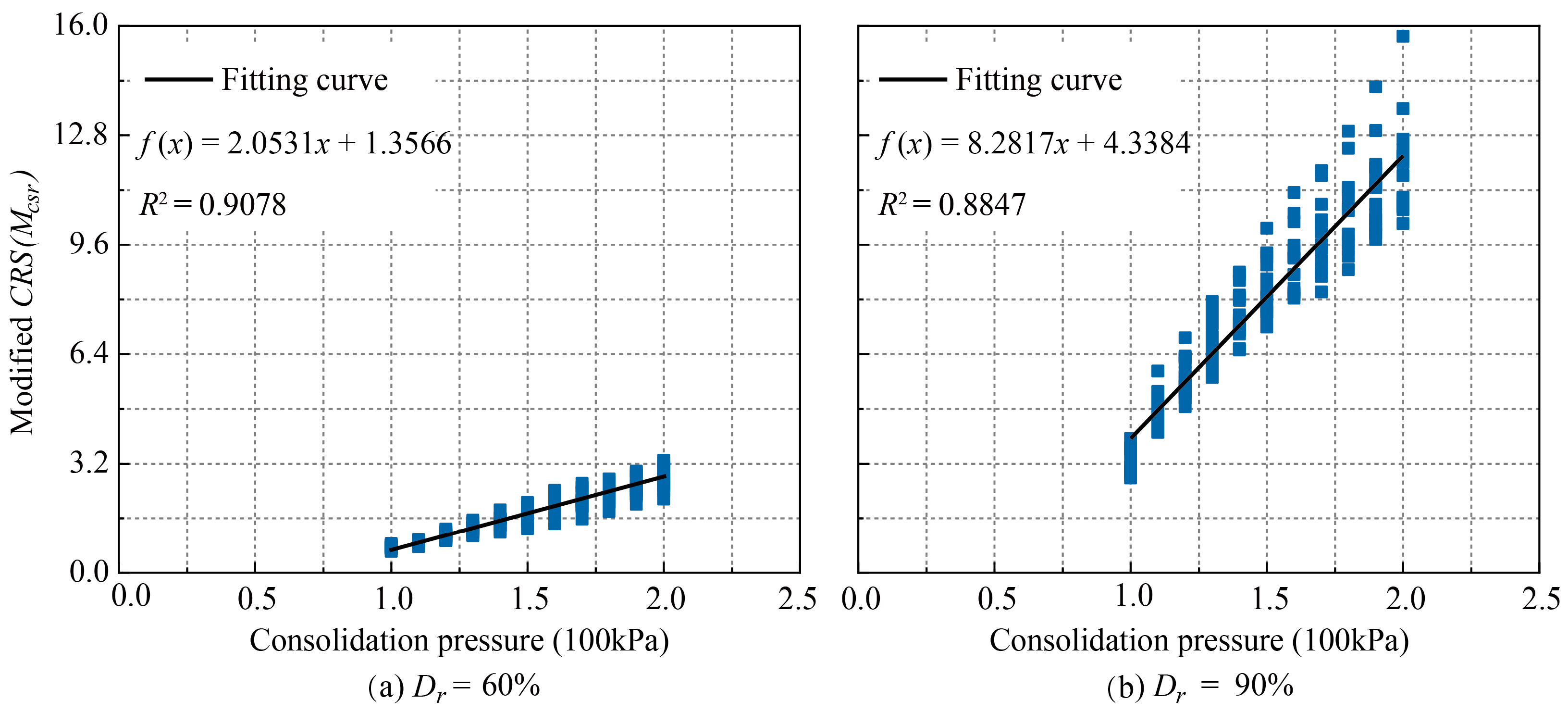
2.5.2. Effect of Consolidation Ratio on Pore Water Pressure Model
- (1)
- For the Dr = 60%:
- (2)
- For the Dr = 90%:
- (1)
- For the Dr = 60%:
- (2)
- For the Dr = 90%:
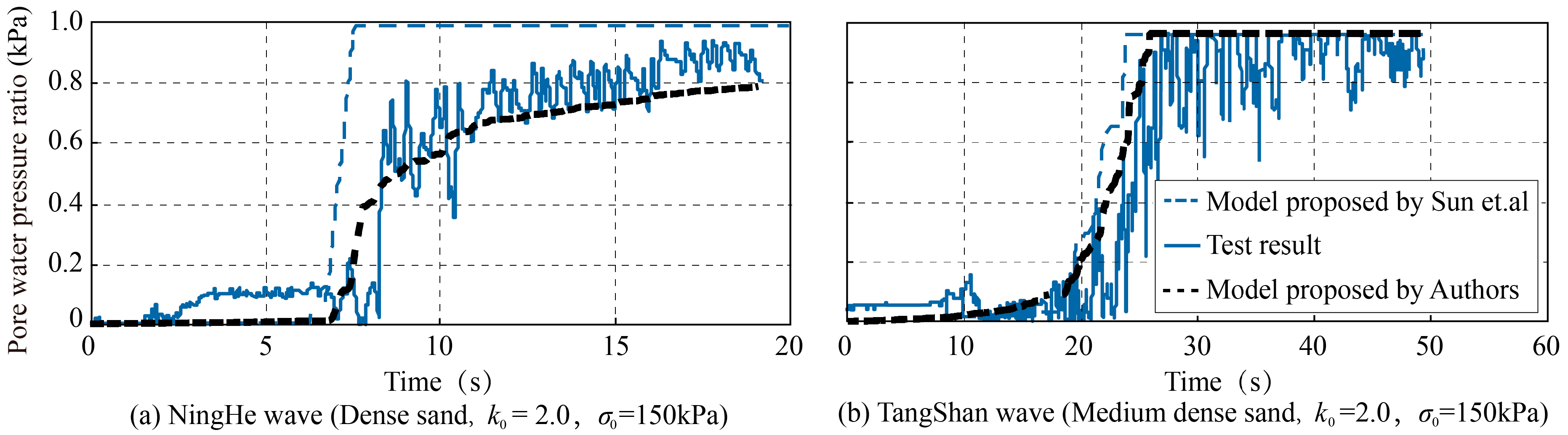
2.5.3. Validation of the Pore Water Pressure Model
3. Liquefaction Potential Assessment Methodology
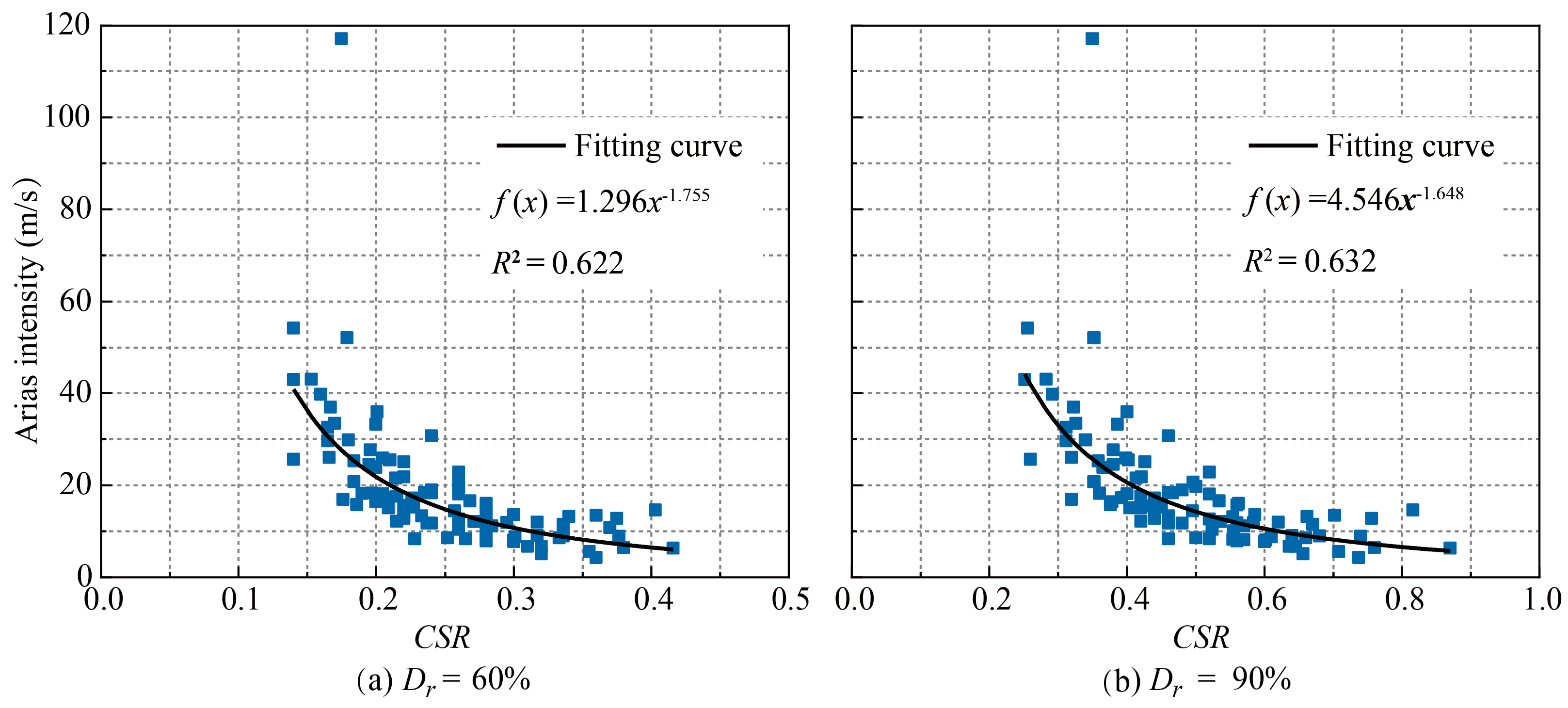
3.1. Cyclic Stress Ratio
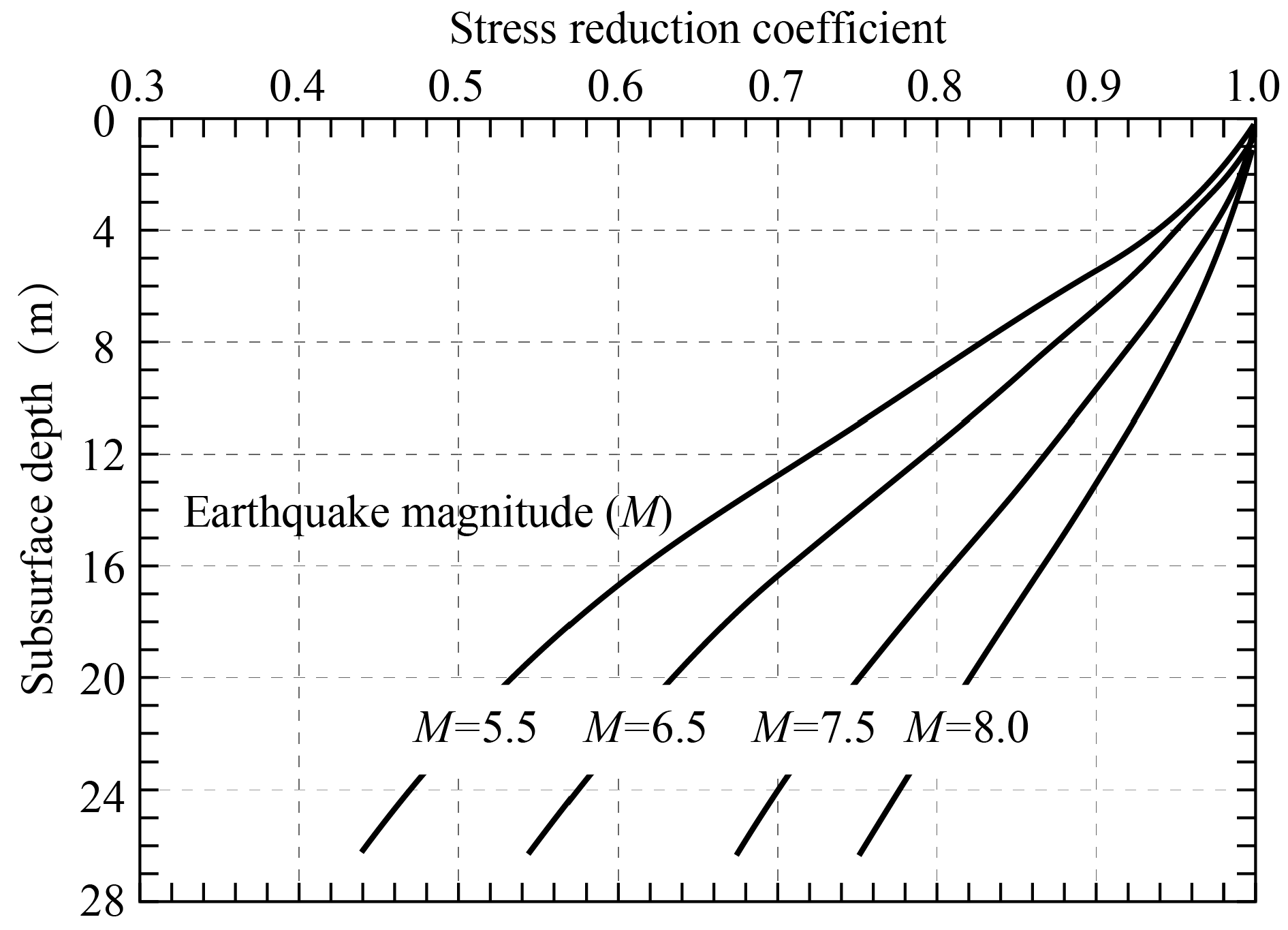
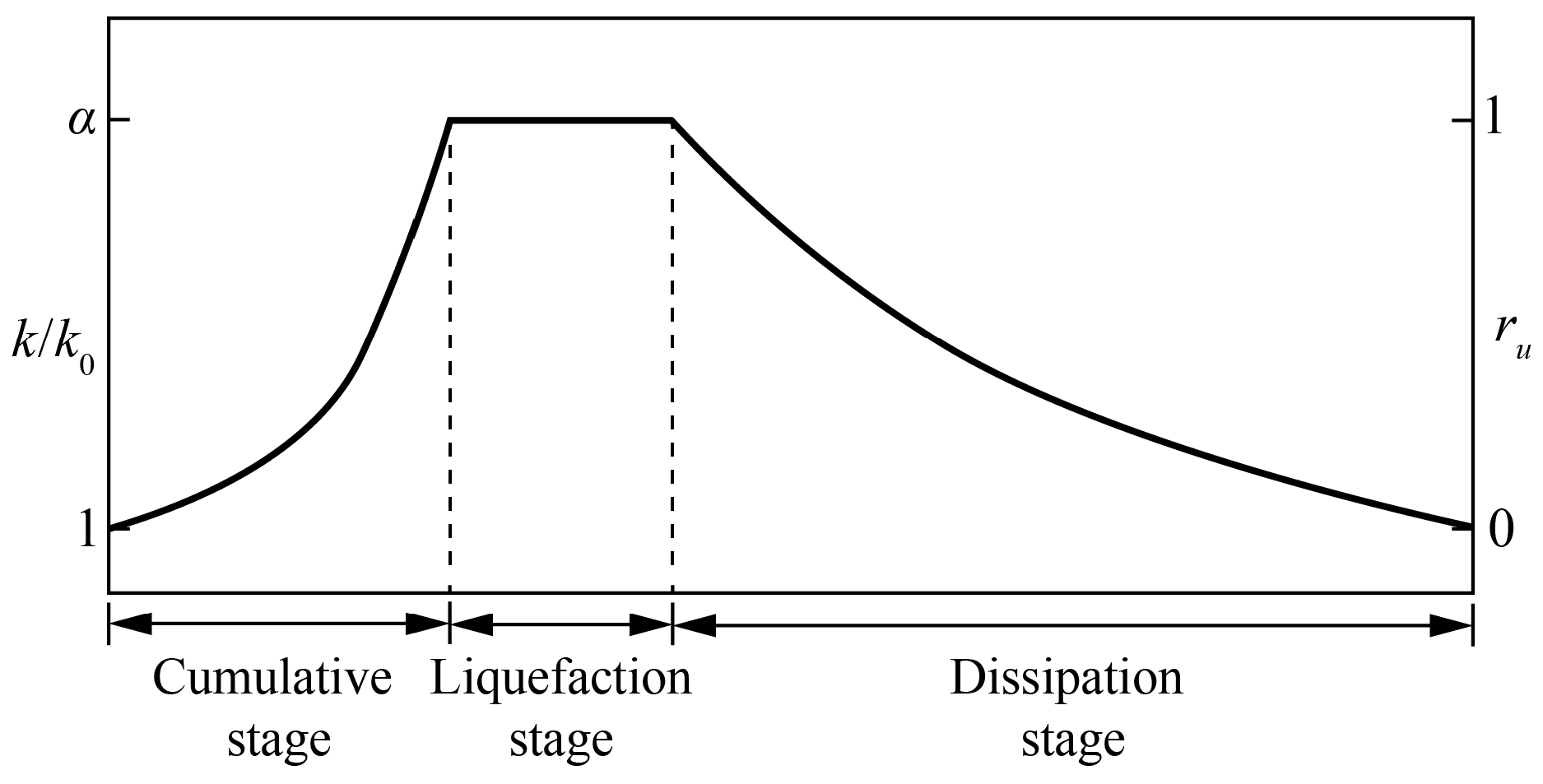
3.2. Effect of Free-Field Permeability Coefficients
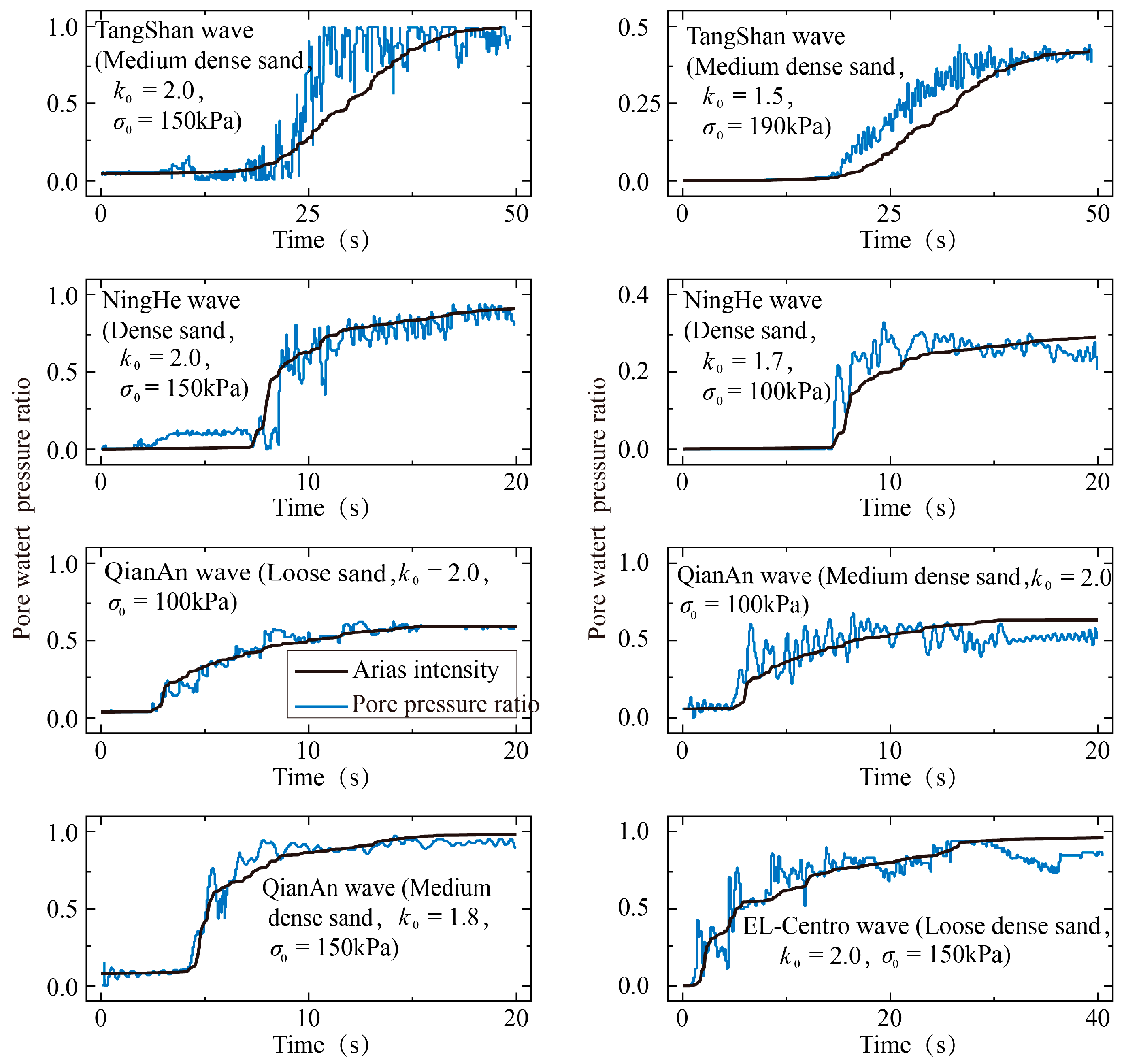
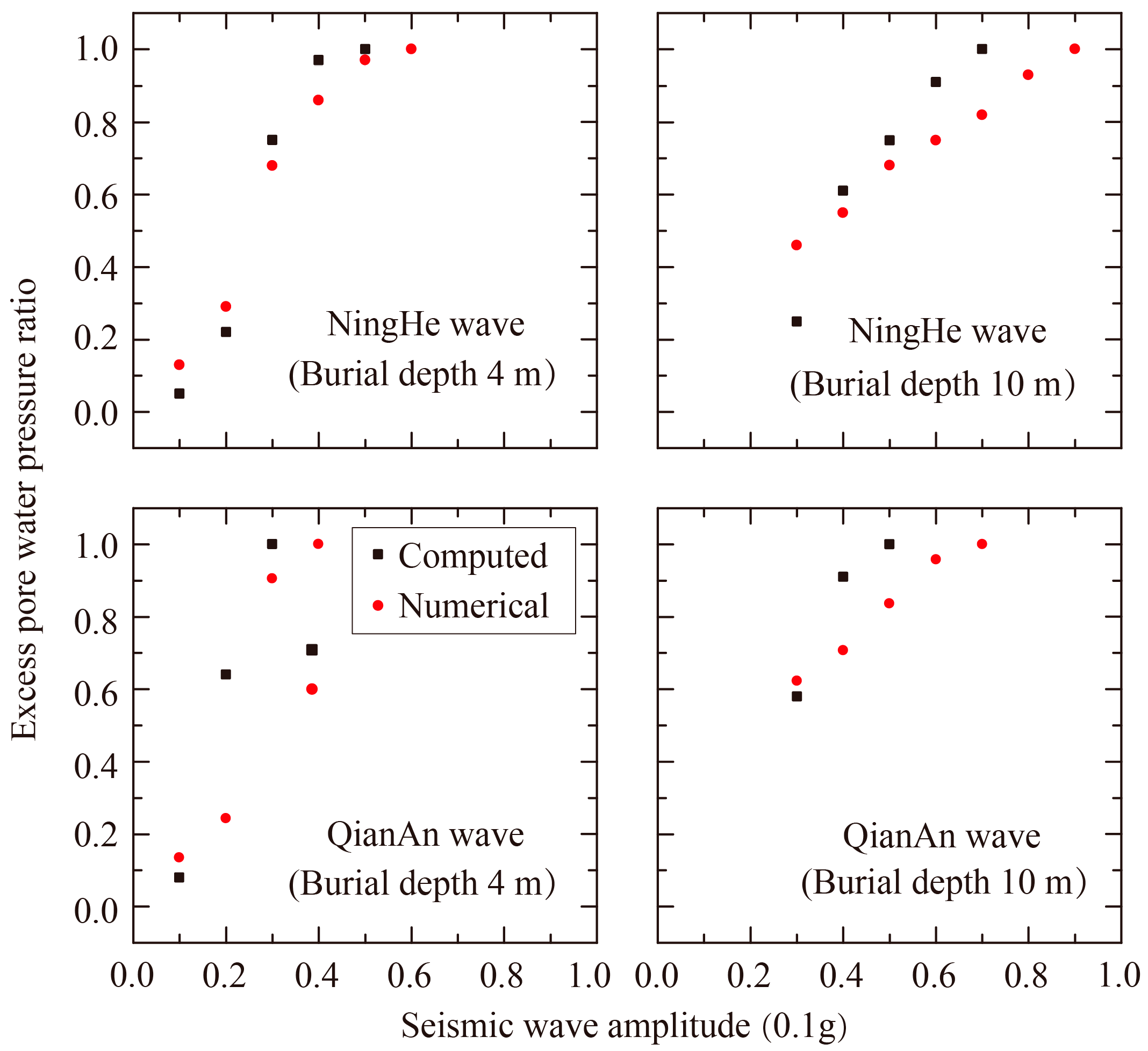
3.3. Validation and Application of Liquefaction Risk Assessment Methodology
4. Conclusions
- (1)
- The results of bi-directional dynamic triaxial tests showed that there was a significant correlation between the accumulation of pore water pressure and the Arias intensity of ground motion in the saturated sand. Additionally, the mean period of the ground motion and the cyclic stress ratio also influence this relationship.
- (2)
- The consolidation pressure and the consolidation ratio of the test significantly influence the modeling of pore water pressure. As both the consolidation pressure and the consolidation ratio increase, the liquefaction resistance of the soil mass exhibits a linear increase.
- (3)
- A novel energy pore water pressure model has been developed based on the results of bi-directional dynamic triaxial tests. The model is capable of accurately predicting the accumulation characteristics of pore water pressure observed during cyclic triaxial tests conducted on dense and medium-dense saturated Fujian standard sand. As the relative density increases, the sand liquefaction potential decreases, making the sand less likely to approach liquefaction.
- (4)
- A methodology for assessing the liquefaction potential has been developed based on the energy pore water pressure model. This method demonstrates enhanced accuracy in predicting the maximum excess pore water pressure ratio of the soil with a shallow burial depth of 4 m. Conversely, the assessment method tends to be conservative when applied to soil bodies with a greater burial depth of 10 m.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hamada, M. Large Ground Deformations and Their Effects on Lifelines: 1964 Niigata Earthquake. In Case Studies of Liquefaction and Lifelines Performance During Past Earthquake; Technical Report NCEER-92-0001; National Centre for Earthquake Engineering Research: Buffalo, NY, USA, 1992. [Google Scholar]
- Youd, T.L.; Driss, I.M. Liquefaction Resistance of Soils: Summary Report from the 1996 NCEER and 1998 NCEER/NSF Workshops on Evaluation of Liquefaction Resistance of Soils. J. Geotech. Geoenviron. Eng. 2001, 127, 297–313. [Google Scholar] [CrossRef]
- Seed, H.B.; Idriss, I.M. Simplified procedure for evaluating soil liquefaction potential. J. Soil Mech. Found. 1971, 97, 1249–1274. [Google Scholar] [CrossRef]
- Dobry, R.; Ladd, R.S.; Yokel, F.Y.; Chung, R.M.; Powell, D. Prediction of Pore Water Pressure Buildup and Liquefaction of Sands During Earthquakes by the Cyclic Strain Method; National Bureau of Standards Building Science Series; US Department of Commerce: Washington, DC, USA, 1982; Volume 138.
- Davis, R.O.; Berrill, J.B. Pore pressure and dissipated energy in earthquakes-field verification. J. Geotech. Geoenviron. Eng. 2001, 127, 269–274. [Google Scholar] [CrossRef]
- Fardad, A.P.; Noorzad, R. Energy-based evaluation of liquefaction of fiber-reinforced sand using cyclic triaxial testing. Soil Dyn. Earthq. Eng. 2018, 104, 45–53. [Google Scholar] [CrossRef]
- Nemat-Nasser, S.; Shokooh, A. A unified approach to densification and liquefaction of cohesionless sand in cyclic shearing. Can. Geotech. J. 1979, 16, 659–678. [Google Scholar] [CrossRef]
- Towhata, I.; Ishihara, K. Shear work and pore water pressure in untrained shear. Soils Found. 1985, 25, 73–84. [Google Scholar] [CrossRef] [PubMed]
- Law, K.T.; Cao, Y.L.; He, G.N. An energy approach for assessing seismic liquefaction potential. Can. Geotech. J. 1990, 27, 320–329. [Google Scholar] [CrossRef]
- Xie, D.Y.; Wu, Z.H. Effect of irregular dynamic impulse history on liquefaction characteristics of saturated sand. Chin. J. Rock Mech. Eng. 1987, 9, 1–12. [Google Scholar]
- Meng, S.J.; Liu, T.H. Study of pore-pressure model of saturated sands under irregular load. Chin. J. Rock Mech. Eng. 2014, 33, 3050–3055. [Google Scholar]
- Wang, T.S.; Lin, Y.; Tong, J.; Qin, X. Generation and dissipation of pore pressure in saturated sand layer due to earthquake loading. Chin. J. Geotech. Eng. 1983, 5, 87–102. [Google Scholar]
- Fu, H.Q. An Approach of Dynamic In-Situ Liquefaction Test and Characteristics of Liquefaction Soil. Ph.D. Thesis, Institute of Engineering Mechanics, Harbin, China, 2016. [Google Scholar]
- Sun, R. Study on Seismic Ground Motion on Liquefiable Soil Layer and Site Liquefaction Detection. Ph.D. Thesis, Institute of Engineering Mechanics, Harbin, China, 2006. [Google Scholar]
- Arias, A. A measure of earthquake intensity. In Seismic Design for Nuclear Power Plants; Hansen, R.J., Ed.; MIT Press: Cambridge, MA, USA, 1970. [Google Scholar]
- Mazzoni, S.; McKenne, F.; Scott, M.; Fenves, G. Open System for Earthquake Engineering Simulation User Manual Version 2.1.0; University of California, Pacific Earthquake Engineering Center: Berkeley, CA, USA, 2009. [Google Scholar]
- McGann, C.R.; Arduino, P.; Mackenzie-Helnwein, P. Stabilized single-point 4-node quadrilateral element for dynamic analysis of fluid saturated porous media. Acta Geotech. 2012, 7, 297–311. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Shiomi, T. Dynamic behavior of saturated porous media: The generalized Biot formulation and its numerical solution. Int. J. Numer. Anal. Met. 1984, 8, 71–96. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of elasticity and consolidation for a porous anisotropic solid. J. Appl. Phys. 1955, 26, 182–185. [Google Scholar] [CrossRef]
- Elgamal, A.; Yang, Z.H.; Parra, E. Computational modeling of cyclic mobility and post-liquefaction site response. Soil Dyn. Earthq. Eng. 2002, 22, 259–271. [Google Scholar] [CrossRef]
- Yang, Z.H.; Elgamal, A.; Parra, E. Computational model for cyclic mobility and associated shear deformation. J. Geotech. Geoenviron. Eng. 2003, 129, 1119–1127. [Google Scholar] [CrossRef]
- Zhang, J.L.; Cheng, Q.G.; Li, Y.; Qiu, Y.; Wang, Y.; Wu, J. Performance of rectangular closed diaphragm walls in gently sloping liquefiable deposits subjected to different earthquake ground motions. Earthq. Eng. Eng. Vib. 2021, 20, 905–923. [Google Scholar] [CrossRef]
- Zhang, J.L.; Cheng, Q.G.; Li, Y.; Zhang, E.M.; Wang, Y.F.; Wu, J.J.; Xie, S.Y. Mechanism of liquefaction mitigation by rectangular closed diaphragm walls in sloping liquefiable deposits. Soil Dyn. Earthq. Eng. 2021, 142, 106582. [Google Scholar] [CrossRef]
- Golesorkhi, R. Factors Influencing the Computational Determination of Earthquake-Induced Shear Stresses in Sandy Soils. Ph.D. Thesis, University of California, Berkeley, CA, USA, 1989. [Google Scholar]
- Idriss, I.M.; Boulanger, R.W. Semi-empirical procedures for evaluating liquefaction potential during earthquakes. Soil Dyn. Earthq. Eng. 2006, 26, 115–130. [Google Scholar] [CrossRef]
- Wang, K.; Sun, R.; Yuan, X.M. Influence factors and formula for dynamic stress reduction coefficient. Chin. J. Rock Mech. Eng. 2018, 37, 177–189. [Google Scholar]
- Idriss, I.M. Earthquake ground motions at soft soil sites. In Proceedings of the Second International Conference on Recent Advances in Geotechnical Earthquake Engineering & Soil Dynamics, St. Louis, MO, USA, 11–15 March 1991; Volume 3, pp. 2265–2271. [Google Scholar]
- Seed, R.B.; Dickenson, S.E.; Mok, C. Site effects on strong shaking and seismic risk: Recent developments and their impact on seismic design codes and practice. In Structures Congress XII 1994; ASCE: New York, NY, USA, 1994; Volume 1, pp. 573–578. [Google Scholar]
- Shahir, H.; Mohammadi-Haji, B.; Ghassemi, A. Employing a variable permeability model in numerical simulation of saturated sand behavior under earthquake loading. Comput. Geotech. 2014, 55, 211–223. [Google Scholar] [CrossRef]
- Arulanandan, K.; Sybico, J.; Schofield, A.N. Post-liquefaction settlement of sands. In Proceedings of the Wroth Memorial Symposium, Oxford, UK, 27–29 July 1992. [Google Scholar]
- Taiebat, M.; Shahir, H.; Pak, A. Study of pore pressure variation during liquefaction using two constitutive models for sand. Soil Dyn. Earthq. Eng. 2007, 27, 60–72. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, G.Y.; Gu, X.Q.; Song, J. A numerical study of the influence of permeability coefficient on the liquefaction-induced settlement of sands. Rock Soil Mech. 2017, 38, 1813–1818. [Google Scholar]
- Rahmani, A.; Ghasemi, F.O.; Pak, A. Investigation of the influence of permeability coefficient on the numerical modeling of the liquefaction phenomenon. Sci. Iran. 2012, 19, 179–187. [Google Scholar] [CrossRef]
- Li, Y.; Cheng, Q.G.; Zhang, J.L.; Lyu, B.; Wang, Y.F.; Wu, J.J. Seismic behavior of rectangular closed diaphragm walls serving as bridge foundations in gently sloping liquefiable deposit: Dynamic centrifuge tests. J. Geotech. Geoenviron. Eng. 2019, 145, 04019105. [Google Scholar] [CrossRef]


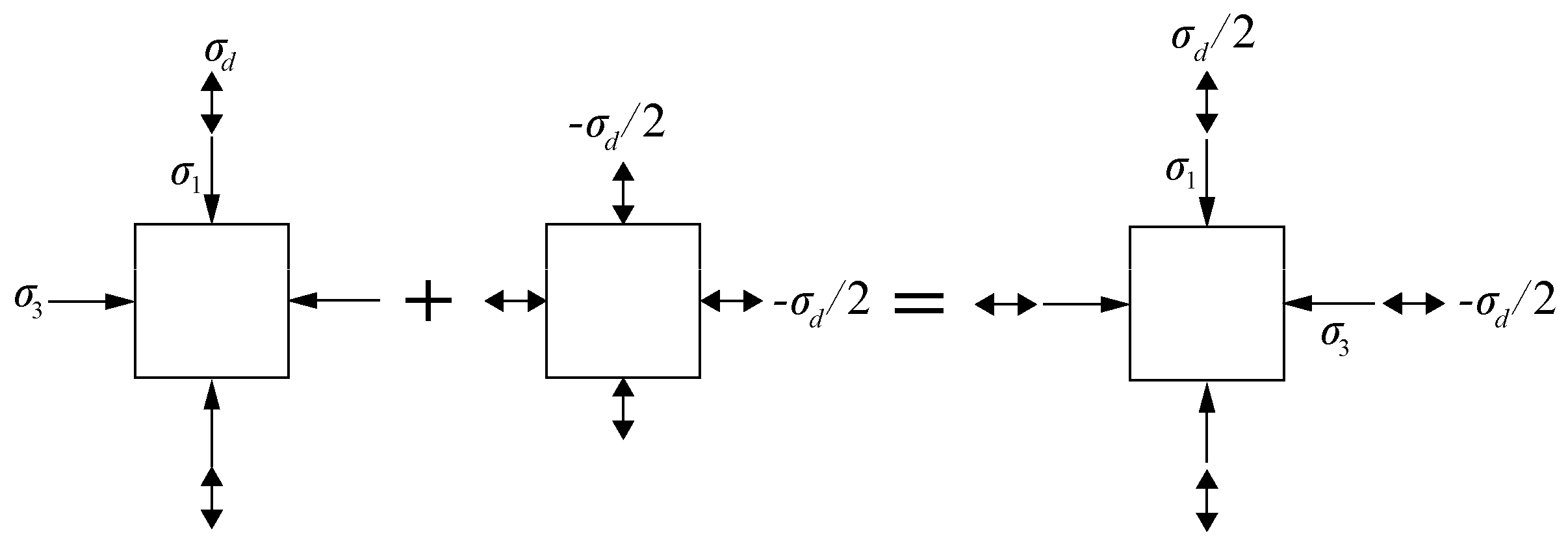


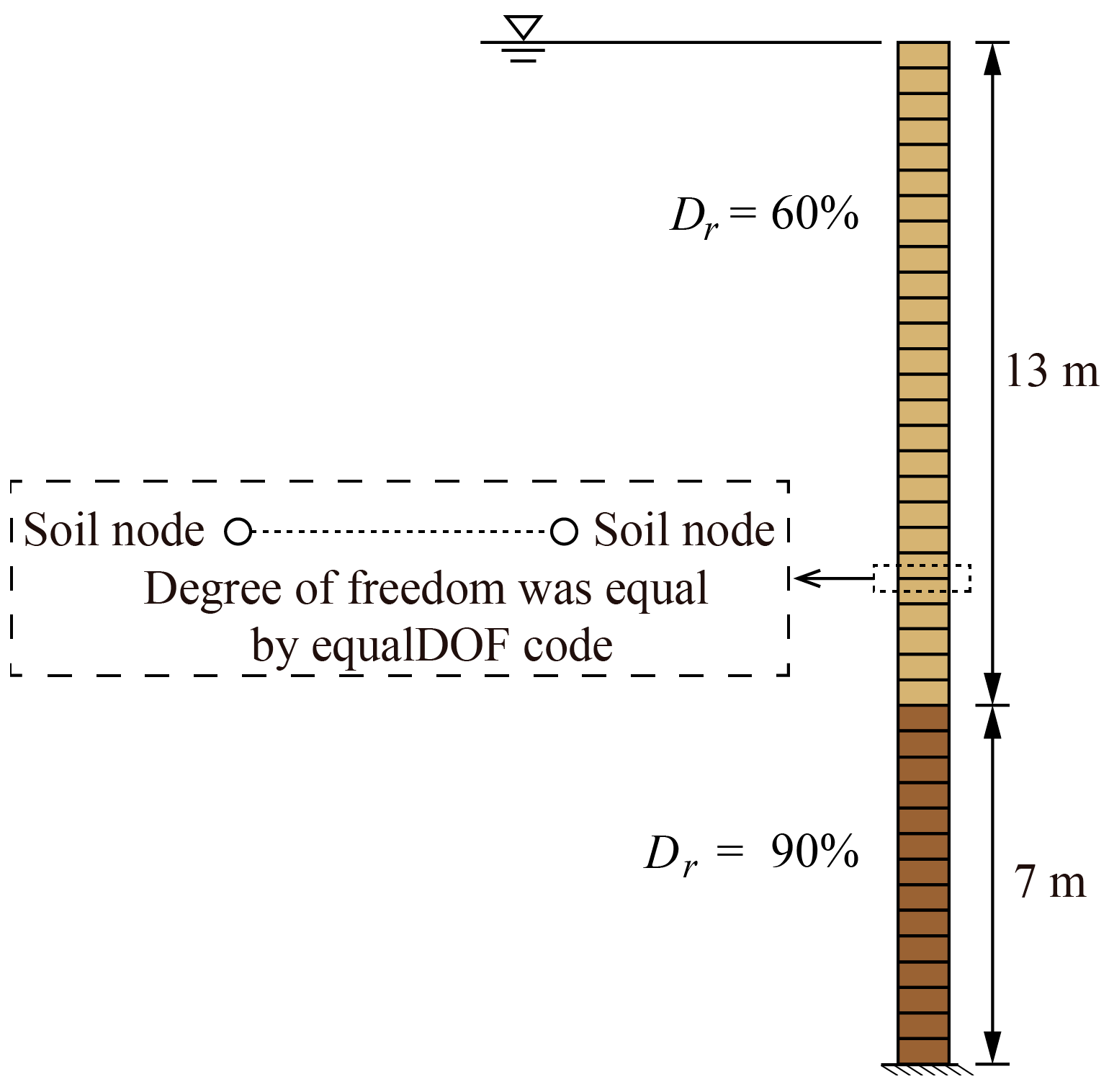

| Dr | Density (kg·m−3) | Reference Pressure (kPa) | Shear Modulus at Pr (MPa) | Bulk Modulus at Pr (MPa) | Friction Angle (°) | Phase Transformation Angle (°) | c1 | c3 | d1 | d3 |
|---|---|---|---|---|---|---|---|---|---|---|
| 60% | 19.38 | 80 | 6.5 × 104 | 1.6 × 105 | 31 | 31 | 0.087 | 0.18 | 0.0 | 0.0 |
| 90% | 19.98 | 800.087 | 1.1 × 105 | 2.4 × 105 | 33 | 26 | 0.28 | 0.05 | 0.1 | 0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Cheng, Q.; Fan, H.; Dai, M.; Li, Y.; Wu, J.; Wang, Y. A New Method for Evaluating Liquefaction by Energy-Based Pore Water Pressure Models. Coatings 2025, 15, 7. https://doi.org/10.3390/coatings15010007
Zhang J, Cheng Q, Fan H, Dai M, Li Y, Wu J, Wang Y. A New Method for Evaluating Liquefaction by Energy-Based Pore Water Pressure Models. Coatings. 2025; 15(1):7. https://doi.org/10.3390/coatings15010007
Chicago/Turabian StyleZhang, Jianlei, Qiangong Cheng, Haozhen Fan, Mengjie Dai, Yan Li, Jiujiang Wu, and Yufeng Wang. 2025. "A New Method for Evaluating Liquefaction by Energy-Based Pore Water Pressure Models" Coatings 15, no. 1: 7. https://doi.org/10.3390/coatings15010007
APA StyleZhang, J., Cheng, Q., Fan, H., Dai, M., Li, Y., Wu, J., & Wang, Y. (2025). A New Method for Evaluating Liquefaction by Energy-Based Pore Water Pressure Models. Coatings, 15(1), 7. https://doi.org/10.3390/coatings15010007







