Numerical Simulation of Gas–Liquid–Solid Erosive Wear in Gas Storage Columns

Abstract

Gas reservoirs play an increasingly important role in oil and gas consumption and safety in China. To study the problem of erosion and wear caused by gas-carrying particles in the process of gas extraction from gas storage reservoirs, a mathematical model of gas–liquid–solid three-phase erosion of gas storage reservoir columns was established through theories of multiphase flow and particle motion. Based on this model, the effects of the water volume fraction, gas extraction rate, particle mass flow rate, particle size, and bending angle on the erosion location and rate of the pipe columns were investigated. The findings indicate that when the water content volume fraction is low, the water production volume minimally affects the maximum erosion rate of pipe columns. Conversely, the gas extraction rate exerted the most significant influence on the column erosion, showing a power function relationship between the two. When gas extraction volume exceeds 60 × 10⁴ m³/d, the maximum erosion rate surpasses the critical erosion rate of 0.076 mm/a. This coincided with the increased sand mass flow rate, although the maximum erosion rate of the pipe columns remained relatively steady. The salt mass flow rate demonstrated a linear relationship with the erosion rate, with the maximum erosion rate exceeding the critical erosion rate of 0.076 mm/a. The maximum erosion rate of the pipe columns increased, stabilized with larger sand and salt particle sizes, and exhibited an increasing trend with the bending angle. For gas extraction volumes exceeding 46.4 × 10⁴ m³/d and salt mass flow rates exceeding 22 kg/d, the maximum erosion rate of pipe columns exceeds the critical erosion rate of 0.076 mm/a. The conclusions of this study are of some importance for the clarification of the influencing law of pipe column erosion under high temperature and high pressure in gas storage reservoirs and for the formulation of measures for the prevention and control of pipe column erosion in gas storage reservoirs.

1. Introduction

In recent years, with the continuous growth in natural gas demand, traditional transmission and distribution methods have struggled to satisfy user needs [1]. Gas storage plays a crucial role in the seasonal peak adjustment and emergency supply, making it essential for China’s rapid development. Most of China’s gas storage reservoirs are of the reservoir type, which differs from the gas production reservoirs. Gas storage facilities often operate with multiple intense injection and extraction cycles. During these processes, pipe columns are subjected to impacts from sand and salt particles, accelerating the erosion of their inner walls and posing threats to reservoir safety.

Numerous scholars have conducted extensive studies using physical experiments and numerical simulations to investigate the erosion patterns of gas storage columns. Finnie [2] and colleagues conducted erosion experiments on gas–solid two-phase flows, revealing that high-speed impacts from solid particles at specific angles can strip material from the target surface in a micro-cutting fashion. Bitter [3] and others approached the erosion of gas storage columns from an energy change perspective, finding that particle impact velocities exceeding the critical velocity of the target surface for inducing plastic strain led to elastic and plastic deformations in the surface material.

Cui Lu et al. [4] conducted liquid–solid two-phase flow erosion experiments on QT1100 continuous pipeline steel. The results indicated that avoiding a scour angle of 45° and using a sand-carrying fluid with a sand mass concentration of 60 kg/m³ could reduce erosion. Lin Yuanyuan et al. [5] simulated erosion experiments on a 90° bend based on full-size real objects. They analyzed the gas flow rate, particle size, particle mass flow rate, and bend-to-diameter ratio as variables and obtained the degree of influence of different factors using the gray correlation method. Zahedi et al. [6] tested gas–solid two-phase and gas–liquid–solid three-phase flows by using 56 elbows with a size of 101.6 mm. The results showed that under conditions of low liquid velocity, erosion in a gas–solid two-phase flow can be reduced by avoiding a scouring angle of 45° and using sand-carrying liquid with a mass concentration of 60 kg/m³. As the apparent liquid velocity increased, the erosion rate decreased, but this trend was reversed at higher liquid rates.

Bilal et al. [7] investigated the relationship between erosion wear and bend diameter ratio for 45° and 90° elbows using a combination of experimental and computational fluid dynamics (CFD) simulations. The results showed that erosion wear decreased as the bend diameter ratio increased, and the erosion wear for the 45° elbow was two times smaller than that for the 90° elbow. Banakermani et al. [8] studied the relationship between erosion wear and the bend diameter ratio for 45° and 90° elbows using a combination of experimental and CFD simulations. They investigated the erosive wear of a gas–solid two-phase flow in 15–90° elbows and obtained the variation rule of the maximum erosive wear rate of the pipeline at different angles.

Vieira et al. [9] studied the gas–solid two-phase flow through 90° elbows with a diameter of 76.2 mm using a combination of indoor physical experiments and numerical simulations. The results indicated that the maximum erosion and wear sites of the elbow were located at 45°. Peng Tao et al. [10] studied the effect of gravel shape on gas storage wellbore erosion based on the CFD theory. The results indicate that the less smooth the gravel boundary, the stronger the sand-carrying capacity of the gas phase, resulting in a smaller abrasion effect.

Li Mingxing et al. [11] investigated the gas–liquid two-phase erosion law of gas storage reservoir injection and extraction wells. The results demonstrated that the temperature, pressure, and flow rate all contributed to an increased tubing erosion rate. He Zuqing et al. [12], based on the API RP 14E model, investigated the erosion law of injection and extraction tubing columns in the Wen23 reservoir. They analyzed the limiting injection and extraction gas volumes and found that during gas injection, the actual flow rate and critical erosion flow rate in the tubing increased and then decreased with well depth.

Currently, the literature predominantly focuses on researching salt formation in gas storage reservoirs, particularly the laws governing salt formation. However, there is a notable lack of research on erosion caused by salt formation on tubing columns. Duan Yuan et al. [13] investigated the salt formation processes in high-mineralization gas reservoir wells, exploring these processes under various pressure and temperature conditions. Shen Chen et al. [14] conducted laboratory experiments to study the evaporation of formation of water and subsequent salt formation, developing a theoretical model to predict salt formation in wellbores. Ren Zhongxin et al. [15] proposed a pressure calculation formula and a corresponding production capacity equation for constructing gas wells prone to salt formation, considering the impact of salt accumulation on the reservoir’s physical properties. Yao Shizhe et al. [16], through indoor experiments and field measurements, examined the salt formation phenomena in Wen96 gas reservoir injection and extraction wells.

In summary, current research on wellbore erosion mainly focuses on the effect of sand on erosion and on gas–solid or liquid–solid erosion research. However, studies that consider the effects of sand, salt formation, and water production on the erosion of gas reservoir columns have not been reported. Because the experiments cannot completely simulate the erosion of the gas reservoir column, this study considers the characteristics of the gas reservoir column, adopts the multiphase flow theory, the particle discrete phase model, considers the high temperature and high pressure, the gas–liquid–solid three-phase medium, the different solid particles (sand and salt), the particle size, and the inclination angle of the column, and establishes the gas–liquid–solid three-phase mathematical erosion model of the gas reservoir column by using CFD. Based on the above research methods and considerations, this study aims to further clarify the rules of gas reservoir column erosion and to provide a reference for the development of gas reservoir column erosion prevention and control strategies and measures.

2. Numerical Method

A mathematical model for pipe column erosion in gas storage reservoirs was developed based on a gas storage reservoir in central China as an engineering context. This model employs multiphase flow theory to handle the gas–liquid two-phase system. It simulates the movement of salt and sand particles by solving the particle motion equations and integrates these processes to construct a gas–liquid–solid three-phase flow model. To quantify the extent of pipe column erosion, an erosion model was introduced.

2.1. Continuous Phase Control Equations

In this gas reservoir well, liquid is extracted along with gas, resulting in a fluid system comprising the gas, liquid, and particle phases simultaneously. Therefore, the mixture model is employed to describe the flow and temperature fields within the tubing column. The continuity Equation (1), momentum Equation (2), and energy Equation (3) in the model are as follows [17,18]:

$${\displaystyle \frac{\partial {\rho }_m}{\partial t}}+\nabla \cdot \left({\rho }_m{\overrightarrow{v}}_m\right)=0$$

(1)

$${\displaystyle \frac{\partial }{\partial t}}\left({\rho }_m{\overrightarrow{v}}_m\right)+\nabla \cdot \left({\rho }_m{\overrightarrow{v}}_m{\overrightarrow{v}}_m\right)=-\nabla p+\nabla \cdot \left[{\mu }_m\left(\nabla {\overrightarrow{v}}_m+\nabla {\overrightarrow{v}}_m^T\right)\right]+{\rho }_{m}g+\overrightarrow{F}-\nabla \cdot \left({\displaystyle \sum _{k=1}^n{\alpha }_k{\rho }_k{\overrightarrow{v}}_{dr,k}{\overrightarrow{v}}_{dr,k}}\right)$$

(2)

$${\displaystyle \frac{\partial }{\partial \mathrm{t}}}{\displaystyle \sum _k\left({\alpha }_k{\rho }_k{E}_k\right)}+\nabla \cdot {\displaystyle \sum _k\left({\alpha }_k{\overrightarrow{v}}_k\left({\rho }_k{E}_k+\mathrm{p}\right)\right)}=\nabla \cdot \left(k_{eff}\nabla T-{\displaystyle \sum _k{\displaystyle \sum _j{h}_{j,k}{\overrightarrow{J}}_{j,k}+\left({\tau }_{eff}\cdot \overrightarrow{v}\right)}}\right)+S_h$$

(3)

where ${\rho }_m$ is the density of the mixture, kg/m³; t is the time, s; ${\overrightarrow{v}}_m$ is the velocity of the mixture, m/s; ${\alpha }_k$ is the volume fraction of phase k; ${\mu }_m$ is the viscosity of the mixture, pa·s; ${\overrightarrow{v}}_{dr,k}$ is the drift velocity of subphase k, m/s; g is the acceleration of gravity, m/s²; $h_{j,k}$ is the enthalpy of substance j in phase k, J; $h_{j,k}$ is the diffusion flux of substance j in phase k; $k_{eff}$ is the effective thermal conductivity, W/(m·k).

2.2. Turbulence Modeling

The daily gas production of this reservoir well is about $5\times {10}^4–60\times {10}^4$ m³/d. The fluid flow, characterized by a Reynolds number greater than 4000, exhibits turbulence. The k–ε model is commonly employed for turbulence calculations, and the Reliable k–ε turbulence model offers enhanced accuracy, particularly in boundary layer and secondary flow within rotating flows. Hence, in this paper, the reliable k–ε model is selected for calculations [19,20,21], and the mathematical model is depicted in Equations (4) and (5):

$${\displaystyle \frac{\partial }{\partial t}}\left(\rho k\right)+{\displaystyle \frac{\partial }{\partial x_i}}\left(\rho {\overrightarrow{u}}_{j}k\right)={\displaystyle \frac{\partial }{\partial x_i}}\left[\left(\mu +{\displaystyle \frac{{\mu }_t}{p{\gamma }_k}}\right){\displaystyle \frac{\partial k}{\partial x_i}}\right]+G_k+G_b-\rho \epsilon -Y_M$$

(4)

$${\displaystyle \frac{\partial }{\partial t}}\left(\rho \epsilon \right)+{\displaystyle \frac{\partial }{\partial x_j}}\left(\rho {\overrightarrow{u}}_j\epsilon \right)={\displaystyle \frac{\partial }{\partial x_j}}\left[\left(\mu +{\displaystyle \frac{{\mu }_t}{p{\gamma }_{\epsilon }}}\right){\displaystyle \frac{\partial \epsilon }{\partial x_j}}\right]+\rho C_1{\overline{S}}_{\epsilon }-C_2\rho {\displaystyle \frac{{\epsilon }^2}{k+\sqrt{v\epsilon }}}+C_{\epsilon 1}{\displaystyle \frac{\epsilon }{k}}{C}_{\epsilon 3}{G}_b$$

(5)

where k is the turbulent kinetic energy, J; $\epsilon$ is the dissipation rate, J/s; ${\overrightarrow{u}}_j$ is the average velocity, m/s; $x_i$ is the spatial coordinate, mm; ${\mu }_t$ is the turbulence viscosity coefficient; G_k is the turbulence kinetic energy generating term; G_b is the turbulence kinetic energy generating term caused by buoyancy; Y_M is the fluctuation energy; $C_{\epsilon 1}$ and $C_{\epsilon 2}$ are the empirical constants.

2.3. Mathematical Modeling of Particle Motion

The gas in the reservoir tubing column transports sand and salt particles toward the wellhead, where their quantity is relatively small compared to the gas itself, which belongs to the discrete phase (or discontinuous phase). The movement of these particles within the continuous gas phase follows Newton’s second law. The equations of motion for the particles account for the drag forces exerted by the sand and salt particles during their movement as well as their own gravitational effects [22], as shown in Equation (6):

$${\displaystyle \frac{d{U}_p}{dt}}=F_D\left(U_f-U_p\right)+{\displaystyle \frac{g\left({\rho }_p-{\rho }_f\right)}{{\rho }_p}}$$

(6)

$$F_D={\displaystyle \frac{18\mu }{{\rho }_p{D}_p^2}}{\displaystyle \frac{C_D{\mathrm{Re}}_p}{24}}$$

(7)

$${\mathrm{Re}}_p={\rho }_f\left|U_f-U_p\right|D_p/\mu$$

(8)

where $F_D$ is the drag force per unit mass of particles, N; $U_f$ is the gas phase velocity, m/s; $U_p$ is the particle velocity, m/s; $D_p$ is the particle diameter, mm; ${\mathrm{Re}}_p$ is the Reynolds number of particles. $C_D$ is the drag force coefficient, which is related to the change in the Reynolds number.

The magnitude of the drag force in Equation (7) depends on the flow conditions of the continuous phase, the characteristics of the particles, and other factors. Currently, the commonly used drag force coefficient models include the Alexander model and the Vince Peel model. The Alexander model is suitable for spherical particles, as shown in Equation (9), while the Vince Peel model is suitable for non-spherical particles, as shown in Equation (10).

$$C_D={\displaystyle \frac{24}{{\mathrm{Re}}_p}}\left(1+b_1{\mathrm{Re}}_p^{b_2}\right)+{\displaystyle \frac{b_3{\mathrm{Re}}_p}{b_4+{\mathrm{Re}}_p}}$$

(9)

$$C_D=a_1+{\displaystyle \frac{a_2}{{\mathrm{Re}}_p}}+{\displaystyle \frac{a_3}{{\mathrm{Re}}_p^2}}$$

(10)

where a₁, a₂, and a₃ are constants; b₁, b₂, b₃, and b₄ are constants.

This study primarily addresses sand and salt particles, which have different shapes: salt particles are spherical, and sand particles are non-spherical. Therefore, the Alexander model [23] is applied to calculate the drag force for salt particles, and the Vince Peel model [24] is applied to sand particles.

2.4. Particle Erosion Modeling

Based on domestic and international research on erosion, factors such as fluid properties inside the pipe, velocity of discrete-phase particles, particle size, and mass flow rate significantly influence erosion. Therefore, by integrating these factors with the fluid properties within the pipe, the erosion model proposed by J.K. Edwards et al. [25], shown in Equation (11), was utilized as the calculation model to determine the erosion rate in the gas storage reservoir tubing column in this study.

$$ER={\displaystyle {\sum }_{n=1}^N\frac{m_{p}C\left(d_p\right)f\left(\alpha \right)U_p^{b\left(v\right)}}{A_{face}}}$$

(11)

where m_p is the particle mass flow rate, kg/s; $C\left(d_p\right)$ is the particle size function, generally take $1.8\times {10}^{-9}$; $f\left(\alpha \right)$ is the impact angle function; $b\left(v\right)$ is the velocity function, generally take 2.6; $A_{face}$ is the sand particles hit the wall area, m².

Where the impact angle function is set using a segmented function; the impact angle and the corresponding coefficients are shown in

Table 1. Impact angles and coefficients.

Serial Number	Impact Angle (°)	Impact Angle Coefficient
1	0	0
2	20	0.8
3	30	1
4	45	0.5
5	90	0.4

:

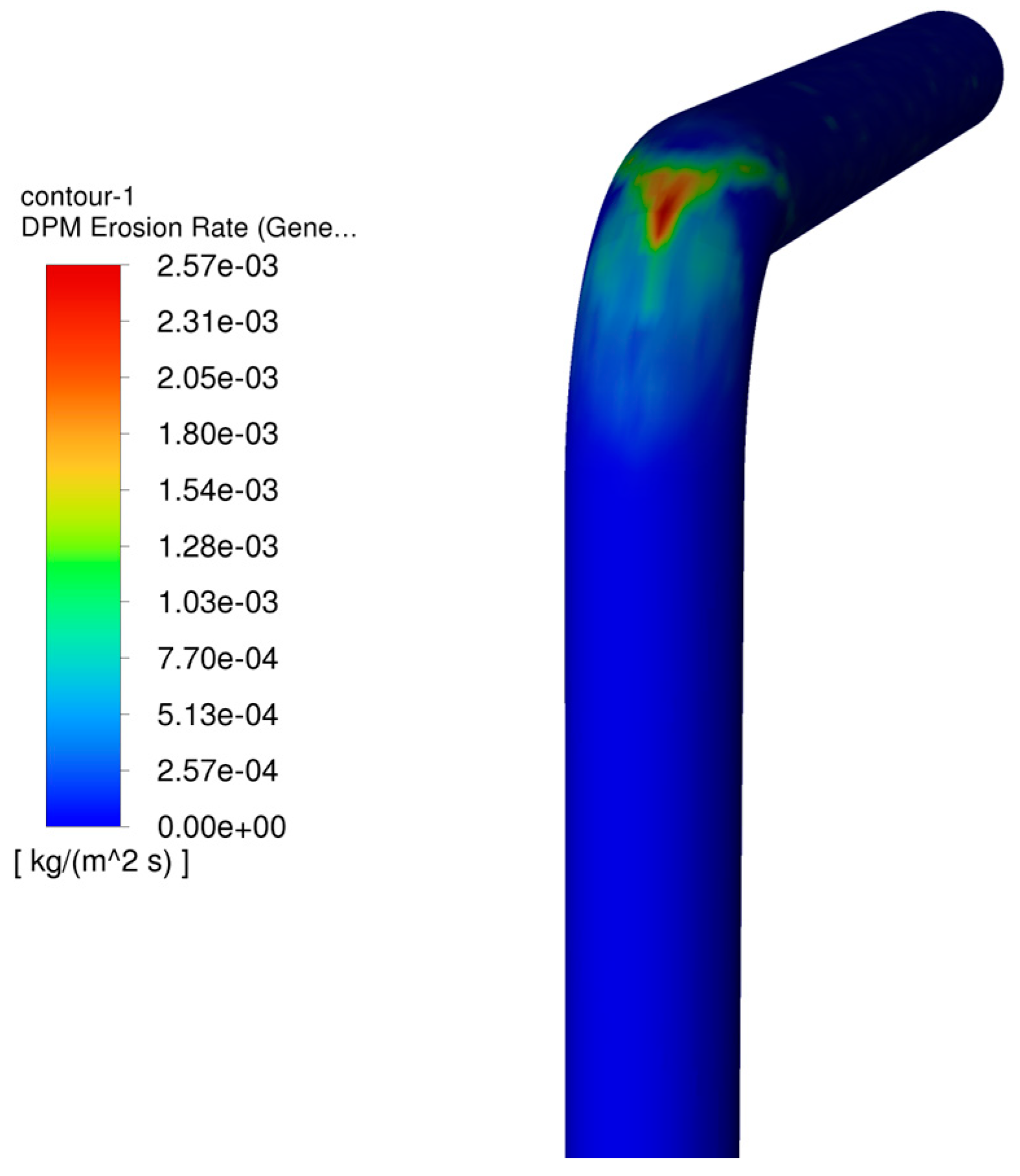
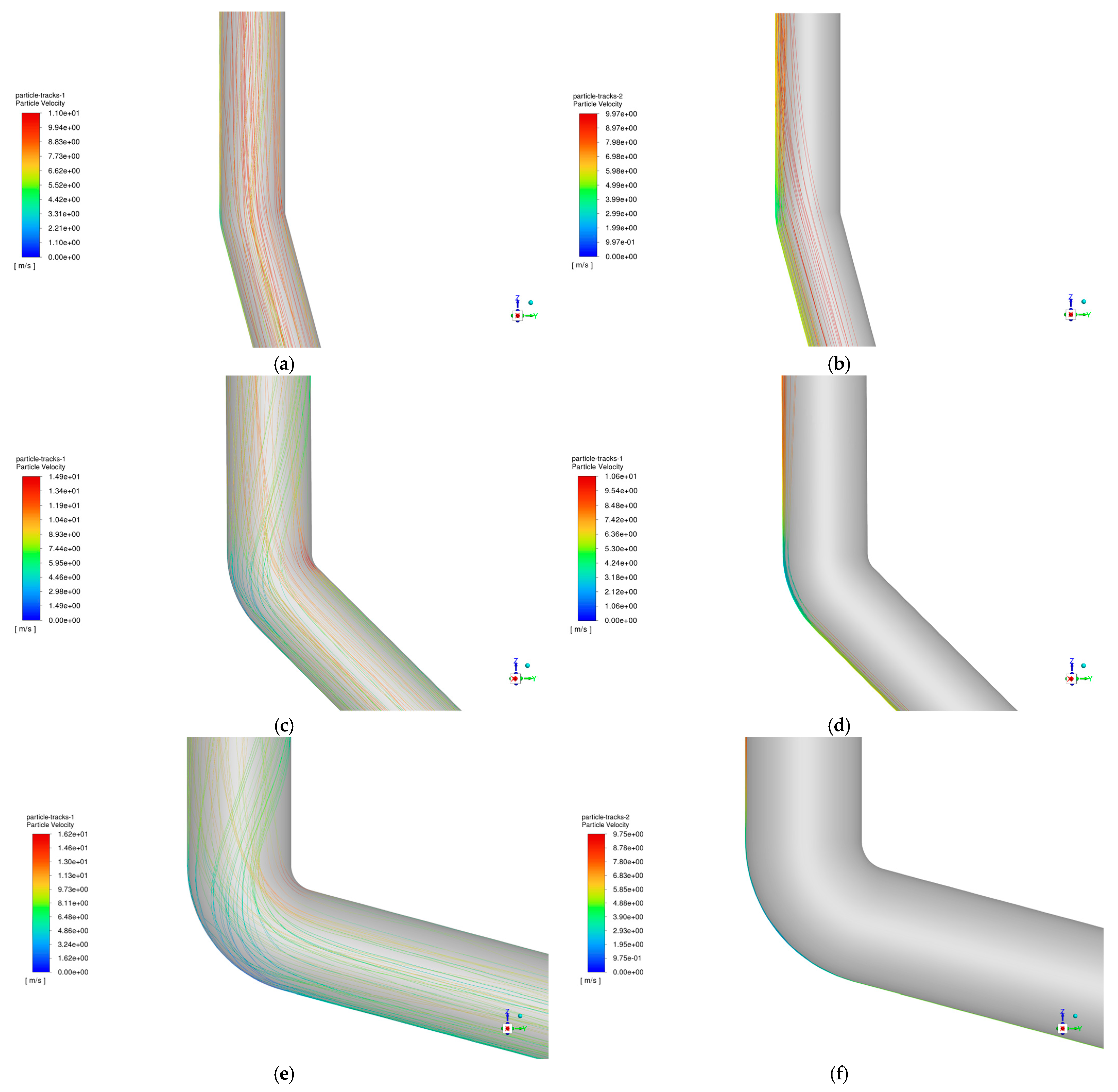
2.5. Model Validation

To verify the reliability of the numerical model, the experimental conditions in the literature [26] are utilized for numerical calculations and compared with the experimental results. The pipe in the experiment is ASTM A216. Grade WCB; the specific parameters are shown in

Table 2. List of specific physical parameters.

Pipe Diameter/mm	Aspect Ratio	Sand Density/(kg·m−3)	Pipe Density/(kg·m−3)	Fluid Velocity/(m·s−1)	Sand Particle Size/mm	Sand Mass Flow Rate/(kg·s−1)
52.5	1.5	2650	7800	47	0.35	0.06758

, and the calculation cloud diagram is shown in Figure 1:

Calculations based on the experimental conditions yielded a maximum erosion rate of 2.57 × 10⁻³ kg/(m²·s). Conversion yields a calculated result of 3.29 × 10⁻⁷ m/s, a relatively small error of 0.76% compared to the experimental result of 3.32 × 10⁻⁷ m/s. Therefore, it is considered that the model developed in this study can be used to predict the erosion rate of the pipe column.

3. CFD Simulation Modeling and Validation

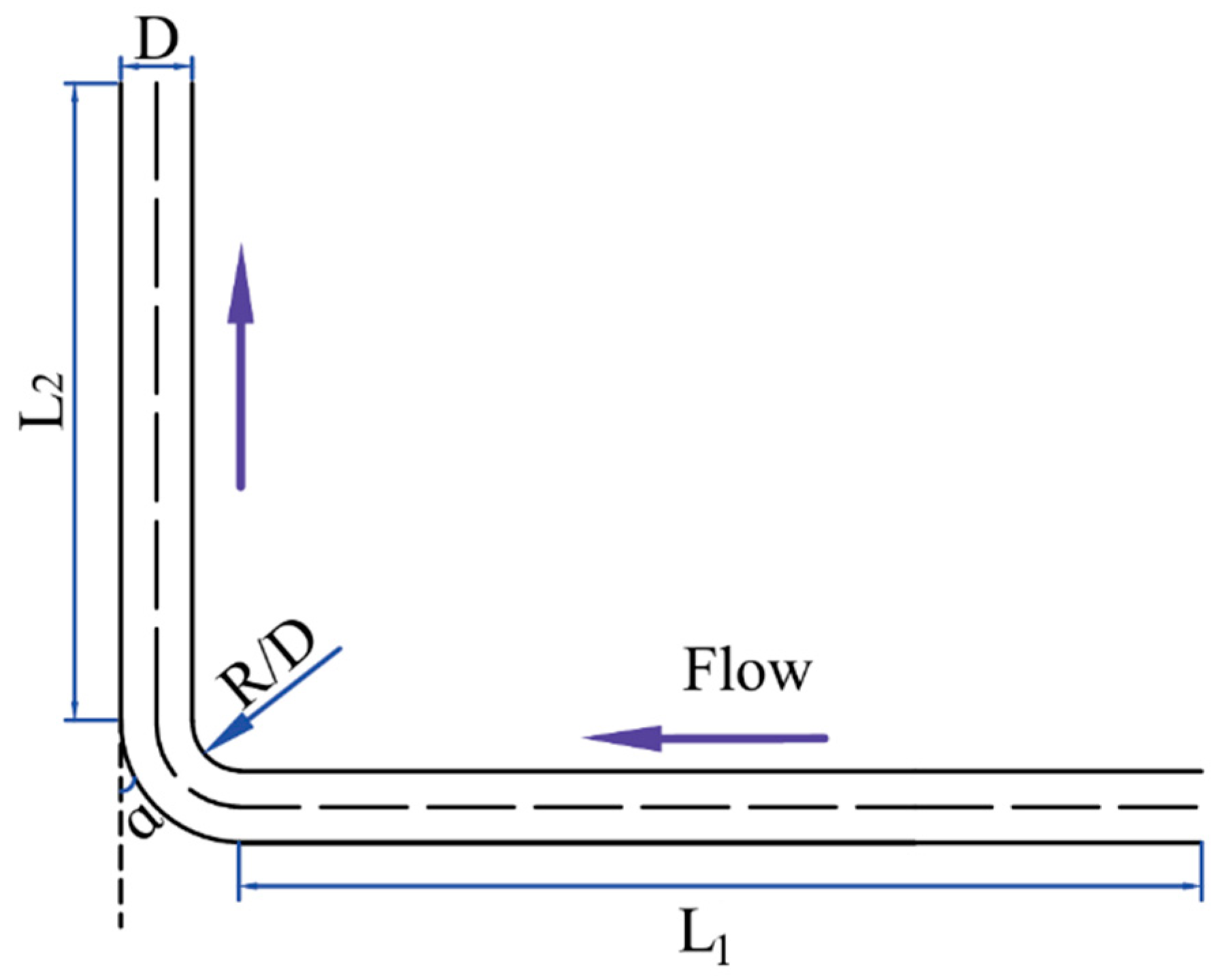
3.1. Geometric Modeling and Meshing of Gas Storage Columns

In this paper, Fluent 2022r1 software is used for simulation, and 90-degree bend pipe is taken as the research object, and the diameter of the pipe is 76 mm; the radius of curvature of the bend is 1.5 times the diameter of the bend, and the lengths of the inlet section, L₁, and the outlet section, L₂, are 50 and 20 times the diameter of the pipe, respectively, as shown in Figure 2. Using mesh to mesh the geometric structure, in order to improve the accuracy of the numerical solution, set 11 boundary layers near the pipe wall; mesh results are shown in Figure 3.

3.2. Boundary Conditions and Calculation Methods for Gas Storage Columns

It is assumed that the particle velocity is the same as the inlet velocity of the continuous phase medium, the boundary is set as the velocity inlet and pressure outlet, the inlet turbulence intensity is 5%, the hydraulic diameter is 0.076 m, the wall has no slip, and the standard wall function is chosen for the near-wall calculation. The SIMPLE algorithm is used for the solution, and the convergence criterion is 10⁻⁶ for the scaled residuals of the energy equation and 10⁻⁴ for the other equations. The wall conditions are reflections, and the normal recovery coefficients and tangential recovery coefficients are shown below:

$$\left\{\begin{array}{l}{e}_n=0.993-1.76\theta +1.56{\theta }^2-0.49{\theta }^3\\ e_t=0.988-1.66\theta +2.11{\theta }^2-0.67{\theta }^3\end{array}\right.$$

(12)

where: $e_n$ is the normal coefficient of recovery; $e_t$ is the tangential coefficient of recovery; $\theta$ is the impact angle of solid particles colliding with the wall.

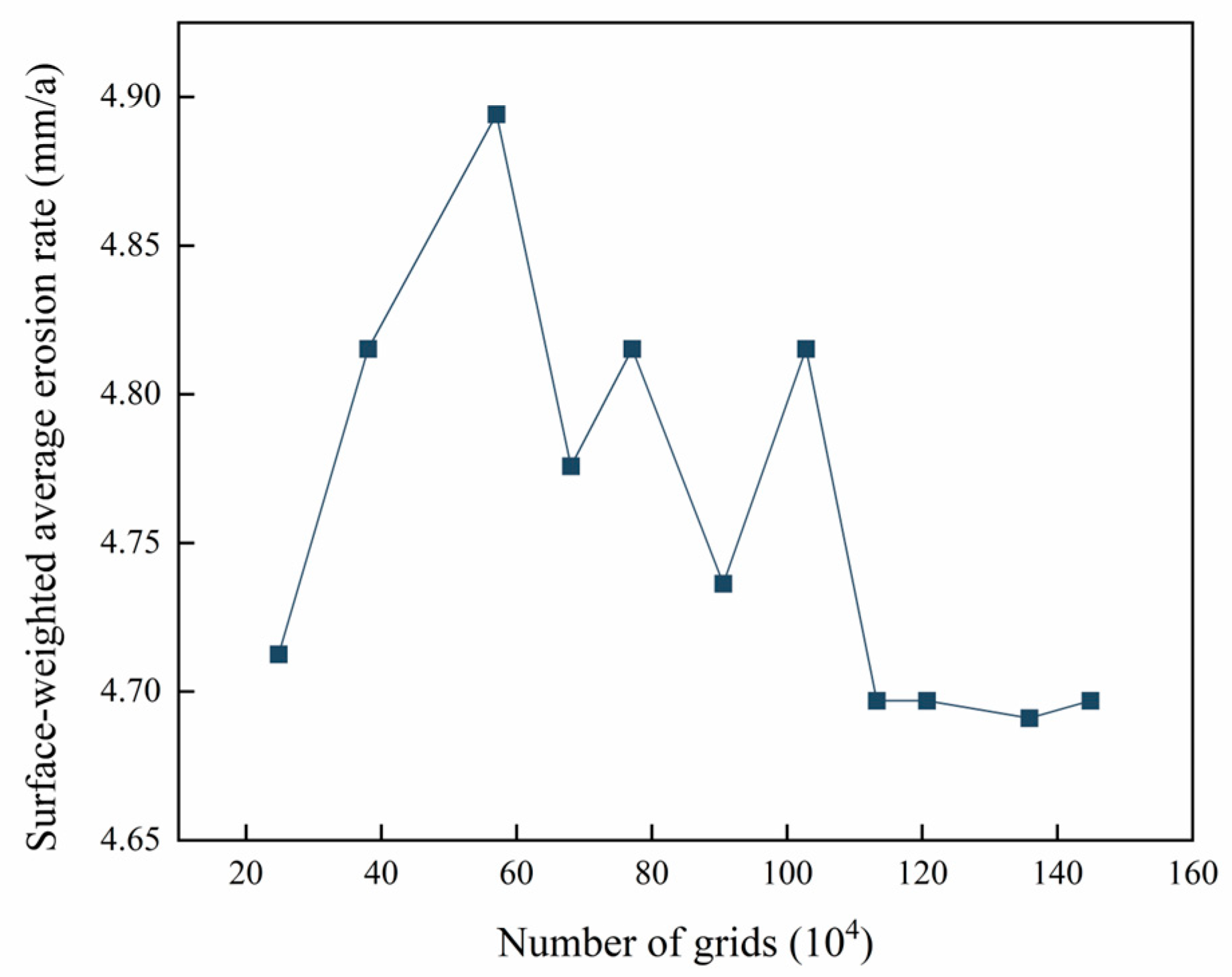
3.3. Grid-Independent Verification

To verify the irrelevance of the grids, a total of 11 sets of unstructured grids with 247,968, 380,268, 570,402, 680,400, 771,120, 905,760, 1,028,016, 1,132,800, 1,207,040, 1,358,400, and 1,448,960 grids were divided for the computation. The face-weighted average erosion rates of the different grids under the same boundary conditions and calculation methods (see

Table 3. Grid-independent boundary condition settings.

Parameters	Worth
Gas velocity	23 m/s
Particle diameter	300 μm
Particle density	2650 kg/m3
Particle mass flow rate	0.3 kg/s
Tube density	7800 kg/m3

for specific conditions) were calculated, and the results are shown in Figure 4.

Figure 4 indicates that there is no significant change in the face-weighted average erosion rate when the grid count exceeds 1,207,040. Therefore, to reduce the computational costs, a grid count of 1,207,040 was selected for the calculations.

4. Study on the Erosion Law of Gas Storage Pipe Columns

The daily gas extraction from the reservoir wells is about 5 × 10⁴–60 × 10⁴ m³/d. During the gas extraction process, the reservoir wells often contain sand particles and salt particles, and according to the field measurement data, the particle size of the sand particles ranges from 0.01 to 7 mm, the particle size of the salt particles ranges from 0.1 to 0.6 mm, and the shape coefficient of the sand particles is determined to be 0.6 based on the sand particle type [10]. Assuming that there is no collision between the particles, sensitivity analysis is carried out for the main factors affecting the column erosion: water volume fraction, gas extraction, particle mass flow rate, particle size, and bending angle of the column, etc., (all the calculated column geometries in this section are shown in Figure 2, and the basic data are shown in

Table 4. Statistical table of basic parameters.

Parameters	Worth
Quantity of gas recovered	60 × 104 m3/d
Sand particle size	0.05 mm
Grain density	2650 kg/m3
Salt particle size	0.3 mm
Salt particle size	2150 kg/m3
Grit mass flow rate	4.32 kg/d
Salt particle mass flow rate	8.64 kg/d
Water content by volume	0.002%
Length of entrance section	50 D
Stresses	20 MPa
Inlet temperature	374 K

) to obtain the relationship between the different factors and the maximum erosion rate of the column. We draw on the oil and gas industry standard SY5329-2022 [27] in the corrosion-related provisions of the 0.076 mm/a set as the critical erosion rate [28], so as to determine in a variety of factors under the influence of the maximum erosion rate of the pipe column whether the column structure will cause damage to the column, for the subsequent protective measures to provide a basis for decision-making.

4.1. Analysis of the Influence of Water Volume Fraction and Gas Recovery Rate on the Erosion Pattern of Pipe Columns

The basic operating parameters of the reservoir are shown in Table 3, and when the gas extraction volume is 6.62 × 10⁴–60 × 10⁴ m³/d, the water production volume is 0–100 m³/d. In order to study the influence of the water production volume on the erosion of the pipe column in this volume, when the volume fraction of the water content is 0.0005%, 0.001%, 0.002%, 0.0032%, 0.004%, the change pattern of the maximum erosion rate of the pipe column is shown in Figure 5.

Figure 5 shows that with a low water content volume fraction, the maximum erosion rate of the column remains relatively unchanged as the water content volume fraction increases. The reason for this is that the fluid production is small and the fluid does not affect the particles during gas extraction, so the erosion rate is essentially unchanged. When the water content volume fraction is kept constant, the maximum erosion rate of the pipe column increases with higher gas extraction rates following a power function relationship. When the gas extraction volume exceeds 60 × 10⁴ m³/d, the maximum erosion rate exceeds the critical erosion rate of 0.076 mm/a. At this point, the safety of the column is severely compromised.

4.2. Analysis of the Influence of Particle Mass Flow Rate on the Erosion Pattern of Pipe Columns

Because the production process involves sand and salt particles, it is necessary to separately analyze the mass flow rates of these two types of particles to clarify their respective roles in column erosion. This analysis aims to identify the primary particles contributing to column erosion damage, thereby providing a theoretical basis for optimizing production methods in the future.

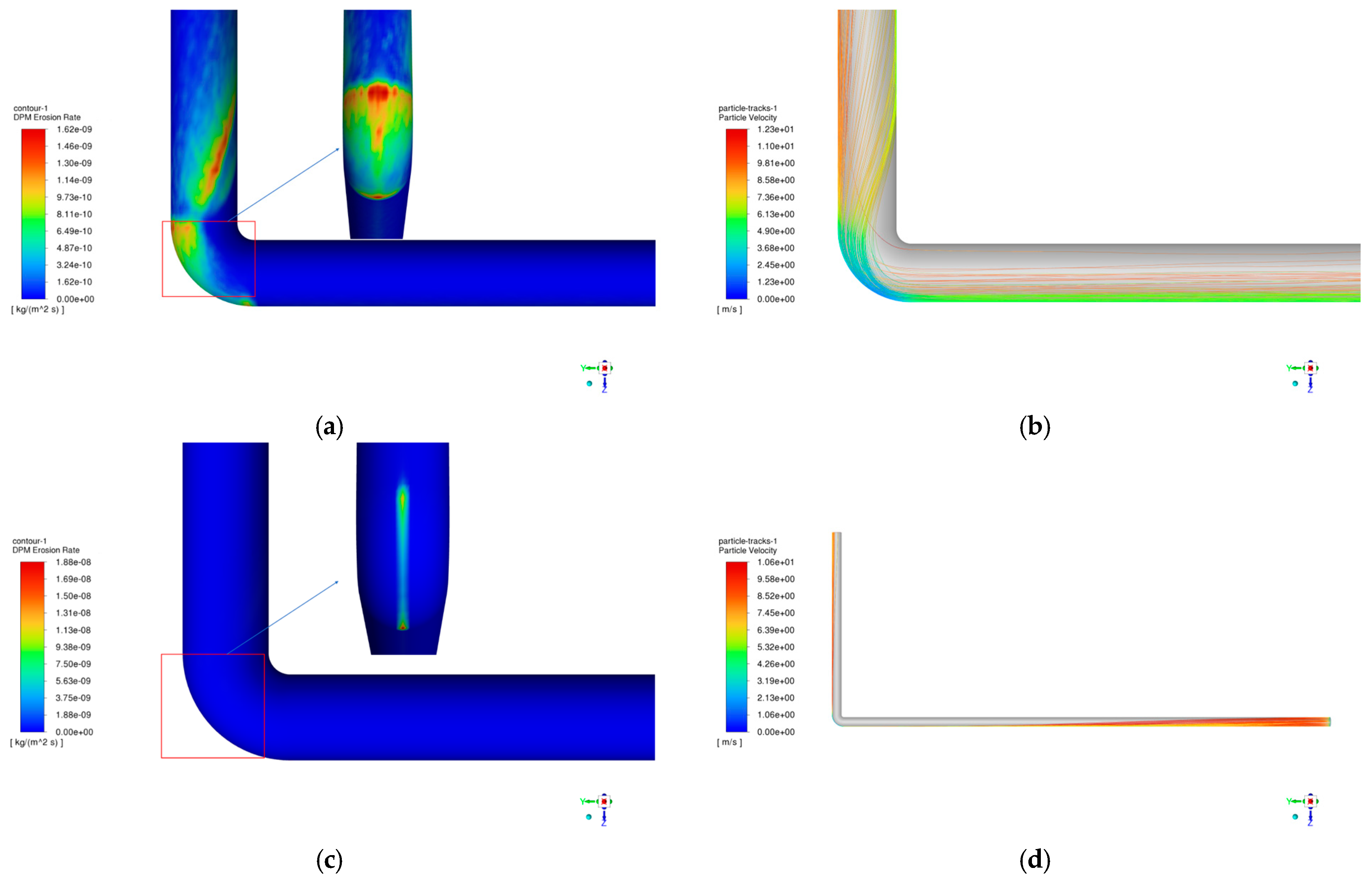
4.2.1. Effect of Sand Mass Flow Rate on Column Erosion

The basic operating parameters of the reservoirs are presented in Table 3. Figure 6 depicts the variation in the maximum erosion rate of the pipe column with changes in the sand mass flow rate, ranging from 0.0864 to 8.64 kg/d. Figure 7 shows the particle trajectory diagram corresponding to the variations in the sand mass flow rate.

Figure 6 shows that the maximum erosion rate of the pipe column remains relatively constant despite the increase in the mass flow rate of sand particles at consistent gas extraction volumes. As depicted in Figure 7c, salt particles gravitate towards the lower part of the pipe owing to their larger size. Figure 7a,b illustrate that the trajectory of sand particles remains consistent, as their smaller size allows them to move freely within the fluid column, reducing the frequency of wall collisions. Consequently, the maximum erosion rate remains stable with varying sand mass flow rates. However, at constant sand mass flow rates, higher gas extraction leads to increased maximum erosion rates, as detailed in Section 4.1.

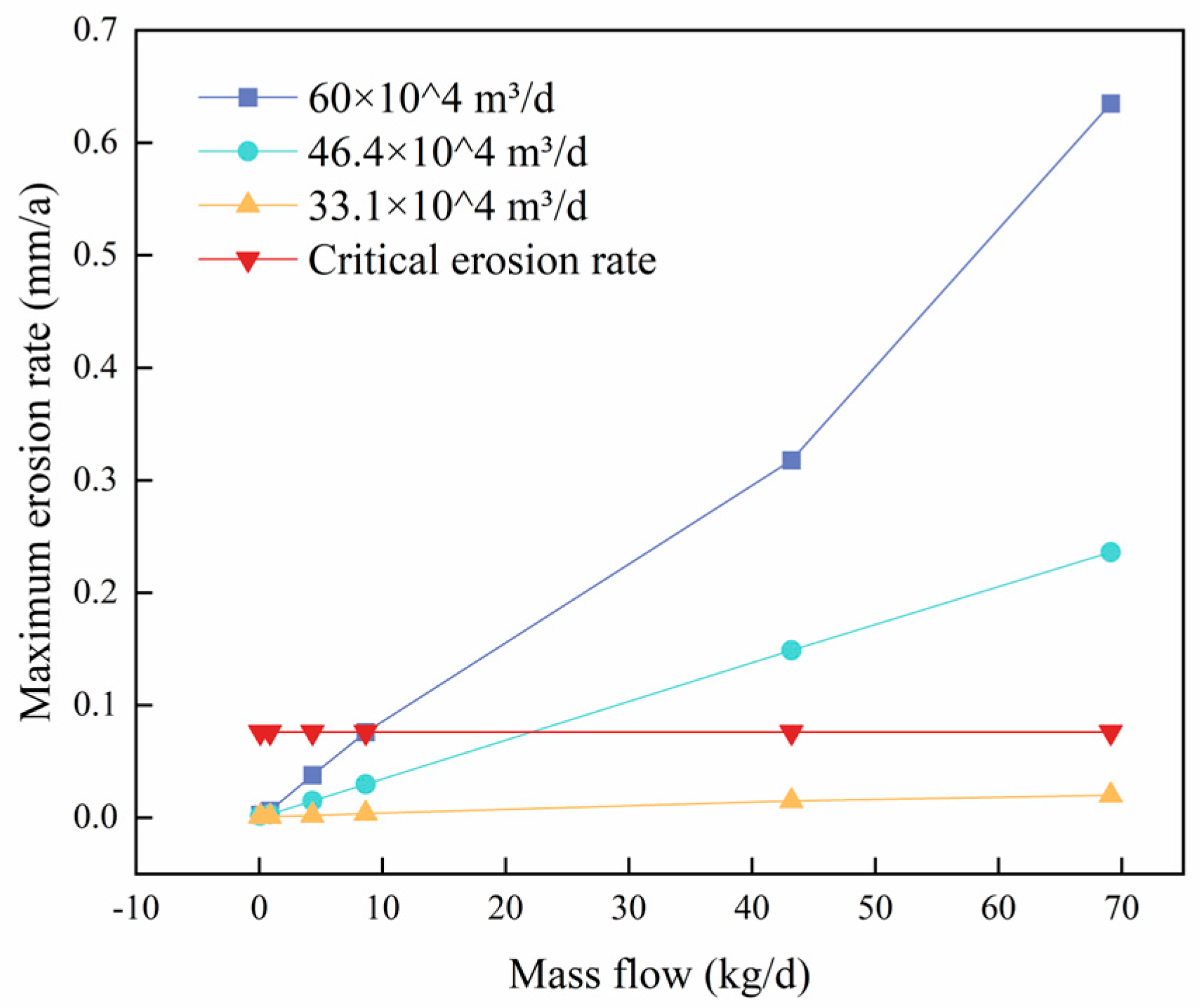
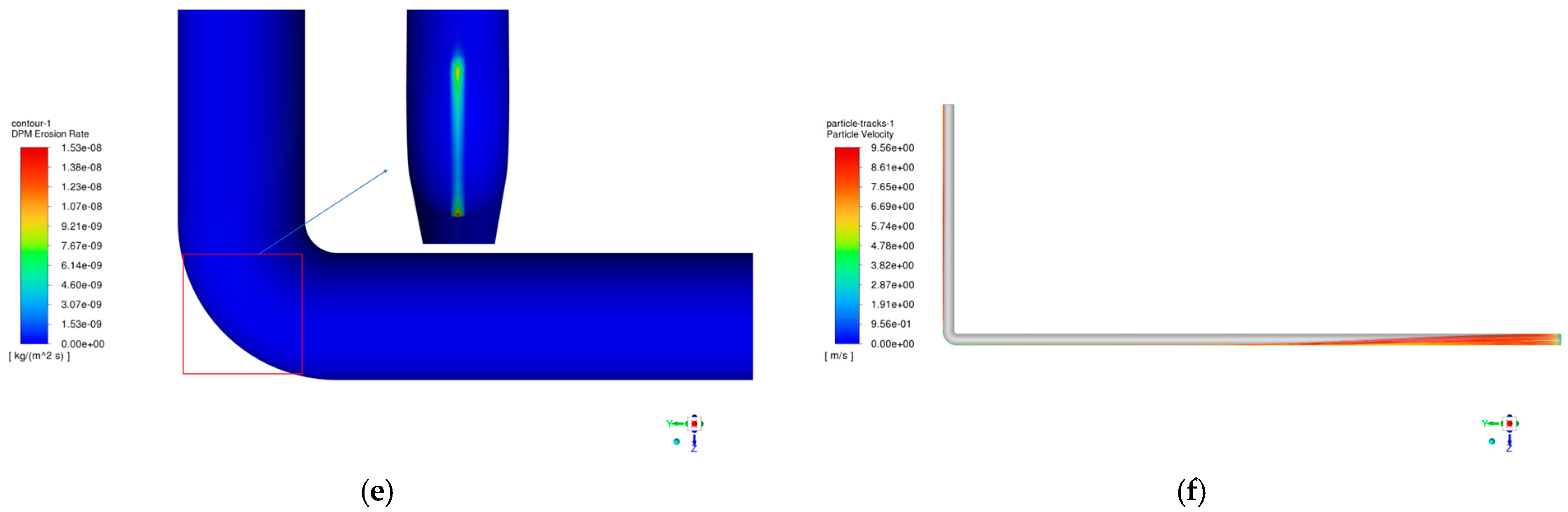
4.2.2. Effect of Salt Mass Flow on Column Erosion

The basic operating parameters of the reservoirs are presented in Table 3. Figure 8 depicts the variation in the maximum erosion rate of the pipe column with changes in the salt mass flow rate ranging from 0.0864 to 69.1 kg/d. Figure 9 depicts the erosion cloud and particle trajectory diagrams corresponding to the variations in the salt mass flow rate.

Figure 8 shows that the maximum erosion rate of the pipe column shows minimal sensitivity to the salt mass flow rate under low gas recovery conditions, whereas it exhibits a linear correlation under high gas recovery. Figure 9a,b show the variations in both the magnitude and location of the maximum erosion rate of the pipe column across different salt mass flow rates.

As shown in Figure 9c,e, at constant particle size, the number of salt particles decreases when the salt mass flow rate is small, and at this time, the area and size of the erosion (see Section 4.2.1 for the reason) is subject to the erosion of sand particles; as shown in Figure 9d,f, the number of salt particles increases when the salt mass flow rate is large, and the velocity of particle flow increases (the maximum velocity of particles with a salt mass flow rate of 69.1 kg/d is 10.6 m/s, the maximum velocity of particles with a salt mass flow rate of 0.0864 kg/d is 9.73 m/s, as shown in Figure 9e,f); at this time, the area and size of erosion are mainly affected by salt particle erosion, resulting in an increase in the degree of erosion of the pipe column. When the gas extraction volume is greater than 46.4 × 10⁴ m³/d and the salt mass flow rate is greater than about 22 kg/d, the maximum erosion rate is greater than the critical erosion rate of 0.076 mm/a at this time, the safety of the pipe column is seriously threatened.

When the gas extraction volume exceeds 46.4 × 10⁴ m³/d and the salt mass flow rate surpasses approximately 22 kg/d, the maximum erosion rate exceeds the critical erosion rate of 0.076 mm/a, posing a serious threat to the safety of the pipe column.

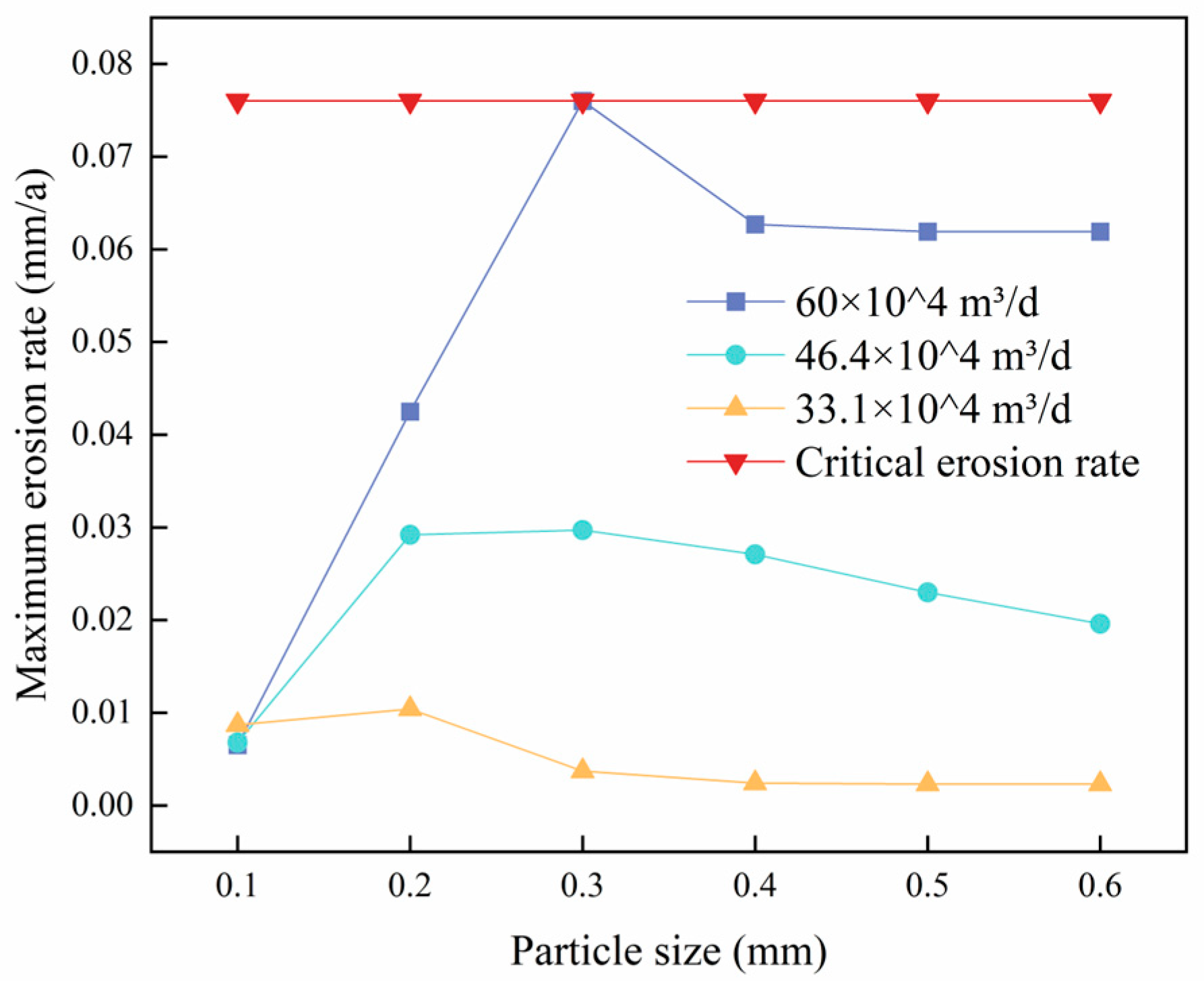
4.3. Effect of Particle Size on Column Erosion

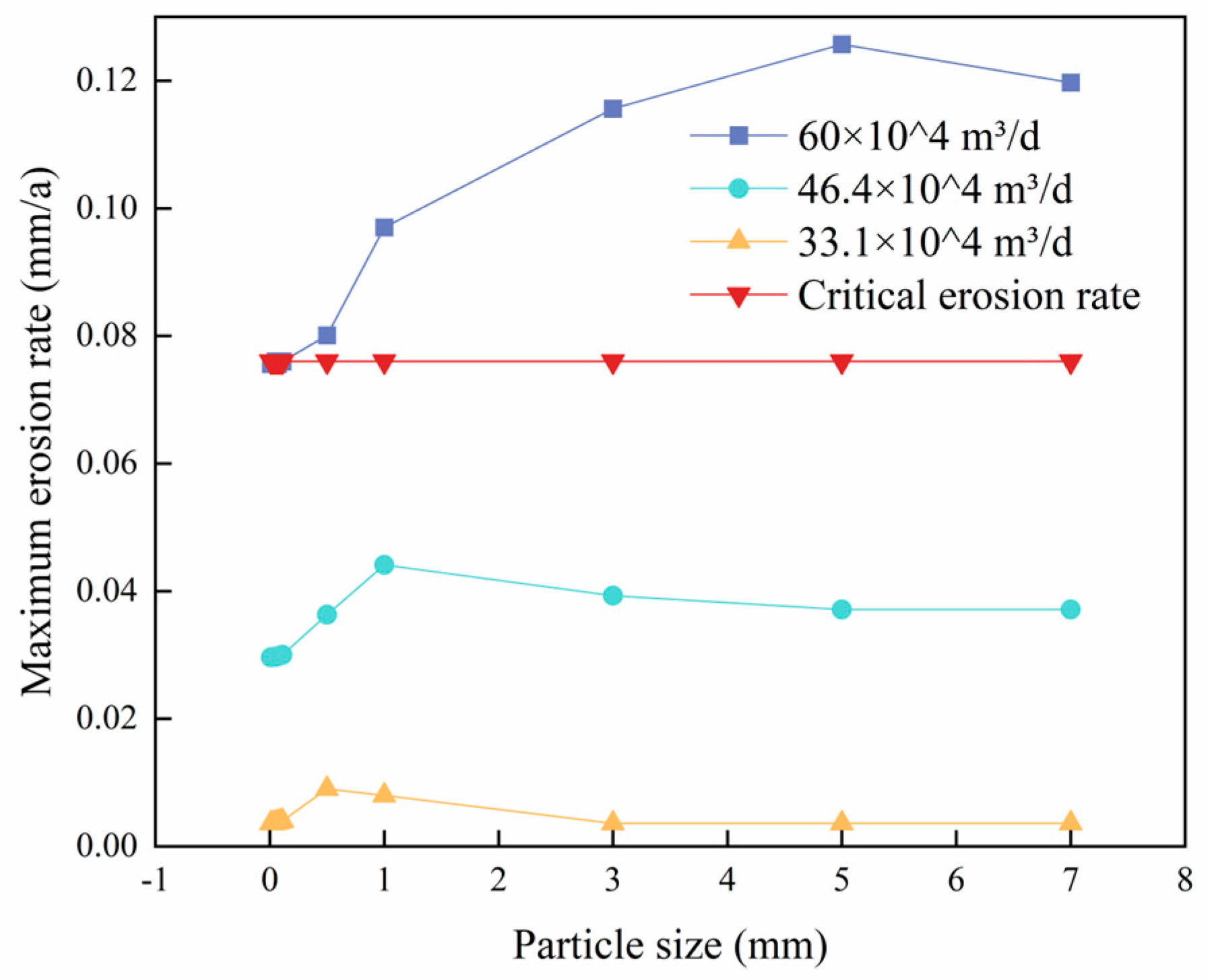
4.3.1. Effect of Sand Particle Size on Column Erosion

The basic operating parameters of the gas storage reservoir are presented in Table 3. Figure 10 depicts the maximum erosion rate of the pipe column for particle sizes ranging from 0.01 to 7 mm, depicting the variation in erosion with particle size. Figure 11 depicts the particle trajectory diagrams for different sand particle sizes.

Figure 10 shows that as grain size increases, the maximum erosion rate of the pipe column initially increases, then decreases, and finally stabilizes. From Figure 11a, it can be observed that the erosion damage is least severe for sand particles of 0.01 mm size, as explained in Section 4.2.1. Additionally, Figure 11b shows that as sand particle size increases due to gravity, their trajectory aligns with that of salt particles (as shown in Figure 11d), leading to erosion damage on the pipe column. Furthermore, Figure 11c reveals that with further increase in particle size, the particles’ velocity decreases (the maximum velocity decreases from 7.59 m/s to 7.12 m/s, as shown in Figure 11b,c), resulting in a nearly unchanged maximum erosion rate of the pipe column after this reduction.

4.3.2. Effect of Salt Particle Size on Column Erosion

The basic operating parameters of the gas storage reservoir are displayed in Table 3. Figure 12 shows the maximum erosion rate of the pipe column with particle sizes ranging from 0.1 to 0.6 mm, illustrating the variation in erosion. Furthermore, Figure 13 presents the particle trajectory diagrams for various salt particle sizes.

Figure 12 indicates that as the particle size increases, the maximum erosion rate of the pipe column initially rises, then declines, and eventually stabilizes. Figure 13a,b indicate that smaller salt particles are influenced by gravity, allowing them to move freely with the fluid, resulting in a wider erosion zone on the column but with less intensity. In contrast, Figure 13c,d show that larger salt particles affected by gravity tend to concentrate erosion towards the central region, resulting in more pronounced erosion. Figure 13e,f further demonstrate that as particle size increases, the maximum erosion rate follows a pattern of initial increase, decrease, and eventual stabilization. In Figure 13f, it is observed that with a further increase beyond 0.3 mm, the erosion intensity decreases. This reduction is attributed to fewer impacts per unit of time on the wall, lowering the frequency of wall collisions. Additionally, particle velocity decreases (from a maximum of 10.6 m/s to 9.5 m/s, as shown in Figure 13d,f), contributing to a reduced maximum erosion rate of the pipe column.

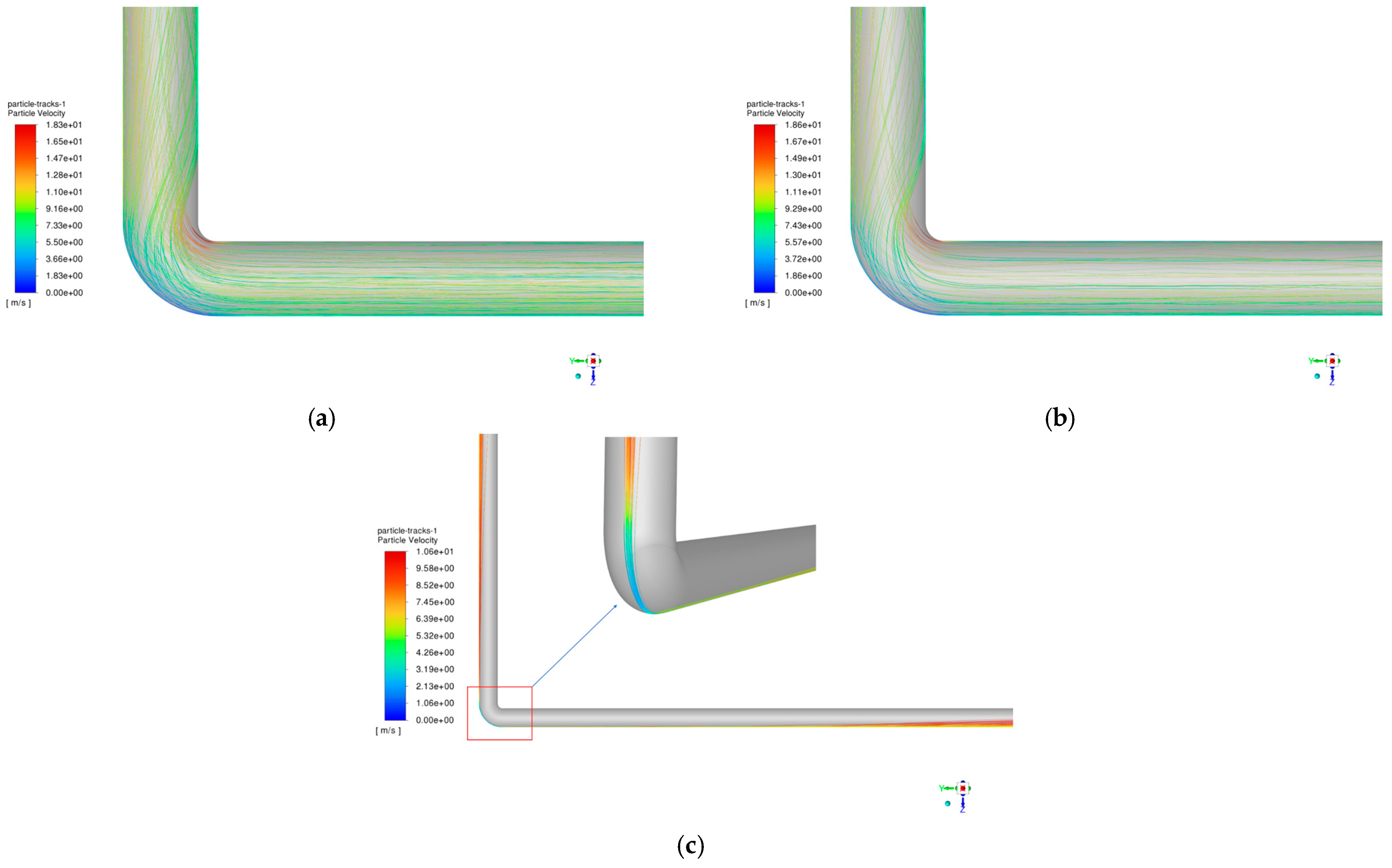
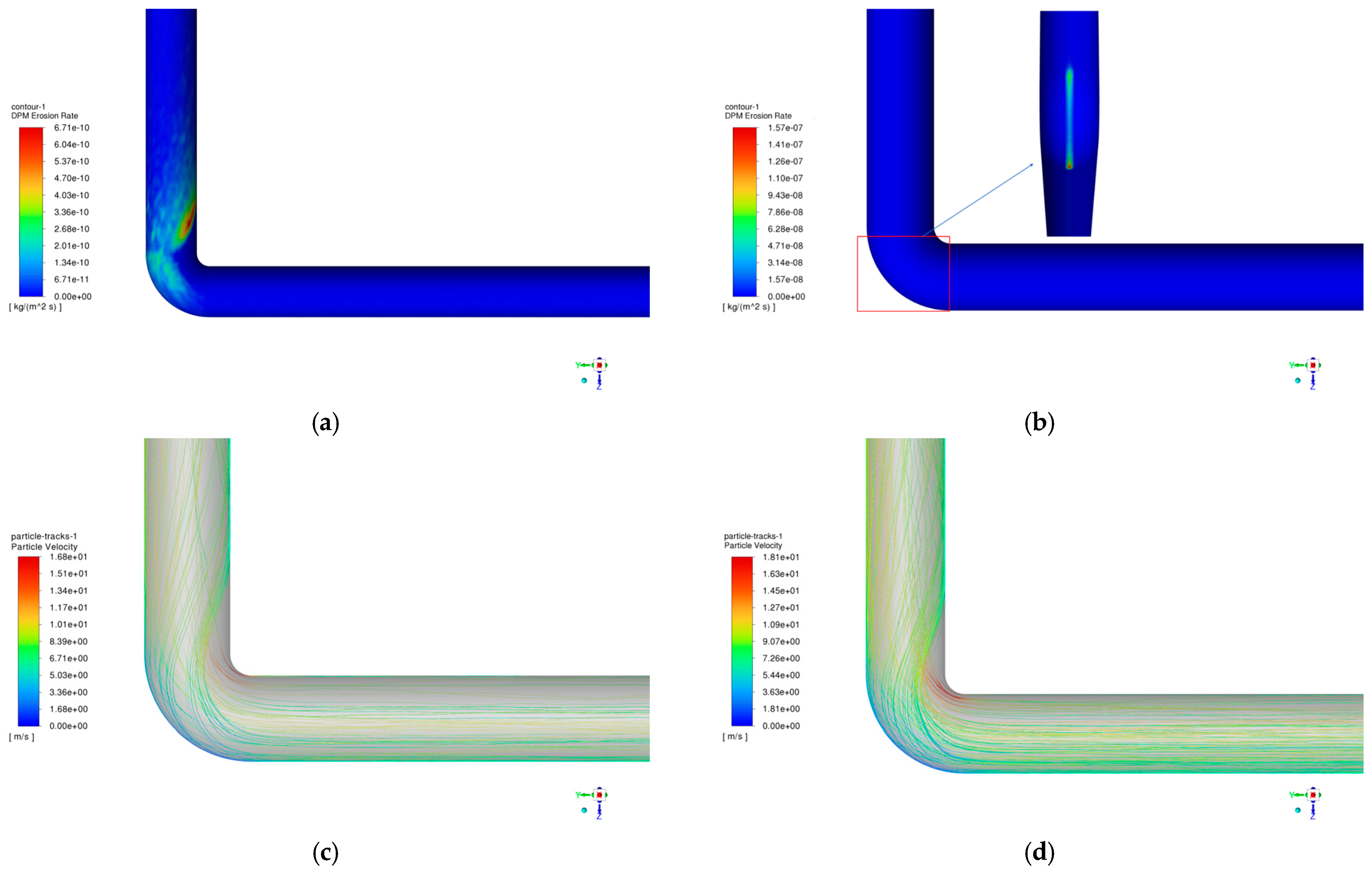
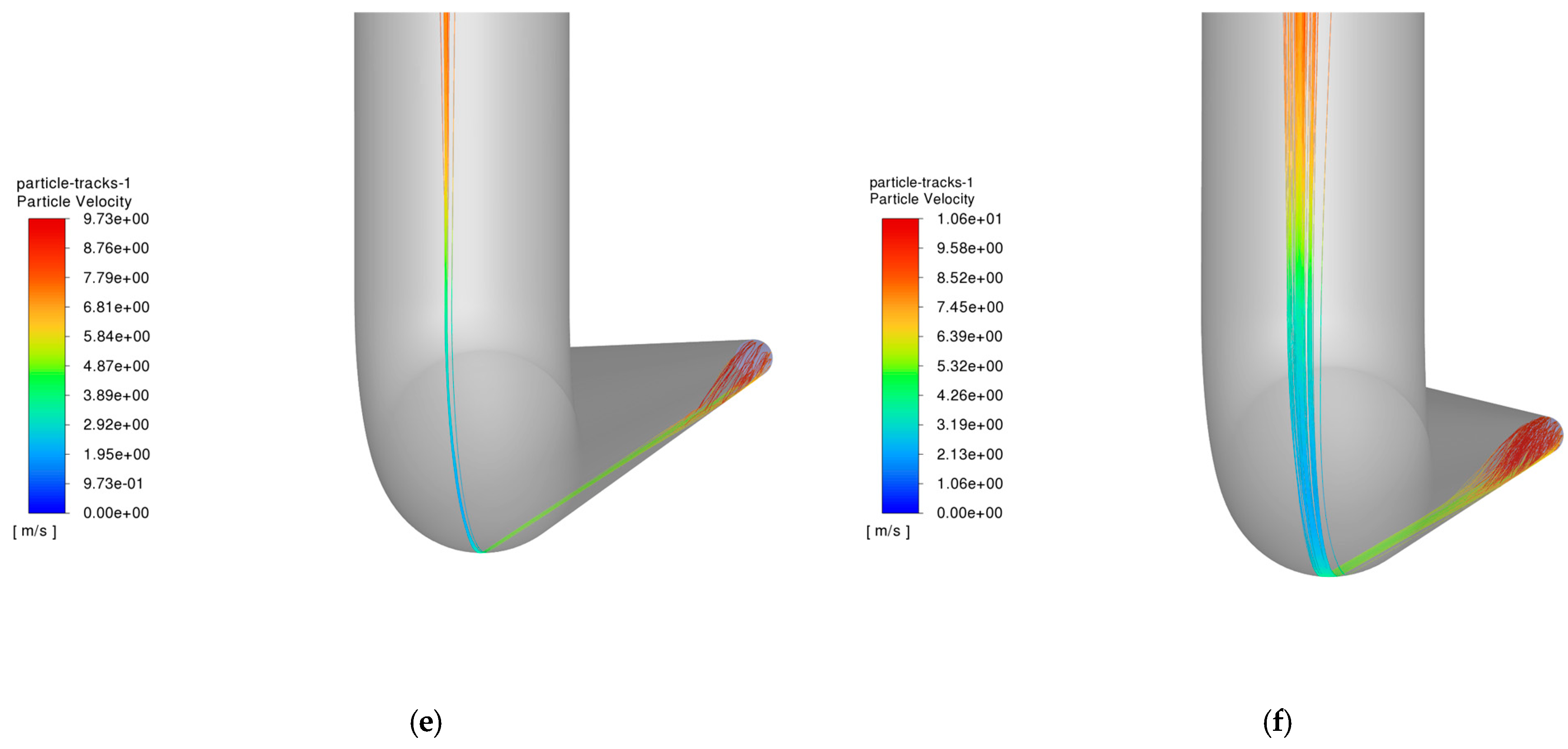
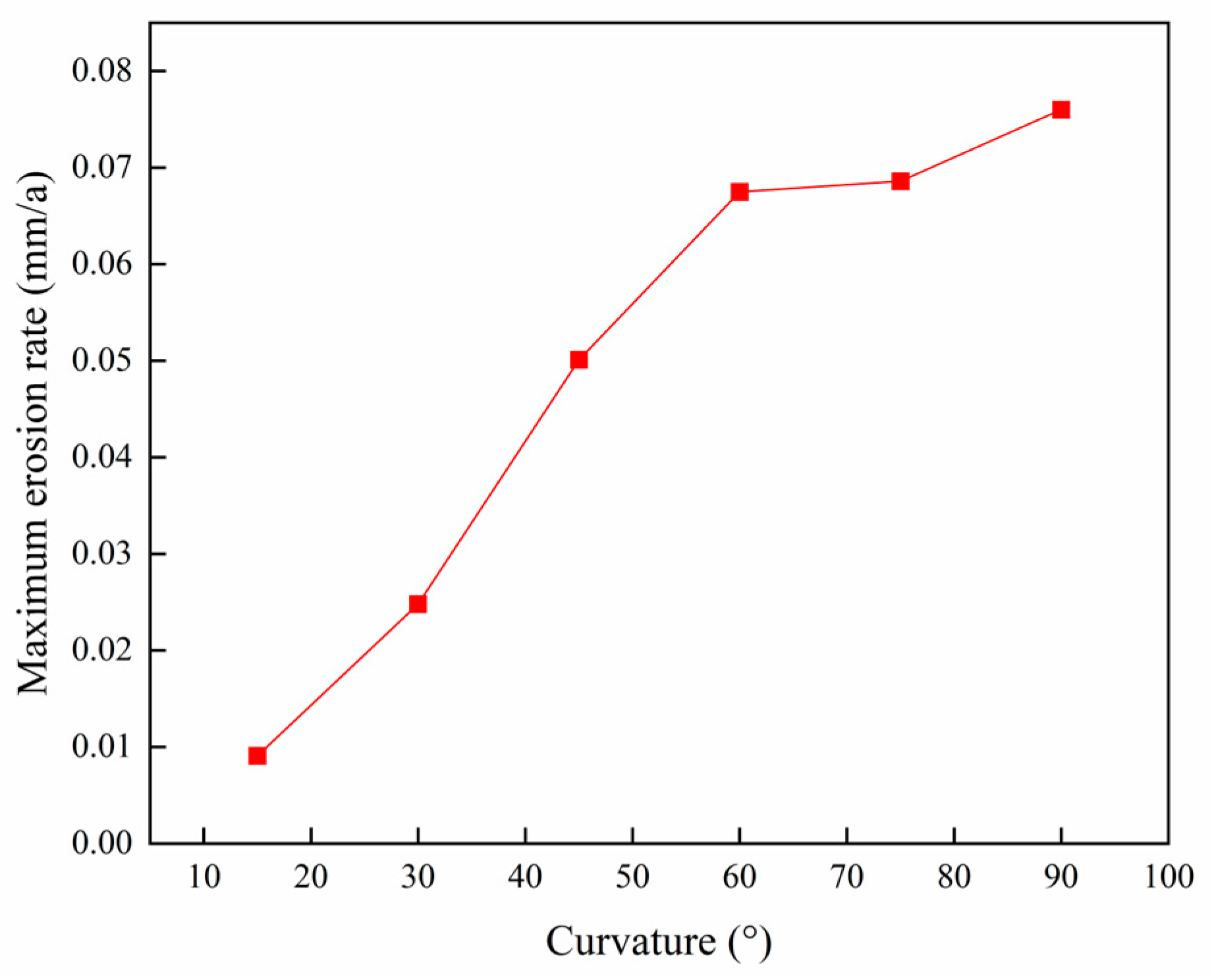
4.4. Effect of Bending Angle on Column Erosion

The basic operating parameters of the gas storage reservoir are presented in Table 3. Figure 14 depicts the maximum erosion rate of the pipe column as the bending angle varies between 15°, 30°, 45°, 60°, 75°, and 90°. Additionally, Figure 15 depicts trajectory diagrams depicting the paths of different particles under varying bending angles.

Figure 14 indicates that the maximum erosion rate of the pipe column tends to increase with higher bending angles. In Figure 15a,b, at smaller bending angles, most sand particles maintain their velocity through the bend, suggesting minimal collision with the pipe wall. Similarly, some salt particles also retain their velocity, indicating fewer collisions. Consequently, the maximum erosion rate of the pipe column is lowest at a 15° bending angle. As seen in Figure 15c,d, with increasing bending angles, some sand particles slow down within the bend, indicating collisions with the pipe wall. By this stage, salt particles consistently collide with the wall, increasing the maximum erosion rate. In Figure 15e,f, at a 75° bending angle, salt particles collide entirely with the wall, while sand particles are more prone to wall collisions within the bend. Hence, the maximum erosion rate of the pipe column continues to rise.

5. Conclusions

The main insights and conclusions of this paper are as follows:

(1)

Grid-independence verification of the pipe column erosion model: when the number of grids is greater than 1,207,040, the face-weighted average erosion rate does not change significantly; considering the savings in computational costs, choose the number of grids for 1,207,040 grids for calculation.

(2)

In scenarios with low liquid volumes, the maximum erosion rate remains largely unaffected by increases in water volume fraction. Within identical liquid volumes, the maximum erosion rate rises alongside higher gas extraction rates, exhibiting a power function relationship with the volume of gas extracted. When the gas extraction volume exceeds 60 × 10⁴ m³/d, the maximum erosion rate surpasses the critical erosion rate of 0.076 mm/a. This study emphasizes that the gas extraction rate is the most influential factor affecting erosion rates in this context.

(3)

Under low gas extraction rates, the salt mass flow rate has minimal influence on the maximum erosion rate of the pipe column. However, at high gas extraction rates, there is a linear correlation between the maximum erosion rate and the salt mass flow rate. Specifically, when the gas extraction rate exceeds 46.4 × 10⁴ m³/d and the salt mass flow rate exceeds 22 kg/d, the maximum erosion rate surpasses the critical erosion rate of 0.076 mm/a. This poses a serious threat to the safety of the pipe column during these conditions.

(4)

As the sand and salt particle sizes increase, the maximum erosion rate of the column exhibits a trend where it initially increases, then decreases, and eventually stabilizes. Similarly, as the bending angle increases, the maximum erosion rate of the column shows an increasing trend.