Simulation of Macroscopic Chloride Ion Diffusion in Concrete Members
Abstract
1. Introduction
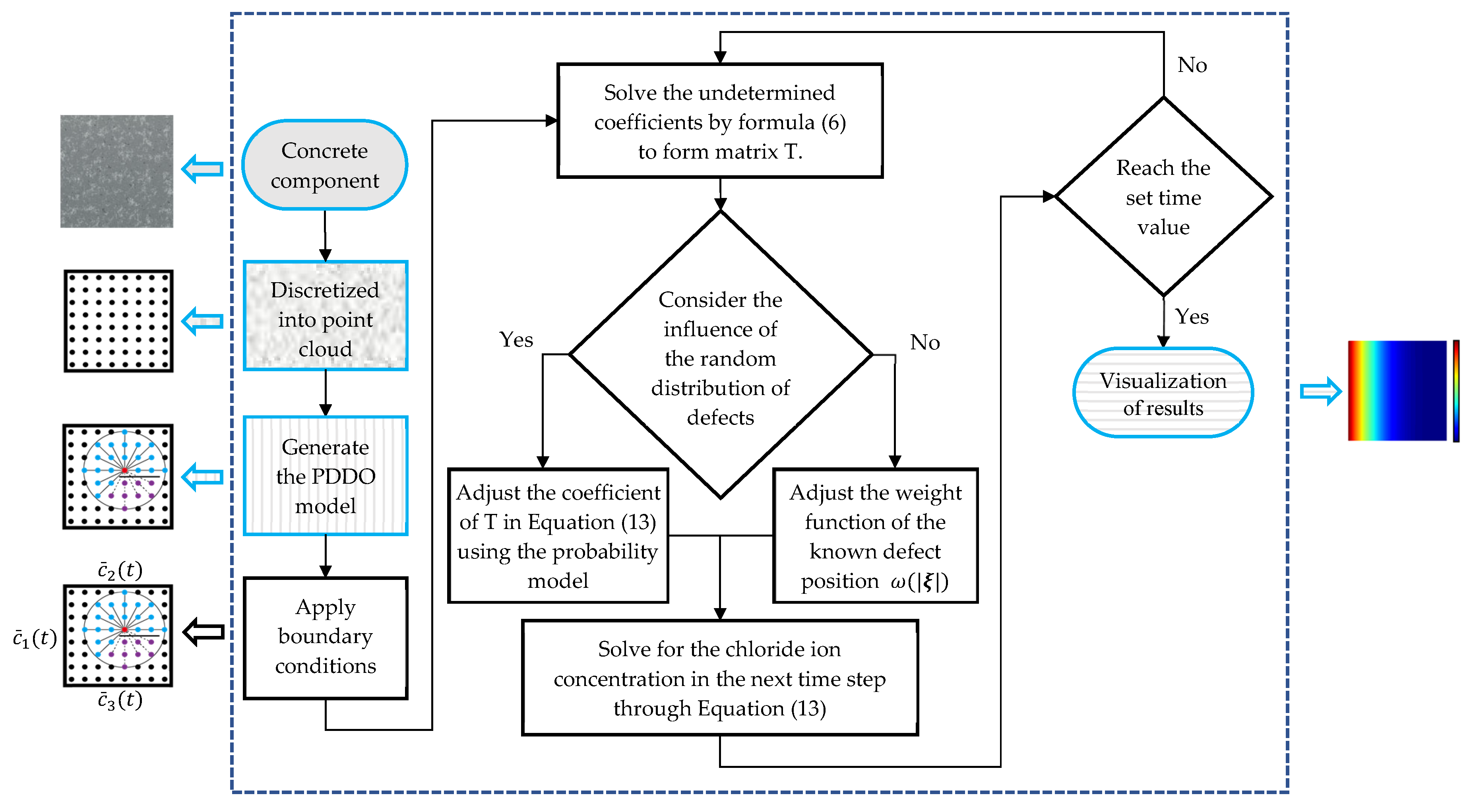
2. Discrete Solution Format of Fick’s Second Law Using PDDO
2.1. Peridynamic Differential Operator
2.2. Spatial Discretization of Fick’s Law Using PDDO
2.3. Time Domain Difference
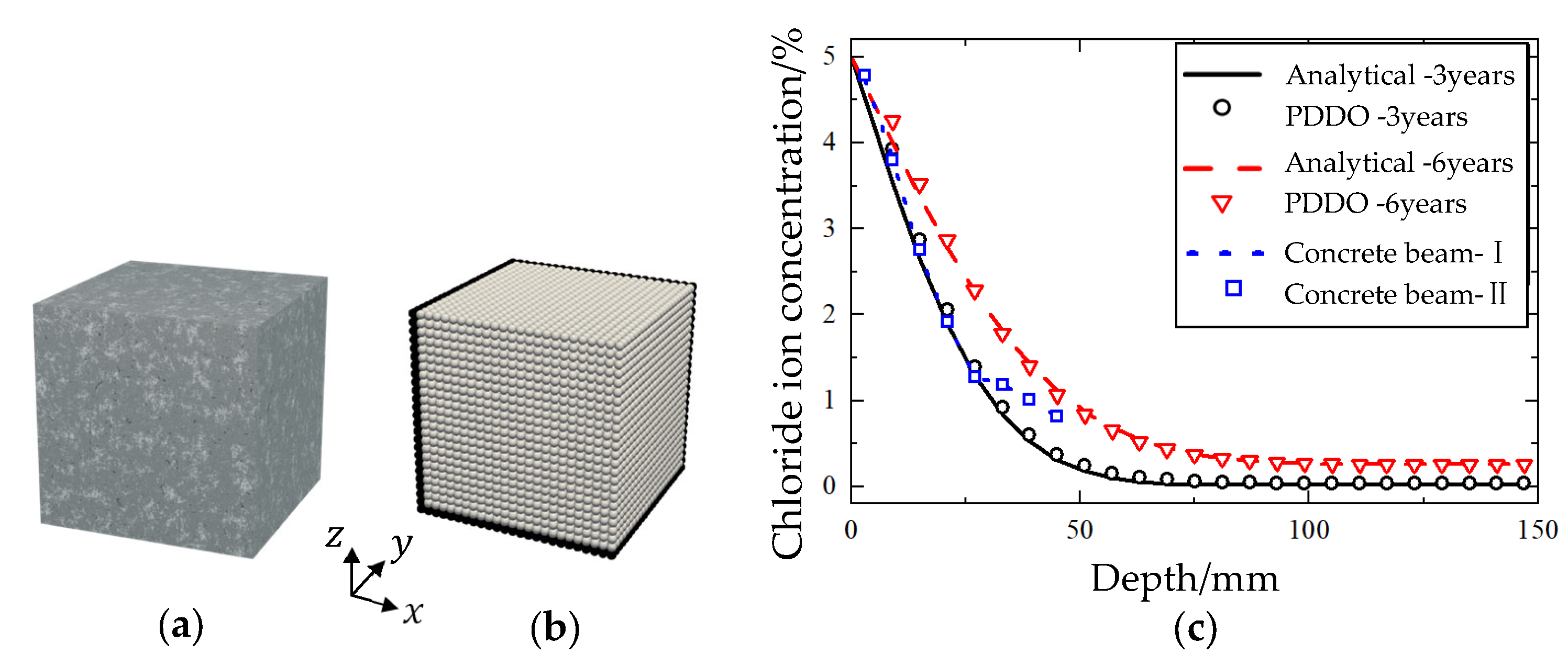
3. Validation of the PDDO Discrete Solution Format
3.1. Determination of the Horizon
3.2. Diffusion Analysis Under Ideal Conditions
4. Simulation of Macroscopic Chloride Ion Diffusion in Concrete
4.1. Influence of Time-Dependent Diffusion Coefficient
4.2. Influence of Complex Boundary Conditions
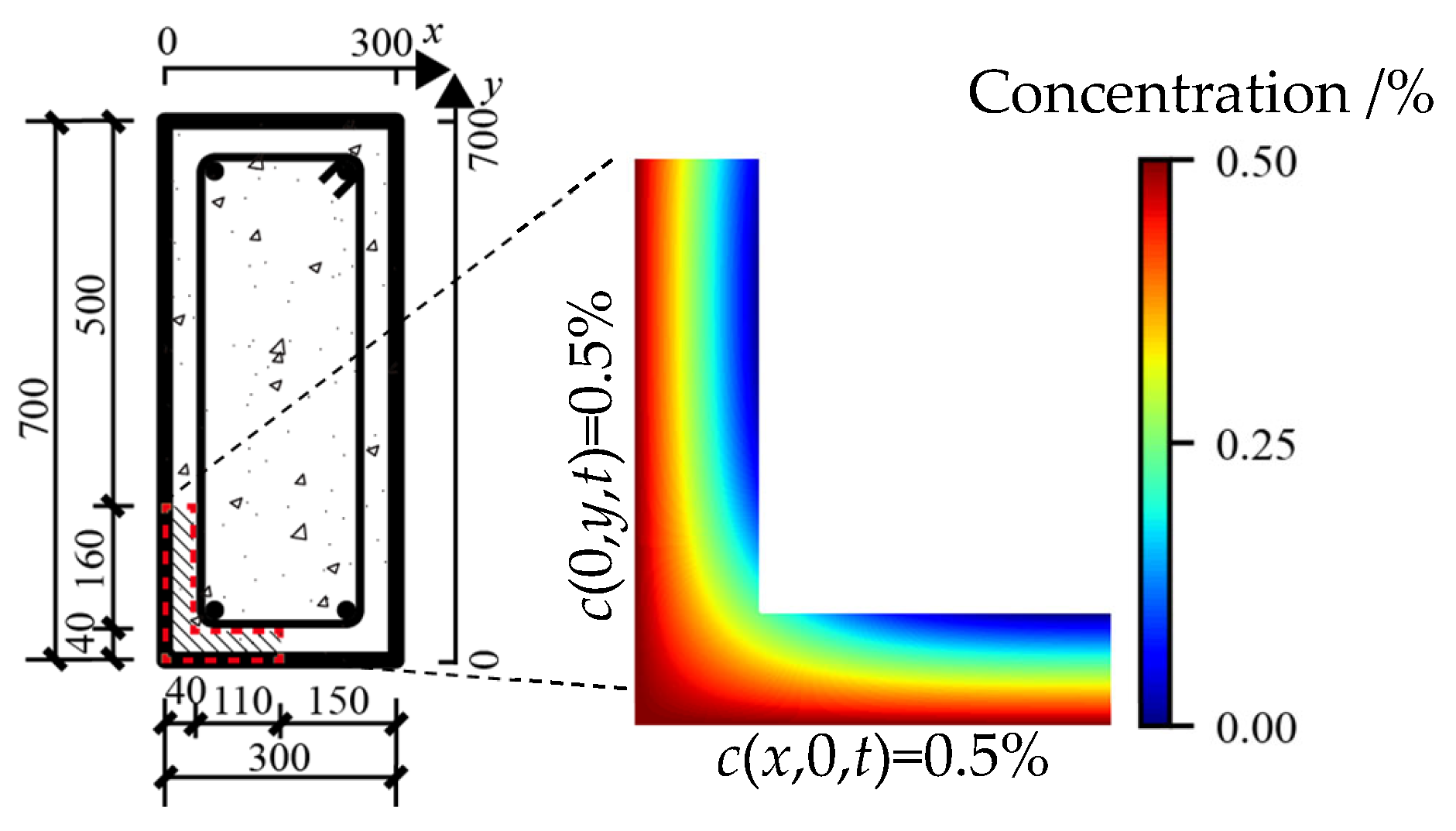
4.3. Influence of Shape of Members
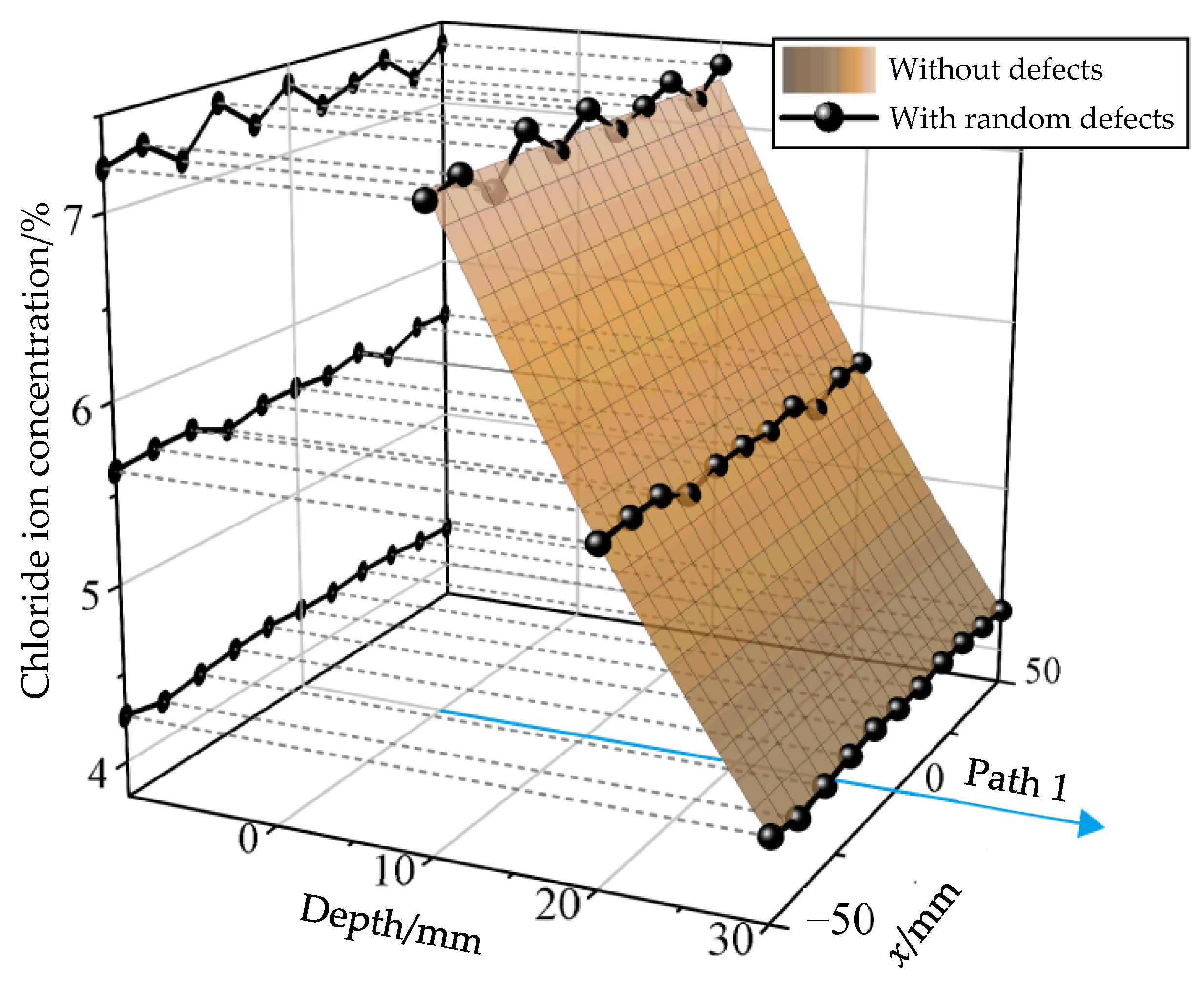
4.4. Influence of Defects
5. Simulation and Prediction of Macroscopic Chloride Ion Diffusion in Concrete Members Under Natural Environments
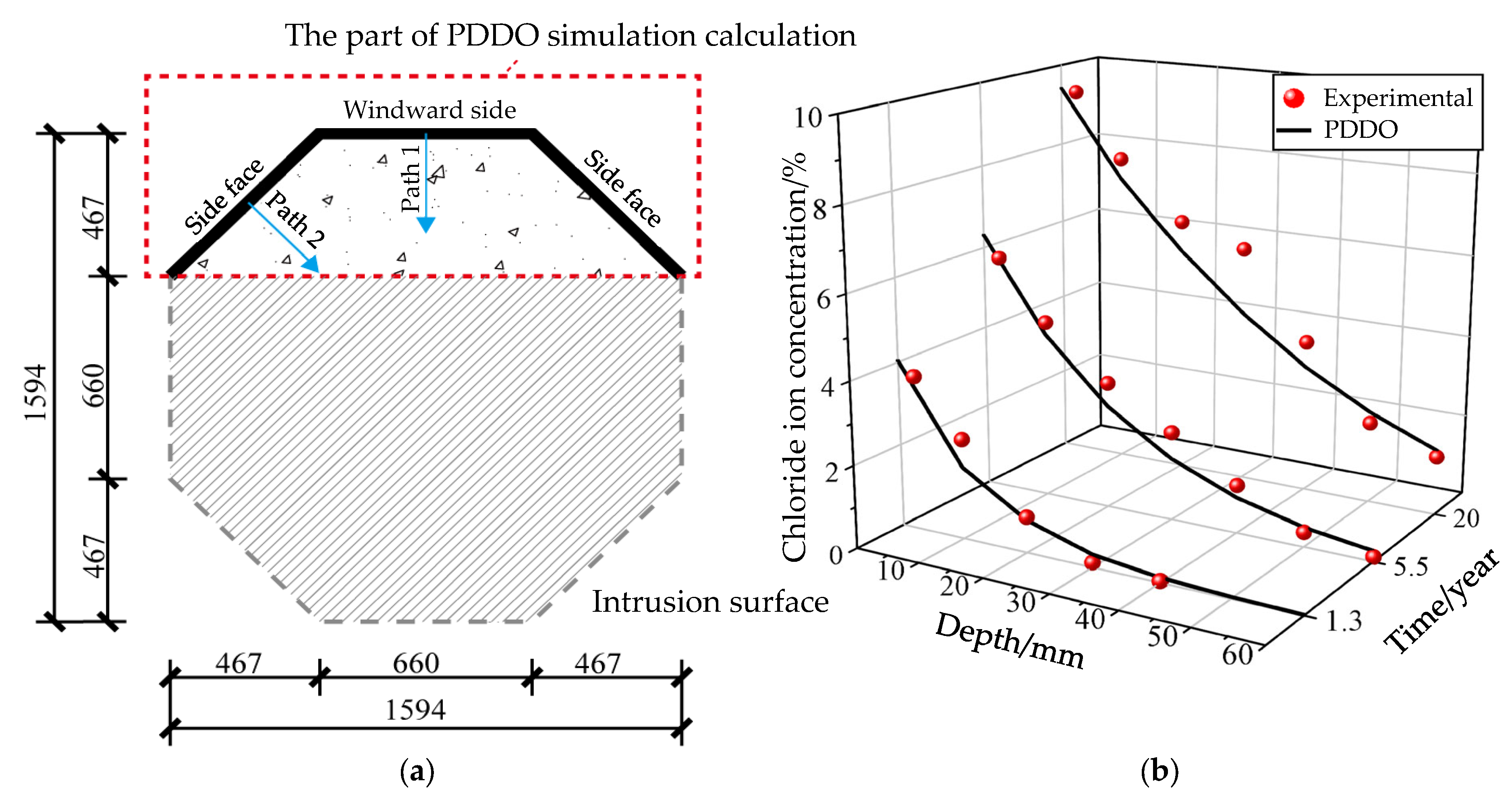
5.1. Simulation of Experiments
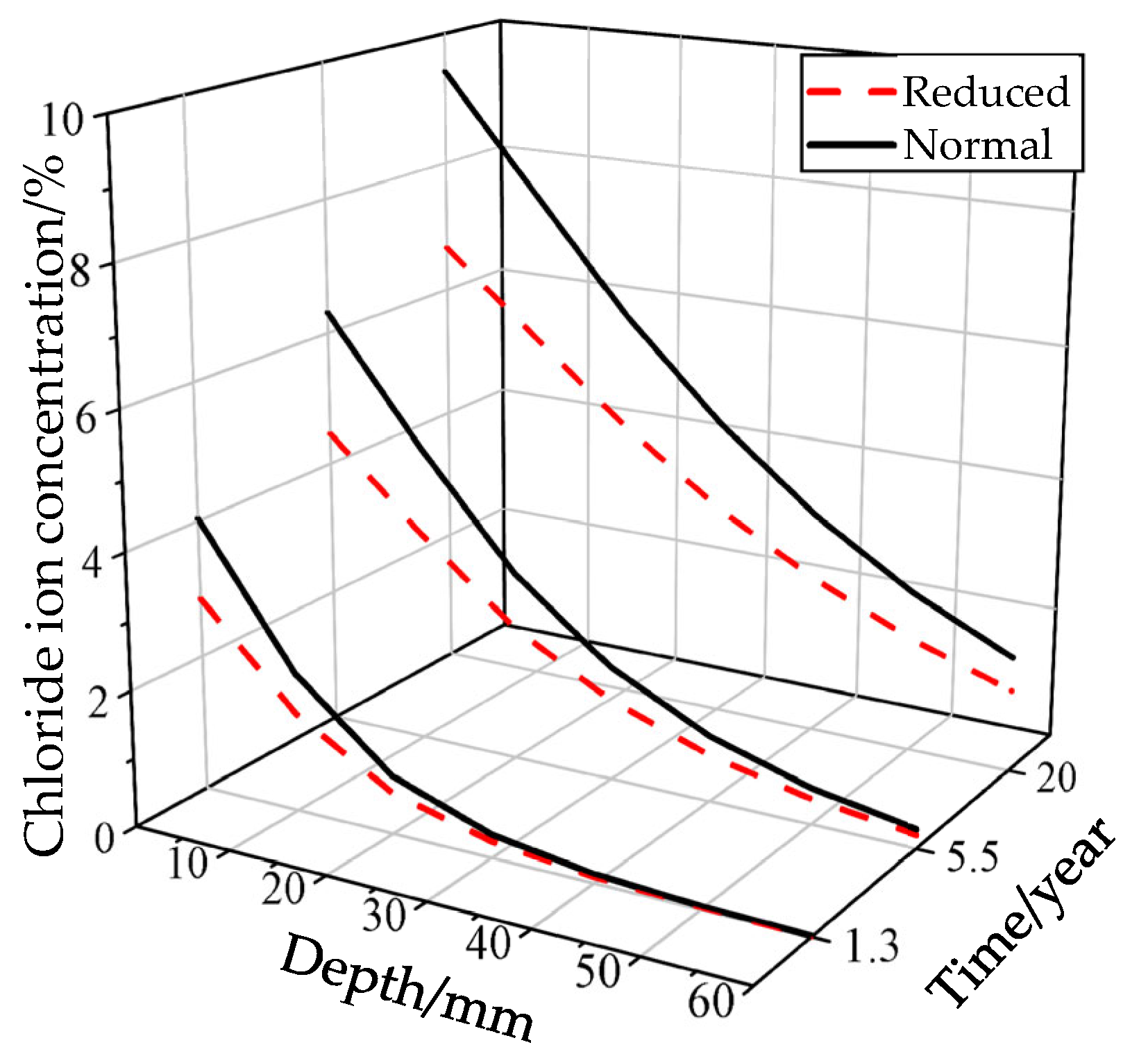
5.2. The Impact of Boundary Conditions
5.3. The Impact of Concrete Quality
6. Conclusions
- Comparisons with analytical or experimental results show the peridynamic model based on the PDDO can effectively simulate the macroscopic diffusion process of chloride ions in concrete. Moreover, the model can be conveniently applied to concrete members with complex geometries and diverse corrosion conditions, while these conditions would result in challenges for other grid-dependent methods;
- The peridynamic model based on the PDDO can effectively quantify the impacts of known and random defects in concrete without the need to re-discretize the solution domain, and it does not increase computational iterations or cumulative errors. This could be difficult for other methods based on the assumption of continuous fields;
- The simulation based on the PDDO suggests specific measures in maintenance strategy for concrete members, including an improvement of the apparent diffusion coefficient of concrete, an appropriate coating that separates adjacent chloride exposure surfaces, and the careful protection of corners in concrete members;
- It is quantitively demonstrated that the defects in concrete result in the peaks of chloride ion concentration shifting forward in the depth direction, and this trend becomes more pronounced with higher concentrations. Under such circumstances, the chloride ions will penetrate the concrete cover and reach the rebars faster. Therefore, to slow the erosion of rebars in existing concrete members and extend their service life, it is important to use good-quality concrete with fewer defects.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Miao, C.W.; Gu, X.L.; Zhang, W.P.; Guo, H.Y. State-of-the-art on performance evolution and control of concrete structures subjected to environmental actions. J. Build. Struct. 2019, 40, 1–10. [Google Scholar]
- Gu, X.L.; Zhang, W.P.; Jiang, C.; Huang, Q.H.; Xu, N. Environmental Actions of Concrete Structures; Science Press: Beijing, China, 2021. [Google Scholar]
- Fu, C.Q.; Tu, Y.J.; Jin, X.Y.; Fang, D.M.; Zhou, J.B. Experimental study on chloride ion transport in concrete under the combined action of load and environment. J. Hydraul. Eng. 2016, 47, 674–684. [Google Scholar]
- Sun, J.; Jin, Z.Q.; Chang, H.L.; Zhang, W. A review of chloride transport in concrete exposed to the marine atmosphere zone environment: Experiments and numerical models. J. Build. Eng. 2024, 84, 108591. [Google Scholar] [CrossRef]
- Zhao, Y.X.; Wang, C.K.; Jin, W.L.; Chen, X. Experimental analysis on time-dependent law of surface chloride ion concentration of concrete. J. Civ. Environ. Eng. 2010, 32, 8–13. [Google Scholar]
- Li, P.; Li, C.F.; Jia, C.H.; Li, D.W. A comparative study on chloride diffusion in concrete exposed to different marine environment conditions. J. Build. Eng. 2024, 94, 109845. [Google Scholar] [CrossRef]
- Yan, S.J.; Liu, Y.; Liang, Y.J. A space fractal derivative crack model for characterizing chloride ions superdiffusion in concrete in the marine tidal zone. Constr. Build. Mater. 2024, 450, 138585. [Google Scholar] [CrossRef]
- Xi, Y.; Bažant, Z.P. Modeling chloride penetration in saturated concrete. J. Mater. Civ. Eng. 1999, 11, 58–65. [Google Scholar] [CrossRef]
- Du, T.; Xiao, J.; Li, C.Y.; Gan, Y.D.; Jiang, X.L. Experimental and numerical study on the chloride ions penetration in recycled aggregate concrete. Constr. Build. Mater. 2024, 451, 138702. [Google Scholar] [CrossRef]
- Tang, L.; Utgenannt, P. Validation of Models and Test Methods for Assessment of Durability of Concrete Structures in the Road Environment; Betonginstitutet: Lund, Sweden, 2012. [Google Scholar]
- Zhang, W.P.; Zhang, Q.Z.; Gu, X.L.; Zhong, L.J.; Huang, Q.H. Effects of environmental conditions and stress level on chloride ion transport in concrete. J. Jiangsu Univ. Nat. Sci. Ed. 2013, 34, 101–106. [Google Scholar]
- Zhou, X.G.; Li, K.F.; Chen, Z.Y. Simulation analysis of chloride penetration in concrete with finite volume method. Eng. Mech. 2013, 30, 34–39. [Google Scholar]
- Engelund, S.; Mohr, L.; Edvardsen, C. General Guidelines for Durability Design and Redesign; CUR: Gouda, The Netherlands, 2000. [Google Scholar]
- Samson, E.; Marchand, J. Modeling the transport of ions in unsaturated cement-based materials. Comput. Struct. 2007, 85, 1740–1756. [Google Scholar] [CrossRef]
- Tian, Y.; Tian, Z.; Jin, N.; Jin, X.; Yu, W. A multiphase numerical simulation of chloride ions diffusion in concrete using electron microprobe analysis for characterizing properties of ITZ. Constr. Build. Mater. 2018, 178, 432–444. [Google Scholar] [CrossRef]
- Liu, Q.; Easterbrook, D.; Yang, J.; Li, L.-Y. A three-phase, multi-component ionic transport model for simulation of chloride penetration in concrete. Eng. Struct. 2015, 86, 122–133. [Google Scholar]
- Hu, H.Y.; Chen, J.S.; Hu, W. Error analysis of collocation method based on reproducing kernel approximation. Numer. Methods Partial Differ. Equ. 2011, 27, 554–580. [Google Scholar] [CrossRef]
- Du, Q.; Gunzburger, M.; Lehoucq, R.B.; Zhou, K. Analysis and approximation of nonlocal diffusion problems with volume constraints. SIAM Rev. 2012, 54, 667–696. [Google Scholar] [CrossRef]
- Du, Q.; Gunzburger, M.; Lehoucq, R.B.; Zhou, K. A nonlocal vector calculus, nonlocal volume-constrained problems, and nonlocal balance laws. Math. Models Methods Appl. Sci. 2013, 23, 493–540. [Google Scholar] [CrossRef]
- Yu, H.; Sun, Y. Bridging the gap between local and nonlocal numerical methods—A unified variational framework for non-ordinary state-based peridynamics. Comput. Methods Appl. Mech. Eng. 2021, 384, 113962. [Google Scholar]
- Silling, S.A.; Lehoucq, R.B. Peridynamic theory of solid mechanics. Adv. Appl. Mech. 2010, 44, 73–168. [Google Scholar]
- Li, W.J.; Guo, L.; Zhou, X.; Hong, J. Peridynamic simulation of chloride penetration into concrete and the influences of mesoscopic parameters. J. Southeast Univ. Nat. Sci. Ed. 2021, 51, 30–37. [Google Scholar]
- Chen, X.; Gu, X.; Liu, P.; Zhang, J.; Xia, X.; Zhang, Q. Peridynamic model for chloride diffusion–reaction in concrete reflecting mesostructure characteristic. Int. J. Fract. 2024, 245, 121–135. [Google Scholar]
- Madenci, E.; Barut, A.; Futch, M. Peridynamic differential operator and its applications. Comput. Methods Appl. Mech. Eng. 2016, 304, 408–451. [Google Scholar] [CrossRef]
- Madenci, E.; Barut, A.; Dorduncu, M. Peridynamic Differential Operator for Numerical Analysis; Springer International Publishing: Berlin, Germany, 2019. [Google Scholar]
- Gu, X.; Madenci, E.; Zhang, Q. Revisit of non-ordinary state-based peridynamics. Eng. Fract. Mech. 2018, 190, 31–52. [Google Scholar]
- Burman, E. Projection stabilisation of Lagrange multipliers for the imposition of constraints on interfaces and boundaries. Numer. Methods Partial Differ. Equ. 2014, 30, 567–592. [Google Scholar]
- Bažant, Z.P.; Luo, W.; Chau, V.T.; Bessa, M.A. Wave dispersion and basic concepts of peridynamics compared to classical nonlocal damage models. J. Appl. Mech. 2016, 83, 111004. [Google Scholar] [CrossRef]
- Bessa, M.A.; Foster, J.T.; Belytschko, T.; Liu, W.K. A meshfree unification: Reproducing kernel peridynamics. Comput. Mech. 2014, 53, 1251–1264. [Google Scholar] [CrossRef]
- Madenci, E.; Oterkus, E. Peridynamic Theory and Its Applications; Springer: New York, NY, USA, 2014. [Google Scholar]
- Li, D.; Wang, X.; Li, L.-Y. An analytical solution for chloride diffusion in concrete with considering binding effect. Ocean Eng. 2019, 191, 106549. [Google Scholar] [CrossRef]
- GB/T 50082-2024; Standard for Test Methods of Long-Term Performance and Durability of Concrete. Standards Press of China: Beijing, China, 2024.
- Silling, S.A.; Lehoucq, R.B. Convergence of peridynamics to classical elasticity theory. J. Elast. 2008, 93, 13–37. [Google Scholar] [CrossRef]
- Kim, J.; McCarter, W.J.; Suryanto, B.; Nanukuttan, S.; Basheer, P.A.M.; Chrisp, T.M. Chloride ingress into marine exposed concrete: A comparison of empirical- and physically-based models. Cem. Concr. Compos. 2016, 72, 133–145. [Google Scholar]
- Cheng, X.; Peng, J.; Cai, C.S.; Zhang, J. Experimental Study on Chloride Ion Diffusion in Concrete under Uniaxial and Biaxial Sustained Stress. Materials 2020, 13, 5717. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhao, M.; Song, L.; Yang, Y.; He, J. The Evolution of Concrete Microstructure and Chloride-Ion Diffusion Coefficient Under Cyclic Axial Compression. Int. J. Concr. Struct. Mater. 2025, 19, 56. [Google Scholar] [CrossRef]
- Wang, J.; Ng, P.-L.; Wang, W.; Du, J.; Song, J. Modelling chloride diffusion in concrete with influence of concrete stress state. J. Civ. Eng. Manag. 2017, 23, 955–965. [Google Scholar] [CrossRef]



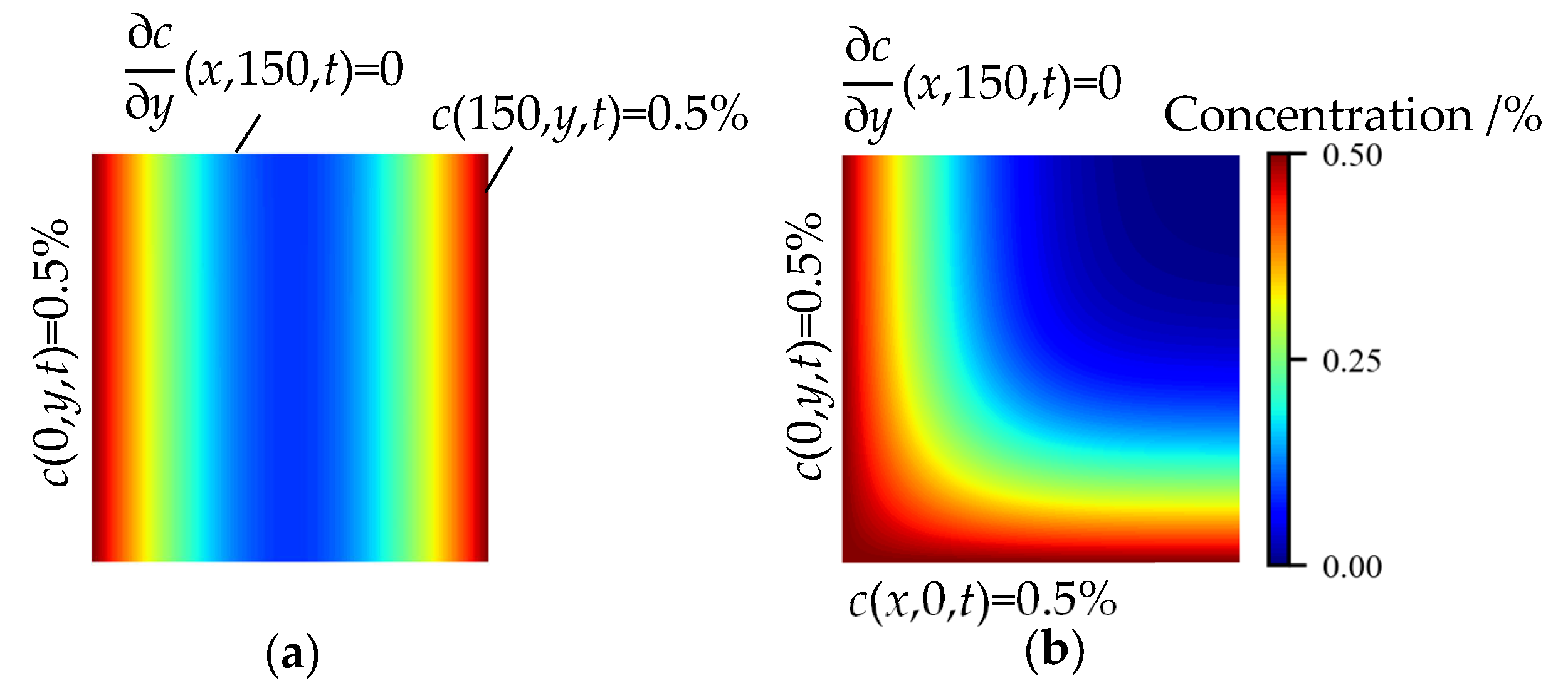

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, Z.; Peng, B.; Guo, W.; Sun, M. Simulation of Macroscopic Chloride Ion Diffusion in Concrete Members. Coatings 2025, 15, 1131. https://doi.org/10.3390/coatings15101131
Ji Z, Peng B, Guo W, Sun M. Simulation of Macroscopic Chloride Ion Diffusion in Concrete Members. Coatings. 2025; 15(10):1131. https://doi.org/10.3390/coatings15101131
Chicago/Turabian StyleJi, Zhaorui, Bin Peng, Wendong Guo, and Mingyang Sun. 2025. "Simulation of Macroscopic Chloride Ion Diffusion in Concrete Members" Coatings 15, no. 10: 1131. https://doi.org/10.3390/coatings15101131
APA StyleJi, Z., Peng, B., Guo, W., & Sun, M. (2025). Simulation of Macroscopic Chloride Ion Diffusion in Concrete Members. Coatings, 15(10), 1131. https://doi.org/10.3390/coatings15101131







