Prediction Model for Material Removal Rate of TC4 Titanium Alloy Processed by Vertical Vibratory Finishing
Abstract
1. Introduction
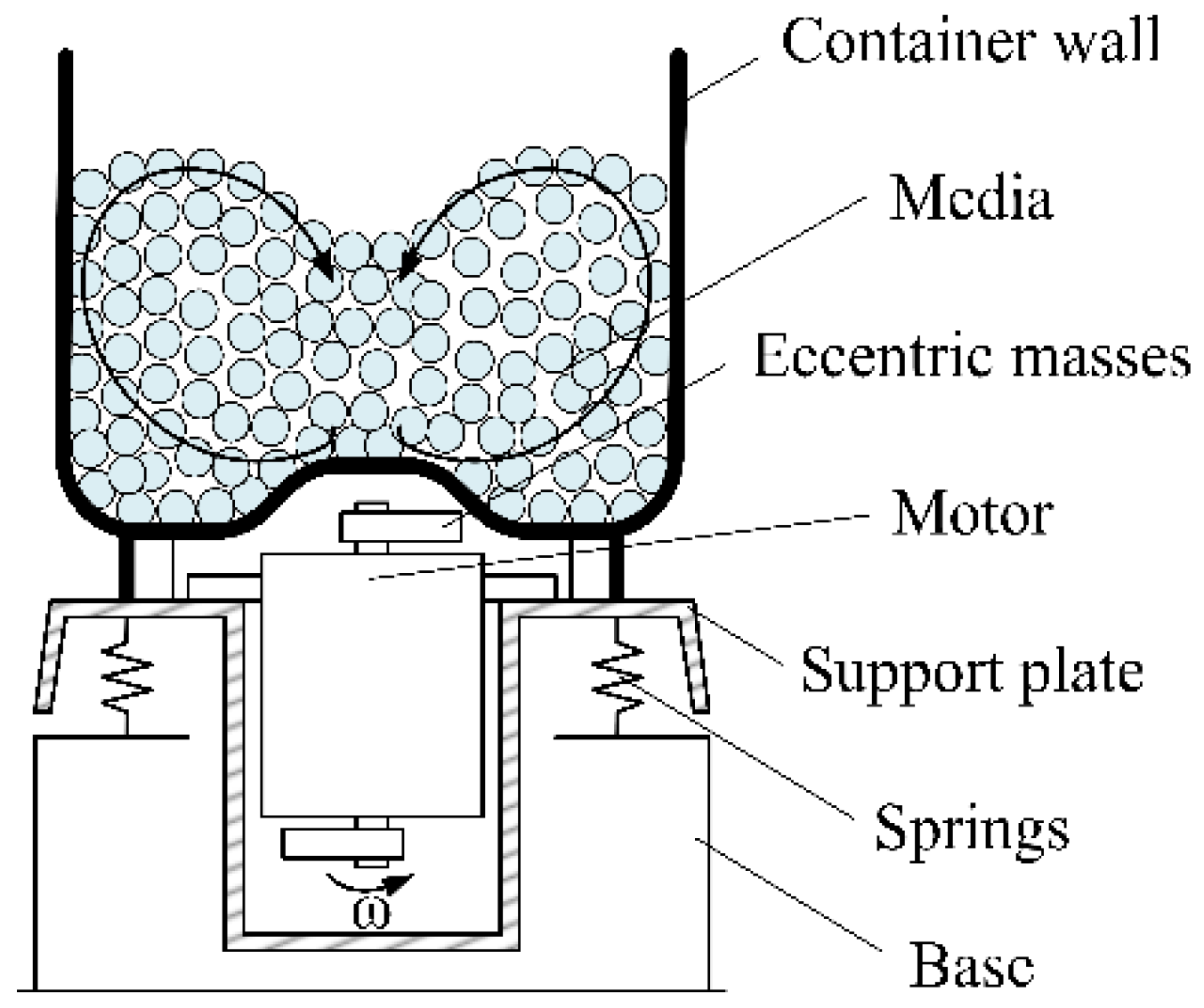
2. Principle of Vertical Vibratory Finishing
3. Experiment
3.1. Experimental Specimen and Processing Environment
3.2. Process Parameters and Experimental Design
4. The Prediction Model of MRR
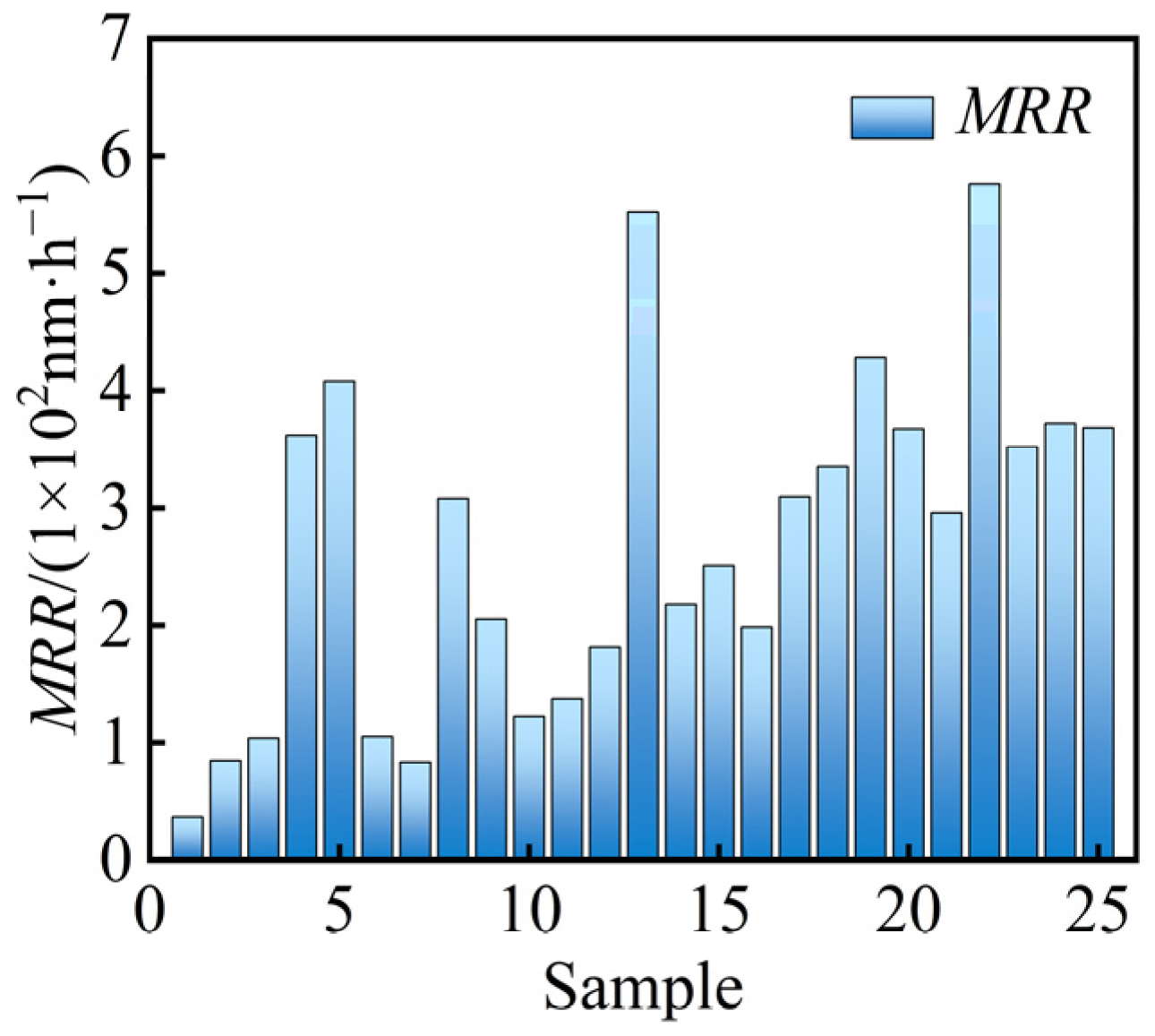
4.1. Experimental Results and Analysis
4.2. MMR Prediction Model Based on Mathematical Regression
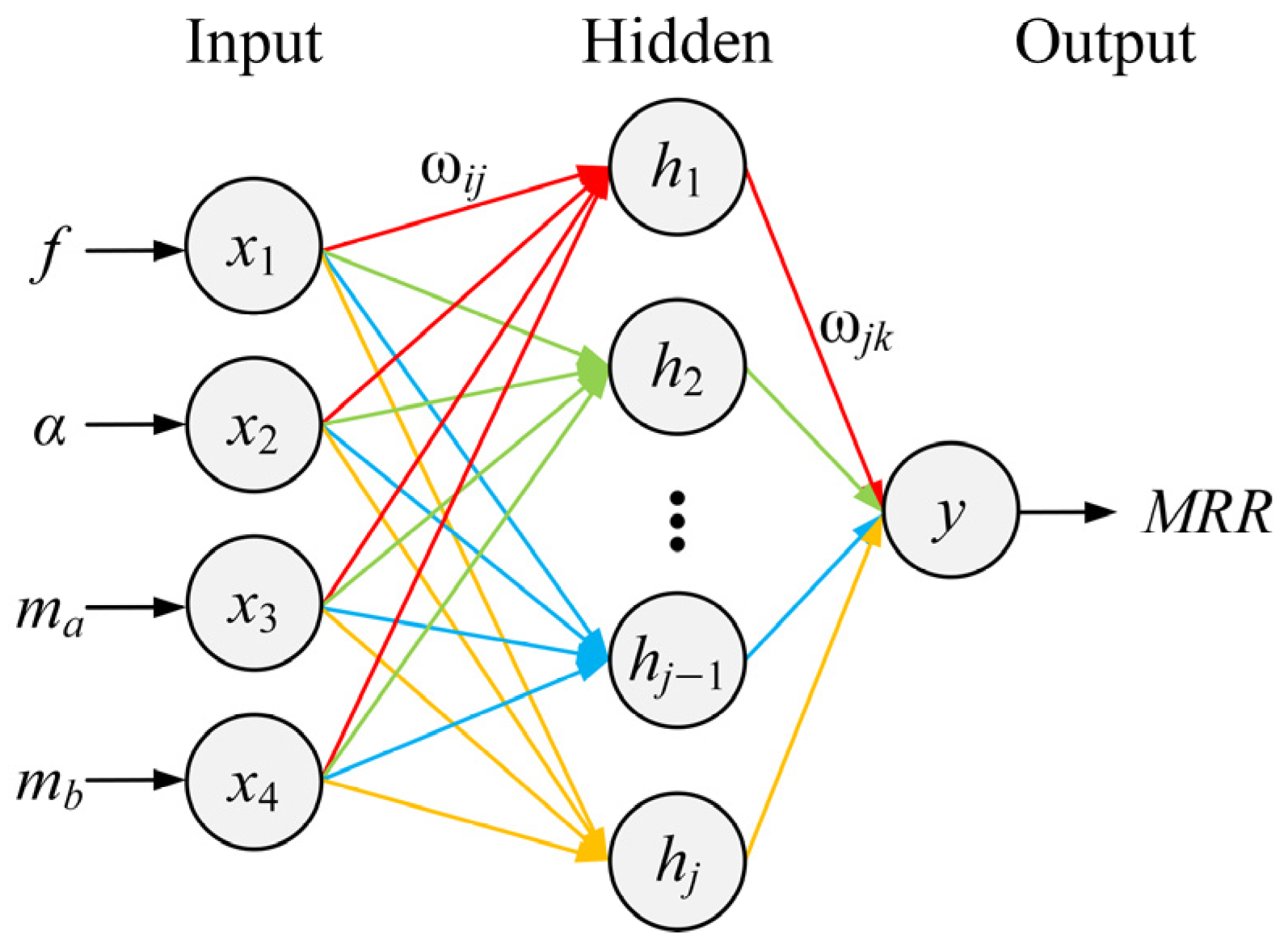
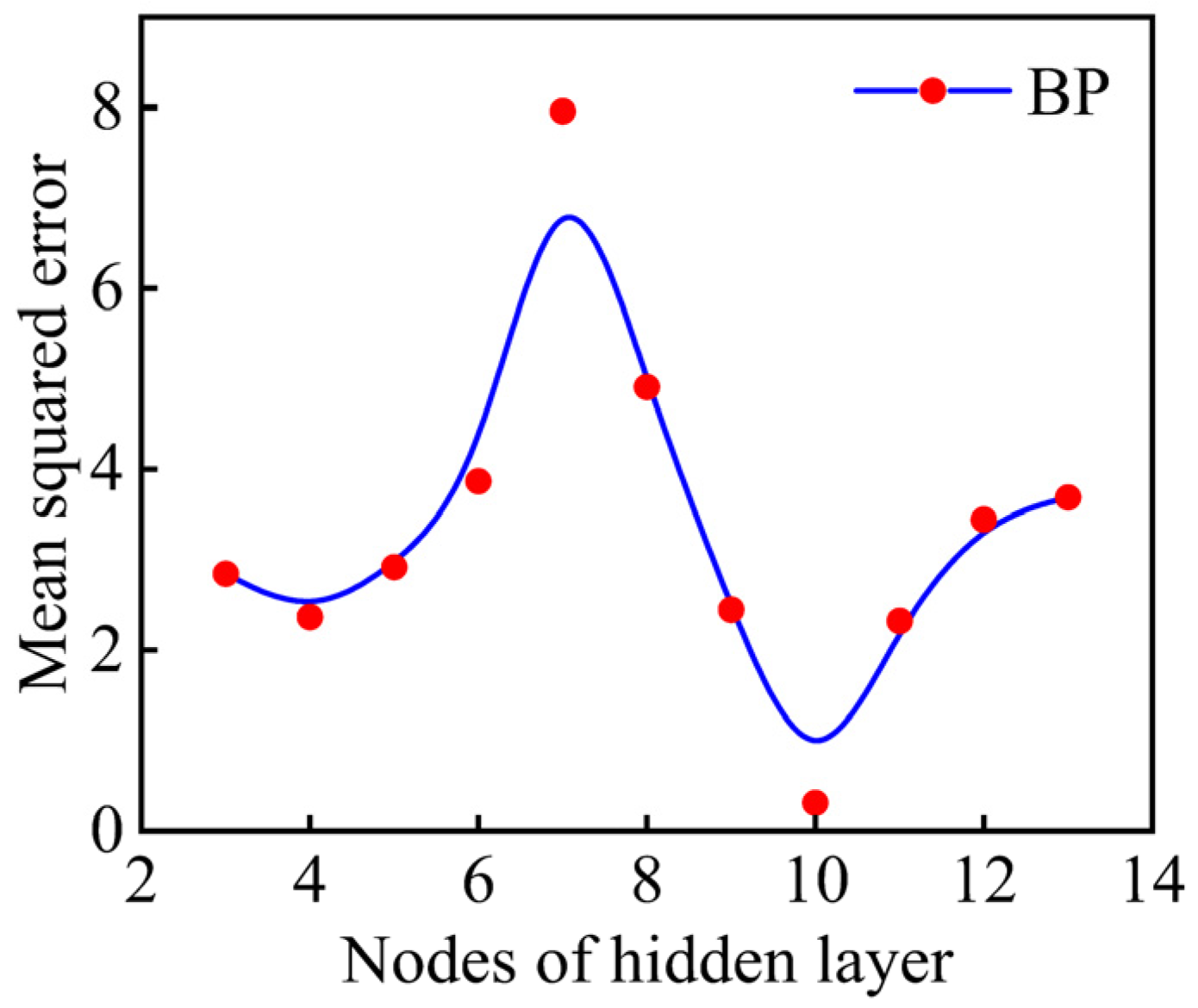
4.3. MMR Prediction Model Based on GABP Neural Network
4.4. Comparative Analysis of Prediction Models
5. Conclusions
- (1)
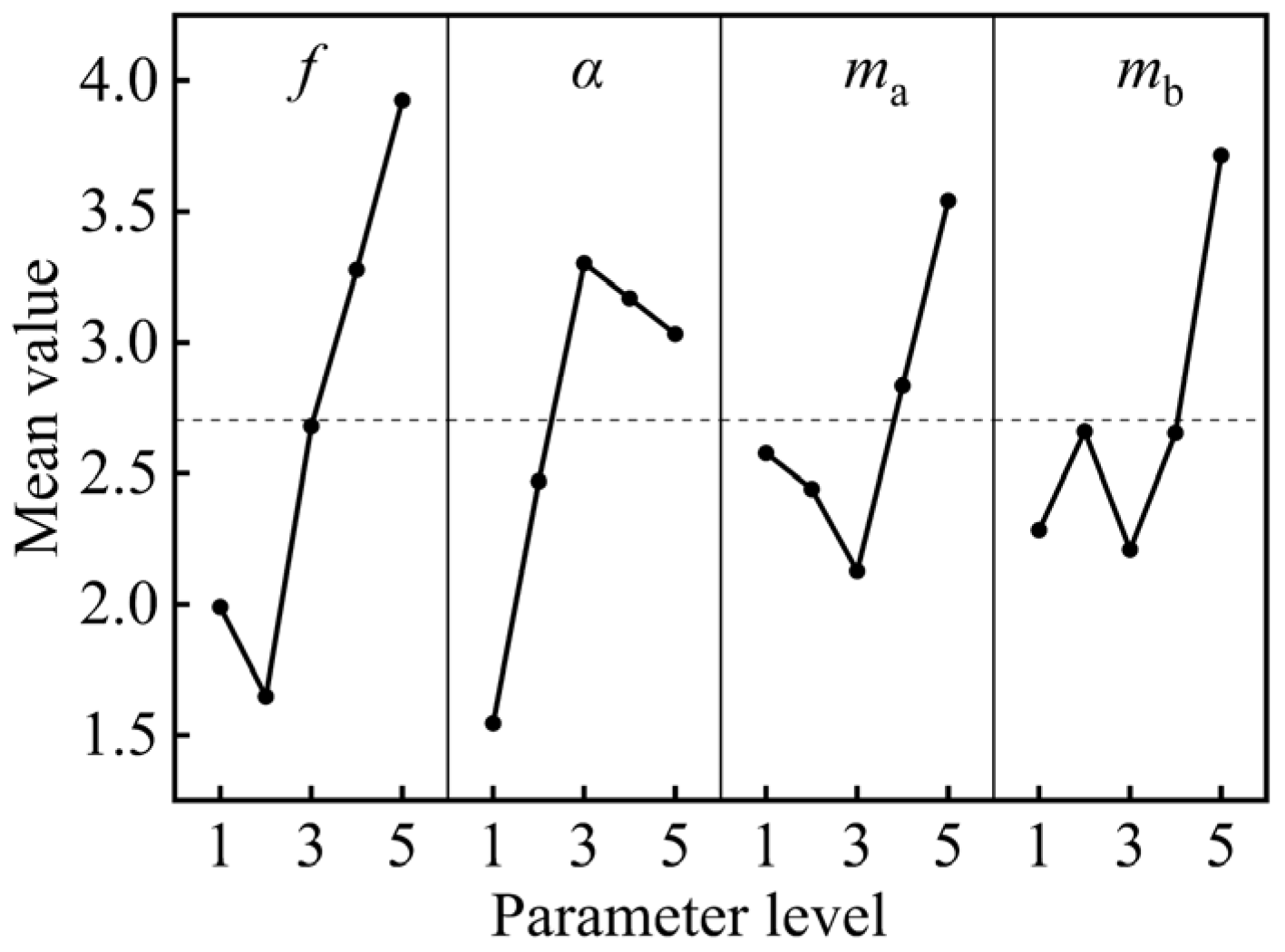
- Through theoretical analysis and variance analysis of orthogonal experiment results, it can be concluded that vibration frequency had the greatest influence on the MRR, and the corresponding F value was 3.372. This was followed by the eccentric block phase difference, corresponding to an F value of 2.033. The influence of the mass of the lower eccentric block and the mass of the upper eccentric block on the material removal rate were small and close, and the corresponding F values were 1.416 and 1.112, respectively.
- (2)
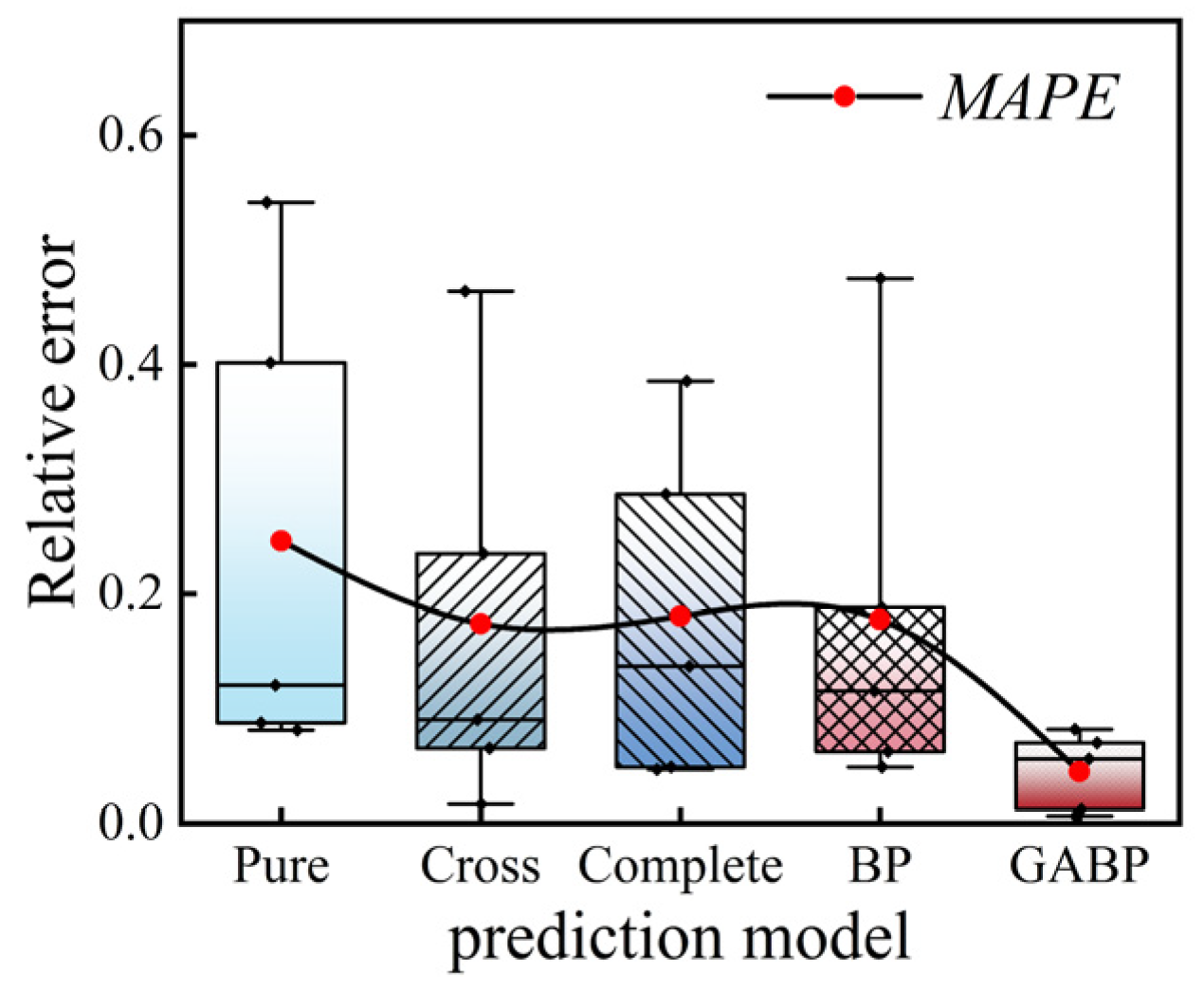
- The prediction model of the MRR was constructed according to the experimental data. In the mathematical regression model, the prediction accuracy of the cross-over model and the complete quadratic model for the verification set hovered around 82%. However, the maximum error reached 2.563. The prediction accuracy of the neural network attained 82.2%; meanwhile, its maximum error decreased to 1.039. Through comparison, it can be clearly seen that the neural network exhibited a superior prediction effect.
- (3)
- The neural network prediction model constructed by coupled GA reduced the error distribution range, reducing the MAPE from 0.178 to 0.045, and increasing the prediction accuracy to 95.5%. The constructed MRR prediction model had the best prediction performance and the highest accuracy, which verified the application of the GABP neural network in vertical vibratory finishing, and provided a new method for the control of process parameters in vibratory finishing.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bu, J.; Gao, Z.; Niu, J.; Cao, Y. Crack Failure Analysis of a Fan Stator Vane. Aeroengine 2021, 47, 91–95. [Google Scholar]
- Yang, S.; Wang, X.; Li, W. Research Status and Further Development of Vibratory Finishing Technology. J. Taiyuan Univ. Technol. 2017, 48, 385–392. [Google Scholar]
- Mediratta, R.; Ahluwalia, K.; Yeo, S. State-of-the-art on vibratory finishing in the aviation industry: An industrial and academic perspective. Int. J. Adv. Manuf. Technol. 2016, 85, 415–429. [Google Scholar] [CrossRef]
- Wong, B.; Maiumdar, K.; Ahluwalia, K.; Yeo, S. Effects of high frequency vibratory finishing of aerospace components. J. Mech. Sci. Technol. 2019, 33, 1809–1815. [Google Scholar] [CrossRef]
- Yang, S.; Li, W.; Chen, H. Surface Finishing Theory and New Technology; National Defense Industry Press: Beijing, China, 2011. [Google Scholar]
- Li, H.; Zhao, Z.; Zhen, C.; Ji, Z.; Zhao, G. Effect of Laser Shock Finishing on the Surface Quality of 2024 Aluminum Alloy with Milled Plane. Surf. Technol. 2023, 52, 388–396. [Google Scholar]
- Wang, J.; Shi, H.; Gao, Z.; Li, X.; Li, W. The Effect of the Physical Properties of the Granular Media on the Finishing of 7075 Aluminum Alloy. Surf. Technol. 2021, 50, 358–366. [Google Scholar]
- Hao, Z.; Li, W.; Li, X.; Wu, F.; Zhao, W. Effect of media parameters on contact forces in centrifugal barrel finishing. China Sci. 2017, 12, 2756–2760. [Google Scholar]
- Maciel, L.S.; Spelt, J.K. Influence of process parameters on average particle speeds in a vibratory finisher. Granul. Matter 2018, 20, 65. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, W.; Wang, S.; Liu, Z.; Morgan, M.; Liu, X. Dynamic modeling and trajectory measurement on vibratory finishing. Int. J. Adv. Manuf. Technol. 2020, 106, 253–263. [Google Scholar] [CrossRef]
- Tian, Y.; Zhong, Z.; Tan, S. Kinematic analysis and experimental investigation on vibratory finishing. Int. J. Adv. Manuf. Technol. 2016, 86, 3113–3121. [Google Scholar] [CrossRef]
- Hashemnia, K.; Mohajerani, A.; Spelt, J.K. Development of a laser displacement probe to measure particle impact velocities in vibrationally fluidized granular flows. Powder Technol. 2013, 235, 940–952. [Google Scholar] [CrossRef]
- Wang, S.; Timsit, R.S.; Spelt, J.K. Experimental investigation of vibratory finishing of aluminum. Wear 2000, 243, 147–156. [Google Scholar] [CrossRef]
- Domblesky, J.; Evans, R.; Cariapa, V. Material removal model for vibratory finishing. Int. J. Prod. Res. 2004, 42, 1029–1041. [Google Scholar] [CrossRef]
- Maciel, L.; Spelt, J. Bulk mass flow in a vibratory finisher: Mechanisms and effect of process parameters. Granul. Matter 2018, 20, 57–70. [Google Scholar] [CrossRef]
- Hashemnia, K.; Spelt, J.K. Particle impact velocities in a vibrationally fluidized granular flow: Measurements and discrete element predictions. Chem. Eng. Sci. 2014, 109, 123–135. [Google Scholar] [CrossRef]
- Tang, L.; Ren, L.; Feng, X.; Zhao, J.; Zhu, Q. Multi-objective Parameter Optimization and Regression Analysis of EDM for SiC/Al Functionally Graded Materials. Electromachining Mould. 2018, 2, 8–13+38. [Google Scholar]
- Naeim, N.; Aboueleaz, M.; Elkaseer, A. Experimental Investigation of Surface Roughness and Material Removal Rate in Wire EDM of Stainless Steel 304. Materials 2023, 16, 1022. [Google Scholar] [CrossRef]
- Song, Z.; Lv, B.; Ke, M.; Yang, Y.B.; Shao, Q.; Yuan, J.L.; Nguyen, D.N. Removal Rate Model of Deterministic Shear Thickening Polishing Material Based on BP Neural Network. Surf. Technol. 2020, 49, 320–325, 357. [Google Scholar]
- Peng, B.; Yan, X.; Du, J. Surface Quality Prediction Based on BP and RBF Neural Networks. Surf. Technol. 2020, 49, 324–328, 337. [Google Scholar]
- Yan, Y.; Li, Z.; Yu, X.; Zhao, J. Research on Measurement Method of Grinding Surface Roughness for Small Samples. Mach. Tool Hydraul. 2023, 51, 1–8. [Google Scholar]
- Tang, S.; Hakim, N.; Khaksar, W. Artificial Neural Network (ANN) Approach for Predicting Friction Coefficient of Roller Burnishing AL6061. Int. J. Mach. Learn. Comput. 2012, 2, 825–830. [Google Scholar] [CrossRef]
- Nguyen, T.; Nguyen, T.; Trinh, Q.; Le, X.B.; Pham, L.H.; Le, X.H. Artificial neural network-based optimization of operating parameters for minimum quantity lubrication-assisted burnishing process in terms of surface characteristics. Neural Comput. Appl. 2022, 34, 7005–7031. [Google Scholar] [CrossRef]
- Kanovic, Z.; Vukelic, D.; el Simunovic, K. The Modelling of Surface Roughness after the Ball Burnishing Process with a High-Stiffness Tool by Using Regression Analysis, Artificial Neural Networks, and Support Vector Regression. Metals 2022, 12, 320. [Google Scholar] [CrossRef]
- Harlal, S.; Alakesh, M. Simulation of surface generated during abrasive flow finishing of Al/SiC_p-MMC using neural networks. Int. J. Adv. Manuf. Technol. 2012, 61, 1263–1268. [Google Scholar]
- Xu, L.; Chen, Y.; Han, B.; Chen, H.; Liu, W. Research on Surface Roughness Prediction Method of Magnetic Abrasive Finishing Based on Evolutionary Neural Network. Surf. Technol. 2021, 50, 94–100, 118. [Google Scholar]
- Ahamd, S.; Singari, R.; Mishra, R. Modelling and optimisation of magnetic abrasive finishing process based on a non-orthogonal array with ANN-GA approach. Trans. Inst. Met. Finish. Int. J. Surf. Eng. Coat. 2020, 98, 186–198. [Google Scholar] [CrossRef]
- Ahamd, S.; Singari, R.; Mishra, R. Tri-objective constrained optimization of pulsating DC sourced magnetic abrasive finishing process parameters using artificial neural network and genetic algorithm. Mater. Manuf. Process. 2021, 36, 843–857. [Google Scholar] [CrossRef]
- Wang, J.; Li, X.; Li, W.; Yang, S. Research of horizontal vibratory finishing for aero-engine blade movement characteristics and action behavior of media. Int. J. Adv. Manuf. Technol. 2023, 126, 2065–2081. [Google Scholar] [CrossRef]
- Wang, N.; Yang, S.; Cao, B.; Zhao, K. Influence of Different Machining Parameters of the Spindle Type Barrel Finishing on Surface Finishing Effect. Mach. Des. Manuf. 2020, 5, 206–209+213. [Google Scholar]
- Huai, C.; Huang, T.; Jia, X. Optimization of Processing Parameters in Grinding and Polishing Coupling Neural Networks with Genetic Algorithms. Mech. Sci. Technol. Aerosp. Eng. 2021, 40, 1025–1030. [Google Scholar]
- Liu, S.; Yi, J.; Xie, H. Research on quality prediction of surface polishing on die and mould parts based on improved BP algorithm. Mould Ind. 2023, 49, 9–19. [Google Scholar]
- Wang, Z.; Qin, K.; Ying, D. Prediction of heavy duty diesal vehicle emission based on GA-BP neural network with double hidden layer. J. Hefei Univ. Technol. (Nat. Sci.) 2019, 42, 735–740. [Google Scholar]
- Pang, C.; Jiang, Y.; Wu, T.; Liao, C.; Ma, W. Effect of Neural Network Parameters on Earthquake Type Recognition. Sci. Technol. Eng. 2022, 22, 7765–7772. [Google Scholar]



| Experimental Conditions | Parameters |
|---|---|
| Specimen | TC4 |
| Specimen size/mm | 40 × 40 × 5 |
| Abrasive | SiC |
| Abrasive size/mm | 4 × 4 |
| Vibration frequency/Hz | 15, 17.5, 20, 22.5, 25 |
| Block phase/° | 0, 30, 60, 90, 120 |
| Upper eccentric block mass/kg | 0.9, 1.15, 1.4, 1.65, 1.9 |
| Lower eccentric block mass/kg | 0.9, 1.15, 1.4, 1.65, 1.9 |
| Finishing time/h | 4 |
| Level | f (Hz) | α (°) | ma (kg) | mb (kg) |
|---|---|---|---|---|
| 1 | 15 | 0 | 0.9 | 0.9 |
| 2 | 17.5 | 30 | 1.15 | 1.15 |
| 3 | 20 | 60 | 1.4 | 1.4 |
| 4 | 22.5 | 90 | 1.65 | 1.65 |
| 5 | 25 | 120 | 1.9 | 1.9 |
| Test Number | f (Hz) | α (°) | ma (kg) | mb (kg) | MRR (1 × 102 nm/h) |
|---|---|---|---|---|---|
| 1 | 15 | 0 | 0.9 | 0.9 | 0.367 |
| 2 | 15 | 30 | 1.15 | 1.15 | 0.847 |
| 3 | 15 | 60 | 1.4 | 1.4 | 1.038 |
| 4 | 15 | 90 | 1.65 | 1.65 | 3.617 |
| 5 | 15 | 120 | 1.9 | 1.9 | 4.080 |
| 6 | 17.5 | 0 | 1.15 | 1.4 | 1.052 |
| 7 | 17.5 | 30 | 1.4 | 1.65 | 0.833 |
| 8 | 17.5 | 60 | 1.65 | 1.9 | 3.081 |
| 9 | 17.5 | 90 | 1.9 | 0.9 | 2.053 |
| 10 | 17.5 | 120 | 0.9 | 1.15 | 1.226 |
| 11 | 20 | 0 | 1.4 | 1.9 | 1.374 |
| 12 | 20 | 30 | 1.65 | 0.9 | 1.816 |
| 13 | 20 | 60 | 1.9 | 1.15 | 5.522 |
| 14 | 20 | 90 | 0.9 | 1.4 | 2.179 |
| 15 | 20 | 120 | 1.15 | 1.65 | 2.509 |
| 16 | 22.5 | 0 | 1.65 | 1.15 | 1.983 |
| 17 | 22.5 | 30 | 1.9 | 1.4 | 3.096 |
| 18 | 22.5 | 60 | 0.9 | 1.65 | 3.353 |
| 19 | 22.5 | 90 | 1.15 | 1.9 | 4.282 |
| 20 | 22.5 | 120 | 1.4 | 0.9 | 3.671 |
| 21 | 25 | 0 | 1.9 | 1.65 | 2.957 |
| 22 | 25 | 30 | 0.9 | 1.9 | 5.759 |
| 23 | 25 | 60 | 1.15 | 0.9 | 3.515 |
| 24 | 25 | 90 | 1.4 | 1.15 | 3.720 |
| 25 | 25 | 120 | 1.65 | 1.4 | 3.682 |
| ω(1) | b(1) | ω(2)T | b(2) | |||
|---|---|---|---|---|---|---|
| 38.03097 | 88.42798 | 9.214891 | 84.56396 | −85.586 | 29.3833 | −3.0525 |
| −21.9475 | 16.34671 | −55.5134 | 61.80692 | 101.7267 | 141.019 | |
| 167.2091 | −45.3575 | −68.1891 | 181.7955 | 41.29363 | 117.1958 | |
| −57.8797 | −55.3923 | −83.2141 | −185.713 | 15.48892 | 32.84436 | |
| −17.7363 | 40.80021 | −76.156 | 29.88119 | 144.0186 | 14.56718 | |
| 10.5136 | −100.326 | −29.97 | 32.25797 | −123.869 | 85.8492 | |
| −125.215 | −117.92 | −55.6022 | −93.7621 | −23.9777 | 44.31186 | |
| 112.4577 | −102.606 | 52.85801 | 66.37956 | 10.15133 | 101.9355 | |
| −138.522 | −7.06086 | −28.1511 | −120.609 | −118.772 | −94.0888 | |
| 39.12697 | −53.8944 | 61.45187 | −92.0853 | 172.9724 | −79.3458 | |
| Validation Set | Pure Quadratic | Interaction | Quadratic | BP | GABP | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Value | Error | Value | Error | Value | Error | Value | Error | Value | Error | ||
| Sample Error | 1 | 1.600 | 0.562 | 1.282 | 0.244 | 1.336 | 0.298 | 1.531 | 0.493 | 1.123 | 0.085 |
| 2 | 3.452 | 0.371 | 2.803 | 0.278 | 2.937 | 0.144 | 3.232 | 0.151 | 3.118 | 0.037 | |
| 3 | 3.305 | 2.217 | 2.959 | 2.563 | 3.394 | 2.128 | 4.483 | 1.039 | 5.212 | 0.31 | |
| 4 | 3.625 | 0.272 | 3.409 | 0.056 | 3.812 | 0.459 | 3.562 | 0.209 | 3.118 | 0.235 | |
| 5 | 3.823 | 0.308 | 3.745 | 0.230 | 3.687 | 0.172 | 3.920 | 0.405 | 3.537 | 0.022 | |
| Integral Error | MAE | 0.746 | 0.674 | 0.640 | 0.459 | 0.138 | |||||
| MSE | 1.108 | 1.352 | 0.976 | 0.311 | 0.032 | ||||||
| RMSE | 1.052 | 1.163 | 0.988 | 0.557 | 0.179 | ||||||
| MAPE | 0.246 | 0.174 | 0.181 | 0.178 | 0.045 | ||||||
| Accuracy | 75.4% | 82.6% | 81.9% | 82.2% | 95.5% | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shan, K.; Zhang, L.; Tan, B.; Zhang, Y.; Li, W.; Li, X.; Wen, X. Prediction Model for Material Removal Rate of TC4 Titanium Alloy Processed by Vertical Vibratory Finishing. Coatings 2025, 15, 286. https://doi.org/10.3390/coatings15030286
Shan K, Zhang L, Tan B, Zhang Y, Li W, Li X, Wen X. Prediction Model for Material Removal Rate of TC4 Titanium Alloy Processed by Vertical Vibratory Finishing. Coatings. 2025; 15(3):286. https://doi.org/10.3390/coatings15030286
Chicago/Turabian StyleShan, Kun, Liaoyuan Zhang, Bo Tan, Yashuang Zhang, Wenhui Li, Xiuhong Li, and Xuejie Wen. 2025. "Prediction Model for Material Removal Rate of TC4 Titanium Alloy Processed by Vertical Vibratory Finishing" Coatings 15, no. 3: 286. https://doi.org/10.3390/coatings15030286
APA StyleShan, K., Zhang, L., Tan, B., Zhang, Y., Li, W., Li, X., & Wen, X. (2025). Prediction Model for Material Removal Rate of TC4 Titanium Alloy Processed by Vertical Vibratory Finishing. Coatings, 15(3), 286. https://doi.org/10.3390/coatings15030286





