Temperature and Depth Sensor Based on Fiber Bragg Gratings with Temperature-Compensated Structure in Marine Environment
Abstract
1. Introduction
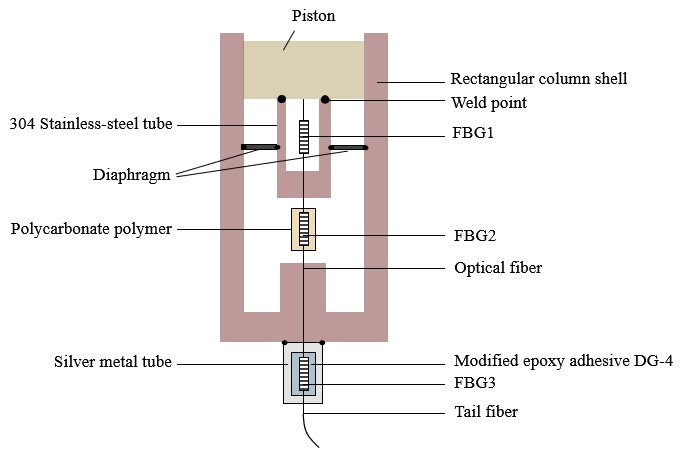
2. Structure Design and Fabrication
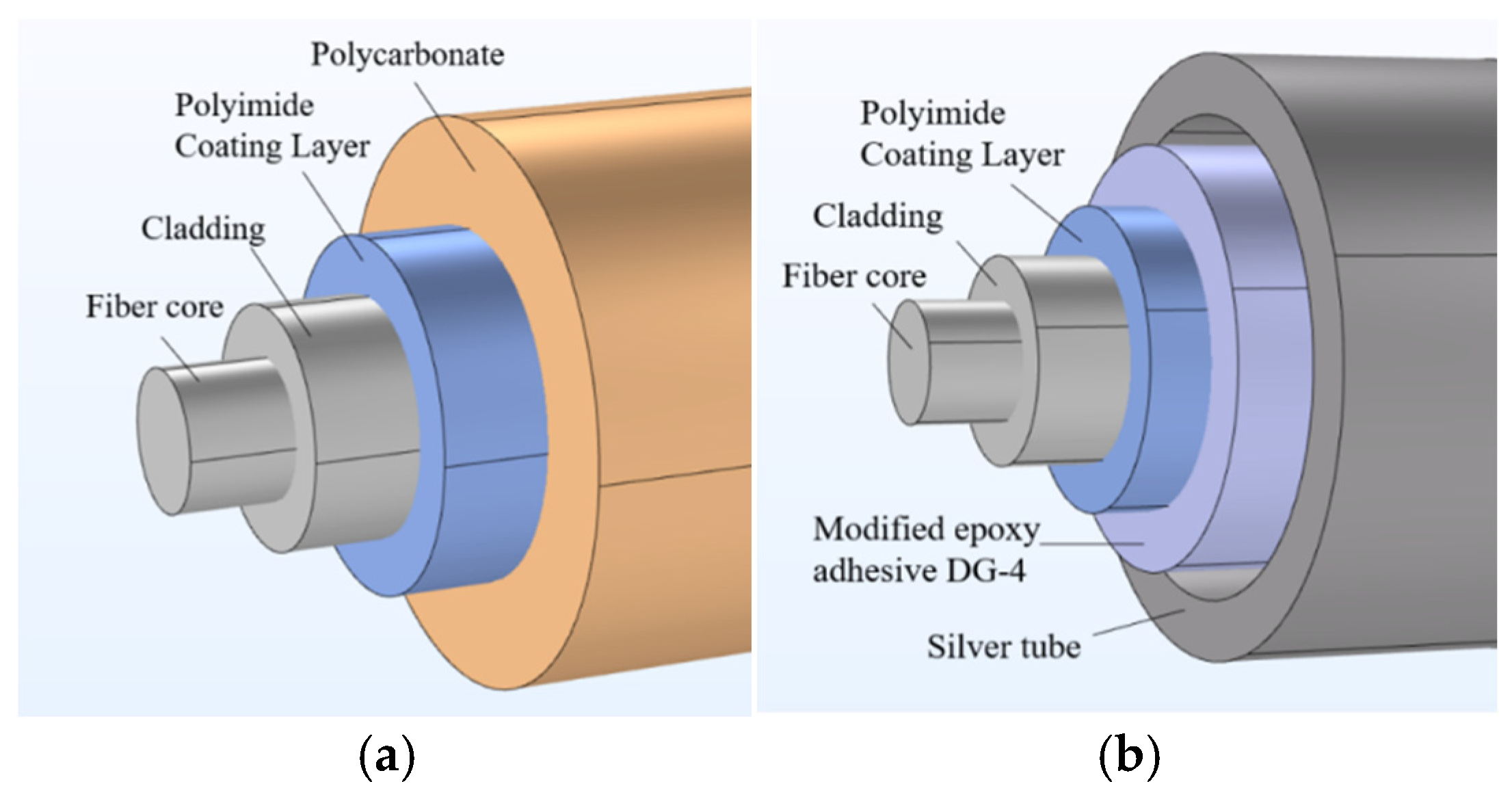
2.1. Temperature Sensing Principle
2.2. Temperature Compensation Principle
2.3. Pressure Sensing Principle
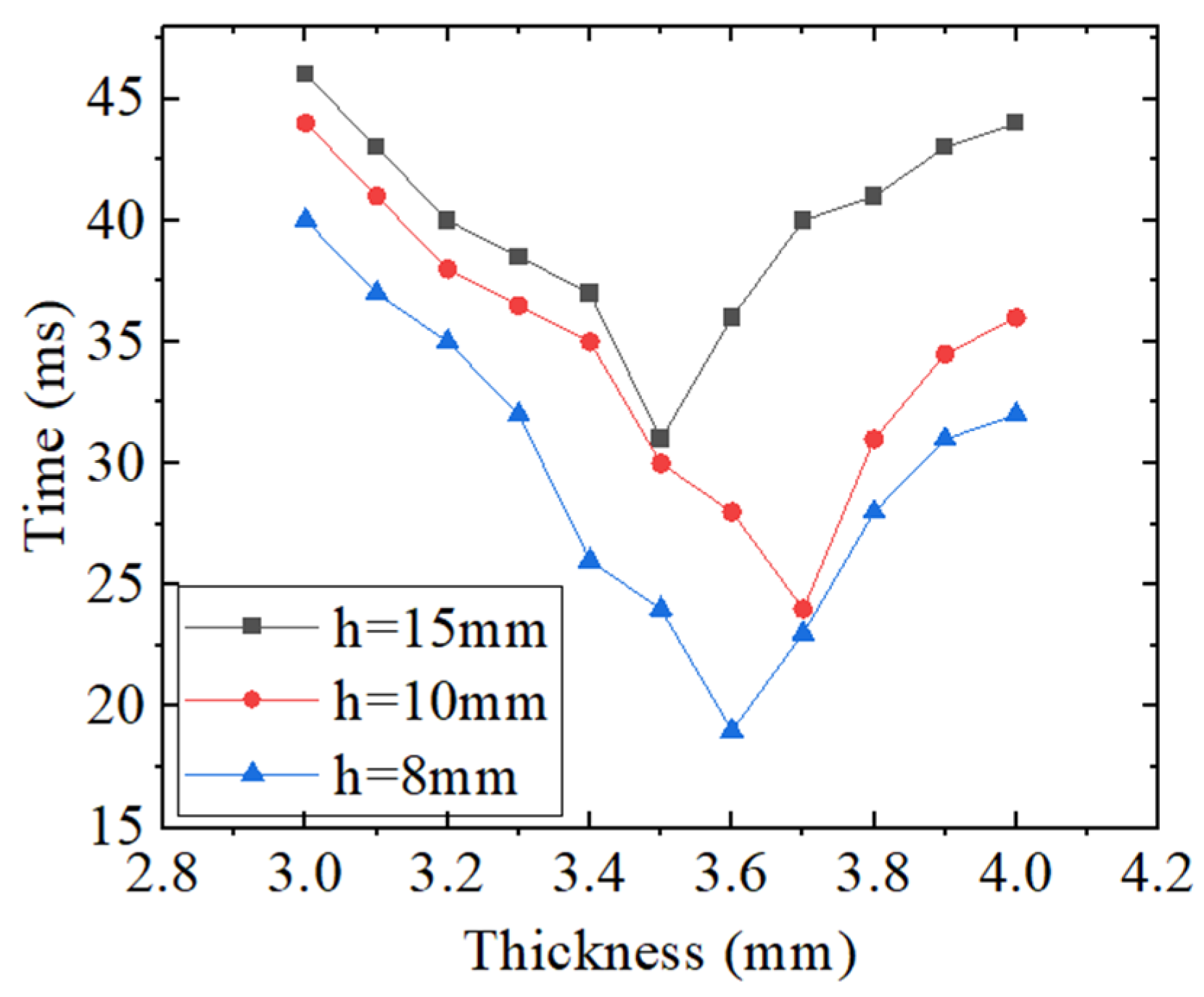
3. Results and Discussion
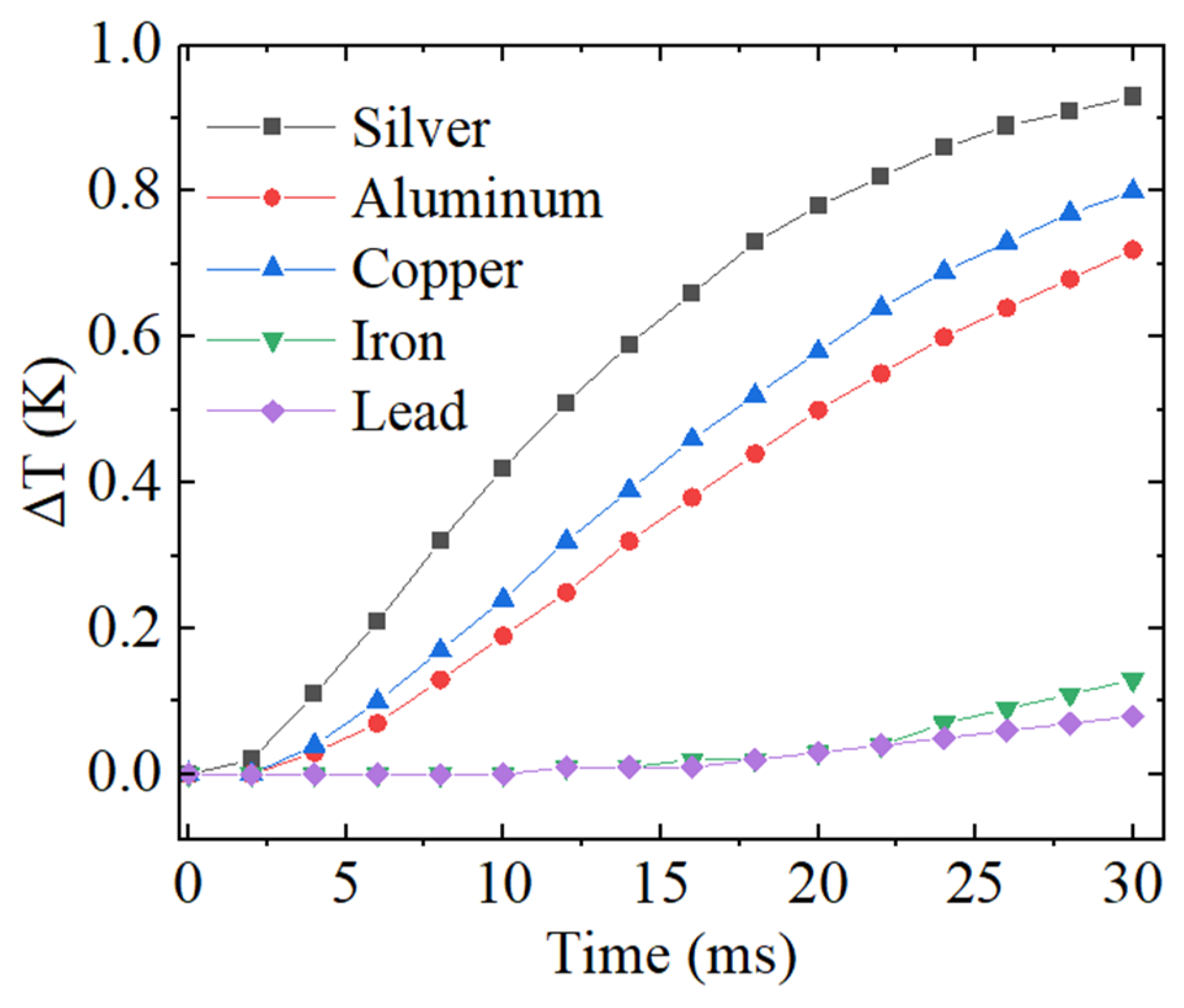
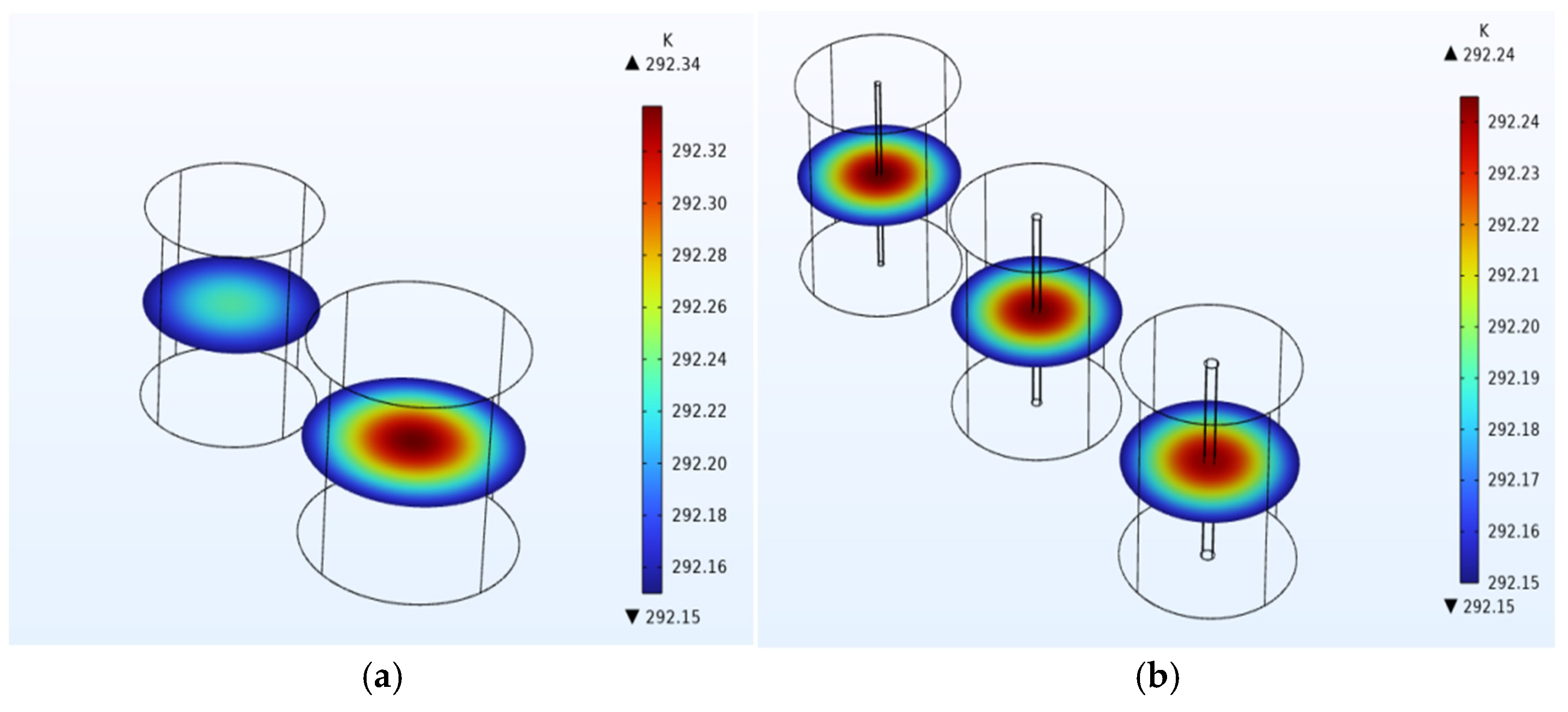
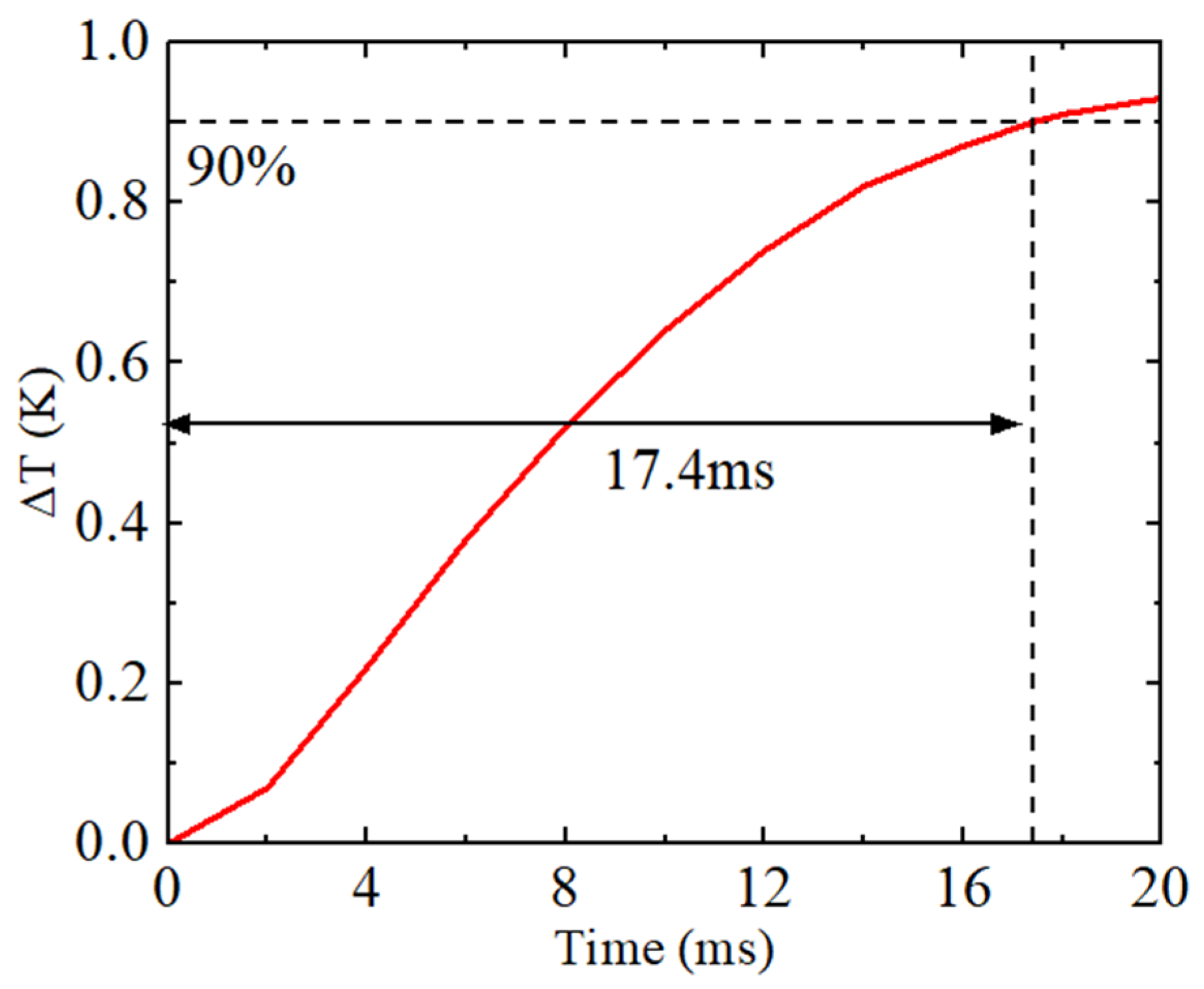
3.1. Simulation Analysis of the Temperature Sensing Structure
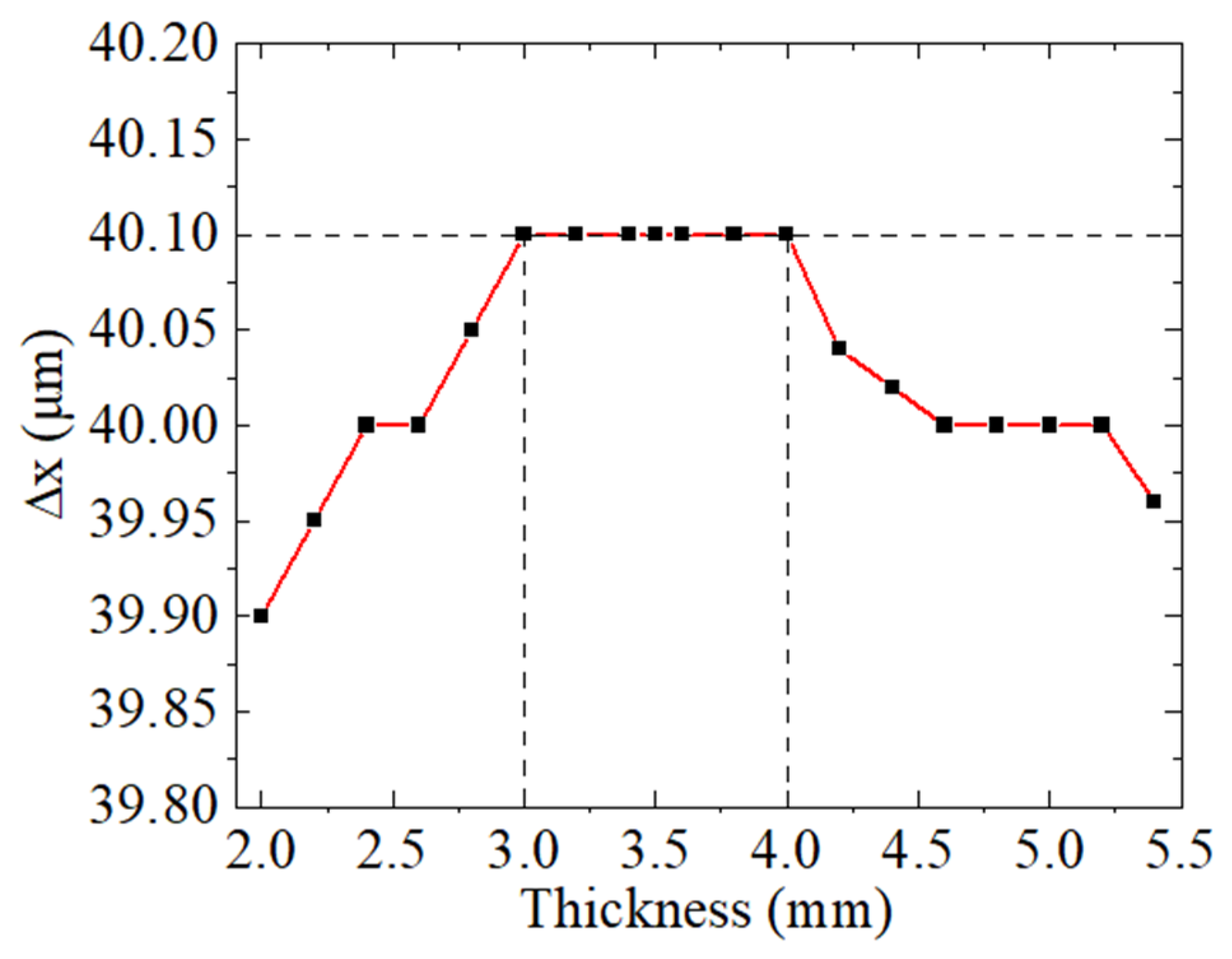
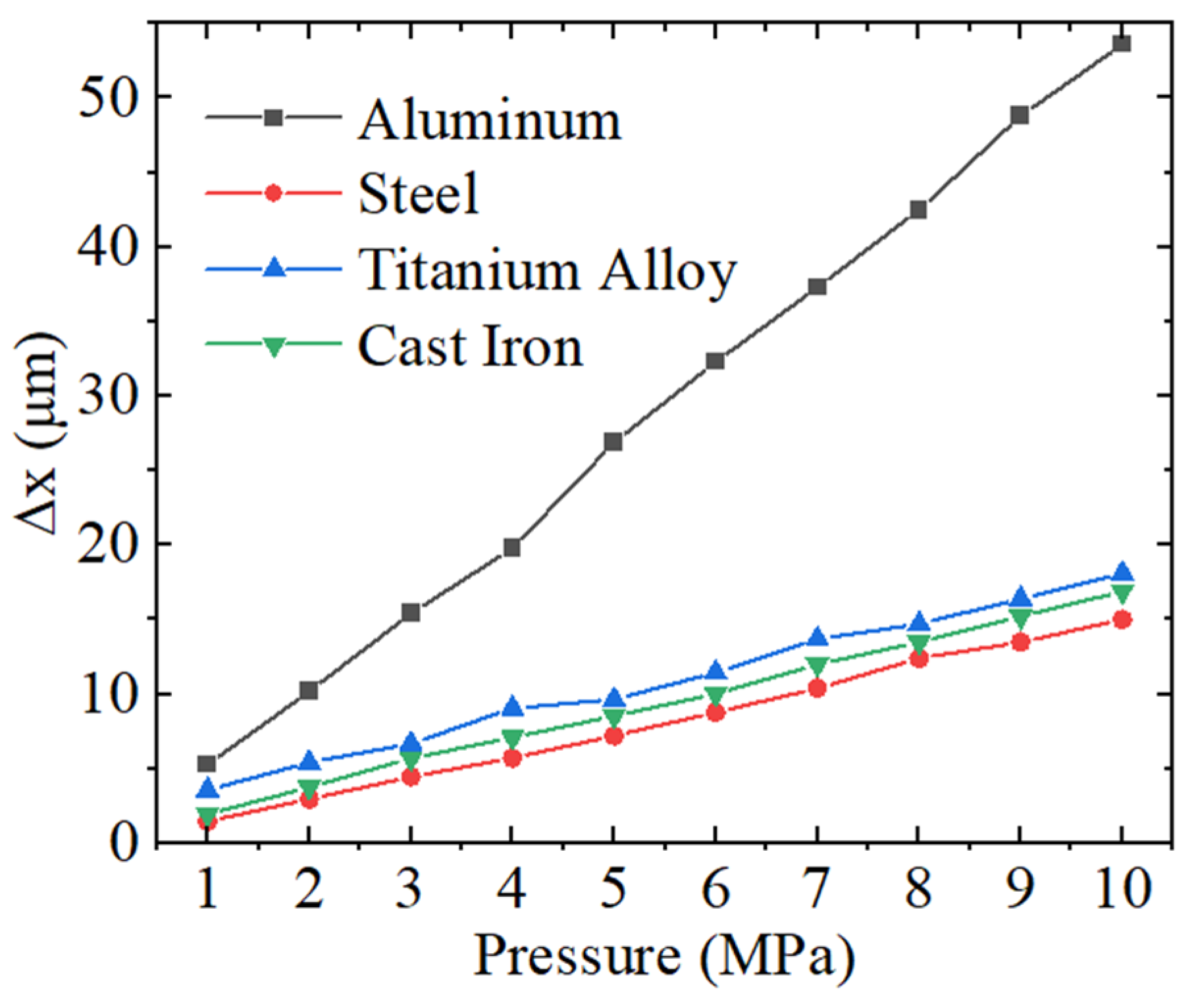
3.2. Simulation Analysis of the Pressure-Sensing Structure
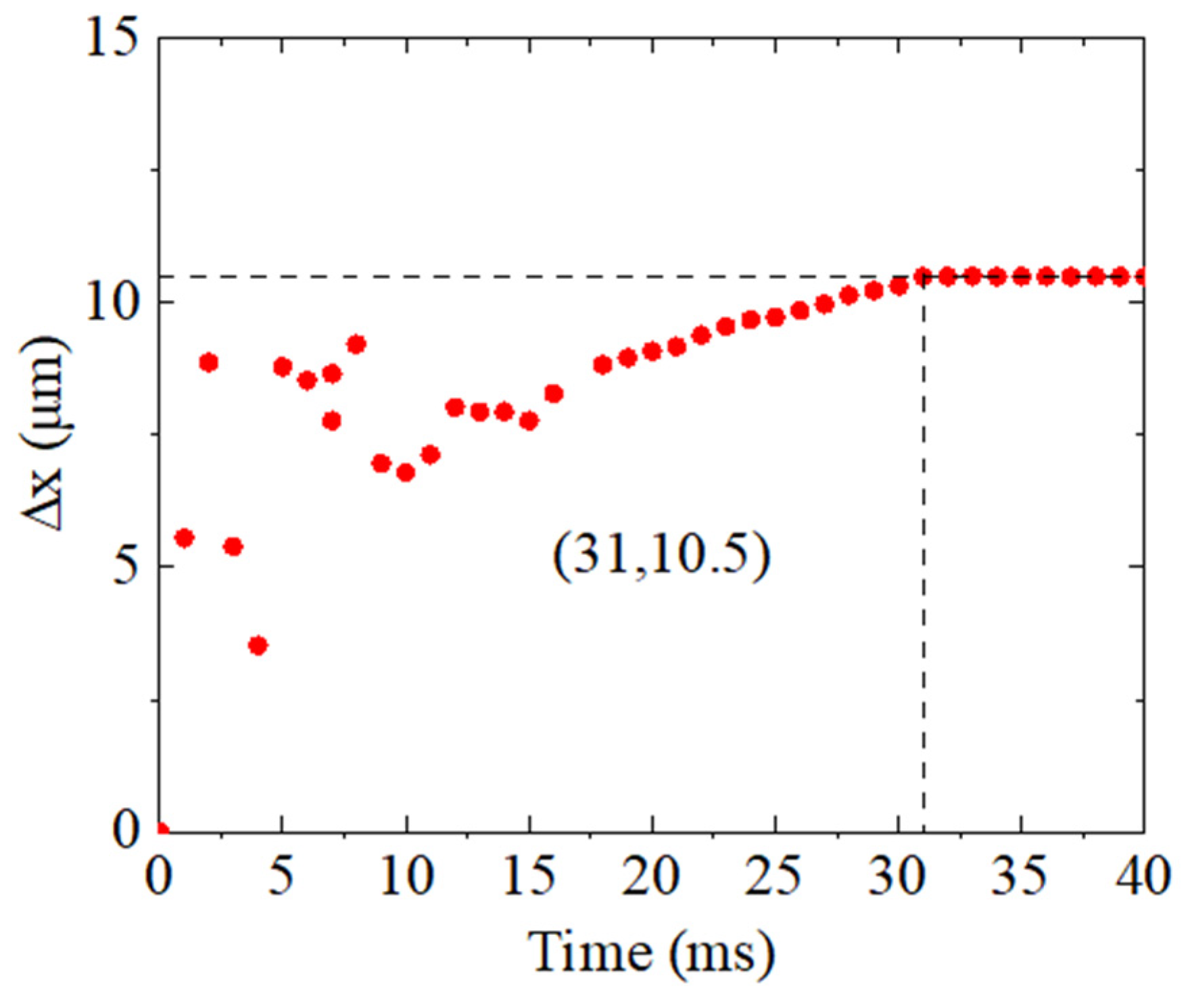
3.3. Experimental Validation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, X.; Wang, J.; Wang, S.S.; Liao, Y.P. Fiber-optic salinity sensing with a panda-microfiber-based multimode interferometer. J. Light. Technol. 2017, 35, 5086–5091. [Google Scholar] [CrossRef]
- Zhao, X.; Wei, C.; Zeng, L.; Sun, L.; Li, Z.; Chen, H.; Liu, G.; Qiao, Z.; Qu, Y.; Xu, D.; et al. Research Progress in Fiber Bragg Grating-Based Ocean Temperature and Depth Sensors. Sensors 2024, 25, 183. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, Y.; Cui, C.; Lv, W.; Liu, X. High-sensitivity ocean temperature sensor using a reflective optical microfiber coupler and machine learning methods. Appl. Opt. 2024, 63, 8771–8779. [Google Scholar] [CrossRef] [PubMed]
- Goes, M.; Goni, G.; Dong, S.; Boyer, T.; Baringer, M. The Complementary Value of XBT and Argo Observations to Monitor Ocean Boundary Currents and Meridional Heat and Volume Transports: A Case Study in the Atlantic Ocean. J. Atmos. Ocean. Technol. 2020, 37, 2267–2282. [Google Scholar] [CrossRef]
- Yan, Y.; Gu, Z.; Wang, Y.; Du, J. Design and simulation of reflective fiber grating sensor for simultaneous monitoring of CTD in marine environment. J. Opt. 2024, 1–12. [Google Scholar] [CrossRef]
- Goes, M.; Goni, G.; Dong, S. An optimal XBT-based monitoring system for the South Atlantic meridional overturning circulation at 34° S. J. Geophys. Res. Oceans 2015, 120, 161–181. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Y.; Zeng, L.; Li, Z.; Chen, H.; Qiao, Z.; Qu, Y.; Liu, G.; Li, L. Structural Design of Ocean Temperature and Depth Sensor with Quick Response and High Sensitivity. Sensors 2022, 22, 7756. [Google Scholar] [CrossRef]
- Liu, Z.; Zeng, L.; Xu, K.; Li, Z.; Chen, H.; Qiao, Z.; Qu, Y.; Liu, G.; Li, L. Design of a Fiber Bragg Grating Pressure Sensor Based on a Metal Diaphragm and Lever Structure. Sensors 2022, 22, 5096. [Google Scholar] [CrossRef]
- Meng, Q.; Wang, J.; Chen, D.; Chen, J.; Xie, B.; Lu, Y. An Ultra-low Thermal Sensitivity Drift Piezoresistive Pressure Sensor Compensated by Passive Resistor/Thermistor Network. J. Phys. Conf. Ser. 2024, 2740, 012042. [Google Scholar] [CrossRef]
- Tagawa, M.; Kato, K.; Ohta, Y. Response Compensation of Thermistors: Frequency Response and Identification of Thermal Time Constant. Rev. Sci. Instrum. 2003, 74 Pt 1, 1350–1358. [Google Scholar] [CrossRef]
- Su, F.; Hu, Y.; Zhu, X.; Lai, T. Enhancing the Thermal Stability and Reducing the Resistance Drift of Sb Phase Change Films by Adding In2Se3 Interlayers. Coatings 2023, 13, 927. [Google Scholar] [CrossRef]
- Cui, C.; Gao, L.; Dai, N.; Xu, Q. Fiber Bragg Grating Inclinometer-enabled IoT Sensing System with Low Power Consumption and Small Size. Sens. Mater. 2021, 33, 2321–2331. [Google Scholar] [CrossRef]
- Xu, B.; Chen, G.; Xu, X.; Liu, S.; Liao, C.; Weng, X.; Liu, L.; Qu, J.; Wang, Y.; He, J. Highly birefringent side-hole fiber Bragg grating for high-temperature pressure sensing. Opt. Lett. 2024, 49, 1233–1236. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, X.; Wang, Z.; Liu, Y. Single Mode Fiber Dislocation Mach–Zehnder Interferometer Cascaded with Fiber Bragg Grating for Monitoring Metal Electrochemical Corrosion. Optoelectron. Lett. 2023, 19, 653–658. [Google Scholar] [CrossRef]
- Kumar, J.; Prakash, O.; Agrawal, S.K.; Mahakud, R.; Mokhariwale, A.; Dixit, S.K.; Nakhe, S.V. Distributed fiber Bragg grating sensor for multipoint temperature monitoring up to 500 °C in high-electromagnetic interference environment. Opt. Eng. 2016, 55, 090502. [Google Scholar] [CrossRef]
- Hnatovsky, C.; Silva, K.D.; Abdukerim, N.; Walker, R.B.; Ding, H.; Mihailov, S.J. Nanoscale Morphology and Thermal Properties of Low Insertion Loss Fiber Bragg Gratings Produced Using the Phase Mask Technique and a Single Femtosecond Laser Pulse. Opt. Express 2022, 30, 47361–47374. [Google Scholar] [CrossRef]
- Purwasih, N.; Shinozaki, H.; Okazaki, S.; Kihira, H.; Kuriyama, Y.; Kasai, N. Atmospheric Corrosion Sensor Based on Strain Measurement with Active–Dummy Fiber Bragg Grating Sensors. Metals 2020, 10, 1076. [Google Scholar] [CrossRef]
- Kanakambaran, S.; Sarathi, R.; Srinivasan, B. Identification and localization of partial discharge in transformer insulation adopting cross recurrence plot analysis of acoustic signals detected using fiber Bragg gratings. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 1773–1780. [Google Scholar] [CrossRef]
- Yan, G.; Wang, T.; Zhu, L.; Meng, F.; Zhuang, W. A Novel Strain-Decoupled Sensitized FBG Temperature Sensor and Its Applications to Aircraft Thermal Management. Opt. Laser Technol. 2021, 140, 106597. [Google Scholar] [CrossRef]
- Hong, L.; Wang, J.; Cai, J.; Teng, Y.; Qiu, Z. Substrate-Type Sensitized FBG Temperature Sensor. Sens. Rev. 2023, 43, 83–91. [Google Scholar] [CrossRef]
- Gu, Y.; Zhao, Y.; Lv, R.Q.; Zhang, W.; Yang, B. A Practical FBG Sensor Based on a Thin-Walled Cylinder for Hydraulic Pressure Measurement. IEEE Photonics Technol. Lett. 2016, 28, 2569–2572. [Google Scholar] [CrossRef]
- Hegde, G.; Prasad, M.V.N.; Asokan, S. Temperature compensated diaphragm based Fiber Bragg Grating (FBG) sensor for high pressure measurement for space applications. Microelectron. Eng. 2021, 248, 111615. [Google Scholar] [CrossRef]
- Fadeev, K.M.; Larionov, D.D.; Zhikina, L.A.; Minkin, A.M.; Shevtsov, D.I. A Fiber-Optic Sensor for Simultaneous Temperature and Pressure Measurements Based on a Fabry–Perot Interferometer and a Fiber Bragg Grating. Instrum. Exp. Tech. 2020, 63, 543–546. [Google Scholar] [CrossRef]
- Zhao, Q.; Wang, Y.; Sun, P.; Du, D.; Yu, L.; Zhang, J.; Ding, B.; Han, G.; Qu, Y. Shipborne expendable all-optical fiber ocean temperature-depth profile sensor. Appl. Opt. 2022, 61, 2089–2095. [Google Scholar] [CrossRef]
- Hopf, B.; Fischer, B.; Bosselmann, T.; Koch, A.W.; Roths, J. Strain-Independent Temperature Measurements with Surface-Glued Polarization-Maintaining Fiber Bragg Grating Sensor Elements. Sensors 2019, 19, 144. [Google Scholar] [CrossRef]
- Kuang, Y.; Guo, Y.; Xiong, L.; Liu, W. Packaging and Temperature Compensation of Fiber Bragg Grating for Strain Sensing: A Survey. Photonic Sens. 2018, 8, 320–331. [Google Scholar] [CrossRef]
- Fajkus, M.; Nedoma, J.; Martinek, R.; Fridrich, M.; Bednar, E.; Zabka, S.; Zmij, P. Pressure Membrane FBG Sensor Realized by 3D Technology. Sensors 2021, 21, 5158. [Google Scholar] [CrossRef]
- Dzipalski, A.; Morton, J.A.S.; Papachristou, N.; Maier, R.R.J.; MacPherson, W.N.; Ristolainen, A.; Reilent, E.; Kruusmaa, M.; Wolf, B.J.; Pirih, P.; et al. A Multiplexed Reconfigurable Modular FBG Based Sensor Platform for Flow and Temperature Measurements in the North Sea. In Remote Sensing for Agriculture, Ecosystems, and Hydrology XXVI; Neale, C.M.U., Maltese, A., Bostater, C.R., Nichol, C., Eds.; SPIE: Bellingham, WA, USA, 2024; Volume 13191, p. 1319104. [Google Scholar] [CrossRef]
- Shang, Q.; Qin, W. Fiber Bragg Grating Dynamic Calibration Based on Online Sequential Extreme Learning Machine. Sensors 2020, 20, 1840. [Google Scholar] [CrossRef]
- Brown, R.T.; MacPherson, W.N.; Maier, R.R.J.; Barton, J.S.; Jones, J.D.C.; Collins, A.T. An Optical Fibre Depth (Pressure) Sensor for Remote Operated Vehicles in Underwater Applications. Sensors 2017, 17, 406. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Fang, J.; Zhang, X.; Chen, R.; Xu, Y. Submarine Optical Fiber Sensing System for the Real-Time Monitoring of Depth, Vibration, and Temperature. Front. Mar. Sci. 2022, 9, 870674. [Google Scholar] [CrossRef]
- Pei, W.; Pei, X.; Xie, Z.; Wang, J. Research progress of marine anti-corrosion and wear-resistant coating. Tribol. Int. 2024, 198, 109864. [Google Scholar] [CrossRef]
- Zhan, W.; Li, X.; Qian, X.; Li, Y.; Ding, Y.; Zu, Y.; Xie, F.; Tian, F. Preparation and Characterization of Synchronous Chemical Conversion Coating on 6061 Aluminum Alloy/7075 Aluminum Alloy/Galvanized Steel Substrates. Metals 2022, 12, 2011. [Google Scholar] [CrossRef]
- Udd, E.; Spillman, W.B. Fiber Optic Sensors: An Introduction for Engineers and Scientists, 2nd ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Zhang, H.; Xue, X. The research progress on corrosion and protection of silver layer. SN Appl. Sci. 2019, 1, 464. [Google Scholar] [CrossRef]
- Raju, B.; Kumar, R.; Dhanalakshmi, S.; Hrbac, R.; Demel, L.; Narayanamoorthi, R. Experimental investigation on polymer coated fibre bragg grating sensor for temperature measurement in sewer environment. Results Eng. 2025, 25, 104319. [Google Scholar] [CrossRef]
- Bakaic, M.; Hanna, M.; Hnatovsky, C.; Grobnic, D.; Mihailov, S.; Zeisler, S.S.; Hoehr, C. Fiber-Optic Bragg Gratings for Temperature and Pressure Measurements in Isotope Production Targets for Nuclear Medicine. Appl. Sci. 2020, 10, 4610. [Google Scholar] [CrossRef]
- Wang, H.-P.; Dai, J.-G.; Wang, X.-Z. Improved Temperature Compensation of Fiber Bragg Grating-Based Sensors Applied to Structures under Different Loading Conditions. Opt. Fiber Technol. 2021, 63, 102506. [Google Scholar] [CrossRef]
- Yu, X.; Shuai, C.; Yang, X.; Lu, G.; Liang, C.; Liu, Z. Design and testing of a smart rubber stave for marine water-lubricated bearings. Sci. Eng. Compos. Mater. 2022, 29, 215–226. [Google Scholar] [CrossRef]
- Cheng, L.; Zhu, J.; Cowley, R.; Boyer, T.; Wijffels, S. Time, Probe Type, and Temperature Variable Bias Corrections to Historical Expendable Bathythermograph Observations. J. Atmos. Ocean. Technol. 2014, 31, 1793–1825. [Google Scholar] [CrossRef]
- Abeywardena, C.L.; Zhang, Q.; Korposh, S.; Morgan, S.P.; Bull, S.; Correia, R. Highly Sensitive Optical Fibre Bragg Grating Contact Pressure Sensor Embedded in a Polymer Layer: Modelling and Experimental Validation. Results Opt. 2024, 14, 100604. [Google Scholar] [CrossRef]
- Moccia, M.; Pisco, M.; Cutolo, A.; Galdi, V.; Bevilacqua, P.; Cusano, A. Opto-acoustic behavior of coated fiber Bragg gratings. Opt. Express 2011, 19, 18842–18860. [Google Scholar] [CrossRef] [PubMed]





| Materials | Linear Expansion Coefficient | Thermal Conductivity | Source |
|---|---|---|---|
| Aluminum | 23.0 × 10−6 pm/°C | 237 W/mK | Goodfellow Cambridge Ltd., Huntingdon, UK |
| Silver | 19.5 × 10−6 pm/°C | 429 W/mK | |
| Copper | 17.5 × 10−6 pm/°C | 401 W/mK | |
| Iron | 11.8 × 10−6 pm/°C | 80 W/mK | |
| Lead | 29.0 × 10−6 pm/°C | 34.8 W/mK |
| Materials | Poisson’s Ratio | Young’s Modulus | Source |
|---|---|---|---|
| Epoxy resin | 0.38 | 3 GPa | Epoxy Technology, Billerica, MA, USA |
| Polycarbonate | 0.24 | 1.448 GPa | Covestro AG, Leverkusen, Germany |
| Polyimide | 0.34 | 2.914 GPa | DuPont, Wilmington, DE, USA |
| Polyethylene | 0.45 | 1.2 GPa | LyondellBasell, Rotterdam, The Netherlands |
| Materials | Density | Young’s Modulus | Source |
|---|---|---|---|
| Aluminum alloy | 2.7 g/cm3 | 75 GPa | Arconic, Pittsburgh, PA, USA |
| Steel | 7.9 g/cm3 | 200 GPa | Ovako, Stockholm, Sweden |
| Titanium alloy | 4.5 g/cm3 | 118 GPa | TIMET, Warrensville Heights, OH, USA |
| Cast iron | 7.2 g/cm3 | 123 GPa | Bradbury Group, Moundridge, KS, USA |
| Components | Piston | 304 Stainless-Steel Tube | Polymer |
|---|---|---|---|
| Materials | Aluminum alloy | 304 Stainless-steel | Polycarbonate |
| Dimensions | Length = 15 mm, width = 8 mm, and thickness = 6 mm | Length = 15 mm, width = 5 mm, and thickness = 1 mm | Radius = 3.5 mm and length = 15 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Wei, C.; Zeng, L.; Li, L.; Liu, S.; Sun, L.; Li, Z.; Chen, H.; Liu, G.; Qu, Y.; et al. Temperature and Depth Sensor Based on Fiber Bragg Gratings with Temperature-Compensated Structure in Marine Environment. Coatings 2025, 15, 795. https://doi.org/10.3390/coatings15070795
Zhao X, Wei C, Zeng L, Li L, Liu S, Sun L, Li Z, Chen H, Liu G, Qu Y, et al. Temperature and Depth Sensor Based on Fiber Bragg Gratings with Temperature-Compensated Structure in Marine Environment. Coatings. 2025; 15(7):795. https://doi.org/10.3390/coatings15070795
Chicago/Turabian StyleZhao, Xinyu, Chenxi Wei, Lina Zeng, Lu Li, Shengjie Liu, Li Sun, Zaijin Li, Hao Chen, Guojun Liu, Yi Qu, and et al. 2025. "Temperature and Depth Sensor Based on Fiber Bragg Gratings with Temperature-Compensated Structure in Marine Environment" Coatings 15, no. 7: 795. https://doi.org/10.3390/coatings15070795
APA StyleZhao, X., Wei, C., Zeng, L., Li, L., Liu, S., Sun, L., Li, Z., Chen, H., Liu, G., Qu, Y., Le, Z., Li, Y., Li, L., & Li, L. (2025). Temperature and Depth Sensor Based on Fiber Bragg Gratings with Temperature-Compensated Structure in Marine Environment. Coatings, 15(7), 795. https://doi.org/10.3390/coatings15070795






