A Comprehensive Review on Fluid Dynamics and Transport of Suspension/Liquid Droplets and Particles in High-Velocity Oxygen-Fuel (HVOF) Thermal Spray
Abstract
:1. Introduction
High-Velocity Oxygen-Fuel (HVOF) Thermal Spray Technique






2. Governing Equations
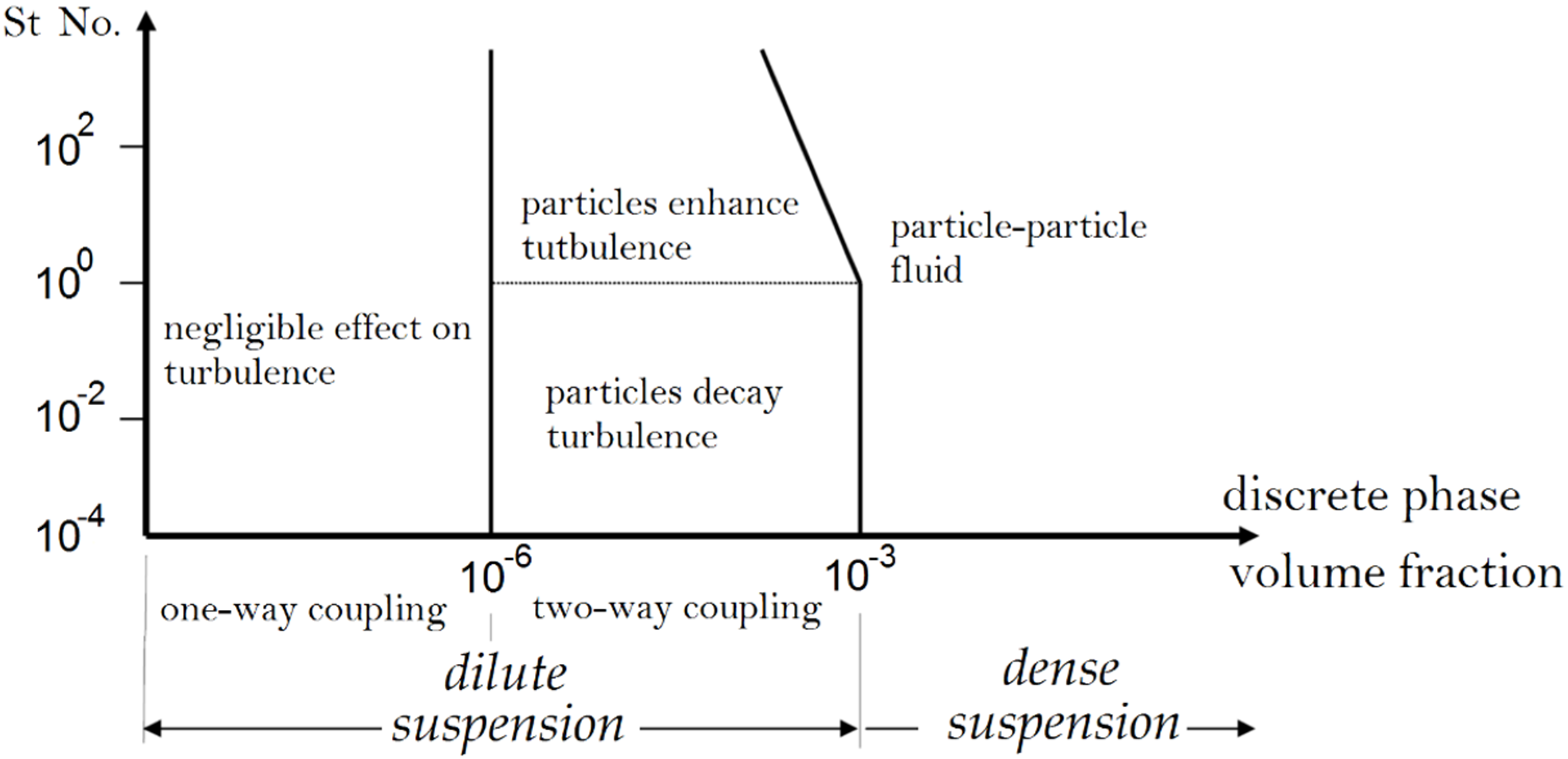

3. Literature Review on HVOF Modeling
3.1. Combustion Simulation
3.2. Operating Conditions Effects
3.3. Particle Size and Shape


3.4. Powder Injector Effects
3.5. Nozzle Shape
3.6. Shock Diamonds
3.7. Particle Oxidation Modeling
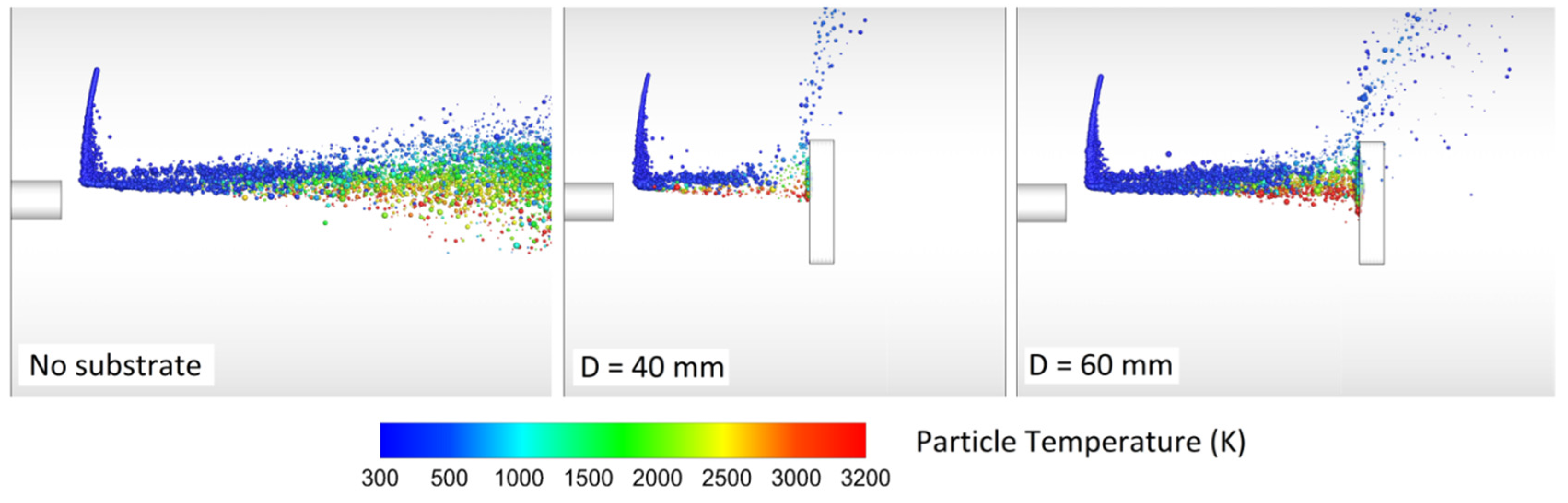
3.8. Substrate Effects
4. High Velocity Suspension Flame Spray (HVSFS) Technique


4.1. Suspension Properties
4.2. Breakup
4.2.1. Primary Breakup
Cylindrical Liquid Jet Breakup


| Breakup Regime | Criteria |
|---|---|
| Region A: dripping regime | WeL < 8 |
| Region B: Rayleigh regime | WeL > 8 WeG < 0.4 or 1.2 + 3.41Oh0.9 |
| Region C: first wind-induced regime | 1.2 + 3.41Oh0.9 < WeG < 13 |
| Region D: second wind-induced regime | 13 < WeG < 40.3 |
| Region E: atomization regime | 40.3 < WeG |

Liquid Jet in Crossflow
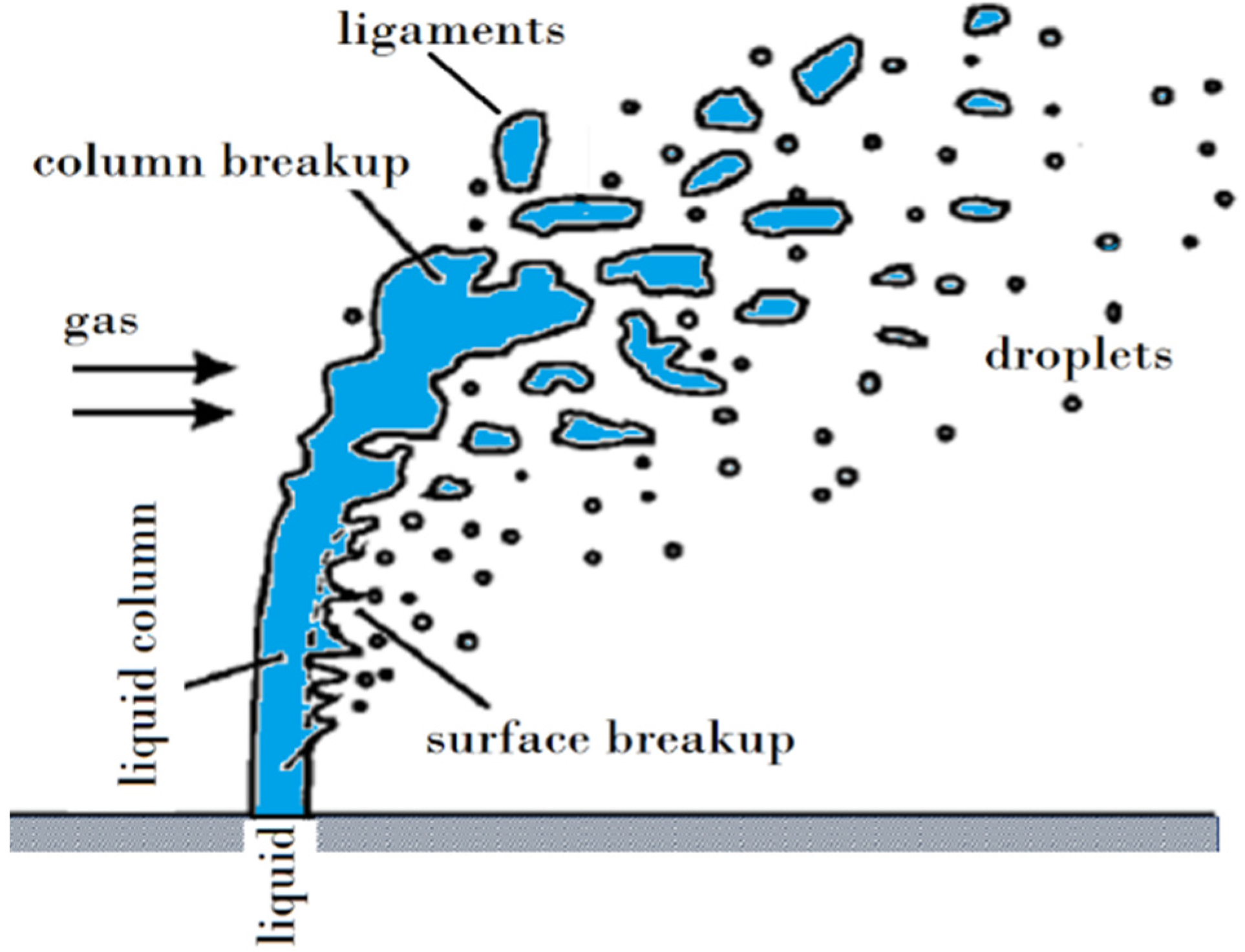
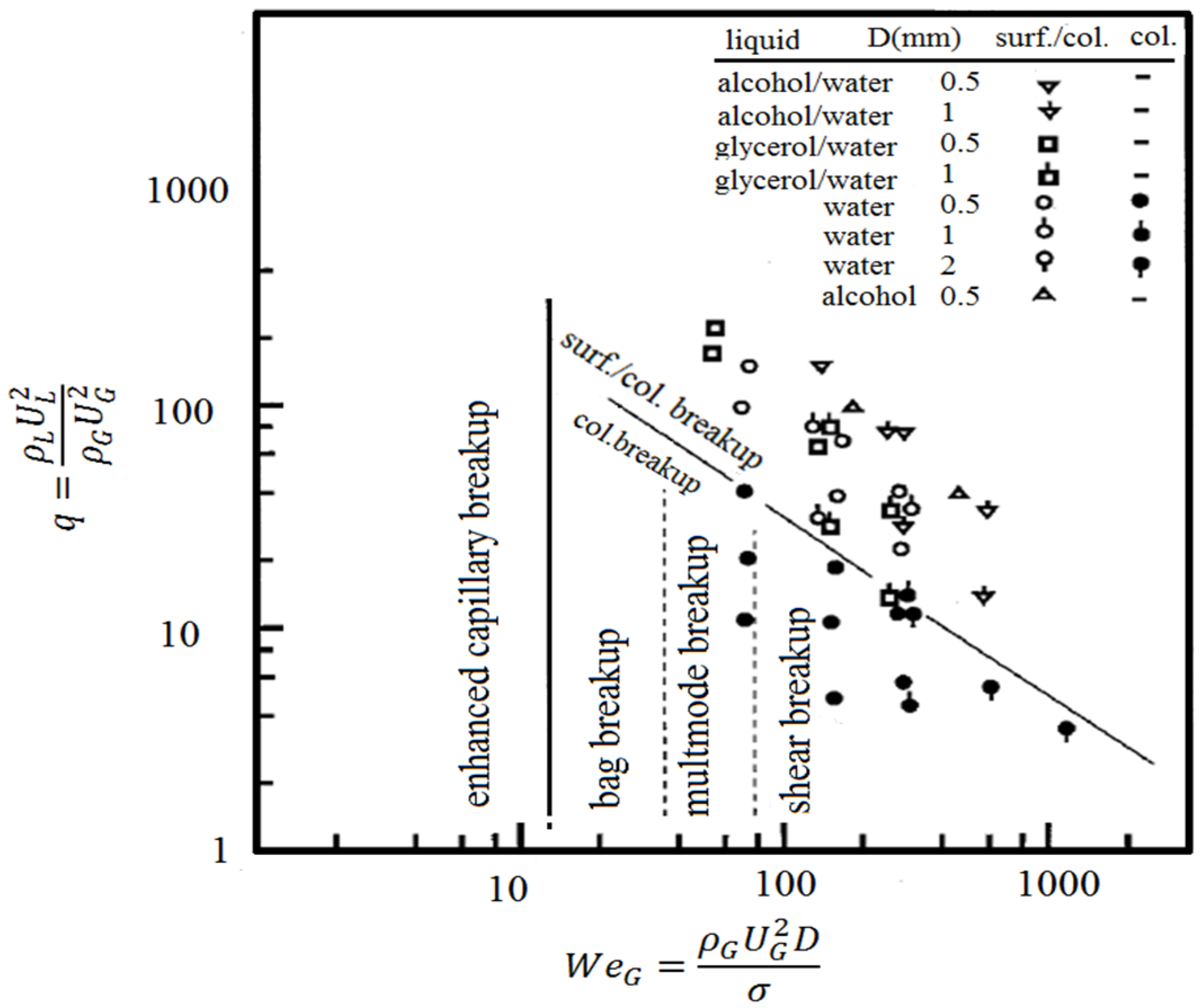

| Injector Type | a1 | a2 | a1 | a2 |
|---|---|---|---|---|
| Sharp edge | 1.2181 | 1.8806 | 1.9866 | 0.7403 |
| Round edge | 1.0724 | 1.8641 | ||
| Penetration | Average | Maximum | ||

Coaxial Jets

4.2.2. Numerical Modeling of Primary Breakup and Atomization
- Mass conservation
- Handling flows with large density ratios (liquid-to-gas ratio)
- Accurate interface representation and advection
- Spurious currents

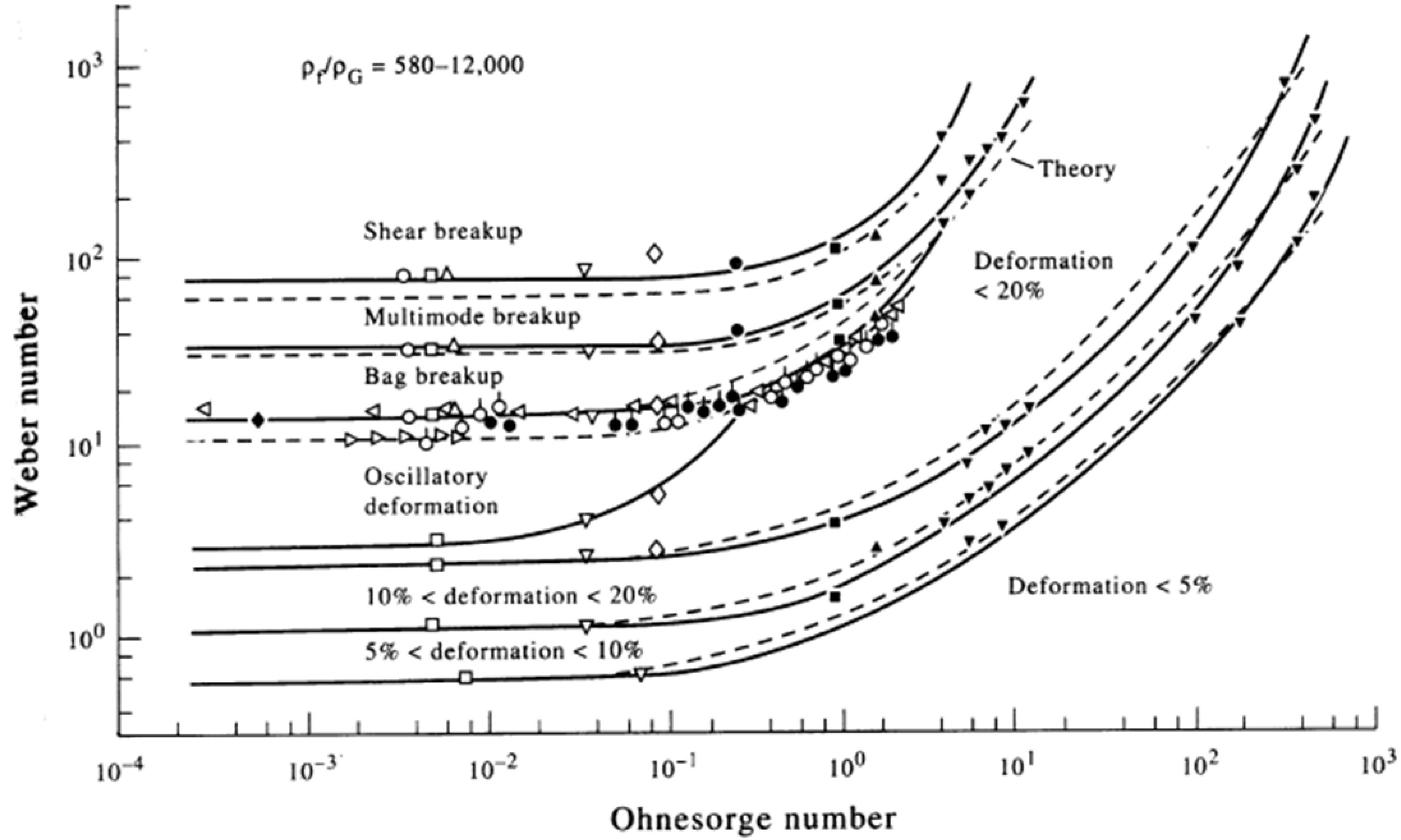
4.2.3. Secondary Breakup

| Vibrational | 0 < We < ~11 |
|---|---|
| Bag | ~11 < We < ~35 |
| Multimode | ~35 < We < ~80 |
| Sheet-thinning | ~80 < We < ~350 |
| Catastrophic | We > ~350 |
4.3. Droplet Evaporation/Combustion


5. Literature Review on HVSFS Modeling

6. Conclusions and Future Works
- Coupling of level set (LS) and volume of fluid (VOF) methods to simulate both inertia-dominated and surface tension-dominated compressible multiphase flows (the CLSVOF method);
- Coupling the mentioned fully Eulerian methods such as CLSVOF and Lagrangian spray models to simulate both primary and secondary atomization;
- After secondary atomization modeling, tracking the droplets/particles in the domain using the Eulerian-Lagrangian approach;
- Using more accurate turbulence models such as large eddy simulation (LES);
- Measuring and correlating suspension properties, especially dynamic and static surface tensions (these parameters has significant effects on the atomization process);
- Understanding the suspension evaporation/combustion mechanisms within the high temperature jets and flames (they have some influence on the particle agglomerations' sizes and, subsequently, on the adhesion of the coating on the substrate);
- Considering the effect of the Knudsen number on the Nusselt number and heat transfer coefficient;
- Considering the thermophoretic force;
- Parametric study to optimize the torch;
- The effect of Weber, Ohnesorge, and Reynolds numbers on the atomization process and droplet size distribution in HVOF torches;
- The effect of suspension/liquid injector shape, type, and location on the droplet size distribution and droplet velocity in HVOF torches;
- The effect of operating conditions such as total flow rate and equivalence ratio on the atomization process and droplet combustion;
- The effect of combustion chamber geometry and injector angle on the droplet size distribution, droplet velocity, droplet combustion, and particle temperature and velocity;
- The effect of torch geometry on the particle temperature and oxidation;
- The effect of standoff distance and substrate shape on the deposition efficiency.
Acknowledgments
Conflicts of Interest
References
- Pawlowski, L. The Science and Engineering of Thermal Spray Coatings, 2nd ed.; John Wiley & Sons: Chichester, West Sussex, UK, 2008. [Google Scholar]
- Heimann, R.B. Plasma Spray Coating: Principles and Applications, 2nd ed.; Wiley-VCH Verlagsgesellschaft mbH: Weinheim, Germany, 1996. [Google Scholar]
- Sobolev, V.V.; Guilemany, J.M.; Nutting, J. High Velocity Oxy-Fuel Spraying: Theory, Structure-Property Relationships and Applications; Maney Publishing: London, UK, 2004. [Google Scholar]
- Li, M.; Christofides, P.D. Modeling and control of high-velocity oxygen-fuel (HVOF) thermal spray: A tutorial review. J. Therm. Spray Technol. 2009, 18, 753–768. [Google Scholar] [CrossRef]
- Cetegen, B.M.; Basu, S. Review of modeling of liquid precursor droplets and particles injected into plasmas and high-velocity oxy-fuel (HVOF) flame jets for thermal spray deposition applications. J. Therm. Spray Technol. 2009, 18, 769–793. [Google Scholar] [CrossRef]
- Oksa, M.; Turunen, E.; Suhonen, T.; Varis, T.; Hannula, S.P. Optimization and characterization of high velocity oxy-fuel sprayed coatings: Techniques, materials, and applications. Coatings 2011, 1, 17–25. [Google Scholar] [CrossRef]
- Fauchais, P.; Montavon, G.; Lima, R.S.; Marple, B.R. Engineering a new class of thermal spray nano-based microstructures from agglomerated nanostructured particles, suspensions and solutions: An invited review. J. Phys. D Appl. Phys. 2011, 44. [Google Scholar] [CrossRef] [Green Version]
- Dolatabadi, A. A Computational Analysis of High Speed Particle-Laden Flows. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 2003. [Google Scholar]
- Gu, S.; McCartney, D.G.; Eastwick, C.N.; Simmons, K.A. Numerical modeling of in-flight characteristics of Inconel 625 particles during high-velocity oxy-fuel thermal spraying. J. Therm. Spray Technol. 2004, 13, 200–213. [Google Scholar] [CrossRef]
- Law, C.K. Combustion physics; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Kobayashi, H.; Nakashima, T.; Tamura, T.; Maruta, K.; Niioka, T. Turbulence measurements and observations of turbulent premixed flames at elevated pressures up to 3.0 MPa. Combust. Flame 1997, 108, 104–117. [Google Scholar] [CrossRef]
- Kobayashi, H.; Tamura, T.; Maruta, K.; Niioka, T.; Williams, F.A. Burning velocity of turbulent premixed flames in a high-pressure environment. In Proceedings of the 26th Symposium (International) on Combustion, Naples, Italy, 28 July–2 August 1996; pp. 389–396.
- Kobayashi, H.; Kawabata, Y.; Maruta, K. Experimental study on general correlation of turbulent burning velocity at high pressure. In Proceedings of the 27th Symposium (International) on Combustion, Boulder, CO, USA, 2–7 August 1998; pp. 941–948.
- Kobayashi, H. Experimental study of high-pressure turbulent premixed flames. Exp. Therm. Fluid Sci. 2002, 26, 375–387. [Google Scholar] [CrossRef]
- Norman, M.L.; Winkler, K.A. Supersonic Jets. In Los Alamos Science; Los Alamos Science Center: Los Alamos National Laboratory, NM, USA, 1985. [Google Scholar]
- Anderson, J.D., Jr. Modern Compressible Flow with Historical Perspective, 2nd ed.; McGraw-Hill: Singapore, Singapore, 1990. [Google Scholar]
- Aerospaceweb. Available online: http://www.aerospaceweb.org/question/propulsion/q0224.shtml (accessed on 14 August 2015).
- Munday, D.; Gutmark, E.; Liu, J.; Kailasanath, K. Flow structure and acoustics of supersonic jets from conical convergent-divergent nozzles. Phys. Fluids 2011, 23. [Google Scholar] [CrossRef]
- Samareh, B.; Stier, O.; Luthen, V.; Dolatabadi, A. Assessment of CFD modeling via flow visualization in cold spray process. J. Therm. Spray Technol. 2009, 18, 934–943. [Google Scholar] [CrossRef]
- Andreopoulos, Y.; Agui, J.H.; Briassulis, G. Shock wave-turbulence interactions. Annu. Rev. Fluid Mech. 2000, 32, 309–345. [Google Scholar] [CrossRef]
- Garnier, E.; Adams, N.; Sagaut, P. Large Eddy Simulation for Compressible Flows; Springer: New York, NY, USA, 2009. [Google Scholar]
- Fan, L.S.; Zhu, C. Principles of Gas-Solid Flows; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Rudinger, G. Relaxation in Gas-Particle Flow. Project SQUID; Technical Report No. CAL-96-PU; July 1968. [Google Scholar]
- Varma, T.D.; Chopra, N.K. Analysis of normal shock waves in a gas-particle mixture. Z. Angew. Math. Phys. 1967, 18, 650–660. [Google Scholar] [CrossRef]
- Srivastava, R.S.; Sharma, J.P. Structure of normal shock waves in a gas-particle mixture. Z. Angew. Math. Phys. 1982, 33, 819–825. [Google Scholar] [CrossRef]
- John, E.A.; Keith, T.G. Gas. Dynamics, 3rd ed.; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2006. [Google Scholar]
- Crowe, C.; Sommerfeld, M.; Tsuji, Y. Multiphase Flows with Droplets and Particles; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Berry, R.A. Ensemble Averaged Conservation Equations for Multiphase, Multi-Component, and Multi-Material Flows. In Idaho National Engineering and Environmental Laboratory, Bechtel BWXT Idaho, INEEL/EXT-03–01011; Idaho National Laboratory: Idaho Falls, ID, USA, 2003. [Google Scholar]
- Kashiwa, B.A.; Rauenzahn, R.M. A Multimaterial Formalism; Technical Report LA-UR-94-771; Los Alamos National Laboratory: Los Alamos, NM, USA, 1994. [Google Scholar]
- Elghobashi, S.E. On predicting particle-laden turbulent flows. Appl. Sci. Res. 1994, 52, 309–329. [Google Scholar] [CrossRef]
- Dolatabadi, A.; Mostaghimi, J.; Pershin, V. Modeling dense suspension of solid particles in highly compressible flows. Int. J. Comput. Fluid Dyn. 2004, 18, 125–131. [Google Scholar] [CrossRef]
- Samareh, B.; Dolatabadi, A. Dense particulate flow in a cold gas dynamic spray system. J. Fluids Eng. 2008, 130. [Google Scholar] [CrossRef]
- Crowe, C.T. Drag coefficient on particles in a rocket nozzle. AIAA J. 1967, 5, 1021–1022. [Google Scholar] [CrossRef]
- Clift, R.; Grace, J.R.; Weber, M.E. Bubbles, Drops and Particles; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- Samareh Abolhassani, B. Two phase flow modeling of cold spray process. Master’s Thesis, Concordia University, Montreal, QC, Canada, 2008. [Google Scholar]
- Siegel, R.; Howell, J.R. Thermal radiation heat transfer, 2nd ed.; Hemisphere Publishing Corp: Washington, DC, USA, 1981. [Google Scholar]
- Li, M.; Shi, D.; Christofides, P.D. Modeling and control of HVOF thermal spray processing of WC-Co coatings. Powder Technol. 2005, 156, 177–194. [Google Scholar] [CrossRef]
- Viskanta, R.; Menguc, M.P. Radiation heat transfer in combustion systems. Prog. Energy Combust. Sci. 1987, 13, 97–160. [Google Scholar] [CrossRef]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; Wiley: New York, NY, USA, 1983. [Google Scholar]
- Van de Hulst, H.C. Light Scattering by Small Particles; Wiley: New York, NY, USA, 1957. [Google Scholar]
- Wickramasinghe, N.C. Light Scattering Functions for Small Particles; Wiley: New York, NY, USA, 1973. [Google Scholar]
- Jones, A.R. Light scattering for particle characterization. Prog. Energy Combust. Sci. 1999, 25, 1–53. [Google Scholar] [CrossRef]
- Ordal, M.A.; Long, L.L.; Bell, R.J.; Bell, S.E.; Bell, R.R.; Alexander, R.W.; Ward, C.A. Optical properties of the metals Al, Co, Cu, Au, Fe, Pb, Ni, Pd, Pt, Ag, Ti, and W in the infrared and far infrared. Appl. Opt. 1983, 22, 1099–1119. [Google Scholar] [CrossRef] [PubMed]
- Bidabadi, M.; Shabani Shahrbabaki, A.; Jadidi, M.; Montazerinejad, S. An analytical study of radiation effect on the premixed laminar flame of aluminum dust clouds. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2010, 224, 1679–1695. [Google Scholar] [CrossRef]
- Plass, G.N. Mie scattering and absorption cross sections for aluminum oxide and magnesium oxide. Appl. Opt. 1964, 3, 867–872. [Google Scholar] [CrossRef]
- Echekki, T.; Mastorakos, E. Turbulent Combustion Modeling, Advances, New Trends and Perspectives; Springer: Dordrecht, The Netherlands, 2010. [Google Scholar]
- ANSYS FLUENT Theory Guide; Release 14.0; ANSYS, Inc.: Cecil Township, PA, USA, 2011.
- Turns, S.R. An Introduction to Combustion, Concepts and Applications, 2nd ed.; McGraw-Hill: New York, NY, USA, 2000. [Google Scholar]
- Glassman, I.; Yetter, R.A. Combustion, 4th ed.; Academic Press: Burlington, MA, USA, 2008. [Google Scholar]
- Jabbari, F.; Jadidi, M.; Wuthrich, R.; Dolatabadi, A. A numerical study of suspension injection in plasma spraying process. J. Therm. Spray Technol. 2014, 23, 3–13. [Google Scholar] [CrossRef]
- Marchand, C.; Chazelas, C.; Mariaux, G.; Vardelle, A. Liquid precursor plasma spraying: Modeling the interactions between the transient plasma jet and the droplets. J. Therm. Spray Technol. 2007, 16, 705–712. [Google Scholar] [CrossRef]
- Vincent, S.; Balmigere, G.; Caruyer, C.; Meillot, E.; Caltagirone, J.P. Contribution to the modeling of the interaction between a plasma flow and a liquid jet. Surf. Coat. Technol. 2009, 203, 2162–2171. [Google Scholar] [CrossRef]
- Caruyer, C.; Vincent, S.; Meillot, E.; Caltagirone, J.P. Modeling the first instant of the interaction between a liquid and a plasma jet with a compressible approach. Surf. Coat. Technol. 2010, 205, 974–979. [Google Scholar] [CrossRef]
- Caruyer, C.; Vincent, S.; Meillot, E.; Caltagirone, J.P.; Damiani, D. Analysis of the unsteadiness of a plasma jet and the related turbulence. Surf. Coat. Technol. 2010, 205, 1165–1170. [Google Scholar] [CrossRef]
- Cheng, C.H.; Moore, R.L. Numerical simulation of gas and particle flow in a high velocity oxygen-fuel (HVOF) torch. J. Therm. Spray Technol. 1995, 4, 358–366. [Google Scholar] [CrossRef]
- Oberkampf, W.L.; Talpallikar, M. Analysis of High Velocity Oxygen Fuel (HVOF) Thermal Spray Torch, Part 1: Numerical formulation. In Proceedings of the 7th National Thermal Spray Conference, Boston, MA, USA, 20–24 June 1994; pp. 381–386.
- Oberkampf, W.L.; Talpallikar, M. Analysis of High Velocity Oxygen Fuel (HVOF) Thermal Spray Torch, Part 2: Computational Results. In Proceedings of the 7th National Thermal Spray Conference, Boston, MA, USA, 20–24 June 1994; pp. 387–392.
- Hassan, B.; Oberkampf, W.L.; Neiser, R.A.; Roemer, T.J. Computational fluid dynamics analysis of a high-velocity oxygen-fuel (HVOF) thermal spray torch. In Proceedings of the 8th National Thermal Spray Conference, Houston, TX, USA, 11–15 September 1995.
- Westbrook, C.K.; Dryer, F.L. Simplified reaction mechanisms for the oxidation of hydrocarbon fuels in flames. Combust. Sci. Technol. 1981, 27, 31–43. [Google Scholar] [CrossRef]
- Li, M.; Christofides, P.D. Multi-scale modeling and analysis of an industrial HVOF thermal spray process. Chem. Eng. Sci. 2005, 60, 3649–3669. [Google Scholar] [CrossRef]
- Hossainpour, S.; Binesh, A.R. A CFD study of sensitive parameters effect on the combustion in a high velocity oxygen-fuel thermal spray gun. Proc. World Acad. Sci. Eng. Technol. 2008, 41, 213–220. [Google Scholar]
- Kamali, R.; Binesh, A.R. The importance of sensitive parameters effect on the combustion in a high velocity oxygen-fuel spray system. Int. Commun. Heat Mass Transf. 2009, 36, 978–983. [Google Scholar] [CrossRef]
- Dolatabadi, A.; Mostaghimi, J.; Pershin, V. Effect of a cylindrical shroud on particle conditions in high velocity oxy-fuel spray process. Sci. Technol. Adv. Mater. 2002, 3, 245–255. [Google Scholar] [CrossRef]
- Dolatabadi, A.; Mostaghimi, J.; Pershin, V. Effect of a cylindrical shroud on particle conditions in high velocity oxy-fuel (HVOF) spray process. J. Mater. Process. Technol. 2003, 137, 214–224. [Google Scholar] [CrossRef]
- Srivatsan, V.R.; Dolatabadi, A. Simulation of particle-shock interaction in a high velocity oxygen fuel process. J. Therm. Spray Technol. 2006, 15, 481–487. [Google Scholar] [CrossRef]
- Kamnis, S.; Gu, S. Numerical modeling of propane combustion in a high velocity oxygen-fuel thermal spray gun. Chem. Eng. Process. 2006, 45, 246–253. [Google Scholar] [CrossRef]
- Kamnis, S.; Gu, S. 3-D modeling of kerosene-fuelled HVOF thermal spray gun. Chem. Eng. Sci. 2006, 61, 5427–5439. [Google Scholar] [CrossRef]
- Tabbara, H.; Gu, S. Computational simulation of liquid-fuelled HVOF thermal spraying. Surf. Coat. Technol. 2009, 204, 676–684. [Google Scholar] [CrossRef]
- Dongmo, E.; Wenzelburger, M.; Gadow, R. Analysis and optimization of the HVOF process by combined experimental and numerical approaches. Surf. Coat. Technol. 2008, 202, 4470–4478. [Google Scholar] [CrossRef]
- Kadyrov, E.; Evdokimenko, Y.; Kisel, V.; Kadyrov, V.; Worzala, F. Interaction of particles with carrier gas in HVOF spraying systems. J. Therm. Spray Technol. 1994, 3, 389–397. [Google Scholar] [CrossRef]
- Cheng, D.; Xu, Q.; Trapaga, G.; Lavernia, E.J. A numerical study of high-velocity oxygen fuel thermal spraying process, part I: Gas phase dynamics. Metall. Mater. Trans. A 2001, 32A, 1609–1620. [Google Scholar] [CrossRef]
- Li, M.; Christofides, P.D. Modeling and analysis of HVOF thermal spray process accounting for powder size distribution. Chem. Eng. Sci. 2003, 58, 849–857. [Google Scholar] [CrossRef]
- Li, M.; Shi, D.; Christofides, P.D. Diamond jet hybrid HVOF thermal spray: Gas-phase and particle behavior modeling and feedback control design. Ind. Eng. Chem. Res. 2004, 43, 3632–3652. [Google Scholar] [CrossRef]
- Gu, S.; Eastwick, C.N.; Simmons, K.A.; McCartney, D.G. Computational fluid dynamic modeling of gas flow characteristics in a high-velocity oxy-fuel thermal spray system. J. Therm. Spray Technol. 2001, 10, 461–469. [Google Scholar]
- Yang, X.; Eidelman, S. Numerical analysis of a high velocity oxygen-fuel thermal spray system. J. Therm. Spray Technol. 1996, 5, 175–184. [Google Scholar] [CrossRef]
- Joshi, S.V.; Sivakumar, R. Particle behaviour during high velocity oxy-fuel spraying. Surf. Coat. Technol. 1991, 50, 67–74. [Google Scholar] [CrossRef]
- Joshi, S.V. A prediction model to assist plasma and HVOF spraying. Mater. Lett. 1992, 14, 31–36. [Google Scholar] [CrossRef]
- Sobolev, V.V.; Guilemany, J.M.; Garmier, J.C.; Calero, J.A. Modeling of particle movement and thermal behaviour during high velocity oxy-fuel spraying. Surf. Coat. Technol. 1994, 63, 181–187. [Google Scholar] [CrossRef]
- Sobolev, V.V.; Guilemany, J.M.; Miguel, J.R.; Calero, J.A. Influence of in-flight dissolution process on composite powder particle (WC-Ni) behaviour during high velocity oxy-fuel spraying. Surf. Coat. Technol. 1996, 81, 136–145. [Google Scholar] [CrossRef]
- Sobolev, V.V.; Guilemany, J.M.; Martin, A.J.; Calero, J.A. Modeling of the in-flight behaviour of the stainless steel powder particles in high velocity oxy-fuel spraying. J. Mater. Process. Technol. 1998, 79, 213–216. [Google Scholar] [CrossRef]
- Ait-Messaoudene, N.; Abdellah El-hadj, A. Effect of the substrate and of thermophoresis on the acceleration and heating of particles during HVOF spraying. Surf. Coat. Technol. 1998, 106, 140–144. [Google Scholar] [CrossRef]
- Cheng, D.; Xu, Q.; Trapaga, G.; Lavernia, E.J. The effect of particle size and morphology on the in-flight behavior of particles during high-velocity oxyfuel thermal spraying. Metall. Mater. Trans. B 2001, 32B, 525–535. [Google Scholar] [CrossRef]
- Ganser, G.H. A rational approach to drag prediction of spherical and nonspherical particles. Powder Technol. 1993, 77, 143–152. [Google Scholar] [CrossRef]
- Gu, S.; Kamnis, S. Numerical modeling of in-flight particle dynamics of non-spherical powder. Surf. Coat. Technol. 2009, 203, 3485–3490. [Google Scholar] [CrossRef]
- Kamnis, S.; Gu, S. Study of in-flight and impact dynamics of nonspherical particles from HVOF guns. J. Therm. Spray Technol. 2010, 19, 31–41. [Google Scholar] [CrossRef]
- Hackett, C.M.; Settles, G.S. The influence of nozzle design on HVOF spray particle velocity and temperature. In Proceedings of 8th National Thermal Spray Conference, Houston, TX, USA, 11–15 September 1995.
- Li, M.; Christofides, P.D. Computational study of particle in-flight behavior in the HVOF thermal spray process. Chem. Eng. Sci. 2006, 61, 6540–6552. [Google Scholar] [CrossRef]
- Lopez, A.R.; Hassan, B.; Oberkampf, W.L.; Neiser, R.A.; Roemer, T.J. Computational fluid dynamics analysis of a wire-feed high-velocity oxygen fuel (HVOF) thermal spray torch. J. Therm. Spray Technol. 1998, 7, 374–382. [Google Scholar] [CrossRef]
- Kamnis, S.; Gu, S.; Zeoli, N. Mathematical modeling of Inconel 718 particles in HVOF thermal spraying. Surf. Coat. Technol. 2008, 202, 2715–2724. [Google Scholar] [CrossRef]
- Kamnis, S.; Gu, S.; Lu, T.J.; Chen, C. Computational simulation of thermally sprayed WC-Co powder. Comput. Mater. Sci. 2008, 43, 1172–1182. [Google Scholar] [CrossRef]
- Katanoda, H.; Yamamoto, H.; Matsuo, K. Numerical simulation on supersonic flow in high-velocity oxy-fuel thermal spray gun. J. Therm. Sci. 2006, 15, 65–70. [Google Scholar] [CrossRef]
- Katanoda, H. Quasi-one dimensional analysis of the effects of pipe friction, cooling and nozzle geometry on gas/particle flows in HVOF thermal spray gun. Mater. Trans. 2006, 47, 2791–2797. [Google Scholar] [CrossRef]
- Hassan, B.; Lopez, A.R.; Oberkampf, W.L. Computational analysis of a three-dimensional high-velocity oxygen fuel (HVOF) thermal spray torch. J. Therm. Spray Technol. 1998, 7, 71–77. [Google Scholar] [CrossRef]
- Zeoli, N.; Gu, S.; Kamnis, S. Numerical simulation of in-flight particle oxidation during thermal spraying. Comput. Chem. Eng. 2008, 32, 1661–1668. [Google Scholar] [CrossRef]
- Neiser, R.A.; Smith, M.F.; Dykhuizen, R.C. Oxidation in wire HVOF sprayed steel. J. Therm. Spray Technol. 1998, 7, 537–545. [Google Scholar] [CrossRef]
- Dobler, K.; Kreye, H.; Schwetzke, R. Oxidation of stainless steel in the high velocity oxy-fuel process. J. Therm. Spray Technol. 2000, 9, 407–413. [Google Scholar] [CrossRef]
- Sakaki, K.; Shimizu, Y. Effect of the increase in the entrance convergent section length of the gun nozzle on the high-velocity oxygen fuel and cold spray process. J. Therm. Spray Technol. 2001, 10, 487–496. [Google Scholar] [CrossRef]
- Baik, J.S.; Kim, Y.J. Effect of nozzle shape on the performance of high velocity oxygen-fuel thermal spray system. Surf. Coat. Technol. 2008, 202, 5457–5462. [Google Scholar] [CrossRef]
- Kim, S.H.; Kim, Y.J. Flow characteristics in compact thermal spray coating systems with minimum length nozzle. Plasma Sci. Technol. 2009, 11, 550–554. [Google Scholar] [CrossRef]
- Dolatabadi, A.; Pershin, V.; Mostaghimi, J. New attachment for controlling gas flow in the HVOF process. J. Therm. Spray Technol. 2005, 14, 91–99. [Google Scholar] [CrossRef]
- Dai, S.L.; Delplanque, J.P.; Lavernia, E.J. Microstructural characteristics of 5083 Al alloys processed by reactive spray deposition for net-shape manufacturing. Metall. Mater. Trans. A 1998, 29, 2597–2611. [Google Scholar] [CrossRef]
- Haider, A.; Levenspiel, O. Drag coefficient and terminal velocity of spherical and nonspherical particles. Powder Technol. 1989, 58, 63–70. [Google Scholar] [CrossRef]
- Eidelman, S.; Yang, X. Three dimensional simulation of HVOF spray deposition of nanoscale materials. Nanostruct. Mater. 1997, 9, 79–84. [Google Scholar] [CrossRef]
- Ma, M.; Hill, R.M. Superhydrophobic surfaces. Curr. Opin. Colloid Interface Sci. 2006, 11, 193–202. [Google Scholar] [CrossRef]
- Nosonovsky, M.; Bhushan, B. Superhydrophobic surfaces and emerging applications: Non-adhesion, energy, green engineering. Curr. Opin. Colloid Interface Sci. 2009, 14, 270–280. [Google Scholar] [CrossRef]
- Bhushan, B.; Jung, Y.C. Natural and biomimetic artificial surfaces for superhydrophobicity, self-cleaning, low adhesion, and drag reduction. Prog. Mater. Sci. 2011, 56, 1–108. [Google Scholar] [CrossRef]
- Moghtadernejad, S.; Tembely, M.; Jadidi, M.; Esmail, N.; Dolatabadi, A. Shear driven droplet shedding and coalescence on a superhydrophobic surface. Phys. Fluids 2015, 27. [Google Scholar] [CrossRef]
- Moghtadernejad, S.; Jadidi, M.; Tembely, M.; Esmail, N.; Dolatabadi, A. Concurrent droplet coalescence and solidification on surfaces with various wettabilities. J. Fluids Eng. 2015, 137. [Google Scholar] [CrossRef]
- Moghtadernejad, S.; Mohammadi, M.; Jadidi, M.; Tembely, M.; Dolatabadi, A. Shear driven droplet shedding on surfaces with various wettabilities. SAE Int. J. Aerosp. 2013, 6, 459–464. [Google Scholar] [CrossRef]
- Moghtadernejad, S.; Jadidi, M.; Esmail, N.; Dolatabadi, A. Shear driven droplet coalescence and rivulet formation. Proc. Inst. Mech. Engrs. Part. C J. Mech. Engng. Sci. 2015, in press. [Google Scholar] [CrossRef]
- Moghtadernejad, S. Dynamics of Droplet Shedding and Coalescence under the Effect of Shear Flow. Ph.D. Thesis, Concordia University, Montreal, QC, Canada, 2014. [Google Scholar]
- Moghtadernejad, S.; Jadidi, M.; Esmail, N.; Dolatabadi, A. SPH simulation of rivulet dynamics on surfaces with various wettabilities. SAE Int. J. Aerosp. 2015. in Press. [Google Scholar] [CrossRef]
- Moghtadernejad, S.; Jadidi, M.; Tembely, M.; Dolatabadi, A. Shear driven rivulet dynamics on surfaces with various wettabilities. In Proceedings of the ASME 2014 International Mechanical Engineering Congress and Exposition, Montreal, QC, Canada, 14–20 November 2014.
- Aghasibeig, M.; Mousavi, M.; Ben Ettouill, F.; Moreau, C.; Wuthrich, R.; Dolatabadi, A. Electrocatalytically active nickel-based electrode coatings formed by atmospheric and suspension plasma spraying. J. Therm. Spray Technol. 2014, 23, 220–226. [Google Scholar] [CrossRef]
- Pawlowski, L. Suspension and solution thermal spray coatings. Surf. Coat. Technol. 2009, 203, 2807–2829. [Google Scholar] [CrossRef]
- Toma, F.L.; Berger, L.M.; Jacquet, D.; Wicky, D.; Villaluenga, I.; de Miguel, Y.R.; Lindelov, J.S. Comparative study on the photocatalytic behavior of titanium oxide thermal sprayed coatings from powders and suspensions. Surf. Coat. Technol. 2009, 203, 2150–2156. [Google Scholar] [CrossRef]
- Killinger, A.; Kuhn, M.; Gadow, R. High-velocity suspension flame spraying (HVSFS), a new approach for spraying nanoparticles with hypersonic speed. Surf. Coat. Technol. 2006, 201, 1922–1929. [Google Scholar] [CrossRef]
- Fazilleau, J.; Delbos, C.; Rat, V.; Coudert, J.F.; Fauchais, P.; Pateyron, B. Phenomena involved in suspension plasma spraying part 1: Suspension injection and behavior. Plasma Chem. Plasma Process 2006, 26, 371–391. [Google Scholar] [CrossRef]
- Fauchais, P.; Montavon, G.; Bertrand, G. From powders to thermally sprayed coatings. J. Therm. Spray Technol. 2010, 19, 56–80. [Google Scholar] [CrossRef]
- Gadow, R.; Killinger, A.; Rauch, J. Introduction to high-velocity suspension flame spraying (HVSFS). J. Therm. Spray Technol. 2008, 17, 655–661. [Google Scholar] [CrossRef]
- Yu, W.; France, D.M.; Routbort, J.L.; Choi, S.U.S. Review and comparison of nanofluid thermal conductivity and heat transfer enhancements. Heat Transfer Eng. 2008, 29, 432–460. [Google Scholar] [CrossRef]
- Ghadimi, A.; Saidur, R.; Metselaar, H.S.C. A review of nanofluid stability properties and characterization in stationary conditions. Int. J. Heat Mass Transfer 2011, 54, 4051–4068. [Google Scholar] [CrossRef]
- Schramm, L.L. Suspensions: Fundamentals and Applications in the Petroleum Industry; The American Chemical Society: Washington, DC, USA, 1996. [Google Scholar]
- Litchfield, D.W.; Baird, D.G. The rheology of high aspect ratio nano-particle filled liquids. Rheol. Rev. 2006, 1–60. [Google Scholar]
- Tanvir, S.; Qiao, L. Surface tension of nanofluid-type fuels containing suspended nanomaterials. Nanoscale Res. Lett. 2012, 7, 226:1–226:10. [Google Scholar] [CrossRef] [PubMed]
- Beck, M.P. Thermal Conductivity of Metal Oxide Nanofluids. PhD Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2008. [Google Scholar]
- Pabst, W. Fundamental considerations on suspension rheology. Ceram. Silik. 2004, 48, 6–13. [Google Scholar]
- Gauglitz, P.A.; Mahoney, L.A.; Blanchard, J.; Bamberger, J.A. Surface tension estimates for droplet formation in slurries with low concentrations of hydrophobic particles, polymer flocculants or surface-active contaminants. Report for the U.S. Department of Energy DE-AC05–76RL01830; Pacific Northwest National Laboratory: Richland, Washington, DC, USA, June 2011. [Google Scholar]
- Berg, J.C. An. Introduction to Interfaces and Colloids: The Bridge to Nanoscience; World Scientific: Singapore, 2010. [Google Scholar]
- Brian, B.W.; Chen, J.C. Surface tension of solid-liquid slurries. AIChE J. 1987, 33, 316–318. [Google Scholar] [CrossRef]
- Okubo, T. Surface tension of structured colloidal suspensions of polystyrene and silica spheres at the air-water interface. J. Colloid Interface Sci. 1995, 171, 55–62. [Google Scholar] [CrossRef]
- Waghmare, P.R.; Mitra, S.K. Contact angle hysteresis of microbead suspensions. Langmuir 2010, 26, 17082–17089. [Google Scholar] [CrossRef] [PubMed]
- Salager, J.L. Surfactants Types and Uses; FIRP Laboratory Booklet No: 300A; University of Los Andes: Merido, Venezuela, 2002. [Google Scholar]
- Schramm, L.L.; Stasiuk, E.N.; Marangoni, D.G. Surfactants and their applications. Annu. Rep. Prog. Chem. Sect. C Phys. Chem. 2003, 99, 3–48. [Google Scholar] [CrossRef]
- Thiessen, D.B.; Man, K.F. Surface Tension Measurement. In Measurement, Instrumentation, and Sensors Hndbook, 2nd ed.; Webster, J.G., Eren, H., Eds.; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Kihm, K.D.; Deignan, P. Dynamic surface tension of coal-water slurry fuels. Fuel 1995, 74, 295–300. [Google Scholar] [CrossRef]
- Bechtel, S.E.; Cooper, J.A.; Forest, M.G.; Petersson, N.A.; Reichard, D.L.; Saleh, A.; Venkataramanan, V. A new model to determine dynamic surface tension and elongational viscosity using oscillating jet measurements. J. Fluid Mech. 1995, 293, 379–403. [Google Scholar] [CrossRef]
- Bechtel, S.E.; Forest, M.G.; Youssef, N.T.; Zhou, H. The effect of dynamic surface tension on the oscillation of slender elliptical Newtonian jets. J. Appl. Mech. 1998, 65, 694–704. [Google Scholar] [CrossRef]
- Bechtel, S.E.; Koelling, K.W.; Nguyen, W.; Tan, G. A new technique for the measurement of the dynamic evolution of surface tension. J. Colloid Interface Sci. 2002, 245, 142–162. [Google Scholar] [CrossRef] [PubMed]
- Amini, G.; Dolatabadi, A. Capillary instability of elliptic liquid jets. Phys. Fluids 2011, 23. [Google Scholar] [CrossRef]
- Amini, G.; Ihme, M.; Dolatabadi, A. Effect of gravity on capillary instability of liquid jets. Phys. Rev. E 2013, 87. [Google Scholar] [CrossRef]
- Amini, G.; Dolatabadi, A. Axis-switching and breakup of low-speed elliptic liquid jets. Int. J. Multiph. Flow 2012, 42, 96–103. [Google Scholar] [CrossRef]
- Ronay, M. Determination of the dynamic surface tension of inks from the capillary instability of jets. J. Colloid Interface Sci. 1978, 66, 55–67. [Google Scholar] [CrossRef]
- Howell, E.A.; Megaridis, C.M.; McNallan, M. Dynamic surface tension measurements of molten Sn/Pb solder using oscillating slender elliptical jets. Int. J. Heat Fluid Flow 2004, 25, 91–102. [Google Scholar] [CrossRef]
- Alakoc, U.; Megaridis, C.M.; McNallan, M.; Wallace, D.B. Dynamic surface tension measurements with submillisecond resolution using a capillary-jet instability technique. J. Colloid Interface Sci. 2004, 276, 379–391. [Google Scholar] [CrossRef] [PubMed]
- Dumouchel, C. On the experimental investigation on primary atomization of liquid streams. Exp. Fluids 2008, 45, 371–422. [Google Scholar] [CrossRef]
- Ashgriz, N. Handbook of Atomization and Sprays: Theory and Applications; Springer: New York, NY, USA, 2011. [Google Scholar]
- Birouk, M.; Lekic, N. Liquid jet breakup in quiescent atmosphere: A review. At. Sprays 2009, 19, 501–528. [Google Scholar] [CrossRef]
- Leroux, S. Stabilite d’un jet Liquide Cylindrique, Influence de Fortes Pressions Ambiantes. Ph.D. Thesis, University of Rouen, Rouen, France, 1996. [Google Scholar]
- Wu, P.K.; Miranda, R.F.; Faeth, G.M. Effects of initial flow conditions on primary breakup of nonturbulent and turbulent round liquid jets. At. Sprays 1995, 5, 175–196. [Google Scholar] [CrossRef]
- Hiroyasu, H.; Arai, M.; Shimizu, M. Break-up length of a liquid jet and internal flow in a nozzle. In Proceedings of the 5th International Conference on Liquid Atomization and Spray Systems, Gaithersburg, MD, USA, 15–18 July 1991; pp. 275–282.
- Hiroyasu, H.; Shimizu, M.; Arai, M. The breakup length of high speed jet in a high pressure gaseous atmosphere. In Proceedings of the 2nd International Conference on Liquid Atomization and Spray Systems, Madison, WI, USA, 20–24 June 1982; pp. 69–74.
- Arai, M.; Shimizu, M.; Hiroyasu, H. Break-up length and spray angle of high speed jet. In Proceedings of the 3rd International Conference on Liquid Atomization and Spray Systems, London, UK, 8–10 July 1985.
- Lin, S.P.; Reitz, R.D. Drop and spray formation from a liquid jet. Annu. Rev. Fluid Mech. 1998, 30, 85–105. [Google Scholar] [CrossRef]
- Wu, P.K.; Tseng, L.K.; Faeth, G.M. Primary breakup in gas/liquid mixing layers for turbulent liquids. At. Sprays 1992, 2, 295–317. [Google Scholar] [CrossRef]
- Hiroyasu, H. Spray breakup mechanism from hole-type nozzle and its applications. At. Sprays 2000, 10, 511–527. [Google Scholar] [CrossRef]
- Arai, M.; Shimizu, M.; Hiroyasu, H. Breakup length and spray formation mechanism of a high speed liquid jet. In Proceedings of the 4th International Conference on Liquid Atomization and Spray Systems, Sendai, Japan, 22–24 August 1988; pp. 177–184.
- Arai, M.; Shimizu, M.; Hiroyasu, H. Similarity between the break-up lengths of a high speed liquid jet in atmospheric and pressurized conditions. In Proceedings of the 5th International Conference on Liquid Atomization and Spray Systems, Gaithersburg, USA, 15–18 July 1991; pp. 563–570.
- Arai, M.; Amagai, K. Surface wave transition before breakup of a laminar liquid jet. Int. J. Heat Fluid Flow 1999, 20, 507–512. [Google Scholar] [CrossRef]
- Reitz, R.D.; Bracco, F.V. Mechanism of atomization of a liquid jet. Phys. Fluids 1982, 25, 1730–1742. [Google Scholar] [CrossRef]
- Sterling, A.M.; Sleicher, C.A. The instability of capillary jets. J. Fluid Mech. 1975, 68, 477–495. [Google Scholar] [CrossRef]
- Ranz, W.E. On Sprays and Spraying; Department of Engineering Research Bulletin 65, The Pennsylvania State University: University Park, PA, USA, 1956. [Google Scholar]
- Miesse, C.C. Correlation of experimental data on the disintegration of liquid jets. Ind. Eng. Chem. 1955, 47, 1690–1701. [Google Scholar] [CrossRef]
- Reitz, R. Atomization and Other Breakup Regimes of a Liquid Jet. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 1978. [Google Scholar]
- Dan, T.; Yamamoto, T.; Senda, J.; Fujimoto, H. Effect of nozzle configurations for characteristics of non-reacting diesel fuel sprays. SAE 1997 Trans. J. Engines 1997, 106. [Google Scholar] [CrossRef]
- Vahedi Tafreshi, H.; Pourdeyhimi, B. The effects of nozzle geometry of water jet breakup at high Reynolds numbers. Exp. Fluids 2003, 35, 364–371. [Google Scholar] [CrossRef]
- Chigier, N.; Reitz, R.D. Regimes of Jet Breakup and Breakup Mechanisms (Physical Aspects). In Recent Advances in Spray Combustion: Spray Atomization and Drop Burning Phenomena; Kuo, K.K., Ed.; American Institute of Aeronautics and Astronautics Inc.: Reston, VA, USA, 1996; Volume 1, pp. 109–135. [Google Scholar]
- Cavaliere, A.; Ragucci, R.; Noviello, C. Bending and break-up of a liquid jet in a high pressure airflow. Exp. Therm. Fluid Sci. 2003, 27, 449–454. [Google Scholar] [CrossRef]
- Inamura, T.; Nagai, N. Spray characteristics of liquid jets traversing subsonic airstreams. J. Propul. Power 1997, 13, 250–256. [Google Scholar] [CrossRef]
- Inamura, T.; Nagai, N.; Hirai, T.; Asano, H. Disintegration phenomena of metalized slurry fuel jets in high speed air stream. In Proceedings of the 5th International Conference on Liquid Atomization and Spray Systems, Gaithersburg, MD, USA, 15–18 July 1991; pp. 839–846.
- Inamura, T. Trajectory of a liquid jet traversing subsonic airstreams. J. Propul. Power 2000, 16, 155–157. [Google Scholar] [CrossRef]
- Ingebo, R.D. Aerodynamic effect of combustor inlet-air pressure on fuel jet atomization. In Proceedings of the AIAA/SAE/ASME 20th Joint Propulsion Conference, Cincinnati, OH, USA, 11–13 June 1984.
- Wu, P.K.; Kirkendall, K.A.; Fuller, R.P.; Nejad, A.S. Breakup processes of liquid jets in subsonic crossflows. J. Propul. Power 1997, 13, 64–72. [Google Scholar] [CrossRef]
- Tambe, S.B.; Jeng, S.M.; Mongia, H.; Hsiao, G. Liquid jets in subsonic crossflow. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, ND, USA, 10–13 January 2005.
- Chen, T.H.; Smith, C.R.; Schommer, D.G.; Nejad, A.S. Multi-zone behavior of transverse liquid jet in high-speed flow. In Proceedings of the 31st AIAA Aerospace Sciences Meeting and Exhibit, Reno, ND, USA, 11–14 January 1993.
- Lubarsky, E.; Shcherbik, D.; Bibik, O.; Gopala, Y.; Zinn, B.T. Fuel Jet in Cross Flow—Experimental Study of Spray Characteristics. In Advanced Fluid Dynamics; Oh, H.W., Ed.; INTECH Open Access Publisher: Vienna, Austria, 2012. [Google Scholar]
- Becker, J.; Hassa, C. Breakup and atomization of a kerosene jet in crossflow at elevated pressure. At. Sprays 2002, 11, 49–67. [Google Scholar] [CrossRef]
- Less, D.M.; Schetz, J.A. Transient behavior of liquid jets injected normal to a high-velocity gas stream. AIAA J. 1986, 24, 1979–1986. [Google Scholar] [CrossRef]
- Bellofiore, A. Experimental and Numerical Study of Liquid Jets Injected in High-Density Air Crossflow. Ph.D. Thesis, University of Studies of Naples Federico II, Naples, Italy, 2007. [Google Scholar]
- Sallam, K.A.; Aalburg, C.; Faeth, G.M. Breakup of round nonturbulent liquid jets in gaseous crossflow. AIAA J. 2004, 42, 2529–2540. [Google Scholar] [CrossRef]
- Ashgriz, N. Atomization of a liquid jet in a crossflow. In Proceedings of the 4th International Meeting of Advances in Thermofluids, Melaka, Malaysia, 3–4 October 2011.
- Stenzler, J.N.; Lee, J.G.; Santavicca, D.A. Penetration of liquid jets in a crossflow. In Proceedings of the 41st Aerospace Science Meeting and Exhibit, Reno, ND, USA, 6–9 January 2003.
- Lakhamraju, R.R.; Jeng, S.M. Liquid jet breakup studies in subsonic air stream at elevated temperatures. In Proceedings of the 18th Annual Conference on Liquid and Atomization and Spray Systems, Irvine, CA, USA, 22–25 May 2005.
- Elshamy, O.M.; Jeng, S.M. Study of liquid jet in crossflow at elevated ambient pressures. In Proceedings of the 18th Annual Conference on Liquid and Atomization and Spray Systems, Irvine, CA, USA, 22–25 May 2005.
- Leong, M.Y.; McDonell, V.G.; Samvelsen, G.S. Effect of ambient pressure on an airblast spray injected into a crossflow. J. Propul. Power 2001, 17, 1076–1084. [Google Scholar]
- Costa, M.; Melo, M.J.; Sousa, J.M.M.; Levy, Y. Spray characteristics of angled liquid injection into subsonic crossflows. AIAA J. 2006, 44, 646–653. [Google Scholar] [CrossRef]
- Ahn, K.; Kim, J.; Yoon, Y. Effect of orifice internal flow on transverse injection into subsonic crossflows: Cavitation and hydraulic flip. At. Sprays 2006, 16, 15–34. [Google Scholar]
- Nguyen, T.T.; Karagozian, A.R. Liquid fuel jet in subsonic crossflow. J. Propul. Power 1992, 8, 21–29. [Google Scholar] [CrossRef]
- Inamura, T.; Nagai, N.; Watanabe, T.; Yatsuyanagi, N. Disintegration of liquid and slurry jets traversing subsonic airstreams. In Proceedings of the 3rd World Conference on Experimental Heat Transfer, Fluid Mechanics, and Thermodynamics, Honolulu, HI, USA, 31 October–5 November 1993.
- Masuda, B.J.; Hack, R.L.; McDonell, V.G.; Oskam, G.W.; Cramb, D.J. Some observations of liquid jet in crossflow. In Proceedings of 18th Annual Conference on Liquid and Atomization and Spray Systems, Irvine, CA, USA, 22–25 May 2005.
- Schetz, J.A.; Padhye, A. Penetration and breakup of liquids in subsonic airstreams. AIAA J. 1977, 15, 1385–1390. [Google Scholar] [CrossRef]
- Birouk, M.; Azzopardi, B.J.; Stabler, T. Primary breakup of a viscous liquid jet in a cross airflow. Part. Part. Syst. Charact. 2003, 20, 283–289. [Google Scholar] [CrossRef]
- Yates, C.L. Liquid Injection into a Supersonic Stream; Technical Report AFAPL-TR-71–97; Air Force Aero Propulsion Laboratory: Wright-Patterson Air Force Base, OH, USA, 1972. [Google Scholar]
- Ghenai, C.; Sapmaz, H.; Lin, C.X. Penetration height correlations for non-aerated and aerated transverse liquid jets in supersonic cross flow. Exp. Fluids 2009, 46, 121–129. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, L.; Li, Q.; Li, C. Experimental investigation on structures and velocity of liquid jets in a supersonic crossflow. Appl. Phys. Lett. 2014, 105. [Google Scholar] [CrossRef]
- Lin, K.C.; Ryan, M.; Carter, C.; Gruber, M.; Raffoul, C. Raman scattering measurements of gaseous ethylene jets in Mach 2 supersonic crossflow. J. Propul. Power 2010, 26, 503–513. [Google Scholar] [CrossRef]
- Farago, Z.; Chigier, N. Morphological classification of disintegration of round liquid jets in a coaxial air stream. At. Sprays 1992, 2, 137–153. [Google Scholar]
- Mayer, W.O.H.; Branam, R. Atomization characteristics on the surface of a round liquid jet. Exp. Fluids 2004, 36, 528–539. [Google Scholar] [CrossRef]
- Lasheras, J.C.; Villermaux, E.; Hopfinger, E.J. Break-up and atomization of a round water jet by a high-speed annular air jet. J. Fluid Mech. 1998, 357, 351–379. [Google Scholar] [CrossRef]
- Lasheras, J.C.; Hopfinger, E.J. Liquid jet instability and atomization in a coaxial gas stream. Annu. Rev. Fluid Mech. 2000, 32, 275–308. [Google Scholar] [CrossRef]
- Marmottant, P.H.; Villermaux, E. On spray formation. J. Fluid Mech. 2004, 498, 73–111. [Google Scholar] [CrossRef]
- Leroux, B.; Delabroy, O.; Lacas, F. Experimental study of coaxial atomizers scaling, part I: Dense core zone. At. Sprays 2007, 17, 381–407. [Google Scholar] [CrossRef]
- Porcheron, E.; Carreau, J.L.; Prevost, L.; Le Visage, D.; Roger, F. Effect of injection gas density on coaxial liquid jet atomization. At. Sprays 2002, 12, 209–227. [Google Scholar] [CrossRef]
- Eroglu, H.; Chigier, N.; Farago, Z. Caoaxial atomizer liquid intact lengths. Phys. Fluids 1991, 3, 303–308. [Google Scholar] [CrossRef]
- Hardalupas, Y.; Tsai, R.F.; Whitelaw, J.H. Primary breakup of coaxial airblast atomizers. In Proceedings of the International Conference on Liquid Atomization and Spray Systems, Manchester, UK, 6–8 July 1998; pp. 42–47.
- Woodward, R.D.; Burch, R.L.; Kuo, K.K.; Cheung, F.B. Correlation of intact-liquid core length for coaxial injectors. In Proceedings of the International Conference on Liquid Atomization and Spray Systems, Rouen, France, 18–22 July 1994; pp. 105–112.
- Gorokhovski, M.; Herrmann, M. Modeling primary atomization. Annu. Rev. Fluid Mech. 2008, 40, 343–366. [Google Scholar] [CrossRef]
- Tryggvason, G.; Scardovelli, R.; Zaleski, S. Direct Numerical Simulations of Gas-Liquid Multiphase Flows; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Prosperetti, A.; Tryggvason, G. Computational Methods for Multiphase Flow; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Violeau, D. Fluid mechanics and the SPH method: Theory and Applications; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Braun, S.; Hofler, C.; Koch, R.; Bauer, H. Modeling fuel injection in gas turbines using the meshless smoothed particle hydrodynamics method. In Proceedings of ASME Turbo Expo, Turbine Technical Conference and Exposition, San Antonio, TX, USA, 3–7 June 2013.
- Muzaferija, S.; Peric, M. Computation of free-surface flows using the finite volume method and moving grids. Numer. Heat Transf. Part B 1997, 32, 369–384. [Google Scholar] [CrossRef]
- Huang, W.; Russell, R.D. Adaptive Moving Mesh Methods; Springer: New York, NY, USA, 2011. [Google Scholar]
- Tukovic, Z.; Jasak, H. A moving mesh finite volume interface tracking method for surface tension dominated interfacial fluid flow. Comput. Fluids 2012, 55, 70–84. [Google Scholar] [CrossRef]
- Unverdi, S.O.; Tryggvason, G. A front-tracking method for viscous, incompressible, multi-fluid flows. J. Comput. Phys. 1992, 100, 25–37. [Google Scholar] [CrossRef]
- Du, J.; Fix, B.; Glimm, J.; Jia, X.; Li, X.; Li, Y.; Wu, L. A simple package for front tracking. J. Comput. Phys. 2006, 213, 613–628. [Google Scholar] [CrossRef]
- Pozrikidis, C. Interfacial dynamics for Stokes flow. J. Comput. Phys. 2001, 169, 250–301. [Google Scholar] [CrossRef]
- Pozrikidis, C. Modeling and Simulation of Capsules and Biological Cells; Chapmann & Hall/CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Rider, W.J.; Kothe, D.B. Reconstructing volume tracking. J. Comput. Phys. 1998, 141, 112–152. [Google Scholar] [CrossRef]
- Osher, S.; Sethian, J.A. Fronts propagating with curvature dependent speed: Algorithms based on Hamilton-Jacobi formulations. J. Comput. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef]
- Sussman, M.; Smereka, P.; Osher, S. A level set approach for computing solutions to incompressible two phase flow. J. Comput. Phys. 1994, 114, 146–159. [Google Scholar] [CrossRef]
- Francois, M.M.; Cummins, S.J.; Dendy, E.D.; Kothe, D.B.; Sicilian, J.M.; Williams, M.W. A balanced-force algorithm for continuous and sharp interfacial surface tension models within a volume tracking framework. J. Comput. Phys. 2006, 213, 141–173. [Google Scholar] [CrossRef]
- Deshpande, S.S.; Anumolu, L.; Trujillo, M.F. Evaluating the performance of the two-phase flow solver interFoam. Comput. Sci. Disc. 2012, 5. [Google Scholar] [CrossRef]
- Buelow, P.; Mao, C.; Smith, S.; Bretz, D. Application of two-phase CFD analysis to a prefilming pure-airblast atomizer. In Proceedings of the 37th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Salt Lake City, UT, USA, 8–11 July 2011.
- De Viliers, E.; Gosman, A.D.; Weller, H.G. Large Eddy Simulation of Primary Diesel Spray Atomization. SAE 2004 Ttans. J. Energies 2004, 113. [Google Scholar] [CrossRef]
- Srinivasan, V.; Salazar, A.; Saito, K. Investigation of the primary breakup of round turbulent liquid jets using LES/VOF technique. In Proceedings of the 36th AIAA Fluid Dynamics Conference and Exhibit, San Francisco, NY, USA, 5–8 June 2006.
- Zeoli, N.; Tabbara, H.; Gu, S. CFD modeling of primary breakup during metal powder atomization. Chem. Eng. Sci. 2011, 66, 6498–6504. [Google Scholar] [CrossRef]
- Farvardin, E.; Dolatabadi, A. Numerical simulation of the breakup of elliptical liquid jet in still air. J. Fluids Eng. 2013, 135. [Google Scholar] [CrossRef]
- Fuster, D.; Bague, A.; Boeck, T.; Moyne, L.L.; Leboissetier, A.; Popinet, S.; Ray, P.; Scardovelli, R.; Zaleski, S. Simulation of primary atomization with an octree adaptive mesh refinement and VOF method. Int. J. Multiph. Flow 2009, 35, 550–565. [Google Scholar] [CrossRef]
- Mehravaran, K. Direct simulations of primary atomization in moderate-speed diesel fuel injection. Int. J. Mater. Mech. Manuf. 2013, 1, 207–209. [Google Scholar] [CrossRef]
- Salvador, F.J.; Romero, J.V.; Rosello, M.D.; Jaramillo, D. Numerical simulation of primary atomization in diesel spray at low injection pressure. J. Comput. Appl. Math. 2016, 291, 94–102. [Google Scholar] [CrossRef]
- Chen, X.; Ma, D.; Yang, V.; Popinet, S. High-fidelity simulations of impinging jet atomization. At. Sprays 2013, 23, 1079–1101. [Google Scholar] [CrossRef]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Ghods, S.; Herrmann, M. A consistent rescaled momentum transport method for simulating large density ratio incompressible multiphase flows using level set methods. Phys. Scr. 2013. [Google Scholar] [CrossRef]
- Rudman, M. A volume-tracking method for incompressible multifluid flows with large density variations. Int. J. Numer. Methods Fluids 1998, 28, 357–378. [Google Scholar] [CrossRef]
- Xiao, F.; Ii, S.; Chen, C. Revisit to the thinc scheme: A simple algebraic VOF algorithm. J. Comput. Phys. 2011, 230, 7086–7092. [Google Scholar] [CrossRef]
- Cummins, S.J.; Francois, M.M.; Kothe, D.B. Estimating curvature from volume fractions. Comput. Struct. 2005, 83, 425–434. [Google Scholar] [CrossRef]
- Renardy, Y.; Renardy, M. PROST: A parabolic reconstruction of surface tension for the volume-of-fluid method. J. Comput. Phys. 2002, 183, 400–421. [Google Scholar] [CrossRef]
- Popinet, S. An accurate adaptive solver for surface-tension-driven interfacial flows. J. Comput. Phys. 2009, 228, 5838–5866. [Google Scholar] [CrossRef]
- Ubbink, O.; Issa, R. A method for capturing sharp fluid interfaces on arbitrary meshes. J. Comput. Phys. 1999, 153, 26–50. [Google Scholar] [CrossRef]
- OpenCFD Ltd. Homepage. Available online: http//www.openfoam.com (accessed on 14 August 2015).
- Rusche, H. Computational Fluid Dynamics of Dispersed Two-Phase Flows at High Phase Fractions. Ph.D. Thesis, Imperial College of Science Technology and Medicine, London, UK, 2002. [Google Scholar]
- Suponitsky, V.; Froese, A.; Barsky, S. Richtmyer-Meshkov instability of a liquid-gas interface driven by a cylindrical imploding pressure wave. Comput. Fluids 2014, 89, 1–19. [Google Scholar] [CrossRef]
- Jadidi, M.; Tembely, M.; Moghtadernejad, S.; Dolatabadi, A. A coupled level set and volume of fluid method with application to compressible two-phase flow. In Proceedings of the 22nd Annual Conference of the CFD Society of Canada, Toronto, ON, Canada, 1–4 June 2014.
- Farvardin, E.; Dolatabadi, A. Simulation of biodiesel jet in cross flow. In Proceedings of the 12th Triennial International Conference on Liquid Atomization and Spray Systems, Heidelberg, Germany, 2–6 September 2012.
- Xiao, F.; Dianat, M.; McGuirk, J.J. Large eddy simulation of liquid-jet primary breakup in air crossflow. AIAA J. 2013, 51, 2878–2893. [Google Scholar] [CrossRef]
- Sussman, M.; Puckett, E.G. A coupled level set and volume-of-fluid method for computing 3D and axisymmetric incompressible two-phase flows. J. Comput. Phys. 2000, 162, 301–337. [Google Scholar] [CrossRef]
- Sussman, M. A second order coupled level set and volume-of-fluid method for computing growth and collapse of vapor bubbles. J. Comput. Phys. 2003, 187, 110–136. [Google Scholar] [CrossRef]
- Kees, C.E.; Akkerman, I.; Farthing, M.W.; Bazilevs, Y. A conservative level set method suitable for variable-order approximations and unstructured meshes. J. Comput. Phys. 2011, 230, 4536–4558. [Google Scholar] [CrossRef]
- Sethian, J.A.; Smereka, P. Level set methods for fluid interfaces. Annu. Rev. Fluid Mech. 2003, 35, 341–372. [Google Scholar] [CrossRef]
- Albadawi, A.; Donoghue, D.B.; Robinson, A.J.; Murray, D.B.; Delaure, Y.M.C. Influence of surface tension implementation in volume of fluid and coupled volume of fluid with level set methods for bubble growth and detachment. Int. J. Multiph. Flow 2013, 53, 11–28. [Google Scholar] [CrossRef]
- Herrmann, M. A parallel Eulerian interface tracking/Lagrangian point particle multi-scale coupling procedure. J. Comput. Phys. 2010, 229, 745–759. [Google Scholar]
- Herrmann, M. Detailed numerical simulations of the primary atomization of a turbulent liquid jet in crossflow. J. Eng. Gas. Turbines Power 2010, 132. [Google Scholar] [CrossRef]
- Herrmann, M. The influence of density ratio on the primary atomization of a turbulent liquid jet in crossflow. Proc. Combust. Inst. 2011, 33, 2079–2088. [Google Scholar] [CrossRef]
- Tomar, G.; Fuster, D.; Zaleski, S.; Popinet, S. Multiscale simulations of primary atomization. Comput. Fluids 2010, 39, 1864–1874. [Google Scholar]
- Arienti, M.; Li, X.; Soteriou, M.C.; Eckett, C.A.; Sussman, M.; Jensen, R.J. Coupled level-set/volume-of-fluid method for simulation of injector atomization. J. Propul. Power 2013, 29, 147–157. [Google Scholar] [CrossRef]
- Guildenbecher, D.R.; Lopez-Rivera, C.; Sojka, P.E. Secondary atomization. Exp. Fluids 2009, 46, 371–402. [Google Scholar] [CrossRef]
- Shraiber, A.A.; Podvysotsky, A.M.; Dubrovsky, V.V. Deformation and breakup of drops by aerodynamic forces. At. Sprays 1996, 6, 667–692. [Google Scholar] [CrossRef]
- Hsiang, L.P.; Faeth, G.M. Near-limit drop deformation and secondary breakup. Int. J. Multiph. Flow 1992, 18, 635–652. [Google Scholar] [CrossRef]
- Pilch, M.; Erdman, C.A. Use of breakup time data and velocity history data to predict the maximum size of stable fragments for acceleration-induced breakup of a liquid drop. Int. J. Multiph. Flow 1987, 13, 741–757. [Google Scholar] [CrossRef]
- Hsiang, L.P.; Faeth, G.M. Drop deformation and breakup due to shock wave and steady disturbances. Int. J. Multiph. Flow 1995, 21, 545–560. [Google Scholar] [CrossRef]
- Brodkey, R.S. The Phenomena of Fluid Motions; Addison-Wesley: Reading, MA, USA, 1967. [Google Scholar]
- Gelfand, B.E. Droplet breakup phenomena in flows with velocity lag. Prog. Energy Combust. Sci. 1996, 22, 201–265. [Google Scholar] [CrossRef]
- Dai, Z.; Faeth, G.M. Temporal properties of secondary drop breakup in the multimode breakup regime. Int. J. Multiph. Flow 2001, 27, 217–236. [Google Scholar] [CrossRef]
- Ranger, A.A.; Nicholls, J.A. Aerodynamic shattering of liquid drops. AIAA J. 1969, 7, 285–290. [Google Scholar]
- Taylor, G.I. The Shape and Acceleration of a Drop in High-Speed Air Stream. In The Scientific Papers of Sir Geoffrey Ingram Taylor; Batchelor, G.K., Ed.; Cambridge University Press: Cambridge, UK, 1963. [Google Scholar]
- Reitz, R.D. Mechanisms of atomization processes in High-pressure Vaporizing Sprays. At. Spray Technol. 1987, 3, 309–337. [Google Scholar]
- Patterson, M.A.; Reitz, R.D. Modeling spray atomization with the kelvin-helmholtz/rayleigh-taylor hybrid model. At. Sprays 1999, 9, 623–650. [Google Scholar]
- Drazin, P.G.; Reid, W.H. Hydrodynamic Stability, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Choudhury, P.R. Slurry fuels. Prog. Energy Combust. Sci. 1992, 18, 409–427. [Google Scholar] [CrossRef]
- Gan, Y.; Qiao, L. Combustion characteristics of fuel droplets with addition of nano and micron-sized aluminum particles. Combust. Flame 2011, 158, 354–368. [Google Scholar] [CrossRef]
- Gan, Y.; Lim, Y.S.; Qiao, L. Combustion of nanofluid fuels with addition of boron and iron particles at dilute and dense concentrations. Combust. Flame 2012, 159, 1732–1740. [Google Scholar] [CrossRef]
- Sirignano, W.A. Fluid Dynamics and Transport of Droplets and Sprays; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Miller, R.S.; Harstad, K.; Bellan, J. Evaluation of equilibrium and non-equilibrium evaporation models for many droplet gas-liquid flow simulations. Int. J. Multiph. Flow 1998, 24, 1025–1055. [Google Scholar] [CrossRef]
- Sazhin, S.S. Advanced models of fuel droplet heating and evaporation. Prog. Energy Combust. Sci. 2006, 32, 162–214. [Google Scholar] [CrossRef]
- Taleby, M.; Hossainpour, S. Numerical investigation of high velocity suspension flame spraying. J. Therm. Spray Technol. 2012, 21, 1163–1172. [Google Scholar] [CrossRef]
- Gozali, E.; Kamnis, S.; Gu, S. Numerical investigation of combustion and liquid feedstock in high velocity suspension flame spraying process. Surf. Coat. Technol. 2013, 228, 176–186. [Google Scholar] [CrossRef]
- Gozali, E.; Mahrukh, M.; Gu, S.; Kamnis, S. Numerical analysis of multicomponent suspension droplets in high-velocity flame spray process. J. Therm. Spray Technol. 2014, 23, 940–949. [Google Scholar] [CrossRef] [Green Version]
- Basu, S.; Cetegen, B.M. Modeling of liquid ceramic precursor droplets in a high velocity oxy-fuel flame jet. Acta Mater. 2008, 56, 2750–2759. [Google Scholar] [CrossRef]
- Tabbara, H.; Gu, S. A study of liquid droplet disintegration for the development of nanostructured coatings. AIChE J. 2012, 58, 3533–3544. [Google Scholar] [CrossRef]
- Dongmo, E.; Killinger, A.; Wenzelburger, M.; Gadow, R. Numerical approach and optimization of the combustion and gas dynamics in high velocity suspension flame spraying (HVSFS). Surf. Coat. Technol. 2009, 203, 2139–2145. [Google Scholar] [CrossRef]
- Dongmo, E.; Gadow, R.; Killinger, A.; Wenzelburger, M. Modeling of combustion as well as heat, mass, and momentum transfer during thermal spraying by HVOF and HVSFS. J. Therm. Spray Technol. 2009, 18, 896–908. [Google Scholar] [CrossRef]
- Jadidi, M.; Mousavi, M.; Moghtadernejad, S.; Dolatabadi, A. A three-dimensional analysis of the suspension plasma spray impinging on a flat substrate. J. Therm. Spray Technol. 2015, 24, 11–23. [Google Scholar] [CrossRef]
- Pourang, K.; Moreau, C.; Dolatabadi, A. A three-dimensional analysis of the suspension plasma spray impinging on a curved substrate. In Proceedings of the International Thermal Spray Conference and Exposition, Long Beach, CA, USA, 11–14 May 2015.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jadidi, M.; Moghtadernejad, S.; Dolatabadi, A. A Comprehensive Review on Fluid Dynamics and Transport of Suspension/Liquid Droplets and Particles in High-Velocity Oxygen-Fuel (HVOF) Thermal Spray. Coatings 2015, 5, 576-645. https://doi.org/10.3390/coatings5040576
Jadidi M, Moghtadernejad S, Dolatabadi A. A Comprehensive Review on Fluid Dynamics and Transport of Suspension/Liquid Droplets and Particles in High-Velocity Oxygen-Fuel (HVOF) Thermal Spray. Coatings. 2015; 5(4):576-645. https://doi.org/10.3390/coatings5040576
Chicago/Turabian StyleJadidi, Mehdi, Sara Moghtadernejad, and Ali Dolatabadi. 2015. "A Comprehensive Review on Fluid Dynamics and Transport of Suspension/Liquid Droplets and Particles in High-Velocity Oxygen-Fuel (HVOF) Thermal Spray" Coatings 5, no. 4: 576-645. https://doi.org/10.3390/coatings5040576
APA StyleJadidi, M., Moghtadernejad, S., & Dolatabadi, A. (2015). A Comprehensive Review on Fluid Dynamics and Transport of Suspension/Liquid Droplets and Particles in High-Velocity Oxygen-Fuel (HVOF) Thermal Spray. Coatings, 5(4), 576-645. https://doi.org/10.3390/coatings5040576







