In Silico Screening and Design of Coating Materials for PEMFC Bipolar Plates
Abstract
:1. Introduction
2. Methods
2.1. Computational Methods
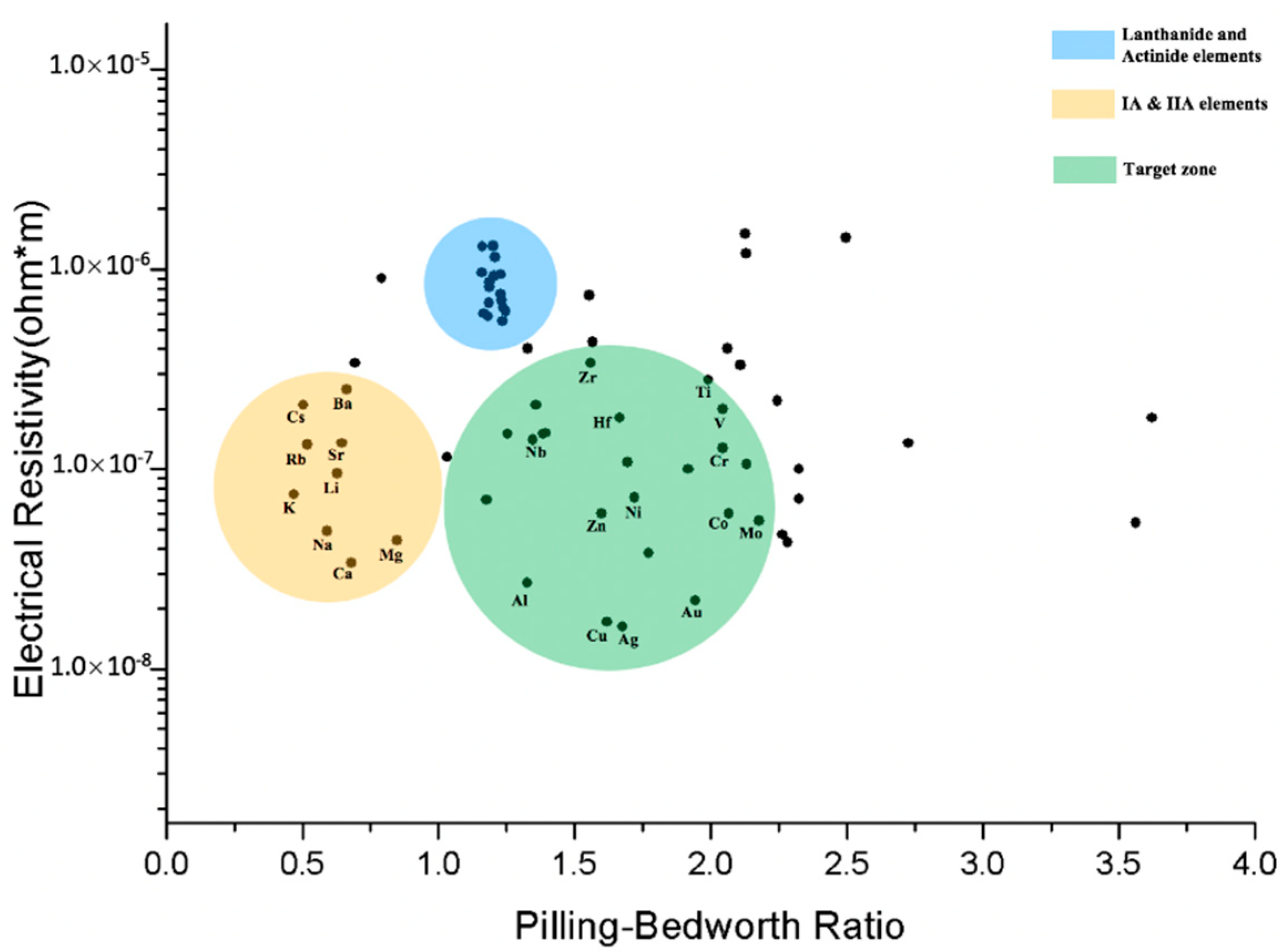
2.1.1. Corrosion Resistance Assessment
2.1.2. Electrical Conductivity Assessment
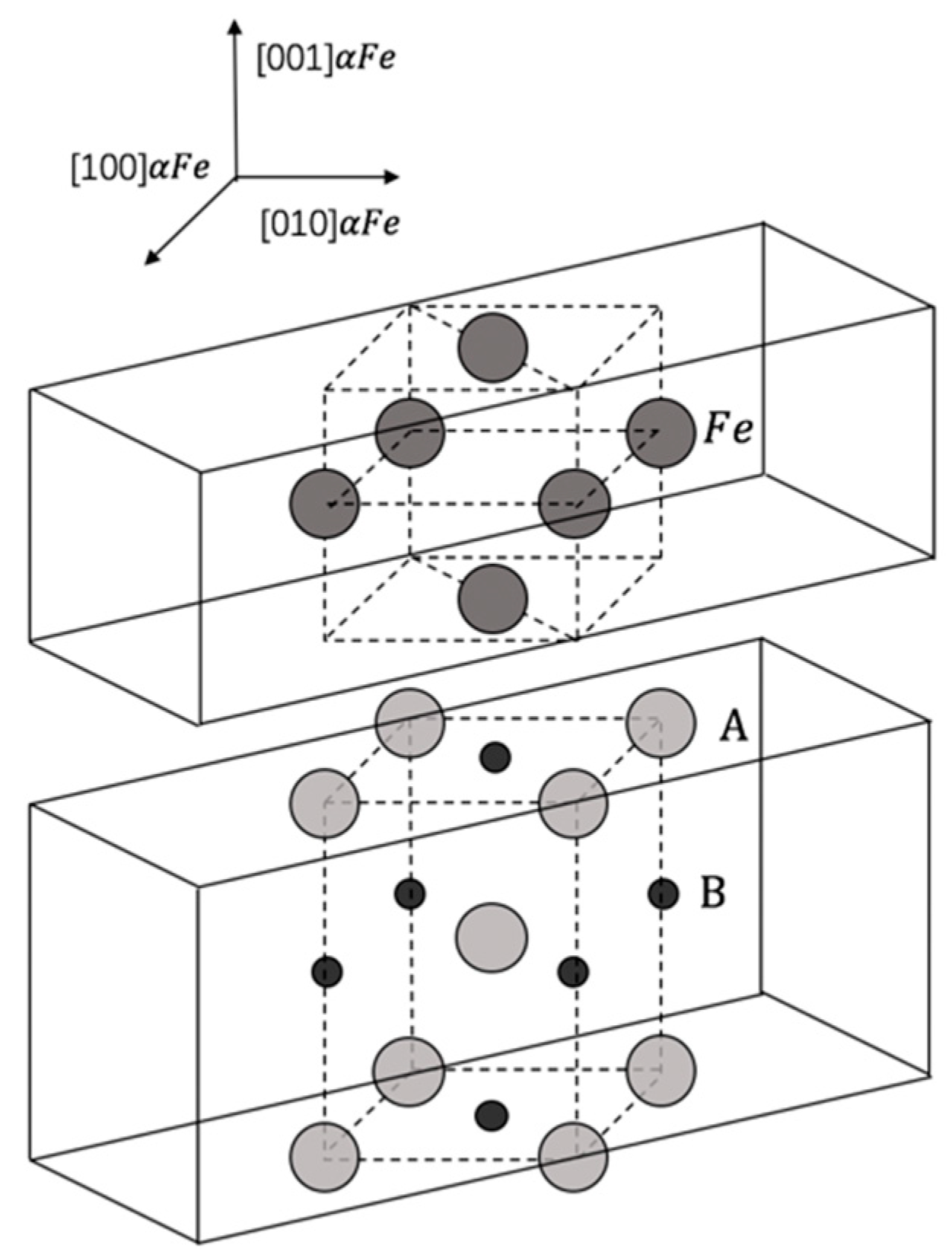
2.1.3. Separation Work of Interface
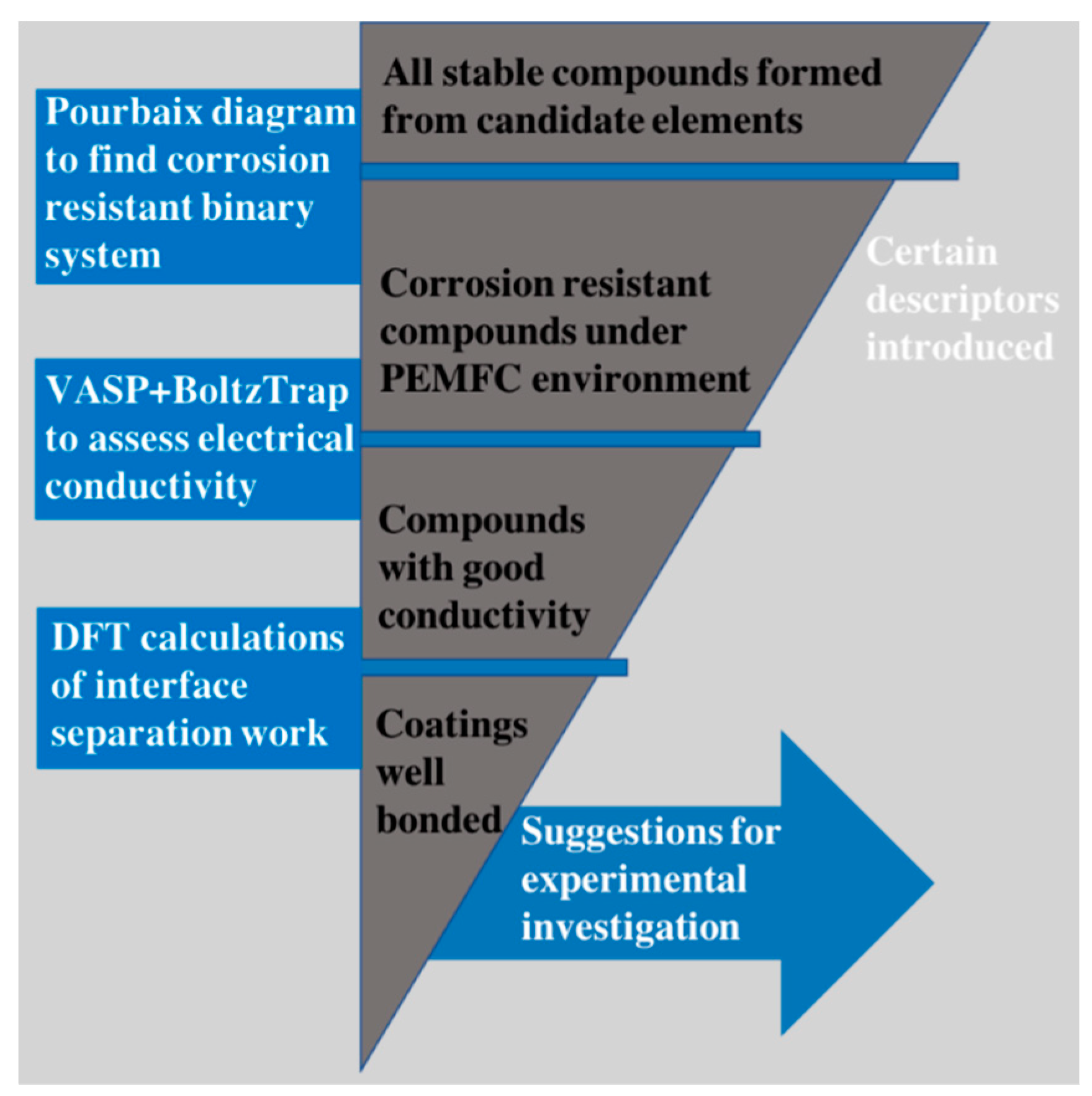
3. Results and Discussion
3.1. Elements Selection
3.2. Electrical Conductivity
3.3. Separation Work
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hinds, G.; Brightman, E. Towards more representative test methods for corrosion resistance of PEMFC metallic bipolar plates. Int. J. Hydrogen Energy 2015, 40, 2785–2791. [Google Scholar] [CrossRef]
- Fetohi, A.E.; Hameed, R.A.; El-Khatib, K.M. Ni–P and Ni–Mo–P modified aluminium alloy 6061 as bipolar plate material for proton exchange membrane fuel cells. J. Power Sources 2013, 240, 589–597. [Google Scholar] [CrossRef]
- Alishahi, M.; Mahboubi, F.; Khoie, S.M.; Aparicio, M.; Hübner, R.; Soldera, F.; Gago, R. Electrochemical behavior of nanocrystalline Ta/TaN multilayer on 316L stainless steel: Novel bipolar plates for proton exchange membrane fuel-cells. J. Power Sources 2016, 322, 1–9. [Google Scholar] [CrossRef]
- Feng, K.; Li, Z.; Sun, H.; Yu, L.; Cai, X.; Wu, Y.; Chu, P.K. C/CrN multilayer coating for polymer electrolyte membrane fuel cell metallic bipolar plates. J. Power Sources 2013, 222, 351–358. [Google Scholar] [CrossRef]
- Bar-On, I.; Kirchain, R.; Roth, R. Technical cost analysis for PEM fuel cells. J. Power Sources 2002, 109, 71–75. [Google Scholar] [CrossRef]
- Mehta, V.; Cooper, J.S. Review and analysis of PEM fuel cell design and manufacturing. J. Power Sources 2003, 114, 32–53. [Google Scholar] [CrossRef]
- Yi, P.; Peng, L.; Zhou, T.; Wu, H.; Lai, X. Cr–N–C multilayer film on 316L stainless steel as bipolar plates for proton exchange membrane fuel cells using closed field unbalanced magnetron sputter ion plating. Int. J. Hydrogen Energy 2013, 38, 1535–1543. [Google Scholar] [CrossRef]
- De Oliveira, M.C.L.; Sayeg, I.J.; Ett, G.; Antunes, R.A. Corrosion behavior of polyphenylene sulfide–carbon black–graphite composites for bipolar plates of polymer electrolyte membrane fuel cells. Int. J. Hydrogen Energy 2014, 39, 16405–16418. [Google Scholar] [CrossRef]
- De Las Heras, N.; Roberts, E.P.L.; Langton, R.; Hodgson, D.R. A review of metal separator plate materials suitable for automotive PEM fuel cells. Energy Environ. Sci. 2009, 2, 206–214. [Google Scholar] [CrossRef]
- Wang, S.; Hou, M.; Zhao, Q.; Jiang, Y.; Wang, Z.; Li, H.; Fu, Y.; Shao, Z. Ti/(Ti, Cr) N/CrN multilayer coated 316L stainless steel by arc ion plating as bipolar plates for proton exchange membrane fuel cells. J. Energy Chem. 2017, 26, 168–174. [Google Scholar] [CrossRef]
- Zhang, H.; Lin, G.; Hou, M.; Hu, L.; Han, Z.; Fu, Y.; Shao, G.S.; Yi, B. CrN/Cr multilayer coating on 316L stainless steel as bipolar plates for proton exchange membrane fuel cells. J. Power Sources 2012, 198, 176–181. [Google Scholar] [CrossRef]
- Yu, H.; Yang, L.; Zhu, L.; Jian, X.; Wang, Z.; Jiang, L. Anticorrosion properties of Ta-coated 316L stainless steel as bipolar plate material in proton exchange membrane fuel cells. J. Power Sources 2009, 191, 495–500. [Google Scholar] [CrossRef]
- Nordin, M.; Herranen, M.; Hogmark, S. Influence of lamellae thickness on the corrosion behaviour of multilayered PVD TiN/CrN coatings. Thin Solid Films 1999, 348, 202–209. [Google Scholar] [CrossRef]
- Chandra, R.; Chawla, A.K.; Kaur, D.; Ayyub, P. Structural, optical and electronic properties of nanocrystalline TiN films. Nanotechnology 2005, 16, 3053. [Google Scholar] [CrossRef]
- Holdren, J.P. Materials Genome Initiative for Global Competitiveness; National Science and Technology Council OSTP: Washington, DC, USA, 2011.
- Greeley, J.; Jaramillo, T.F.; Bonde, J.; Chorkendorff, I.B.; Nã¸Rskov, J.K. Computational high-throughput screening of electrocatalytic materials for hydrogen evolution. Nat. Mater. 2006, 5, 909–913. [Google Scholar] [CrossRef] [PubMed]
- Kirklin, S.; Meredig, B.; Wolverton, C. High-Throughput computational screening of new Li-ion battery anode materials. Adv. Energy Mater. 2013, 3, 252–262. [Google Scholar] [CrossRef]
- Toher, C.; Plata, J.J.; Levy, O.; de Jong, M.; Asta, M.; Nardelli, M.B.; Curtarolo, S. High-throughput computational screening of thermal conductivity, Debye temperature and Grüneisen parameter using a quasi-harmonic Debye Model. Phys. Rev. B 2014, 90, 174107. [Google Scholar] [CrossRef]
- Okimoto, N.; Futatsugi, N.; Fuji, H.; Suenaga, A.; Morimoto, G.; Yanai, R.; Ohno, Y.; Narumi, T.; Taiji, M. High-performance drug discovery: Computational screening by combining docking and molecular dynamics simulations. PLoS Comput. Biol. 2009, 5, e1000528. [Google Scholar] [CrossRef] [PubMed]
- Tong, M.; Lan, Y.; Yang, Q.; Zhong, C. High-throughput computational screening and design of nanoporous materials for methane storage and carbon dioxide capture. Green Energy Environ. 2018, 3, 107–119. [Google Scholar] [CrossRef]
- Xu, C.; Gao, W. Pilling-Bedworth ratio for oxidation of alloys. Mater. Res. Innov. 2000, 3, 231–235. [Google Scholar] [CrossRef]
- Jain, A.; Ong, S.P.; Hautier, G.; Chen, W.; Richards, W.D.; Dacek, S.; Gholia, S.; Gunter, D.; Skinner, D.; Ceder, G.; et al. Commentary: The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater. 2013, 1, 011002. [Google Scholar] [CrossRef] [Green Version]
- Pourbaix, D.; O’KEEKE, T.J. Encyclopedia of Materials: Science and Technology; Elsevier: Amsterdam, The Netherlands, 2001; Volume 3, pp. 7774–7781. [Google Scholar]
- Ding, R.; Shang, J.X.; Wang, F.H.; Chen, Y. Electrochemical Pourbaix diagrams of Ni Ti alloys from first-principles calculations and experimental aqueous states. Comput. Mater. Sci. 2018, 143, 431–438. [Google Scholar] [CrossRef]
- Schweitzer, G.K.; Pesterfield, L.L. The Aqueous Chemistry of the Elements; Oxford University Press: New York, NY, USA, 2010. [Google Scholar]
- Persson, K.A.; Waldwick, B.; Lazic, P.; Ceder, G. Prediction of solid-aqueous equilibria: Scheme to combine first-principles calculations of solids with experimental aqueous states. Phys. Rev. B 2012, 85, 235–438. [Google Scholar] [CrossRef]
- Singh, A.K.; Zhou, L.; Shinde, A.; Suram, S.K.; Montoya, J.H.; Winston, D.; Gregoire, J.M.; Persson, K.A. Electrochemical stability of metastable materials. Chem. Mater. 2017, 29, 10159–10167. [Google Scholar] [CrossRef]
- Madsen, G.K.; Singh, D.J. BoltzTraP. A code for calculating band-structure dependent quantities. Comput. Phys. Commun. 2006, 175, 67–71. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, S.; Ahmad, R.; Bilal, M.; Rehman, N.U. DFT studies of thermoelectric properties of R–Au intermetallics at 300 K. J. Rare Earths 2018, 36, 197–202. [Google Scholar] [CrossRef]
- Lee, S.C. Robust mechanical stability, electronic structure, magnetism and thermoelectric properties of CoFeMnSb quaternary Heusler alloy: A first principle study. J. Alloys Compd. 2018, 742, 903–909. [Google Scholar]
- Reshak, A.H. Electronic structure and transport properties of Ba2Cd2Pn3 (Pn = As and Sb): An efficient materials for energy conversion. J. Alloys Compd. 2016, 670, 1–11. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E.; Jepsen, O.; Andersen, O.K. Improved tetrahedron method for Brillouin-zone integrations. Phys. Rev. B 1994, 49, 16223. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Fors, D.H.; Johansson, S.A.; Petisme, M.V.; Wahnström, G. Theoretical investigation of moderate misfit and interface energetics in the Fe/VN system. Comput. Mater. Sci. 2010, 50, 550–559. [Google Scholar] [CrossRef]
- Fors, D.H.; Wahnström, G. Theoretical study of interface structure and energetics in semicoherent Fe(001)/MX(001) systems (M = Sc, Ti, V, Cr, Zr, Nb, Hf, Ta; X = C or N). Phys. Rev. B 2010, 82, 1616–1622. [Google Scholar] [CrossRef]
- Choi, G.; Kim, H.S.; Lee, K.; Park, S.H.; Cha, J.; Chung, I.; Lee, W.B. Study on thermal conductivity and electrical resistivity of Al-Cu alloys obtained by Boltzmann transport equation and first-principles simulation: Semi-empirical approach. J. Alloys Compd. 2017, 727, 1237–1242. [Google Scholar] [CrossRef]
- Gowtham, S.; Arunnellaiappan, T.; Rameshbabu, N. An investigation on pulsed DC plasma electrolytic oxidation of cp-Ti and its corrosion behaviour in simulated body fluid. Surf. Coat. Technol. 2016, 301, 63–73. [Google Scholar]
- Dai, N.; Zhang, L.C.; Zhang, J.; Chen, Q.; Wu, M. Corrosion behavior of selective laser melted Ti-6Al-4V alloy in NaCl solution. Corros. Sci. 2016, 102, 484–489. [Google Scholar] [CrossRef]
- Lawley, A.; Gotman, I.; Gutmanas, E.Y.; Koczak, M.J. Design and Processing of Alloys and Composites from Ultrafine Powders. Adv. Powder Metall. Part. Mater. 1993, 6, 135. [Google Scholar]
- Martinez-Sanchez, R.; Gabanas-Moreno, J.G.; Calderon, H.A.; Umemoto, M. Co-Ti Intermetallics Made by Mechanical Alloying. Mater. Sci. Forum 1996, 225–227, 435–440. [Google Scholar]
- Fatoba, O.S.; Adesina, O.S.; Popoola, A.P.I. Evaluation of microstructure, microhardness, and electrochemical properties of laser-deposited Ti-Co coatings on Ti-6Al-4V Alloy. Int. J. Adv. Manuf. Technol. 2018, 97, 2341–2350. [Google Scholar] [CrossRef]


| Compounds | Common | |||||
|---|---|---|---|---|---|---|
| HfN | 3.12 | −30.61 | −85.19 | −118.21 | 17.1 | 3.9 |
| ZrN | 3.15 | −30.48 | −78.99 | −111.74 | 15.3 | 3.6 |
| TaC | 3.10 | −30.67 | −86.95 | −120.13 | 13.6 | 4.2 |
| CoN | 2.92 | −30.16 | −95.32 | −125.59 | 10.8 | 0.2 |
| Ta2N | 2.98 | −30.61 | −74.57 | −114.43 | 6.41 | 16.7 |
| NbN | 3.06 | −30.34 | −88.94 | −119.51 | 6.33 | 0.4 |
| TiCo | 2.85 | −30.81 | −98.65 | −133.74 | 5.35 | 8.4 |
| CrN | 3.02 | −30.48 | −97.99 | −132.84 | 5.09 | 7.6 |
| TiAl | 2.85 | −30.82 | −85.45 | −117.02 | 4.93 | 1.5 |
| TiCo3 | 3.23 | −30.54 | −70.54 | −114.41 | 4.48 | 20.5 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Yao, L.; Feng, K.; Luo, Z.; Liu, K.; Zhu, H.; Chu, P.K. In Silico Screening and Design of Coating Materials for PEMFC Bipolar Plates. Coatings 2018, 8, 386. https://doi.org/10.3390/coatings8110386
Liu L, Yao L, Feng K, Luo Z, Liu K, Zhu H, Chu PK. In Silico Screening and Design of Coating Materials for PEMFC Bipolar Plates. Coatings. 2018; 8(11):386. https://doi.org/10.3390/coatings8110386
Chicago/Turabian StyleLiu, Longjie, Li Yao, Kai Feng, Zhe Luo, Ke Liu, Hong Zhu, and Paul. K. Chu. 2018. "In Silico Screening and Design of Coating Materials for PEMFC Bipolar Plates" Coatings 8, no. 11: 386. https://doi.org/10.3390/coatings8110386
APA StyleLiu, L., Yao, L., Feng, K., Luo, Z., Liu, K., Zhu, H., & Chu, P. K. (2018). In Silico Screening and Design of Coating Materials for PEMFC Bipolar Plates. Coatings, 8(11), 386. https://doi.org/10.3390/coatings8110386





