Carbon-Coated Nickel Nanoparticles: Effect on the Magnetic and Electric Properties of Composite Materials
Abstract
:1. Introduction
2. Methodology
3. Experimental Results
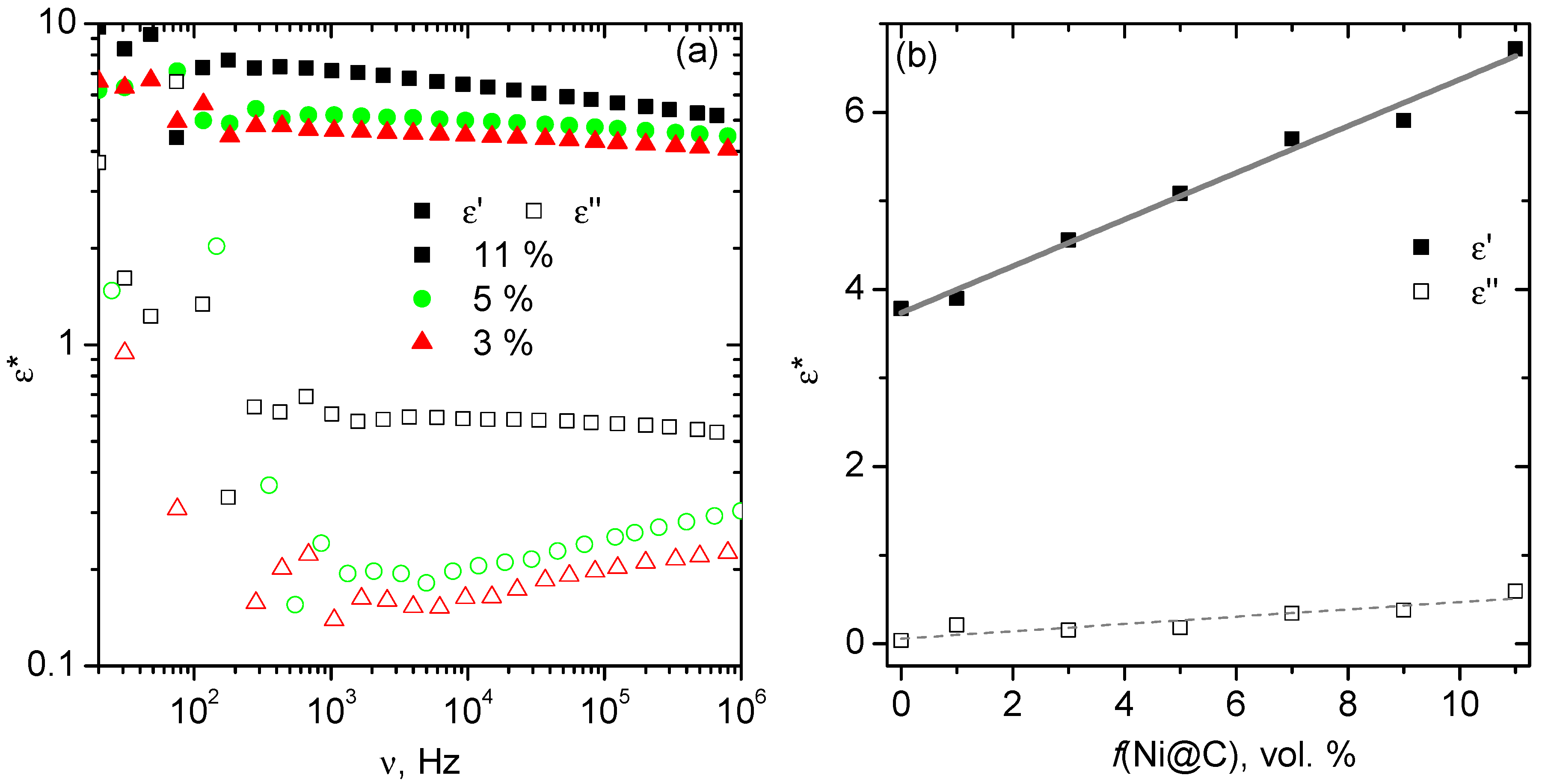
3.1. Dielectric Properties
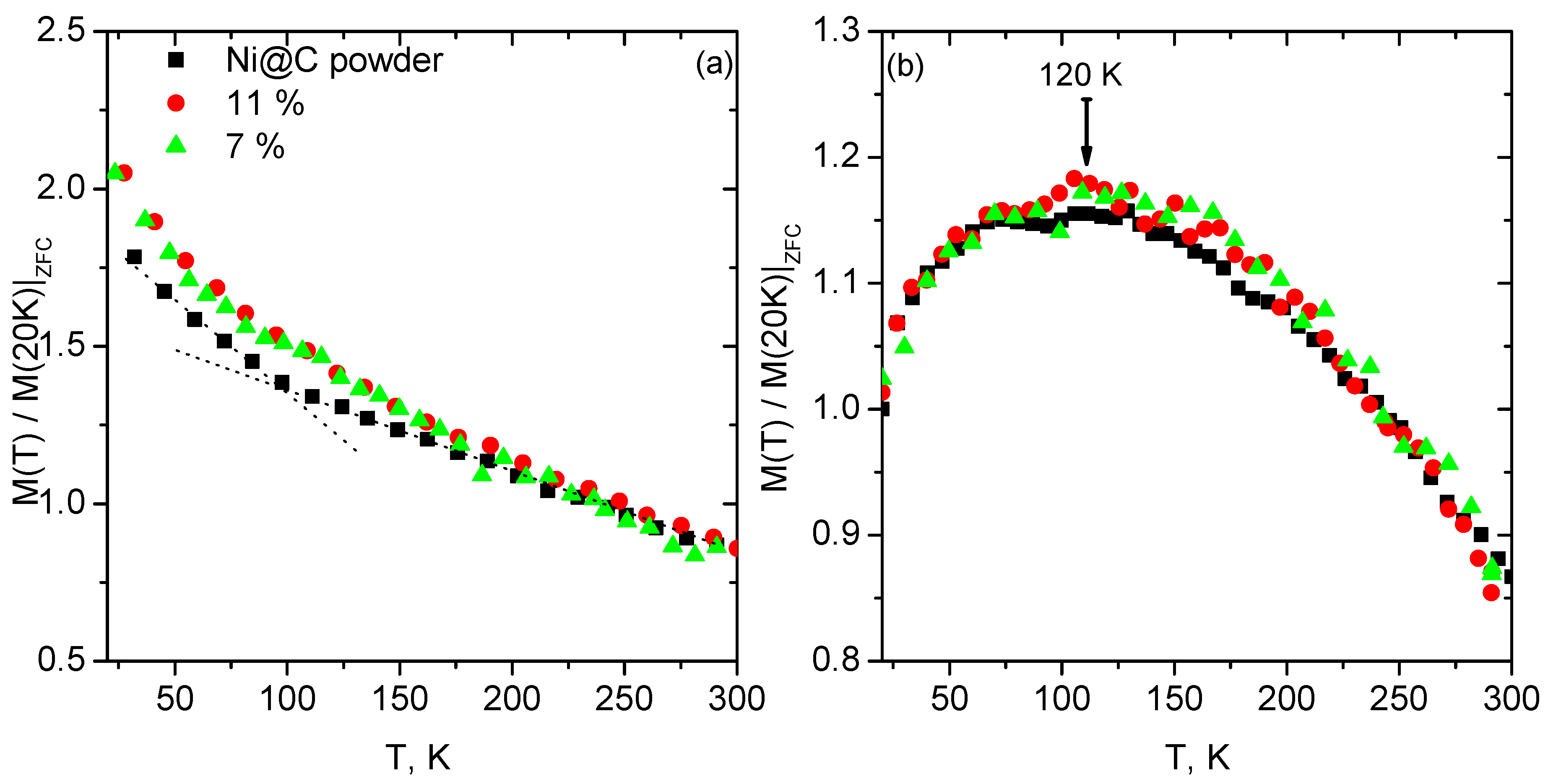
3.2. Magnetic Properties
4. Discussion and Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Ausanio, G.; Hison, C.L.; Iannotti, V.; Lanotte, L.; Lanotte, L. Magneto-piezoresistance in elastomagnetic composites. J. Appl. Phys. 2011, 110, 063903. [Google Scholar] [CrossRef]
- Rocha-Santos, T.A. Sensors and biosensors based on magnetic nanoparticles. TrAC Trends Anal. Chem. 2014, 62, 28–36. [Google Scholar] [CrossRef]
- Freitas, P.; Ferreira, R.; Cardoso, S.; Cardoso, F. Magnetoresistive sensors. J. Phys. Condens. Matter 2007, 19, 165221. [Google Scholar] [CrossRef]
- Mocanu, Z.; Airimioaei, M.; Ciomaga, C.; Curecheriu, L.; Tudorache, F.; Tascu, S.; Iordan, A.; Palamaru, N.; Mitoseriu, L. Investigation of the functional properties of MgxNi1−xFe2O4 ceramics. J. Mater. Sci. 2014, 49, 3276–3286. [Google Scholar] [CrossRef]
- Dumitrescu, A.; Lisa, G.; Iordan, A.; Tudorache, F.; Petrila, I.; Borhan, A.; Palamaru, M.; Mihailescu, C.; Leontie, L.; Munteanu, C. Ni ferrite highly organized as humidity sensors. Mater. Chem. Phys. 2015, 156, 170–179. [Google Scholar] [CrossRef]
- Mohr, R.; Kratz, K.; Weigel, T.; Lucka-Gabor, M.; Moneke, M.; Lendlein, A. Initiation of shape-memory effect by inductive heating of magnetic nanoparticles in thermoplastic polymers. Proc. Nat. Acad. Sci. USA 2006, 103, 3540–3545. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, A.M. Electromagnetic activation of shape memory polymer networks containing magnetic nanoparticles. Macromol. Rapid Commun. 2006, 27, 1168–1172. [Google Scholar] [CrossRef]
- Pankhurst, Q.A.; Connolly, J.; Jones, S.; Dobson, J. Applications of magnetic nanoparticles in biomedicine. J. Phys. D Appl. Phys. 2003, 36, R167. [Google Scholar] [CrossRef]
- Berry, C.C.; Curtis, A.S. Functionalisation of magnetic nanoparticles for applications in biomedicine. J. Phys. D Appl. Phys. 2003, 36, R198. [Google Scholar] [CrossRef]
- Liu, X.; Li, B.; Geng, D.; Cui, W.; Yang, F.; Xie, Z.; Kang, D.; Zhang, Z. (Fe, Ni)/C nanocapsules for electromagnetic-wave-absorber in the whole Ku-band. Carbon 2009, 47, 470–474. [Google Scholar] [CrossRef]
- Wu, N.; Liu, X.; Zhao, C.; Cui, C.; Xia, A. Effects of particle size on the magnetic and microwave absorption properties of carbon-coated nickel nanocapsules. J. Alloys Compd. 2016, 656, 628–634. [Google Scholar] [CrossRef]
- Li, Y.; Wang, J.; Liu, R.; Zhao, X.; Wang, X.; Zhang, X.; Qin, G. Dependence of gigahertz microwave absorption on the mass fraction of Co@C nanocapsules in composite. J. Alloys Compd. 2017, 724, 1023–1029. [Google Scholar] [CrossRef]
- Xie, Z.; Geng, D.; Liu, X.; Ma, S.; Zhang, Z. Magnetic and microwave-absorption properties of graphite-coated (Fe, Ni) nanocapsules. J. Mater. Sci. Technol. 2011, 27, 607–614. [Google Scholar] [CrossRef]
- Liu, X.; Ou, Z.; Geng, D.; Han, Z.; Jiang, J.; Liu, W.; Zhang, Z. Influence of a graphite shell on the thermal and electromagnetic characteristics of FeNi nanoparticles. Carbon 2010, 48, 891–897. [Google Scholar] [CrossRef]
- Fujii, T. PDMS-based microfluidic devices for biomedical applications. Microelectron. Eng. 2002, 61, 907–914. [Google Scholar] [CrossRef]
- Comina, G.; Suska, A.; Filippini, D. PDMS lab-on-a-chip fabrication using 3D printed templates. Lab Chip 2014, 14, 424–430. [Google Scholar] [CrossRef] [PubMed]
- Clarson, S.; Dodgson, K.; Semlyen, J. Studies of cyclic and linear poly (dimethylsiloxanes): 19. Glass transition temperatures and crystallization behavior. Polymer 1985, 26, 930–934. [Google Scholar] [CrossRef]
- Choi, K.M.; Rogers, J.A. A photocurable poly (dimethylsiloxane) chemistry designed for soft lithographic molding and printing in the nanometer regime. J. Am. Chem. Soc. 2003, 125, 4060–4061. [Google Scholar] [CrossRef] [PubMed]
- Xia, Y.; Whitesides, G.M. Soft lithography. Ann. Rev. Mater. Sci. 1998, 28, 153–184. [Google Scholar] [CrossRef]
- Whitesides, G.M.; Ostuni, E.; Takayama, S.; Jiang, X.; Ingber, D.E. Soft lithography in biology and biochemistry. Ann. Rev. Biomed. Eng. 2001, 3, 335–373. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Yang, B. Patterning colloidal crystals and nanostructure arrays by soft lithography. Adv. Funct. Mater. 2010, 20, 3411–3424. [Google Scholar] [CrossRef]
- Jin, X.; Deng, M.; Kaps, S.; Zhu, X.; Hölken, I.; Mess, K.; Adelung, R.; Mishra, Y.K. Study of tetrapodal ZnO-PDMS composites: A comparison of fillers shapes in stiffness and hydrophobicity improvements. PLoS ONE 2014, 9, e106991. [Google Scholar] [CrossRef] [PubMed]
- Canavese, G.; Lombardi, M.; Stassi, S.; Pirri, C.F. Comprehensive characterization of large piezoresistive variation of Ni-PDMS composites. In Applied Mechanics and Materials; Trans Tech Publications: Zurich, Switzerland, 2012; Volume 110, pp. 1336–1344. [Google Scholar]
- Chu, K.; Kim, D.; Sohn, Y.; Lee, S.; Moon, C.; Park, S. Electrical and thermal properties of carbon-nanotube composite for flexible electric heating-unit applications. IEEE Electron Device Lett. 2013, 34, 668–670. [Google Scholar] [CrossRef]
- Chen, D.; Chen, F.; Hu, X.; Zhang, H.; Yin, X.; Zhou, Y. Thermal stability, mechanical and optical properties of novel addition cured PDMS composites with nano-silica sol and MQ silicone resin. Compos. Sci. Technol. 2015, 117, 307–314. [Google Scholar] [CrossRef]
- Varga, Z.; Filipcsei, G.; Zrínyi, M. Magnetic field sensitive functional elastomers with tuneable elastic modulus. Polymer 2006, 47, 227–233. [Google Scholar] [CrossRef]
- Letellier, M.; Macutkevic, J.; Bychanok, D.; Kuzhir, P.; Delgado-Sanchez, C.; Naguib, H.; Mosanenzadeh, S.G.; Fierro, V.; Celzard, A. Modelling the physical properties of glasslike carbon foams. In Journal of Physics: Conference Series; IOP Publishing: Bristow, UK, 2017; Volume 879, p. 012014. [Google Scholar]
- Letellier, M.; Macutkevic, J.; Kuzhir, P.; Banys, J.; Fierro, V.; Celzard, A. Electromagnetic properties of model vitreous carbon foams. Carbon 2017, 122, 217–227. [Google Scholar] [CrossRef]
- Kuzhir, P.P.; Letellier, M.; Bychanok, D.S.; Paddubskaya, O.; Suslyaev, V.I.; Korovin, E.Y.; Baturkin, S.; Fierro, V.; Celzard, A. Electrical properties of carbon foam in the microwave range. Rus. Phys. J. 2017, 59, 1703–1709. [Google Scholar] [CrossRef]
- Galakhov, V.; Shkvarin, A.; Semenova, A.; Uimin, M.; Mysik, A.; Shchegoleva, N.; Yermakov, A.Y.; Kurmaev, E. Characterization of carbon-encapsulated nickel and iron nanoparticles by means of X-ray absorption and photoelectron spectroscopy. J. Phys. Chem. C 2010, 114, 22413–22416. [Google Scholar] [CrossRef]
- Erokhin, A.; Lokteva, E.; Yermakov, A.Y.; Boukhvalov, D.; Maslakov, K.; Golubina, E.; Uimin, M. Phenylacetylene hydrogenation on Fe@C and Ni@C core–shell nanoparticles: about intrinsic activity of graphene-like carbon layer in H2 activation. Carbon 2014, 74, 291–301. [Google Scholar] [CrossRef]
- Tsurin, V.; Yermakov, A.Y.; Uimin, M.; Mysik, A.; Shchegoleva, N.; Gaviko, V.; Maikov, V. Synthesis, structure, and magnetic properties of iron and nickel nanoparticles encapsulated into carbon. Phys. Solid State 2014, 56, 287–301. [Google Scholar] [CrossRef]
- Macutkevic, J.; Kranauskaite, I.; Banys, J.; Moseenkov, S.; Kuznetsov, V.; Shenderova, O. Metal-insulator transition and size dependent electrical percolation in onion-like carbon/polydimethylsiloxane composites. J. Appl. Phys. 2014, 115, 213702. [Google Scholar] [CrossRef]
- Garnett, J.C.M. Colours in Metal Glasses and in Metallic Films. Phils. Trans. R. Soc. Lond. A 1904, 203, 385–420. [Google Scholar] [CrossRef]
- Garboczi, E.J.; Snyder, K.A.; Douglas, J.F.; Thorpe, M.F. Geometrical percolation threshold of overlapping ellipsoids. Phys. Rev. E 1995, 52, 819–828. [Google Scholar] [CrossRef]
- Kirkpatrick, S. Percolation phenomena in higher dimensions: Approach to the mean-field limit. Phys. Rev. Lett. 1976, 36, 69. [Google Scholar] [CrossRef]
- Bychanok, D.; Kanygin, M.; Okotrub, A.V.; Shuba, M.; Paddubskaya, A.; Pliushch, A.; Kuzhir, P.; Maksimenko, S. Anisotropy of the electromagnetic properties of polymer composites based on multiwall carbon nanotubes in the gigahertz frequency range. JETP Lett. 2011, 93, 607–611. [Google Scholar] [CrossRef]
- Fragiadakis, D.; Pissis, P.; Bokobza, L. Glass transition and molecular dynamics in poly (dimethylsiloxane)/silica nanocomposites. Polymer 2005, 46, 6001–6008. [Google Scholar] [CrossRef]
- Vogel, H. The law of the relation between the viscosity of liquids and the temperature. Physical Z 1921, 22, 645–646. [Google Scholar]
- Bai, Y.; Jin, L. Characterization of frequency-dependent glass transition temperature by Vogel–Fulcher relationship. J. Phys. D Appl. Phys. 2008, 41, 152008. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, Z.; Moon, K.S.; Wong, C. Glass transition and relaxation behavior of epoxy nanocomposites. J. Polym. Sci. Part B Polym. Phys. 2004, 42, 3849–3858. [Google Scholar] [CrossRef]
- Becker, C.; Krug, H.; Schmidt, H. Tailoring of thermomechanical properties of thermoplastic nanocomposites by surface modification of nanoscale silica particles. MRS Online Proc. Libr. Arch. 1996, 435. [Google Scholar] [CrossRef]
- Chen, K.; Yang, S. Synthesis of epoxy–montmorillonite nanocomposite. J. Appl. Polym. Sci. 2002, 86, 414–421. [Google Scholar] [CrossRef]
- Ash, B.; Schadler, L.; Siegel, R. Glass transition behavior of alumina/polymethylmethacrylate nanocomposites. Mater. Lett. 2002, 55, 83–87. [Google Scholar] [CrossRef]
- Arrighi, V.; McEwen, I.; Qian, H.; Prieto, M.S. The glass transition and interfacial layer in styrene-butadiene rubber containing silica nanofiller. Polymer 2003, 44, 6259–6266. [Google Scholar] [CrossRef]
- Belovickis, J.; Macutkevic, J.; Svirskas, Š.; Samulionis, V.; Banys, J.; Shenderova, O.; Borjanovic, V. Ultrasonic and dielectric relaxations in PDMS/ZnO nanocomposite. Phys. Status Solidi B 2015, 252, 2778–2783. [Google Scholar] [CrossRef]
- Gass, J.; Poddar, P.; Almand, J.; Srinath, S.; Srikanth, H. Superparamagnetic polymer nanocomposites with uniform Fe3O4 nanoparticle dispersions. Adv. Funct. Mater. 2006, 16, 71–75. [Google Scholar] [CrossRef]
- Kumar, A.; Tandon, R.; Awana, V. Successive spin glass, cluster ferromagnetic, and superparamagnetic transitions in RuSr2Y1.5Ce0.5Cu2O10 complex magneto-superconductor. Eur. Phys. J. B 2012, 85, 238. [Google Scholar] [CrossRef]
- Liu, X.; Huang, K.; Zhou, S.; Zhao, P.; Meridor, U.; Frydman, A.; Gedanken, A. Phase transition from the ferromagnetic to superparamagnetic with a loop shift in 5-nm nickel particles. J. Magn. Magn. Mater. 2006, 305, 504–508. [Google Scholar] [CrossRef]
- Virlan, C.; Tudorache, F.; Pui, A. Tertiary NiCuZn ferrites for improved humidity sensors: A systematic study. Arabian J. Chem. 2018. [Google Scholar] [CrossRef]
- Hou, Y.; Gao, S. Monodisperse nickel nanoparticles prepared from a monosurfactant system and their magnetic properties. J. Mater. Chem. 2003, 13, 1510–1512. [Google Scholar] [CrossRef]
- Ngo, A.; Bonville, P.; Pileni, M. Spin canting and size effects in nanoparticles of nonstoichiometric cobalt ferrite. J. Appl. Phys. 2001, 89, 3370–3376. [Google Scholar] [CrossRef]
- Mishra, A.; Bandyopadhyay, S.; Das, D. Structural and magnetic properties of pristine and Fe-doped NiO nanoparticles synthesized by the co-precipitation method. Mater. Res. Bull. 2012, 47, 2288–2293. [Google Scholar] [CrossRef]
- Sardar, D.; Sengupta, M.; Bordoloi, A.; Ahmed, M.A.; Neogi, S.; Bandyopadhyay, S.; Jain, R.; Gopinath, C.S.; Bala, T. Multiple functionalities of Ni nanoparticles embedded in carboxymethyl guar gum polymer: catalytic activity and superparamagnetism. Appl. Surf. Sci. 2017, 405, 231–239. [Google Scholar] [CrossRef]





| Ni@C vol % | , K | , K | , kHz | , K |
|---|---|---|---|---|
| 11 | 154.9 | 71.1 | 484.4 | 20,206 |
| 9 | 152.3 | 69.7 | 172.1 | 18,423 |
| 7 | 142.8 | 144.6 | 1870.01 | 16,926 |
| 5 | 142.4 | 238.2 | 13,224.7 | 18,199 |
| 3 | 136.3 | 139.5 | 857.8 | 17,960 |
| 1 | 130.1 | 298.0 | 8763.9 | - |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Plyushch, A.; Macutkevič, J.; Banys, J.; Kuzhir, P.; Kalanda, N.; Petrov, A.; Silvestre, C.; Uimin, M.A.; Yermakov, A.Y.; Shenderova, O. Carbon-Coated Nickel Nanoparticles: Effect on the Magnetic and Electric Properties of Composite Materials. Coatings 2018, 8, 165. https://doi.org/10.3390/coatings8050165
Plyushch A, Macutkevič J, Banys J, Kuzhir P, Kalanda N, Petrov A, Silvestre C, Uimin MA, Yermakov AY, Shenderova O. Carbon-Coated Nickel Nanoparticles: Effect on the Magnetic and Electric Properties of Composite Materials. Coatings. 2018; 8(5):165. https://doi.org/10.3390/coatings8050165
Chicago/Turabian StylePlyushch, Artyom, Jan Macutkevič, Jūras Banys, Polina Kuzhir, Nikolay Kalanda, Alexander Petrov, Clara Silvestre, Mikhail A. Uimin, Anatoly Ye. Yermakov, and Olga Shenderova. 2018. "Carbon-Coated Nickel Nanoparticles: Effect on the Magnetic and Electric Properties of Composite Materials" Coatings 8, no. 5: 165. https://doi.org/10.3390/coatings8050165
APA StylePlyushch, A., Macutkevič, J., Banys, J., Kuzhir, P., Kalanda, N., Petrov, A., Silvestre, C., Uimin, M. A., Yermakov, A. Y., & Shenderova, O. (2018). Carbon-Coated Nickel Nanoparticles: Effect on the Magnetic and Electric Properties of Composite Materials. Coatings, 8(5), 165. https://doi.org/10.3390/coatings8050165








