Tunable Perfect Narrow-Band Absorber Based on a Metal-Dielectric-Metal Structure
Abstract
:1. Introduction
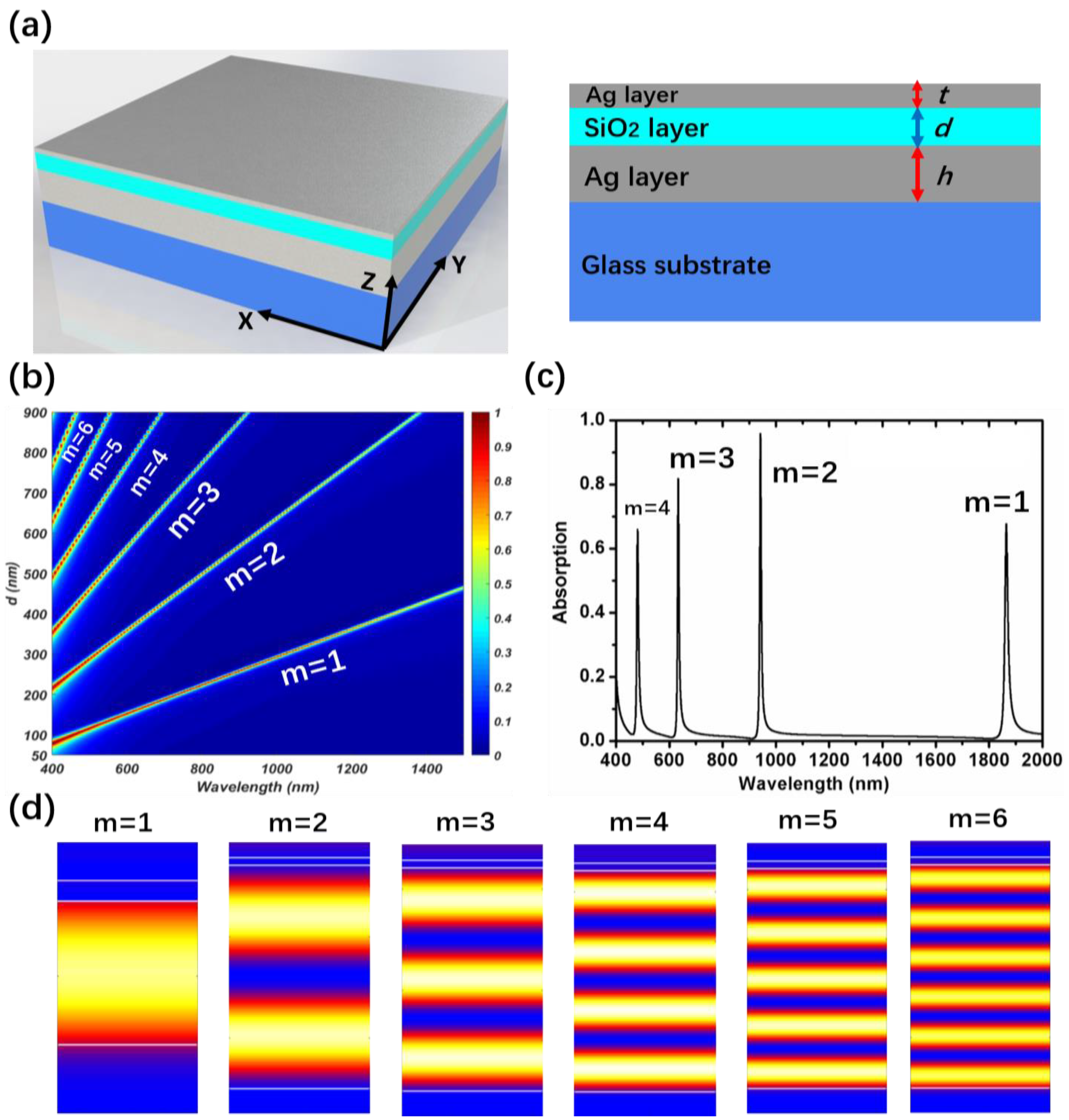
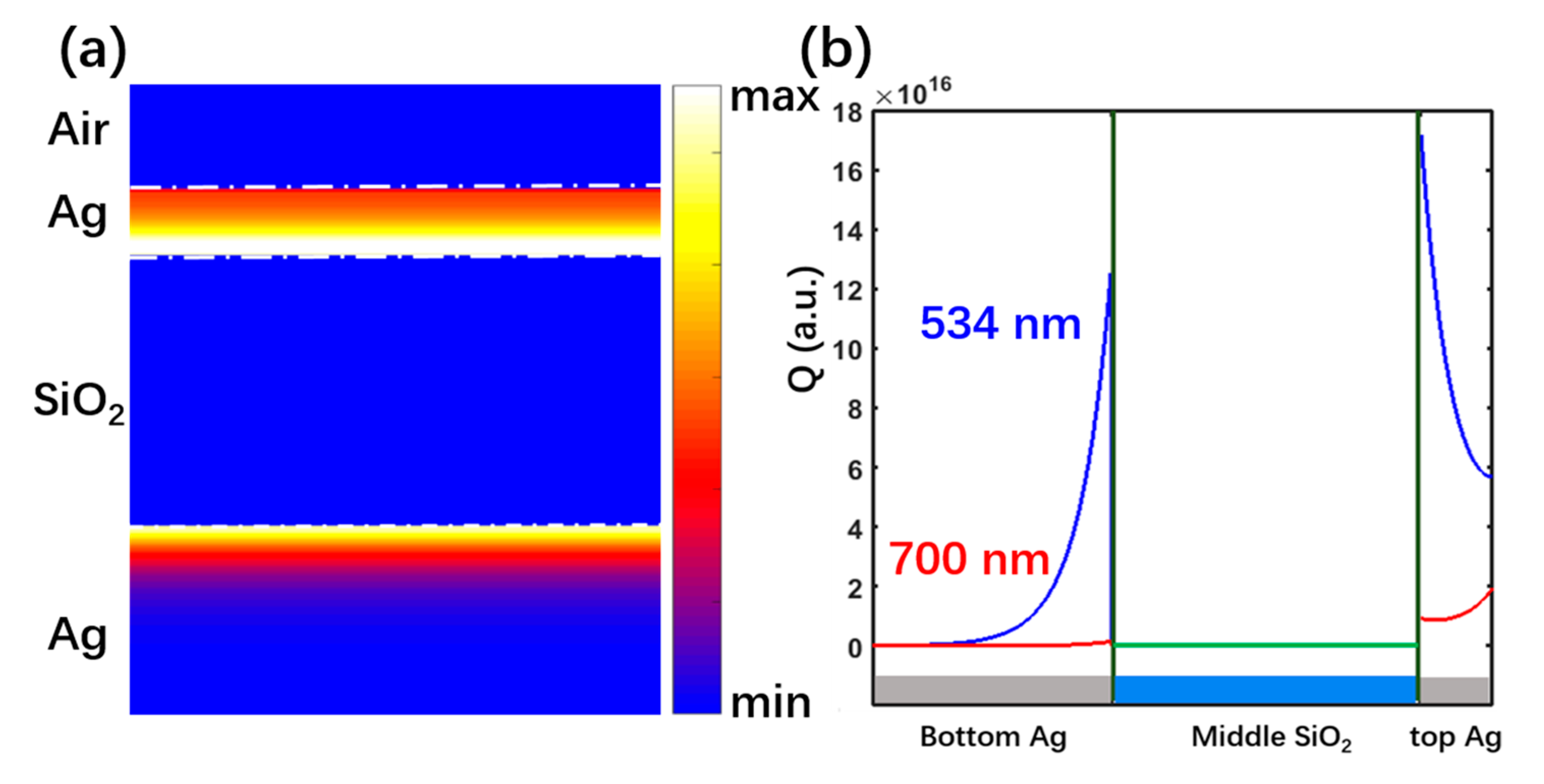
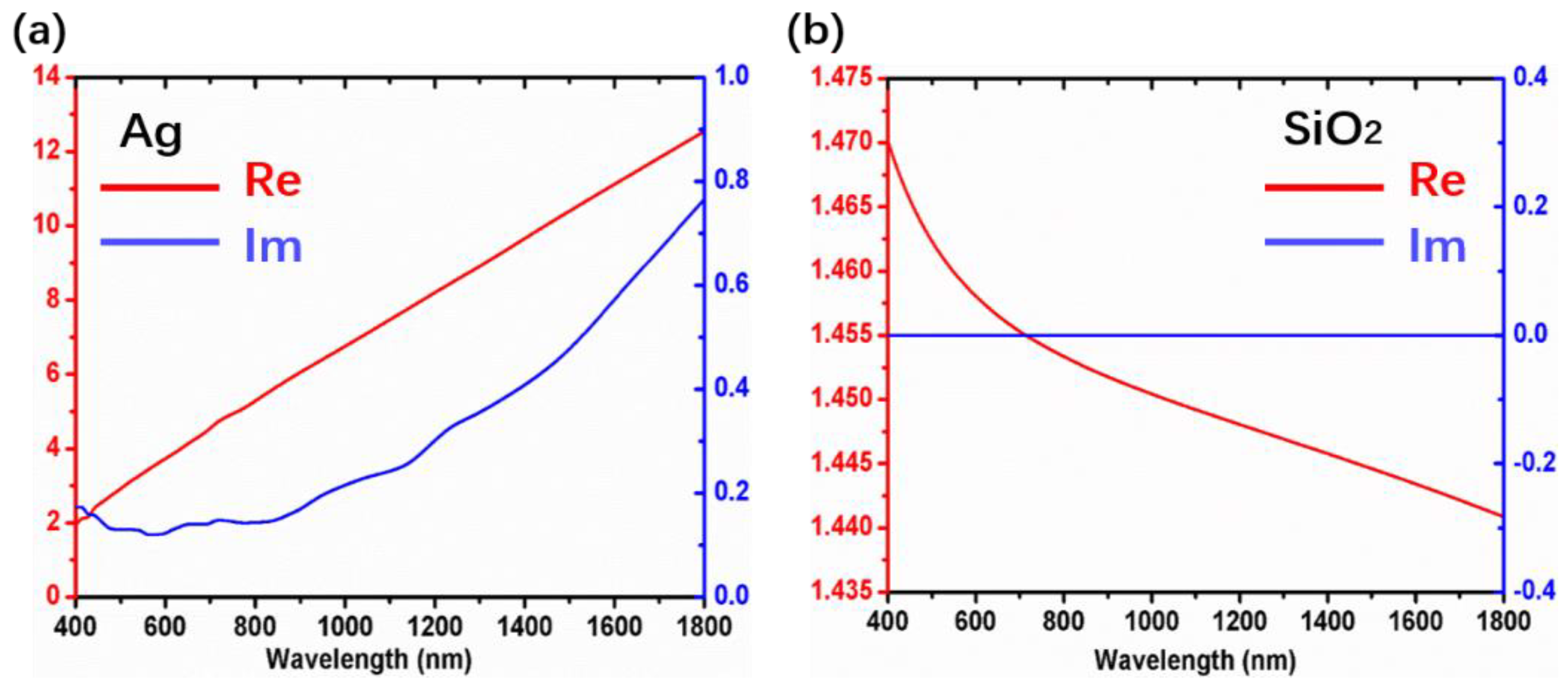
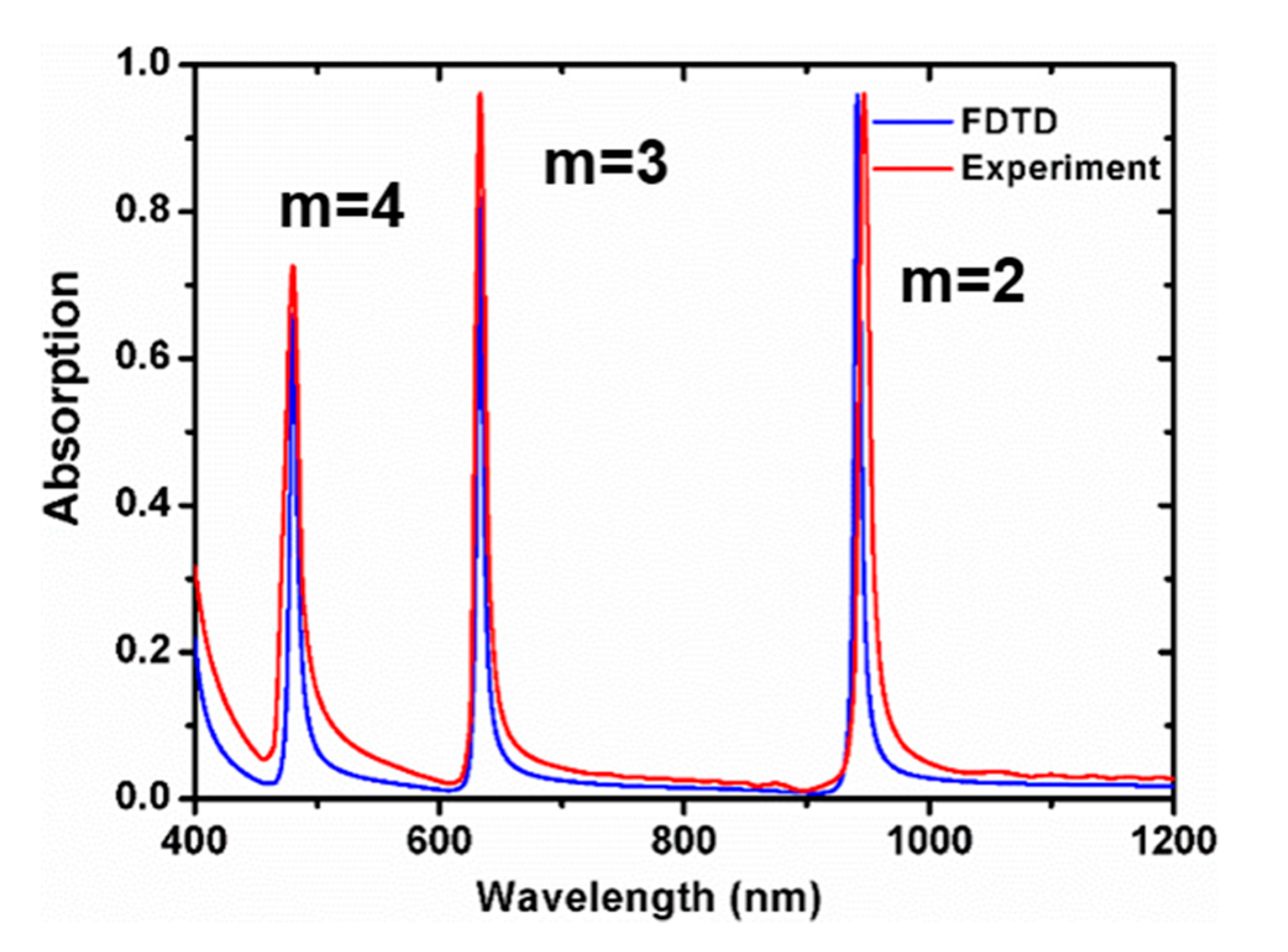
2. Simulation and Analysis
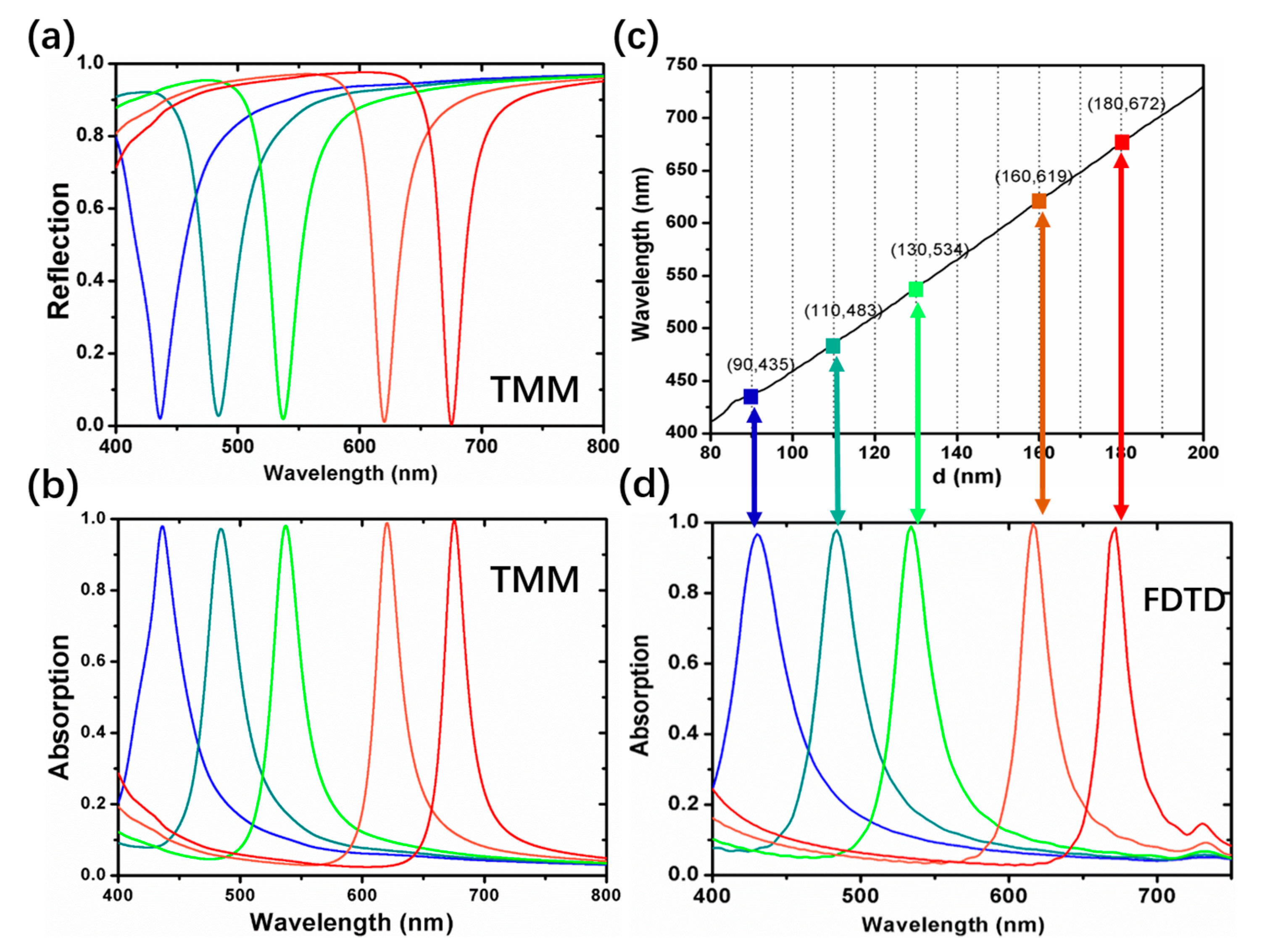
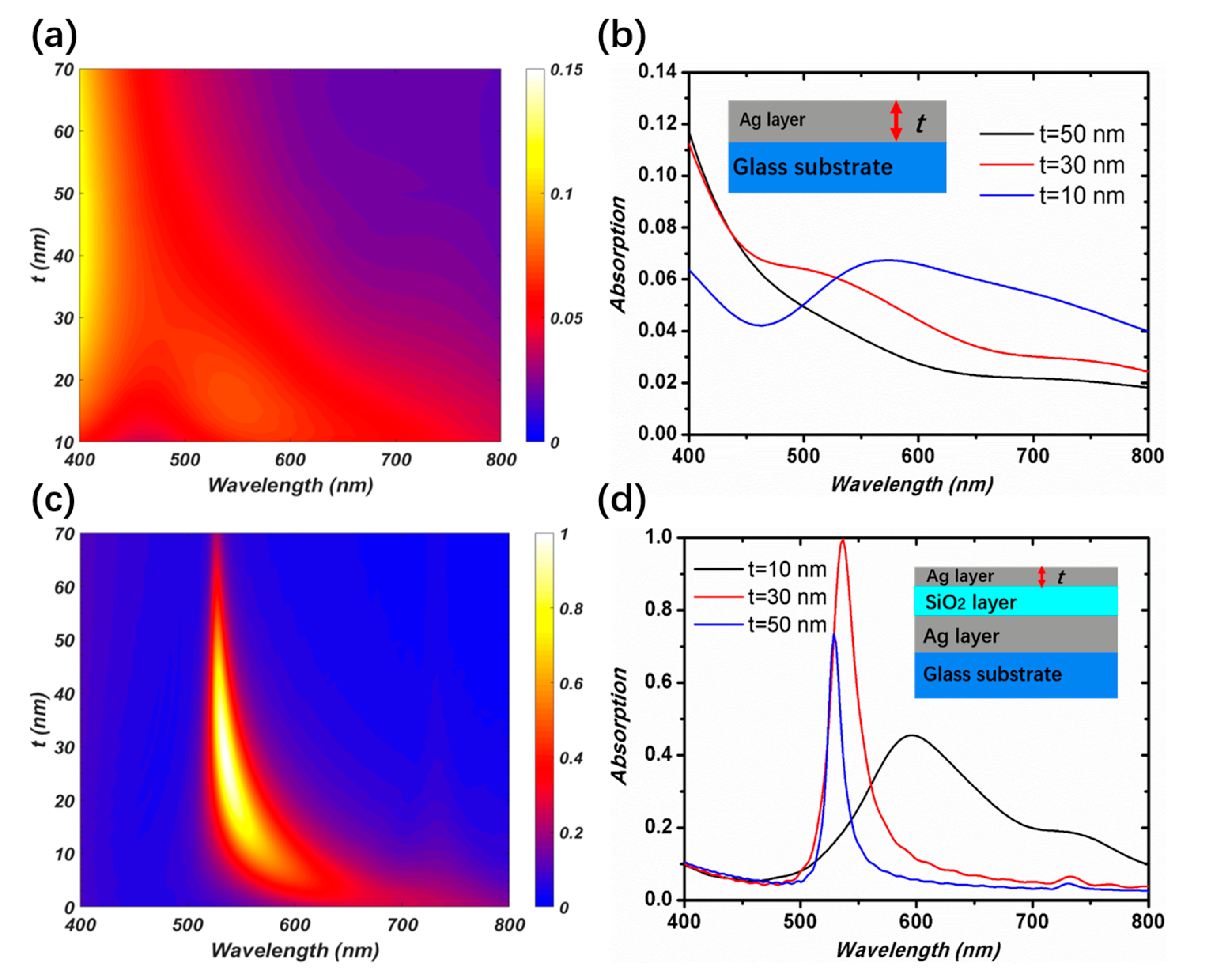
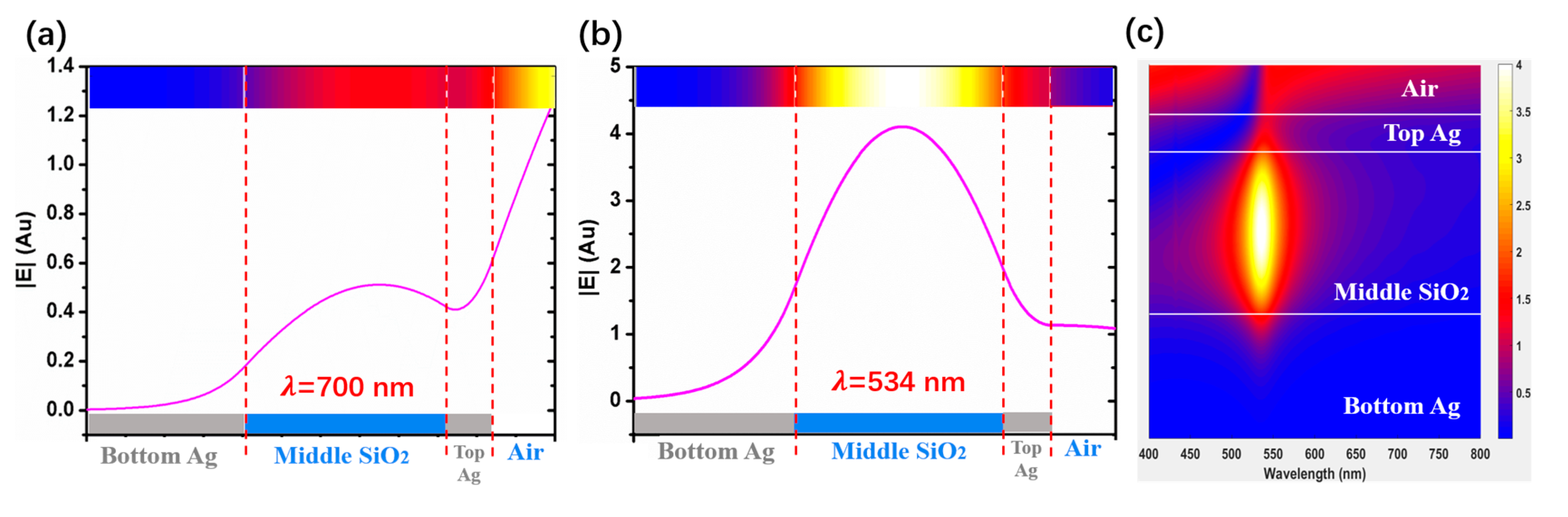
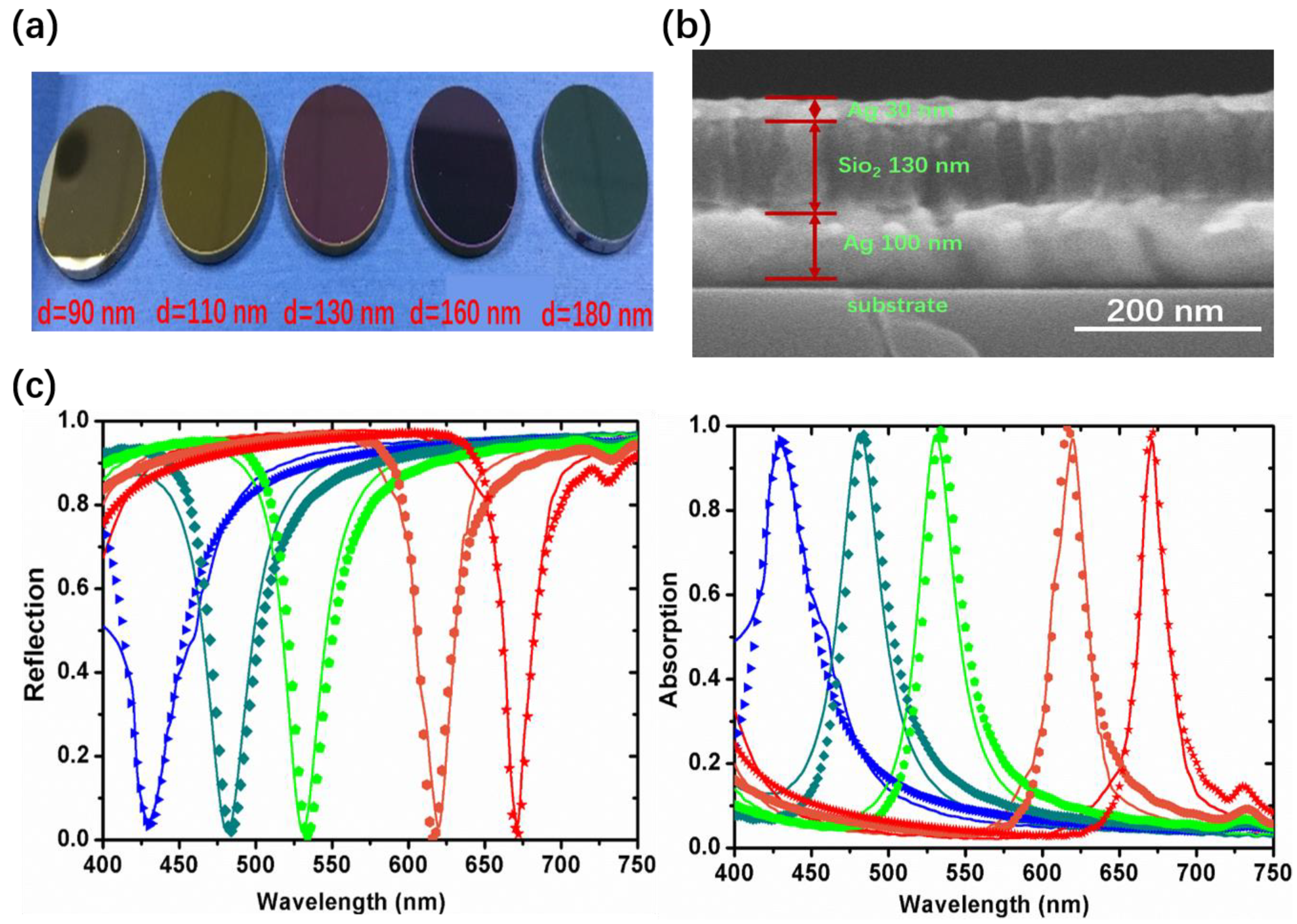
3. Experiment Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, G.; Finefrock, S.; Liang, D.; Yadav, G.G.; Yang, H.; Fang, H.; Wu, Y. Semiconductor nanostructure-based photovoltaic solar cells. Nanoscale 2011, 3, 2430. [Google Scholar] [CrossRef] [PubMed]
- Guo, C.F.; Sun, T.; Cao, F.; Liu, Q.; Ren, Z. Metallic nanostructures for light trapping in energy-harvesting devices. Light Sci. Appl. 2014, 3, e161. [Google Scholar]
- Su, Y.-H.; Ke, Y.-F.; Cai, S.-L.; Yao, Q.-Y. Surface plasmon resonance of layer-by-layer gold nanoparticles induced photoelectric current in environmentally-friendly plasmon-sensitized solar cell. Light Sci. Appl. 2012, 1, e14. [Google Scholar] [CrossRef]
- Yu, M.; Long, Y.Z.; Sun, B.; Fan, Z. Recent advances in solar cells based on one-dimensional nanostructure arrays. Nanoscale 2012, 4, 2783–2796. [Google Scholar]
- Azad, A.K.; Kort-Kamp, W.J.M.; Sýkora, M.; Weisse-Bernstein, N.R.; Luk, T.S.; Taylor, A.J.; Dalvit, D.A.R.; Chen, H.-T. Metasurface Broadband Solar Absorber. Sci. Rep. 2016, 6, 20347. [Google Scholar] [CrossRef]
- Zheng, J.; Yang, W.; Wang, J.; Zhu, J.; Qian, L.; Yang, Z. An ultranarrow SPR linewidth in the UV region for plasmonic sensing. Nanoscale 2019, 11, 4061–4066. [Google Scholar] [CrossRef] [PubMed]
- Yong, Z.; Zhang, S.; Gong, C.; He, S. Narrow band perfect absorber for maximum localized magnetic and electric field enhancement and sensing applications. Sci. Rep. 2016, 6, 24063. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Park, B.; Yun, S.H.; Cho, C.Y.; Kim, Y.C.; Shin, J.C.; Jeon, H.G.; Huh, Y.H.; Hwang, I.; Baik, K.Y.; Lee, Y.I.; et al. Surface plasmon excitation in semitransparent inverted polymer photovoltaic devices and their applications as label-free optical sensors. Light Sci. Appl. 2014, 3, e222. [Google Scholar] [CrossRef]
- Lu, X.; Zhang, T.; Wan, R.; Xu, Y.; Zhao, C.; Guo, S. Numerical investigation of narrowband infrared absorber and sensor based on dielectric-metal metasurface. Opt. Express 2018, 26, 10179–10187. [Google Scholar] [CrossRef]
- Allsop, T.; Arif, R.; Neal, R.; Kalli, K.; Kundrát, V.; Rozhin, A.; Culverhouse, P.; Webb, D.J. Photonic gas sensors exploiting directly the optical properties of hybrid carbon nanotube localized surface plasmon structures. Light Sci. Appl. 2016, 5, e16036. [Google Scholar] [CrossRef]
- Li, W.; Valentine, J. Metamaterial Perfect Absorber Based Hot Electron Photodetection. Nano Lett. 2014, 14, 3510–3514. [Google Scholar] [CrossRef] [PubMed]
- Chalabi, H.; Schoen, D.; Brongersma, M.L. Hot-Electron Photodetection with a Plasmonic Nanostripe Antenna. Nano Lett. 2014, 14, 1374–1380. [Google Scholar] [CrossRef] [PubMed]
- Costantini, D.; Lefebvre, A.; Coutrot, A.-L.; Moldovan-Doyen, I.; Hugonin, J.-P.; Boutami, S.; Marquier, F.; Benisty, H.; Greffet, J.-J. Plasmonic Metasurface for Directional and Frequency-Selective Thermal Emission. Phys. Rev. Appl. 2015, 4, 014023. [Google Scholar] [CrossRef]
- Liu, X.; Tyler, T.; Starr, T.; Starr, A.F.; Jokerst, N.M.; Padilla, W.J. Taming the Blackbody with Infrared Metamaterials as Selective Thermal Emitters. Phys. Rev. Lett. 2011, 107, 045901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ameling, R.; Dregely, D.; Giessen, H. Strong coupling of localized and surface plasmons to microcavity modes. Opt. Lett. 2011, 36, 2218–2220. [Google Scholar] [CrossRef]
- Li, Q.; Gao, J.; Yang, H.; Liu, H.; Wang, X.; Li, Z.; Guo, X. Tunable plasmonic absorber based on propagating and localized surface plasmons using metal-dielectric-metal structure. Plasmonics 2017, 12, 1037–1043. [Google Scholar] [CrossRef]
- Yu, P.; Li, J.; Tang, C.; Cheng, H.; Liu, Z.; Li, Z.; Liu, Z.; Gu, C.; Li, J.; Chen, S.; et al. Controllable optical activity with non-chiral plasmonic metasurfaces. Light Sci. Appl. 2016, 5, e16096. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, X.; Li, J.; Ma, L.; Zhang, Z. Analytical plasmon dispersion in subwavelength closely spaced Au nanorod arrays from planar metal–insulator–metal waveguides. J. Mater. Chem. C 2017, 5, 6079–6085. [Google Scholar] [CrossRef]
- Sannomiya, T.; Saito, H.; Junesch, J.; Yamamoto, N. Coupling of plasmonic nanopore pairs: Facing dipoles attract each other. Light Sci. Appl. 2016, 5, e16146. [Google Scholar] [CrossRef]
- Nelson, J.W.; Knefelkamp, G.R.; Brolo, A.G.; Lindquist, N.C. Digital plasmonic holography. Light Sci. Appl. 2018, 7, 52. [Google Scholar] [CrossRef]
- Ding, T.; Sigle, D.; Zhang, L.; Mertens, J.; De Nijs, B.; Baumberg, J. Controllable Tuning Plasmonic Coupling with Nanoscale Oxidation. ACS Nano 2015, 9, 6110–6118. [Google Scholar] [CrossRef] [Green Version]
- Nazirzadeh, M.A.; Atar, F.B.; Turgut, B.B.; Okyay, A.K. Random sized plasmonic nanoantennas on Silicon for low-cost broad-band near-infrared photodetection. Sci. Rep. 2014, 4, 7103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Z.; Liu, X.; Huang, S.; Pan, P.; Chen, J.; Liu, G.; Gu, G. Automatically Acquired Broadband Plasmonic-Metamaterial Black Absorber during the Metallic Film-Formation. ACS Appl. Mater. Interfaces 2015, 7, 4962–4968. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Gao, J.; Li, Z.; Yang, H.; Liu, H.; Wang, X.; Li, Y. Absorption enhancement in nanostructured silicon fabricated by self-assembled nanosphere lithography. Opt. Mater. 2017, 70, 165–170. [Google Scholar] [CrossRef]
- He, X.; Yan, S.; Lu, G.; Zhang, Q.; Wu, F.; Jiang, J. An ultra-broadband polarization-independent perfect absorber for the solar spectrum. RSC Adv. 2015, 5, 61955–61959. [Google Scholar]
- Liu, H.; Wang, X.; Zhao, J.; Li, Z.; Yang, H.; Gao, J.; Li, Q. Novel aluminum plasmonic absorber enhanced by extraordinary optical transmission. Opt. Express 2016, 24, 25885. [Google Scholar] [CrossRef]
- Siddique, R.H.; Mertens, J.; Hölscher, H.; Vignolini, S. Scalable and controlled self-assembly of aluminum-based random plasmonic metasurfaces. Light Sci. Appl. 2017, 6, e17015. [Google Scholar] [CrossRef]
- Li, Q.; Li, Z.; Wang, X.; Wang, T.; Liu, H.; Yang, H.; Gong, Y.; Gao, J. Structurally tunable plasmonic absorption bands in a self-assembled nano-hole array. Nanoscale 2018, 10, 19117–19124. [Google Scholar] [CrossRef]
- Sain, B.; Kaner, R.; Prior, Y. Phase-controlled propagation of surface plasmons. Light Sci. Appl. 2017, 6, e17072. [Google Scholar] [CrossRef]
- Lu, J.Y.; Nam, S.H.; Wilke, K.; Raza, A.; Lee, Y.E.; Alghaferi, A.; Fang, N.X.; Zhang, T. Localized Surface Plasmon-Enhanced Ultrathin Film Broadband Nanoporous Absorbers. Adv. Opt. Mater. 2016, 4, 1255–1264. [Google Scholar] [CrossRef]
- Shan, H.; Yu, Y.; Wang, X.; Luo, Y.; Zu, S.; Du, B.; Han, T.; Li, B.; Li, Y.; Wu, J.; et al. Direct observation of ultrafast plasmonic hot electron transfer in the strong coupling regime. Light Sci. Appl. 2019, 8, 9. [Google Scholar] [CrossRef]
- Li, G.; Shen, Y.; Xiao, G.; Jin, C. Double-layered metal grating for high-performance refractive index sensing. Opt. Express 2015, 23, 8995. [Google Scholar] [CrossRef] [PubMed]
- Floess, D.; Chin, J.Y.; Kawatani, A.; Dregely, D.; Habermeier, H.-U.; Weiss, T.; Giessen, H. Tunable and switchable polarization rotation with non-reciprocal plasmonic thin films at designated wavelengths. Light Sci. Appl. 2015, 4, e284. [Google Scholar] [CrossRef]
- Willey, R. Achieving narrow bandpass filters which meet the requirements for DWDM. Thin Solid Films 2001, 398, 1–9. [Google Scholar] [CrossRef]
- Tang, H.; Gao, J.; Zhang, J.; Wang, X.; Fu, X. Preparation and Spectrum Characterization of a High Quality Linear Variable Filter. Coatings 2018, 8, 308. [Google Scholar] [CrossRef]
- Loh, J.Y.Y.; Kherani, N. Design of Nano-Porous Multilayer Antireflective Coatings. Coatings 2017, 7, 134. [Google Scholar] [CrossRef]
- Matsuoka, Y.; Mathonnèire, S.; Peters, S.; Masselink, W.T. Broadband multilayer anti-reflection coating for mid-infrared range from 7 μm to 12 μm. Appl. Opt. 2018, 57, 1645–1649. [Google Scholar] [CrossRef]
- Li, Z.; Li, Q.; Quan, X.; Zhang, X.; Song, C.; Yang, H.; Wang, X.; Gao, J. Broadband High-Reflection Dielectric PVD Coating with Low Stress and High Adhesion on PMMA. Coatings 2019, 9, 237. [Google Scholar] [CrossRef]
- Hu, C.; Liu, J.; Wang, J.; Gu, Z.; Li, C.; Li, Q.; Li, Y.; Zhang, S.; Bi, C.; Fan, X.; et al. New design for highly durable infrared-reflective coatings. Light Sci. Appl. 2018, 7, 17175. [Google Scholar] [CrossRef]
- Salisbury, W.W. Absorbent Body for Electromagnetic Waves. U.S. Patent 2599944, 10 June 1952. [Google Scholar]
- Mikhail, A.K.; Romain, B.; Patrice, G.; Federico, C. Nanometre optical coatings based on strong interference effects in highly absorbing media. Nat. Mater. 2013, 12, 20–24. [Google Scholar] [CrossRef]
- Park, J.; Kang, J.-H.; Vasudev, A.P.; Schoen, D.T.; Kim, H.; Hasman, E.; Brongersma, M.L. Omnidirectional Near-Unity Absorption in an Ultrathin Planar Semiconductor Layer on a Metal Substrate. ACS Photonics 2014, 1, 812–821. [Google Scholar] [CrossRef]
- Pu, M.; Feng, Q.; Wang, M.; Hu, C.; Huang, C.; Ma, X.; Zhao, Z.; Wang, C.; Luo, X. Ultrathin broadband nearly perfect absorber with symmetrical coherent illumination. Opt. Express 2012, 20, 2246. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Palacios, E.; Butun, S.; Kocer, H.; Aydin, K. Omnidirectional, broadband light absorption using large-area, ultrathin lossy metallic film coatings. Sci. Rep. 2015, 5, 15137. [Google Scholar] [CrossRef] [PubMed]
- Kats, M.A.; Capasso, F. Ultra-thin optical interference coatings on rough and flexible substrates. Appl. Phys. Lett. 2014, 105, 131108. [Google Scholar] [CrossRef]
- Kats, M.A.; Sharma, D.; Lin, J.; Genevet, P.; Blanchard, R.; Yang, Z.; Qazilbash, M.M.; Basov, D.N.; Ramanathan, S.; Capasso, F. Ultra-thin perfect absorber employing a tunable phase change material. Appl. Phys. Lett. 2012, 101, 221101. [Google Scholar] [CrossRef]
- Palik, E.D. Handbook of Optical Constants of Solids; Academic Press: New York, NY, USA, 1985. [Google Scholar]
- Hao, J.; Zhou, L.; Qiu, M. Nearly total absorption of light and heat generation by plasmonic metamaterials. Phys. Rev. B 2011, 83, 165107. [Google Scholar] [CrossRef]
| Material | Power (W) | Ar (Sccm) | O2 (Sccm) | Vacuum Degree (Pa) | Deposition Rate (Å/s) |
|---|---|---|---|---|---|
| Ag | 150 | 80 | 0 | 1.0 | 4.28 |
| SiO2 | 200 | 80 | 20 | 1.5 | 2.63 |
| d (nm) | Simulated Resonance Wavelength (nm) | Simulated Max Absorption | Experimental Resonance Wavelength (nm) | Experimental Max Absorption | FWHM (nm) |
|---|---|---|---|---|---|
| 90 | 436 | 0.9779 | 440 | 0.9868 | 54 |
| 110 | 485 | 0.9887 | 482 | 0.9865 | 30 |
| 130 | 534 | 0.9899 | 530 | 0.9937 | 26 |
| 160 | 617 | 0.9966 | 620 | 0.9925 | 24 |
| 180 | 671 | 0.9984 | 675 | 0.9917 | 20 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Li, Z.; Xiang, X.; Wang, T.; Yang, H.; Wang, X.; Gong, Y.; Gao, J. Tunable Perfect Narrow-Band Absorber Based on a Metal-Dielectric-Metal Structure. Coatings 2019, 9, 393. https://doi.org/10.3390/coatings9060393
Li Q, Li Z, Xiang X, Wang T, Yang H, Wang X, Gong Y, Gao J. Tunable Perfect Narrow-Band Absorber Based on a Metal-Dielectric-Metal Structure. Coatings. 2019; 9(6):393. https://doi.org/10.3390/coatings9060393
Chicago/Turabian StyleLi, Qiang, Zizheng Li, Xiangjun Xiang, Tongtong Wang, Haigui Yang, Xiaoyi Wang, Yan Gong, and Jinsong Gao. 2019. "Tunable Perfect Narrow-Band Absorber Based on a Metal-Dielectric-Metal Structure" Coatings 9, no. 6: 393. https://doi.org/10.3390/coatings9060393
APA StyleLi, Q., Li, Z., Xiang, X., Wang, T., Yang, H., Wang, X., Gong, Y., & Gao, J. (2019). Tunable Perfect Narrow-Band Absorber Based on a Metal-Dielectric-Metal Structure. Coatings, 9(6), 393. https://doi.org/10.3390/coatings9060393





