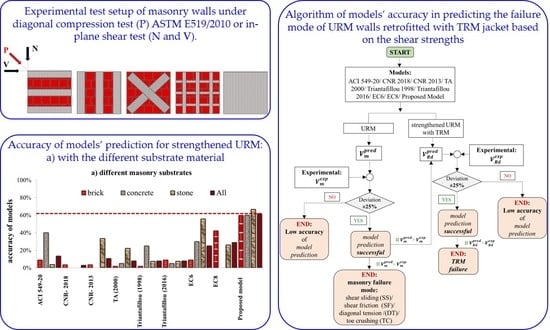
Failure Mode Prediction of Unreinforced Masonry (URM) Walls Retrofitted with Cementitious Textile Reinforced Mortar (TRM)
Abstract
:1. Introduction
1.1. Literature Overview
1.2. Brick Masonry Walls
1.3. Cement Masonry Walls
1.4. Stone Masonry Walls
1.5. Research Gap and Novelty
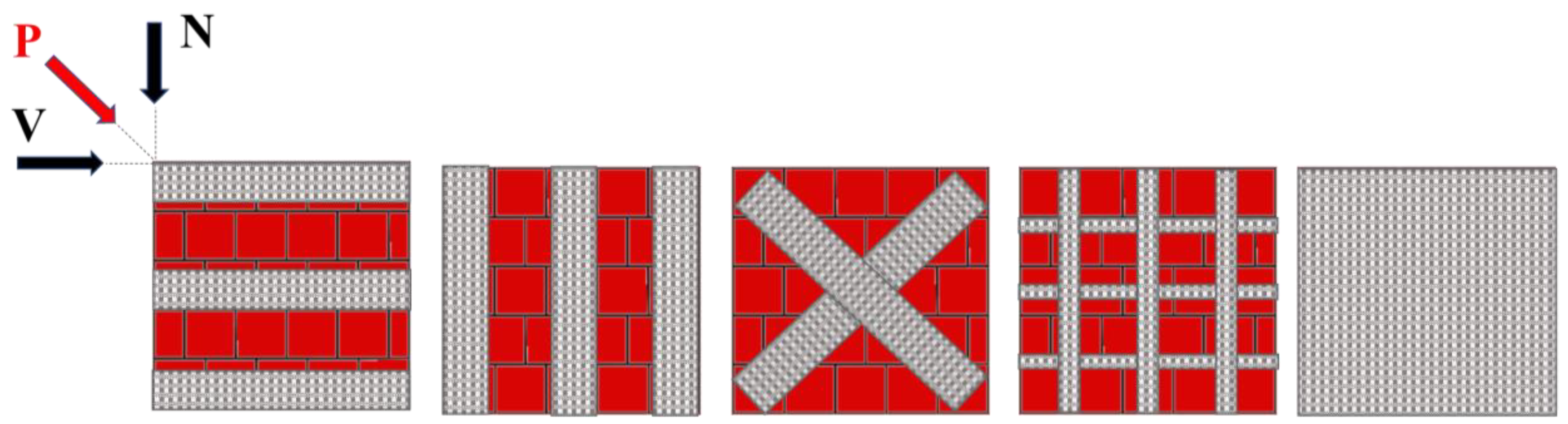
2. Database Assembly
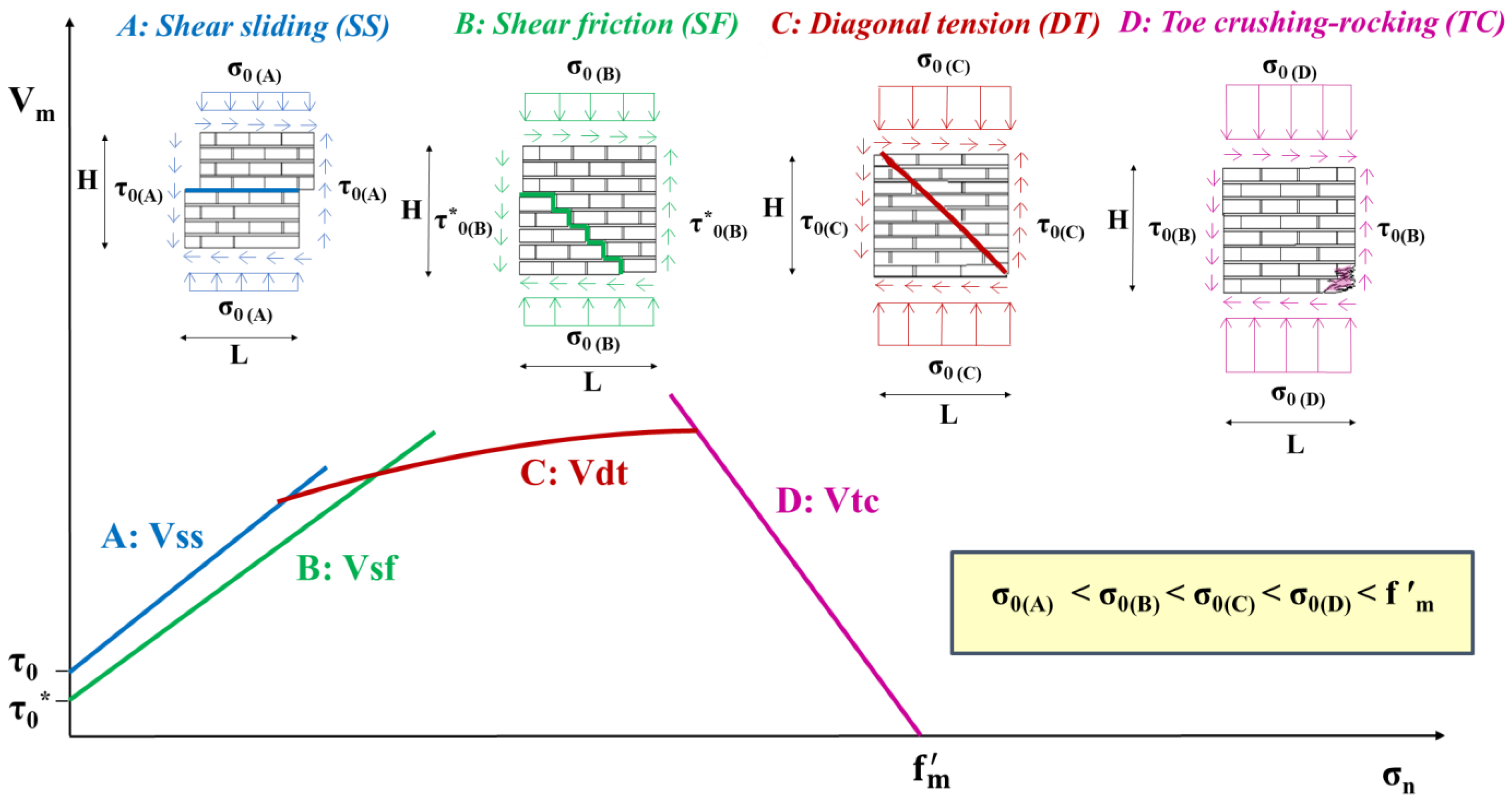
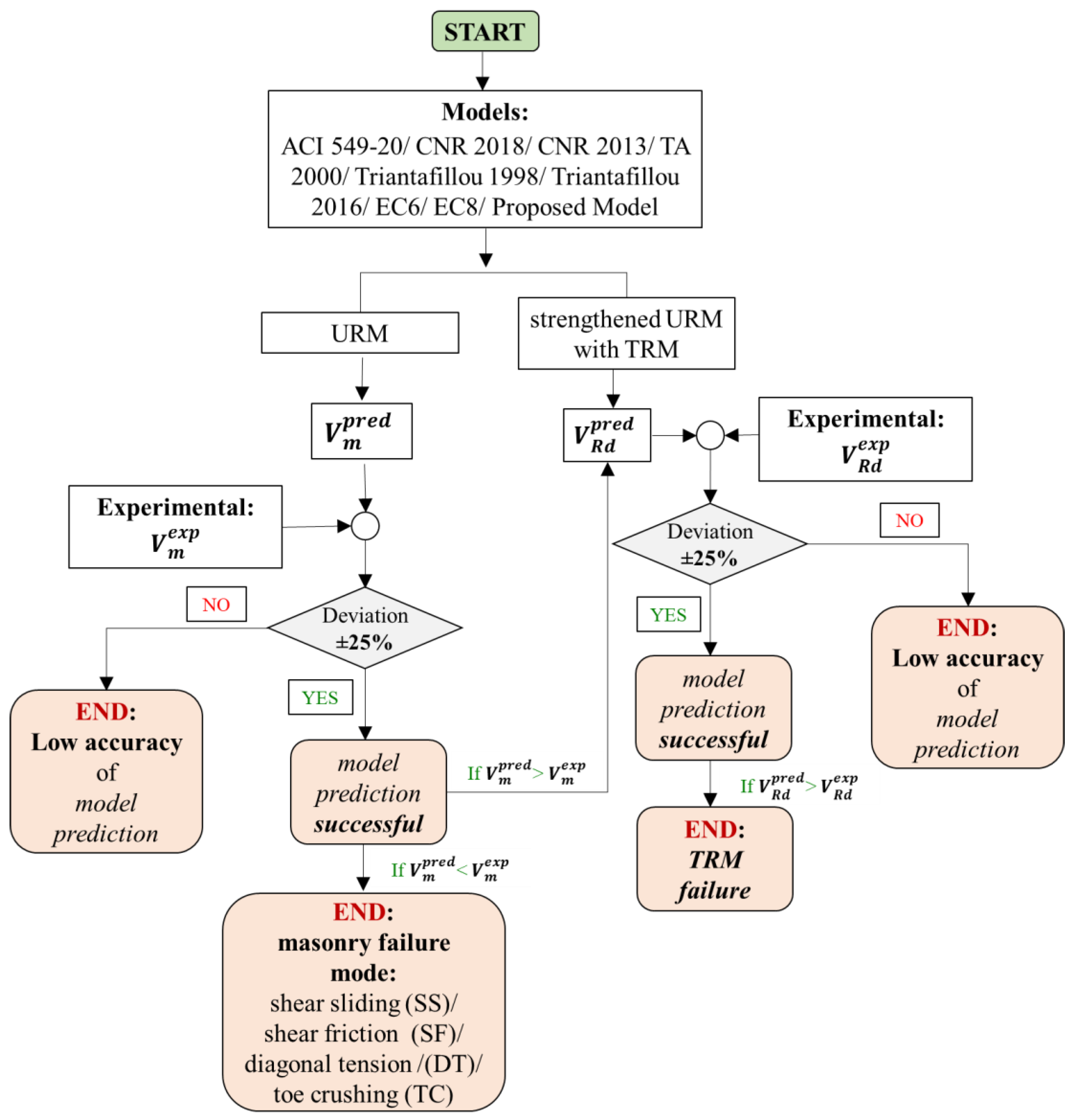
3. Design Models
3.1. Existing Models
3.2. Proposed Model
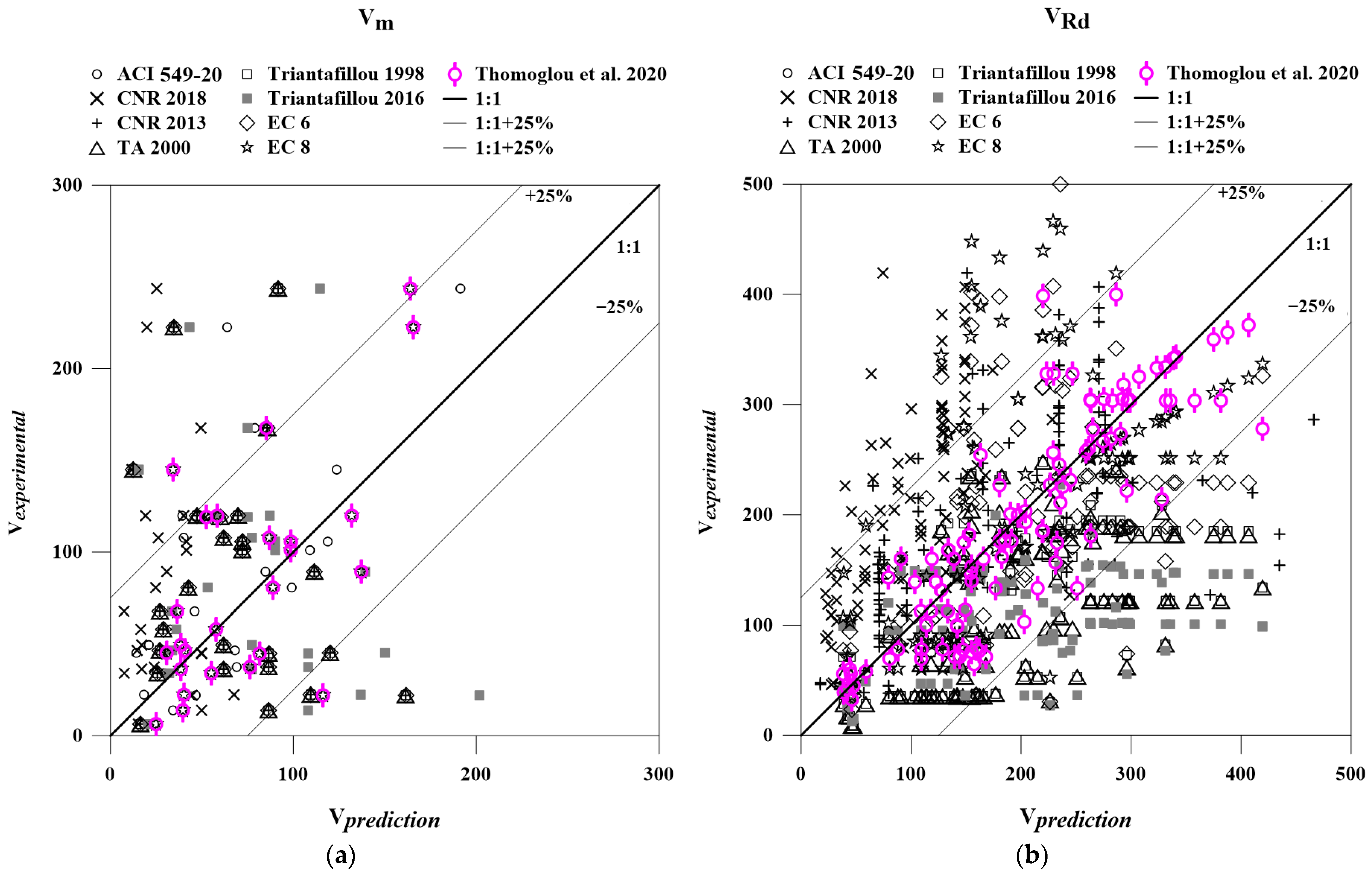
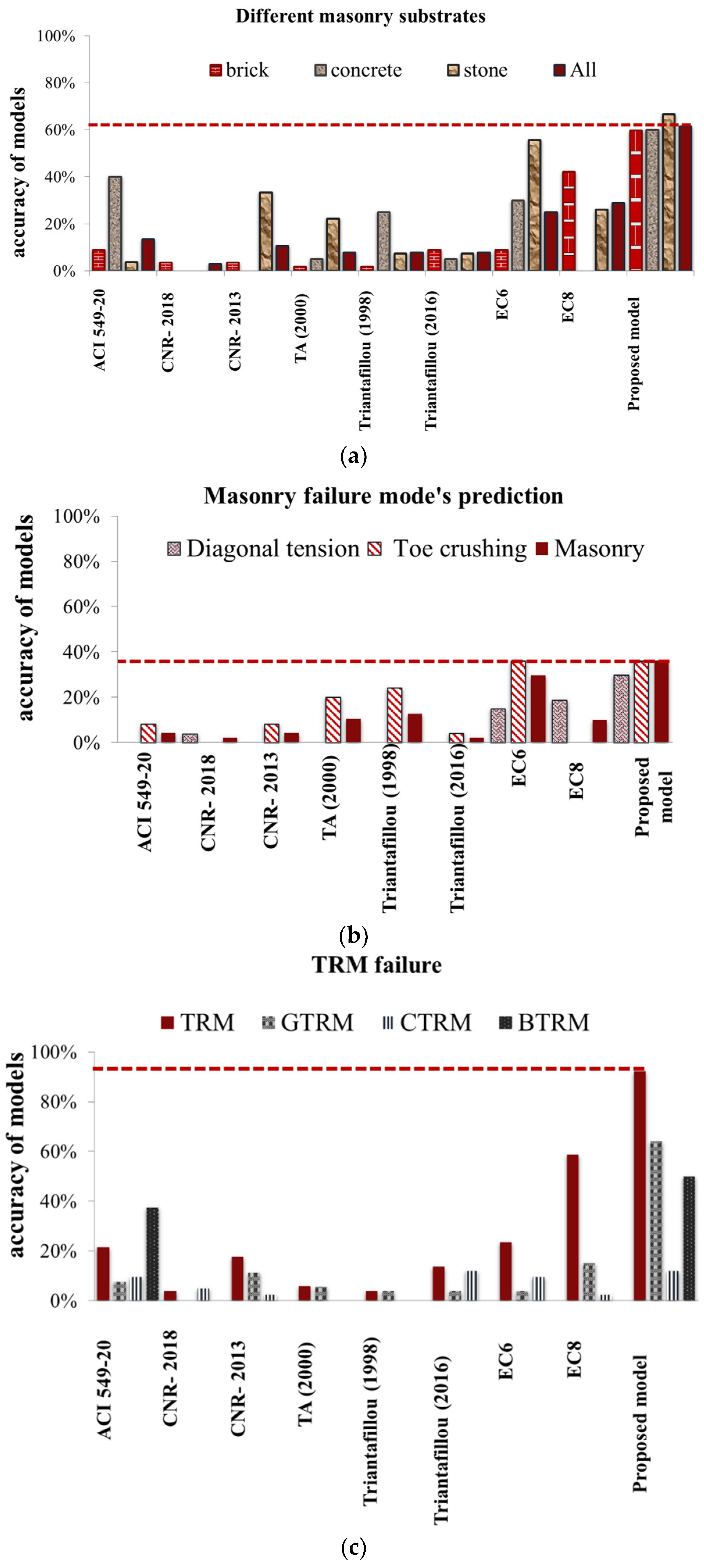
4. Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Authors | Type of Masonry | Type of TRM | Specimen Code | Experimental Failure Mode | ACI | CNR (2018) | CNR (2013) | TA 2000 | Trantafillou 1998 | Trantafillou 2016 | EC6 | EC8 | Proposed Model |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [12] | brick | G | SO-UMG1 | TRM | SF | NA | NA | NA | NA | NA | NA | NA | TRM |
| brick | G | SO-UMG2 | TC | TRM | M | M | M | M | M | M | TRM | TC | |
| brick | G | SO-UMG3 | TC | NA | NA | NA | NA | NA | NA | NA | NA | TC | |
| [30] | brick | G | 1GRWN25 | TC | NA | NA | NA | NA | NA | NA | NA | NA | TC |
| brick | G | 2GRWN15 | DT | NA | NA | NA | NA | NA | NA | NA | NA | NA | |
| brick | G | 2GRWN25 | TC | NA | NA | NA | NA | NA | NA | NA | NA | NA | |
| brick | G | 2GRWN25 | TC | NA | NA | NA | NA | NA | NA | NA | NA | NA | |
| [29] | brick | G | W16-G | TRM/DT | TRM | NA | NA | NA | NA | NA | NA | NA | TRM |
| brick | G | W17-G | TRM/DT | TRM | NA | NA | NA | NA | NA | NA | NA | TRM | |
| brick | G | W18-G | TRM/DT | TRM | NA | NA | TRM | NA | NA | NA | NA | TRM | |
| G | |||||||||||||
| [32] | concrete | G | T1F-3 | DT/TRM | TRM | NA | NA | NA | NA | NA | NA | NA | TRM |
| concrete | G | T1F-4 | DT/TRM | TRM | NA | NA | NA | NA | NA | NA | NA | TRM | |
| concrete | C | T1F-5 | DT/TRM | TRM | NA | NA | NA | NA | NA | NA | NA | TRM | |
| concrete | C | T1F-6 | DT/TRM | TRM | NA | NA | NA | NA | NA | NA | NA | TRM | |
| concrete | B | T1F-7 | TC/ DT | TRM | NA | NA | TC | NA | NA | NA | NA | TRM | |
| concrete | B | T1F-8 | TC DT | NA | NA | NA | TC | NA | NA | NA | NA | TRM | |
| concrete | B | T1F-9a | TC/ DT | TRM | NA | TC | TC | NA | NA | NA | NA | TRM | |
| concrete | G | T2F-10 | DT/TC | DT | NA | NA | TC | NA | NA | NA | NA | TC | |
| concrete | G | T2F-11 | DT/TC | DT | NA | NA | TC | NA | NA | NA | NA | TC | |
| concrete | C | T2F-12 | DT-TRM | DT | NA | NA | NA | NA | NA | NA | NA | TRM | |
| concrete | C | T2F-13 | TC | NA | NA | NA | NA | NA | NA | NA | NA | TC | |
| concrete | B | T2F-14 | DT/TRM | TRM | NA | NA | NA | NA | NA | NA | NA | TRM | |
| concrete | B | T2F-15 | DT/TRM | TRM | NA | NA | NA | NA | NA | NA | NA | TRM | |
| concrete | B | T2F-16 | DT/TRM | DT | NA | NA | NA | NA | NA | NA | NA | TRM | |
| [29] | brick | G | W4 | TRM | NA | NA | NA | NA | NA | NA | NA | NA | TRM |
| brick | G | W5 | TRM | NA | NA | NA | NA | NA | NA | NA | NA | TRM | |
| brick | G | W6 | TRM | NA | NA | NA | NA | NA | NA | NA | NA | TRM | |
| [23] | brick | C | FRMCom_01 | DT | NA | NA | NA | NA | NA | NA | NA | NA | NA |
| [25] | brick | C | CFRCM 01 | SS | TC | NA | NA | NA | NA | NA | M | NA | SS-SF |
| brick | G | CFRCM 02 | SS | TC | NA | NA | NA | NA | NA | M | NA | SS-SF | |
| [24] | brick | C | CD_FRCM | TRM | NA | TRM | TRM | NA | NA | NA | NA | NA | NA |
| [40] | brick | G | A-3 | DT | TC | M | TC | TC | TC | M | TRM | TRM | TC |
| [34] | stone | G | CD-07-U-IP | SF | NA | NA | NA | NA | NA | NA | NA | NA | NA |
| [38] * | stone | G | 7 | DT/TRM | NA | NA | NA | NA | NA | NA | M | DT | DT |
| stone | G | SM-10S | DT/TRM | SF/SS | NA | TRM | NA | NA | TRM | NA | DT | DT | |
| [35] | brick | G | CD-11-S-IP | TRM | SF | TRM | TRM | TC | TC | TRM | TRM | TRM | TRM |
| stone | G | CD-12-P-IP | DT/TRM | NA | NA | TRM | TRM | TRM | NA | TRM | NA | TRM | |
| stone | G | CD-13-P-IP | DT-TRM | NA | NA | TRM | TRM | TRM | NA | TRM | NA | TRM | |
| [26] | brick | G | B2A-F33S-1 | DT/TRM | NA | NA | NA | NA | NA | NA | NA | TRM | TRM |
| brick | G | B2A-F33S-2 | DT/TRM | NA | NA | NA | NA | NA | NA | NA | TRM | TRM | |
| brick | G | B2A-F66S-1 | DT/TRM | NA | NA | NA | NA | NA | NA | NA | TRM | TRM | |
| brick | G | B2A-F66S-2 | DT/TRM | NA | NA | NA | NA | NA | NA | NA | TRM | TRM | |
| brick | G | B2A-F99S-1 | DT/TRM | NA | NA | NA | NA | NA | NA | NA | TRM | TRM | |
| brick | G | B2A-F99S-2 | DT/TRM | NA | NA | NA | NA | NA | NA | NA | TRM | TRM | |
| brick | G | B2C-F33S-1 | DT/TRM | NA | NA | NA | NA | NA | NA | NA | TRM | TRM | |
| brick | G | B2C-F33S-2 | DT/TRM | NA | NA | NA | NA | NA | NA | NA | TRM | TRM | |
| brick | G | B2C-F66S-1 | DT/TRM | NA | NA | NA | NA | NA | NA | NA | TRM | TRM | |
| brick | G | B2C-F66S-2 | DT/TRM | NA | NA | NA | NA | NA | NA | NA | TRM | TRM | |
| brick | G | B2C-F99S-1 | DT/TRM | NA | NA | NA | NA | NA | NA | NA | TRM | TRM | |
| brick | G | B2C-F99S-2 | DT/TRM | NA | NA | NA | NA | NA | NA | NA | TRM | TRM | |
| brick | G | B3A-F33S-1 | DT/TRM | NA | NA | NA | NA | NA | NA | NA | TRM | TRM | |
| brick | G | B3A-F33S-2 | DT/TRM | NA | NA | NA | NA | NA | NA | NA | TRM | TRM | |
| brick | G | B3A-F66S-1 | DT/TRM | NA | NA | NA | NA | NA | NA | NA | TRM | TRM | |
| brick | G | B3A-F66S-2 | DT/TRM | NA | NA | NA | NA | NA | NA | NA | TRM | TRM | |
| brick | G | B3A-F66D-1 | DT/TRM | NA | NA | NA | NA | NA | NA | NA | TRM | TRM | |
| brick | G | B3A-F66D-2 | DT/TRM | NA | NA | NA | NA | NA | NA | NA | TRM | TRM | |
| brick | G | B3A-F99D-1 | DT/TRM | NA | NA | NA | NA | NA | NA | NA | TRM | TRM | |
| brick | G | B3A-F99D-2 | DT/TRM | NA | NA | NA | NA | NA | NA | NA | TRM | TRM | |
| rub stone | G | RA-F33S-1 | DT/TRM | NA | NA | TRM | NA | NA | NA | NA | TRM | TRM | |
| rub stone | G | RA-F33S-2 | DT/TRM | NA | NA | TRM | NA | NA | NA | NA | TRM | TRM | |
| rub stone | G | RA-F66S-1 | DT/TRM | NA | NA | TRM | NA | NA | NA | NA | TRM | TRM | |
| rub stone | G | RA-F66S-2 | DT/TRM | NA | NA | TRM | NA | NA | NA | NA | TRM | TRM | |
| rub stone | G | RA-F66D-1 | DT/TRM | NA | NA | TRM | NA | NA | NA | NA | TRM | TRM | |
| rub stone | G | RA-F66D-2 | DT/TRM | NA | NA | TRM | NA | NA | NA | NA | TRM | TRM | |
| [22] | concrete | C | CMU-1 ply-1 | TC | NA | NA | NA | NA | NA | NA | M | NA | NA |
| concrete | C | CMU-1 ply-2 | TC | NA | TC | NA | NA | NA | NA | M | NA | NA | |
| concrete | C | CMU-1 ply-3 | TC | NA | TC | NA | NA | NA | NA | M | NA | NA | |
| concrete | C | CMU-4 ply-1 | TC | NA | NA | NA | NA | NA | NA | M | NA | NA | |
| concrete | C | CMU-4 ply-2 | TC | NA | NA | NA | NA | NA | NA | M | NA | NA | |
| concrete | C | CMU-4 ply-3 | TC | NA | NA | NA | NA | NA | NA | M | NA | NA | |
| clay brick | C | 1 ply-1 | TRM | TRM | NA | NA | NA | NA | NA | NA | NA | TRM | |
| clay brick | C | 1 ply-2 | TRM | TRM | NA | NA | NA | NA | NA | NA | NA | TRM | |
| clay brick | C | 1 ply-3 | TRM | TRM | NA | NA | NA | NA | NA | NA | NA | TRM | |
| clay brick | C | 4 ply-1 | TC | NA | NA | NA | NA | NA | NA | M | NA | NA | |
| clay brick | C | 4 ply-2 | TC | NA | NA | NA | NA | NA | NA | M | NA | NA | |
| clay brick | C | 4 ply-3 | TC | NA | NA | NA | NA | NA | NA | M | NA | NA | |
| [37] | tuff | G | PRR1 | SF/SS | NA | NA | NA | NA | NA | NA | M | NA | NA |
| tuff | G | PRR2 | DT | NA | NA | NA | NA | NA | NA | M | NA | NA | |
| [39] * | clay brick | C | I10%_SW_RC1 | TRM | NA | TRM | NA | NA | NA | TRM | NA | NA | NA |
| clay brick | C | I10%_SW_RC2 | TC | NA | NA | TC | NA | NA | NA | NA | NA | NA | |
| clay brick | C | I_SC_PC1 | TRM | NA | NA | NA | NA | NA | TRM | NA | NA | NA | |
| clay brick | C | I_SC_PC2 | DT | NA | NA | NA | NA | NA | NA | NA | NA | NA | |
| clay brick | C | I25%_F_PC1 | DT | NA | NA | NA | NA | NA | NA | NA | NA | NA | |
| clay brick | C | I25%_F_PC2 | DT | NA | NA | NA | NA | NA | NA | NA | NA | NA | |
| stone blocks | B | I3%_SW_LB1 | TC | NA | NA | NA | NA | NA | NA | NA | NA | NA | |
| stone blocks | B | I3%_SW_FB1 | TC | NA | NA | NA | NA | NA | NA | NA | NA | NA | |
| [21] | clay brick | C | specimen#4 | DT | NA | NA | NA | NA | NA | NA | NA | NA | NA |
| clay brick | C | specimen#5 | TRM | NA | NA | NA | NA | NA | TRM | NA | TRM | NA | |
| clay brick | C | specimen#6 | TRM | NA | NA | NA | NA | NA | TRM | NA | TRM | NA | |
| clay brick | C | specimen#7 | DT | NA | NA | NA | NA | NA | NA | NA | NA | NA | |
| clay brick | C | specimen#8 | DT | NA | NA | NA | NA | NA | NA | NA | NA | NA | |
| clay brick | C | specimen#9 | TRM | NA | NA | NA | NA | NA | TRM | NA | TRM | NA | |
| [33] | tuff | G | PS#3 | TC | NA | NA | NA | TC | NA | NA | NA | NA | NA |
| tuff | G | PS#4 | TC | NA | NA | TC | TC | NA | NA | NA | NA | NA | |
| tuff | G | PS#1 | TC | NA | NA | NA | TC | NA | NA | NA | NA | NA | |
| tuff | G | PS#2 | TC | NA | NA | NA | TC | NA | NA | NA | NA | NA | |
| [14] | tuff | G | PS#1 | DT | NA | NA | NA | NA | NA | NA | NA | NA | DT |
| tuff | G | PS#2 | DT | NA | NA | NA | NA | NA | NA | NA | NA | DT | |
| tuff | G | PS#3 | SS/DT/TRM | NA | NA | NA | NA | NA | NA | TRM | NA | NA | |
| tuff | G | PS#4 | SS/DT | NA | NA | NA | NA | NA | NA | TRM | NA | DT | |
| tuff | G | PT#1 | SS/TRM | NA | NA | NA | NA | NA | NA | TRM | NA | NA | |
| tuff | G | PT#2 | SS/TRM | NA | NA | NA | NA | NA | TRM | TRM | NA | TRM | |
| tuff | G | PT#3 | SS | NA | NA | NA | NA | NA | NA | NA | NA | NA | |
| tuff | G | PT#4 | SS, out-of-plane | NA | NA | NA | NA | NA | NA | NA | NA | NA |
References
- ACI 549-20; Guide to Design and Construction of Externally Bonded Fabric-Reinforced Cementitious Matrix (FRCM) and Steel-Reinforced Grout (SRG) Systems for Repair and Strengthening Masonry Structures. ACI 549.6R. ACI: Farmington Hills, MI, USA, 2020.
- CNR-DT 215; Istruzioni per la Progettazione, l’Esecuzione ed il Controllo di Interventi di Consolidamento Statico mediante l’utilizzo di Compositi Fibrorinforzati a Matrice Inorganica. Consiglio Nazionale delle Ricerche: Roma, Italy, 2018.
- Triantafillou, T. Strengthening of Existing Masonry Structures: Design Models. In Textile Fibre Composites in Civil Engineering; Elsevier Inc.: Amsterdam, The Netherlands, 2016; pp. 375–388. [Google Scholar]
- CNR-DT 200 R1/2012; Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Existing Structures. National Research Council: Rome, Italy, 2013.
- Triantafillou, T.C. Strengthening of masonry structures using epoxy-bonded FRP laminates. J. Compos. Constr. ASCE 1998, 2, 96–104. [Google Scholar] [CrossRef]
- Triantafillou, T.C.; Antonopoulos, C.P. Design of concrete flexural members strengthened in shear with FRP. J. Compos. Constr. ASCE 2000, 4, 198–204. [Google Scholar] [CrossRef]
- Eurocode 6; Design of Masonry Structures, Part 1-1: General Rules for Building-Rules for Reinforced and Unreinforced Masonry. European Committee for Standardization, CEN: Brussels, Belgium, 2005.
- EN 1998-3; Design of Structures for Earthquake Resistance, Part 3: Assessment and Retrofitting of Buildings. European Standard: Brussels, Belgium, 1998.
- Thomoglou, A.K.; Rousakis, T.C.; Achillopoulou, D.V.; Karabinis, A.I. Ultimate shear strength prediction model for unreinforced masonry retrofitted externally with textile reinforced mortar. Earthq. Struct. 2020, 19, 4411–4425. [Google Scholar]
- Roca, P.; Lourenço, P.B.; Gaetani, A. Damage and collapse mechanisms in masonry buildings. In Historic Construction and Conservation; Routledge: England, UK, 2019; pp. 239–293. [Google Scholar]
- Thomoglou, A.K.; Rousakis, T.C.; Karabinis, A.I. Investigation of failure modes of URM walls strengthened with TRM subjected to in-plane seismic loads. In Proceedings of the 2nd International Conference on Natural Hazards & Infrastructure, Chania, Greece, 23–26 June 2019. [Google Scholar]
- Thomoglou, A.K.; Rousakis, T.C.; Karabinis, A.I. Experimental Investigation of Shear Behavior of URM strengthened with TRM. In Proceedings of the 4nd Hellenic Conference Mechanical Seismology, Athens, Greece, 5–7 September 2019. [Google Scholar]
- Viskovic, A.; Zuccarino, L.; Kwiecień, A.; Zając, B. Masonry panels composite reinforcements with epoxy matrix, inorganic mortar matrix and PS polymer matrix. Key Eng. Mater. 2015, 624, 214–221. [Google Scholar] [CrossRef]
- Prota, A.; Marcari, G.; Fabbrocino, G.; Manfredi, G.; Aldea, C. Experimental In-Plane Behavior of Tuff Masonry Strengthened with Cementitious Matrix–Grid. Composites. J. Comp. Constr. ASCE 2006, 10, 223–233. [Google Scholar] [CrossRef]
- Papanicolaou, C.G.; Triantafillou, T.C.; Karlos, K.; Papathanasiou, M. Textile-reinforced mortar (TRM) versus FRP as strengthening material of URM walls: In-plane cyclic loading. Mater. Struct. 2007, 40, 1081–1097. [Google Scholar] [CrossRef]
- Del Zoppo, M.; Di Ludovico, M.; Prota, A. Analysis of FRCM and CRM parameters for the in-plane shear strengthening of different URM types. Compos. B Eng. 2019, 171, 20–33. [Google Scholar] [CrossRef]
- Saleh, H.M.; Eskander, S.B.; Fahmy, H.M. Mortar composite based on wet oxidative degraded cellulosic spinney waste fibers. Int. J. Environ. Sci. Technol. 2014, 11, 1297–1304. [Google Scholar] [CrossRef] [Green Version]
- Saleh, H.M.; Salman, A.A.; Faheim, A.A.; Abeer, A.E. Influence of aggressive environmental impacts on clean, lightweight bricks made from cement kiln dust and grated polystyrene. Case Stud. Constr. Mater. 2021, 15, e00759. [Google Scholar] [CrossRef]
- Eskander, S.B.; Saleh, H.M. Cement mortar-degraded spinney waste composite as a matrix for immobilizing some low and intermediate level radioactive wastes: Consistency under frost attack. J. Nucl. Mater. 2012, 420, 491–496. [Google Scholar] [CrossRef]
- Thomoglou, A.K.; Falara, M.G.; Gkountakou, F.I.; Elenas, A.; Chalioris, C.E. Smart Cementitious Sensors with Nano-, Micro-, and Hybrid-Modified Reinforcement: Mechanical and Electrical Properties. Sensors 2023, 23, 2405. [Google Scholar] [CrossRef] [PubMed]
- Faella, C.; Martinelli, E.; Nigro, E.; Paciello, S. Shear capacity of masonry walls externally strengthened by a cement-based composite material: An experimental campaign. Constr. Build. Mater. 2010, 24, 84–93. [Google Scholar] [CrossRef]
- Babaeidarabad, S.; De Caso, F.; Nanni, A. URM Walls Strengthened with Fabric-Reinforced Cementitious Matrix Composite Subjected to Diagonal Compression. J. Compos. Constr. 2014, 18, 04013045. [Google Scholar] [CrossRef]
- Almeida, J.A.P.P.; Pereira, E.B.; Barros, J.A.O. Assessment of Overlay Masonry Strengthening System Under In-Plane 1 Monotonic and Cyclic Loading Using the Diagonal Tensile Test; 2, ISISE, University of Minho, Department of Civil Engineering, School of Engineering: Guimarães, Portugal, 2015. [Google Scholar]
- Ferretti, F.; Tilocca, A.R.; Ferracuti, B.; Mazzotti, C. In situ diagonal compression tests on masonry panels strengthened by FRP and FRCM. In Proceedings of the 12th International Symposium on Fiber Reinforced Polymers for Reinforced Concrete Structures (FRPRCS-12) & 5th Asia-Pacific Conference on Fiber Reinforced Polymers in Structures (APFIS-2015) Joint Conference, Nanjing, China, 14–16 December 2015. [Google Scholar]
- Mazzotti, C.; Ferretti, F.; Ferracuti, B.; Incerti, A. Diagonal Compression Tests on Masonry Panels Strengthened by FRP and FRCM; © Taylor & Francis Group: London, UK, 2016; ISBN 978-1-138-02951-4. [Google Scholar]
- Gattesco, N.; Boem, I. Experimental and analytical study to evaluate the effectiveness of an in-plane reinforcement for masonry walls using GFRP meshes. Constr. Build. Mater. 2015, 88, 94–104. [Google Scholar] [CrossRef]
- Ismail, N.; Ingham, J.M. In-plane and out-of-plane testing of unreinforced masonry walls strengthened using polymer textile reinforced mortar. Eng. Struct. 2016, 118, 167–177. [Google Scholar] [CrossRef]
- Tomaževič, M.; Gams, M.; Berset, T. Seismic strengthening of brick masonry walls with composites: An experimental study. In Proceedings of the 4th Structural Engineering World Congress, International Association for Shell and Spatial Structures, Madrid, Spain, 2011; p. 307. [Google Scholar]
- Mustafaraj, E.; Yardim, Y. In-plane Shear Strengthening of Unreinforced Masonry Walls Using GFRP Jacketing. Period. Polytech. Civ. Eng. 2018, 62, 330–336. [Google Scholar] [CrossRef] [Green Version]
- Shabdin, M.; Zargaran, M.; Attari, N.K.A. Experimental DT (shear) test of Un-Reinforced Masonry (URM) walls strengthened with textile reinforced mortar (TRM). Constr. Build. Mater. 2018, 164, 704–715. [Google Scholar] [CrossRef]
- Babaeidarabad, S.; Arboleda, D.; Loreto, G.; Nanni, A. Shear strengthening of un-reinforced concrete masonry walls with fabric-reinforced-cementitious-matrix. Constr. Build. Mater. 2014, 65, 243–253. [Google Scholar] [CrossRef]
- Ismail, N.; El-Maaddawy, T.; Khattak, N.; Najmal, A. In-plane shear strength improvement of hollow concrete masonry panels using a fabric-reinforced cementitious matrix. J. Compos. Constr. 2018, 22, 04018004. [Google Scholar] [CrossRef]
- Lignola, G.; Prota, A.; Manfredi, G. Nonlinear analyses of tuff masonry walls strengthened with cementitious matrix-grid composites. J. Compos. Constr. 2009, 13, 243–251. [Google Scholar] [CrossRef]
- Borri, A.; Corradi, M.; Castori, G.; Sisti, R. Reinforcement of masonry panels with GFRP grids. In Proceedings of the SAHC2014, 9th International Conference on Structural Analysis of Historical Constructions, Mexico City, Mexico, 14–17 October 2014. [Google Scholar]
- Corradi, M.; Borri, A.; Castori, G.; Sisti, R. Shear strengthening of wall panels through jacketing with cement mortar reinforced by GFRP grids. Compos. B Eng. 2014, 64, 33–42. [Google Scholar] [CrossRef] [Green Version]
- Mustafaraj, E. External Shear Strengthening of Unreinforced Damaged Masonry Walls. Ph.D. Thesis, Epoka University, Tirana, Albania, 2016. [Google Scholar]
- Parisi, F.; Iovinella, I.; Balsamo, A.; Augenti, N.; Prota, A. In-plane behaviour of tuff masonry strengthened with inorganic matrix-grid composites. Compos. Part B 2013, 45, 1657–1666. [Google Scholar] [CrossRef]
- Gams, M.; Kwiecien, A.; Zajac, B.; Tomacevic, M. Seismic Strengthening of Brick Masonry Walls with Flexible Polymer Coating. In Proceedings of the 9th International Masonry Conference, Guimarães, Portugal, 7–9 July 2014; ISBN 978-972-8692-85-8. ID 1502. [Google Scholar]
- Tomaževič, M.; Gams, M.; Berset, T. Strengthening of stone masonry walls with composite reinforced coatings. Bull. Earthq. Eng. 2014, 13, 2003–2027. [Google Scholar] [CrossRef]
- Papanicolaou, C.; Triantafillou, T.; Lekka, M. Externally bonded grids as strengthening and seismic retrofitting materials of masonry panels. Constr. Build. Mater. 2011, 25, 504–514. [Google Scholar] [CrossRef]
- Wang, X.; Lam, C.C.; Iu, V.P. Comparison of different types of TRM composites for strengthening masonry panels. Constr. Build. Mater. 2019, 219, 184–194. [Google Scholar] [CrossRef]
- Calderini, C.; Cattari, S.; Lagomarsino, S. In-plane strength of unreinforced masonry piers. Earthq. Eng. Struc. 2009, 38, 243–267. [Google Scholar] [CrossRef]
- Carozzi, F.G.; Milani, G.; Poggi, C. Mechanical properties and numerical modeling of Fabric Reinforced Cementitious Matrix (FRCM) systems for strengthening of masonry Structures. Compos. Struct. 2014, 117, 711–725. [Google Scholar] [CrossRef]
- Ferrara, G.; Pepe, M.; Martinelli, E. Influence of fibres impregnation on the tensile response of flax textile reinforced mortar composite systems. In Fiber Reinforced Concrete: Improvements and Innovations, RILEM-Fib International Symposium on FRC (BEFIB); Serna, P., Llano-Torre, A., Vargas, J.R.M., Navarro-Gregori, J., Eds.; Springer: Valencia, Spain, 2021. [Google Scholar]
- Gaetani, A.; Fascetti, A.; Nistico, N. Parametric investigation on the tensile response of GFRP elements through a discrete lattice modeling approach. Compos. B Eng. 2019, 176, 107254. [Google Scholar] [CrossRef]
- De Santis, S.; Hadad, A.; De Caso, B.; De Felice, G.; Nanni, A. Acceptance Criteria for Tensile Characterization of Fabric-Reinforced Cementitious Matrix Systems for Concrete and Masonry Repair. ASCE J. Compos. Constr. 2018, 22, 04018048. [Google Scholar] [CrossRef]
- Türkmen, Ö.S.; De Vries, B.T.; Wijte, S.N.M.; Vermeltfoort, A.T. In-plane behaviour of clay brick masonry wallettes retrofitted with single-sided fabric-reinforced cementitious matrix and deep mounted carbon fibre strips. Bull. Earthq. Eng. 2020, 18, 725–765. [Google Scholar] [CrossRef] [Green Version]
- Mann, W.; Müller, H. Failure of shear-stressed masonry—An enlarged theory. Tests and application to shear walls. Proc. Br. Ceram. Soc. 1982, 30, 223–235. [Google Scholar]
- Li, T.; Galati, N.; Tumialan, J.G.; Nanni, A. Analysis of unreinforced masonry concrete walls strengthened with glass fiber-reinforced polymer bars. Aci. Struct. J. 2005, 102, 569–577. [Google Scholar]
- D’Ambrisi, F.A.; Focacci, F. Experimental and analytical investigation on bond between Carbon-FRCM materials and masonry. Compos. B Eng. 2013, 46, 15–20. [Google Scholar] [CrossRef]
- Sagar, S.L.; Singhal, V.; Rai, D.C.; Gudur, P. Diagonal shear and out-of-plane flexural strength of fabric-reinforced cementitious matrix-strengthened masonry wallets. J. Compos. Constr. 2017, 21, 04017016. [Google Scholar] [CrossRef]
- Ferrara, G.; Caggegi, C.; Martinelli, E.; Gabor, A. Shear capacity of masonry walls externally strengthened using Flax–TRM composite systems: Experimental tests and comparative assessment. Constr. Build. Mater. 2020, 261, 120490. [Google Scholar] [CrossRef]
- Trochoutsou, N.; Di Benedetti, M.; Pilakoutas, K.; Guadagnini, M. Mechanical characterisation of flax and jute textile-reinforced mortars. Constr. Build. Mater. 2021, 271, 121564. [Google Scholar] [CrossRef]
- Trochoutsou, N.; Di Benedetti, M.; Pilakoutas, K.; Guadagnini, M. Bond of flax textile-reinforced mortars to masonry. Constr. Build. Mater. 2021, 284, 122849. [Google Scholar] [CrossRef]
- Papadopoulos, N.A.; Naoum, M.C.; Sapidis, G.M.; Chalioris, C.E. Cracking and Fiber Debonding Identification of Concrete Deep Beams Reinforced with C-FRP Ropes against Shear Using a Real-Time Monitoring System. Polymers 2023, 15, 473. [Google Scholar] [CrossRef]
- Zapris, A.G.; Naoum, M.C.; Kytinou, V.K.; Sapidis, G.M.; Chalioris, C.E. Fiber Reinforced Polymer Debonding Failure Identification Using Smart Materials in Strengthened T-Shaped Reinforced Concrete Beams. Polymers 2023, 15, 278. [Google Scholar] [CrossRef]
- Ali, A.H.; Mohamed, H.M.; Chalioris, C.E.; Deifalla, A. Evaluating the shear design equations of FRP-reinforced concrete beams without shear reinforcement. Eng. Struct. 2021, 235, 112017. [Google Scholar] [CrossRef]
- Askouni, P.D.; Papanicolaou, C.G. Experimental investigation of bond between glass textile reinforced mortar overlays and masonry: The effect of bond length. Mater. Struct. 2017, 50, 164. [Google Scholar] [CrossRef]
- Hojdys, Ł.; Krajewski, P. Tensile Behaviour of FRCM Composites for Strengthening of Masonry Structures—An Experimental Investigation. Materials 2021, 14, 3626. [Google Scholar] [CrossRef]
- Yardim, Y.; Lalaj, O. Shear strengthening of unreinforced masonry wall with different fiber reinforced mortar jacketing. Constr. Build. Mater. 2016, 102, 149–154. [Google Scholar] [CrossRef]
- Tarek, D.; Ahmed, M.M.; Hussein, H.S.; Zeyad, A.M.; Al-Enizi, A.M.; Yousef, A.; Ragab, A. Building envelope optimization using geopolymer bricks to improve the energy efficiency of residential buildings in hot arid regions. Case Stud. Constr. Mater. 2022, 17, e01657. [Google Scholar] [CrossRef]
- Jagadesh, P.; Nagarajan, V.; Karthik prabhu, T.; Karthik Arunachalam, K. Effect of nano titanium di oxide on mechanical properties of fly ash and ground granulated blast furnace slag based geopolymer concrete. J. Build. Eng. 2022, 61, 105235. [Google Scholar]

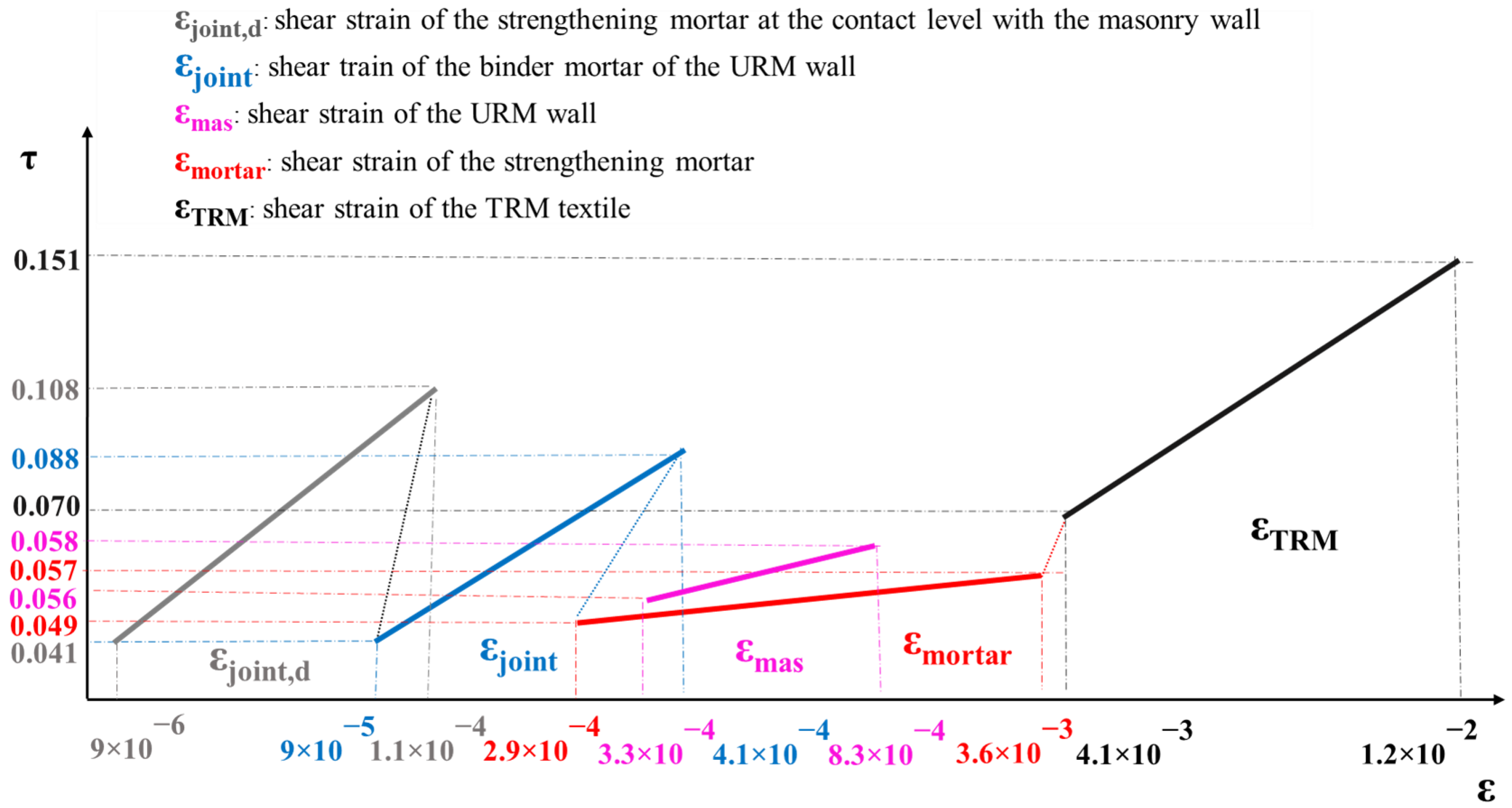
| τexp | Range (MPa) | ε | Range (mm/mm) | Failure Mode | Type of TRM | |
|---|---|---|---|---|---|---|
| Masonry substrate | τεjoint | 0.041–0.088 | εjoint | 0.000095–0.000410 | SS-SF | GTRM-CTRM |
| τεmas | 0.056–0.058 | εmas | 0.000330–0.000830 | DT-TC | GTRM-CTRM | |
| TRM | τεjoint,d | 0.041–0.108 | εjoint,d | 0.000009–0.000110 | TRM Failure | GTRM-CTRM |
| τεmortar | 0.049–0.057 | εmortar | 0.000288–0.003590 | TRM Failure | GTRM-CTRM | |
| τTRM | 0.070–0.151 | εTRM | 0.004100–0.011700 | TRM Failure | CTRM-CTRM |
| Types of Masonry Units | Types of Textile Reinforcement | Coefficient k | εtm (%) |
|---|---|---|---|
| brick | glass | 0.55 | 0.057 |
| carbon | 0.60 | 0.112 | |
| cement | glass | 0.52 | 0.038 |
| carbon | 0.52 | 0.015 | |
| stone | glass | 0.59 | 0.038 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thomoglou, A.K.; Karabini, M.A.; Achillopoulou, D.V.; Rousakis, T.C.; Chalioris, C.E. Failure Mode Prediction of Unreinforced Masonry (URM) Walls Retrofitted with Cementitious Textile Reinforced Mortar (TRM). Fibers 2023, 11, 53. https://doi.org/10.3390/fib11060053
Thomoglou AK, Karabini MA, Achillopoulou DV, Rousakis TC, Chalioris CE. Failure Mode Prediction of Unreinforced Masonry (URM) Walls Retrofitted with Cementitious Textile Reinforced Mortar (TRM). Fibers. 2023; 11(6):53. https://doi.org/10.3390/fib11060053
Chicago/Turabian StyleThomoglou, Athanasia K., Martha A. Karabini, Dimitra V. Achillopoulou, Theodoros C. Rousakis, and Constantin E. Chalioris. 2023. "Failure Mode Prediction of Unreinforced Masonry (URM) Walls Retrofitted with Cementitious Textile Reinforced Mortar (TRM)" Fibers 11, no. 6: 53. https://doi.org/10.3390/fib11060053
APA StyleThomoglou, A. K., Karabini, M. A., Achillopoulou, D. V., Rousakis, T. C., & Chalioris, C. E. (2023). Failure Mode Prediction of Unreinforced Masonry (URM) Walls Retrofitted with Cementitious Textile Reinforced Mortar (TRM). Fibers, 11(6), 53. https://doi.org/10.3390/fib11060053