Anisotropy and Fiber Orientation: A Key Player in the Lateral Imbibition of Cellulose Paper
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
3. Results
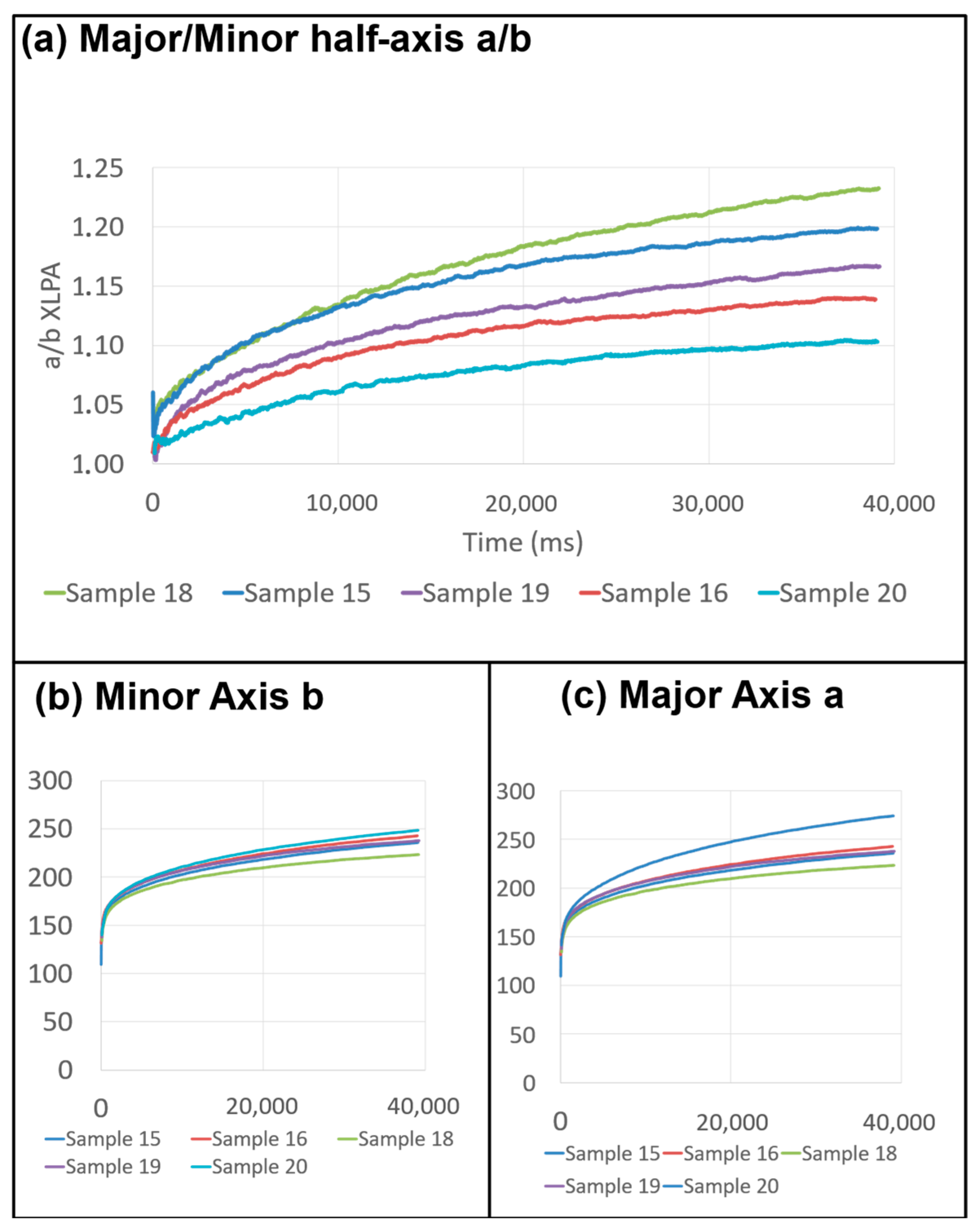
- The same evolution for all the papers. However, the curves differ in their course and position in the coordinate system.
- We recognize a global square root, which corresponds to Lucas–Washburn’s model [27]. For more details about the modeling of such behavior, the interested reader may refer to Bloch et al., 2023 [23], where two regimes are distinguished, namely the initial linear rate then the classical square root shape.
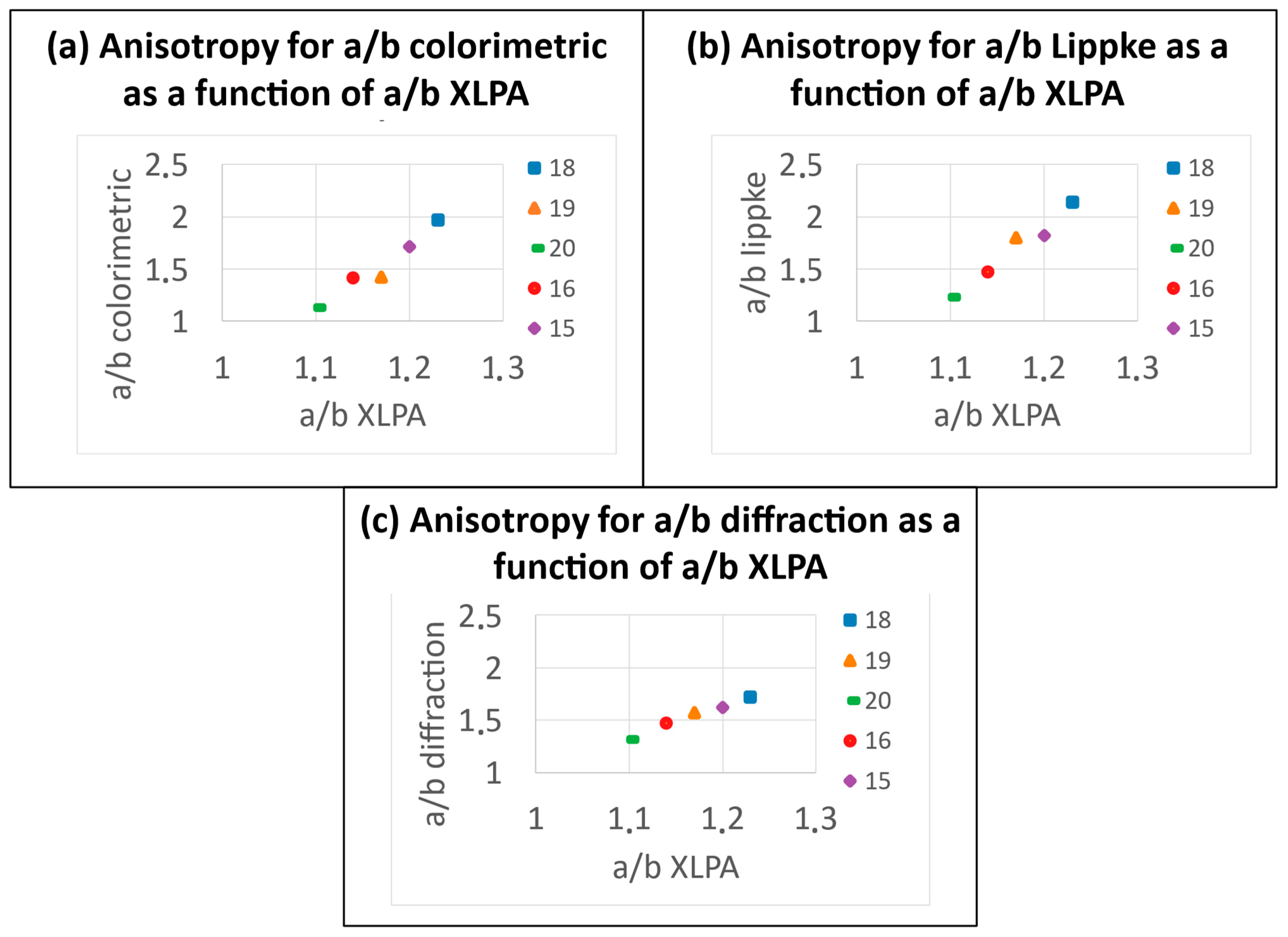
- The imbibition anisotropy (a/b) leads to the following order: 18, 15, 19, 16, 20.
- The minor and major axes lead exactly to the same order (18, 15, 19, 16, 20) from the smaller to the larger values.
- As the mean pore size is related to the porosity, the evolution of the major axis mainly depends on the porosity, which itself depends on the fiber orientation. The more oriented, the less porous a fibrous structure is. Hence, the time evolution of the imbibition in each main direction should be analyzed based on the porosity.
4. Discussion
- Our results fit with all the data presented in Table 2. The anisotropy is well characterized.
- Furthermore, linear relationships exist between each anisotropy characterization and the one obtained from imbibition. The imbibition anisotropy is, hence, due to fiber orientation.
- The main axes (a, b) of the ellipse are related to porosity, as expected, and therefore to velocities, which are the time derivative of a and b.
5. Conclusions
- The main axes representing the main directions of liquid penetration through the paper structure are influenced by the porosity of the fibrous structure.
- Unevenness in the spread of liquid in the tested paper samples was observed during imbibition measurements. It was found that there is a correlation between this effect and anisotropy of paper structure (i.e., differences in fiber orientation).
- The greater the paper anisotropy, the greater the differences in the lengths of the main axes of the ellipse that were observed. A linear dependence is exhibited in our results.
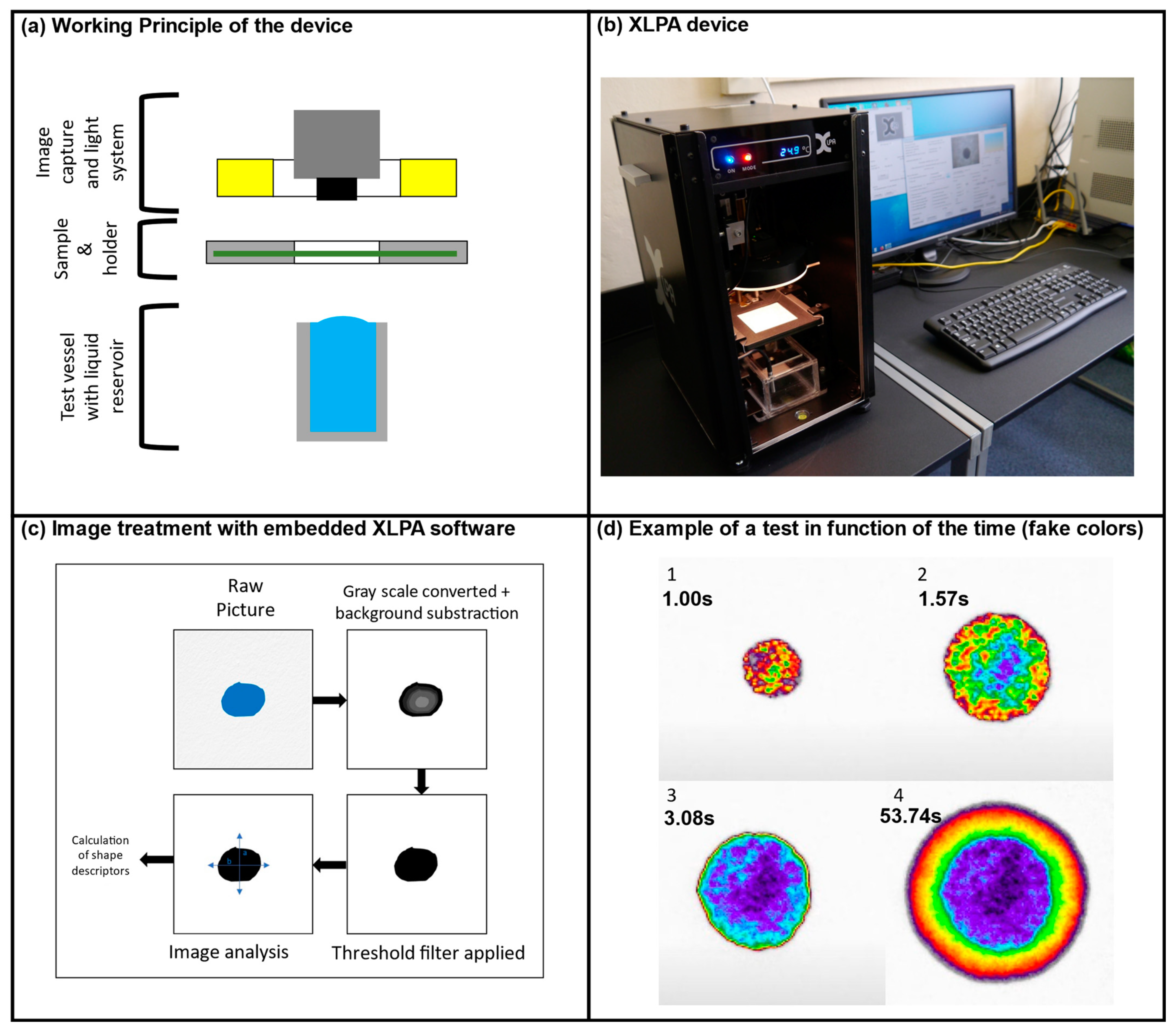
- An experimental device used in the presented research allowed us to characterize the kinetics of imbibition, including small time scales (ms) and larger time (s).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
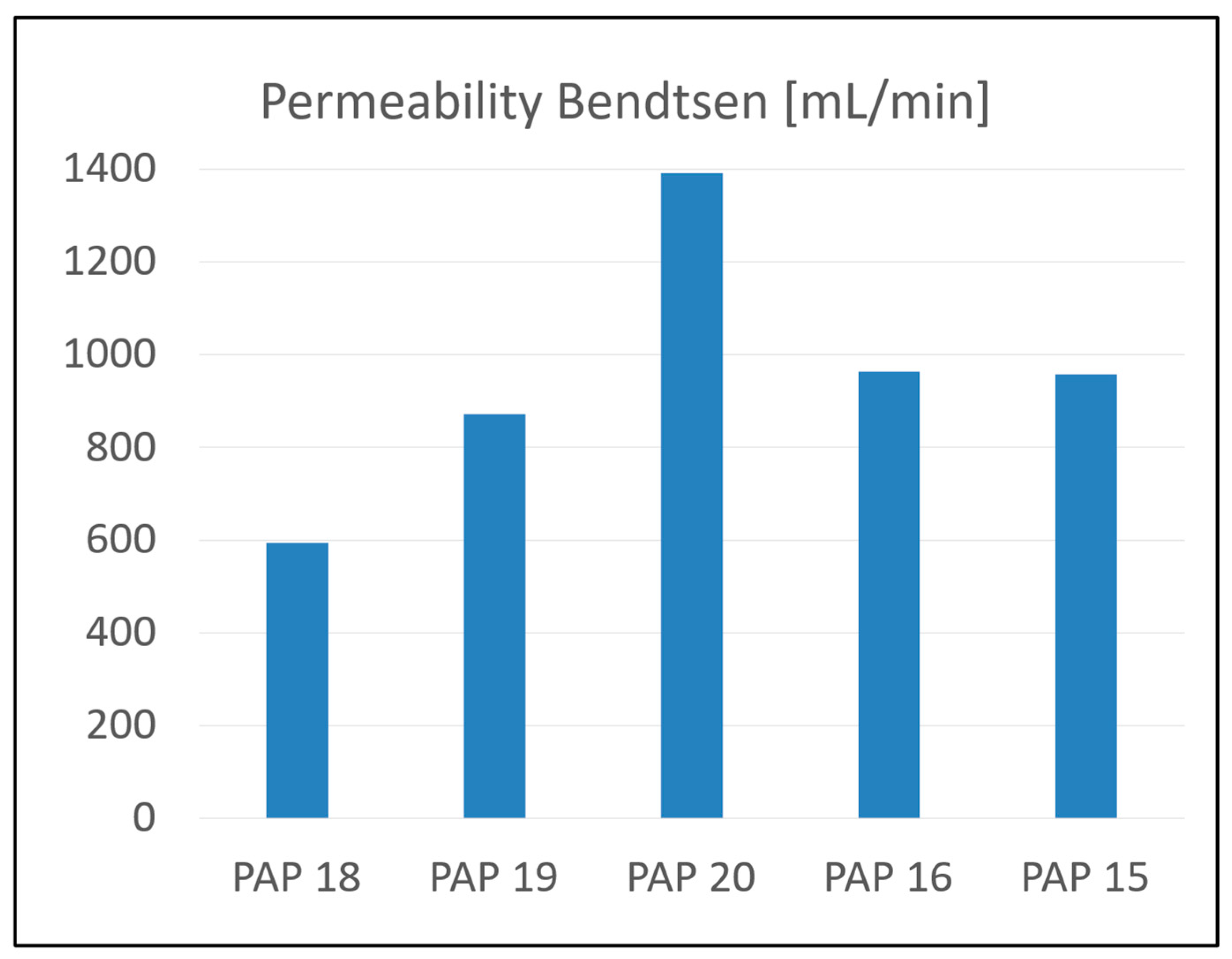
Appendix A. S1—Experimental Data for Permeability
| TESTS | Papers | 18 | 19 | 20 | 16 | 15 |
| Permeability Bendtsen (mL/min) | Rep1 | 582 | 802 | 1327 | 896 | 918 |
| Rep2 | 524 | 766 | 1350 | 996 | 912 | |
| Rep3 | 589 | 826 | 1563 | 922 | 1080 | |
| Rep4 | 558 | 762 | 1243 | 997 | 811 | |
| Rep5 | 604 | 739 | 1692 | 1095 | 1077 | |
| Rep6 | 688 | 974 | 1588 | 905 | 1253 | |
| Rep7 | 566 | 922 | 1253 | 984 | 890 | |
| Rep8 | 621 | 874 | 1480 | 1028 | 1043 | |
| Rep9 | 553 | 1055 | 1494 | 943 | 732 | |
| Rep10 | 539 | 1052 | 1405 | 870 | 1076 | |
| Rep11 | 636 | 786 | 1172 | 933 | 924 | |
| Rep12 | 632 | 786 | 1361 | 938 | 1097 | |
| Rep13 | 676 | 1023 | 1177 | 929 | 837 | |
| Rep14 | 560 | 837 | 1382 | 1053 | 749 | |
| Average | 595 | 872 | 1392 | 964 | 957 | |
| Std-Dev | 50 | 113 | 157 | 64 | 151 | |
| Coef Var | 0.084 | 0.229 | 0.113 | 0.066 | 0.157 | |
| Thickness (µm) | Rep1 | 82 | 90 | 85 | 82 | 82 |
| Rep2 | 82 | 87 | 88 | 79 | 78 | |
| Rep3 | 81 | 89 | 86 | 81 | 77 | |
| Rep4 | 83 | 86 | 90 | 84 | 82 | |
| Rep5 | 84 | 85 | 89 | 83 | 79 | |
| Rep6 | 84 | 82 | 91 | 81 | 84 | |
| Rep7 | 86 | 83 | 94 | 85 | 79 | |
| Rep8 | 84 | 85 | 86 | 79 | 76 | |
| Rep9 | 82 | 85 | 89 | 81 | 80 | |
| Rep10 | 83 | 89 | 87 | 79 | 86 | |
| Average | 83 | 86 | 89 | 81 | 80 | |
| Std-Dev | 1 | 2 | 3 | 2 | 3 | |
| Coef Var | 0.018 | 0.029 | 0.031 | 0.028 | 0.042 |
References
- Htun, M.; Fellers, C. The In-Plane Anisotry of Paper in Relation to Fiber Orientation and Drying Restrains. In Paper Structure and Properties (International Fiber Science and Technology); Bristow, J.A., Kolsteh, P., Eds.; CRC Press: Boca Raton, FL, USA, 1986; Volume 327, pp. 327–345. [Google Scholar]
- Niskanen, K. Paper Structure. In Paper Physics (Papermaking Science and Technology); Tappi Pr: Peachtree Corners, GA, USA, 1998; Volume PST Book 16, pp. 15–51. [Google Scholar]
- Schaffnit, C.; Silvy, J.; Dodson, C.T.J. Orientation Density Distributions of Fibres in Paper. Nord. Pulp. Pap. Res. J. 1992, 7, 121–125. [Google Scholar] [CrossRef]
- Shakespeare, J. Tutorial: Fibre Orientation Angle Profiles—Process Principles and Cross Machine Control. TAPPI Process Control Electr. Info. Conf. Proc. 1998, 98, e593–e636. [Google Scholar]
- Niskanen, K. Papermaking Science and Technology; Finnish Paper Engineers’ Association: Helsinki, Finland, 2005; Volume 16. [Google Scholar]
- Yang, C.-F.; Crosby, C.M.; Eusufzai, A.R.K.; Mark, R.E. Determination of Paper Sheet Fiber Orientation Distributions by a Laser Optical Diffraction Method. J. Appl. Polym. Sci. 1987, 34, 1145–1157. [Google Scholar] [CrossRef]
- Fiadeiro, P.T.; Pereira, M.J.T.; Jesus, M.E.P.; Silvy, J.J. The Surface Measurement of Fibre Orientation Anisotropy and Misalignment Angle by Laser Diffraction. J. Pulp Pap. Sci. 2002, 28, 341–346. [Google Scholar]
- Dias, P.A.N.; Rodrigues, R.J.; Reis, M.S. Fast Characterization of In-Plane Fiber Orientation at the Surface of Paper Sheets through Image Analysis. Chemom. Intell. Lab. Syst. 2023, 234, 104761. [Google Scholar] [CrossRef]
- Wharen, D.; Haglund, L.; Norman, B. The Power Spectrum of the Basis Weight of Random Sheets. In Proceedings of the International Paper Physics Conference, Montreal, PQ, Canada, 1971; pp. 57–59. [Google Scholar]
- Helbrecht, C.; Langhans, M.; Meckel, T.; Biesalski, M.; Schabel, S. Analyses of the Effects of Fiber Diameter, Fiber Fibrillation, and Fines Content on the Pore Structure and Capillary Flow Using Laboratory Sheets of Regenerated Fibers. Nord. Pulp. Pap. Res. J. 2023, 38, 425–440. [Google Scholar] [CrossRef]
- Ferreira, E.S.; Drummond, J.; Veiga, A.T.V.; Sibellas, A.; Brown, S.; Cranston, E.D.; Martinez, D.M. Mapping Absorbency in Cellulosic Fibres with Iron Tracers. Carbohydr. Polym. 2023, 311, 120785. [Google Scholar] [CrossRef] [PubMed]
- Olejnik, K.; Bloch, J.-F.; Pelczynski, P. Measurement of the Dynamics of Fluid Sorption for Tissue Papers. Tappi J. 2019, 18, 417–426. [Google Scholar] [CrossRef]
- Yang, L.; Liu, J.; Gu, L. Detailed Insights to Liquid Absorption and Liquid-Paper Interaction. In Proceedings of the Transactions of the XVth Fundamental Research Symposium Cambridge, 2013; I’ Anson, S.J., Ed.; Fundamental Research Committee (FRC): Manchester, UK, 2013; pp. 585–598. [Google Scholar]
- Schoelkopf, J.; Matthews, G.P. Influence of Inertia on Liquid Absorption into Paper Coating Structures. Nord. Pulp. Pap. Res. J. 2000, 15, 422–430. [Google Scholar] [CrossRef]
- von Bahr, M.; Kizling, J. Spreading and Penetration of Aqueous Solutions and Water-Borne Inks in Contact with Paper and Model Substrates. In Advances in Printing Science and Technology; Pira International: Surrey, UK, 2001; pp. 87–102. [Google Scholar]
- Liana, D.D.; Raguse, B.; Gooding, J.J.; Chow, E. Recent Advances in Paper-Based Sensors. Sensors 2012, 12, 11505–11526. [Google Scholar] [CrossRef] [PubMed]
- Songok, J.; Salminen, P.; Toivakka, M. Temperature Effects on Dynamic Water Absorption into Paper. J. Colloid Interface Sci. 2014, 418, 373–377. [Google Scholar] [CrossRef] [PubMed]
- Iglesias, M.C.; Gomez-Maldonado, D.; Via, B.K.; Jiang, Z.; Peresin, M.S. Pulping Processes and Their Effects on Cellulose Fibers and Nanofibrillated Cellulose Properties: A Review. For. Prod. J. 2020, 70, 10–21. [Google Scholar] [CrossRef]
- Silvy, J. La Transformation Conforme Du Pore Équivalent, Méthode d’homogénéisation de La Texture Des Milieux Polyphasés. Récents Progrès Génie Procédés Diffus. Lavoisier Tech. Doc. 1989, 3, 506–514. [Google Scholar]
- Drouin, B.; Gagnon, R.; Schroder, A.; Butel, M.; Silvy, J. L’Orientation Des Fibres et Les Propriétés Mécaniques Du Papier: Méthodes de Contrôle de l’Anisotropie de La Feuille. REVUE-ATIP 1995, 49, 66–72. [Google Scholar]
- Silvy, J. Etude Structurale Des Milieux Fibreux: Cas Des Fibres Cellulosiques. Ph.D. Thesis, Institut National Polytechnique de Grenoble, Grenoble, France, 1980. [Google Scholar]
- Silvy, J.; Caret, C.; Belamaalem, B.; Marhous, M. The Tridimensional Structure of Paper, Methods of Analysis and Implications on His Physical Properties. In Proceedings of the International Paper Physics Conference; CPPA TAPPI: Niagara on the Lake, ON, Canada, 1995; pp. 1–5. [Google Scholar]
- Bloch, P.-Y.; Olejnik, K.; Bloch, J.-F.; Bloch, A.; Hammond, J.; Brissaud, D. Time Scales of Spontaneous Imbibition into Porous Material: From Classic Models to Papers Applications. Bioresources 2023, 19, 345–365. [Google Scholar] [CrossRef]
- ISO 5636-3:2013; Paper and Board—Determination of Air Permeance (Medium Range)—Part 3: Bendtsen Method. International Organization for Standardization: Geneva, Switzerland, 2013.
- ISO 534:2011; Paper and Board—Determination of Thickness, Density and Specific Volume. International Organization for Standardization: Geneva, Switzerland, 2011.
- Mercer, P. On-Line Instrumentation for Wet-Ended Control. Appita 1988, 41, 308–312. [Google Scholar]
- Hamraoui, A.; Nylander, T. Analytical Approach for the Lucas-Washburn Equation. J. Colloid Interface Sci. 2002, 250, 415–421. [Google Scholar] [CrossRef] [PubMed]

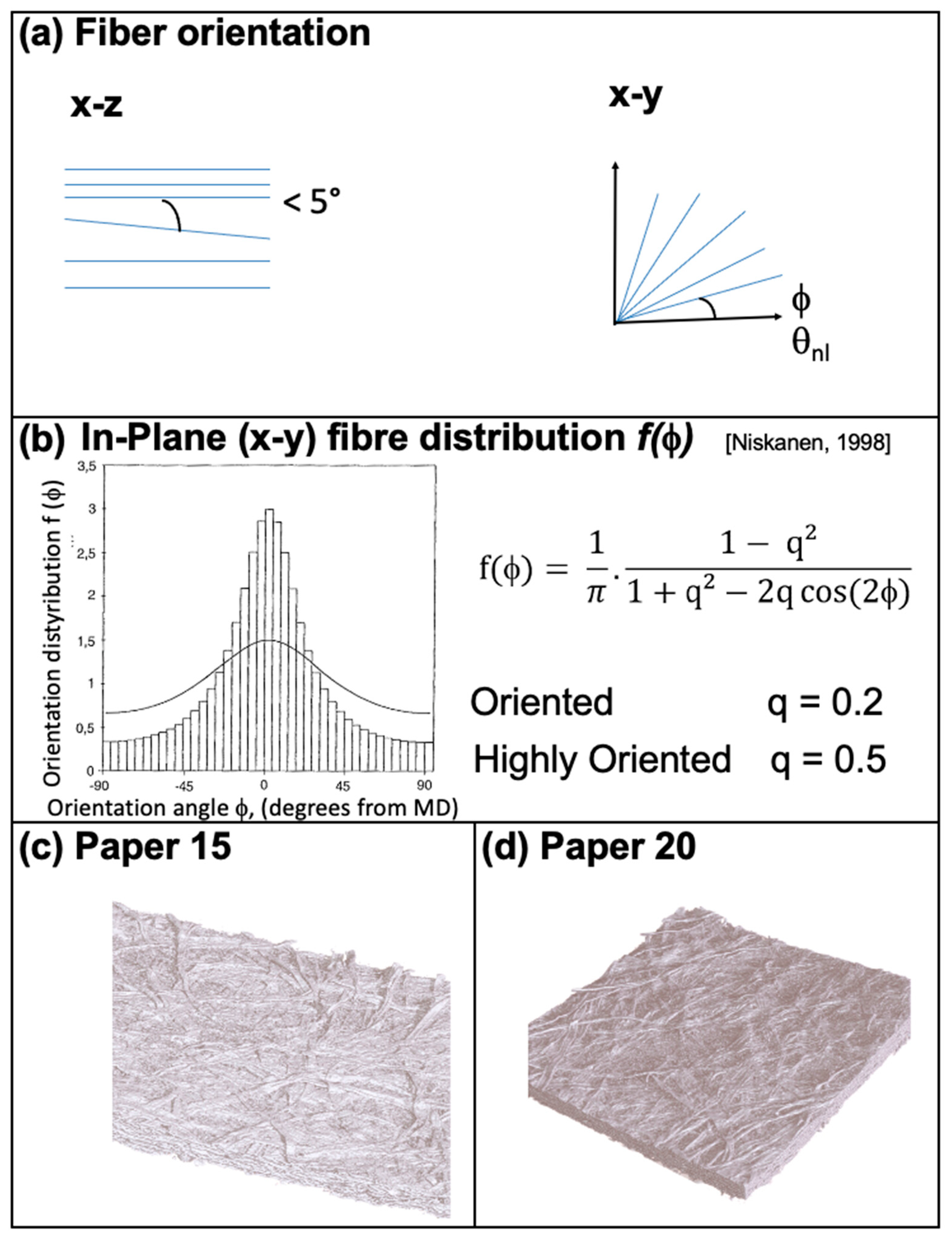
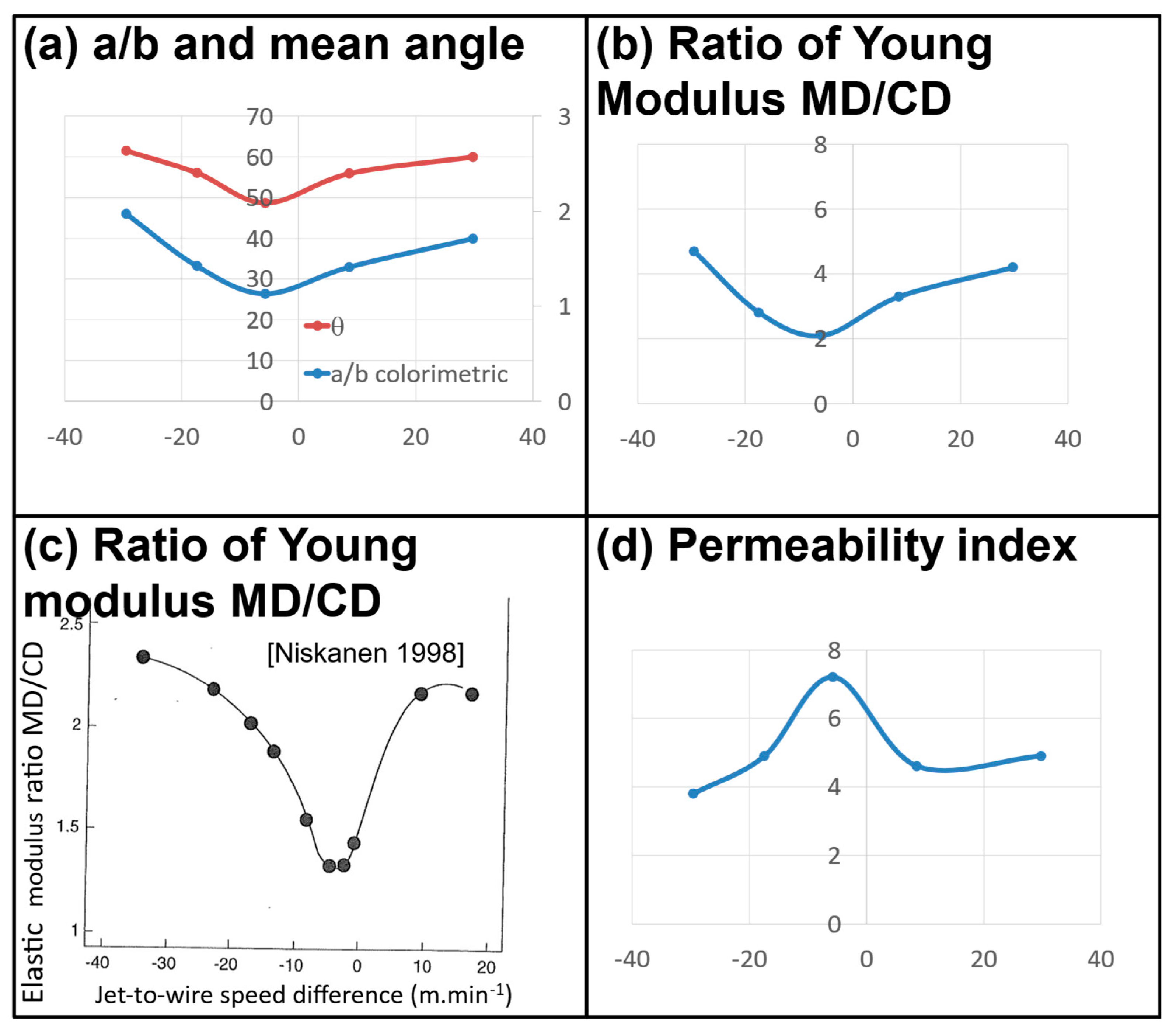
| Paper Samples Data from the Literature | 18 | 19 | 20 | 16 | 15 |
|---|---|---|---|---|---|
| Vjet − Vwire (m·min−1) | −29.5 | −17.4 | −5.7 | 8.6 | 29.8 |
| θnl | 61.5 | 56.1 | 48.7 | 55.9 | 60 |
| a/b colorimetric | 1.97 | 1.42 | 1.13 | 1.41 | 1.71 |
| W (g·m−2) | 50.9 | 48.6 | 48.5 | 48.2 | 47.7 |
| e (µm) | 86 | 82 | 90 | 87 | 89 |
| Porosity | 0.615 | 0.615 | 0.650 | 0.640 | 0.652 |
| Young Modulus (kN·cm−2) | |||||
| MD | 532 | 434 | 317 | 378 | 466 |
| CD | 114 | 152 | 150 | 113 | 111 |
| Mean | 323 | 293 | 235 | 264 | 288 |
| MD/CD | 4.7 | 2.8 | 2.1 | 3.3 | 4.2 |
| Paper | 18 | 19 | 20 | 16 | 15 |
|---|---|---|---|---|---|
| a/b colorimetric | 1.97 | 1.42 | 1.13 | 1.41 | 1.71 |
| a/b Lippke | 2.14 | 1.8 | 1.23 | 1.47 | 1.82 |
| a/b diffraction | 1.72 | 1.57 | 1.32 | 1.47 | 1.62 |
| TSI (EMD/ECD) | 4.53 | 2.81 | 1.72 | 2.39 | 3.69 |
| a/b XLPA | 1.23 | 1.17 | 1.1 | 1.14 | 1.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bloch, P.-Y.; Bloch, J.-F.; Olejnik, K.; Brissaud, D. Anisotropy and Fiber Orientation: A Key Player in the Lateral Imbibition of Cellulose Paper. Fibers 2024, 12, 56. https://doi.org/10.3390/fib12070056
Bloch P-Y, Bloch J-F, Olejnik K, Brissaud D. Anisotropy and Fiber Orientation: A Key Player in the Lateral Imbibition of Cellulose Paper. Fibers. 2024; 12(7):56. https://doi.org/10.3390/fib12070056
Chicago/Turabian StyleBloch, Pierre-Yves, Jean-Francis Bloch, Konrad Olejnik, and Daniel Brissaud. 2024. "Anisotropy and Fiber Orientation: A Key Player in the Lateral Imbibition of Cellulose Paper" Fibers 12, no. 7: 56. https://doi.org/10.3390/fib12070056
APA StyleBloch, P.-Y., Bloch, J.-F., Olejnik, K., & Brissaud, D. (2024). Anisotropy and Fiber Orientation: A Key Player in the Lateral Imbibition of Cellulose Paper. Fibers, 12(7), 56. https://doi.org/10.3390/fib12070056







