Modelling Pore Size Distribution Function of Twist-Texturized Yarns and Single-Jersey Knitted Fabrics
Abstract
:1. Introduction
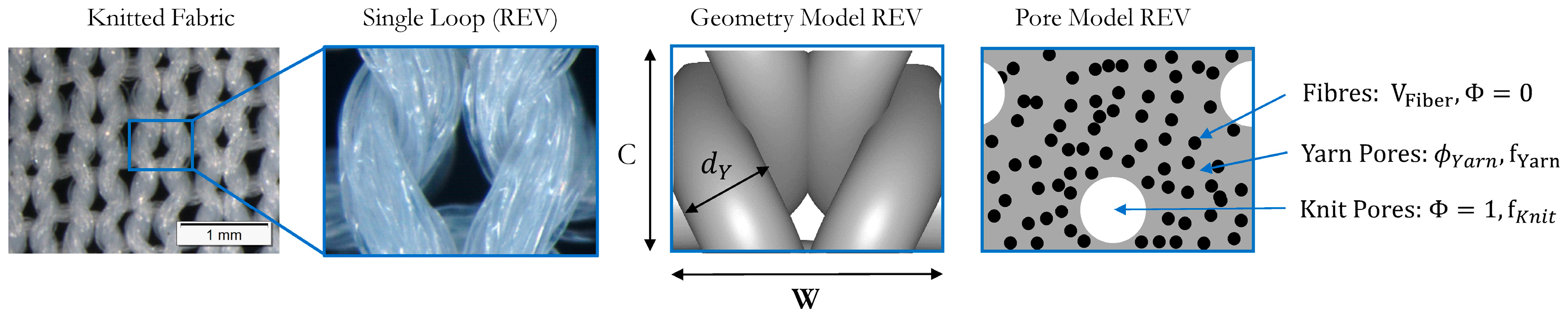
2. Model for PDF of Single-Jersey Fabrics
2.1. General Model
2.2. Modelling PDF of Twist-Texturized Yarns
- Yarn Diameter
- Fibre Diameter
- Fibre Count
- Yarn Linear Density
2.3. Modelling PDF of Single-Jersey Knitted Fabrics
3. Validation of Model
3.1. Extraction of Yarn Parameters from Cross-Sections
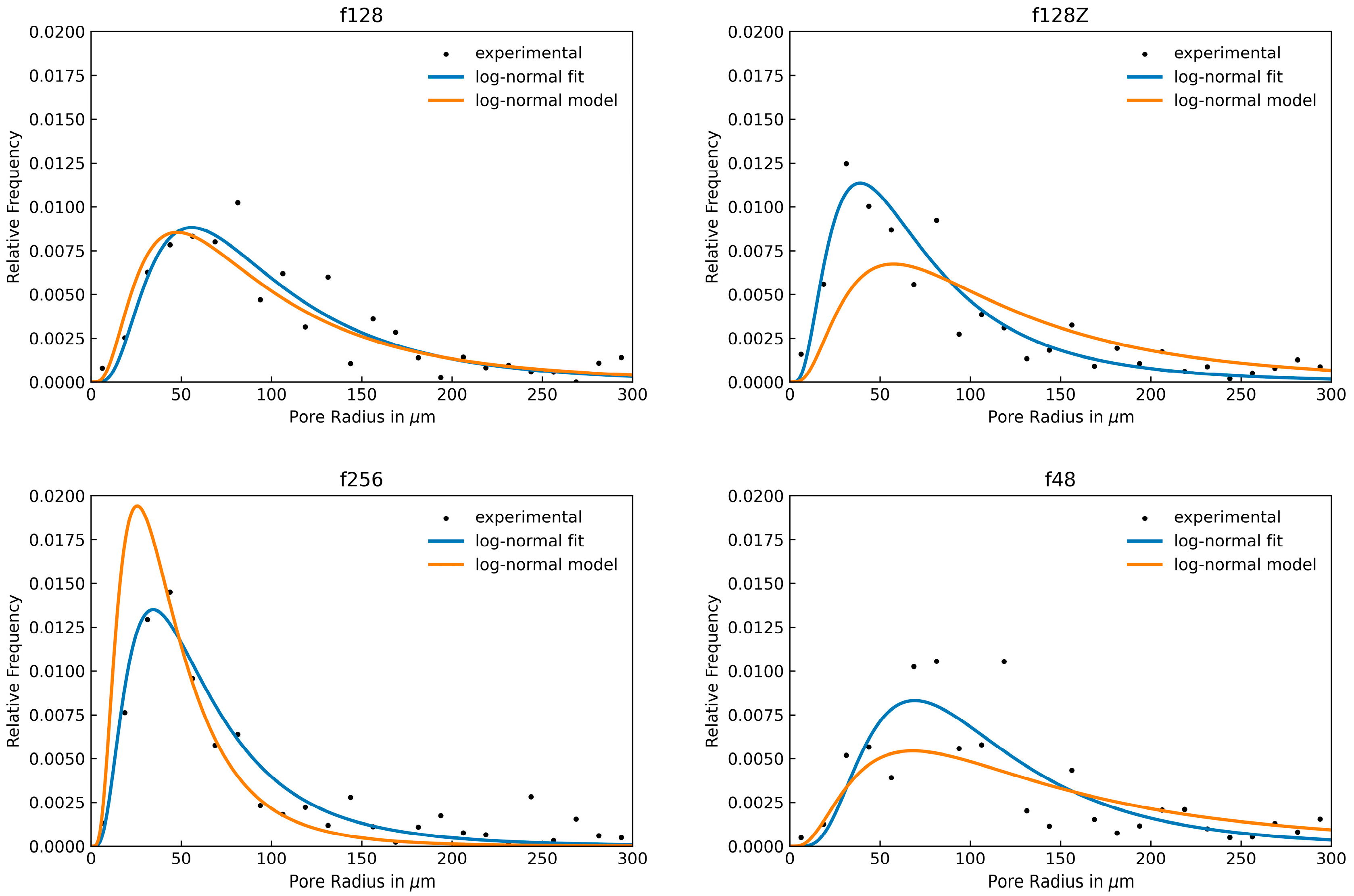
3.2. Experimental Derivation of Yarn PDF and Validation of Yarn Model
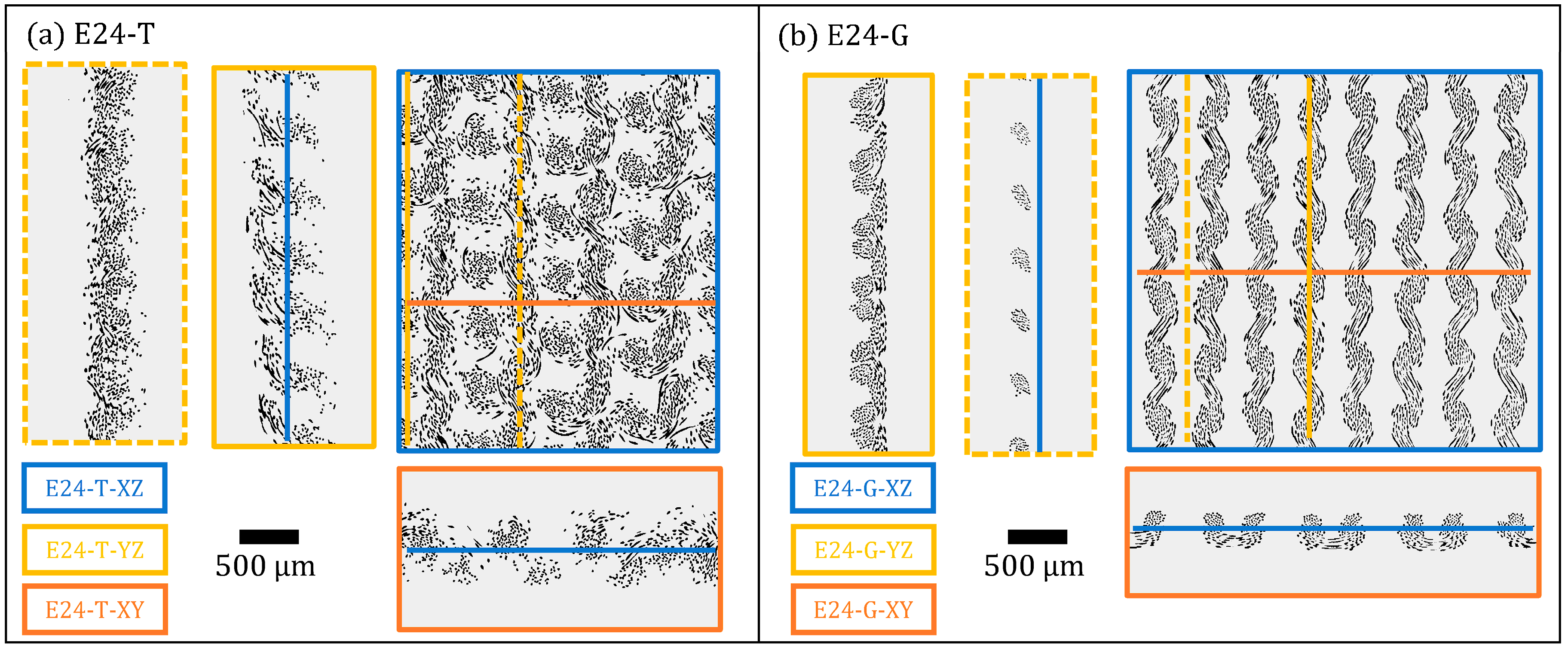
3.3. CT Scans of Single-Jersey Fabrics
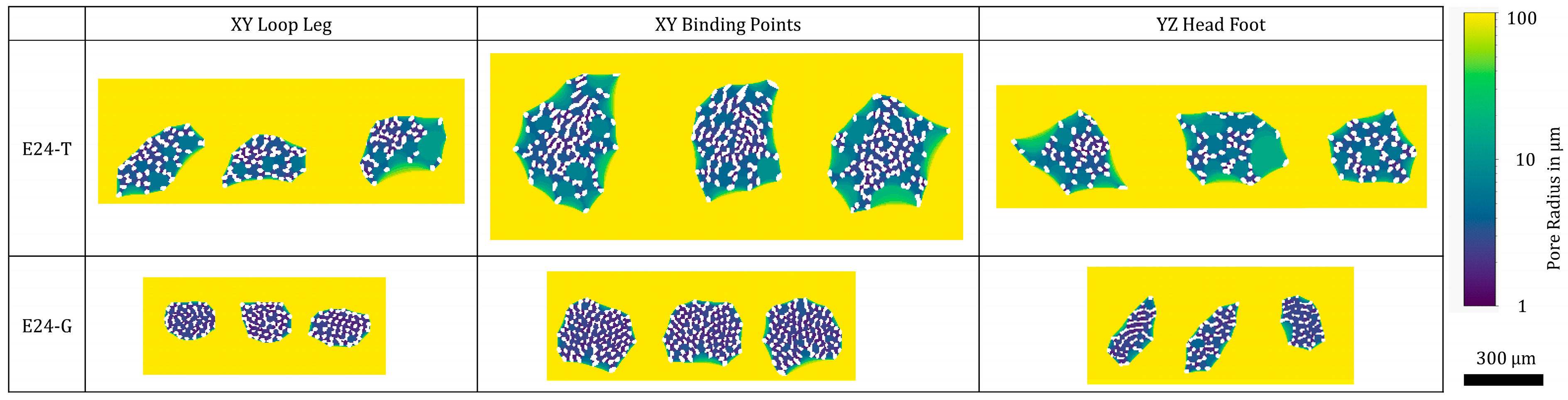
3.4. Validation of Yarn PDF in Knitted Fabrics
3.5. Validation of Fabric PDF
4. Parameter Study on Model
4.1. Fibre Diameter and Yarn Count
4.2. Fibre Orientation and Yarn Porosity
4.3. Knitting Parameters
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Name | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E24-G | 818 | 513 | 186 | 275 | 48 | 1.38 | 18.8 | 1.01 | 3032 | 1.42 | 0.77 | 0.59 | 0.84 | 199 | 32 |
| E24-T | 631 | 477 | 194 | 372 | 48 | 1.38 | 16.3 | 1.40 | 2556 | 1.72 | 0.87 | 0.44 | 0.81 | 146 | 55 |
| Name | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 500 | 350 | 186 | 186 | 961 | 1.38 | 3 | 1.2 | 1966 | 2.19 | 0.7 | 0.56 | 0.87 | 124 | 10 | |
| 500 | 350 | 186 | 186 | 346 | 1.38 | 5 | 1.2 | 1970 | 2.19 | 0.7 | 0.55 | 0.87 | 124 | 17 | |
| 500 | 350 | 186 | 186 | 177 | 1.38 | 7 | 1.2 | 1976 | 2.18 | 0.7 | 0.56 | 0.87 | 124 | 23 | |
| 500 | 350 | 186 | 185 | 86 | 1.38 | 10 | 1.2 | 1978 | 2.18 | 0.7 | 0.56 | 0.87 | 125 | 34 | |
| 500 | 350 | 186 | 186 | 60 | 1.38 | 12 | 1.2 | 1981 | 2.18 | 0.7 | 0.55 | 0.87 | 124 | 40 |
| Name | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 500 | 350 | 73 | 99 | 50 | 1.38 | 7 | 1.2 | 1798 | 1.50 | 0.70 | 0.66 | 0.90 | 136 | 23 | |
| 500 | 350 | 146 | 140 | 100 | 1.38 | 7 | 1.2 | 1879 | 2.03 | 0.70 | 0.47 | 0.85 | 115 | 24 | |
| 500 | 350 | 219 | 171 | 150 | 1.38 | 7 | 1.2 | 1944 | 2.41 | 0.70 | 0.36 | 0.80 | 100 | 23 | |
| 500 | 350 | 291 | 198 | 200 | 1.38 | 7 | 1.2 | 1999 | 2.70 | 0.70 | 0.27 | 0.75 | 87 | 23 | |
| 500 | 350 | 364 | 221 | 250 | 1.38 | 7 | 1.2 | 2050 | 2.94 | 0.70 | 0.22 | 0.71 | 78 | 23 |
| Name | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 500 | 350 | 163 | 232 | 128 | 1.38 | 7 | 1.05 | 1917 | 2.25 | 0.7 | 0.42 | 0.84 | 108 | 25 | |
| 500 | 350 | 171 | 232 | 128 | 1.38 | 7 | 1.1 | 1917 | 2.25 | 0.7 | 0.42 | 0.83 | 108 | 24 | |
| 500 | 350 | 186 | 232 | 128 | 1.38 | 7 | 1.2 | 1917 | 2.25 | 0.7 | 0.42 | 0.82 | 108 | 22 | |
| 500 | 350 | 202 | 232 | 128 | 1.38 | 7 | 1.3 | 1917 | 2.25 | 0.7 | 0.42 | 0.80 | 108 | 20 | |
| 500 | 350 | 233 | 232 | 128 | 1.38 | 7 | 1.5 | 1917 | 2.25 | 0.7 | 0.42 | 0.77 | 108 | 17 |
| Name | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 500 | 350 | 186 | 123 | 128 | 1.38 | 7 | 1.2 | 1917 | 2.25 | 0.5 | 0.69 | 0.78 | 138 | 4 | |
| 500 | 350 | 186 | 137 | 128 | 1.38 | 7 | 1.2 | 1917 | 2.25 | 0.6 | 0.65 | 0.79 | 135 | 5 | |
| 500 | 350 | 186 | 158 | 128 | 1.38 | 7 | 1.2 | 1917 | 2.25 | 0.7 | 0.60 | 0.80 | 129 | 8 | |
| 500 | 350 | 186 | 194 | 128 | 1.38 | 7 | 1.2 | 1917 | 2.25 | 0.8 | 0.50 | 0.81 | 118 | 14 | |
| 500 | 350 | 186 | 274 | 128 | 1.38 | 7 | 1.2 | 1917 | 2.25 | 0.9 | 0.34 | 0.83 | 97 | 31 |
| Name | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E80 | 318 | 222 | 79 | 80 | 16 | 1.38 | 10 | 1.2 | 1181 | 2.38 | 0.7 | 0.70 | 0.85 | 89 | 12 |
| E66 | 385 | 269 | 92 | 92 | 21 | 1.38 | 10 | 1.2 | 1419 | 2.14 | 0.7 | 0.72 | 0.86 | 109 | 12 |
| E50 | 508 | 356 | 117 | 117 | 34 | 1.38 | 10 | 1.2 | 1862 | 1.84 | 0.7 | 0.74 | 0.87 | 146 | 12 |
| E28 | 907 | 635 | 221 | 221 | 122 | 1.38 | 10 | 1.2 | 3339 | 1.41 | 0.7 | 0.72 | 0.86 | 257 | 12 |
| E20 | 1270 | 889 | 344 | 344 | 296 | 1.38 | 10 | 1.2 | 4736 | 1.24 | 0.7 | 0.68 | 0.83 | 349 | 12 |
| Name | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 500 | 330 | 186 | 232 | 128 | 1.38 | 7 | 1.2 | 1820 | 2.37 | 0.7 | 0.36 | 0.80 | 93 | 24 | |
| 500 | 325 | 186 | 232 | 128 | 1.38 | 7 | 1.2 | 1867 | 2.31 | 0.7 | 0.38 | 0.81 | 99 | 24 | |
| 500 | 350 | 186 | 232 | 128 | 1.38 | 7 | 1.2 | 1917 | 2.25 | 0.7 | 0.40 | 0.82 | 106 | 24 | |
| 500 | 400 | 186 | 232 | 128 | 1.38 | 7 | 1.2 | 2025 | 2.13 | 0.7 | 0.43 | 0.83 | 117 | 24 | |
| 500 | 500 | 186 | 232 | 128 | 1.38 | 7 | 1.2 | 2256 | 1.91 | 0.7 | 0.48 | 0.84 | 138 | 24 |
References
- Ortega, M.; Saynisch, A.; Yurtseven, B.-M.; Gries, T. A Review on False-Twist Texturing. Fibers 2024, 12, 36. [Google Scholar] [CrossRef]
- Mezarcioz, S.; Ogulata, R.T. Modelling of Porosity in Knitted Fabrics. J. Fash. Technol. Text. Eng. 2017, s1, 5. [Google Scholar] [CrossRef]
- Khalil, E. Effect of Stitch Length on Physical and Mechanical Properties of Single Jersey Cotton Knitted Fabric. Int. J. Sci. Res. 2012, 3, 593–596. [Google Scholar]
- Pauly, L.; Maier, L.; Nieken, U.; Gresser, G.T. Functional design of porous systems by systematic patterning of flat knits. In Proceedings of the 15th Annual International Conference on Porous Media, Edinburgh, UK, 22–25 May 2023; Available online: https://events.interpore.org/event/41/contributions/5685/contribution.pdf (accessed on 1 November 2024).
- Kabir, S.M.F.; Uluturk, I.; Pang, R.; Khadse, N.; Stapleton, S.E.; Park, J.H. Structure–Property Investigation of Knit Patterns on Thermal Comfort: A Holistic Approach. ACS Appl. Eng. Mater. 2023, 1, 1455–1466. [Google Scholar] [CrossRef]
- Chen, Q.; Tang, K.-P.M.; Ma, P.; Jiang, G.; Xu, C. Thermophysiological comfort properties of polyester weft-knitted fabrics for sports T-shirt. J. Text. Inst. 2017, 108, 1421–1429. [Google Scholar] [CrossRef]
- Çil, M.; Nergis, U.; Candan, C. An Experimental Study of Some Comfort-related Properties of Cotton—Acrylic Knitted Fabrics. Text. Res. J. 2009, 79, 917–923. [Google Scholar] [CrossRef]
- Rouquerol, J.; Avnir, D.; Fairbridge, C.W.; Everett, D.H.; Haynes, J.M.; Pernicone, N.; Ramsay, J.D.F.; Sing, K.S.W.; Unger, K.K. Recommendations for the characterization of porous solids (Technical Report). Pure Appl. Chem. 1994, 66, 1739–1758. [Google Scholar] [CrossRef]
- Dal, V.; Atmaca, M.; Yildiz, Z.; Ceviz, N.O.; Hes, L. Thermal Comfort of Woolen Fabrics Depending on Physical Properties. J. Nat. Fibers 2016, 13, 714–725. [Google Scholar] [CrossRef]
- Mao, Z.; Yu, H.; Wang, Y.; Zhang, L.; Zhong, Y.; Xu, H. States of Water and Pore Size Distribution of Cotton Fibers with Different Moisture Ratios. Ind. Eng. Chem. Res. 2014, 53, 8927–8934. [Google Scholar] [CrossRef]
- Nagy, V.; Vas, L.M. Pore characteristic determination with mercury porosimetry in polyester staple yarns. Fibres Text. East. Eur. 2005, 13, 21–26. [Google Scholar]
- Miller, B.; Tyomkin, I. An Extended Range Liquid Extrusion Method for Determining Pore Size Distributions. Text. Res. J. 1986, 56, 35–40. [Google Scholar] [CrossRef]
- Jakšić, D.; Jakšić, N. Assessment of Porosity of Flat Textile Fabrics. Text. Res. J. 2007, 77, 105–110. [Google Scholar] [CrossRef]
- Pan, N.; Gibson, P. Thermal and Moisture Transport in Fibrous Materials, 1st ed.; Woodhead Publishing: Cambridge, UK, 2006; Available online: https://shop.elsevier.com/books/thermal-and-moisture-transport-in-fibrous-materials/pan/978-1-84569-057-1 (accessed on 24 August 2024).
- Gostick, J.; Khan, Z.; Tranter, T.; Kok, M.; Agnaou, M.; Sadeghi, M.; Jervis, R. PoreSpy: A Python Toolkit for Quantitative Analysis of Porous Media Images. J. Open Source Softw. 2019, 4, 1296. [Google Scholar] [CrossRef]
- Ogulata, R.T.; Mavruz, S. Investigation of porosity and air permeability values of plain knitted fabrics. Fibres Text. East. Eur. 2010, 82, 71–75. [Google Scholar]
- Dias, T.; Delkumburewatte, G.B. Changing porosity of knitted structures by changing tightness. Fibers Polym. 2008, 9, 76–79. [Google Scholar] [CrossRef]
- Abd elzaher Eltahan, E.; Sultan, M.; Mito, A.-B. Determination of loop length, tightness factor and porosity of single jersey knitted fabric. Alex. Eng. J. 2016, 55, 851–856. [Google Scholar] [CrossRef]
- Ramratan, R.; Choudhary, A.K. The Influence of Yarn and Knit Structure on Comfort Properties of Sportswear Fabric. J. Text. Appar. Technol. Manag. 2020, 11, 10. [Google Scholar]
- Abdolmaleki, S.; Jeddi, A.A.A.; Amani, M. Estimation on the 3D porosity of plain knitted fabric under uniaxial extension. Fibers Polym. 2012, 13, 535–541. [Google Scholar] [CrossRef]
- Abdolmaleki, S.; Jeddi, A. Estimation on the 3D Porosity of Plain Weft Knitted Fabric under Wale Extension. J. Text. Polym. 2014, 2, 65–70. [Google Scholar]
- Daukantiene, V.; Vadeike, G. Evaluation of the air permeability of elastic knitted fabrics and their assemblies. Int. J. Cloth. Sci. Technol. 2018, 30, 839–853. [Google Scholar] [CrossRef]
- Du, Y.; Shen, W.; Feng, X. Analysis of the Porosity Changing after Moisture Absorption in Functional Knitted Fabrics. J. Donghua Univ. Engl. Ed. 2007, 24, 740–743. [Google Scholar]
- Gebart, B.R. Permeability of Unidirectional Reinforcements for RTM. J. Compos. Mater. 1992, 26, 1100–1133. [Google Scholar] [CrossRef]
- Neckář, B.; Ibrahim, S. Theoretical Approach for Determining Pore Characteristics Between Fibers. Text. Res. J. 2003, 73, 611–619. [Google Scholar] [CrossRef]
- Li, Y.F.; Huang, L.Q.; Yu, J.Y. Study on the Pore Structure of Cotton-Like Polyester Knitted Fabrics. Adv. Mater. Res. 2013, 821–822, 270–273. [Google Scholar] [CrossRef]
- Mark, A.; Bauer, B.; Gresser, G. Quantification of hierarchic multimodal pore structures in textiles by the example of knitted fabric structures. In Proceedings of the Aachen Dresden International Textile Conference, Aachen, Germany, 26–27 November 2015. [Google Scholar]
- Benltoufa, S.; Fayala, F.; BenNasrallah, S. Capillary Rise in Macro and Micro Pores of Jersey Knitting Structure. J. Eng. Fibers Fabr. 2008, 3, 155892500800300. [Google Scholar] [CrossRef]
- Maier, L.; Pauly, L.; Gostick, J.T.; Gresser, G.T.; Nieken, U. Spontaneous imbibition in thin anisotropic fibrous media: Experiments and numerical modelling. Text. Res. J. 2024, 00405175241268794. [Google Scholar] [CrossRef]
- Rebenfeld, L.; Miller, B. Using Liquid Flow to Quantify the Pore Structure of Fibrous Materials. J. Text. Inst. 1995, 86, 241–251. [Google Scholar] [CrossRef]
- Birrfelder, P.; Dorrestijn, M.; Roth, C.; Rossi, R.M. Effect of fiber count and knit structure on intra- and inter-yarn transport of liquid water. Text. Res. J. 2013, 83, 1477–1488. [Google Scholar] [CrossRef]
- Fischer, R.; Schlepütz, C.M.; Hegemann, D.; Rossi, R.M.; Derome, D.; Carmeliet, J. Four-dimensional imaging and free-energy analysis of sudden pore-filling events in wicking of yarns. Phys. Rev. E 2021, 103, 053101. [Google Scholar] [CrossRef]
- Fischer, R.; Schlepütz, C.M.; Zhao, J.; Boillat, P.; Hegemann, D.; Rossi, R.M.; Derome, D.; Carmeliet, J. Wicking dynamics in yarns. J. Colloid Interface Sci. 2022, 625, 1–11. [Google Scholar] [CrossRef]
- Benltoufa, S.; Fayala, F.; Cheikhrouhou, M.; Ben Nasrallah, S. Porosity determination of jersey structure. AUTEX Res. J. 2007, 7, 63–69. [Google Scholar] [CrossRef]
- Siddiqui, M.O.R.; Sun, D. Porosity Prediction of Plain Weft Knitted Fabrics. Fibers 2014, 3, 1–11. [Google Scholar] [CrossRef]
- Karaguzel, B. Characterization and Role of Porosity in Knitted Fabrics. Master’s Thesis, North Carolina State University, Raleigh, NC, USA, 2004. [Google Scholar]
- Huang, R. Characterization and Modeling of Pore Size in Weft-Knitted Fabrics; North Carolina State University: Raleigh, NC, USA, 2023; Available online: https://repository.lib.ncsu.edu/server/api/core/bitstreams/0eff62d3-7f05-4907-aac5-179f0cf499b4/content (accessed on 26 January 2025).
- Sampson, W.W. A multiplanar model for the pore radius distribution in isotropic near-planar stochastic fibre networks. J. Mater. Sci. 2003, 38, 1617–1622. [Google Scholar] [CrossRef]
- Rawal, A.; Rao, P.V.K.; Russell, S.; Jeganathan, A. Effect of fiber orientation on pore size characteristics of nonwoven structures. J. Appl. Polym. Sci. 2010, 118, 2668–2673. [Google Scholar] [CrossRef]
- Bai, H.; Qian, X.; Fan, J.; Qian, Y.; Duo, Y.; Liu, Y.; Wang, X. Computing Pore Size Distribution in Non-woven Fibrous Filter Media. Fibers Polym. 2020, 21, 196–203. [Google Scholar] [CrossRef]
- Wang, F.; Schiller, U.D. Computational characterization of nonwoven fibrous media: I. Pore-network extraction and morphological analysis. Phys. Rev. Mater. 2020, 4, 083803. [Google Scholar] [CrossRef]
- Komori, T.; Makishima, K. Geometrical Expressions of Spaces in Anisotropic Fiber Assemblies. Text. Res. J. 1979, 49, 550–555. [Google Scholar] [CrossRef]
- Ren, J.; Li, Z.; Wong, F.-S. A new method for the prediction of pore size distribution and MWCO of ultrafiltration membranes. J. Membr. Sci. 2006, 279, 558–569. [Google Scholar] [CrossRef]
- D’Hollander, E.H. Estimation of the pore size distribution from the moisture characteristic. Water Resour. Res. 1979, 15, 107–112. [Google Scholar] [CrossRef]
- Boributh, S.; Jiraratananon, R.; Li, K. Analytical solutions for membrane wetting calculations based on log-normal and normal distribution functions for CO2 absorption by a hollow fiber membrane contactor. J. Membr. Sci. 2013, 429, 459–472. [Google Scholar] [CrossRef]
- Limpert, E.; Stahel, W.A.; Abbt, M. Log-normal Distributions across the Sciences: Keys and Clues. BioScience 2001, 51, 341–352. [Google Scholar] [CrossRef]
- Crow, E.L. Lognormal Distributions: Theory and Applications; Statistics: Textbooks and Monographs Series; Dekker: New York, NY, USA, 1988. [Google Scholar]
- Kyosev, Y. Topology-Based Modeling of Textile Structures and Their Joint Assemblies: Principles, Algorithms and Limitations; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Brown, L.P. TexGen. In Advanced Weaving Technology; Kyosev, Y., Boussu, F., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 253–291. [Google Scholar] [CrossRef]
- Kyosev, Y.; Angelova, Y.; Kovar, R. 3D Modeling of Plain Weft Knitted Structures of Compressible Yarn. Res. J. Text. Appar. 2005, 9, 88–97. [Google Scholar] [CrossRef]
- Choi, K.F.; Lo, T.Y. An Energy Model of the Plain Knitted Loop. Text. Res. J. 2003, 73, 739–748. [Google Scholar] [CrossRef]
- Specht, E. The Best Known Packings of Equal Circles in a Circle (Complete up to N = 2600). Available online: http://hydra.nat.uni-magdeburg.de/packing/cci/cci.html#References (accessed on 28 June 2023).
- Mezarcioz, S.; Mezarcioz, S.; Ogulata, R.T. Prediction of air permeability of knitted fabrics by means of computational fluid dynamics. Tekst. Konfeksiyon 2014, 24, 202–211. [Google Scholar]
- Team, O.D. OpenCV: Open Source Computer Vision Library. Available online: https://opencv.org (accessed on 16 December 2024).
- Sozumert, E.; Kiyak, Y.; Demirci, E.; Silberschmidt, V.V. Effect of microstructure on porosity of random fibrous networks. J. Text. Inst. 2020, 111, 1713–1723. [Google Scholar] [CrossRef]






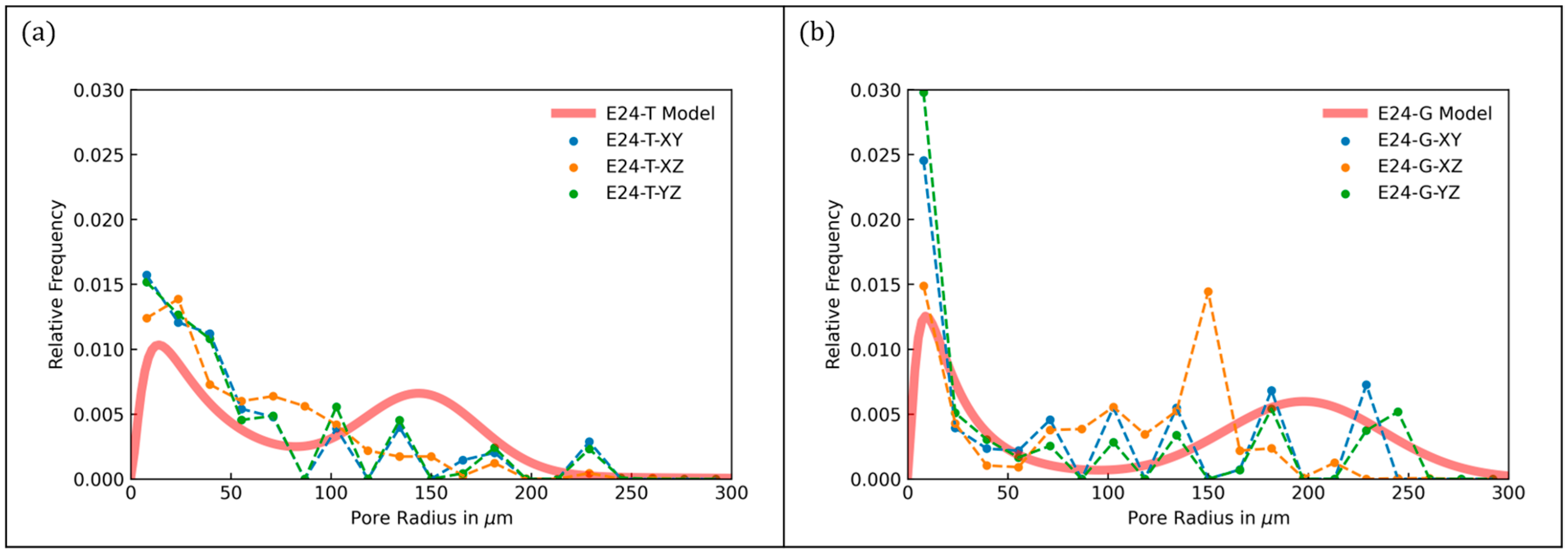
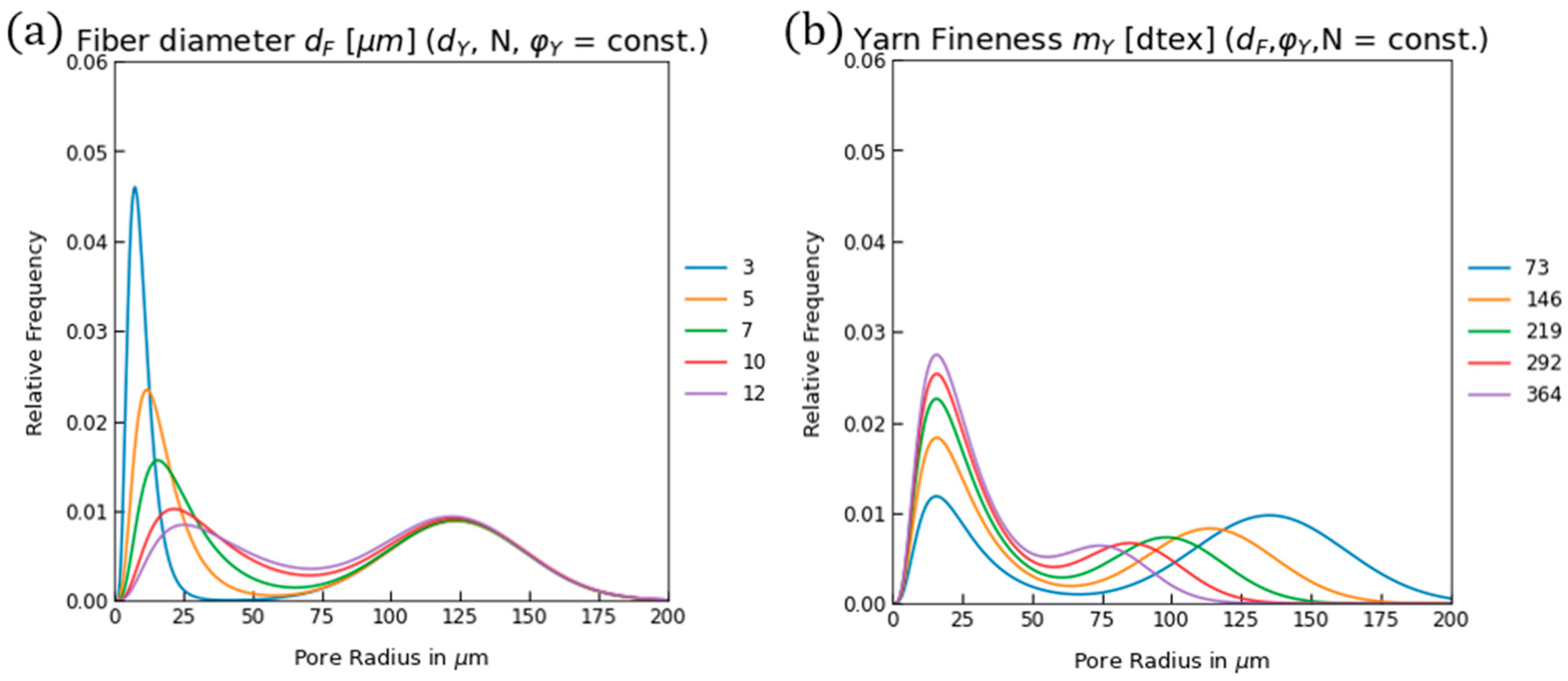
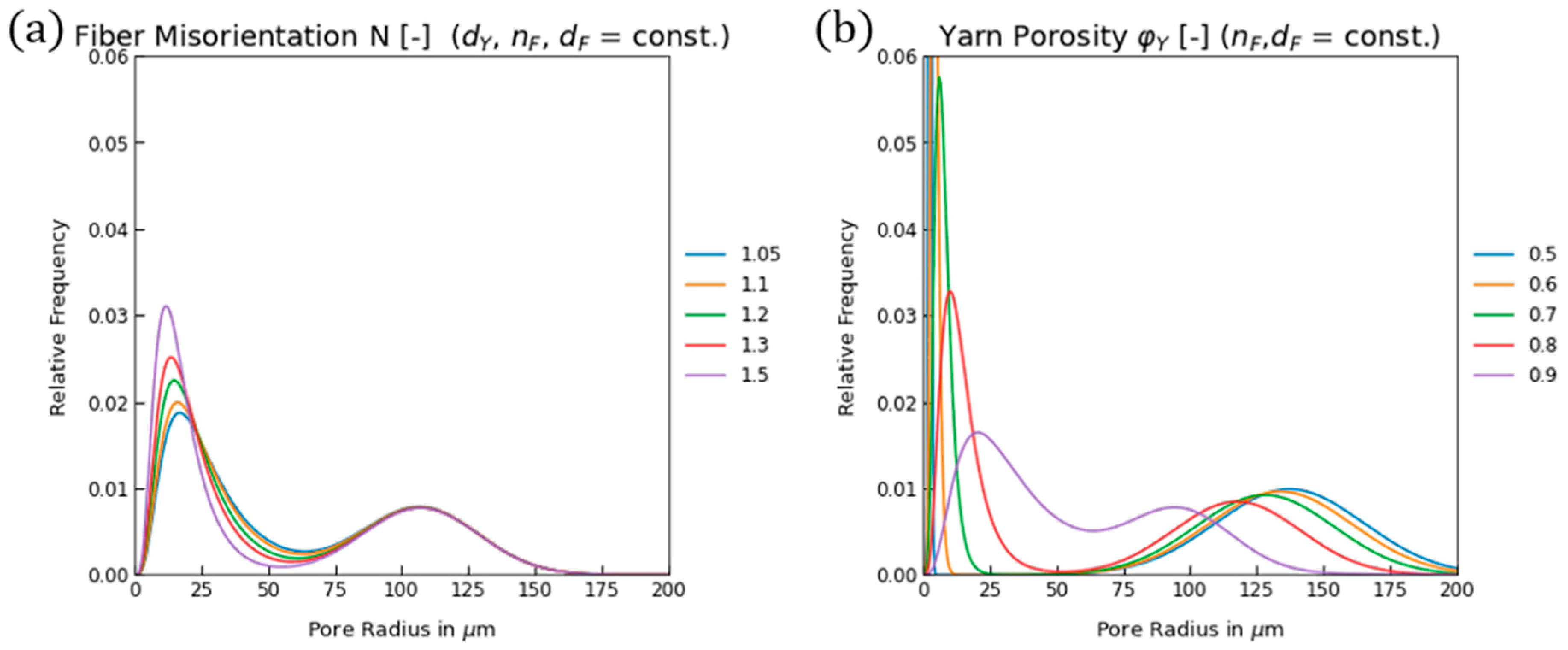
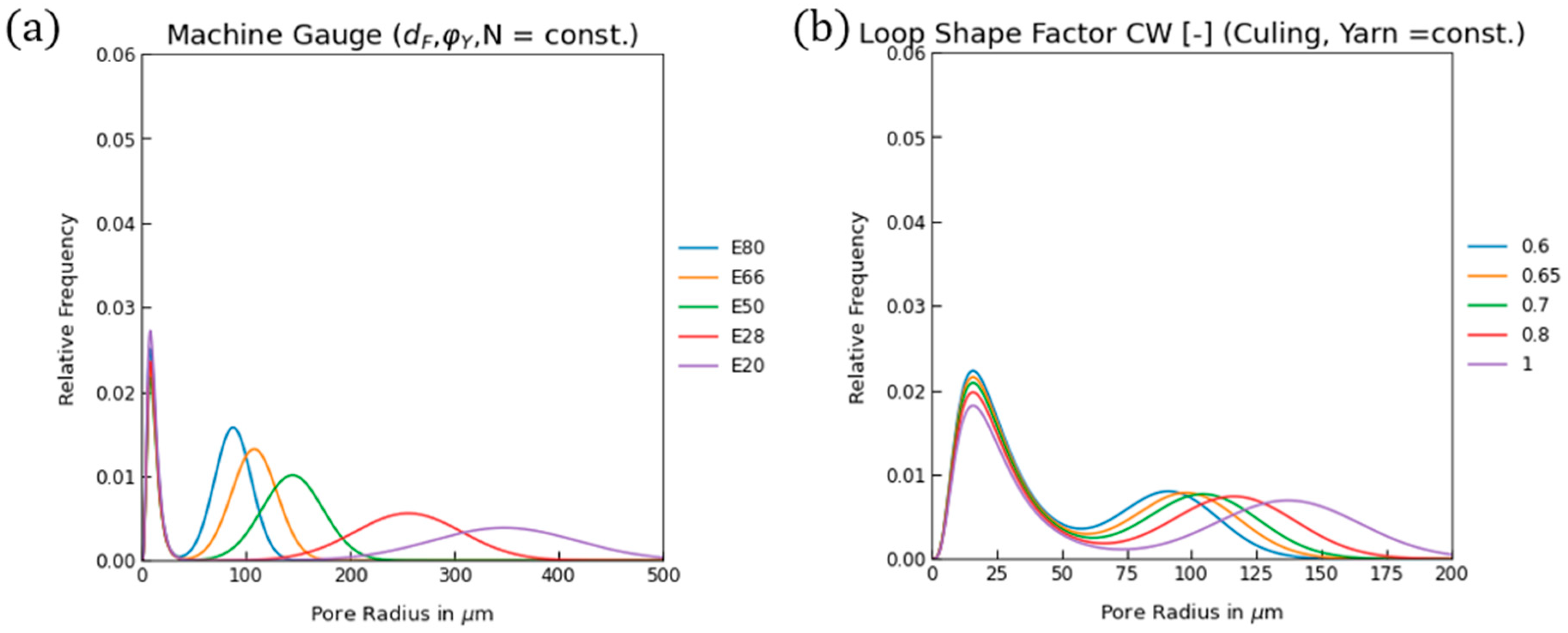
| Scale | Property | Abbreviation | Unit |
|---|---|---|---|
| Yarn | Fibre diameter | ||
| Fibre count | |||
| Yarn linear density | |||
| Yarn diameter | |||
| Fabric | Coarse spacing | ||
| Wale spacing |
| Name | [dtex] | [µm] | [−] | [dtex] | [µm] | [−] | [−] |
|---|---|---|---|---|---|---|---|
| f48 | 182 | 518 | 48 | 1.38 | 19.32 | 0.93 | 1.06 |
| f128 | 180 | 814 | 128 | 1.38 | 12.51 | 0.96 | 1.34 |
| f128Z | 180 | 596 | 128 | 1.38 | 12.51 | 0.94 | 1.01 |
| f256 | 180 | 508 | 256 | 1.38 | 8.33 | 0.90 | 1.40 |
| Name | [µm] | [µm] | Deviation [%] |
|---|---|---|---|
| f48 | 97 | 126 | −23 |
| f128 | 83 | 86 | +3 |
| f128Z | 104 | 64 | +63 |
| f256 | 39 | 55 | −29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pauly, L.; Maier, L.; Schmied, S.; Dinkelmann, A.; Nieken, U.; Gresser, G.T. Modelling Pore Size Distribution Function of Twist-Texturized Yarns and Single-Jersey Knitted Fabrics. Fibers 2025, 13, 48. https://doi.org/10.3390/fib13040048
Pauly L, Maier L, Schmied S, Dinkelmann A, Nieken U, Gresser GT. Modelling Pore Size Distribution Function of Twist-Texturized Yarns and Single-Jersey Knitted Fabrics. Fibers. 2025; 13(4):48. https://doi.org/10.3390/fib13040048
Chicago/Turabian StylePauly, Leon, Lukas Maier, Sibylle Schmied, Albrecht Dinkelmann, Ulrich Nieken, and Götz T. Gresser. 2025. "Modelling Pore Size Distribution Function of Twist-Texturized Yarns and Single-Jersey Knitted Fabrics" Fibers 13, no. 4: 48. https://doi.org/10.3390/fib13040048
APA StylePauly, L., Maier, L., Schmied, S., Dinkelmann, A., Nieken, U., & Gresser, G. T. (2025). Modelling Pore Size Distribution Function of Twist-Texturized Yarns and Single-Jersey Knitted Fabrics. Fibers, 13(4), 48. https://doi.org/10.3390/fib13040048







