A Dual Hollow Core Antiresonant Optical Fiber Coupler Based on a Highly Birefringent Structure-Numerical Design and Analysis
Abstract
:1. Introduction
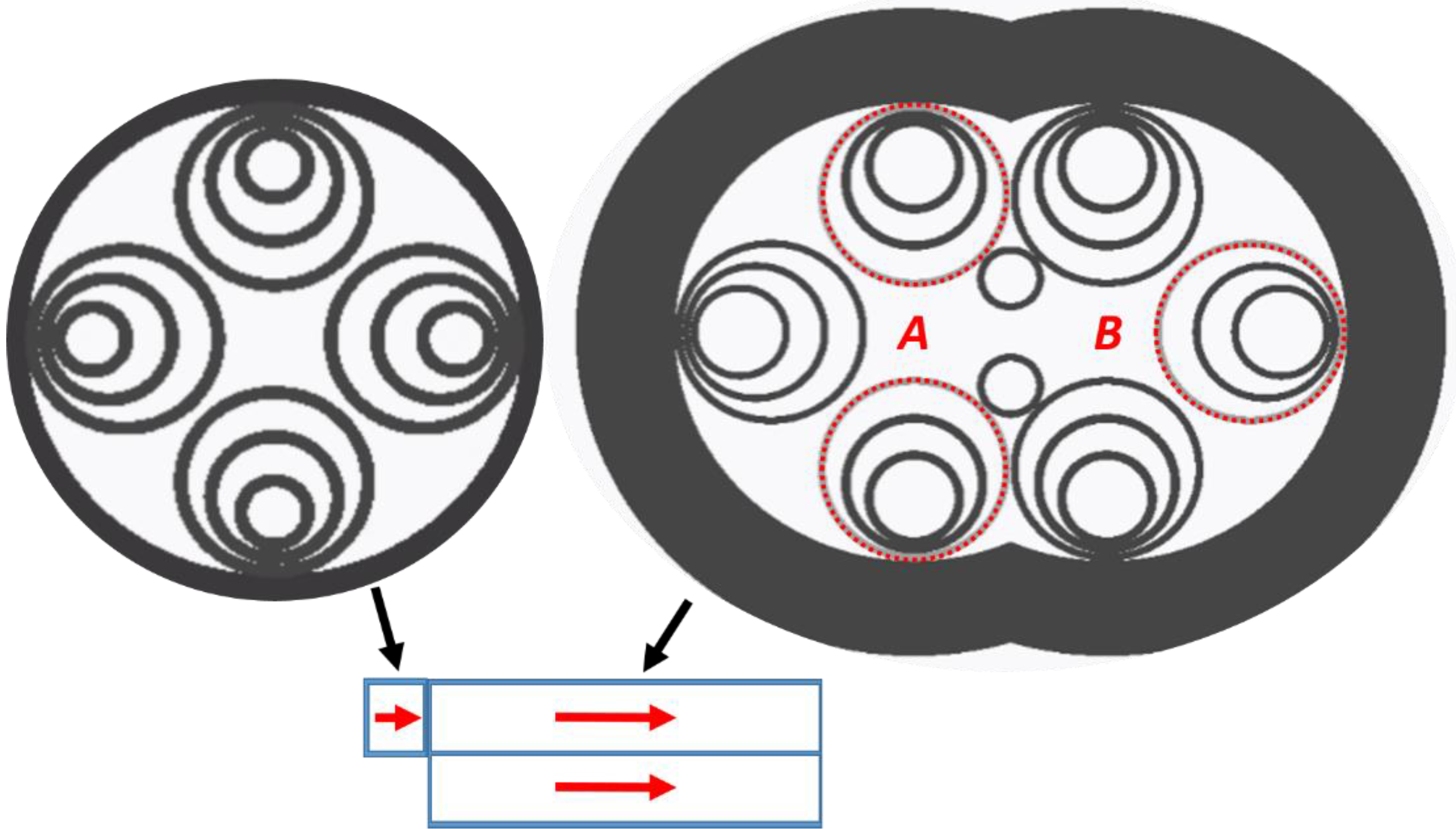
2. Basic Formulas and Principle of Operation
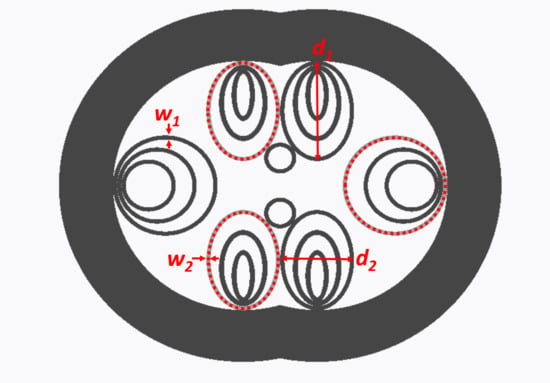
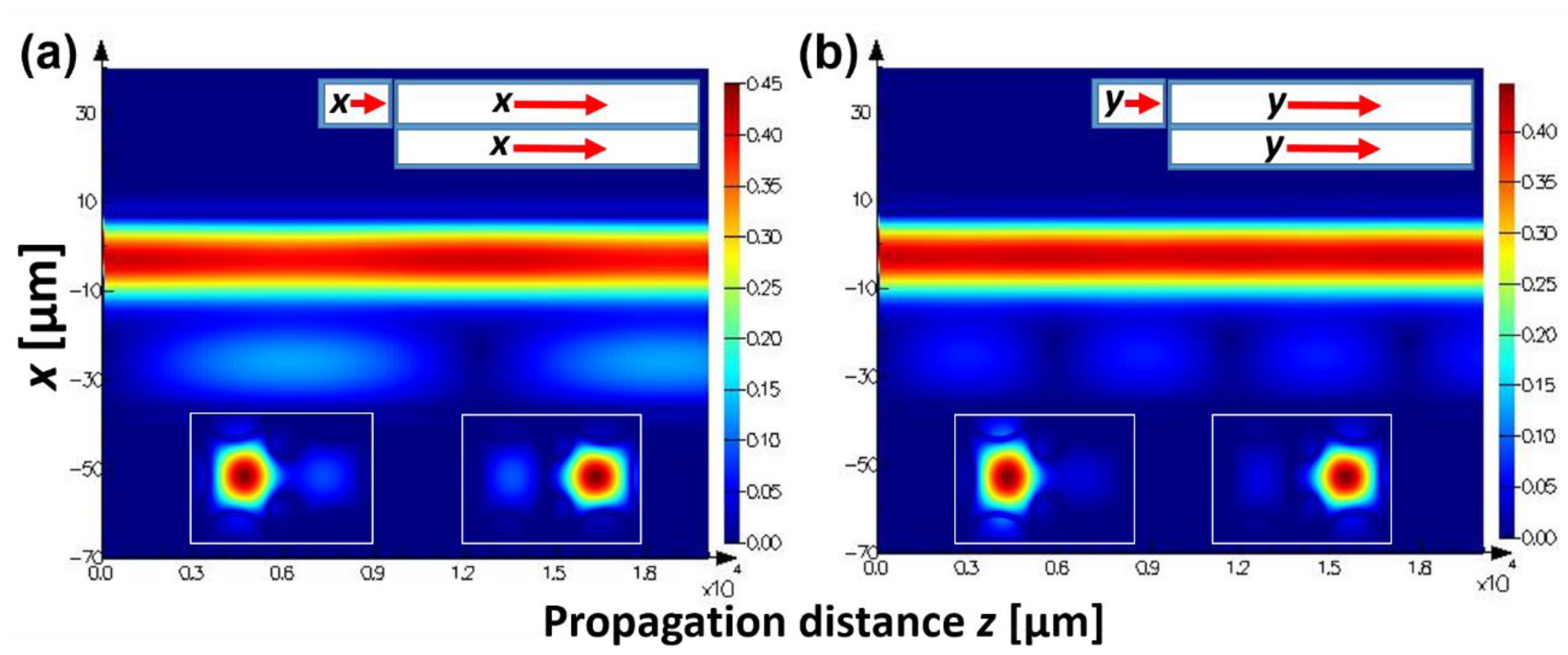
3. Polarization-Splitting DHC-ARF—Analysis of Several Geometrical Parameters
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cregan, R.F.; Mangan, B.J.; Knight, J.C.; Birks, T.A.; Russell, P.S.J.; Roberts, P.J.; Allan, D.C. Single-Mode Photonic Band Gap Guidance of Light in Air. Science 1999, 285, 1537–1539. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Markos, C.; Travers, J.C.; Abdolvand, A.; Eggleton, B.J.; Bang, O. Hybrid photonic-crystal fiber. Rev. Mod. Phys. 2017, 89, 045003. [Google Scholar] [CrossRef] [Green Version]
- Wei, C.; Weiblen, R.J.; Menyuk, C.R.; Hu, J. Negative curvature fibers. Adv. Opt. Photonics 2017, 9, 504–561. [Google Scholar] [CrossRef]
- Bufetov, I.; Kosolapov, A.; Pryamikov, A.; Gladyshev, A.; Kolyadin, A.; Krylov, A.; Yatsenko, Y.; Biriukov, A. Revolver Hollow Core Optical Fibers. Fibers 2018, 6, 39. [Google Scholar] [CrossRef] [Green Version]
- Poletti, F.; Wheeler, N.V.; Petrovich, M.N.; Baddela, N.; Numkam Fokoua, E.; Hayes, J.R.; Gray, D.R.; Li, Z.; Slavík, R.; Richardson, D.J. Towards high-capacity fibre-optic communications at the speed of light in vacuum. Nat. Photonics 2013, 7, 279. [Google Scholar] [CrossRef]
- Sakr, H.; Bradley, T.D.; Hong, Y.; Jasion, G.T.; Hayes, J.R.; Kim, H.; Davidson, I.A.; Fokoua, E.N.; Chen, Y.; Bottrill, K.R.H.; et al. Ultrawide Bandwidth Hollow Core Fiber for Interband Short Reach Data Transmission. In Proceedings of the Optical Fiber Communication Conference Postdeadline Papers 2019, San Diego, CA, USA, 3 March 2019; p. Th4A.1. [Google Scholar]
- Gao, S.-F.; Wang, Y.-Y.; Ding, W.; Jiang, D.-L.; Gu, S.; Zhang, X.; Wang, P. Hollow-core conjoined-tube negative-curvature fibre with ultralow loss. Nat. Commun. 2018, 9, 2828. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nissen, M.; Doherty, B.; Hamperl, J.; Kobelke, J.; Weber, K.; Henkel, T.; Schmidt, A.M. UV Absorption Spectroscopy in Water-Filled Antiresonant Hollow Core Fibers for Pharmaceutical Detection. Sensors 2018, 18, 478. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.-L.; Ding, W.; Wang, Y.-Y.; Gao, S.-F.; Cao, L.; Feng, X.; Wang, P. Characterization of a liquid-filled nodeless anti-resonant fiber for biochemical sensing. Opt. Lett. 2017, 42, 863–866. [Google Scholar] [CrossRef]
- Popenda, M.A.; Stawska, H.I.; Syperek, M.; Kosolapov, A.F.; Kolyadin, A.N.; Bereś-Pawlik, E. Multiphoton fluorescence excitation and detection with a single negative curvature hollow core fibre. Laser Phys. Lett. 2019, 16, 015103. [Google Scholar] [CrossRef]
- Nikodem, M.; Krzempek, K.; Dudzik, G.; Abramski, K. Hollow core fiber-assisted absorption spectroscopy of methane at 3.4 µm. Opt. Express 2018, 26, 21843–21848. [Google Scholar] [CrossRef]
- Nikodem, M.; Gomółka, G.; Klimczak, M.; Pysz, D.; Buczyński, R. Laser absorption spectroscopy at 2 µm inside revolver-type anti-resonant hollow core fiber. Opt. Express 2019, 27, 14998–15006. [Google Scholar] [CrossRef] [PubMed]
- Popenda, M.A.; Stawska, H.I.; Mazur, L.M.; Jakubowski, K.; Kosolapov, A.; Kolyadin, A.; Bereś-Pawlik, E. Application of Negative Curvature Hollow-Core Fiber in an Optical Fiber Sensor Setup for Multiphoton Spectroscopy. Sensors 2017, 17, 2278. [Google Scholar] [CrossRef] [PubMed]
- Cassataro, M.; Novoa, D.; Günendi, M.C.; Edavalath, N.N.; Frosz, M.H.; Travers, J.C.; Russell, P.S.J. Generation of broadband mid-IR and UV light in gas-filled single-ring hollow-core PCF. Opt. Express 2017, 25, 7637–7644. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Belli, F.; Abdolvand, A.; Chang, W.; Travers, J.C.; Russell, P.S.J. Vacuum-ultraviolet to infrared supercontinuum in hydrogen-filled photonic crystal fiber. Optica 2015, 2, 292–300. [Google Scholar] [CrossRef]
- Michieletto, M.; Lyngsø, J.K.; Jakobsen, C.; Lægsgaard, J.; Bang, O.; Alkeskjold, T.T. Hollow-core fibers for high power pulse delivery. Opt. Express 2016, 24, 7103–7119. [Google Scholar] [CrossRef] [Green Version]
- Urich, A.; Maier, R.R.J.; Mangan, B.J.; Renshaw, S.; Knight, J.C.; Hand, D.P.; Shephard, J.D. Delivery of high energy Er: YAG pulsed laser light at 2.94 µm through a silica hollow core photonic crystal fibre. Opt. Express 2012, 20, 6677–6684. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.; Choi, H.; Yazdanfar, S.; So, P.T.C. Ultrafast optical pulse delivery with fibers for nonlinear microscopy. Microsc. Res. Tech. 2008, 71, 887–896. [Google Scholar] [CrossRef] [Green Version]
- Pryamikov, A.D.; Biriukov, A.S.; Kosolapov, A.F.; Plotnichenko, V.G.; Semjonov, S.L.; Dianov, E.M. Demonstration of a waveguide regime for a silica hollow-core microstructured optical fiber with a negative curvature of the core boundary in the spectral region > 3.5 μm. Opt. Express 2011, 19, 1441–1448. [Google Scholar] [CrossRef]
- Shephard, J.D.; MacPherson, W.N.; Maier, R.R.J.; Jones, J.D.C.; Hand, D.P.; Mohebbi, M.; George, A.K.; Roberts, P.J.; Knight, J.C. Single-mode mid-IR guidance in a hollow-core photonic crystal fiber. Opt. Express 2005, 13, 7139–7144. [Google Scholar] [CrossRef]
- Yu, F.; Cann, M.; Brunton, A.; Wadsworth, W.; Knight, J. Single-mode solarization-free hollow-core fiber for ultraviolet pulse delivery. Opt. Express 2018, 26, 10879–10887. [Google Scholar] [CrossRef]
- Colombe, Y.; Slichter, D.H.; Wilson, A.C.; Leibfried, D.; Wineland, D.J. Single-mode optical fiber for high-power, low-loss UV transmission. Opt. Express 2014, 22, 19783–19793. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lombardini, A.; Mytskaniuk, V.; Sivankutty, S.; Andresen, E.R.; Chen, X.; Wenger, J.; Fabert, M.; Joly, N.; Louradour, F.; Kudlinski, A.; et al. High-resolution multimodal flexible coherent Raman endoscope. Light Sci. Appl. 2018, 7, 10. [Google Scholar] [CrossRef] [PubMed]
- Piyawattanametha, W.; Cocker, E.D.; Burns, L.D.; Barretto, R.P.J.; Jung, J.C.; Ra, H.; Solgaard, O.; Schnitzer, M.J. In vivo brain imaging using a portable 2.9 g two-photon microscope based on a microelectromechanical systems scanning mirror. Opt. Lett. 2009, 34, 2309–2311. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mangan, B.J.; Knight, J.C.; Birks, T.A.; Russell, P.S.J.; Greenaway, A.H. Experimental study of dual-core photonic crystal fibre. Electron. Lett. 2000, 36, 1358–1359. [Google Scholar] [CrossRef]
- Saitoh, K.; Sato, Y.; Koshiba, M. Coupling characteristics of dual-core photonic crystal fiber couplers. Opt. Express 2003, 11, 3188–3195. [Google Scholar] [CrossRef]
- Lin, Z.; Changxi, Y.; Changyuan, Y.; Ting, L.; Willner, A.E. PCF-based polarization splitters with simplified structures. J. Lightwave Technol. 2005, 23, 3558–3565. [Google Scholar] [CrossRef]
- Wang, Z.; Taru, T.; Birks, T.A.; Knight, J.C.; Liu, Y.; Du, J. Coupling in dual-core photonic bandgap fibers: Theory and experiment. Opt. Express 2007, 15, 4795–4803. [Google Scholar] [CrossRef]
- Bookey, H.; Buczynski, R.; Wischnewski, A.; Pysz, D.; Kasztelanic, R.; Waddie, A.; Stepien, R.; Kar, A.; Taghizadeh, M.R. Near infrared transmission in dual core lead silicate photonic crystal fibres. Opt. Appl. 2012, 42, 75–83. [Google Scholar] [CrossRef]
- Wang, Z.; Kai, G.; Liu, Y.; Liu, J.; Zhang, C.; Sun, T.; Wang, C.; Zhang, W.; Yuan, S.; Dong, X. Coupling and decoupling of dual-core photonic bandgap fibers. Opt. Lett. 2005, 30, 2542–2544. [Google Scholar] [CrossRef]
- Skorobogatiy, M.; Saitoh, K.; Koshiba, M. Transverse light guides in microstructured optical fibers. Opt. Lett. 2006, 31, 314–316. [Google Scholar] [CrossRef]
- Han, S.; Wang, Z.; Liu, Y.; Li, H.; Liang, H.; Wang, Z. Mode Couplers and Converters Based on Dual-Core Hollow-Core Photonic Bandgap Fiber. IEEE Photonics J. 2018, 10, 1–8. [Google Scholar] [CrossRef]
- Meng, L.; Fini, J.M.; Nicholson, J.W.; Windeler, R.S.; DeSantolo, A.; Monberg, E.; DiMarcello, F.; Hassan, M.; Ortiz, R. Bend Tunable Coupling in Dual-Hollow-Core Photonic Bandgap Fiber. In Proceedings of the OFC/NFOEC, Los Angeles, CA, USA, 4–8 March 2012; pp. 1–3. [Google Scholar]
- Debord, B.; Amsanpally, A.; Chafer, M.; Baz, A.; Maurel, M.; Blondy, J.M.; Hugonnot, E.; Scol, F.; Vincetti, L.; Gérôme, F.; et al. Ultralow transmission loss in inhibited-coupling guiding hollow fibers. Optica 2017, 4, 209–217. [Google Scholar] [CrossRef] [Green Version]
- Habib, M.S.; Antonio-Lopez, J.E.; Markos, C.; Schülzgen, A.; Amezcua-Correa, R. Single-mode, low loss hollow-core anti-resonant fiber designs. Opt. Express 2019, 27, 3824–3836. [Google Scholar] [CrossRef] [PubMed]
- Couny, F.; Benabid, F.; Light, P.S. Large-pitch kagome-structured hollow-core photonic crystal fiber. Opt. Lett. 2006, 31, 3574–3576. [Google Scholar] [CrossRef] [PubMed]
- Stawska, H.; Popenda, M.; Bereś-Pawlik, E. Anti-Resonant Hollow Core Fibers with Modified Shape of the Core for the Better Optical Performance in the Visible Spectral Region—A Numerical Study. Polymers 2018, 10, 899. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Argyros, A.; Leon-Saval, S.G.; van Eijkelenborg, M.A. Twin-hollow-core optical fibres. Opt. Commun. 2009, 282, 1785–1788. [Google Scholar] [CrossRef]
- Wheeler, N.V.; Bradley, T.D.; Hayes, J.R.; Jasion, G.T.; Chen, Y.; Sandoghchi, S.R.; Horak, P.; Poletti, F.; Petrovich, M.N.; Richardson, D.J. Dual Hollow-Core Anti-Resonant Fibres; SPIE: Bellingham, WA, USA, 2016; Volume 9886. [Google Scholar]
- Liu, X.; Fan, Z.; Shi, Z.; Ma, Y.; Yu, J.; Zhang, J. Dual-core antiresonant hollow core fibers. Opt. Express 2016, 24, 17453–17458. [Google Scholar] [CrossRef]
- Huang, X.; Ma, J.; Tang, D.; Yoo, S. Hollow-core air-gap anti-resonant fiber couplers. Opt. Express 2017, 25, 29296–29306. [Google Scholar] [CrossRef]
- Huang, X.; Zang, J.; Yoo, S. Sensing applications of double hollow-core anti-resonant fiber based modal interferometer. In Proceedings of the 2018 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 13–18 May 2018; pp. 1–2. [Google Scholar]
- Huang, X.; Zang, J.; Yoo, S. Multiple hollow-core anti-resonant fiber as a supermodal fiber interferometer. Sci. Rep. 2019, 9, 9342. [Google Scholar] [CrossRef]
- Mousavi, S.A.; Sandoghchi, S.R.; Richardson, D.J.; Poletti, F. Broadband high birefringence and polarizing hollow core antiresonant fibers. Opt. Express 2016, 24, 22943–22958. [Google Scholar] [CrossRef]
- Zhao, T.; Jia, H.; Lian, Z.; Benson, T.; Lou, S. Ultra-broadband dual hollow-core anti-resonant fiber polarization splitter. Opt. Fiber Technol. 2019, 53, 102005. [Google Scholar] [CrossRef]
- Rajeswari, D.; Sivanantha Raja, A.; Selvendran, S. Design and analysis of polarization splitter based on dual-core photonic crystal fiber. Optik 2017, 144, 15–21. [Google Scholar] [CrossRef]
- Hayes, J.R.; Poletti, F.; Abokhamis, M.S.; Wheeler, N.V.; Baddela, N.K.; Richardson, D.J. Anti-resonant hexagram hollow core fibers. Opt. Express 2015, 23, 1289–1299. [Google Scholar] [CrossRef] [PubMed]
- Debord, B.; Amrani, F.; Vincetti, L.; Gérôme, F.; Benabid, F. Hollow-Core Fiber Technology: The Rising of “Gas Photonics”. Fibers 2019, 7, 16. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Ding, W. Confinement loss in hollow-core negative curvature fiber: A multi-layered model. Opt. Express 2017, 25, 33122–33133. [Google Scholar] [CrossRef] [Green Version]
- Yu, F.; Knight, J.C. Negative Curvature Hollow-Core Optical Fiber. IEEE J. Sel. Top. Quantum Electron. 2016, 22, 146–155. [Google Scholar] [CrossRef] [Green Version]




© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stawska, H.I.; Popenda, M.A. A Dual Hollow Core Antiresonant Optical Fiber Coupler Based on a Highly Birefringent Structure-Numerical Design and Analysis. Fibers 2019, 7, 109. https://doi.org/10.3390/fib7120109
Stawska HI, Popenda MA. A Dual Hollow Core Antiresonant Optical Fiber Coupler Based on a Highly Birefringent Structure-Numerical Design and Analysis. Fibers. 2019; 7(12):109. https://doi.org/10.3390/fib7120109
Chicago/Turabian StyleStawska, Hanna Izabela, and Maciej Andrzej Popenda. 2019. "A Dual Hollow Core Antiresonant Optical Fiber Coupler Based on a Highly Birefringent Structure-Numerical Design and Analysis" Fibers 7, no. 12: 109. https://doi.org/10.3390/fib7120109
APA StyleStawska, H. I., & Popenda, M. A. (2019). A Dual Hollow Core Antiresonant Optical Fiber Coupler Based on a Highly Birefringent Structure-Numerical Design and Analysis. Fibers, 7(12), 109. https://doi.org/10.3390/fib7120109