Terahertz Hollow Core Antiresonant Fiber with Metamaterial Cladding
Abstract
1. Introduction
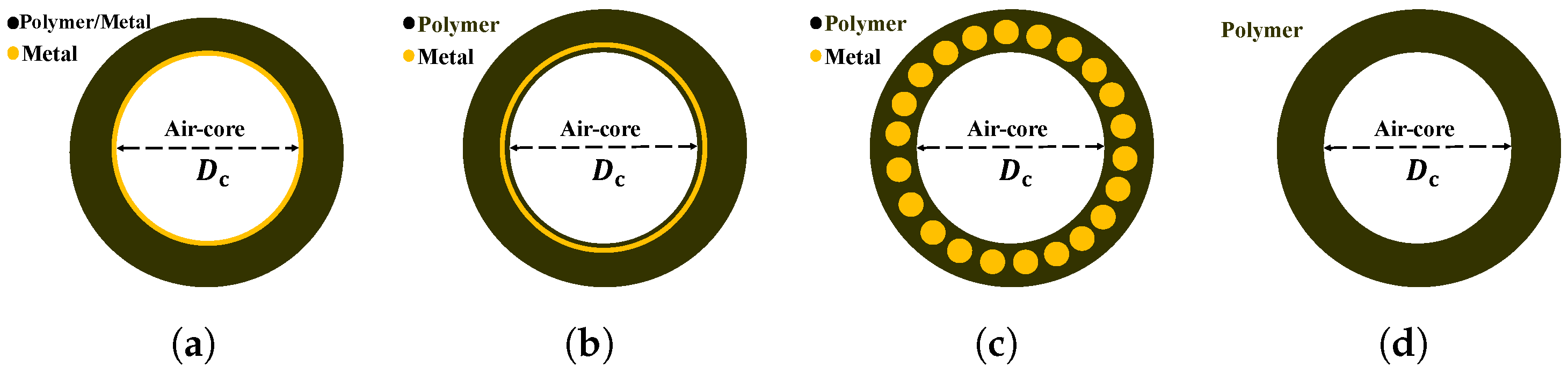
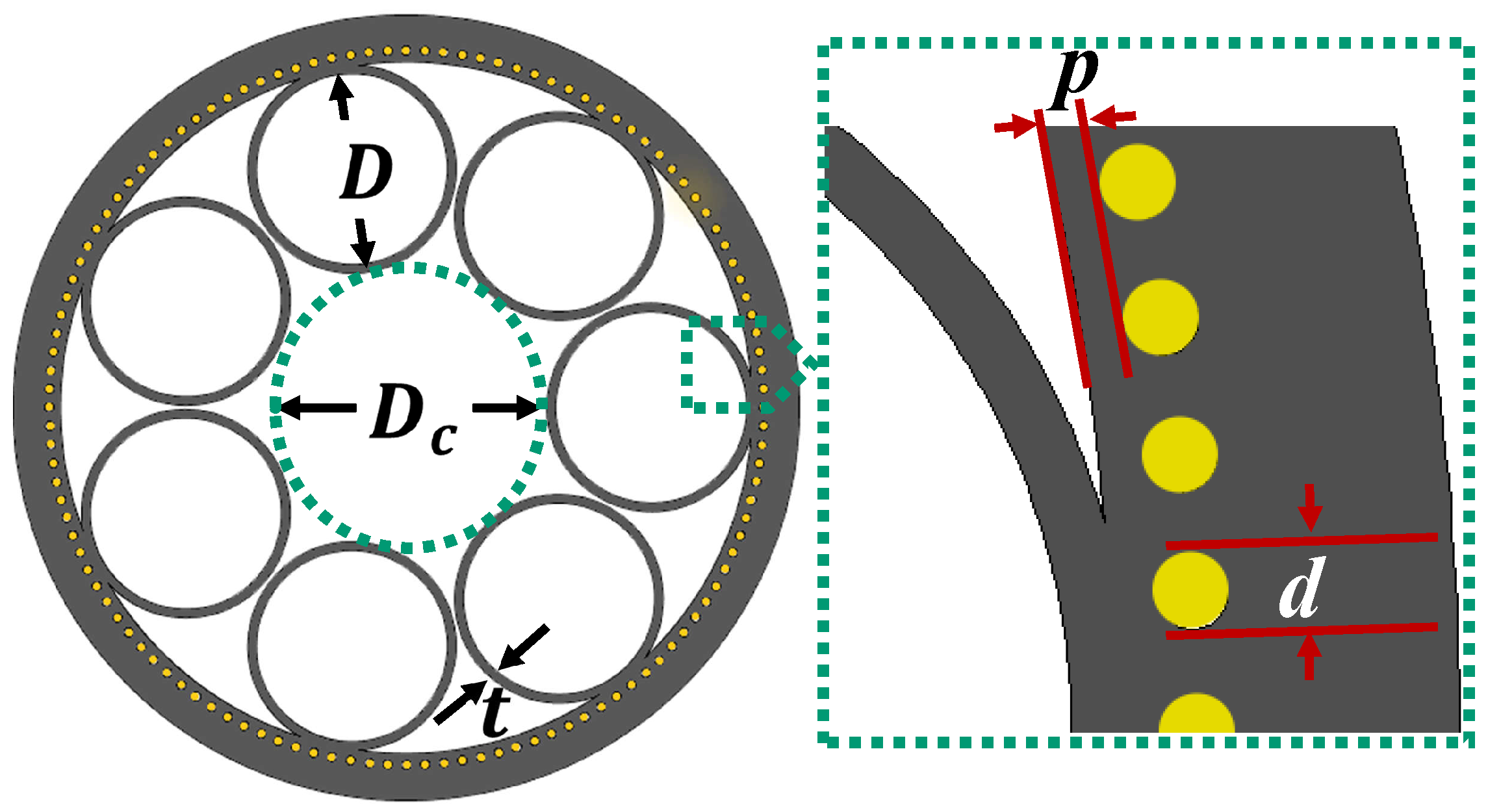
2. Design Methodology
Methodology of Characterizing the AR Fibers With Metal-Wire Inclusions
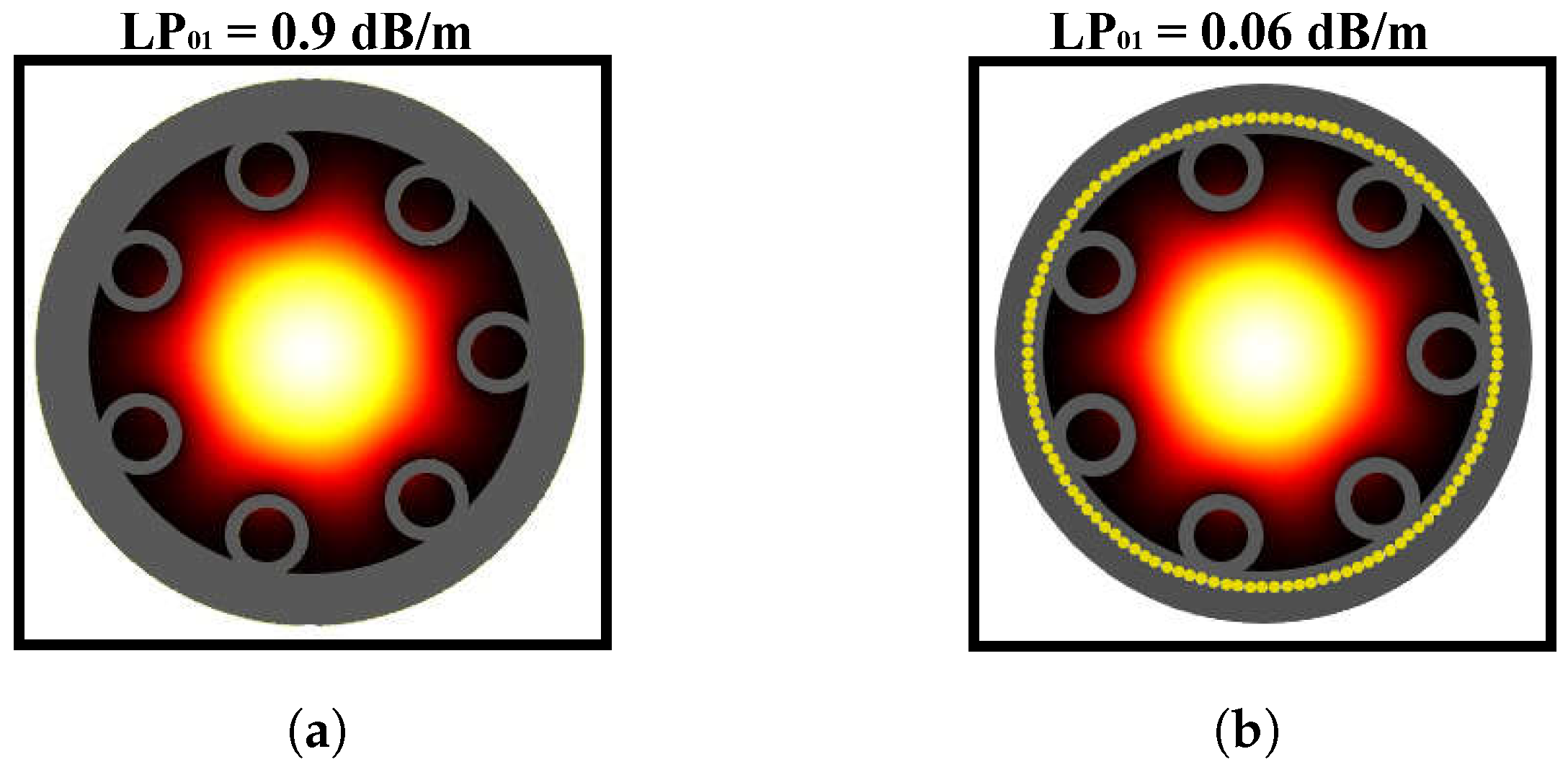
3. Results and Discussion
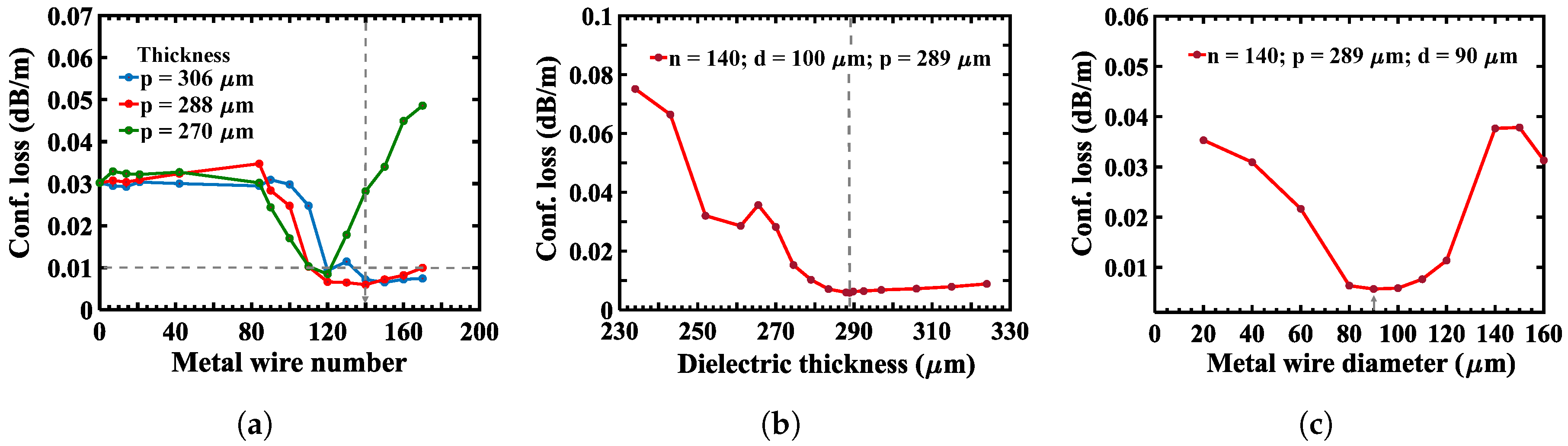
3.1. Effect of Metal Wire Number
3.2. Effect of Inner Cladding Dielectric Layer Thickness and Metal Wire Diameter
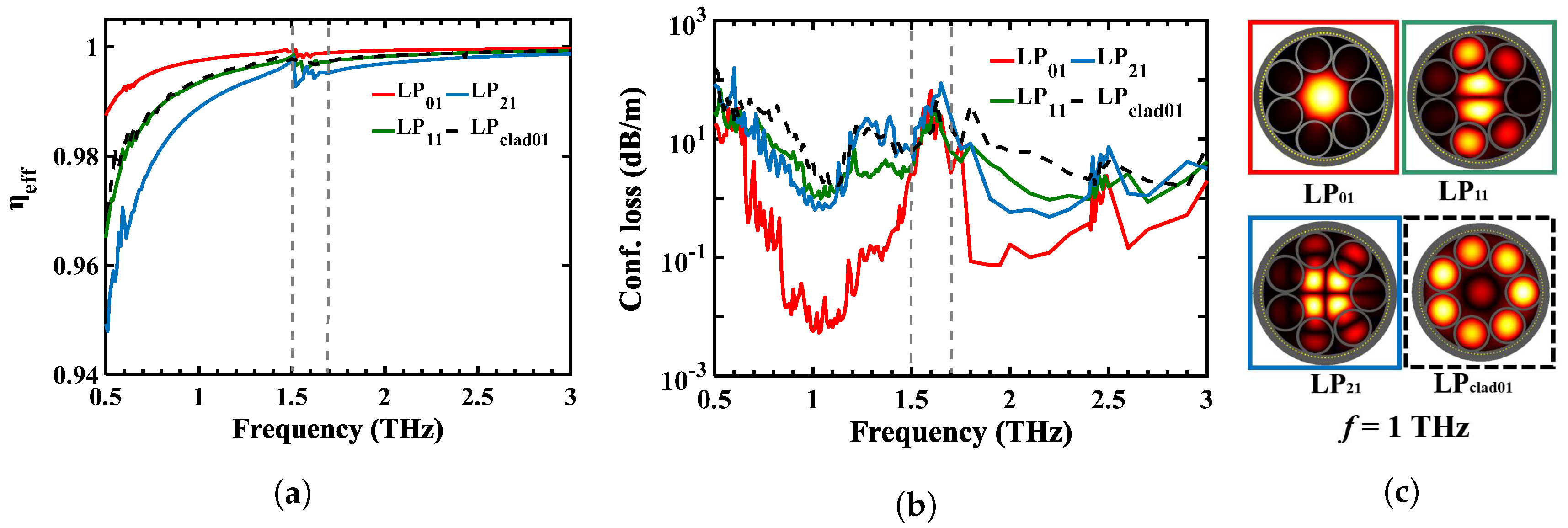
3.3. Comparison between Dielectric AR Fiber with and without Metal Wire Inclusion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AR | Antiresonant |
| HWG | Hollow Waveguide |
| LP | Linearly Polarized |
| FOP | Fraction of Power |
| HOM | Higher Order Mode |
| HC-ARPCF | Hollow Core Antiresonant Photonic Crystal Fiber |
References
- Tonouchi, M. Cutting-edge terahertz technology. Nat. Photonics 2007, 1, 97–105. [Google Scholar] [CrossRef]
- Islam, M.S.; Sultana, J.; Rifat, A.A.; Dinovitser, A.; Ng, B.W.-H.; Abbott, D. Terahertz sensing in a hollow core photonic crystal fiber. IEEE Sens. J. 2018, 18, 4073–4080. [Google Scholar] [CrossRef]
- Islam, M.S.; Sultana, J.; Rana, S.; Islam, M.R.; Faisal, M.; Kaijage, S.F.; Abbott, D. Extremely low material loss and dispersion flattened Topas based circular porous fiber for long distance terahertz wave transmission. Opt. Fiber Technol. 2017, 34, 6–11. [Google Scholar] [CrossRef]
- Islam, M.S.; Rana, S.; Islam, M.R.; Faisal, M.; Rahman, H.; Sultana, J. Porous core photonic crystal fibre for ultra-low material loss in THz regime. IET Commun. 2016, 10, 2179–2183. [Google Scholar] [CrossRef]
- Gallot, G.; Jamison, S.P.; McGowan, R.W.; Grischkowsky, D. Terahertz waveguides. J. Opt. Soc. Am. B 2000, 17, 851–863. [Google Scholar] [CrossRef]
- Atakaramians, S.; Shahraam, A.V.; Monro, T.M.; Abbott, D. Terahertz dielectric waveguides. Adv. Opt. Photonics 2013, 5, 169–215. [Google Scholar] [CrossRef]
- Islam, M.S.; Sultana, J.; Ahmed, K.; Dinovitser, A.; Islam, M.R.; Ng, B.W.-H.; Abbott, D. A novel approach for spectroscopic chemical identification using photonic crystal fiber in the terahertz regime. IEEE Sens. J. 2018, 18, 575–582. [Google Scholar] [CrossRef]
- Mittleman, D.M.; Jacobsen, R.H.; Neelamani, R.; Baraniuk, R.G.; Nuss, M.C. Gas sensing using terahertz time domain spectroscopy. Appl. Phys. B. 1998, 67, 379–390. [Google Scholar] [CrossRef]
- Gerecht, E.; Douglass, K.O.; Plusquellic, D.F. Chirped-pulse terahertz spectroscopy for broadband trace gas sensing. Opt. Express 2011, 19, 8973–8984. [Google Scholar] [CrossRef]
- Lin, H.; Withayachumnankul, W.; Fischer, B.M.; Mickan, S.P.; Abbott, D. Gas recognition with terahertz time-domain spectroscopy and spectral catalog: A preliminary study. Proc. SPIE Terahertz Photonics 2007, 6840, 68400X. [Google Scholar]
- Pickwell, E.; Wallace, V.P. Biomedical applications of terahertz technology. J. Phys. D Appl. Phys. 2006, 39, R301–R310. [Google Scholar] [CrossRef]
- Wu, Z.; Ng, W.; Gehm, M.E.; Xin, H. Terahertz electromagnetic crystal waveguide fabricated by polymer jetting rapid prototyping. Opt. Express 2011, 19, 3962–3972. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, K.; Rasmussen, H.K.; Jepsen, P.U.; Bang, O. Porous-core honeycomb bandgap THz fiber. Opt. Lett. 2011, 36, 666–668. [Google Scholar] [CrossRef] [PubMed]
- Anthony, J.; Leonhardt, R.; Leon-Saval, S.G.; Argyros, A. THz propagation in Kagome hollow-core microstructured fibers. Opt. Express 2011, 19, 18470–18478. [Google Scholar] [CrossRef] [PubMed]
- Vincetti, L.; Setti, V. Extra loss due to Fano resonances in inhibited coupling fibers based on a lattice of tubes. Opt. Express 2012, 20, 14350–14361. [Google Scholar] [CrossRef] [PubMed]
- Argyros, A.; Pla, J. Hollow-core polymer fibers with a kagome lattice: Potential for transmission in the infrared. Opt. Express 2007, 15, 7713–7719. [Google Scholar] [CrossRef] [PubMed]
- Benabid, F.; Knight, J.C.; Antonopoulos, G.; Russell, P.S.J. Stimulated Raman scattering in hydrogen-filled hollow-core photonic crystal fiber. Science 2002, 298, 399–402. [Google Scholar] [CrossRef]
- Ito, T.; Matsuura, Y.; Miyagi, M.; Minamide, H.; Ito, H. Flexible terahertz fiber optics with low bend-induced losses. J. Opt. Soc. Am. B 2007, 24, 1230–1235. [Google Scholar] [CrossRef]
- McGowan, R.W.; Gallot, G.; Grischkowsky, D. Propagation of ultrawideband short pulses of terahertz radiation through submillimeter-diameter circular waveguides. Opt. Lett. 1999, 24, 1431–1433. [Google Scholar] [CrossRef]
- Hidaka, T.; Minamide, H.; Ito, H.; Nishizawa, J.-I.; Tamura, K.; Ichikawa, S. Ferroelectric PVDF cladding terahertz waveguide. J. Light. Technol. 2005, 23, 2469–2473. [Google Scholar] [CrossRef]
- Ponseca, C.S.; Pobre, R.; Estacio, E.; Sarukura, N.; Argyros, A.; Large, M.C.J.; van Eijkelenborg, M.A. Transmission of terahertz radiation using a microstructured polymer optical fiber. Opt. Lett. 2008, 33, 902–904. [Google Scholar] [CrossRef]
- Nagel, M.; Marchewka, A.; Kurz, H. Low-index discontinuity terahertz waveguides. Opt. Express 2006, 14, 9944–9954. [Google Scholar] [CrossRef]
- Harrington, J.A.; George, R.; Pedersenand, P. Hollow polycarbonate waveguides with inner Cu coatings for delivery of terahertz radiation. Opt. Express 2004, 12, 5263–5268. [Google Scholar] [CrossRef]
- Bowden, B.; Harrington, J.A.; Mitrofanov, O. Silver/polystyrene-coated hollow glass waveguides for the transmission of terahertz radiation. Opt. Lett. 2007, 32, 2945–2947. [Google Scholar] [CrossRef]
- Bowden, B.; Harrington, J.A.; Mitrofanov, O. Fabrication of terahertz hollow-glass metallic waveguides with inner dielectric coatings. J. Appl. Phys. 2008, 104, 093110. [Google Scholar] [CrossRef]
- Matsuura, Y.; Takeda, E. Hollow optical fibers loaded with an inner dielectric film for terahertz broadband spectroscopy. J. Opt. Soc. Am. B 2008, 25, 1949–1954. [Google Scholar] [CrossRef]
- Bowden, B.; Harrington, J.A.; Mitrofanov, O. Low-loss modes in hollow metallic terahertz waveguides with dielectric coatings. J. Appl. Phys. Lett. 2008, 93, 181104. [Google Scholar] [CrossRef]
- Themistos, C.; Rahman, B.M.A.; Rajarajan, M.; Grattan, K.T.V.; Bowden, B.; Harrington, J.A. Characterization of Silver/Polystyrene (PS)-coated hollow glass waveguides at THz frequency. J. Light. Technol. 2007, 25, 2456–2462. [Google Scholar] [CrossRef]
- Mitrofanovand, O.; Harrington, J.A. Dielectric-lined cylindrical metallic THz waveguides: Mode structure and dispersion. Opt. Express 2010, 18, 1898–1903. [Google Scholar] [CrossRef]
- Tian, D.; Zhang, H.; Wen, Q.; Wang, Z.; Li, S.; Chen, Z.; Guo, X. Dual cylindrical metallic grating-cladding polymer hollow waveguide for terahertz transmission with low loss. Appl. Phys. Lett. 2010, 97, 133502. [Google Scholar] [CrossRef]
- Anthony, J.; Leonhardt, R.; Argyros, A. Hybrid hollow core fibers with embedded wires as THz waveguides. Opt. Express 2013, 21, 2903–2912. [Google Scholar] [CrossRef]
- Yudasari, N.; Anthony, J.; Leonhardt, R. Terahertz pulse propagation in 3D-printed waveguide with metal wires component. Opt. Express 2014, 22, 26042–26054. [Google Scholar] [CrossRef]
- Li, H.; Atakaramians, S.; Lwin, R.; Tang, X.; Yu, Z.; Argyros, A.; Kuhlme, B.T. Flexible single-mode hollow-core terahertz fiber with metamaterial cladding. Optica 2016, 3, 941–947. [Google Scholar] [CrossRef]
- Tuniz, A.; Lwin, R.; Argyros, A.; Fleming, S.C.; Kuhlmey, B.T. Fabricating metamaterials using the fiber drawing method. J. Vis. Exp. 2012, 68, 4299. [Google Scholar] [CrossRef]
- van Putten, L.D.; Gorecki, J.; Fokoua, E.N.; Apostolopoulos, V.; Poletti, F. 3D-printed polymer antiresonant wave-guides for short-reach terahertz applications. Appl. Opt. 2018, 57, 3953–3958. [Google Scholar] [CrossRef]
- Cruz, A.L.S.; Franco, M.A.R.; Cordeiro, C.M.B.; Rodrigues, G.S.; Osório, J.H.; da Silva, L.E. Exploring THz Hollow-Core Fiber Designs Manufactured by 3D Printing. In Proceedings of the 2017 SBMO/IEEE MTT-S International Microwave and Optoelectronics Conference, Aguas de Lindoia, Brazil, 27–30 August 2017. [Google Scholar] [CrossRef]
- Cruz, A.L.S.; Serrão, V.A.; Barbosa, C.L.; Franco, M.A.R. 3D printed hollow core fiber with negative curvature for terahertz applications. J. Microw. Optoelectron. Electromagn. Appl. 2015, 14, SI-45–SI-53. [Google Scholar]
- Setti, V.; Vincetti, L.; Argyros, A. Flexible tube lattice fibers for terahertz applications. Opt. Express 2013, 21, 3388–3399. [Google Scholar] [CrossRef]
- Lu, W.; Lou, S.; Wang, X.; Shen, Y.; Sheng, X. Demonstration of low-loss flexible fiber with Zeonex tube-lattice cladding for terahertz transmission. In Proceedings of the 2015 Optical Fiber Communications Conference and Exhibition (OFC), Los Angeles, CA, USA, 22–26 March 2015. [Google Scholar] [CrossRef]
- Nazarov, M.M.; Shilov, A.V.; Bzheumikhov, K.A.; Margushev, Z.C.; Sokolov, V.I.; Sotsky, A.B.; Shkurinov, A.P. Eight-capillary cladding THz waveguide with low propagation losses and dispersion. IEEE Trans. Terahertz Sci. Technol. 2018, 8, 183–191. [Google Scholar] [CrossRef]
- Vincetti, L. Single-mode propagation in triangular tube lattice hollow core terahertz fiber. Opt. Commun. 2010, 283, 979–984. [Google Scholar] [CrossRef]
- Vincetti, L.; Setti, V.; Zoboli, M. Terahertz tube lattice fibers with octagonal symmetry. IEEE Photonics Technol. Lett. 2010, 22, 972–974. [Google Scholar] [CrossRef]
- Chesini, G.; Serrão, V.A.; Franco, M.A.R.; Cordeiro, C.M.B. Analysis and optimization of an all-fiber device based on photonic crystal fiber with integrated electrodes. Opt. Express 2010, 18, 2842–2848. [Google Scholar] [CrossRef]
- Refractive index Info. Available online: https://refractiveindex.info/?shelf=main&book=Al&page=Hagemann (accessed on 25 January 2020).
- Islam, M.S.; Sultana, J.; Cordeiro, C.M.B.; Cruz, A.L.S.; Dinovitser, A.; Ng, B.W.-H.; Abbott, D. Broadband characterization of glass and polymer materials using THz-TDS. In Proceedings of the 44th International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz), Paris, France, 1–6 September 2019. [Google Scholar] [CrossRef]
- Rugeland, P.; Sterner, C.; Margulis, W. Visible light guidance in silica capillaries by anti-resonant reflection. Opt. Express 2013, 21, 29217–29222. [Google Scholar] [CrossRef]
- Vincetti, L. Numerical analysis of plastic hollow core microstructured fiber for Terahertz applications. Opt. Fiber Technol. 2009, 15, 398–401. [Google Scholar] [CrossRef]
- Lu, W.; Argyros, A. Terahertz spectroscopy and imaging with flexible tube-lattice fiber probe. J. Light. Technol. 2014, 32, 4621–4627. [Google Scholar]
- Liang, J.; Ren, L.; Chen, N.; Zhou, C. Broadband, low-loss, dispersion flattened porous-core photonic bandgap fiber for terahertz (THz)-wave propagation. Opt. Commun. 2013, 295, 257–261. [Google Scholar] [CrossRef]
- Cordeiro, C.M.B. Microstructured-core optical fiber for evanescent sensing applications. Opt. Express 2006, 14, 13056–13066. [Google Scholar] [CrossRef]
- Gloge, D. Weakly guiding fibers. Appl. Opt. 1971, 10, 2252–2258. [Google Scholar] [CrossRef]
- Ma, Y.Z.; Sych, Y.; Onishchukov, G.; Ramachandran, S.; Peschel, U.; Schmauss, B.; Leuchs, G. Fiber-modes and fiber-anisotropy characterization using low-coherence interferometry. Appl. Phys. B 2009, 96, 345–353. [Google Scholar] [CrossRef][Green Version]
- Vincetti, L.; Setti, V. Waveguiding mechanism in tube lattice fibers. Opt. Express 2010, 18, 23133–23146. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sultana, J.; Islam, M.S.; Cordeiro, C.M.B.; Dinovitser, A.; Kaushik, M.; W.-H. Ng, B.; Abbott, D. Terahertz Hollow Core Antiresonant Fiber with Metamaterial Cladding. Fibers 2020, 8, 14. https://doi.org/10.3390/fib8020014
Sultana J, Islam MS, Cordeiro CMB, Dinovitser A, Kaushik M, W.-H. Ng B, Abbott D. Terahertz Hollow Core Antiresonant Fiber with Metamaterial Cladding. Fibers. 2020; 8(2):14. https://doi.org/10.3390/fib8020014
Chicago/Turabian StyleSultana, Jakeya, Md. Saiful Islam, Cristiano M. B. Cordeiro, Alex Dinovitser, Mayank Kaushik, Brian W.-H. Ng, and Derek Abbott. 2020. "Terahertz Hollow Core Antiresonant Fiber with Metamaterial Cladding" Fibers 8, no. 2: 14. https://doi.org/10.3390/fib8020014
APA StyleSultana, J., Islam, M. S., Cordeiro, C. M. B., Dinovitser, A., Kaushik, M., W.-H. Ng, B., & Abbott, D. (2020). Terahertz Hollow Core Antiresonant Fiber with Metamaterial Cladding. Fibers, 8(2), 14. https://doi.org/10.3390/fib8020014





