Direct Comparison of the Structural Compression Characteristics of Natural and Synthetic Fiber-Epoxy Composites: Flax, Jute, Hemp, Glass and Carbon Fibers
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Channel Fabrications
2.3. Channel Tests
3. Results
3.1. Laminate Thickness
3.2. Fiber Volume Fractions
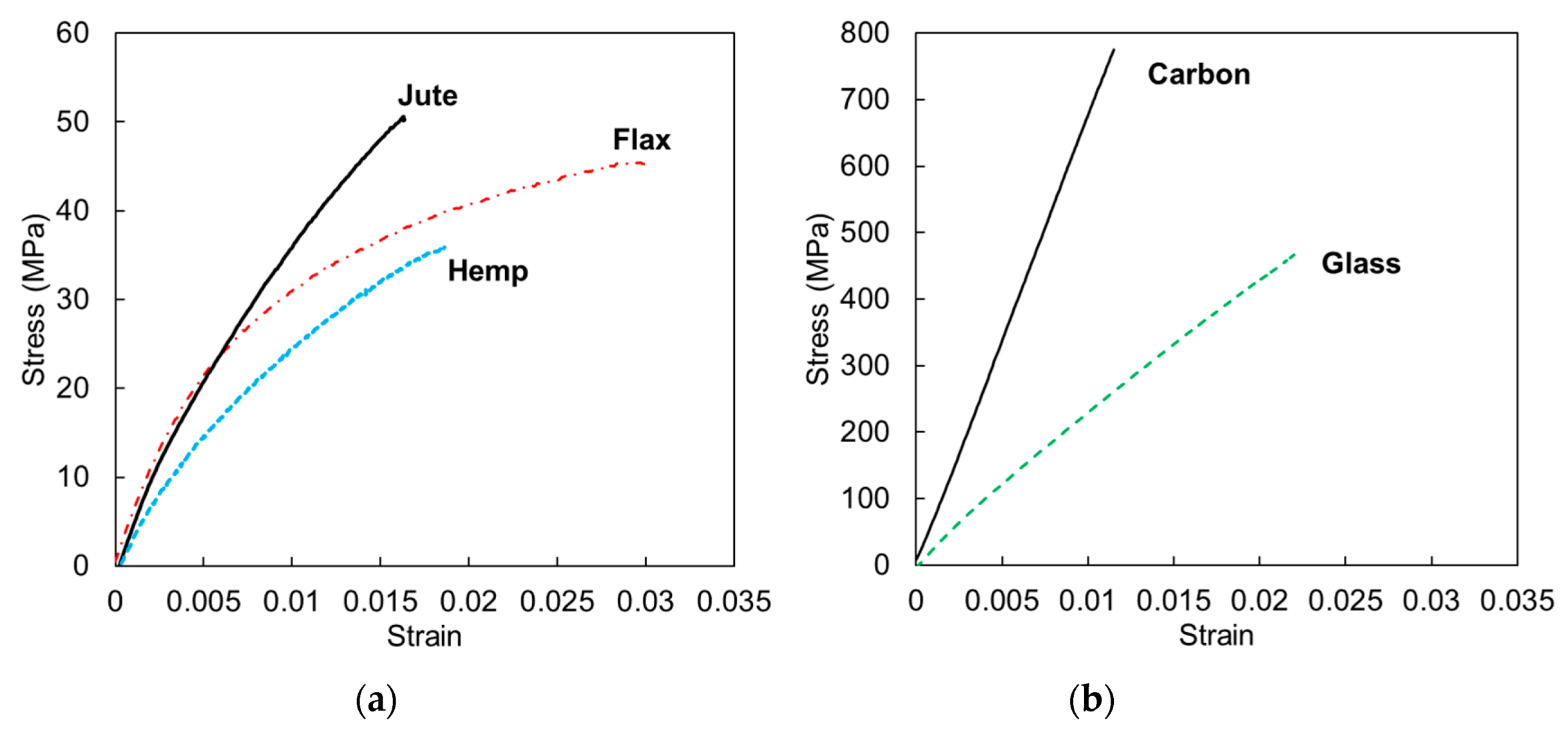
3.3. Material Tension Test Results
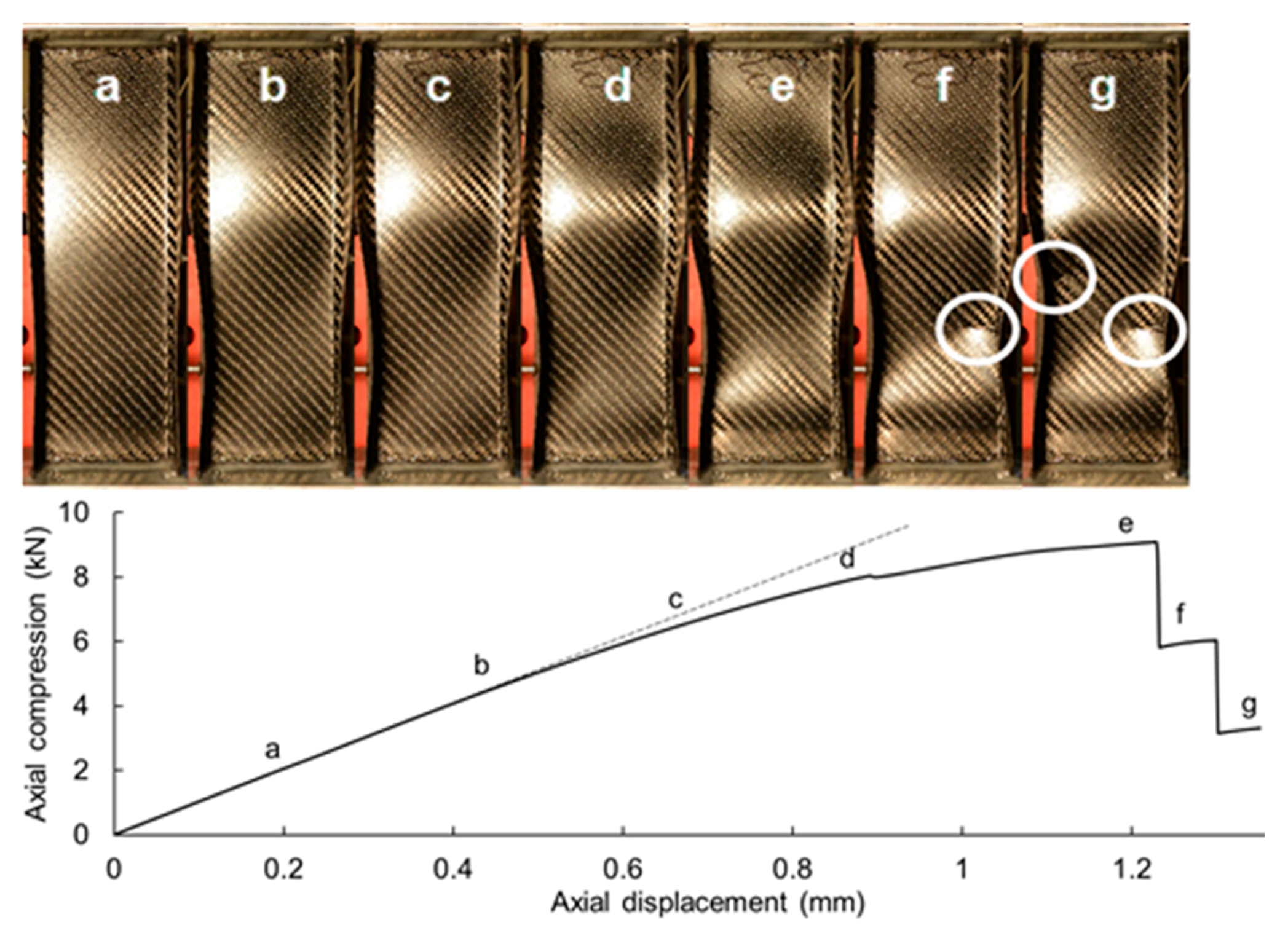
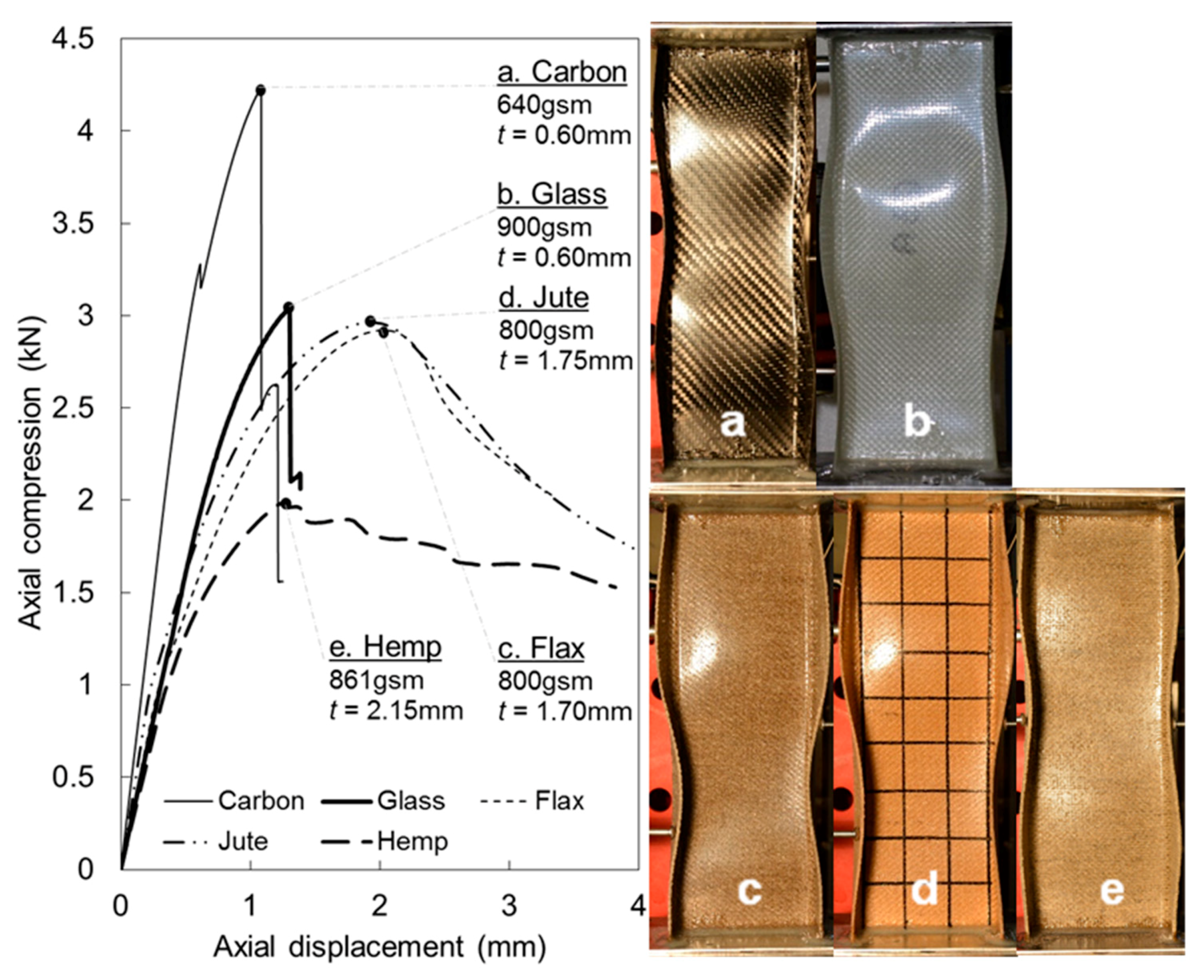
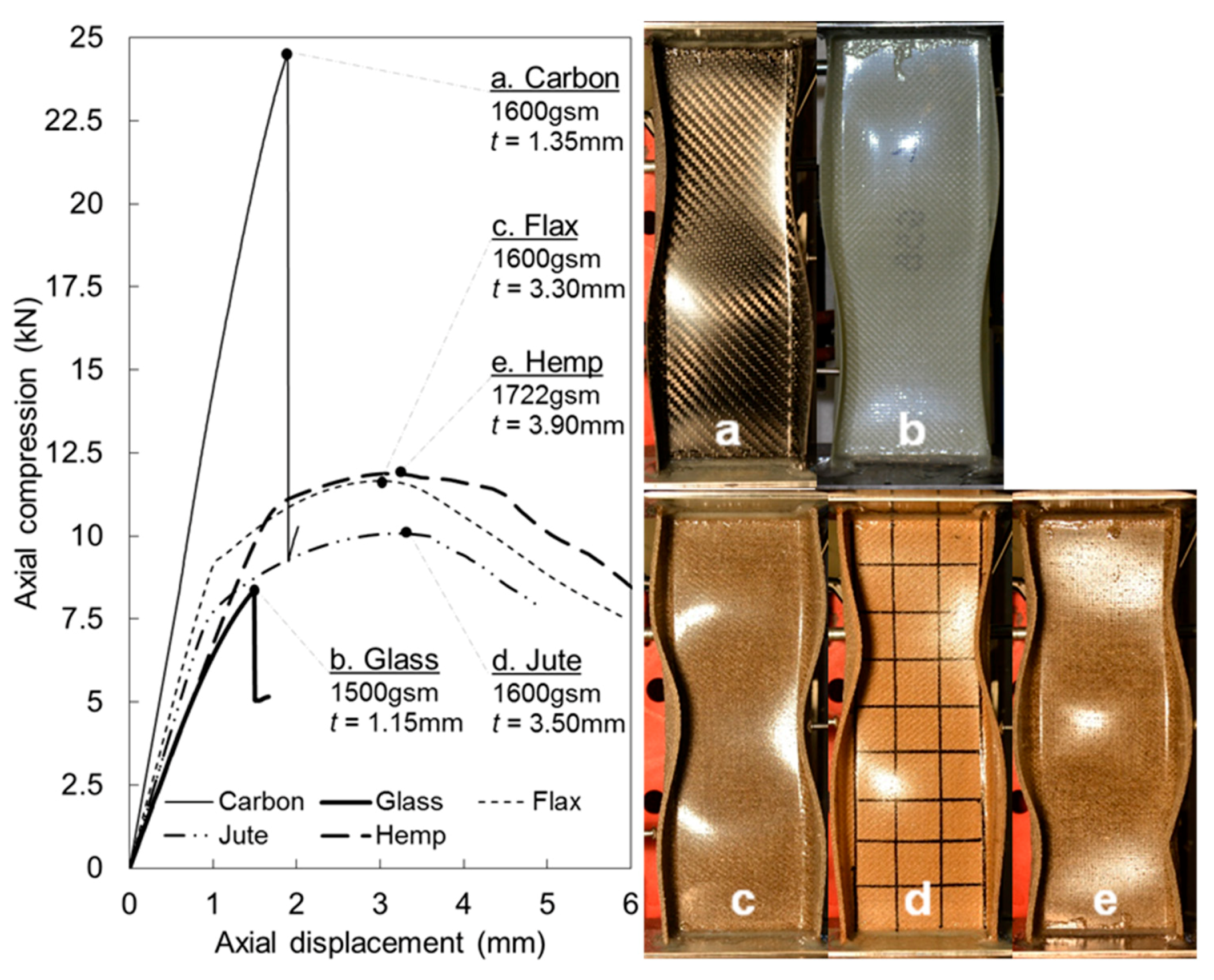
3.4. Channel Test Results
3.5. Failure Modes
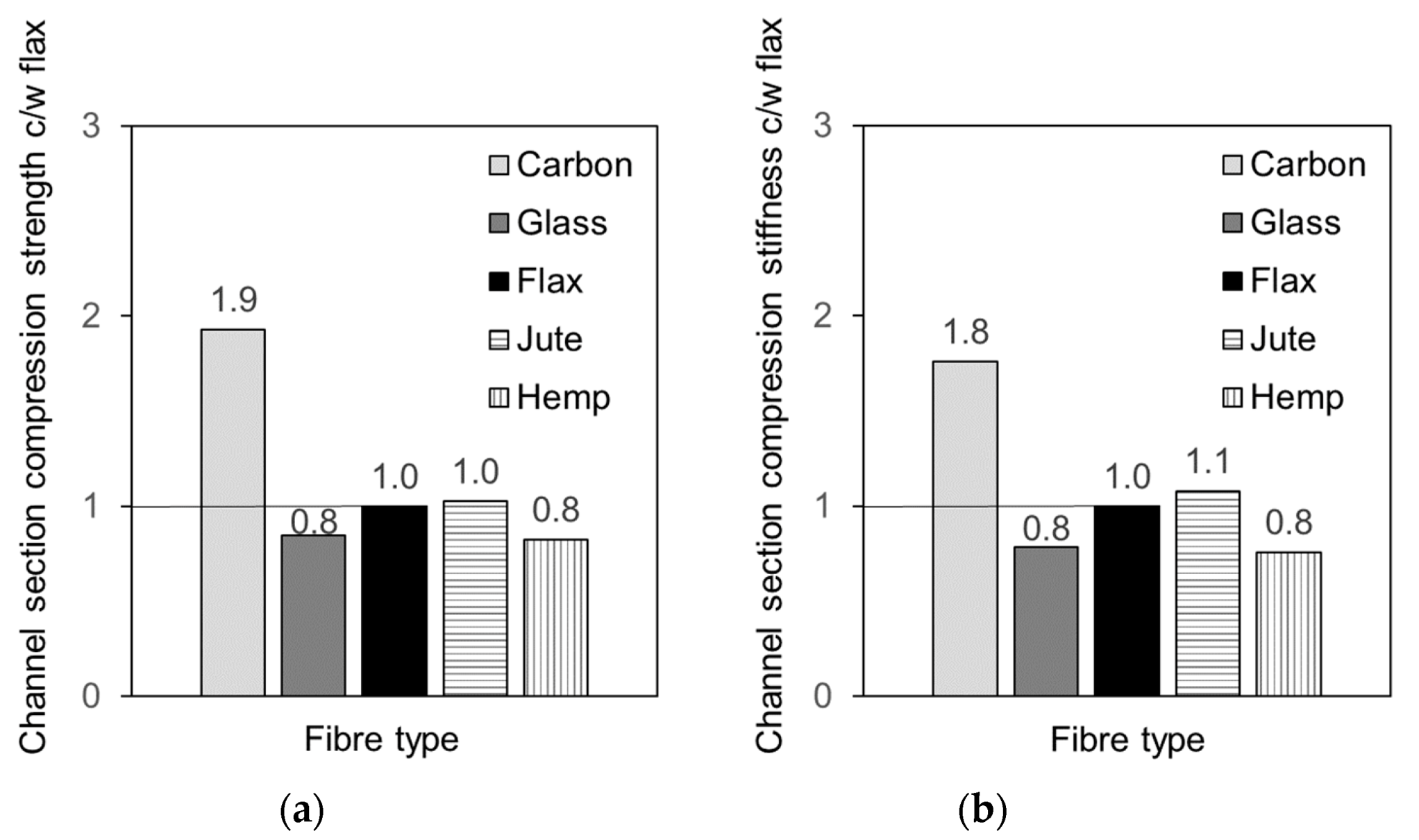
3.6. Comparisons of Structural Compression Characteristics—Compressive Strength and Stiffness
4. Discussion
5. Conclusions
Funding
Conflicts of Interest
References
- Summerscales, J.; Dissanayake, N.P.J.; Virk, A.S.; Hall, W. A review of bast fibers and their composites. Part 1—Fibers as reinforcements. Compos. Part A 2010, 41, 1329–1335. [Google Scholar] [CrossRef]
- Summerscales, J.; Dissanayake, N.P.J.; Virk, A.S.; Hall, W. A review of bast fibers and their composites. Part 2—Composites. Compos. Part A 2010, 41, 1336–1344. [Google Scholar] [CrossRef]
- Ku, H.; Wang, H.; Pattarachaiyakoop, N.; Trada, M. A review on the tensile properties of natural fiber reinforced polymer composites. Compos. Part B Eng. 2011, 42, 856–873. [Google Scholar] [CrossRef]
- Yan, L.B.; Chouw, N.; Jayaraman, K. Flax fibe and its composites—A review. Compos. Part B. 2014, 56, 296–317. [Google Scholar] [CrossRef]
- Pickering, K.L.; Efendy, M.G.A.; Le, T.M. A review of recent developments in natural fiber composites and their mechanical performance. Compos. Part A 2016, 83, 98–112. [Google Scholar] [CrossRef]
- Faruk, O.; Bledzki, A.K.; Fink, H.-P.; Sain, M. Biocomposites reinforced with natural fibers: 2000–Prog. Polym. Sci. 2012, 37, 1552–1596. [Google Scholar] [CrossRef]
- Dicker, M.P.M.; Duckworth, P.F.; Baker, A.B.; François, G.; Hazzard, M.K.; Weaver, P.M. Green composites: A review of material attributes and complementary applications. Compos. Part A Appl. Sci. Manuf. 2014, 56, 280–289. [Google Scholar] [CrossRef]
- Weclawski, B.T.; Fan, M.; Hui, D. Compressive behaviour of natural fiber composite. Compos. Part B 2014, 67, 183–191. [Google Scholar] [CrossRef]
- Costa, F.H.M.M.; D’Almeida, J.R.M. Effect of Water Absorption on the Mechanical Properties of Sisal and Jute Fiber Composites. Polym. Technol. Eng. 1999, 38, 1081–1094. [Google Scholar] [CrossRef]
- Hargitai, H.; Rácz, I.; Anandjiwala, R.D. Development of HEMP Fiber Reinforced Polypropylene Composites. J. Thermoplast. Compos. Mater. 2008, 21, 165–174. [Google Scholar] [CrossRef]
- Oksman, K. High quality flax fiber composites manufactured by the resin transfer moulding process. J. Reinf. Plast. Comp. 2001, 20, 621–627. [Google Scholar] [CrossRef]
- Da Silva, H.S.P.; Júnior, H.L.O.; Júnior, J.H.A.; Zattera, A.J.; Amico, S.C. Mechanical behavior and correlation between dynamic fragility and dynamic mechanical properties of curaua fiber composites. Polym. Compos. 2013, 35, 1078–1086. [Google Scholar] [CrossRef]
- Da Silva, L.V.; Júnior, J.H.A.; Angrizani, C.C.; Amico, S.C. Short beam strength of curaua, sisal, glass and hybrid composites. J. Reinf. Plast. Compos. 2012, 32, 197–206. [Google Scholar] [CrossRef]
- ISO 604: Plastics—Determination of Compressive Properties; ISO: Geneva, Switzerland, 2002.
- ISO 527-4: Plastics—Determination of Tensile Properties. Part 4: Test Conditions for Isotropic and Orthotropic Fiber-Reinforced Plastic Composites; ISO: Geneva, Switzerland, 1997.
- ISO 14125: Fiber-Reinforced Plastic Composites—Determination of Flexural Properties; ISO: Geneva, Switzerland, 1998.
- Bambach, M.R. Compression strength of natural fiber composite plates and sections of flax, jute and hemp. Thin Walled Struct. 2017, 119, 103–113. [Google Scholar] [CrossRef]
- Bambach, M.R. Geometric optimisation and compression design of natural fiber composite structural channel sections. Compos. Struct. 2018, 185, 549–560. [Google Scholar] [CrossRef]
- Bambach, M. Durability of natural fibre epoxy composite structural columns: High cycle compression fatigue and moisture ingress. Compos. Part C Open Access 2020, 2, 100013. [Google Scholar] [CrossRef]
- Shah, D.U.; Schubel, P.J.; Clifford, M.J. Can flax replace E-glass in structural composites? A small wind turbine blade case study. Compos. Part B Eng. 2013, 52, 172–181. [Google Scholar] [CrossRef]
- Yan, L.B.; Chouw, N. Crashworthiness characteristics of flax fiber reinforced epoxy tubes for energy absorption application. Mat. Des. 2013, 51, 629–640. [Google Scholar] [CrossRef]
- Yan, L.B.; Chouw, N. Behaviour and analytical modelling of natural flax fiber reinforced polymer tube encased coir fiber reinforced concrete composite column. J. Comp. Mater 2013, 47, 2133–2148. [Google Scholar] [CrossRef]
- Mak, K.; Fam, A.; MacDougall, C. Flexural Behavior of Sandwich Panels with Bio-FRP Skins Made of Flax Fibers and Epoxidized Pine-Oil Resin. J. Compos. Constr. 2015, 19, 04015005. [Google Scholar] [CrossRef]
- Le Duigou, A.; Deux, J.-M.; Davies, P.; Baley, C. PLLA/Flax Mat/Balsa Bio-Sandwich Manufacture and Mechanical Properties. Appl. Compos. Mater. 2010, 18, 421–438. [Google Scholar] [CrossRef]
- Uddin, N.; Kalyankar, R. Manufacturing and Structural Feasibility of Natural Fiber Reinforced Polymeric Structural Insulated Panels for Panelized Construction. Int. J. Polym. Sci. 2011, 2011, 963549. [Google Scholar] [CrossRef]
- Lansiaux, H.; Soulat, D.; Boussu, F.; Labanieh, A.R. Development and Multiscale Characterization of 3D Warp Interlock Flax Fabrics with Different Woven Architectures for Composite Applications. Fibers 2020, 8, 15. [Google Scholar] [CrossRef]
- Wahab, N.; Srinophakun, P.; Hussain, Q.; Chaimahawan, P. Performance of Concrete Confined with a Jute–Polyester Hybrid Fiber Reinforced Polymer Composite: A Novel Strengthening Technique. Fibers 2019, 7, 72. [Google Scholar] [CrossRef]
- Manaia, J.P.; Manaia, A.T.; Rodriges, L. Industrial Hemp Fibers: An Overview. Fibers 2019, 7, 106. [Google Scholar] [CrossRef]
- Ateş, B.; Koytepe, S.; Ulu, A.; Gurses, C.; Thakur, V. Chemistry, Structures, and Advanced Applications of Nanocomposites from Biorenewable Resources. Chem. Rev. 2020, 120, 9304–9362. [Google Scholar] [CrossRef]
- Singha, A.; Thakur, V. Physical, Chemical and Mechanical Properties of Hibiscus sabdariffa Fiber/Polymer Composite. Int. J. Polym. Mater. 2009, 58, 217–228. [Google Scholar] [CrossRef]
- Singha, A.; Thakur, V. Fabrication and characterization of S. cilliare fibre reinforced polymer composites. Bull. Mater. Sci. 2009, 32, 49–58. [Google Scholar] [CrossRef]
- Bambach, M. Axial capacity and crushing of thin-walled metal, fibre–epoxy and composite metal–fibre tubes. Thin Walled Struct. 2010, 48, 440–452. [Google Scholar] [CrossRef]
- Bambach, M. Photogrammetry measurements of buckling modes and interactions in channels with edge-stiffened flanges. Thin Walled Struct. 2009, 47, 485–504. [Google Scholar] [CrossRef]





| Fiber | Total Areal Mass | Web Depth (D) | Flange Width (B) | Thick- ness (t) | Ultimate Load (Pu) | Strength Efficiency | Axial Stiffness | Buckling Load (Pb) | Pu/Pb |
|---|---|---|---|---|---|---|---|---|---|
| (gsm) | (mm) | (mm) | (mm) | (N) | (N/gsm) | (N/mm) | (N) | ||
| Flax | 800 | 104.1 | 39.8 | 1.70 | 2683 | 3.35 | 3409 | 949 | 2.8 |
| Flax | 800 | 104.0 | 39.8 | 1.70 | 2922 | 3.65 | 3433 | 982 | 3.0 |
| Flax | 1200 | 105.5 | 41.2 | 2.45 | 6898 | 5.75 | 7249 | 3898 | 1.8 |
| Flax | 1200 | 105.9 | 41.4 | 2.45 | 6381 | 5.32 | 7270 | 3667 | 1.7 |
| Flax | 1600 | 107.5 | 41.3 | 3.30 | 11,023 | 6.89 | 9240 | 8933 | 1.2 |
| Flax | 1600 | 107.4 | 41.2 | 3.30 | 11,655 | 7.28 | 8670 | 9287 | 1.3 |
| Jute | 800 | 104.0 | 41.2 | 1.75 | 2996 | 3.75 | 4422 | 825 | 3.6 |
| Jute | 800 | 104.1 | 41.1 | 1.75 | 2967 | 3.71 | 4313 | 1027 | 2.9 |
| Jute | 1200 | 106.1 | 42.0 | 2.75 | 7678 | 6.40 | 7742 | 4414 | 1.7 |
| Jute | 1200 | 105.9 | 42.0 | 2.75 | 7611 | 6.34 | 7755 | 4253 | 1.8 |
| Jute | 1600 | 107.1 | 41.7 | 3.50 | 9555 | 5.97 | 8243 | 7655 | 1.2 |
| Jute | 1600 | 107.3 | 41.8 | 3.50 | 10,078 | 6.30 | 8705 | 7514 | 1.3 |
| Hemp | 861 | 104.8 | 41.8 | 2.15 | 1985 | 2.31 | 2849 | 1031 | 1.9 |
| Hemp | 861 | 104.6 | 42.1 | 2.15 | 2207 | 2.56 | 2850 | 985 | 2.2 |
| Hemp | 1148 | 106.2 | 41.2 | 2.70 | 4663 | 4.06 | 4949 | 3205 | 1.5 |
| Hemp | 1148 | 106.0 | 41.0 | 2.70 | 4903 | 4.27 | 6365 | 2748 | 1.8 |
| Hemp | 1722 | 109.0 | 41.5 | 3.90 | 11,879 | 6.90 | 6669 | 10,780 | 1.1 |
| Hemp | 1722 | 108.9 | 41.7 | 3.90 | 13,262 | 7.70 | 6598 | 11,687 | 1.1 |
| Carbon | 640 | 101.6 | 39.6 | 0.60 | 4231 | 6.61 | 5825 | 3275 | 1.3 |
| Carbon | 640 | 101.5 | 39.3 | 0.60 | 4122 | 6.44 | 5786 | 3095 | 1.3 |
| Carbon | 960 | 102.5 | 41.2 | 0.90 | 9089 | 9.47 | 9629 | 7246 | 1.3 |
| Carbon | 960 | 102.4 | 42.2 | 0.90 | 9340 | 9.73 | 9699 | 7452 | 1.3 |
| Carbon | 1600 | 103.5 | 42.0 | 1.35 | 25,270 | 15.79 | 14,311 | 15,584 | 1.6 |
| Carbon | 1600 | 103.3 | 40.3 | 1.35 | 24,527 | 15.33 | 14,175 | 14,714 | 1.7 |
| Glass | 900 | 101.8 | 39.1 | 0.60 | 3041 | 3.38 | 3191 | 2094 | 1.5 |
| Glass | 900 | 101.8 | 39.3 | 0.60 | 3028 | 3.36 | 3432 | 2036 | 1.5 |
| Glass | 1200 | 102.4 | 41.7 | 0.80 | 5488 | 4.57 | 5303 | 3645 | 1.5 |
| Glass | 1200 | 102.5 | 41.9 | 0.80 | 5241 | 4.37 | 5222 | 3591 | 1.5 |
| Glass | 1500 | 103.3 | 39.3 | 1.15 | 7857 | 5.24 | 6495 | 4912 | 1.6 |
| Glass | 1500 | 103.2 | 39.5 | 1.15 | 8373 | 5.58 | 6840 | 5044 | 1.7 |
| ET | εuT | fuT | |
|---|---|---|---|
| (GPa) | (%) | (MPa) | |
| Flax | 6.03 | 3.1 | 45.4 |
| Jute | 5.18 | 1.6 | 52.1 |
| Hemp | 3.83 | 1.8 | 35.3 |
| Carbon | 72.9 | 1.1 | 771 |
| Glass | 22.9 | 2.3 | 484 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bambach, M.R. Direct Comparison of the Structural Compression Characteristics of Natural and Synthetic Fiber-Epoxy Composites: Flax, Jute, Hemp, Glass and Carbon Fibers. Fibers 2020, 8, 62. https://doi.org/10.3390/fib8100062
Bambach MR. Direct Comparison of the Structural Compression Characteristics of Natural and Synthetic Fiber-Epoxy Composites: Flax, Jute, Hemp, Glass and Carbon Fibers. Fibers. 2020; 8(10):62. https://doi.org/10.3390/fib8100062
Chicago/Turabian StyleBambach, Mike R. 2020. "Direct Comparison of the Structural Compression Characteristics of Natural and Synthetic Fiber-Epoxy Composites: Flax, Jute, Hemp, Glass and Carbon Fibers" Fibers 8, no. 10: 62. https://doi.org/10.3390/fib8100062
APA StyleBambach, M. R. (2020). Direct Comparison of the Structural Compression Characteristics of Natural and Synthetic Fiber-Epoxy Composites: Flax, Jute, Hemp, Glass and Carbon Fibers. Fibers, 8(10), 62. https://doi.org/10.3390/fib8100062





