Enhanced Piezoelectric Fibered Extracellular Matrix to Promote Cardiomyocyte Maturation and Tissue Formation: A 3D Computational Model
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Assumptions
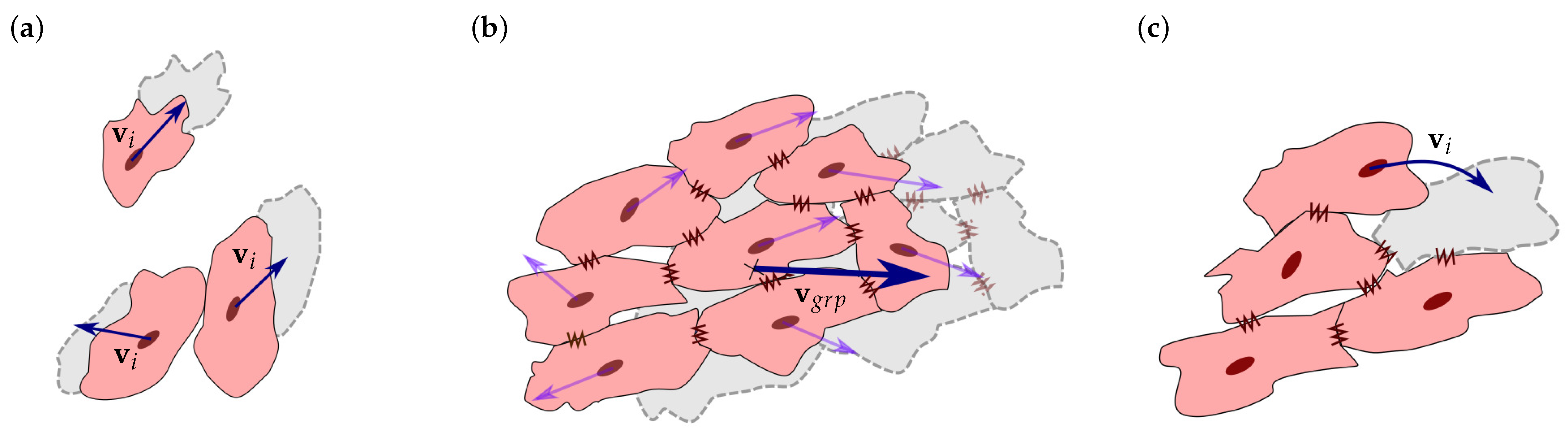
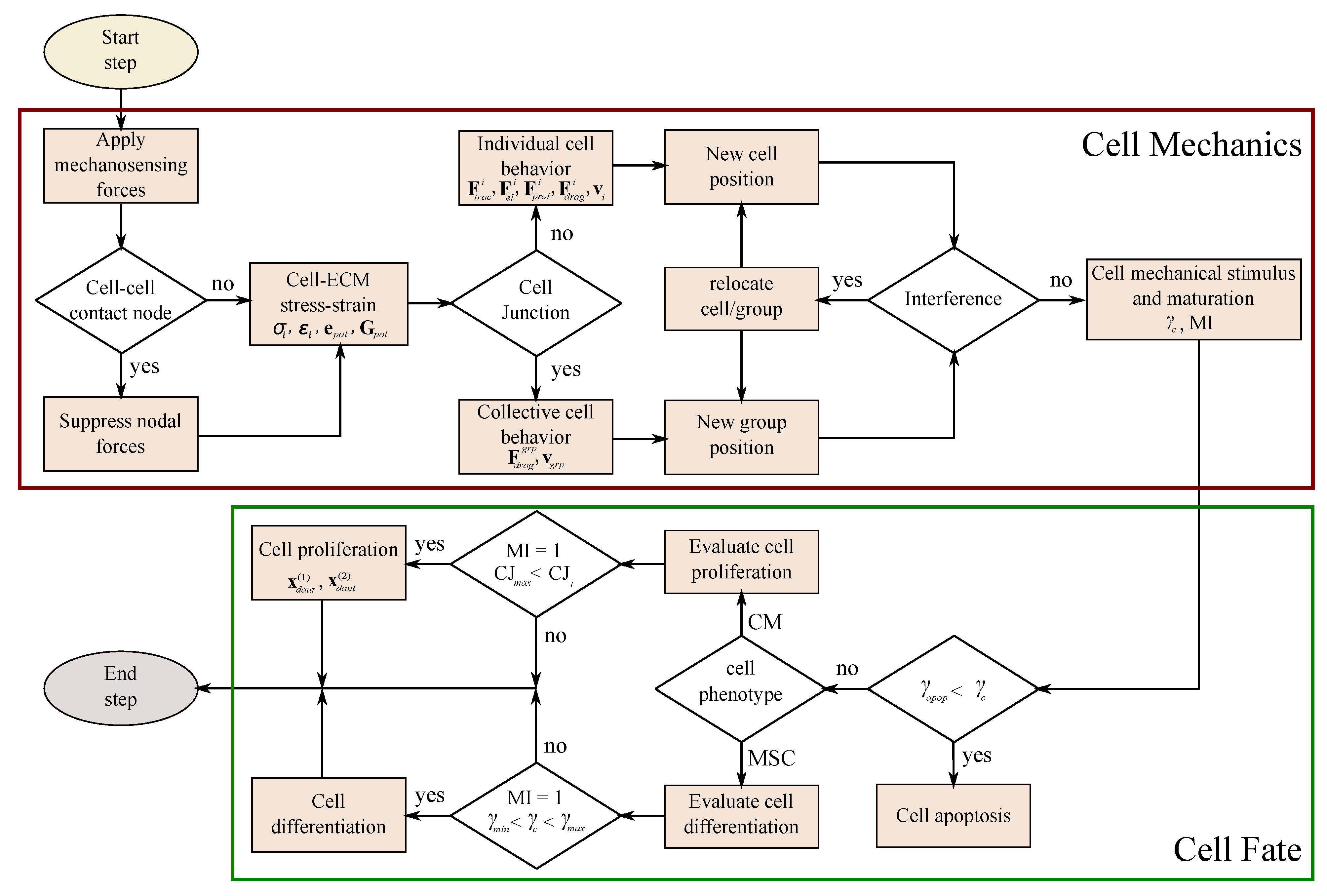
2.2. Cell Migration
2.3. Cell Interaction
2.4. Cell Fate
2.5. ECM Mechanical Behavior
2.6. Electric Field Generated by the PZE Fiber
2.7. Finite Element Model
3. Numerical Examples and Results
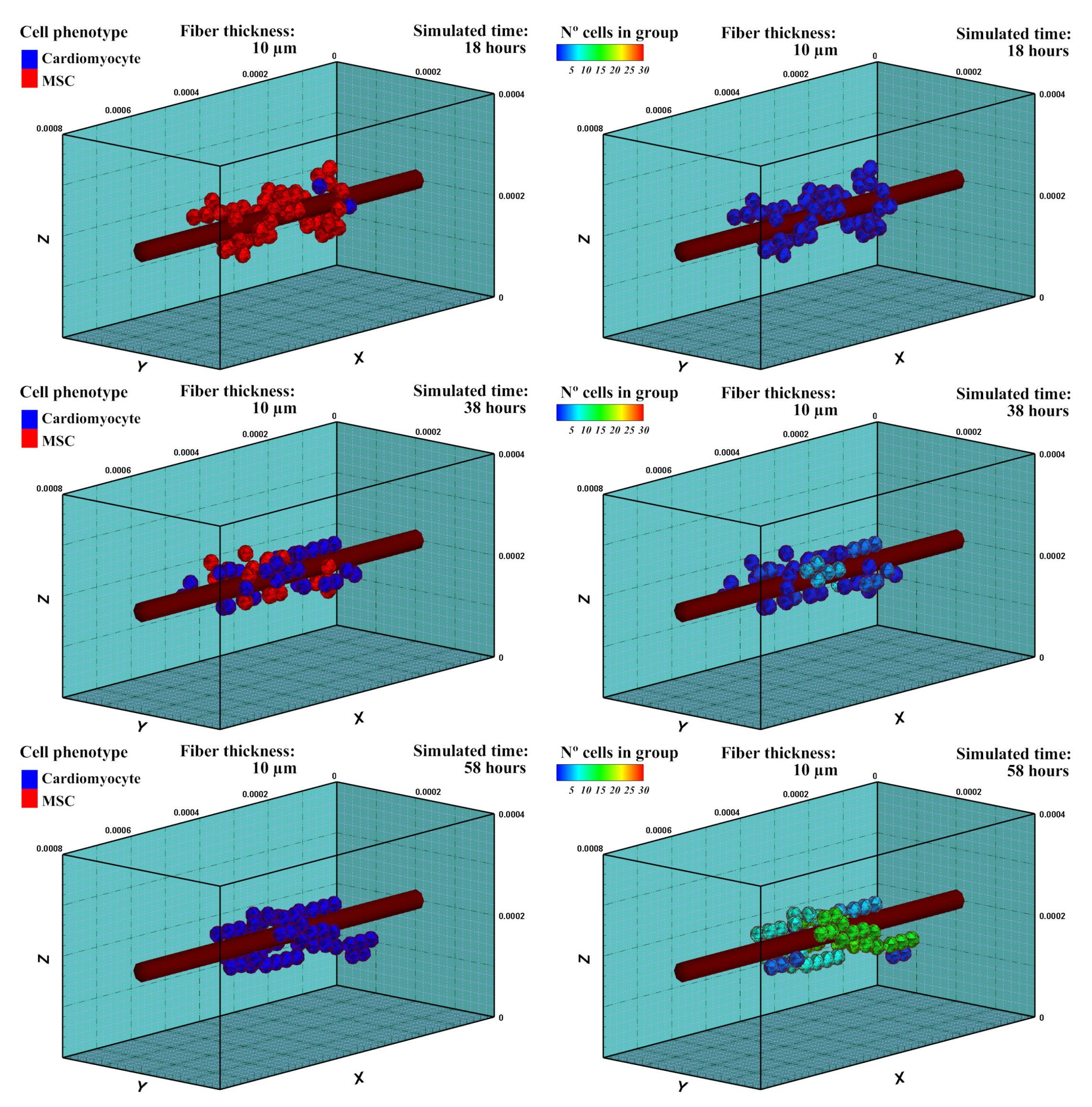
3.1. Mesenchymal Stem Cells Differentiation into Cardiac Cells
3.1.1. Description
3.1.2. Experiment Setup
3.1.3. Results
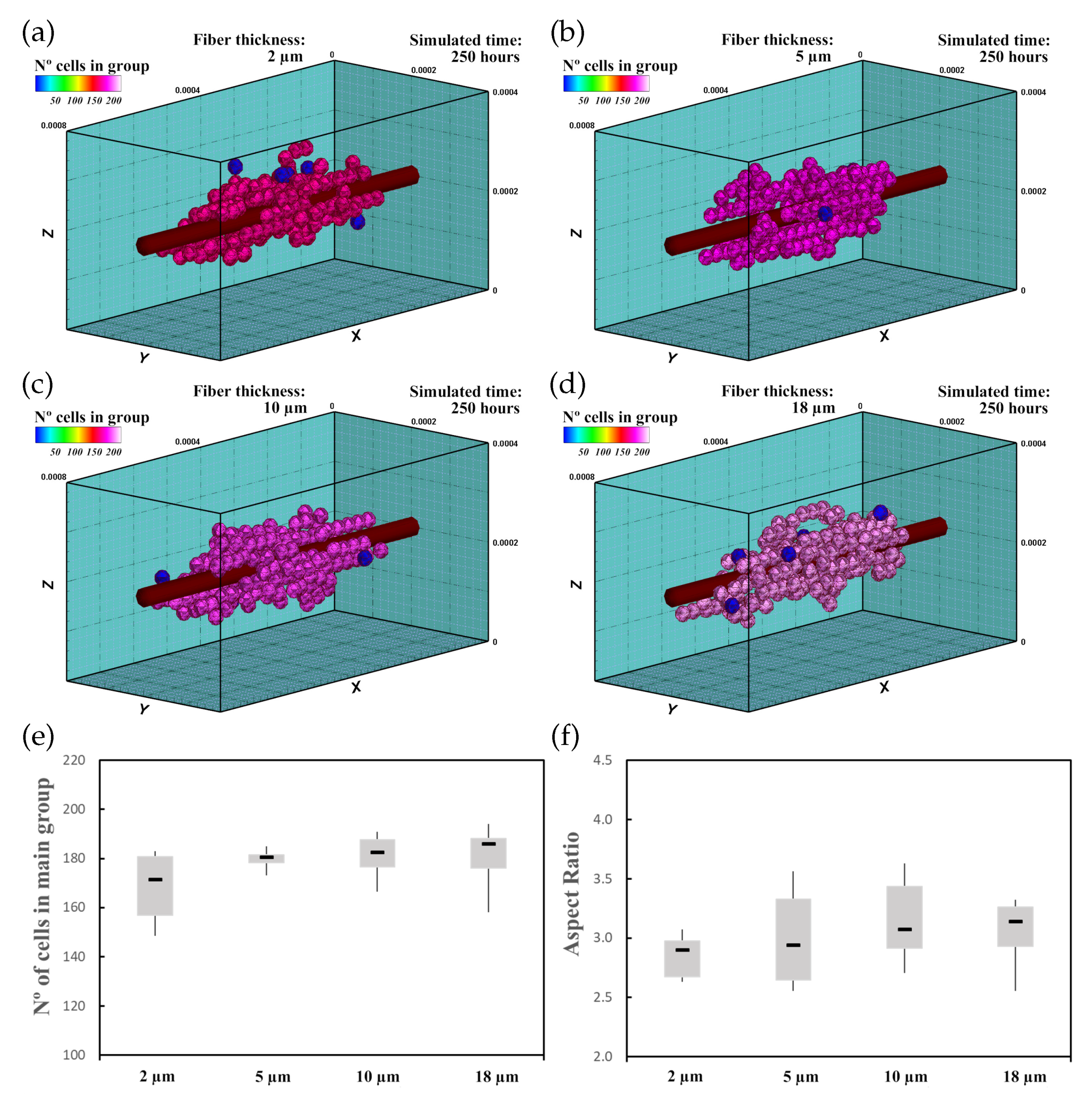
3.2. Fibered ECM
3.2.1. Description
3.2.2. Experiment Setup
3.2.3. Results
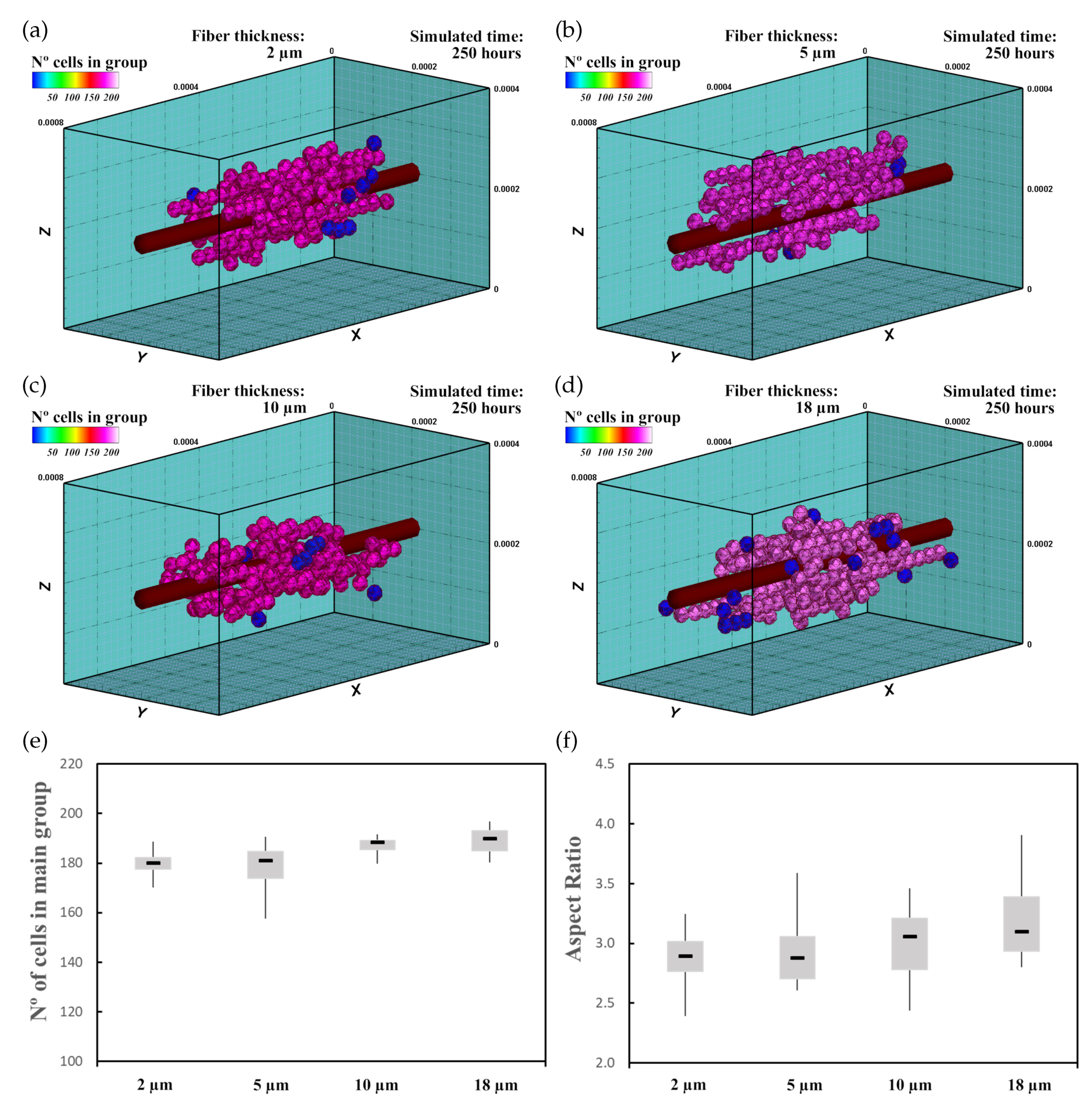
3.3. Mechanically Stimulated Fibered ECM
3.3.1. Description
3.3.2. Experiment Setup
3.3.3. Results
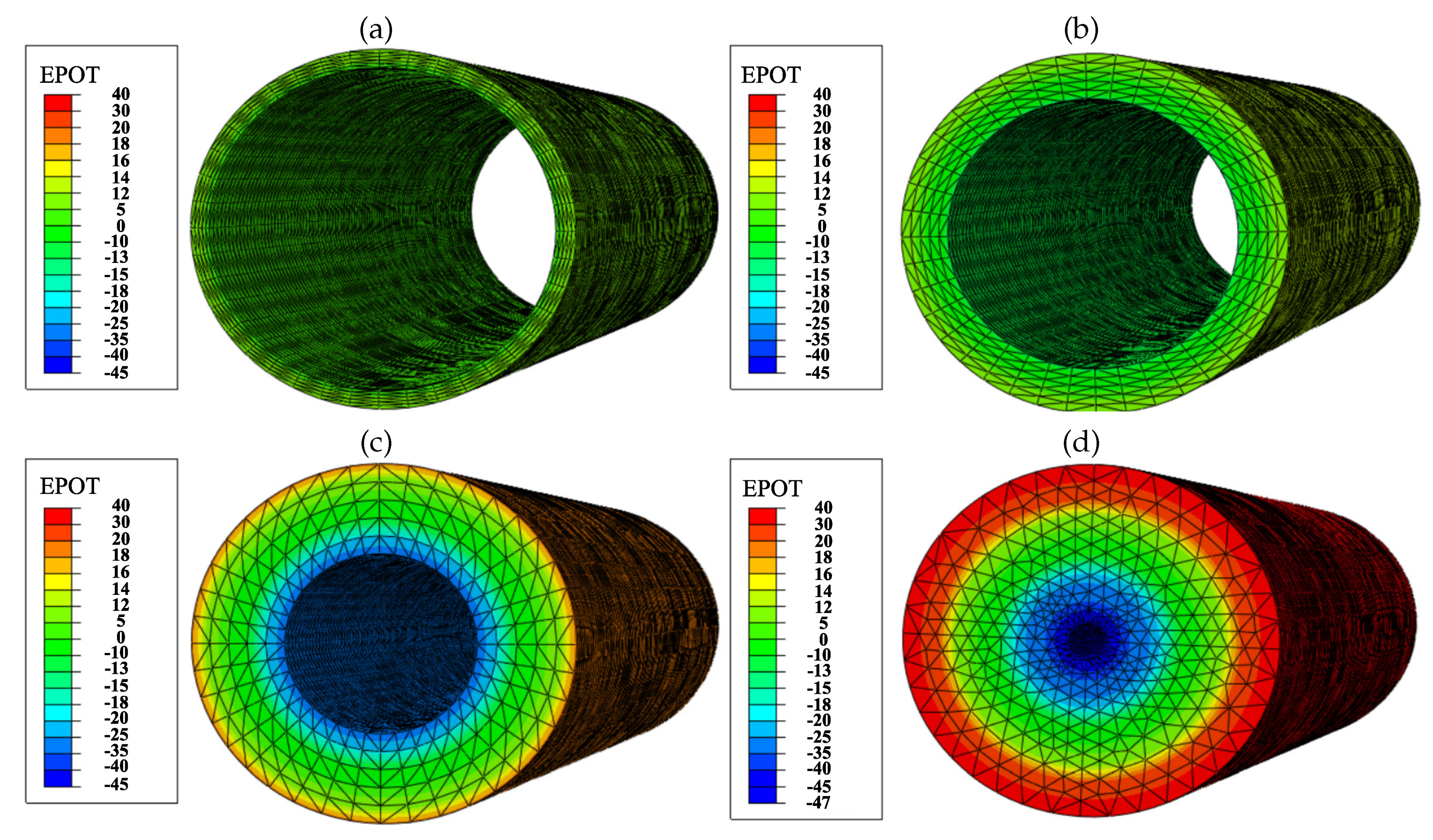
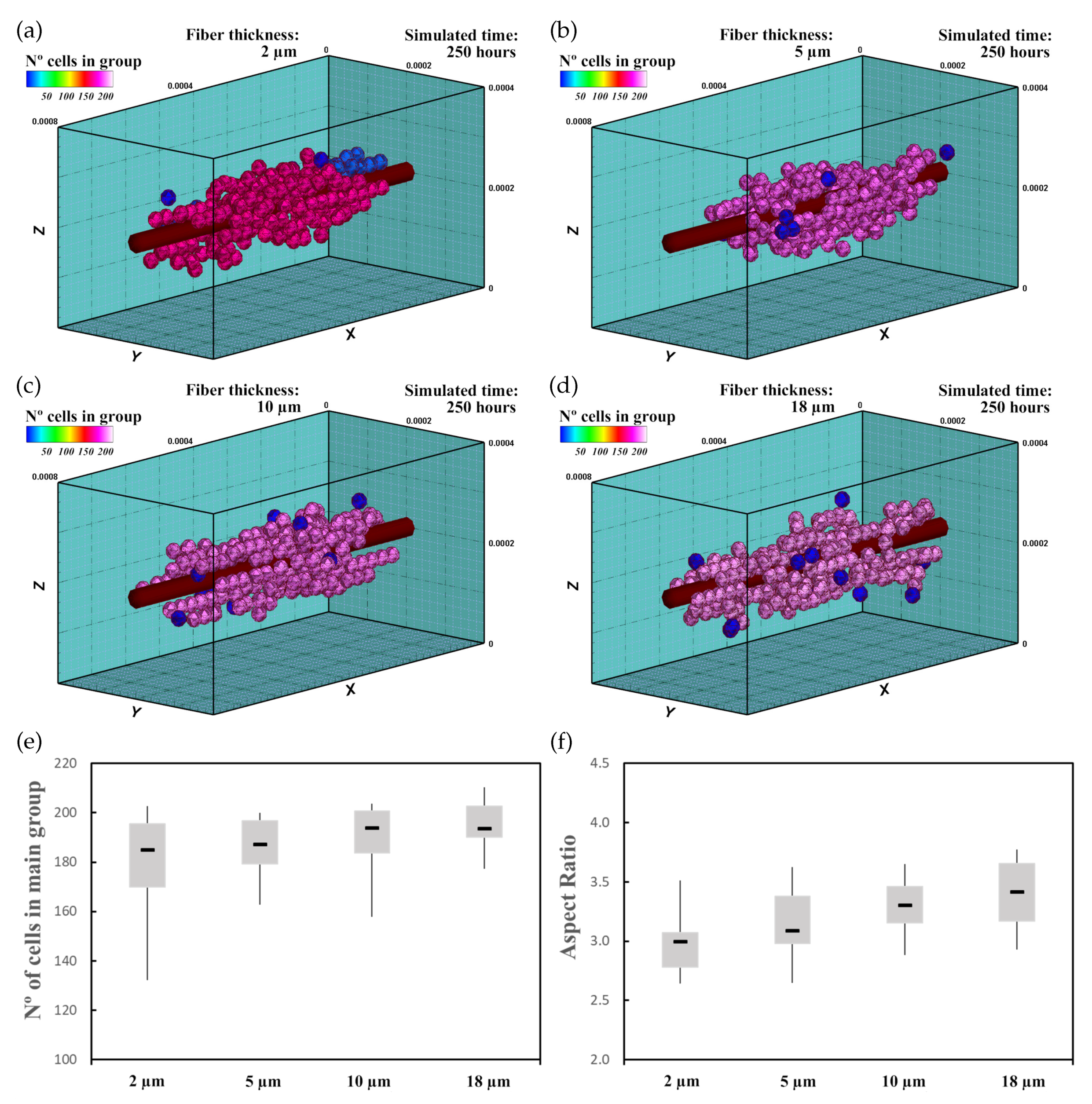
3.4. Mechanically Stimulated PZE Fibered ECM
3.4.1. Description
3.4.2. Experiment Setup
3.4.3. Results
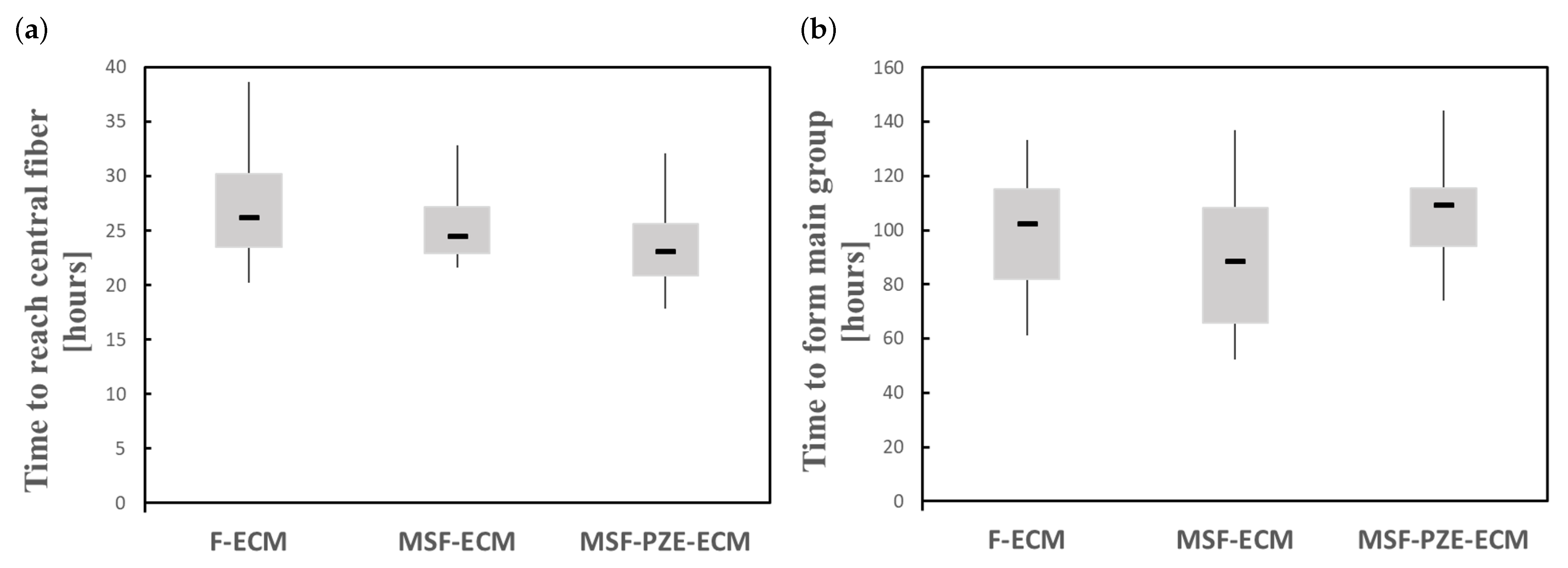
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Wang, J.H.C.; Thampatty, B.P. An Introductory Review of Cell Mechanobiology. Biomech. Model. Mechanobiol. 2006, 5, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Maul, T.M.; Chew, D.W.; Nieponice, A.; Vorp, D.A. Mechanical stimuli differentially control stem cell behavior: Morphology, proliferation, and differentiation. Biomech. Model. Mechanobiol. 2011, 10, 939–953. [Google Scholar] [CrossRef] [Green Version]
- Roth, S.; Hütter, G.; Mühlich, U.; Nassauer, B.; Zybell, L.; Kuna, M. Visualisation of User Defined Finite Elements with ABAQUS/Viewer. GACM Rep. 2012, 5, 7–14. [Google Scholar]
- Mayor, R.; Etienne-Manneville, S. The front and rear of collective cell migration. Nat. Rev. Mol. Cell Biol. 2016, 17, 97–109. [Google Scholar] [CrossRef] [Green Version]
- te Boekhorst, V.; Preziosi, L.; Friedl, P. Plasticity of Cell Migration In Vivo and In Silico. Annu. Rev. Cell Dev. Biol. 2016, 32, 491–526. [Google Scholar] [CrossRef]
- Bissell, M.J.; Rizki, A.; Mian, I.S. Tissue architecture: The ultimate regulator of breast epithelial function. Curr. Opin. Cell Biol. 2003, 15, 753. [Google Scholar] [CrossRef] [Green Version]
- Gumbiner, B.M. Cell Adhesion: The Molecular Basis of Tissue Architecture and Morphogenesis. Cell 1996, 84, 345–357. [Google Scholar] [CrossRef] [Green Version]
- Engler, A.J.; Sen, S.; Sweeney, H.L.; Discher, D.E. Matrix Elasticity Directs Stem Cell Lineage Specification. Cell 2006, 126, 677–689. [Google Scholar] [CrossRef] [Green Version]
- Huebsch, N.; Arany, P.R.; Mao, A.S.; Shvartsman, D.; Ali, O.A.; Bencherif, S.A.; Rivera-Feliciano, J.; Mooney, D.J. Harnessing traction-mediated manipulation of the cell/matrix interface to control stem-cell fate. Nat. Mater. 2010, 9, 518–526. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Guo, X.; Palmer, A.F.; Das, H.; Guan, J. High-efficiency matrix modulus-induced cardiac differentiation of human mesenchymal stem cells inside a thermosensitive hydrogel. Acta Biomater. 2012, 8, 3586–3595. [Google Scholar] [CrossRef]
- Yang, G.; Xiao, Z.; Ren, X.; Long, H.; Ma, K.; Qian, H.; Guo, Y. Obtaining spontaneously beating cardiomyocyte-like cells from adipose-derived stromal vascular fractions cultured on enzyme-crosslinked gelatin hydrogels. Sci. Rep. 2017, 7, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Yamaguchi, H.; Condeelis, J. Regulation of the actin cytoskeleton in cancer cell migration and invasion. Biochim. Et Biophys. Acta (BBA)—Mol. Cell Res. 2007, 1773, 642–652. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- van Helvert, S.; Storm, C.; Friedl, P. Mechanoreciprocity in cell migration. Nat. Cell Biol. 2018, 20, 8–20. [Google Scholar] [CrossRef]
- Chen, Q.Z.; Harding, S.E.; Ali, N.N.; Lyon, A.R.; Boccaccini, A.R. Biomaterials in cardiac tissue engineering: Ten years of research survey. Mater. Sci. Eng. R: Rep. 2008, 59, 1–37. [Google Scholar] [CrossRef]
- Fischer, S.; Glas, K.E. A Review of cardiac transplantation. Anesthesiol. Clin. 2013, 31, 383–403. [Google Scholar] [CrossRef]
- Stoppel, W.L.; Kaplan, D.L.; Black, L.D. Electrical and mechanical stimulation of cardiac cells and tissue constructs. Adv. Drug Deliv. Rev. 2016, 96, 135–155. [Google Scholar] [CrossRef] [Green Version]
- Radisic, M.; Park, H.; Shing, H.; Consi, T.; Schoen, F.J.; Langer, R.; Freed, L.E.; Vunjak-Novakovic, G. Functional assembly of engineered myocardium by electrical stimulation of cardiac myocytes cultured on scaffolds. Proc. Natl. Acad. Sci. USA 2004, 101, 18129–18134. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.; Shadrin, I.Y.; Lam, J.; Xian, H.Q.; Snodgrass, H.R.; Bursac, N. Tissue-engineered cardiac patch for advanced functional maturation of human ESC-derived cardiomyocytes. Biomaterials 2013, 34, 5813–5820. [Google Scholar] [CrossRef] [Green Version]
- Shadrin, I.Y.; Allen, B.W.; Qian, Y.; Jackman, C.P.; Carlson, A.L.; Juhas, M.E.; Bursac, N. Cardiopatch platform enables maturation and scale-up of human pluripotent stem cell-derived engineered heart tissues. Nat. Commun. 2017, 8, 1825. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jackman, C.P.; Ganapathi, A.M.; Asfour, H.; Qian, Y.; Allen, B.W.; Li, Y.; Bursac, N. Engineered cardiac tissue patch maintains structural and electrical properties after epicardial implantation. Biomaterials 2018, 159, 48–58. [Google Scholar] [CrossRef] [PubMed]
- Ott, H.C.; Matthiesen, T.S.; Goh, S.K.K.; Black, L.D.; Kren, S.M.; Netoff, T.I.; Taylor, D.A. Perfusion-decellularized matrix: Using nature’s platform to engineer a bioartificial heart. Nat. Med. 2008, 14, 213–221. [Google Scholar] [CrossRef]
- Di Meglio, F.; Nurzynska, D.; Romano, V.; Miraglia, R.; Belviso, I.; Sacco, A.M.; Barbato, V.; Di Gennaro, M.; Granato, G.; Maiello, C.; et al. Optimization of Human Myocardium Decellularization Method for the Construction of Implantable Patches. Tissue Eng. Part C Methods 2017, 23, 525–539. [Google Scholar] [CrossRef]
- Rao, L.; Qian, Y.; Khodabukus, A.; Ribar, T.; Bursac, N. Engineering human pluripotent stem cells into a functional skeletal muscle tissue. Nat. Commun. 2018, 9, 126. [Google Scholar] [CrossRef] [PubMed]
- Gavagnin, E.; Yates, C.A. Stochastic and Deterministic Modeling of Cell Migration. In Handbook of Statistics; Elsevier: Amsterdam, The Netherlands, 2018; Volume 39, pp. 37–91. [Google Scholar] [CrossRef]
- Carlier, A.; Skvortsov, G.A.; Hafezi, F.; Ferraris, E.; Patterson, J.; Koc, B.; Van Oosterwyck, H. Computational model-informed design and bioprinting of cell-patterned constructs for bone tissue engineering. Biofabrication 2016, 8, 025009. [Google Scholar] [CrossRef] [PubMed]
- Galbusera, F.; Cioffi, M.; Raimondi, M.T.; Pietrabissa, R. Computational modeling of combined cell population dynamics and oxygen transport in engineered tissue subject to interstitial perfusion. Comput. Methods Biomech. Biomed. Eng. 2007, 10, 279–287. [Google Scholar] [CrossRef] [PubMed]
- Galbusera, F.; Cioffi, M.; Raimondi, M.T. An in silico bioreactor for simulating laboratory experiments in tissue engineering. Biomed. Microdevices 2008, 10, 547–554. [Google Scholar] [CrossRef]
- Khayyeri, H.; Checa, S.; Tägil, M.; O’Brien, F.J.; Prendergast, P.J. Tissue differentiation in an in vivo bioreactor: In silico investigations of scaffold stiffness. J. Mater. Science. Mater. Med. 2010, 21, 2331–2336. [Google Scholar] [CrossRef] [PubMed]
- Sandino, C.; Planell, J.A.; Lacroix, D. A finite element study of mechanical stimuli in scaffolds for bone tissue engineering. J. Biomech. 2008, 41, 1005–1014. [Google Scholar] [CrossRef]
- Zaman, M.H.; Kamm, R.D.; Matsudaira, P.; Lauffenburger, D.A. Computational Model for Cell Migration in Three-Dimensional Matrices. Biophys. J. 2005, 89, 1389–1397. [Google Scholar] [CrossRef] [Green Version]
- Mousavi, S.J.; Doweidar, M.H.; Doblaré, M. Computational modelling and analysis of mechanical conditions on cell locomotion and cell–cell interaction. Comput. Methods Biomech. Biomed. Eng. 2014, 17, 678–693. [Google Scholar] [CrossRef]
- Ribeiro, F.O.; Gómez-Benito, M.J.; Folgado, J.; Fernandes, P.R.; García-Aznar, J.M. Computational model of mesenchymal migration in 3D under chemotaxis. Comput. Methods Biomech. Biomed. Eng. 2017, 20, 59–74. [Google Scholar] [CrossRef] [Green Version]
- Stéphanou, A.; Mylona, E.; Chaplain, M.; Tracqui, P. A computational model of cell migration coupling the growth of focal adhesions with oscillatory cell protrusions. J. Theor. Biol. 2008, 253, 701–716. [Google Scholar] [CrossRef]
- Marzban, B.; Yuan, H. The Effect of Thermal Fluctuation on the Receptor-Mediated Adhesion of a Cell Membrane to an Elastic Substrate. Membranes 2017, 7, 24. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Göktepe, S.; Abilez, O.J.; Parker, K.K.; Kuhl, E. A multiscale model for eccentric and concentric cardiac growth through sarcomerogenesis. J. Theor. Biol. 2010, 265, 433–442. [Google Scholar] [CrossRef] [PubMed]
- Shao, D.; Rappel, W.J.; Levine, H. Computational Model for Cell Morphodynamics. Phys. Rev. Lett. 2010, 105, 108104. [Google Scholar] [CrossRef]
- Mousavi, S.J.; Doweidar, M.H. A novel mechanotactic 3D modeling of cell morphology. Phys. Biol. 2014, 11, 046005. [Google Scholar] [CrossRef] [PubMed]
- Mousavi, S.J.; Hamdy Doweidar, M. Three-Dimensional Numerical Model of Cell Morphology during Migration in Multi-Signaling Substrates. PLoS ONE 2015, 10, e0122094. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Urdeitx, P.; Doweidar, M.H. Mechanical stimulation of cell microenvironment for cardiac muscle tissue regeneration: A 3D in-silico model. Comput. Mech. 2020, 66, 1003–1023. [Google Scholar] [CrossRef]
- Urdeitx, P.; Doweidar, M.H. A Computational Model for Cardiomyocytes Mechano-Electric Stimulation to Enhance Cardiac Tissue Regeneration. Mathematics 2020, 8, 1875. [Google Scholar] [CrossRef]
- Mousavi, S.J.; Doweidar, M.H. Role of mechanical cues in cell differentiation and proliferation: A 3D numerical model. PLoS ONE 2015, 10, e0124529. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Urdeitx, P.; Farzaneh, S.; Mousavi, S.J.; Doweidar, M.H. Role of oxygen concentration in the osteoblasts behavior: A finite element model. J. Mech. Med. Biol. 2020, 20, 1950064. [Google Scholar] [CrossRef]
- Dassault Systemes. Abaqus 6.14. 2014. Available online: https://www.3ds.com/products-services/simulia/services-support/support/documentation/ (accessed on 6 November 2020).
- Bernheim-Groswasser, A.; Prost, J.; Sykes, C. Mechanism of Actin-Based Motility: A Dynamic State Diagram. Biophys. J. 2005, 89, 1411–1419. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mogilner, A. Mathematics of cell motility: Have we got its number? J. Math. Biol. 2009, 58, 105–134. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Selmeczi, D.; Mosler, S.; Hagedorn, P.H.; Larsen, N.B.; Flyvbjerg, H. Cell Motility as Persistent Random Motion: Theories from Experiments. Biophys. J. 2005, 89, 912–931. [Google Scholar] [CrossRef] [Green Version]
- Reig, G.; Pulgar, E.; Concha, M.L. Cell migration: From tissue culture to embryos. Development 2014, 141, 1999–2013. [Google Scholar] [CrossRef] [Green Version]
- Ridley, A.J.; Schwartz, M.A.; Burridge, K.; Firtel, R.A.; Ginsberg, M.H.; Borisy, G.; Parsons, J.T.; Horwitz, A.R. Cell Migration: Integrating Signals from Front to Back. Science 2003. [Google Scholar] [CrossRef] [Green Version]
- Mousavi, S.J.; Doweidar, M.H.; Doblaré, M. 3D computational modelling of cell migration: A mechano-chemo-thermo-electrotaxis approach. J. Theor. Biol. 2013, 329, 64–73. [Google Scholar] [CrossRef]
- Mousavi, S.J.; Doblaré, M.; Doweidar, M.H. Computational modelling of multi-cell migration in a multi-signalling substrate. Phys. Biol. 2014, 11, 026002. [Google Scholar] [CrossRef]
- Mousavi, S.J.; Doweidar, M.H. Encapsulated piezoelectric nanoparticle–hydrogel smart material to remotely regulate cell differentiation and proliferation: A finite element model. Comput. Mech. 2019, 63, 471–489. [Google Scholar] [CrossRef]
- Mycielska, M.E.; Djamgoz, M.B.A. Cellular mechanisms of direct-current electric field effects: Galvanotaxis and metastatic disease. J. Cell Sci. 2004, 117, 1631–1639. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Z.; Watt, C.; Karystinou, A.; Roelofs, A.; McCaig, C.; Gibson, I.; De Bari, C. Directed migration of human bone marrow mesenchymal stem cells in a physiological direct current electric field. Eur. Cells Mater. 2011, 22, 344–358. [Google Scholar] [CrossRef] [PubMed]
- Frederich, B.J.; Timofeyev, V.; Thai, P.N.; Haddad, M.J.; Poe, A.J.; Lau, V.C.; Moshref, M.; Knowlton, A.A.; Sirish, P.; Chiamvimonvat, N. Electrotaxis of cardiac progenitor cells, cardiac fibroblasts, and induced pluripotent stem cell-derived cardiac progenitor cells requires serum and is directed via PI3K pathways. Heart Rhythm 2017, 14, 1685–1692. [Google Scholar] [CrossRef]
- Nishimura, K.Y.; Isseroff, R.R.; Nucciteili, R. Human keratinocytes migrate to the negative pole in direct current electric fields comparable to those measured in mammalian wounds. J. Cell Sci. 1996, 109, 199–207. [Google Scholar] [PubMed]
- Mousavi, S.J.; Doweidar, M.H. Numerical modeling of cell differentiation and proliferation in force-induced substrates via encapsulated magnetic nanoparticles. Comput. Methods Programs Biomed. 2016, 130, 106–117. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aragona, M.; Panciera, T.; Manfrin, A.; Giulitti, S.; Michielin, F.; Elvassore, N.; Dupont, S.; Piccolo, S. A mechanical checkpoint controls multicellular growth through YAP/TAZ regulation by actin-processing factors. Cell 2013, 154, 1047–1059. [Google Scholar] [CrossRef] [Green Version]
- Low, B.C.; Pan, C.Q.; Shivashankar, G.V.; Bershadsky, A.; Sudol, M.; Sheetz, M. YAP/TAZ as mechanosensors and mechanotransducers in regulating organ size and tumor growth. FEBS Lett. 2014, 588, 2663–2670. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, M. Electrical fields in wound healing—An overriding signal that directs cell migration. Semin. Cell Dev. Biol. 2009, 20, 674–682. [Google Scholar] [CrossRef]
- Abercrombie, M. Contact inhibition and malignancy. Nature 1979, 281, 259–262. [Google Scholar] [CrossRef]
- Walker, C.A.; Spinale, F.G. The structure and function of the cardiac myocyte: A review of fundamental concepts. J. Thorac. Cardiovasc. Surg. 1999, 118, 375–382. [Google Scholar] [CrossRef] [Green Version]
- Jackman, C.P.; Carlson, A.L.; Bursac, N. Dynamic culture yields engineered myocardium with near-adult functional output. Biomaterials 2016, 111, 66–79. [Google Scholar] [CrossRef] [Green Version]
- Tahara, N.; Brush, M.; Kawakami, Y. Cell migration during heart regeneration in zebrafish. Dev. Dyn. 2016. [Google Scholar] [CrossRef] [Green Version]
- Planat-Bénard, V.; Menard, C.; André, M.; Puceat, M.; Perez, A.; Garcia-Verdugo, J.M.; Pénicaud, L.; Casteilla, L. Spontaneous Cardiomyocyte Differentiation from Adipose Tissue Stroma Cells. Circ. Res. 2004, 94, 223–229. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ghafar-Zadeh, E.; Waldeisen, J.R.; Lee, L.P. Engineered approaches to the stem cell microenvironment for cardiac tissue regeneration. Lab A Chip 2011, 11, 3031. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hirt, M.N.; Boeddinghaus, J.; Mitchell, A.; Schaaf, S.; Börnchen, C.; Müller, C.; Schulz, H.; Hubner, N.; Stenzig, J.; Stoehr, A.; et al. Functional improvement and maturation of rat and human engineered heart tissue by chronic electrical stimulation. J. Mol. Cell. Cardiol. 2014, 74, 151–161. [Google Scholar] [CrossRef] [Green Version]
- Nunes, S.S.; Miklas, J.W.; Liu, J.; Aschar-Sobbi, R.; Xiao, Y.; Zhang, B.; Jiang, J.; Massé, S.; Gagliardi, M.; Hsieh, A.; et al. Biowire: A platform for maturation of human pluripotent stem cell–derived cardiomyocytes. Nat. Methods 2013, 10, 781–787. [Google Scholar] [CrossRef] [Green Version]
- Schmelter, M.; Ateghang, B.; Helmig, S.; Wartenberg, M.; Sauer, H. Embryonic stem cells utilize reactive oxygen species as transducers of mechanical strain-induced cardiovascular differentiation. FASEB J. 2006, 20, 1182–1184. [Google Scholar] [CrossRef]
- Camelliti, P.; McCulloch, A.D.; Kohl, P. Microstructured Cocultures of Cardiac Myocytes and Fibroblasts: A Two-Dimensional In Vitro Model of Cardiac Tissue. Microsc. Microanal. 2005, 11, 249–259. [Google Scholar] [CrossRef]
- Costa, K.D.; Lee, E.J.; Holmes, J.W. Creating Alignment and Anisotropy in Engineered Heart Tissue: Role of Boundary Conditions in a Model Three-Dimensional Culture System. Tissue Eng. 2003, 9, 567–577. [Google Scholar] [CrossRef]
- Sassoli, C.; Pini, A.; Mazzanti, B.; Quercioli, F.; Nistri, S.; Saccardi, R.; Orlandini, S.Z.; Bani, D.; Formigli, L. Mesenchymal stromal cells affect cardiomyocyte growth through juxtacrine Notch-1/Jagged-1 signaling and paracrine mechanisms: Clues for cardiac regeneration. J. Mol. Cell. Cardiol. 2011, 51, 399–408. [Google Scholar] [CrossRef]
- Kresh, J.Y.; Chopra, A. Intercellular and extracellular mechanotransduction in cardiac myocytes. Pflugers Arch.—Eur. J. Physiol. 2011. [Google Scholar] [CrossRef] [PubMed]
- Holtzman, N.G.; Schoenebeck, J.J.; Tsai, H.J.; Yelon, D. Endocardium is necessary for cardiomyocyte movement during heart tube assembly. Development 2007, 134, 2379–2386. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ye, J.; Boyle, A.J.; Shih, H.; Sievers, R.E.; Wang, Z.E.; Gormley, M.; Yeghiazarians, Y. CD45-positive cells are not an essential component in cardiosphere formation. Cell Tissue Res. 2013, 351, 201–205. [Google Scholar] [CrossRef] [PubMed]
- Wu, Q.Q.; Chen, Q. Mechanoregulation of chondrocyte proliferation, maturation, and hypertrophy: Ion-channel dependent transduction of matrix deformation signals. Exp. Cell Res. 2000, 256, 383–391. [Google Scholar] [CrossRef] [PubMed]
- Delaine-Smith, R.M.; Reilly, G.C. Mesenchymal stem cell responses to mechanical stimuli. Muscles Ligaments Tendons J. 2012, 2, 169–180. [Google Scholar]
- Ulrich, T.A.; De Juan Pardo, E.M.; Kumar, S. The mechanical rigidity of the extracellular matrix regulates the structure, motility, and proliferation of glioma cells. Cancer Res. 2009, 69, 4167–4174. [Google Scholar] [CrossRef] [Green Version]
- Ahuja, P.; Sdek, P.; MacLellan, W.R. Cardiac Myocyte Cell Cycle Control in Development, Disease, and Regeneration. Physiol. Rev. 2007, 87, 521–544. [Google Scholar] [CrossRef] [Green Version]
- Kang, K.T.; Park, J.H.; Kim, H.J.; Lee, H.M.; Lee, K.I.; Jung, H.H.; Lee, H.Y.; Jang, J.W. Study of Tissue Differentiation of Mesenchymal Stem Cells by Mechanical Stimuli and an Algorithm for Bone Fracture Healing. Tissue Eng. Regen. Med. 2011, 8, 359–370. [Google Scholar]
- Roveimiab, Z.; Lin, F.; Anderson, J.E. Emerging Development of Microfluidics-Based Approaches to Improve Studies of Muscle Cell Migration. Tissue Eng. Part B Rev. 2019, 25, 30–45. [Google Scholar] [CrossRef]
- Asumda, F.Z. Towards the development of a reliable protocol for mesenchymal stem cell cardiomyogenesis. Stem Cell Discov. 2013, 3, 13–21. [Google Scholar] [CrossRef] [Green Version]
- Yutzey, K.E. Cardiomyocyte Proliferation. Circ. Res. 2017, 120, 627–629. [Google Scholar] [CrossRef]
- Zhang, R.; Han, P.; Yang, H.; Ouyang, K.; Lee, D.; Lin, Y.F.; Ocorr, K.; Kang, G.; Chen, J.; Stainier, D.Y.R.; et al. In vivo cardiac reprogramming contributes to zebrafish heart regeneration. Nature 2013, 498, 497–501. [Google Scholar] [CrossRef]
- Tibbitt, M.W.; Anseth, K.S. Hydrogels as extracellular matrix mimics for 3D cell culture. Biotechnol. Bioeng. 2009, 103, 655–663. [Google Scholar] [CrossRef] [Green Version]
- Ikonen, L.; Kerkelä, E.; Metselaar, G.; Stuart, M.C.A.; de Jong, M.R.; Aalto-Setälä, K. 2D and 3D Self-Assembling Nanofiber Hydrogels for Cardiomyocyte Culture. Biomed. Res. Int. 2013, 2013, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Silva, C.C.; Pinheiro, A.G.; Figueiró, S.D.; Góes, J.C.; Sasaki, J.M.; Miranda, M.A.; Sombra, A.S. Piezoelectric properties of collagen-nanocrystalline hydroxyapatite composites. J. Mater. Sci. 2002, 37, 2061–2070. [Google Scholar] [CrossRef]
- Pietronave, S.; Zamperone, A.; Oltolina, F.; Colangelo, D.; Follenzi, A.; Novelli, E.; Diena, M.; Pavesi, A.; Consolo, F.; Fiore, G.B.; et al. Monophasic and biphasic electrical stimulation induces a precardiac differentiation in progenitor cells isolated from human heart. Stem Cells Dev. 2014, 23, 888–898. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Banks, T.A.; Luckman, P.S.B.; Frith, J.E.; Cooper-White, J.J. Effects of electric fields on human mesenchymal stem cell behaviour and morphology using a novel multichannel device. Integr. Biol. 2015, 7, 693–712. [Google Scholar] [CrossRef]
- Baumgartner, S.; Halbach, M.; Krausgrill, B.; Maass, M.; Srinivasan, S.P.; Sahito, R.G.A.; Peinkofer, G.; Nguemo, F.; Müller-Ehmsen, J.; Hescheler, J. Electrophysiological and morphological maturation of murine fetal cardiomyocytes during electrical stimulation in vitro. J. Cardiovasc. Pharmacol. Ther. 2015, 20, 104–112. [Google Scholar] [CrossRef]
- Schäfer, A.; Radmacher, M. Influence of myosin II activity on stiffness of fibroblast cells. Acta Biomater. 2005, 1, 273–280. [Google Scholar] [CrossRef]
- Darling, E.M.; Topel, M.; Zauscher, S.; Vail, T.P.; Guilak, F. Viscoelastic properties of human mesenchymally-derived stem cells and primary osteoblasts, chondrocytes, and adipocytes. J. Biomech. 2008, 41, 454–464. [Google Scholar] [CrossRef] [Green Version]
- Discher, D.E. Tissue Cells Feel and Respon to the Stiffness of Their Substrate. Science 2005, 310, 1139–1143. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ramtani, S. Mechanical modelling of cell/ECM and cell/cell interactions during the contraction of a fibroblast-populated collagen microsphere: Theory and model simulation. J. Biomech. 2004, 37, 1709–1718. [Google Scholar] [CrossRef]
- Rodriguez, M.L.; Graham, B.T.; Pabon, L.M.; Han, S.J.; Murry, C.E.; Sniadecki, N.J.; Pabon, L.M.; Murry, C.E.; Graham, B.T.; Han, S.J.; et al. Measuring the Contractile Forces of Human Induced Pluripotent Stem Cell-Derived Cardiomyocytes With Arrays of Microposts. J. Biomech. Eng. 2014, 136, 051005. [Google Scholar] [CrossRef] [Green Version]
- Gardel, M.L.; Sabass, B.; Ji, L.; Danuser, G.; Schwarz, U.S.; Waterman, C.M. Traction stress in focal adhesions correlates biphasically with actin retrograde flow speed. J. Cell Biol. 2008, 183, 999–1005. [Google Scholar] [CrossRef] [PubMed]
- Bhana, B.; Iyer, R.K.; Chen, W.L.K.; Zhao, R.; Sider, K.L.; Likhitpanichkul, M.; Simmons, C.A.; Radisic, M. Influence of substrate stiffness on the phenotype of heart cells. Biotechnol. Bioeng. 2010, 105, 1148–1160. [Google Scholar] [CrossRef] [PubMed]
- Mathur, A.B.; Collinsworth, A.M.; Reichert, W.M.; Kraus, W.E.; Truskey, G.A. Endothelial, cardiac muscle and skeletal muscle exhibit different viscous and elastic properties as determined by atomic force microscopy. J. Biomech. 2001, 34, 1545–1553. [Google Scholar] [CrossRef]
- Huang, Y.X.; Zheng, X.J.; Kang, L.L.; Chen, X.Y.; Liu, W.J.; Huang, B.T.; Wu, Z.J. Quantum dots as a sensor for quantitative visualization of surface charges on single living cells with nano-scale resolution. Biosens. Bioelectron. 2011, 26, 2114–2118. [Google Scholar] [CrossRef]
- Fearnley, C.J.; Roderick, H.L.; Bootman, M.D. Calcium Signaling in Cardiac Myocytes. Cold Spring Harb. Perspect. Biol. 2011, 3, a004242. [Google Scholar] [CrossRef] [Green Version]
- Ye, L.; Zhang, S.; Greder, L.; Dutton, J.; Keirstead, S.A.; Lepley, M.; Zhang, L.; Kaufman, D.; Zhang, J. Effective Cardiac Myocyte Differentiation of Human Induced Pluripotent Stem Cells Requires VEGF. PLoS ONE 2013, 8, e53764. [Google Scholar] [CrossRef]
- Hatzistergos, K.E.; Quevedo, H.; Oskouei, B.N.; Hu, Q.; Feigenbaum, G.S.; Margitich, I.S.; Mazhari, R.; Boyle, A.J.; Zambrano, J.P.; Rodriguez, J.E.; et al. Bone marrow mesenchymal stem cells stimulate cardiac stem cell proliferation and differentiation. Circ. Res. 2010, 107, 913–922. [Google Scholar] [CrossRef] [Green Version]
- Tandon, N.; Cannizzaro, C.; Chao, P.P.H.G.H.G.; Maidhof, R.; Marsano, A.; Au, H.T.H.; Radisic, M.; Vunjak-Novakovic, G. Electrical stimulation systems for cardiac tissue engineering. Nat. Protoc. 2009, 4, 155–173. [Google Scholar] [CrossRef] [Green Version]
- Yim, E.K.F.; Darling, E.M.; Kulangara, K.; Guilak, F.; Leong, K.W. Nanotopography-induced changes in focal adhesions, cytoskeletal organization, and mechanical properties of human mesenchymal stem cells. Biomaterials 2010, 31, 1299–1306. [Google Scholar] [CrossRef] [Green Version]
- Bian, W.; Bursac, N. Engineered skeletal muscle tissue networks with controllable architecture. Biomaterials 2009, 30, 1401–1412. [Google Scholar] [CrossRef] [Green Version]
- Sheehy, S.P.; Grosberg, A.; Parker, K.K. The contribution of cellular mechanotransduction to cardiomyocyte form and function. Biomech. Model. Mechanobiol. 2012, 11, 1227–1239. [Google Scholar] [CrossRef] [Green Version]
- Lee, E.J.; Holmes, J.W.; Costa, K.D. Remodeling of engineered tissue anisotropy in response to altered loading conditions. Ann. Biomed. Eng. 2008, 36, 1322–1334. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Heidi Au, H.T.; Cui, B.; Chu, Z.E.; Veres, T.; Radisic, M. Cell culture chips for simultaneous application of topographical and electrical cues enhance phenotype of cardiomyocytes. Lab Chip 2009, 9, 564–575. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Bai, X.; Ding, Y.; Lee, I.S. Electrical stimulation as a novel tool for regulating cell behavior in tissue engineering. Biomater. Res. 2019, 23, 25. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Formigli, L.; Francini, F.; Nistri, S.; Margheri, M.; Luciani, G.; Naro, F.; Silvertown, J.D.; Orlandini, S.Z.; Meacci, E.; Bani, D. Skeletal myoblasts overexpressing relaxin improve differentiation and communication of primary murine cardiomyocyte cell cultures. J. Mol. Cell. Cardiol. 2009, 47, 335–345. [Google Scholar] [CrossRef] [PubMed]



| Parameter | Description | Value | Ref. |
|---|---|---|---|
| Stiffness of the cell passive elements | 2.8 kPa | [90,91] | |
| Stiffness of the actin-myosin machinery | 7.0 kPa | [90,92] | |
| Maximum strain of the cell | 0.09 | [38,93] | |
| Minimum strain of the cell | −0.09 | [38,93] | |
| Maximum contractile stress exerted by the actin-myosin machinery | 0.25 kPa | [94,95] | |
| ECM Poisson ratio | 0.4 | [96,97] | |
| ECM viscosity | 1000 Pa·s | [30,77] | |
| k | Binding constant of the cell | mol | [30,51] |
| Number of available receptors of the cell | [30,51] | ||
| Saturation value of electric field | [54] | ||
| Saturation value of cell charge density | [98,99] | ||
| Cell ligand concentration | mol | [30,51] | |
| Minimum projection bound to consider cell adhesion | 0.50 | [70] | |
| Minimum time needed for maturation | 6 days | [64,81] | |
| Time proportionality | 200 days | [79,90] | |
| Minimum mechanical stimuli for cardiac cell differentiation | −0.04 | [10,16] | |
| Maximum mechanical stimuli for cardiac cell differentiation | −0.01 | [10,16] | |
| Maximum mechanical stimuli that trigger apoptosis | 0.6 | [14,79] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Urdeitx, P.; Doweidar, M.H. Enhanced Piezoelectric Fibered Extracellular Matrix to Promote Cardiomyocyte Maturation and Tissue Formation: A 3D Computational Model. Biology 2021, 10, 135. https://doi.org/10.3390/biology10020135
Urdeitx P, Doweidar MH. Enhanced Piezoelectric Fibered Extracellular Matrix to Promote Cardiomyocyte Maturation and Tissue Formation: A 3D Computational Model. Biology. 2021; 10(2):135. https://doi.org/10.3390/biology10020135
Chicago/Turabian StyleUrdeitx, Pau, and Mohamed H. Doweidar. 2021. "Enhanced Piezoelectric Fibered Extracellular Matrix to Promote Cardiomyocyte Maturation and Tissue Formation: A 3D Computational Model" Biology 10, no. 2: 135. https://doi.org/10.3390/biology10020135
APA StyleUrdeitx, P., & Doweidar, M. H. (2021). Enhanced Piezoelectric Fibered Extracellular Matrix to Promote Cardiomyocyte Maturation and Tissue Formation: A 3D Computational Model. Biology, 10(2), 135. https://doi.org/10.3390/biology10020135







