Mechanisms of Flexible Information Sharing through Noisy Oscillations
Abstract
:Simple Summary
Abstract
1. Introduction
- Zero-delay-coupled quasi-cycles can exhibit robust phase-synchronization even in more realistic cases where asymmetry and heterogeneity are considered;
- The system of two coupled quasi-cycles oscillations does not show dynamic connectivity. The information is predominantly shared from one network to the other in the asymmetric inter-areal connectivity case and in the heterogeneous population case. Therefore it lacks flexibility in information sharing;
- When the system is in the noisy limit cycle regime, we may observe dynamic connectivity highlighted by the presence of two out-of-phase locking states for a single and fixed value of the inter-areal coupling. Information can then be shared from one network to the other and vice versa: there is a flexibility in information sharing. Such flexibility persists in the presence of asymmetry and heterogeneity but with some bias.
2. Methods
2.1. The Model
2.2. Dynamics of a Single Stochastic Wilson–Cowan Network
2.3. Dynamics of Two Coupled Stochastic Wilson–Cowan Networks
2.4. Phase Locking
2.5. Delayed Mutual Information
3. Results
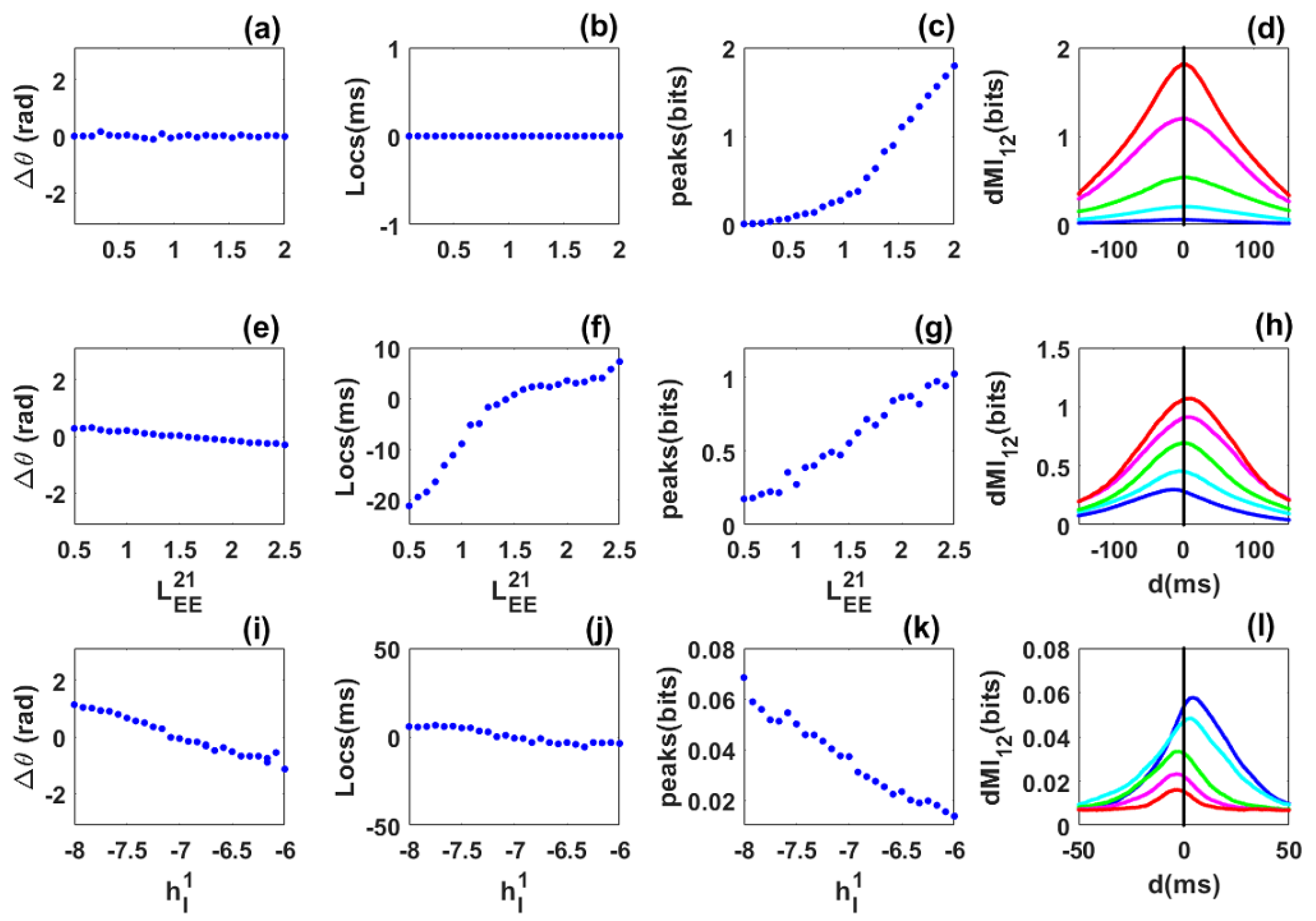
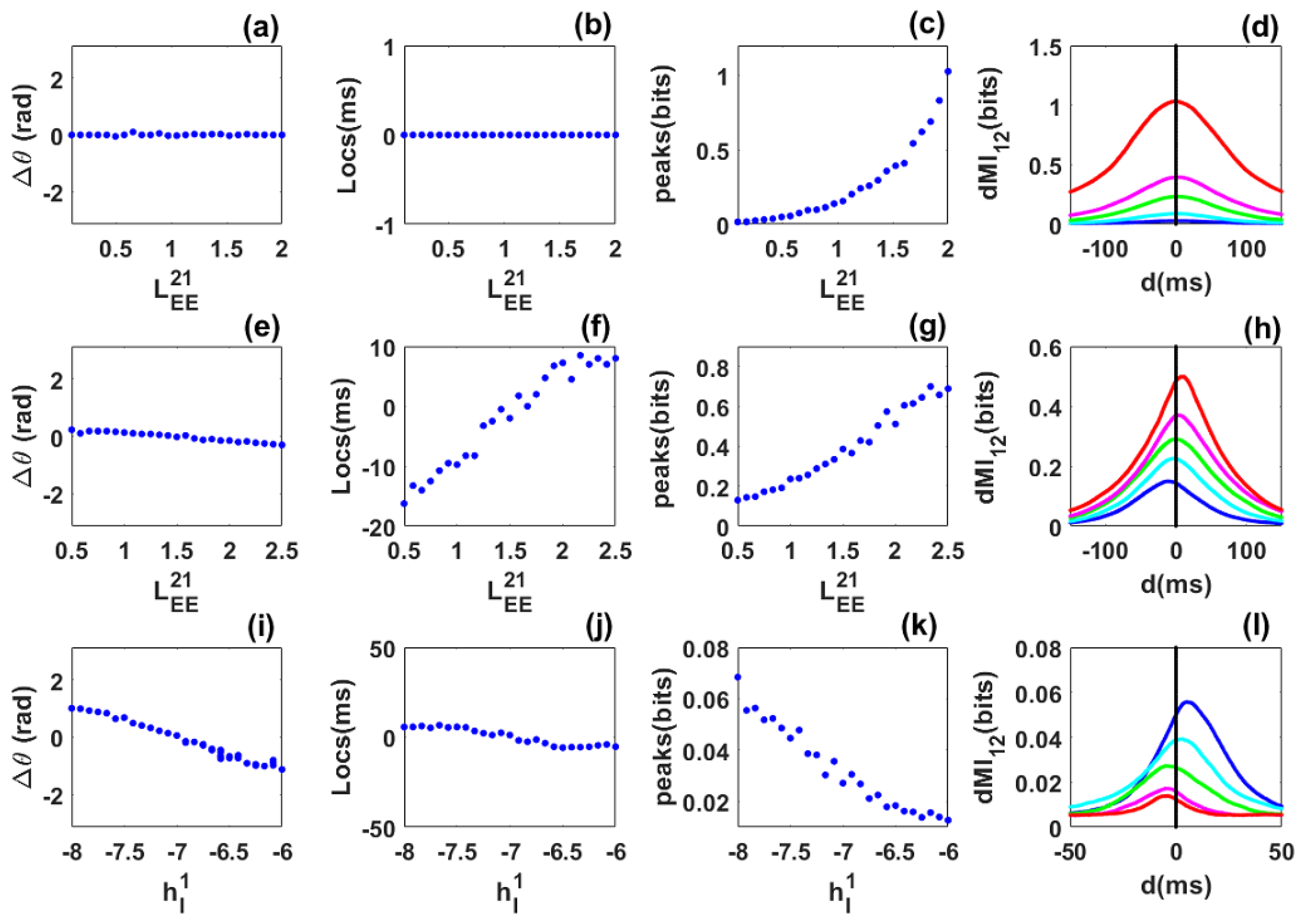
3.1. Information Sharing between Quasi-Cycle Rhythms
3.2. Information Sharing between Quasi-Cycles: Envelope-Phase Decomposition Framework
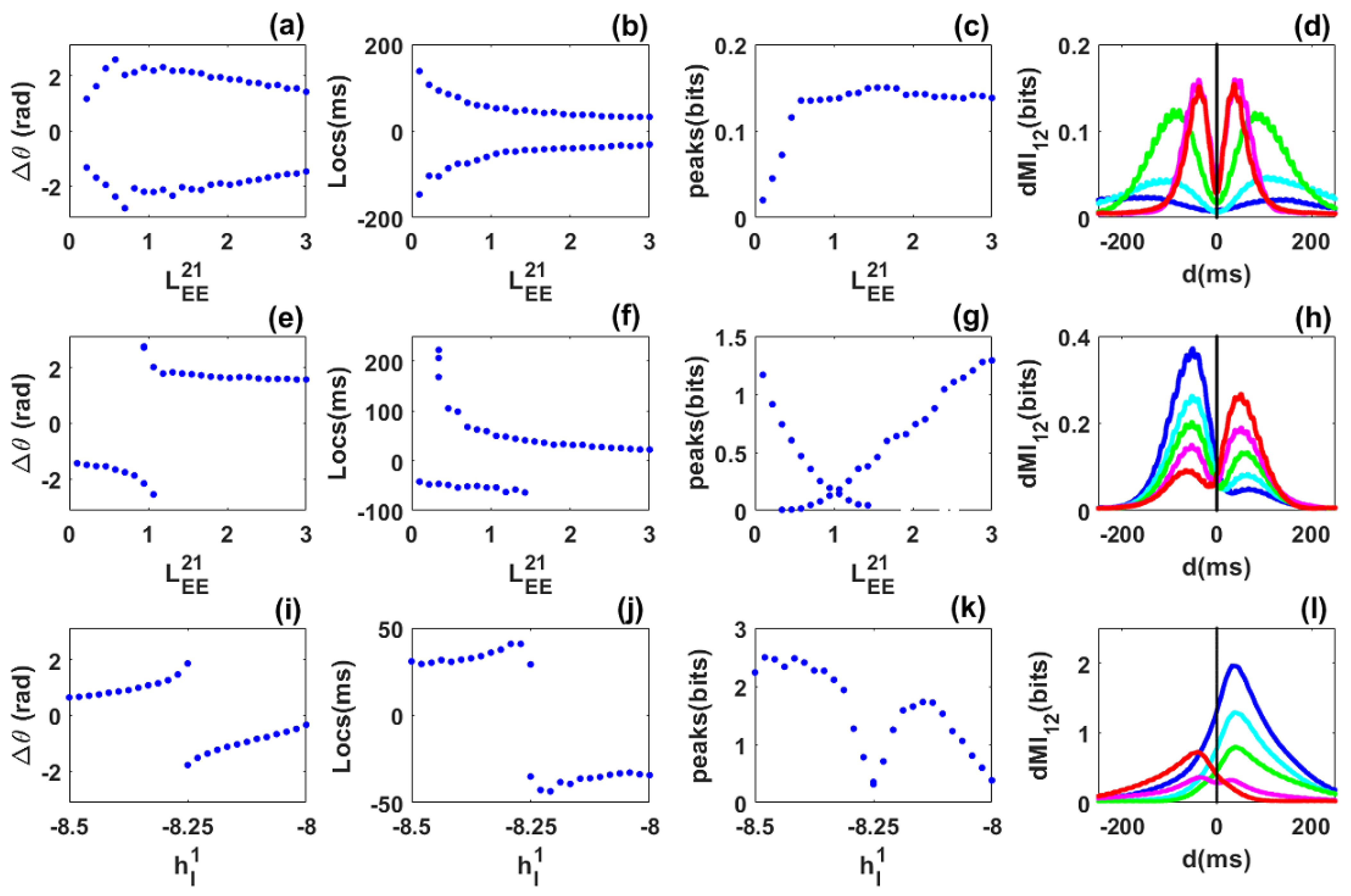
3.3. Information Sharing through Noisy Limit Cycles
4. Discussion
4.1. Summary of Results
4.2. Limitations and Future Work
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Buzsaki, G. Rhythms of the Brain; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Xing, D.; Shen, Y.; Burns, S.; Yeh, C.I.; Shapley, R.; Li, W. Stochastic generation of gamma-band activity in primary visual cortex of awake and anesthetized monkeys. J. Neurosci. 2012, 32, 13873–13880a. [Google Scholar] [CrossRef] [Green Version]
- Fries, P.; Nikolić, D.; Singer, W. The gamma cycle. Trends Neurosci. 2007, 30, 309–316. [Google Scholar] [CrossRef]
- Jia, X.; Kohn, A. Gamma rhythms in the brain. PLoS Biol 2011, 9, e1001045. [Google Scholar] [CrossRef]
- Buzsáki, G.; Wang, X.J. Mechanisms of gamma oscillations. Annu. Rev. Neurosci. 2012, 35, 203–225. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fries, P. A mechanism for cognitive dynamics: Neuronal communication through neuronal coherence. Trends Cogn. Sci. 2005, 9, 474–480. [Google Scholar] [CrossRef] [PubMed]
- Bastos, A.M.; Vezoli, J.; Fries, P. Communication through coherence with inter-areal delays. Curr. Opin. Neurobiol. 2015, 31, 173–180. [Google Scholar] [CrossRef] [Green Version]
- Fries, P. Rhythms for cognition: Communication through coherence. Neuron 2015, 88, 220–235. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Strogatz, S. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; Studies in Nonlinearity; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Wallace, E.; Benayoun, M.; Van Drongelen, W.; Cowan, J.D. Emergent oscillations in networks of stochastic spiking neurons. PLoS ONE 2011, 6, e14804. [Google Scholar]
- Burns, S.P.; Xing, D.; Shapley, R.M. Is gamma-band activity in the local field potential of V1 cortex a “clock” or filtered noise? J. Neurosci. 2011, 31, 9658–9664. [Google Scholar] [CrossRef] [Green Version]
- Powanwe, A.S.; Longtin, A. Determinants of Brain Rhythm Burst Statistics. Sci. Rep. 2019, 9, 18335. [Google Scholar] [CrossRef]
- Pikovsky, A.; Kurths, J.; Rosenblum, M.; Kurths, J. Synchronization: A Universal Concept in Nonlinear Sciences; Cambridge University Press: Cambridge, UK, 2003; Volume 12. [Google Scholar]
- Winfree, A.T. Biological rhythms and the behavior of populations of coupled oscillators. J. Theor. Biol. 1967, 16, 15–42. [Google Scholar] [CrossRef]
- Acebrón, J.A.; Bonilla, L.L.; Vicente, C.J.P.; Ritort, F.; Spigler, R. The Kuramoto model: A simple paradigm for synchronization phenomena. Rev. Mod. Phys. 2005, 77, 137. [Google Scholar] [CrossRef] [Green Version]
- Rodrigues, F.A.; Peron, T.K.D.; Ji, P.; Kurths, J. The Kuramoto model in complex networks. Phys. Rep. 2016, 610, 1–98. [Google Scholar] [CrossRef] [Green Version]
- Schuster, H.; Wagner, P. A model for neuronal oscillations in the visual cortex. Biol. Cybern. 1990, 64, 77–82. [Google Scholar] [CrossRef]
- Daffertshofer, A.; van Wijk, B. On the influence of amplitude on the connectivity between phases. Front. Neuroinform. 2011, 5, 6. [Google Scholar] [CrossRef] [Green Version]
- Dumont, G.; Gutkin, B. Macroscopic phase resetting-curves determine oscillatory coherence and signal transfer in inter-coupled neural circuits. PLoS Comput. Biol. 2019, 15, e1007019. [Google Scholar] [CrossRef]
- Varela, F.; Lachaux, J.P.; Rodriguez, E.; Martinerie, J. The brainweb: Phase synchronization and large-scale integration. Nat. Rev. Neurosci. 2001, 2, 229–239. [Google Scholar] [CrossRef]
- Powanwe, A.S.; Longtin, A. Phase dynamics of delay-coupled quasi-cycles with application to brain rhythms. Phys. Rev. Res. 2020, 2, 043067. [Google Scholar] [CrossRef]
- Battaglia, D.; Brunel, N.; Hansel, D. Temporal decorrelation of collective oscillations in neural networks with local inhibition and long-range excitation. Phys. Rev. Lett. 2007, 99, 238106. [Google Scholar] [CrossRef] [Green Version]
- Witt, A.; Palmigiano, A.; Neef, A.; El Hady, A.; Wolf, F.; Battaglia, D. Controlling the oscillation phase through precisely timed closed-loop optogenetic stimulation: A computational study. Front. Neural Circuits 2013, 7, 49. [Google Scholar] [CrossRef] [Green Version]
- Battaglia, D.; Witt, A.; Wolf, F.; Geisel, T. Dynamic effective connectivity of inter-areal brain circuits. PLoS Comput. Biol. 2012, 8, e1002438. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Greenwood, P.E.; McDonnell, M.D.; Ward, L.M. A kuramoto coupling of quasi-cycle oscillators with application to neural networks. J. Coupled Syst. Multiscale Dyn. 2016, 4, 1–13. [Google Scholar] [CrossRef]
- Palmigiano, A.; Geisel, T.; Wolf, F.; Battaglia, D. Flexible information routing by transient synchrony. Nat. Neurosci. 2017, 20, 1014. [Google Scholar] [CrossRef]
- Schreiber, T. Measuring information transfer. Phys. Rev. Lett. 2000, 85, 461. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Deschle, N.; Daffertshofer, A.; Battaglia, D.; Martens, E.A. Directed flow of information in chimera states. Front. Appl. Math. Stat. 2019, 5, 28. [Google Scholar] [CrossRef]
- Byrne, Á.; O’Dea, R.D.; Forrester, M.; Ross, J.; Coombes, S. Next-generation neural mass and field modeling. J. Neurophysiol. 2020, 123, 726–742. [Google Scholar] [CrossRef] [PubMed]
- Lowet, E.; Roberts, M.J.; Peter, A.; Gips, B.; De Weerd, P. A quantitative theory of gamma synchronization in macaque V1. eLife 2017, 6, e26642. [Google Scholar] [CrossRef]
- Pariz, A.; Fischer, I.; Valizadeh, A.; Mirasso, C. Transmission delays and frequency detuning can regulate information flow between brain regions. PLoS Comput. Biol. 2021, 17, e1008129. [Google Scholar] [CrossRef] [PubMed]
- Kirst, C.; Timme, M.; Battaglia, D. Dynamic information routing in complex networks. Nat. Commun. 2016, 7, 11061. [Google Scholar] [CrossRef] [PubMed] [Green Version]

| Network Parameters | Description | Values |
|---|---|---|
| recurrent excitation of each network | 27.4/30.4 | |
| feedback inhibition of each network | 26.3 | |
| feedback excitation of each network | 32 | |
| recurrent inhibition of each network | 1.3 | |
| decay rate of excitatory neurons | 0.1 ms−1 | |
| decay rate of inhibitory neurons | 0.2 ms−1 | |
| scaling coefficient of the E population response function | 1 | |
| scaling coefficient of the I population response function | 2 | |
| number of excitatory neurons | 80,000 | |
| number of inhibitory neurons | 20,000 | |
| external input to the E population of each network | −3.8 | |
| external input to the I population of network 1 | see caption Figure 1, Figure 2, Figure 3 and Figure 4 | |
| external input to the I population of network 2 | see caption Figure 1, Figure 2, Figure 3 and Figure 4 | |
| long-range connection from to | see caption Figure 2, Figure 3 and Figure 4 | |
| long-range connection from to | see caption Figure 2, Figure 3 and Figure 4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Powanwe, A.S.; Longtin, A. Mechanisms of Flexible Information Sharing through Noisy Oscillations. Biology 2021, 10, 764. https://doi.org/10.3390/biology10080764
Powanwe AS, Longtin A. Mechanisms of Flexible Information Sharing through Noisy Oscillations. Biology. 2021; 10(8):764. https://doi.org/10.3390/biology10080764
Chicago/Turabian StylePowanwe, Arthur S., and Andre Longtin. 2021. "Mechanisms of Flexible Information Sharing through Noisy Oscillations" Biology 10, no. 8: 764. https://doi.org/10.3390/biology10080764
APA StylePowanwe, A. S., & Longtin, A. (2021). Mechanisms of Flexible Information Sharing through Noisy Oscillations. Biology, 10(8), 764. https://doi.org/10.3390/biology10080764







