Digital Reconstructions Using Linear Regression: How Well Can It Estimate Missing Shape Data from Small Damaged Areas?
Abstract
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample
| Sample Origin | Total | Males | Females | Digitalization Technique | Collection |
|---|---|---|---|---|---|
| African Americans | 20 | 9 | 11 | CT scan [19] | Terry collection of the Natural History Museum (Washington, DC, USA) |
| Spanish | 11 | 8 | 3 | Photogrammetry [23] | Olóriz Collection at the Universidad Complutense de Madrid (Madrid, Spain) |
| Italian | 77 | 43 | 34 | Photogrammetry [23] | Anthropological Museum of Florence (University of Florence, Florence, Italy) |
| 42 | 16 | 26 | Photogrammetry [23] | Museum of Anthropology G. Sergi (Sapienza University of Rome, Rome, Italy) |
2.2. Data Acquisition
| Number | Landmark | Definition |
|---|---|---|
| 1 | Inferior zygotemporale | Most inferior point in the temporozygomatic suture |
| 2 | Superior zygotemporale | Most superior point in the temporozygomatic suture |
| 3 | Frontomalare temporale | Most posterior point in the frontozygomatic suture |
| 4 | Frontomalare orbitale | Most anterior point in the frontozygomatic suture |
| 5 | Zygomaxillare orbitale | Most superior point in the zygomaticomaxillary suture |
| 6 | Inferior Zygomaxillare | Most inferior point in the zygomaticomaxillary suture |
| 7 | Inferior zygosphenoid1 | Most inferior point in the zygomaticosphenoid suture, in the orbit |
2.3. Identifying Outliers
2.4. Simulation Design
2.5. Testing Accuracy within Each Case
2.6. Testing Accuracy across Cases
2.7. Evaluating the Population Effect
3. Results
3.1. Accuracy for the Reconstruction Method in Each Case
3.2. Accuracy for the Reconstruction Method across all Cases
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Claes, P.; Vandermeulen, D.; De Greef, S.; Willems, G.; Clement, J.G.; Suetens, P. Bayesian Estimation of Optimal Craniofacial Reconstructions. Forensic Sci. Int. 2010, 201, 146–152. [Google Scholar] [CrossRef] [PubMed]
- Gunz, P.; Mitteroecker, P.; Neubauer, S.; Weber, G.W.; Bookstein, F.L. Principles for the Virtual Reconstruction of Hominin Crania. J. Hum. Evol. 2009, 57, 48–62. [Google Scholar] [CrossRef] [PubMed]
- Guyomarc’h, P.; Dutailly, B.; Charton, J.; Santos, F.; Desbarats, P.; Coqueugniot, H. Anthropological Facial Approximation in Three Dimensions (AFA3D): Computer-Assisted Estimation of the Facial Morphology Using Geometric Morphometrics. J. Forensic Sci. 2014, 59, 1502–1516. [Google Scholar] [CrossRef] [PubMed]
- Jurda, M.; Urbanová, P.; Chmelík, J. Digital Restoration of Fragmentary Human Skeletal Remains: Testing the Feasibility of Virtual Reality. J. Forensic Leg. Med. 2019, 66, 50–57. [Google Scholar] [CrossRef] [PubMed]
- Mori, T.; Profico, A.; Reyes-Centeno, H.; Harvati, K. Frontal Bone Virtual Reconstruction and Geometric Morphometric Analysis of the Mid-Pleistocene Hominin KNM-OG 45500 (Olorgesailie, Kenya). J. Anthropol. Sci. 2020, 98, 49–72. [Google Scholar] [CrossRef] [PubMed]
- Senck, S.; Bookstein, F.L.; Benazzi, S.; Kastner, J.; Weber, G.W. Virtual Reconstruction of Modern and Fossil Hominoid Crania: Consequences of Reference Sample Choice. Anat. Rec. 2015, 298, 827–841. [Google Scholar] [CrossRef]
- Shui, W.; Zhou, M.; Maddock, S.; Ji, Y.; Deng, Q.; Li, K.; Fan, Y.; Li, Y.; Wu, X. A Computerized Craniofacial Reconstruction Method for an Unidentified Skull Based on Statistical Shape Models. Multimed. Tools Appl. 2020, 79, 25589–25611. [Google Scholar] [CrossRef]
- Godinho, R.M.; O’Higgins, P.; Gonçalves, C. Assessing the Reliability of Virtual Reconstruction of Mandibles. Am. J. Phys. Anthropol. 2020, 172, 723–734. [Google Scholar] [CrossRef] [PubMed]
- Benazzi, S.; Senck, S. Comparing 3-Dimensional Virtual Methods for Reconstruction in Craniomaxillofacial Surgery. J. Oral Maxillofac. Surg. 2011, 69, 1184–1194. [Google Scholar] [CrossRef]
- Neeser, R.; Ackermann, R.R.; Gain, J. Comparing the Accuracy and Precision of Three Techniques Used for Estimating Missing Landmarks When Reconstructing Fossil Hominin Crania. Am. J. Phys. Anthropol. 2009, 140, 1–18. [Google Scholar] [CrossRef]
- Miranda, G.E.; Wilkinson, C.; Roughley, M.; Beaini, T.L.; Melani, R.F.H. Assessment of Accuracy and Recognition of Three-Dimensional Computerized Forensic Craniofacial Reconstruction. PLoS ONE 2018, 13, e0196770. [Google Scholar] [CrossRef] [PubMed]
- Gietzen, T.; Brylka, R.; Achenbach, J.; Hebel, K.Z.; Schömer, E.; Botsch, M.; Schwanecke, U.; Schulze, R. A Method for Automatic Forensic Facial Reconstruction Based on Dense Statistics of Soft Tissue Thickness. PLoS ONE 2019, 14, e0210257. [Google Scholar] [CrossRef] [PubMed]
- Amano, H.; Kikuchi, T.; Morita, Y.; Kondo, O.; Suzuki, H.; De León, M.S.P.; Zollikofer, C.P.E.; Bastir, M.; Stringer, C.; Ogihara, N. Virtual Reconstruction of the Neanderthal Amud 1 Cranium. Am. J. Phys. Anthropol. 2015, 158, 185–197. [Google Scholar] [CrossRef]
- Hefner, J.T. Cranial Nonmetric Variation and Estimating Ancestry. J. Forensic Sci. 2009, 54, 985–995. [Google Scholar] [CrossRef] [PubMed]
- Relethford, J.H. Population-Specific Deviations of Global Human Craniometric Variation from a Neutral Model. Am. J. Phys. Anthropol. 2010, 142, 105–111. [Google Scholar] [CrossRef]
- Von Cramon-Taubadel, N.; Lycett, S.J. Brief Communication: Human Cranial Variation Fits Iterative Founder Effect Model with African Origin. Am. J. Phys. Anthropol. 2008, 136, 108–113. [Google Scholar] [CrossRef]
- Von Cramon-Taubadel, N. Evolutionary Insights into Global Patterns of Human Cranial Diversity: Population History, Climatic and Dietary Effects. J. Anthropol. Sci. 2014, 92, 43–77. [Google Scholar] [CrossRef]
- Von Cramon-Taubadel, N. Revisiting the Homoiology Hypothesis: The Impact of Phenotypic Plasticity on the Reconstruction of Human Population History from Craniometric Data. J. Hum. Evol. 2009, 57, 179–190. [Google Scholar] [CrossRef]
- Copes, L. Comparative and Experimental Investigations of Cranial Robusticity in Mid-Pleistocene Hominins. Master’s Thesis, Arizona State University, Tempe, AZ, USA, 2012. [Google Scholar]
- Chui Chui, W.-C. Estudio Antropológico de La Colección de Cráneos Federico Olóriz. Ph.D. Thesis, Univesidad Complutense de Madrid, Madrid, Spain, 2017. [Google Scholar]
- Rubini, M.; Scarani, P. Studio Antropologico e Patologico Su 38 Crani Di Individui Deceduti Durante La Prima Metà Del XIX Secolo Presso Il Manicomio Dell’ospedale Di S. Orsola in Bologna. Patologie Associate e Variabilità Dei Caratteri Metrici e Discontinui. Riv. Antropol. 1989, 67, 273–2986. [Google Scholar] [CrossRef]
- Moggi-Cecchi, J.; Stanyon, R. Il Museo Di Storia Naturale Dell’Universitá Degli Studi Di Firenze: Volume V: Le Collezioni Antropologiche Ed Etnologiche. Il Museo Di Storia Naturale Dell’Universitá Degli Studi Di Firenze, 1–331. Mus. Storia Nat. Univ. Degli Studi Firenze 2014, 23, 1–331. [Google Scholar]
- Del Bove, A.; Profico, A.; Riga, A.; Bucchi, A.; Lorenzo, C. A Geometric Morphometric Approach to the Study of Sexual Dimorphism in the Modern Human Frontal Bone. Am. J. Phys. Anthropol. 2020, 173, 643–654. [Google Scholar] [CrossRef] [PubMed]
- Goswami, A.; Watanabe, A.; Felice, R.N.; Bardua, C.; Fabre, A.C.; Polly, P.D. High-Density Morphometric Analysis of Shape and Integration: The Good, the Bad, and the Not-Really-a-Problem. Integr. Comp. Biol. 2019, 59, 669–683. [Google Scholar] [CrossRef] [PubMed]
- Profico, A.; Schlager, S.; Valoriani, V.; Buzi, C.; Melchionna, M.; Veneziano, A.; Raia, P.; Moggi-Cecchi, J.; Manzi, G. Package ‘Arothron’. Am. J. Phys. Anthropol. 2018, 166, 979–986. [Google Scholar] [CrossRef] [PubMed]
- Schlager, S.; Jefferis, G.; Ian, D. Packege Morpho; R Package Version 3.0.6. 2019. Available online: https://CRAN.R-project.org/package=Morpho (accessed on 18 March 2021).
- Buikstra, E.J.; Ubelaker, D.H. Standards for Data Collection from Human Skeletal Remains; Arkansas Archeological Survey Press: Fayetteville, AR, USA, 1994. [Google Scholar]
- Franklin, D.; Freedman, L.; Milne, N.; Oxnard, C.E. A Geometric Morphometric Study of Sexual Dimorphism in the Crania of Indigenous Southern Africans. S. Afr. J. Sci. 2006, 102, 229–238. [Google Scholar]
- Adams, D.C.; Collyer, M.L.; Kaliontzopoulou, A. Geomorph: Software for Geometric Morphometric Analysis. R Package Version 3.0.6. 2019. Available online: https://CRAN.R-project.org/package=geomorph (accessed on 18 March 2021).
- Arbour, J.H.; Brown, C.M. Incomplete Specimens in Geometric Morphometric Analyses. Methods Ecol. Evol. 2014, 5, 16–26. [Google Scholar] [CrossRef]
- Oettlé, A.C.; Demeter, F.P.; L’abbé, E.N. Ancestral Variations in the Shape and Size of the Zygoma. Anat. Rec. 2017, 300, 196–208. [Google Scholar] [CrossRef] [PubMed]
- Inoue, M.; Ono, T.; Kameo, Y.; Sasaki, F.; Ono, T.; Adachi, T.; Nakashima, T. Forceful Mastication Activates Osteocytes and Builds a Stout Jawbone. Sci. Rep. 2019, 9, 4404. [Google Scholar] [CrossRef]
- Steen, S.L.; Lane, R.W. Evaluation of Habitual Activities among Two Alaskan Eskimo Populations Based on Musculoskeletal Stress Markers. Int. J. Osteoarchaeol. 1998, 8, 341–353. [Google Scholar] [CrossRef]
- Gunz, P.; Mitteroecker, P.; Bookstein, F.L.; Weber, G.W. Computer-Aided Reconstruction of Incomplete Human Crania Using Statistical and Geometrical Estimation Methods. Enter Past Comput. Appl. Quant. Methods Archaeol. 2004, 1227, 92–94. [Google Scholar]

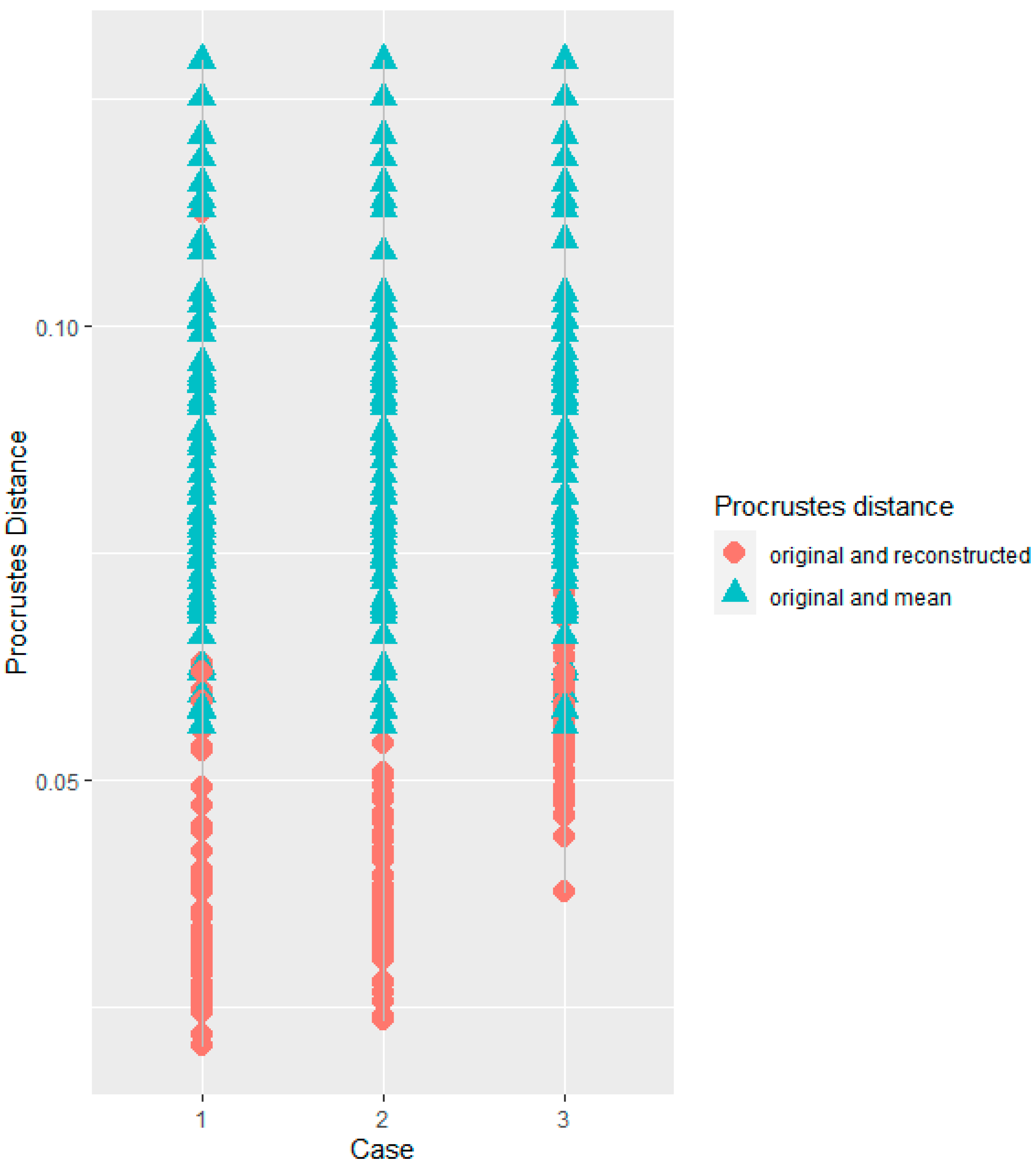

| Procrustes Distance Comparison | Case 1–Case 2 | Case 1–Case 3 | Case 2–Case 3 |
|---|---|---|---|
| Original-Reconstructed Landmark sets in the complete sample | 0.002 (0.6) | −0.016 (p < 0.01) | 0.018 (p < 0.01) |
| Original-Reconstructed Landmark sets in the Italian sample | 0.002 (0.8) | −0.017 (p < 0.01) | −0.017 (p < 0.01) |
| Original-Mean Landmark sets in the complete sample | 0.002 (0.8) | −0.008 (0.02) | −0.009 (p < 0.01) |
| Original-Mean Landmark sets in the Italian sample | −0.001 (0.8) | −0.009 (p < 0.01) | −0.004 (p < 0.01) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bucchi, A.; Del Bove, A.; López-Lázaro, S.; Quevedo-Díaz, F.; Fonseca, G.M. Digital Reconstructions Using Linear Regression: How Well Can It Estimate Missing Shape Data from Small Damaged Areas? Biology 2022, 11, 1741. https://doi.org/10.3390/biology11121741
Bucchi A, Del Bove A, López-Lázaro S, Quevedo-Díaz F, Fonseca GM. Digital Reconstructions Using Linear Regression: How Well Can It Estimate Missing Shape Data from Small Damaged Areas? Biology. 2022; 11(12):1741. https://doi.org/10.3390/biology11121741
Chicago/Turabian StyleBucchi, Ana, Antonietta Del Bove, Sandra López-Lázaro, Fernanda Quevedo-Díaz, and Gabriel M. Fonseca. 2022. "Digital Reconstructions Using Linear Regression: How Well Can It Estimate Missing Shape Data from Small Damaged Areas?" Biology 11, no. 12: 1741. https://doi.org/10.3390/biology11121741
APA StyleBucchi, A., Del Bove, A., López-Lázaro, S., Quevedo-Díaz, F., & Fonseca, G. M. (2022). Digital Reconstructions Using Linear Regression: How Well Can It Estimate Missing Shape Data from Small Damaged Areas? Biology, 11(12), 1741. https://doi.org/10.3390/biology11121741







