Influence of Graft Positioning during the Latarjet Procedure on Shoulder Stability and Articular Contact Pressure: Computational Analysis of the Bone Block Effect
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Geometric Model
2.2. Finite Element Models
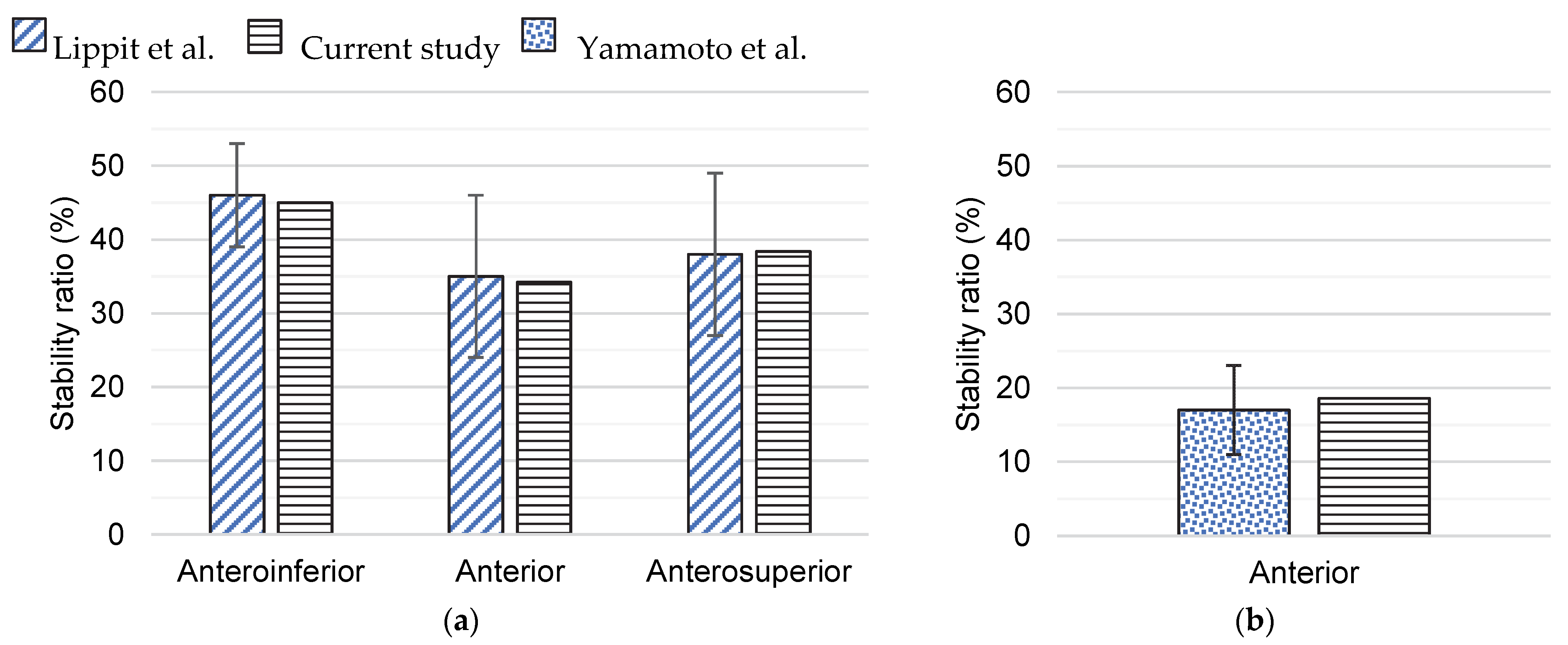
2.3. Validation of Finite Element Models
2.4. Analysis of the Medial–Lateral Bone Graft Positions
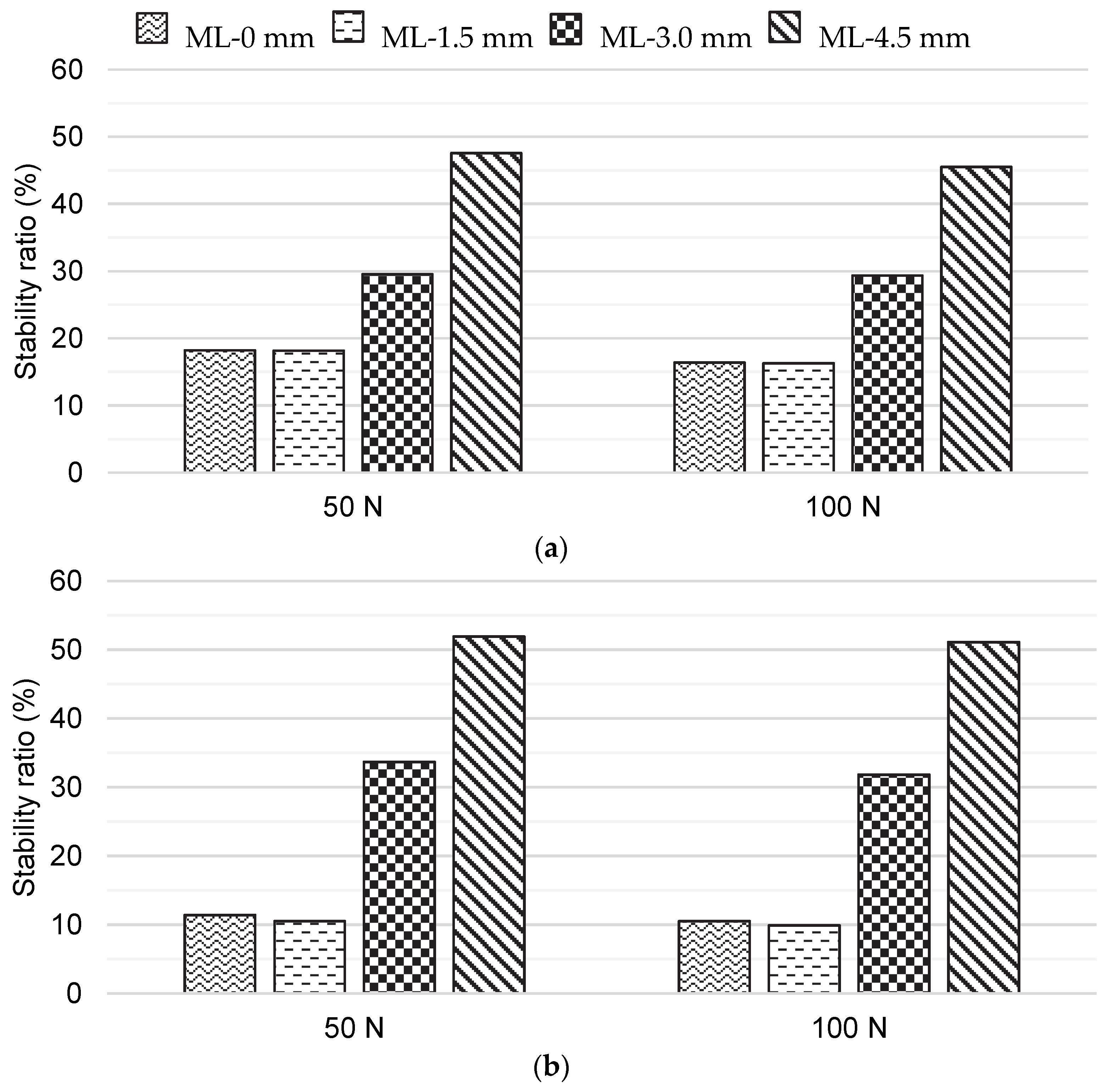
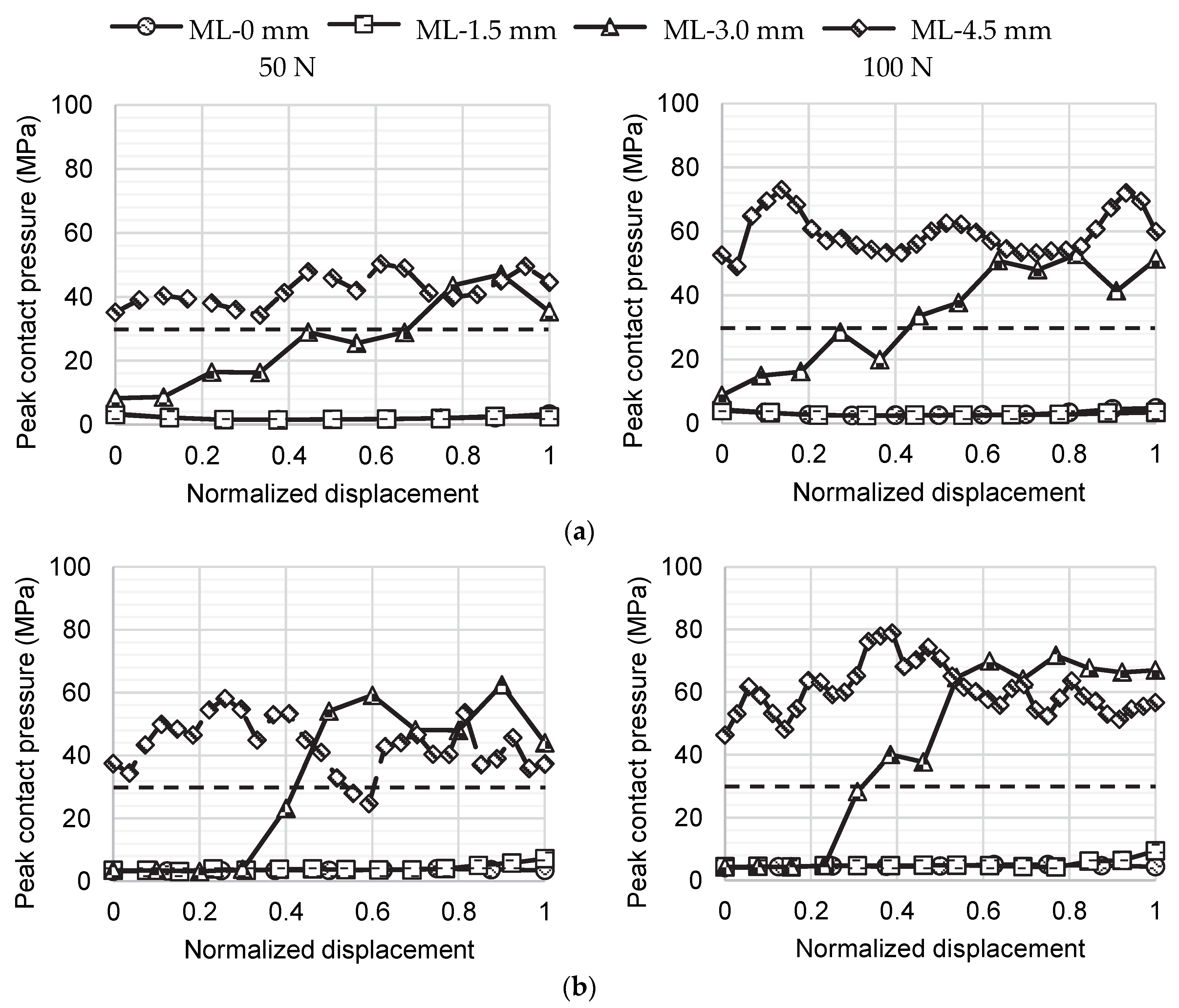
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zacchilli, M.A.; Owens, B.D. Epidemiology of Shoulder Dislocations Presenting to Emergency Departments in the United States. J. Bone Jt. Surg. Ser. A 2010, 92, 542–549. [Google Scholar] [CrossRef] [PubMed]
- Hasebroock, A.W.; Brinkman, J.; Foster, L.; Bowens, J.P. Management of Primary Anterior Shoulder Dislocations: A Narrative Review. Sports Med. Open 2019, 5, 31. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- van der Linde, J.A.; Bosmans, J.E.; ter Meulen, D.P.; van Kampen, D.A.; van Deurzen, D.F.P.; Haverlag, R.; Saris, D.B.F.; van den Bekerom, M.P.J. Direct and Indirect Costs Associated with Nonoperative Treatment for Shoulder Instability: An Observational Study in 132 Patients. Shoulder Elb. 2019, 11, 265–274. [Google Scholar] [CrossRef]
- Pickett, A.; Svoboda, S. Anterior Glenohumeral Instability. Sports Med. Arthrosc. 2017, 25, 156–162. [Google Scholar] [CrossRef]
- Mehl, J.; Otto, A.; Imhoff, F.B.; Murphy, M.; Dyrna, F.; Obopilwe, E.; Cote, M.; Lädermann, A.; Collin, P.; Beitzel, K.; et al. Dynamic Anterior Shoulder Stabilization With the Long Head of the Biceps Tendon: A Biomechanical Study. Am. J. Sports Med. 2019, 47, 1441–1450. [Google Scholar] [CrossRef] [PubMed]
- Hovelius, L.; Sandström, B.; Olofsson, A.; Svensson, O.; Rahme, H. The Effect of Capsular Repair, Bone Block Healing, and Position on the Results of the Bristow-Latarjet Procedure (Study III): Long-Term Follow-up in 319 Shoulders. J. Shoulder Elb. Surg. 2012, 21, 647–660. [Google Scholar] [CrossRef]
- Mizuno, N.; Denard, P.J.; Raiss, P.; Melis, B.; Walch, G. Long-Term Results of the Latarjet Procedure for Anterior Instability of the Shoulder. J. Shoulder Elb. Surg. 2014, 23, 1691–1699. [Google Scholar] [CrossRef]
- Sano, H.; Komatsuda, T.; Abe, H.; Ozawa, H.; Yokobori, T.A. Proximal-Medial Part in the Coracoid Graft Demonstrates the Most Evident Stress Shielding Following the Latarjet Procedure: A Simulation Study Using the 3-Dimensional Finite Element Method. J. Shoulder Elb. Surg. 2020, 29, 2632–2639. [Google Scholar] [CrossRef]
- Imai, S. A New Guide for the Arthroscopically Assisted Latarjet Procedure. JBJS Open Access 2021, 6, e20.00141. [Google Scholar] [CrossRef]
- Boileau, P.; Gendre, P.; Baba, M.; Thélu, C.É.; Baring, T.; Gonzalez, J.F.; Trojani, C. A Guided Surgical Approach and Novel Fixation Method for Arthroscopic Latarjet. J. Shoulder Elb. Surg. 2016, 25, 78–89. [Google Scholar] [CrossRef]
- Spitzer, V.; Ackerman, M.J.; Scherzinger, A.L.; Whitlock, D. The Visible Human Male: A Technical Report. Emerg. Infect. Dis. 1996, 3, 118–130. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Soslowsky, L.J.; Flatow, E.L.; Bigliani, L.U.; Mow, V.C. Articular Geometry of the Glenohumeral Joint. Clin. Orthop. Relat. Res. 1992, 285, 181–190. [Google Scholar] [CrossRef]
- Yeh, L.R.; Kwak, S.; Kim, Y.S.; Chou, D.S.W.; Muhle, C.; Skaf, A.; Trudell, D.; Resnick, D. Evaluation of Articular Cartilage Thickness of the Humeral Head and the Glenoid Fossa by MR Arthrography: Anatomic Correlation in Cadavers. Skelet. Radiol. 1998, 27, 500–504. [Google Scholar] [CrossRef]
- Favre, P.; Senteler, M.; Hipp, J.; Scherrer, S.; Gerber, C.; Snedeker, J.G. An Integrated Model of Active Glenohumeral Stability. J. Biomech. 2012, 45, 2248–2255. [Google Scholar] [CrossRef] [PubMed]
- Fox, J.A.; Cole, B.J.; Romeo, A.A.; Meininger, A.K.; Williams, J.M.; Glenn, R.E.; Bicos, J.; Hayden, J.K.; Dorow, C.B. Articular Cartilage Thickness of the Humeral Head: An Anatomic Study. Orthopedics 2008, 31, 216. [Google Scholar] [CrossRef] [Green Version]
- Griesser, M.J.; Harris, J.D.; McCoy, B.W.; Hussain, W.M.; Jones, M.H.; Bishop, J.Y.; Miniaci, A. Complications and Re-Operations after Bristow-Latarjet Shoulder Stabilization: A Systematic Review. J. Shoulder Elb. Surg. 2013, 22, 286–292. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, N.; Itoi, E.; Abe, H.; Kikuchi, K.; Seki, N.; Minagawa, H.; Tuoheti, Y. Effect of an Anterior Glenoid Defect on Anterior Shoulder Stability: A Cadaveric Study. Am. J. Sports Med. 2009, 37, 949–954. [Google Scholar] [CrossRef] [PubMed]
- Kany, J.; Flamand, O.; Grimberg, J.; Guinand, R.; Croutzet, P.; Amaravathi, R.; Sekaran, P. Arthroscopic Latarjet Procedure: Is Optimal Positioning of the Bone Block and Screws Possible? A Prospective Computed Tomography Scan Analysis. J. Shoulder Elb. Surg. 2016, 25, 69–77. [Google Scholar] [CrossRef]
- Ghodadra, N.; Gupta, A.; Romeo, A.A.; Bach, B.R.; Verma, N.; Shewman, E.; Goldstein, J.; Provencher, M.T. Normalization of Glenohumeral Articular Contact Pressures after Latarjet or Iliac Crest Bone-Grafting. J. Bone Jt. Surg. Ser. A 2010, 92, 1478–1489. [Google Scholar] [CrossRef]
- Boons, H.W.; Giles, J.W.; Elkinson, I.; Johnson, J.A.; Athwal, G.S. Classic versus Congruent Coracoid Positioning during the Latarjet Procedure: An in Vitro Biomechanical Comparison. Arthrosc. J. Arthrosc. Relat. Surg. 2013, 29, 309–316. [Google Scholar] [CrossRef]
- Terrier, A.; Reist, A.; Vogel, A.; Farron, A. Effect of Supraspinatus Deficiency on Humerus Translation and Glenohumeral Contact Force during Abduction. Clin. Biomech. 2007, 22, 645–651. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gupta, S.; Dan, P. Bone Geometry and Mechanical Properties of the Human Scapula Using Computed Tomography Data. Trends Biomater. Artif. Organs 2004, 17, 61–70. [Google Scholar]
- Santos, B.; Quental, C.; Folgado, J.; Sarmento, M.; Monteiro, J. Bone Remodelling of the Humerus after a Resurfacing and a Stemless Shoulder Arthroplasty. Clin. Biomech. 2018, 59, 78–84. [Google Scholar] [CrossRef] [PubMed]
- Quental, C.; Vasconcelos, S.; Folgado, J.; Guerra-Pinto, F. Influence of the PFNA Screw Position on the Risk of Cut-out in an Unstable Intertrochanteric Fracture: A Computational Analysis. Med. Eng. Phys. 2021, 97, 70–76. [Google Scholar] [CrossRef]
- Smith, C.D.; Masouros, S.D.; Hill, A.M.; Wallace, A.L.; Amis, A.A.; Bull, A.M.J. The Compressive Behavior of the Human Glenoid Labrum May Explain the Common Patterns of SLAP Lesions. Arthrosc. J. Arthrosc. Relat. Surg. 2009, 25, 504–509. [Google Scholar] [CrossRef] [Green Version]
- Butz, K.D.; Chan, D.D.; Nauman, E.A.; Neu, C.P. Stress Distributions and Material Properties Determined in Articular Cartilage from MRI-Based Finite Strains. J. Biomech. 2011, 44, 2667–2672. [Google Scholar] [CrossRef]
- Yamamoto, N.; Muraki, T.; An, K.N.; Sperling, J.W.; Cofield, R.H.; Itoi, E.; Walch, G.; Steinmann, S.P. The Stabilizing Mechanism of the Latarjet Procedure: A Cadaveric Study. J. Bone Jt. Surg. Ser. A 2013, 95, 1390–1397. [Google Scholar] [CrossRef] [Green Version]
- Quental, C.; Fernandes, P.R.; Monteiro, J.; Folgado, J. Bone Remodelling of the Scapula after a Total Shoulder Arthroplasty. Biomech. Model. Mechanobiol. 2014, 13, 827–838. [Google Scholar] [CrossRef]
- Lee, H.K.; Kim, S.M.; Lim, H.S. Computational Wear Prediction of TKR with Flatback Deformity during Gait. Appl. Sci. 2022, 12, 3698. [Google Scholar] [CrossRef]
- Erbulut, D.U.; Sadeqi, S.; Summers, R.; Goel, V.K. Tibiofemoral Cartilage Contact Pressures in Athletes During Landing: A Dynamic Finite Element Study. J. Biomech. Eng. 2021, 143, 101006. [Google Scholar] [CrossRef]
- Lippitt, S.B.; Vanderhooft, J.E.; Harris, S.L.; Sidles, J.A.; Harryman, D.T.; Matsen, F.A. Glenohumeral Stability from Concavity-Compression: A Quantitative Analysis. J. Shoulder Elb. Surg. 1993, 2, 27–35. [Google Scholar] [CrossRef] [PubMed]
- Riemenschneider, P.E.; Rose, M.D.; Giordani, M.; McNary, S.M. Compressive Fatigue and Endurance of Juvenile Bovine Articular Cartilage Explants. J. Biomech. 2019, 95, 109304. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, A.; Massimini, D.F.; Distefano, J.; Higgins, L.D. Glenohumeral Contact Pressure with Simulated Anterior Labral and Osseous Defects in Cadaveric Shoulders before and after Soft Tissue Repair. Am. J. Sports Med. 2014, 42, 1947–1954. [Google Scholar] [CrossRef] [PubMed]
- Moroder, P.; Schulz, E.; Wierer, G.; Auffarth, A.; Habermeyer, P.; Resch, H.; Tauber, M. Neer Award 2019: Latarjet Procedure vs. Iliac Crest Bone Graft Transfer for Treatment of Anterior Shoulder Instability with Glenoid Bone Loss: A Prospective Randomized Trial. J. Shoulder Elb. Surg. 2019, 28, 1298–1307. [Google Scholar] [CrossRef] [Green Version]
- Wong, I.H.; King, J.P.; Boyd, G.; Mitchell, M.; Coady, C. Radiographic Analysis of Glenoid Size and Shape After Arthroscopic Coracoid Autograft Versus Distal Tibial Allograft in the Treatment of Anterior Shoulder Instability. Am. J. Sports Med. 2018, 46, 2717–2724. [Google Scholar] [CrossRef]
- Ogimoto, S.; Miyazaki, M.; Tsuruta, T.; Tsumura, H. Arthroscopic Glenoid Reconstruction for Glenoid Bone Loss in Recurrent Anterior Glenohumeral Instability, Using Osteochondral Autograft from the Contralateral Lateral Femoral Condyle: A New Technique and Case Report. JSES Open Access 2018, 2, 104–108. [Google Scholar] [CrossRef]
- Petersen, S.A.; Bernard, J.A.; Langdale, E.R.; Belkoff, S.M. Autologous Distal Clavicle versus Autologous Coracoid Bone Grafts for Restoration of Anterior-Inferior Glenoid Bone Loss: A Biomechanical Comparison. J. Shoulder Elb. Surg. 2016, 25, 960–966. [Google Scholar] [CrossRef]
- Zhang, J.A.; Lam, P.H.; Beretov, J.; Murrell, G.A.C. A Review of Bone Grafting Techniques for Glenoid Reconstruction. Shoulder Elb. 2022, 14, 123–134. [Google Scholar] [CrossRef]
- Goetti, P.; Denard, P.J.; Collin, P.; Ibrahim, M.; Hoffmeyer, P.; Lädermann, A. Shoulder Biomechanics in Normal and Selected Pathological Conditions. EFORT Open Rev. 2020, 5, 508–518. [Google Scholar] [CrossRef]
- Walia, P.; Miniaci, A.; Jones, M.H.; Fening, S.D. Theoretical Model of the Effect of Combined Glenohumeral Bone Defects on Anterior Shoulder Instability: A Finite Element Approach. J. Orthop. Res. 2013, 31, 601–607. [Google Scholar] [CrossRef]
- Dalmas, Y.; Thélu, C.E.; Laumonerie, P.; Martinel, V.; Robert, S.; Mansat, P.; Bonnevialle, N. Arthroscopic Double-Button Latarjet Osteolysis and Remodeling at 1-Year Follow-Up. J. Shoulder Elb. Surg. 2022, 31, e603–e612. [Google Scholar] [CrossRef] [PubMed]
- Boileau, P.; Saliken, D.; Gendre, P.; Seeto, B.L.; d’Ollonne, T.; Gonzalez, J.F.; Bronsard, N. Arthroscopic Latarjet: Suture-Button Fixation Is a Safe and Reliable Alternative to Screw Fixation. Arthrosc. J. Arthrosc. Relat. Surg. 2019, 35, 1050–1061. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Liu, H.; Lu, W.; Deng, Z.; Zhu, W.; Peng, L.; Ouyang, K.; Li, H.; Wang, D. Modified Arthroscopic Latarjet Procedure: Suture-Button Fixation Achieves Excellent Remodeling at 3-Year Follow-Up. Am. J. Sports Med. 2020, 48, 39–47. [Google Scholar] [CrossRef] [PubMed]

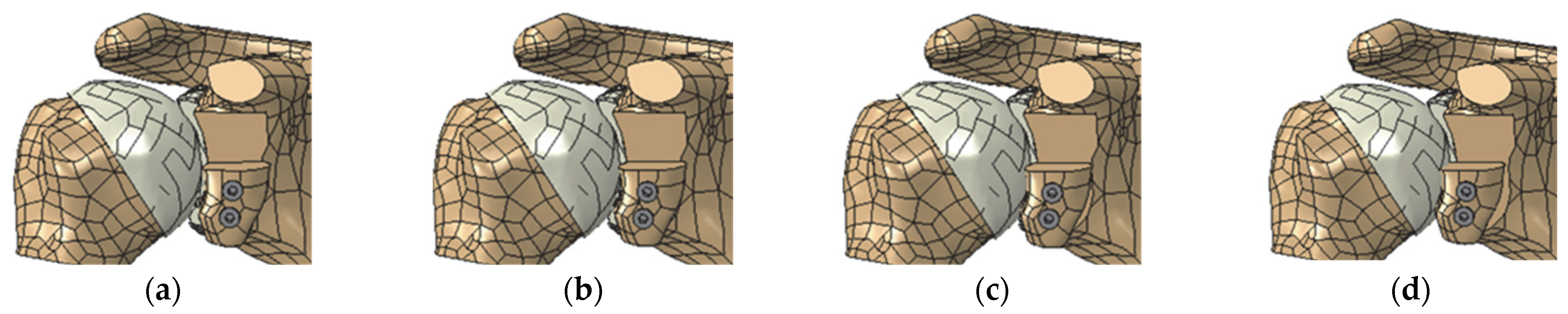

| Latarjet Model | Distance (mm) |
|---|---|
| ML-0 mm | −3.2 |
| ML-1.5 mm | −1.8 |
| ML-3.0 mm | +0.4 |
| ML-4.5 mm | +1.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martins, R.; Quental, C.; Folgado, J.; Ângelo, A.C.; de Campos Azevedo, C. Influence of Graft Positioning during the Latarjet Procedure on Shoulder Stability and Articular Contact Pressure: Computational Analysis of the Bone Block Effect. Biology 2022, 11, 1783. https://doi.org/10.3390/biology11121783
Martins R, Quental C, Folgado J, Ângelo AC, de Campos Azevedo C. Influence of Graft Positioning during the Latarjet Procedure on Shoulder Stability and Articular Contact Pressure: Computational Analysis of the Bone Block Effect. Biology. 2022; 11(12):1783. https://doi.org/10.3390/biology11121783
Chicago/Turabian StyleMartins, Rita, Carlos Quental, João Folgado, Ana Catarina Ângelo, and Clara de Campos Azevedo. 2022. "Influence of Graft Positioning during the Latarjet Procedure on Shoulder Stability and Articular Contact Pressure: Computational Analysis of the Bone Block Effect" Biology 11, no. 12: 1783. https://doi.org/10.3390/biology11121783
APA StyleMartins, R., Quental, C., Folgado, J., Ângelo, A. C., & de Campos Azevedo, C. (2022). Influence of Graft Positioning during the Latarjet Procedure on Shoulder Stability and Articular Contact Pressure: Computational Analysis of the Bone Block Effect. Biology, 11(12), 1783. https://doi.org/10.3390/biology11121783






