Inverted Covariate Effects for First versus Mutated Second Wave Covid-19: High Temperature Spread Biased for Young
Abstract
:1. Introduction
2. Methods
3. Results
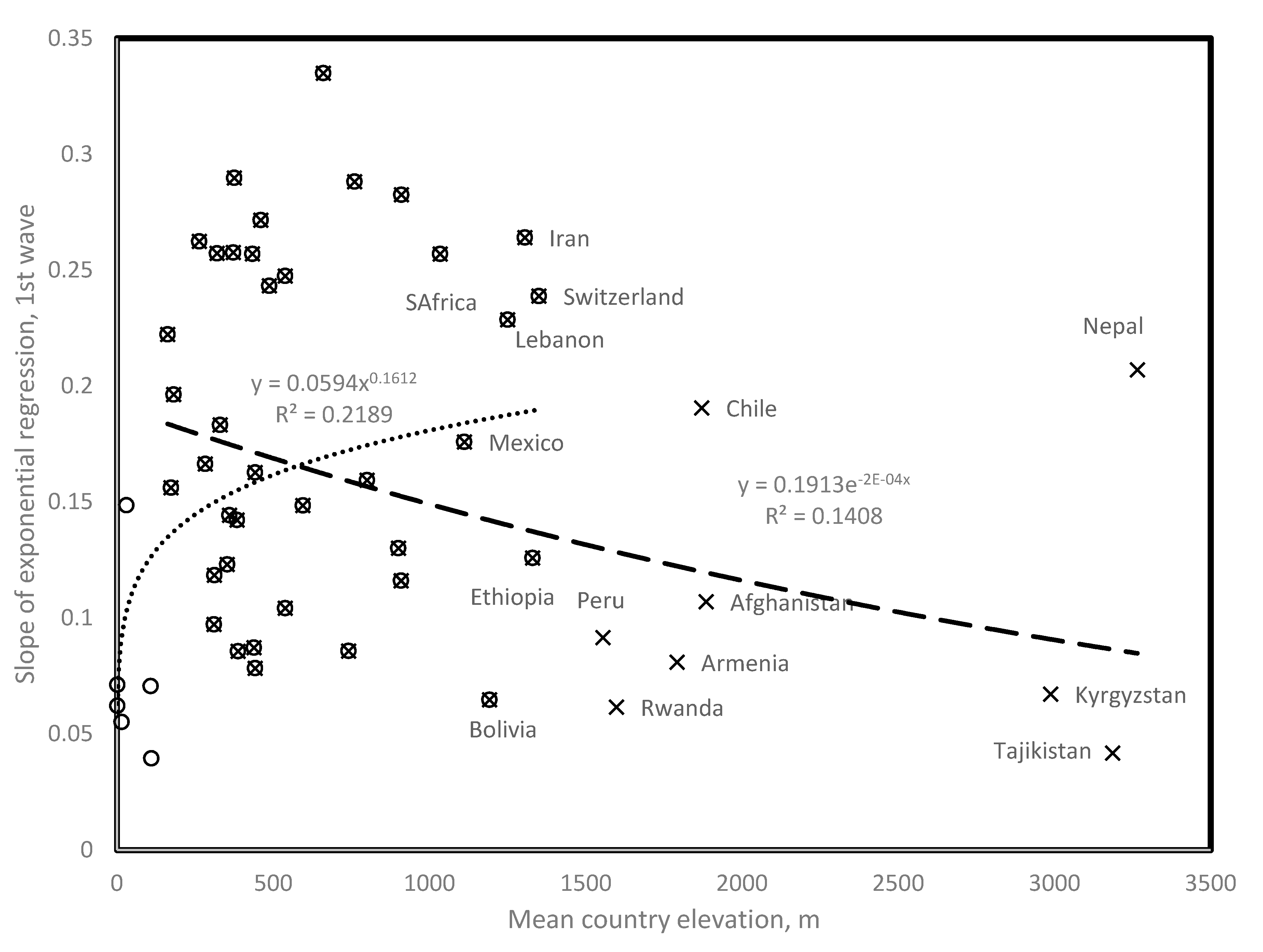
3.1. Relationship between Covid-19 Cases and Mean Elevation
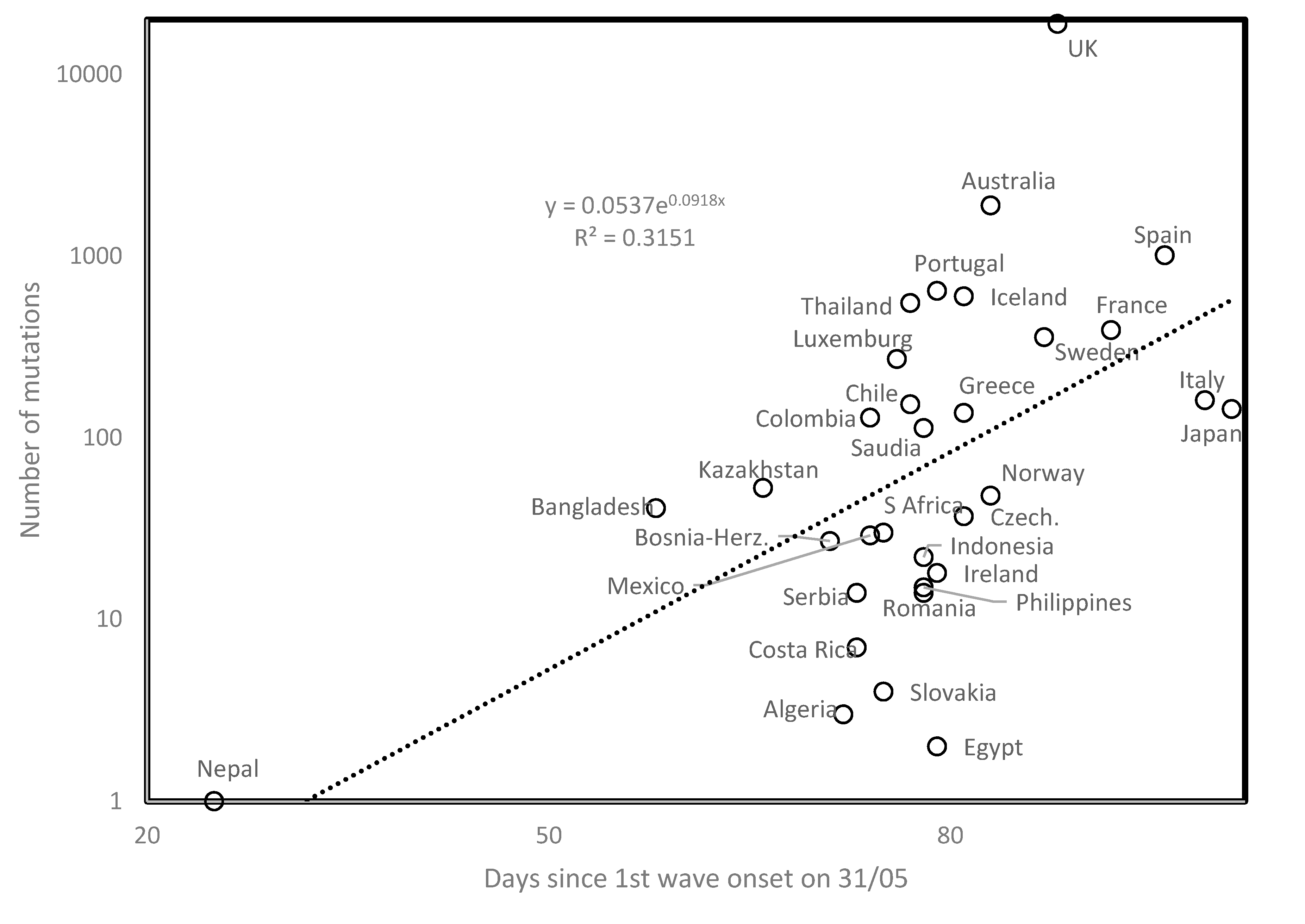
3.2. Covid-19 Viruses Evolve Over Time
3.3. Determination of First and Second Waves
| Country | T | E | D | A | 1st wStart | S1 | 2nd wStart | S2 |
|---|---|---|---|---|---|---|---|---|
| Africa | ||||||||
| Algeria | 22.5 | 800 | 18 | 28.1 | 20/3 | 0.1594 | 07/4 −4 | 0.0316 |
| Kenya | 24.75 | 752 | 82 | 19.7 | 12/5 1 5 | 0.0740 | ||
| Ethiopia * | 22.2 | 1330 | 101 | 17.9 | 21/4 | 0.1259 | ||
| Morocco * | 17.1 | 909 | 80 | 29.3 | 21/3 | 0.1161 | ||
| Rwanda * | 17.85 | 1598 | 470 | 19.0 | 04/4 | 0.0615 | ||
| South Africa * | 17.75 | 1034 | 48 | 27.1 | 17/3 | 0.257 | ||
| Asia | ||||||||
| Afghanistan * | 12.6 | 1885 | 49 | 18.9 | 26/3 | 0.107 | ||
| Bahrain [1] | 27.15 | 1 | 1983 | 32.3 | 09/3 | 0.1884 | ||
| Iran | 17.25 | 1305 | 51 | 30.3 | 26/2 | 0.2641 | 01/5 −1 24 | 0.0438 |
| Iraq | 14.03 | 312 | 90 | 20.0 | 14/3 | 0.1184 | 15/4 1 | 0.041 |
| Japan [1] | 11.15 | 438 | 333 | 47.3 | 20/2 | 0.0872 | ||
| Kazakhstan | 6.4 | 387 | 7 | 30.6 | 26/3 | 0.0856 | 08/5 −4 22 | 0.0933 |
| Kyrgyzstan | 1.55 | 2988 | 32 | 26.5 | 30/3 | 0.0671 | 25/4 3 | 0.0271 |
| Lebanon | 16.4 | 1250 | 672 | 30.5 | 14/3 | 0.2286 | 19/4 −2 | 0.0757 |
| Malaysia [1] | 25.4 | 538 | 99 | 28.5 | 08/3 | 0.1042 | 12/5 5 0 | 0.0794 |
| Nepal * | 8.1 | 3265 | 201 | 24.1 | 06/5 | 0.207 | ||
| Oman | 25.6 | 310 | 15 | 25.6 | 25/3 | 0.0972 | 02/5 −3 7 | 0.0936 |
| Pakistan * | 20.20 | 900 | 274 | 23.8 | 15/3 | 0.1301 | ||
| Philippines | 25.85 | 442 | 362 | 23.5 | 14/3 | 0.1627 | 22/5 7 9 | 0.1772 |
| Singapore [1] | 26.45 | 15 | 7894 | 34.6 | 28/2 | 0.0551 | 02/5 28 3 | 0.0641 |
| South Korea | 11.5 | 282 | 517 | 41.8 | 20/2 | 0.1664 | 06/5 −10 6 | 0.0585 |
| Sri Lanka | 26.95 | 228 | 332 | 32.8 | 08/5 0 | 0.1347 | ||
| Tajikistan * | 2.00 | 3186 | 64 | 24.5 | 02/5 | 0.0418 | ||
| Uzbekistan | 12.05 | 353 $ | 73 | 28.6 | 28/3 | 0.1231 | 26/4 1 | 0.0238 |
| Australia [1] | 21.65 | 330 | 3 | 38.7 | 09/3 | 0.1832 | ||
| Europe | ||||||||
| Armenia | 7.15 | 1792 | 99 | 35.1 | 18/3 | 0.0809 | 05/4 −1 4 | 0.057 |
| Austria [1] | 6.35 | 910 | 106 | 44.0 | 08/3 | 0.2825 | ||
| Azerbaijan | 11.95 | 384 | 116 | 32.3 | 25/3 | 0.1422 | 25/4 0 | 0.0676 |
| Belgium [1] | 9.55 | 181 | 378 | 41.4 | 06/3 | 0.1963 | ||
| Czech Rep. [1] | 7.55 | 433 | 135 | 42.1 | 11/3 | 0.257 | 13/5 11 15 | 0.0474 |
| Denmark | 42.2 | |||||||
| France [1] | 10.7 | 375 | 123 | 41.4 | 29/2 | 0.2898 | ||
| Germany [1] | 8.5 | 263 | 233 | 47.1 | 29/2 | 0.2624 | ||
| Italy [1] | 12.45 | 538 | 200 | 45.5 | 22/2 | 0.2475 | ||
| Lithuania | 6.2 | 110 | 73 | 43.7 | 21/3 | 0.0394 | 05/5 −6 5 | 0.0554 |
| Malta | 19.2 | 1 | 1567 | 41.8 | 23/3 | 0.0712 | 19/4 −13 −10 | 0.0536 |
| N Macedonia | 9.8 | 741 | 81 | 37.9 | 21/3 | 0.0858 | 03/5 1 | 0.0528 |
| Netherlands [1] | 9.25 | 30 | 421 | 42.6 | 05/3 | 0.2485 | ||
| Norway [1] | 1.5 | 460 | 17 | 39.2 | 09/3 | 0.2716 | ||
| Poland | 7.85 | 173 | 123 | 40.7 | 14/3 | 0.1562 | 05/4 −21 −36 | 0.0094 |
| Portugal | 15.15 | 372 | 112 | 42.2 | 13/3 | 0.0301 | 09/5 −1 13 | 0.0431 |
| Spain [1] | 13.3 | 660 | 93 | 42.7 | 25/2 | 0.335 | ||
| Sweden [1] | 2.1 | 320 | 23 | 41.2 | 05/3 | 0.2572 | ||
| Switzerland [1] | 5.5 | 1350 | 208 | 42.4 | 04/3 | 0.2388 | ||
| UK [1] | 8.45 | 162 | 280 | 40.5 | 04/3 | 0.2223 | ||
| North America | ||||||||
| Canada [1] | −5.35 | 487 | 4 | 42.2 | 10/3 | 0.2432 | ||
| Cuba | 25.2 | 108 | 102 | 41.5 | 27/3 | 0.0706 | 17/5 −2 4 | 0.0517 |
| El Salvador | 24.45 | 442 | 319 | 27.1 | 10/4 | 0.0783 | 21/4 2 2 | 0.0535 |
| Guatemala | 23.56 | 759 | 162 | 22.1 | 09/3 | 0.088 | 01/5 −2 −1 | 0.1109 |
| Panama | 25.4 | 360 | 56 | 29.2 | 18/3 | 0.1443 | 19/5 5 7 | 0.1195 |
| Mexico * | 21.00 | 1111 | 64 | 28.3 | 18/3 | 0.1759 | ||
| USA [1] | 8.55 | 760 | 34 | 38.1 | 02/3 | 0.2882 | ||
| South America | ||||||||
| Argentina | 14.8 | 595 | 16 | 31.7 | 18/3 | 0.1485 | 05/5 3 20 | 0.0427 |
| Bolivia * | 21.55 | 1192 | 10 | 24.3 | 30/3 | 0.0647 | ||
| Brazil | 32.6 | |||||||
| Chile | 8.45 | 1871 | 23 | 34.4 | 15/3 | 0.1906 | 30/4 2 10 | 0.0586 |
| Peru * | 19.6 | 1555 | 25 | 28.0 | 29/3 | 0.0915 |
3.4. Geographical Second Wave Clusters
3.5. Second Wave Slopes versus First Wave Slopes
3.6. Second Wave Spread Rates and Temperature
3.7. Time Since Start of First Wave for Low Slopes
3.8. Slopes and Times Since Start of First and Second Waves
3.9. Elevation and Population Density
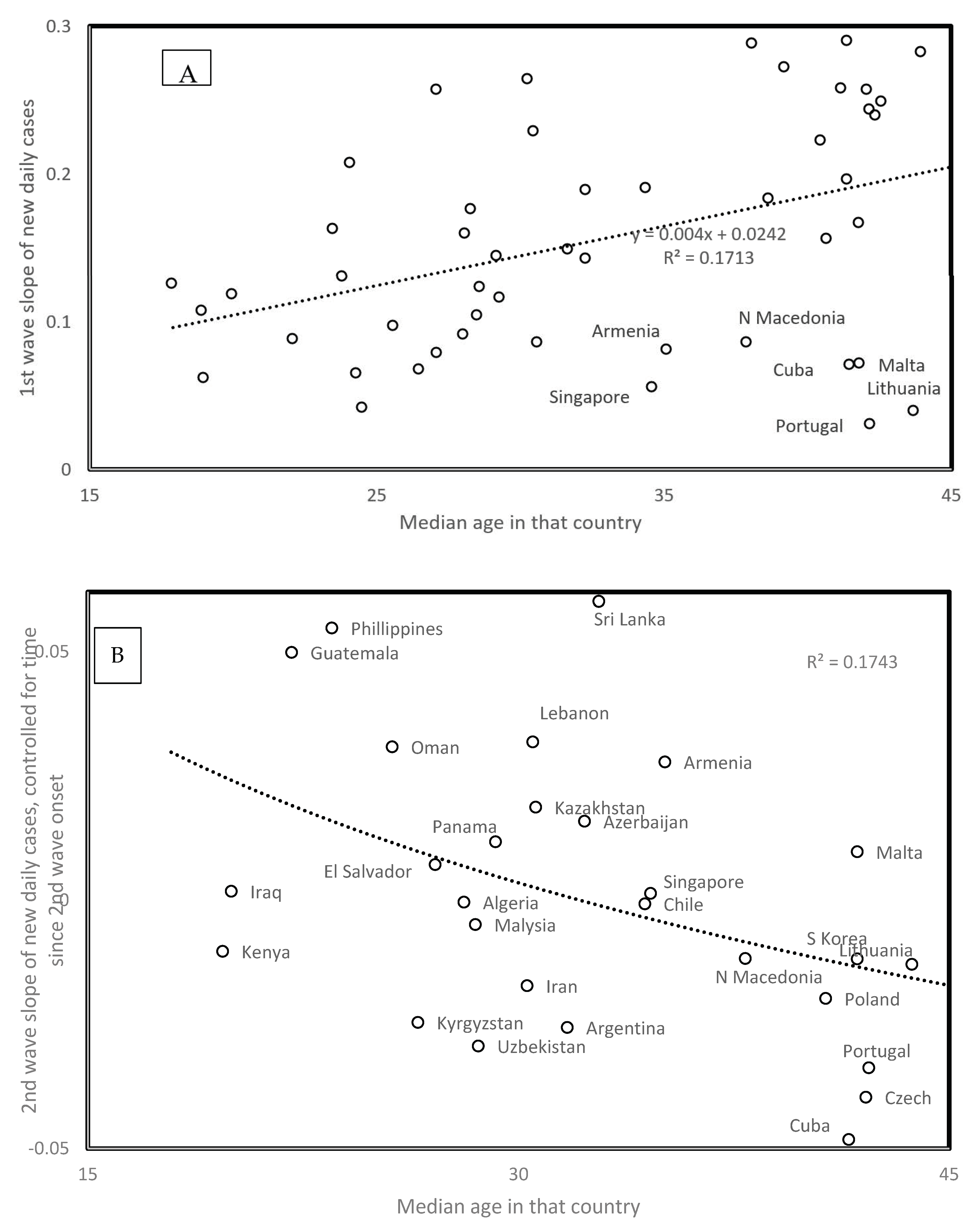
3.10. Median Age and Spread Rates
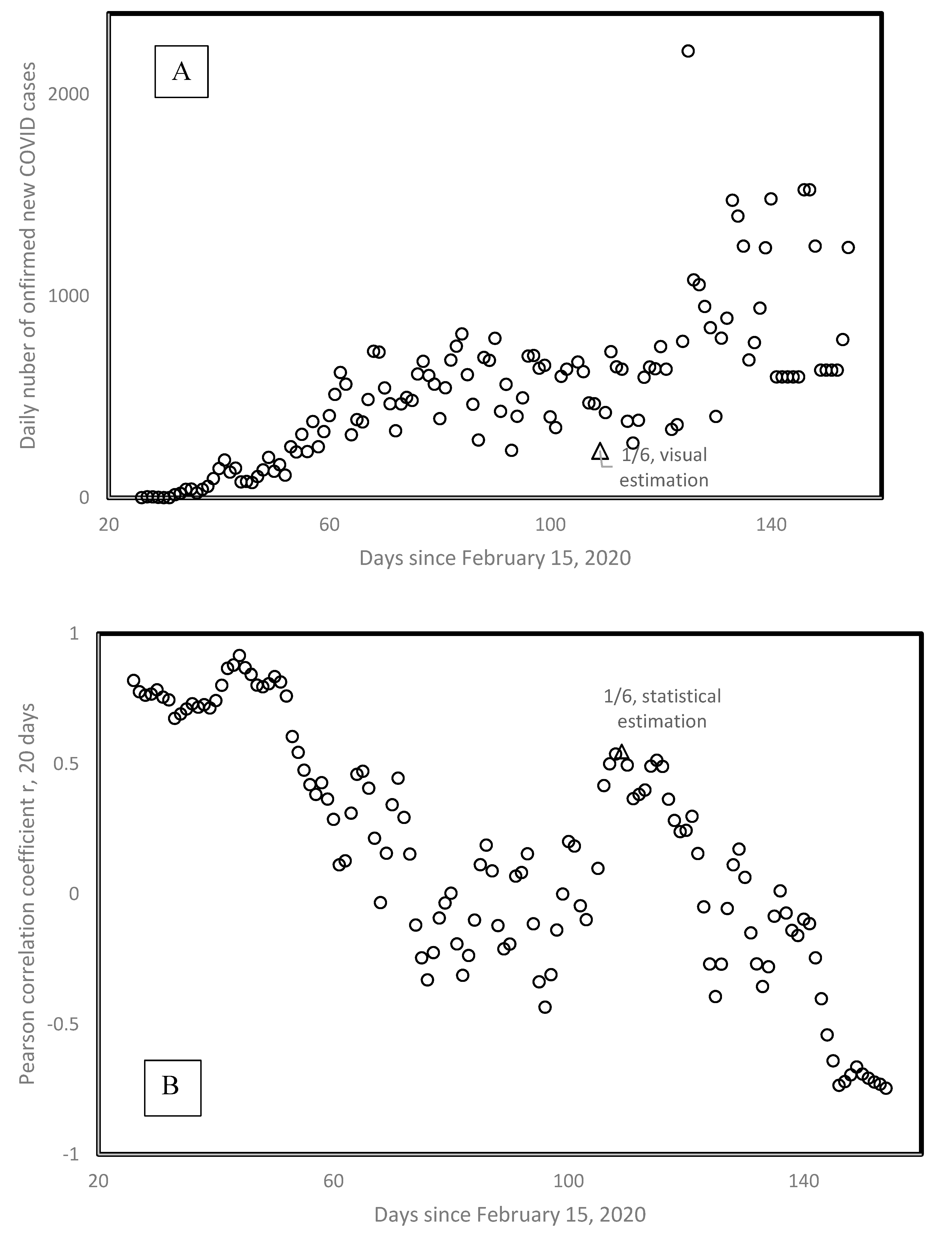
3.11. Eyeballing versus Statistical Evaluation of Second Wave Onset Date
3.12. Total Numbers of Tests
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Demongeot, J.; Flet-Berliac, Y.; Seligmann, H. Temperature decreases spread parameters of the new covid-19 cases dynamics. Biology 2020, 9, 94. [Google Scholar] [CrossRef] [PubMed]
- Renardy, M.; Kirschner, D.E. Predicting the second wave of COVID-19 in Washtenaw county, MI. medRxiv 2020. [Google Scholar] [CrossRef]
- Scarpino, S.V.; Petri, G. On the predictability of infectious disease outbreaks. Nature Comm. 2019, 10, 898. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pramanik, M.; Udmale, P.; Bisht, P.; Chowdhury, K.; Szabo, S.; Pal, I. Climatic factors influence the spread of COVID-19 in Russia. Int. J. Environ. Health Res. 2020, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Steiger, E.; Mussgnug, T.; Kroll, L.E. Causal analysis of COVID-19 observational data in German districts reveals effects of mobility, awareness, and temperature. medRxiv 2020. [Google Scholar] [CrossRef]
- Malki, Z.; Atlam, E.-S.; Hassanien, A.E.; Dagnew, G.; Elhosseini, M.A.; Gad, I. Association between weather data and COVID-19 pandemic predicting mortality rate: Machine learning approaches. Chaos Solut. Fractals 2020, 138, 110137. [Google Scholar] [CrossRef]
- Worldometer. 2020. Available online: https://www.worldometers.info/coronavirus/ (accessed on 6 June 2020).
- Wikipedia. 2016. Available online: https://en.wikipedia.org/wiki/List_of_countries_by_average_elevation (accessed on 6 June 2020).
- Wikipedia. 2015. Available online: https://en.wikipedia.org/wiki/List_of_countries_by_average_yearly_ temperature (accessed on 6 June 2020).
- CNCB. 2019. Available online: https://bigd.big.ac.cn/ncov/variation/annotation/variant/24751 (accessed on 6 June 2020).
- Yao, H.; Lu, X.; Chen, Q.; Xu, K.; Chen, Y.; Cheng, L.; Liu, F.; Wu, Z.; Wu, H.; Jin, C.; et al. Patient-derived mutations impact pathogenicity of SARS-CoV-2. medRxiv 2020. [Google Scholar] [CrossRef]
- Wikipedia. 2020. Available online: https://en.wikipedia.org/wiki/List_of_countries_and_dependencies_by_ population_ density (accessed on 6 June 2020).
- Wikipedia. 2020. Available online: https://en.wikipedia.org/wiki/List_of_countries_by_median_age (accessed on 6 June 2020).
- Percival, D.B.; Rothrock, D.A. “Eyeballing” trends in climate time series: A cautionary note. J. Clim. 2005, 18, 886–891. [Google Scholar] [CrossRef] [Green Version]
- Lund, R.; Reeves, J. Detection of undocumented changepoints: A revision of the two-phase regression model. J. Clim. 2002, 15, 2547–2554. [Google Scholar] [CrossRef]
- Ghorbanzadeh, D.; Picard, D. Etude asymptomatique et pratique du comportement de deux tests de détection de rupture. Stat. Anal. Données 1992, 16, 63–84. [Google Scholar]
- Ondo, J.-C. Étude Comparative des Tests de Stationnarité. Ph.D. Thesis, Québec University, Quebec, QC, Canada, 2002; p. 288. [Google Scholar]
- Forster, P.; Forster, L.; Renfrew, C.; Forster, M. Phylogenetic network analysis of SARS-CoV-2 genomes. Proc. Nat. Acad. Sci. USA 2020, 117, 9241–9243. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Manzourolajdad, A.; Xu, Y.; Ebrahimi, D. Novel polybasic cleavage site in SARS-CoV-2 genome is likely to induce a major change in the RNA secondary structure. Preprints 2020. [Google Scholar] [CrossRef]
- Liu, Z.; Magal, P.; Seydi, O.; Webb, G. Understanding unreported cases in the COVID-19 epidemic outbreak in Wuhan, China, and the importance of major public health interventions. Biology 2020, 9, 50. [Google Scholar] [CrossRef] [PubMed] [Green Version]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seligmann, H.; Iggui, S.; Rachdi, M.; Vuillerme, N.; Demongeot, J. Inverted Covariate Effects for First versus Mutated Second Wave Covid-19: High Temperature Spread Biased for Young. Biology 2020, 9, 226. https://doi.org/10.3390/biology9080226
Seligmann H, Iggui S, Rachdi M, Vuillerme N, Demongeot J. Inverted Covariate Effects for First versus Mutated Second Wave Covid-19: High Temperature Spread Biased for Young. Biology. 2020; 9(8):226. https://doi.org/10.3390/biology9080226
Chicago/Turabian StyleSeligmann, Hervé, Siham Iggui, Mustapha Rachdi, Nicolas Vuillerme, and Jacques Demongeot. 2020. "Inverted Covariate Effects for First versus Mutated Second Wave Covid-19: High Temperature Spread Biased for Young" Biology 9, no. 8: 226. https://doi.org/10.3390/biology9080226
APA StyleSeligmann, H., Iggui, S., Rachdi, M., Vuillerme, N., & Demongeot, J. (2020). Inverted Covariate Effects for First versus Mutated Second Wave Covid-19: High Temperature Spread Biased for Young. Biology, 9(8), 226. https://doi.org/10.3390/biology9080226







