Dual-Channel Supply Chain Pricing Decisions under Discounted Advertising Value
Abstract
:1. Introduction
1.1. Backgrounds and Motivations
1.2. Research Questions and Main Findings
- (i)
- What is the impact of advertising strategies in different sales channels on the profitability of a dual-channel retailer?
- (ii)
- What should advertise levels and pricing decisions be for a dual-channel retailer across different sales channels?
- (iii)
- Given optimal advertising levels and pricing decisions, which is more profitable for retailers, online or offline sales channels?
1.3. Contributions and Paper Arrangements
2. Literature Review
2.1. Dual-Channel Operation
2.2. Advertising Strategies
3. The Problems and Assumptions
4. Models and Analysis
4.1. Online Sales Model
4.2. Offline Sales Model
4.3. Sensitivity Analysis
- (i)
- decreases with, increases with,, and.
- (ii)
- decreases withand, increases withand.
- (iii)
- decreases withand, increases withand.
- (i)
- decreases withand; increases with.
- (ii)
- decreases with,, and.
- (iii)
- decreases with,, and.
5. The Retailer’s Channel Decision
6. Extended Models: Advertising Effect
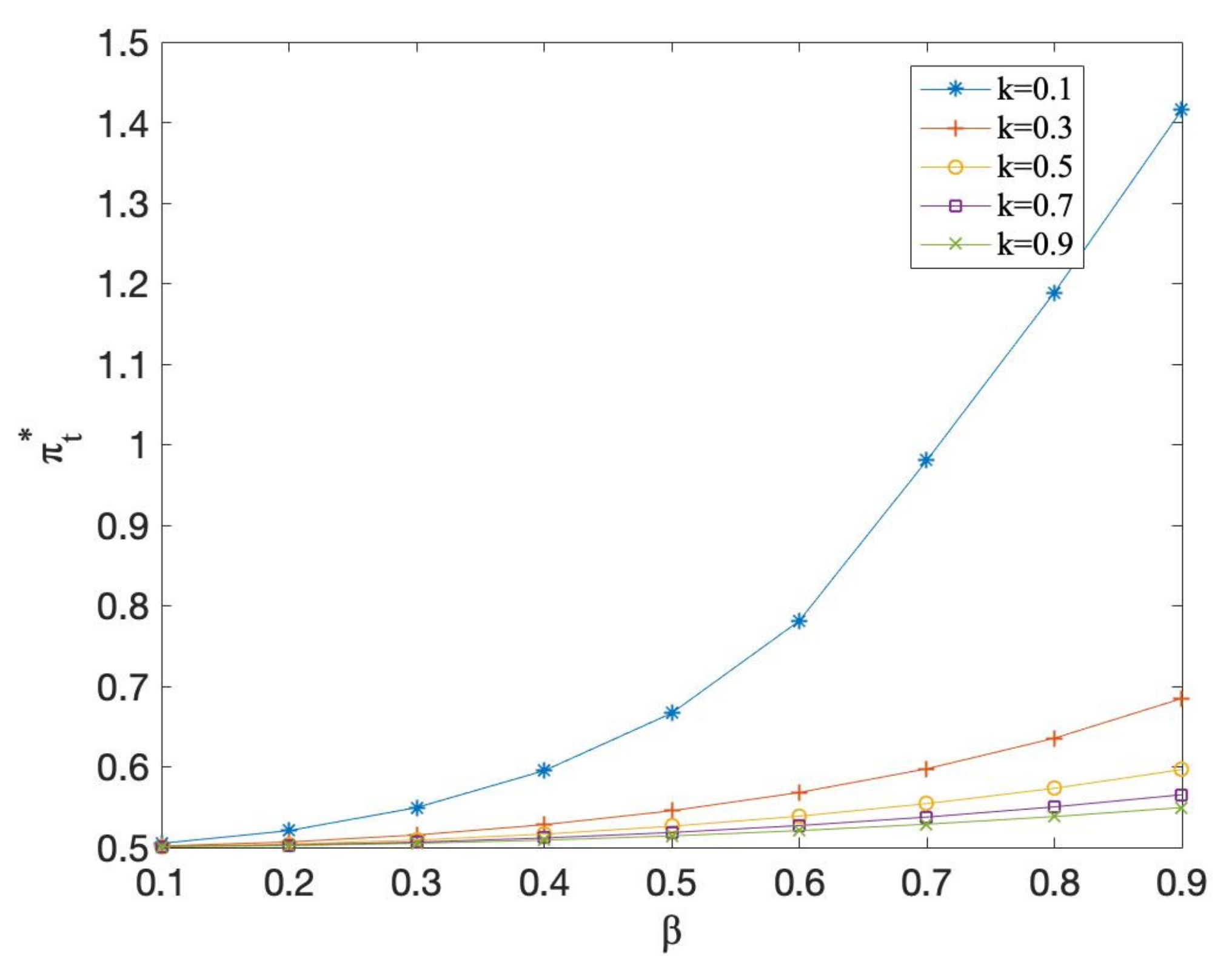
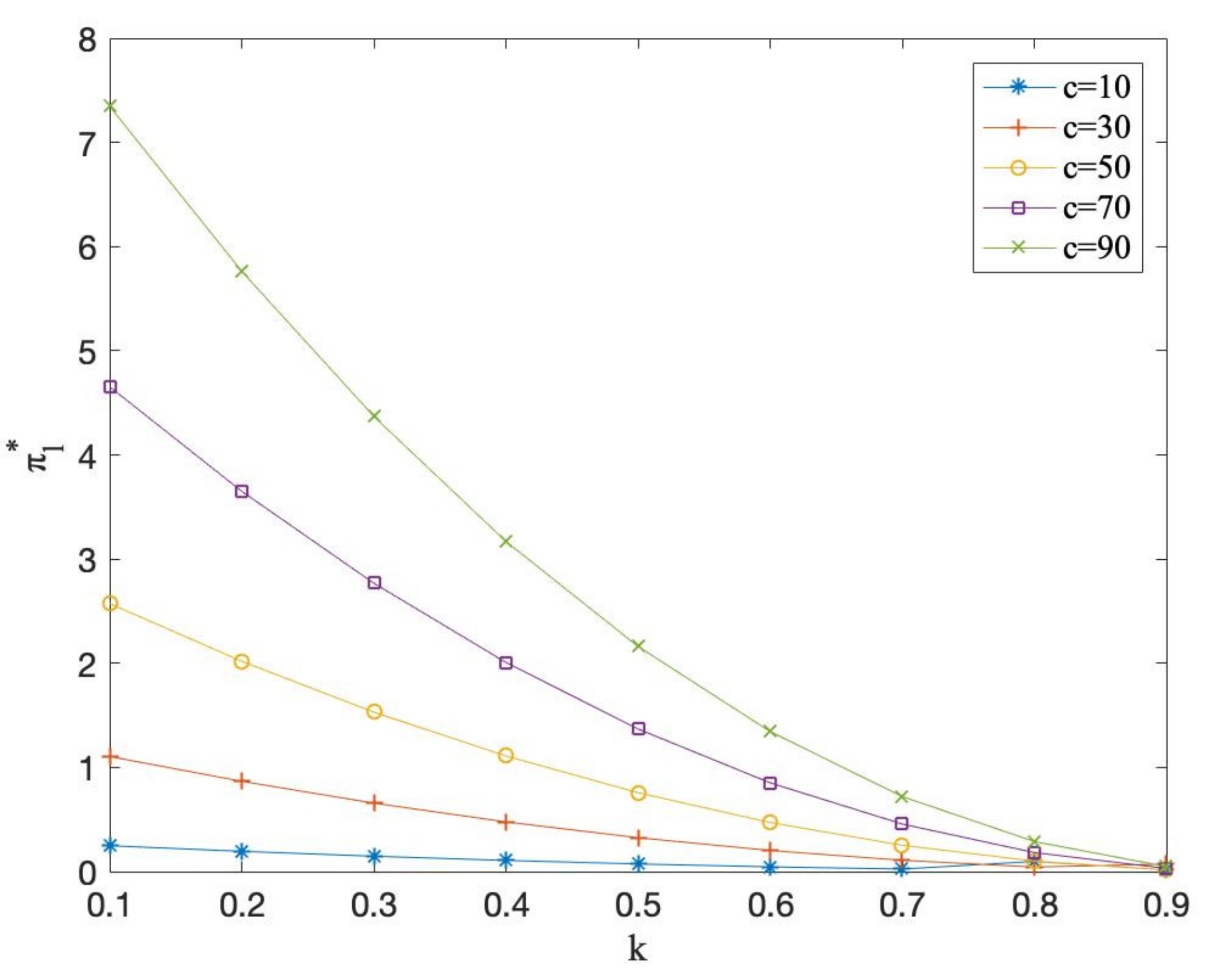
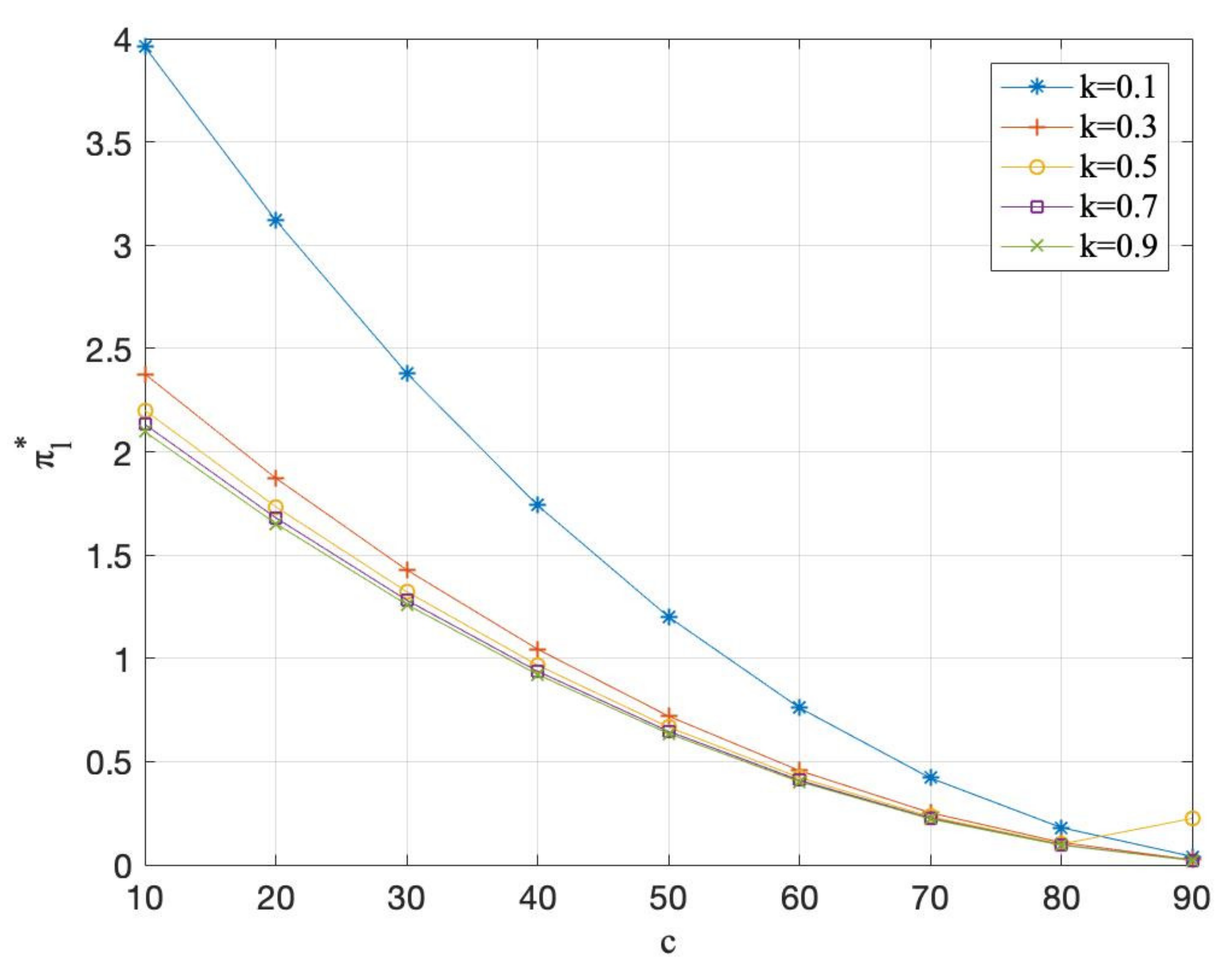
7. Numerical Analysis
8. Conclusions
8.1. Conclusion Remarks
8.2. Managerial Insights
8.3. Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- The COVID-19 Fuels Online Retail Global E-Commerce Sales Jump to $26.7 Trillion. Available online: https://news.un.org/zh/story/2021/05/1083402 (accessed on 3 April 2022).
- Lu, L.; Navas, J. Advertising and quality improving strategies in a supply chain when facing potential crises. Eur. J. Oper. Res. 2021, 288, 839–851. [Google Scholar] [CrossRef]
- Karray, S.; Amin, S.H. Cooperative advertising in a supply chain with retail competition. Int. J. Prod. Res. 2015, 53, 88–105. [Google Scholar] [CrossRef]
- Ahmadi-Javid, A.; Hoseinpour, P. On a cooperative advertising model for a supply chain with one manufacturer and one retailer. Eur. J. Oper. Res. 2012, 219, 458–466. [Google Scholar] [CrossRef]
- Siqin, T.; Choi, T.-M.; Chung, S.-H. Optimal E-tailing channel structure and service contracting in the platform era. Transp. Res. Part E Logist. Transp. Rev. 2022, 160, 102614. [Google Scholar] [CrossRef]
- Jena, S.K.; Meena, P. Shopping in the omnichannel supply chain under price competition and product return. J. Retail Consum. Serv. 2022, 65, 102848. [Google Scholar] [CrossRef]
- Ullah, M.; Asghar, I.; Zahid, M.; Omair, M.; AlArjani, A.; Sarkar, B. Ramification of remanufacturing in a sustainable three-echelon closed-loop supply chain management for returnable products. J. Clean. Prod. 2021, 290, 125609. [Google Scholar] [CrossRef]
- Mahapatra, A.S.; Soni, H.N.; Mahapatra, M.S.; Sarkar, B.; Majumder, S. A continuous review production-inventory system with a variable preparation time in a fuzzy random environment. Mathematics 2021, 9, 747. [Google Scholar] [CrossRef]
- Yadav, D.; Kumari, R.; Kumar, N.; Sarkar, B. Reduction of waste and carbon emission through the selection of items with cross-price elasticity of demand to form a sustainable supply chain with preservation technology. J. Clean. Prod. 2021, 297, 126298. [Google Scholar] [CrossRef]
- Liu, M.; Liang, K.; Perera, S.; Huang, R.; Ghose, S. Game theoretical analysis of service effort timing scheme strategies in dual-channel supply chains. Transp. Res. Part E Logist. Transp. Rev. 2022, 158, 102620. [Google Scholar] [CrossRef]
- Wang, N.; Xing, W.; Zhao, X. Strategic inventory in the presence of socially responsible dual distribution channels. Transp. Res. Part E Logist. Transp. Rev. 2022, 159, 102604. [Google Scholar] [CrossRef]
- Zhang, Z.; Song, H.; Shi, V.; Yang, S. Quality differentiation in a dual-channel supply chain. Eur. J. Oper. Res. 2021, 290, 1000–1013. [Google Scholar] [CrossRef]
- Wang, R.; Nan, G.; Chen, L.; Li, M. Channel integration choices and pricing strategies for competing dual-channel retailers. IEEE Trans. Eng. Manag. 2020, 1–15. [Google Scholar] [CrossRef]
- Shao, X. Omnichannel retail move in a dual-channel supply chain. Eur. J. Oper. Res. 2021, 294, 936–950. [Google Scholar] [CrossRef]
- Wang, J.; He, S. Optimal decisions of modularity, prices and return policy in a dual-channel supply chain under mass customization. Transp. Res. Part E Logist. Transp. Rev. 2022, 160, 102675. [Google Scholar] [CrossRef]
- Liu, W.; Liang, Y.; Tang, O.; Ma, X. Channel competition and collaboration in the presence of hybrid retailing. Transp. Res. Part E Logist. Transp. Rev. 2022, 160, 102658. [Google Scholar] [CrossRef]
- Bhuniya, S.; Pareek, S.; Sarkar, B. A supply chain model with service level constraints and strategies under uncertainty. Alex. Eng. J. 2021, 60, 6035–6052. [Google Scholar] [CrossRef]
- Bhuniya, S.; Pareek, S.; Sarkar, B.; Sett, B.K. A smart production process for the optimum energy consumption with maintenance policy under a supply chain management. Processes 2021, 9, 19. [Google Scholar] [CrossRef]
- Habib, M.S.; Asghar, O.; Hussain, A.; Imran, M.; Mughal, M.P.; Sarkar, B. A robust possibilistic programming approach toward animal fat-based biodiesel supply chain network design under uncertain environment. J. Clean. Prod. 2021, 278, 122403. [Google Scholar] [CrossRef]
- Matsui, K. Optimal timing of acquisition price announcement for used products in a dual-recycling channel reverse supply chain. Eur. J. Oper. Res. 2022, 300, 615–632. [Google Scholar] [CrossRef]
- Shao, X.F. Integrated product and channel decision in mass customization. IEEE Trans. Eng. Manag. 2013, 60, 30–45. [Google Scholar] [CrossRef]
- Yang, W.; Zhang, J.; Yan, H. Impacts of online consumer reviews on a dual-channel supply chain. Omega 2021, 101, 102266. [Google Scholar] [CrossRef]
- Mahar, S.; Wright, P.D. In-store pickup and returns for a dual channel retailer. IEEE Trans. Eng. Manag. 2017, 64, 491–504. [Google Scholar] [CrossRef]
- Tian, C.; Xiao, T.; Shang, J. Channel differentiation strategy in a dual-channel supply chain considering free riding behavior. Eur. J. Oper. Res. 2021, 301, 473–485. [Google Scholar] [CrossRef]
- Gao, D.; Wang, N.; He, Z.; Jia, T. The bullwhip effect in an online retail supply chain: A perspective of price-sensitive demand based on the price discount in e-commerce. IEEE Trans. Eng. Manag. 2017, 64, 134–148. [Google Scholar] [CrossRef]
- Choi, T.M.; Wen, X.; Sun, X.; Chung, S.H. The mean-variance approach for global supply chain risk analysis with air logistics in the blockchain era. Transp. Res. Part E Logist. Transp. Rev. 2019, 127, 178–191. [Google Scholar] [CrossRef]
- Li, Z.; Nan, G.; Li, M. Advertising or freemium: The impacts of social effects and service quality on competing platforms. IEEE Trans. Eng. Manag. 2020, 67, 220–233. [Google Scholar] [CrossRef]
- Yu, L.; He, X.; Zhang, J.; Xu, C. Horizontal cooperative advertising with advertising threshold effects. Omega 2021, 98, 102104. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, X.; Xie, J.; Zhu, W. Inequality aversion in cooperative advertising in supply chain: An experimental study. Int. J. Prod. Res. 2021, 1–23. [Google Scholar] [CrossRef]
- Huang, S.; Zhang, X.; Chen, S. Information acquisition with advertising threshold effect under manufacturer encroachment in a supply chain. Transp. Res. Part E Logist. Transp. Rev. 2021, 153, 102439. [Google Scholar] [CrossRef]
- Yan, K.; Hua, G.; Cheng, T.C.E.; Wang, S.; Dong, J.X. Joint promotion of cross-market retailers: Models and analysis. Int. J. Prod. Res. 2021, 1–22. [Google Scholar] [CrossRef]
- Karray, S.; Martín-Herrán, G.; Sigué, S.P. Managing advertising investments in marketing channels. J. Retail Consum. Serv. 2022, 65, 201852. [Google Scholar] [CrossRef]
- Liu, C.; Chen, W.; Zhou, Q.; Mu, J. Modelling dynamic freshness-keeping effort over a finite time horizon in a two-echelon online fresh product supply chain. Eur. J. Oper. Res. 2021, 293, 511–528. [Google Scholar] [CrossRef]
- Choi, T.M.; Liu, N. Optimal advertisement budget allocation and coordination in luxury fashion supply chains with multiple brand-tier products. Transp. Res. Part E Logist. Transp. Rev. 2019, 130, 95–107. [Google Scholar] [CrossRef]
- Ma, P. Optimal generic and brand advertising efforts in a decentralized supply chain considering customer surplus. J. Retail Consum. Serv. 2021, 60, 102502. [Google Scholar] [CrossRef]
- Liu, S.; Hua, G.; Cheng, T.C.E.; Choi, T.M. Optimal pricing and quality decisions in supply chains with consumers’anticipated regret and online celebrity retailers. IEEE Trans. Eng. Manag 2022, 1–15. [Google Scholar] [CrossRef]
- Du, S.; Wang, L.; Hu, L.; Zhu, Y. Platform-led green advertising: Promote the best or promote by performance. Transp. Res. Part E Logist. Transp. Rev. 2019, 128, 115–131. [Google Scholar] [CrossRef]
- Farshbaf-Geranmayeh, A.; Zaccour, G. Pricing and advertising in a supply chain in the presence of strategic consumers. Omega 2021, 101, 102239. [Google Scholar] [CrossRef]
- Niu, B.; Yue, H.; Luo, H.; Shang, W. Pricing for newly-launched experience products: Free trial or not? Transp. Res. Part E Logist. Transp. Rev. 2019, 126, 149–176. [Google Scholar] [CrossRef]
- Khorshidvand, B.; Soleimani, H.; Sibdari, S.; Seyyed Esfahani, M.M. Revenue management in a multi-level multi-channel supply chain considering pricing, greening, and advertising decisions. J. Retail. Consum. Serv. 2021, 59, 102425. [Google Scholar] [CrossRef]
- Karray, S.; Martín-Herrán, G. The impact of a store brand introduction in a supply chain with competing manufacturers: The strategic role of pricing and advertising decision timing. Int. J. Prod. Econ. 2022, 244, 108378. [Google Scholar] [CrossRef]


| Notations | Explanation |
|---|---|
| The consumers’ utility when purchasing the product, where . | |
| The demand for the product, where . | |
| The number of consumers. | |
| The advertisement levels, where . | |
| The cost for sale channels, where . | |
| The cost for the advertisement, where . | |
| The cost coefficient for the advertisements, where . | |
| The discount factor for the online advertisements, where . | |
| The retail prices, where . | |
| Consumers’ valuation for the product, where . | |
| The retailer’s profits, where . | |
| The difference in profits between online and offline channels. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, K.; Liu, S.; Zuo, M.; Zheng, J.; Xu, Y. Dual-Channel Supply Chain Pricing Decisions under Discounted Advertising Value. Systems 2022, 10, 76. https://doi.org/10.3390/systems10030076
Yan K, Liu S, Zuo M, Zheng J, Xu Y. Dual-Channel Supply Chain Pricing Decisions under Discounted Advertising Value. Systems. 2022; 10(3):76. https://doi.org/10.3390/systems10030076
Chicago/Turabian StyleYan, Ke, Shuai Liu, Min Zuo, Jiamin Zheng, and Yadong Xu. 2022. "Dual-Channel Supply Chain Pricing Decisions under Discounted Advertising Value" Systems 10, no. 3: 76. https://doi.org/10.3390/systems10030076
APA StyleYan, K., Liu, S., Zuo, M., Zheng, J., & Xu, Y. (2022). Dual-Channel Supply Chain Pricing Decisions under Discounted Advertising Value. Systems, 10(3), 76. https://doi.org/10.3390/systems10030076






