A Study on the Drivers of Carbon Emissions in China’s Power Industry Based on an Improved PDA Method
Abstract
:1. Introduction
2. Materials and Methods
2.1. Methods
2.1.1. Environmental Production Technology
2.1.2. LMDI Model
2.1.3. Production Theory Decomposition Method Based on LMDI
2.2. Data Description
- (1)
- Data related to the power industry: The electricity industry data required for the DEA method’s input–output include coal-fired power generation energy consumption, coal-fired power generation output, total power generation output, coal-fired power generation industry installed capacity, and coal-fired power generation industry employment. Thermal power generation, total power generation, and thermal energy consumption data are all derived from the Energy Statistics Yearbook, where thermal energy consumption data are summed by converting various fuels used in thermal power generation into standard coal volumes. The number of people employed in thermal power generation is mainly derived from provincial statistical yearbooks and the installed capacity of the thermal power industry, which is taken from the Electricity Statistical Yearbook. The descriptive statistics of input and output variables are shown in Table 1 below.
- (2)
- Macrodata by province: The macrodata for each province include the gross regional product, the area of each province and municipality, the number of people in each province, and the annual rainfall of each province and municipality. Gross regional product is from the China Statistical Yearbook, and the area of each region is from the official website of the Central People’s Government of the People’s Republic of China. Population figures for each province were taken from provincial and municipal statistical yearbooks. Annual rainfall data are generated by processing the China daily ground climate dataset, where the annual provincial rainfall is the sum of the annual rainfall of each urban area in the province.
- (3)
- Data on carbon emissions from the power sector: The carbon emissions from the power sector calculated in this study are mainly derived from direct carbon emissions from the combustion of fuels for thermal power generation without considering indirect carbon emissions from other inputs. The calculation method is “activity data × emission factor × oxidation rate × global warming potential parameter”. Activity data comprise the fuel consumption used for thermal power generation from the Energy Statistics Yearbook, and the emission factor and oxidation rate are shown in Table A1. The potential global warming parameters for carbon dioxide, methane, and nitric oxides are 1, 21, and 310, respectively [33].
3. Results
3.1. National Power Sector Carbon Emission Ratio Decomposition Results
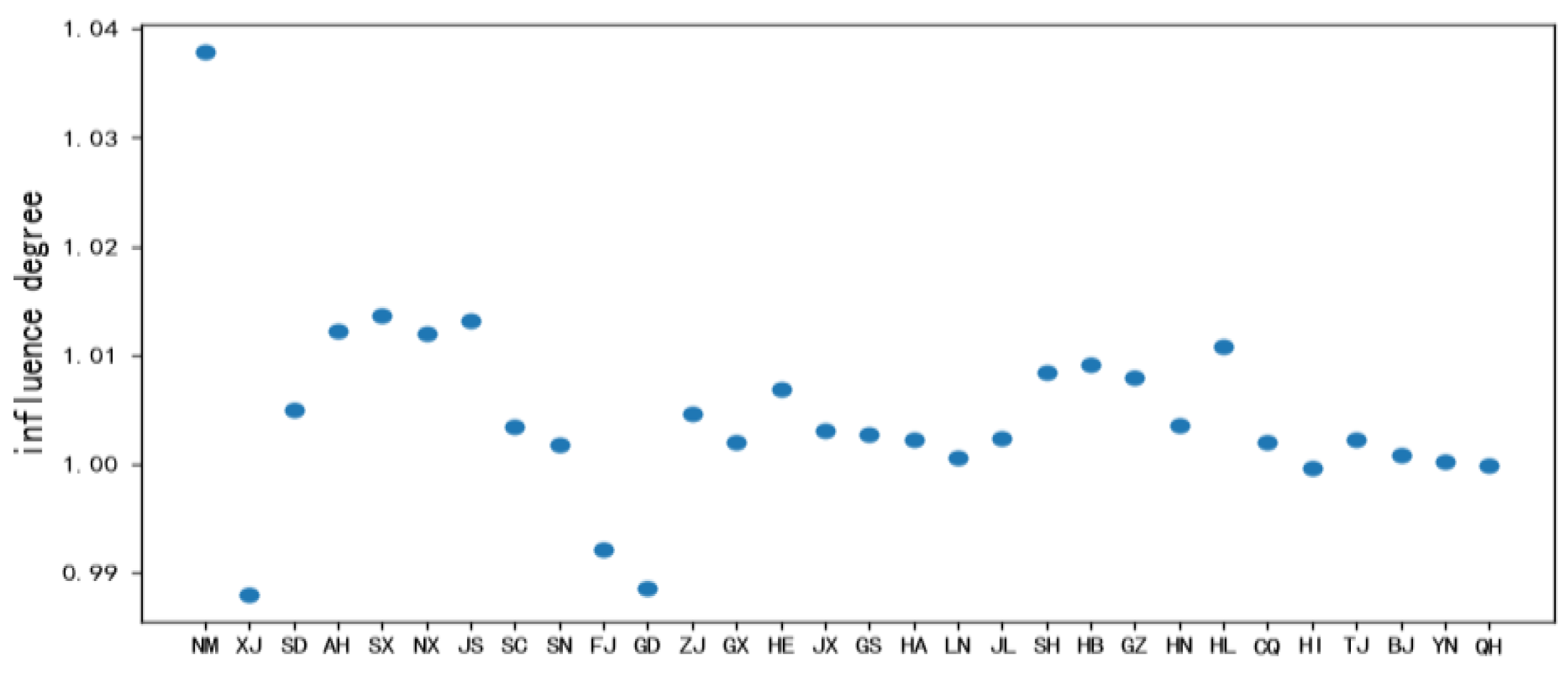
3.2. Results of the Decomposition of Carbon Emission Ratios in Different Provinces
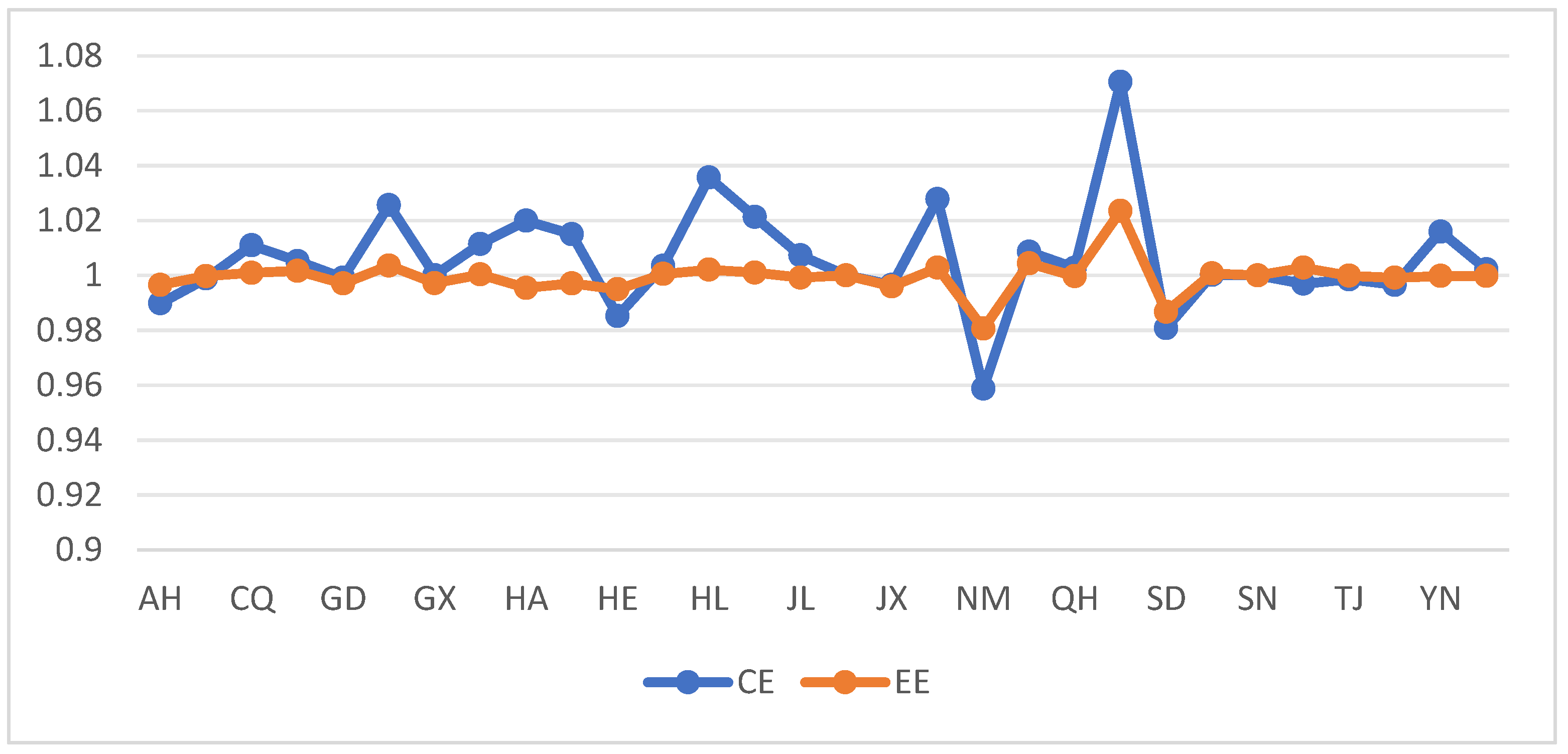
3.3. Efficiency and Technology Impact Factors
3.3.1. Thermal Power Energy and Emission Efficiency Factors
3.3.2. Technical Factors for Energy Saving and Emission Reduction in Thermal Power
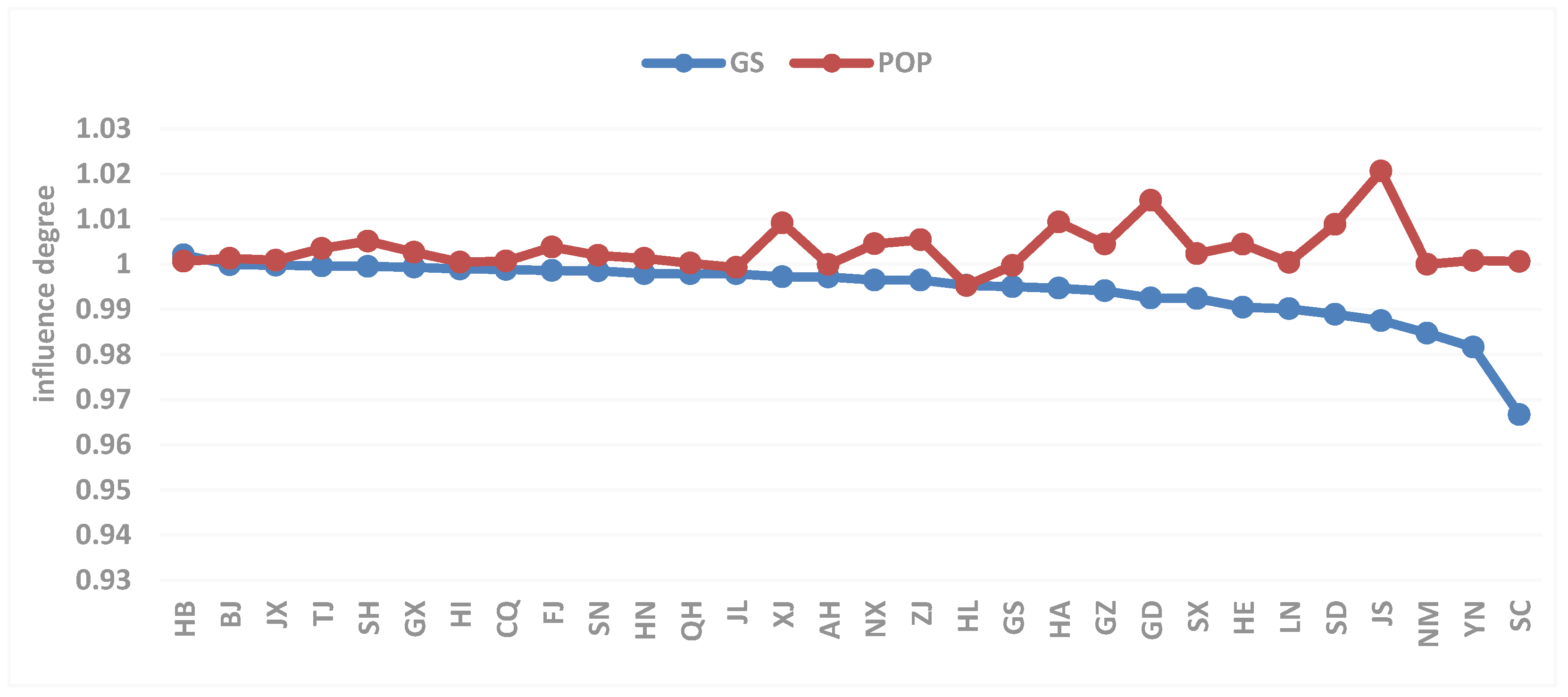
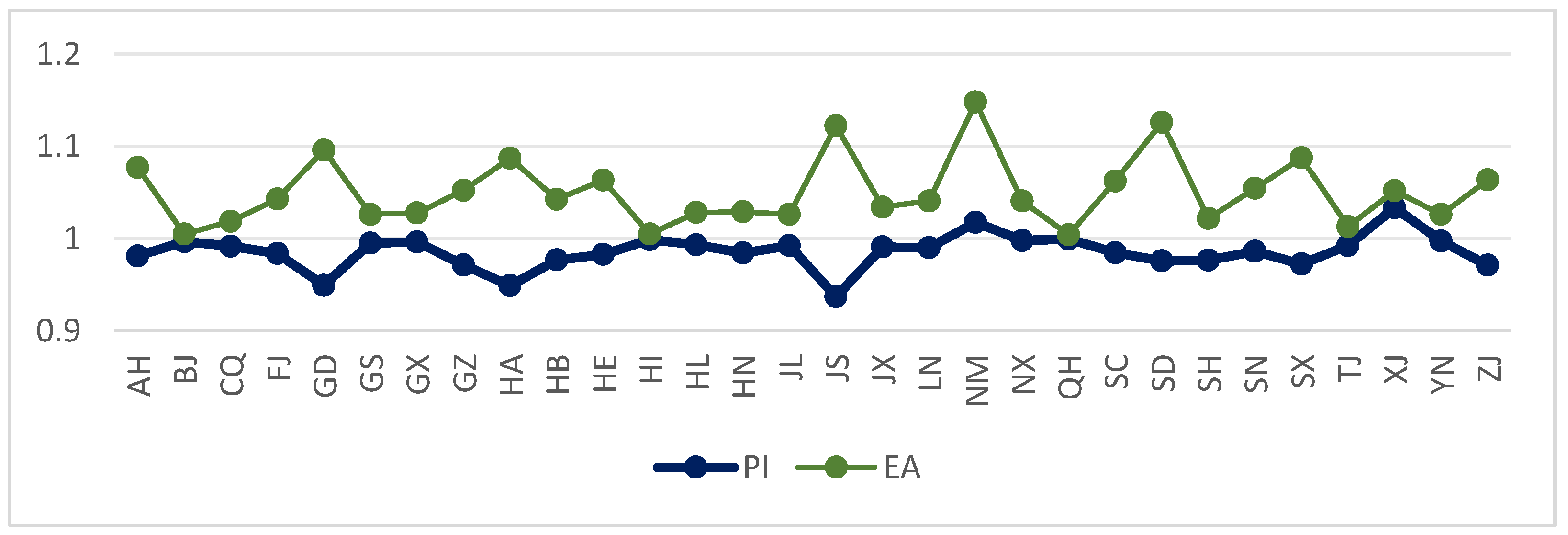
3.4. Other Influencing Factors
3.4.1. Potential Drivers in the Thermal Power Sector
3.4.2. Power Generation Mix and Population Density Drivers
3.4.3. Analysis of Economic Drivers
3.4.4. Analysis of Climate Drivers
4. Discussion
5. Conclusions
- (1)
- Carbon emissions from the power sector, with the national power sector’s carbon emission ratio being greater than 1, indicate that carbon emissions from China’s power sector still increased during the study period, while provincial carbon emission ratios show that super tier 1 cities, such as Beijing, Shanghai, and Qinghai, and provinces with low electricity consumption have a better effect in reducing emissions from the power sector compared to other provinces and cities.
- (2)
- With respect to driving factors, economic development is the most important reason for the growth of carbon emissions in China’s power sector. Growth in GDP per capita has more than double the impact on carbon emissions in the power sector than all other drivers of carbon emissions growth combined. Electricity generation per unit of GDP is the main driver of carbon emission reduction in the power sector, and the generation mix, thermal power reduction technologies, and thermal power energy efficiency technologies are also positive factors in achieving carbon reduction in the power sector.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Energy | Average Net Calorific Value (108 J/ton) | EFCO2i (ton/1012 J) | EFCH4i (ton/1012 J) | EFN2Oi (ton/1012 J) | Oxygenation Efficiency (%) |
|---|---|---|---|---|---|
| Raw Coal | 209.08 | 94.60 | 0.001 | 0.0015 | 91.80 |
| Cleaned Coal | 263.44 | 94.60 | 0.001 | 0.0015 | 91.80 |
| Other Washed Coal | 83.63 | 94.60 | 0.001 | 0.0015 | 91.80 |
| Briquettes | 209.08 | 97.53 | 0.001 | 0.0015 | 92.80 |
| Coke | 284.35 | 107.07 | 0.001 | 0.0015 | 92.80 |
| Other Coking Products | 284.35 | 94.60 | 0.001 | 0.0015 | 92.80 |
| Crude Oil | 418.16 | 73.33 | 0.003 | 0.0006 | 97.90 |
| Gasoline | 430.70 | 69.30 | 0.003 | 0.0006 | 98.60 |
| Diesel Oil | 426.52 | 74.07 | 0.003 | 0.0006 | 98.20 |
| Fuel Oil | 418.16 | 77.37 | 0.003 | 0.0006 | 98.50 |
| Other Petroleum Products | 418.16 | 73.33 | 0.003 | 0.0006 | 97.90 |
| Coke Oven Gas | 167.26 * | 44.37 | 0.001 | 0.0001 | 99.00 |
| Other Gas | 52.27 * | 44.37 | 0.001 | 0.0001 | 99.00 |
| Liquefied Petroleum Gas | 501.79 | 63.07 | 0.001 | 0.0001 | 98.90 |
| Refinery Gas | 460.55 | 57.57 | 0.001 | 0.0001 | 98.90 |
| Natural Gas | 389.31 * | 56.10 | 0.001 | 0.0001 | 99.00 |
| Liquefied Natural Gas | 514.86 | 56.10 | 0.001 | 0.0001 | 99.00 |
| Other Energy | 292.71 | 91.67 | 0.001 | 0.0001 | 99.00 |
| Province | Province Abbreviations |
|---|---|
| Anhui | AH |
| Beijing | BJ |
| Chongqing | CQ |
| Fujian | FJ |
| Gansu | GS |
| Guangdong | GD |
| Guangxi | GX |
| Guizhou | GZ |
| Hainan | HI |
| Hebei | HE |
| Heilongjiang | HL |
| Henan | HA |
| Hubei | HB |
| Hunan | HN |
| Inner Mongolia | NM |
| Jiangsu | JS |
| Jiangxi | JX |
| Jiangxi | SX |
| Jilin | JL |
| Liaoning | LN |
| Ningxia | NX |
| Qinhai | QH |
| Shaanxi | SN |
| Shandong | SD |
| Shanghai | SH |
| Sichuan | SC |
| Tianjin | TJ |
| Xinjiang | XJ |
| Yunnan | YN |
| Zhejiang | ZJ |
References
- Lyu, J.; Li, J. Coupling and Coordinated Spatiotemporal Evolution of the Three-Dimensional System among Carbon Emission-Economic Growth-Ecological Environment in China. Ecol. Econ. 2022, 38, 36–43. [Google Scholar]
- Zhao, Y.; Wang, W.; Yan, S. Distributionally robust optimization scheduling of a joint wind-solar-storage system considering step-type carbon trading. Power Syst. Prot. Control 2023, 51, 127–136. [Google Scholar] [CrossRef]
- Yang, L.S.; Lin, B.Q. Carbon dioxide-emission in China’s power industry: Evidence and policy implications. Renew. Sustain. Energy Rev. 2016, 60, 258–267. [Google Scholar] [CrossRef]
- Kou, Y.; Wu, J.; Zhang, H.; Yang, J.; Jiang, H. Low carbon economic dispatch for a power system considering carbon capture and CVaR. Power Syst. Prot. Control 2023, 51, 131–140. [Google Scholar] [CrossRef]
- Ding, T.; Yang, J.; Song, P. Decomposition Analysis of Carbon Emissions between Eight Comprehensive Economic Areas of China—Based on the Perspective of Temporal and Spatial Technical Heterogeneities. China Soft Sci. 2022, 36, 89–96. [Google Scholar]
- Zhou, X.; Zhou, D.; Wang, Q. Who shapes China’s carbon intensity and how? A demand-side decomposition analysis. Energy Econ. 2020, 85, 104600. [Google Scholar] [CrossRef]
- Li, J.; Meng, G.; Li, C.; Du, K. Tracking carbon intensity changes between China and Japan: Based on the decomposition technique. J. Clean. Prod. 2022, 349, 131090. [Google Scholar] [CrossRef]
- De Oliveira-De Jesus, P.M. Effect of generation capacity factors on carbon emission intensity of electricity of Latin America & theCaribbean, a temporal IDA-LMDI analysis. Renew. Sustain. Energy Rev. 2019, 101, 516–526. [Google Scholar]
- Xu, S.C.; He, Z.X.; Long, R.Y.; Chen, H.; Han, H.M.; Zhang, W.W. Comparative analysis of the regional contributions to carbon emissions in China. J. Clean. Prod. 2016, 127, 406–417. [Google Scholar] [CrossRef]
- Yan, Q.; Zhang, Q.; Zou, X. Decomposition analysis of carbon dioxide emissions in China’s regional thermal electricity generation, 2000–2020. Energy 2016, 112, 788–794. [Google Scholar] [CrossRef]
- Chang, N.; Lahr, M.L. Changes in China’s production-source CO2 emissions: Insights from structural decomposition analysis and linkage analysis. Econ. Syst. Res. 2016, 28, 224–242. [Google Scholar] [CrossRef]
- Chang, Y.F.; Lin, S.J. Structural decomposition of industrial CO2 emission in Taiwan: An input-output approach. Energy Policy 1998, 26, 5–12. [Google Scholar] [CrossRef]
- de Araújo, I.F.; Jackson, R.W.; Neto AB, F.; Perobelli, F.S. European union membership and CO2 emissions: A structural decomposition analysis. Struct. Chang. Econ. Dyn. 2020, 55, 190–203. [Google Scholar] [CrossRef]
- Dietzenbacher, E.; Kulionis, V.; Capurro, F. Measuring the effects of energy transition: A structural decomposition analysis of the change in renewable energy use between 2000 and 2014. Appl. Energy 2020, 258, 114040. [Google Scholar] [CrossRef]
- Wang, Q.; Han, X. Is decoupling embodied carbon emissions from economic output in Sino-US trade possible? Technol. Forecast. Soc. Chang. 2021, 169, 120805. [Google Scholar] [CrossRef]
- Zhang, C.; Su, B.; Zhou, K.; Yang, S. Analysis of electricity consumption in China (1990–2016) using index decomposition and decoupling approach. J. Clean. Prod. 2019, 209, 224–235. [Google Scholar] [CrossRef]
- Lin, B.; Tan, R. Sustainable development of China’s energy intensive industries: From the aspect of carbon dioxide emissions reduction. Renew. Sustain. Energy Rev. 2017, 77, 386–394. [Google Scholar] [CrossRef]
- Chong, C.; Liu, P.; Ma, L.; Li, Z.; Ni, W.; Li, X.; Song, S. LMDI decomposition of energy consumption in Guangdong Province, China, based on an energy allocation diagram. Energy 2017, 133, 525–544. [Google Scholar] [CrossRef]
- Yang, J.; Hao, Y.; Feng, C. A race between economic growth and carbon emissions: What play important roles towards global low-carbon development? Energy Econ. 2021, 100, 105327. [Google Scholar] [CrossRef]
- Zheng, X.; Wang, R.; Du, Q. How does industrial restructuring influence carbon emissions: City-level evidence from China. J. Environ. Manag. 2020, 276, 111093. [Google Scholar] [CrossRef]
- Zhou, P.; Ang, B.W. Decomposition of aggregate CO2 emissions: A production-theoretical approach. Energy Econ. 2008, 30, 1054–1067. [Google Scholar] [CrossRef]
- Wang, Q.; Han, X.; Li, R. Does technical progress curb India’s carbon emissions? A novel approach of combining extended index decomposition analysis and production-theoretical decomposition analysis. J. Environ. Manag. 2022, 310, 114720. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Zhao, Y.; Qiao, X.; Liu, Y.; Cao, Y.; Li, Y.; Wang, S.; Zhang, Z.; Zhang, Y.; Wang, J. Identifying the driving forces of national and regional CO2 emissions in China: Based on temporal and spatial decomposition analysis models. Energy Econ. 2017, 68, 522–538. [Google Scholar] [CrossRef]
- Zhou, P.; Zhang, H.; Zhang, L. The drivers of energy intensity changes in Chinese cities: A production-theoretical decomposition analysis. Appl. Energy 2022, 30, 118230. [Google Scholar] [CrossRef]
- Tian, Y.; Wang, Y.Z.; Hang, Y.; Wang, Q.W. The two-stage factors driving changes in China’s industrial SO2 emission intensity: A production-theoretical decomposition analysis. Sci. Total Environ. 2021, 814, 152426. [Google Scholar] [CrossRef]
- Zhang, X.P.; Tan, Y.K.; Tan, Q.L.; Yuan, J.H. Decomposition of aggregate CO2 emissions within a joint production framework. Energy Econ. 2012, 34, 1088–1097. [Google Scholar] [CrossRef]
- Wang, C. Changing energy intensity of economies in the world and its decomposition. Energy Econ. 2013, 40, 637–644. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, P.; Xie, B.C.; Zhang, N. Assessing drivers of CO2 emissions in China’s electricity sector: A metafrontier production-theoretical decomposition analysis. Eur. J. Oper. Res. 2019, 275, 1096–1107. [Google Scholar] [CrossRef]
- Liu, X.; Zhou, D.; Zhou, P.; Wang, Q. Factors driving energy consumption in China: A joint decomposition approach. J. Clean. Prod. 2018, 172, 724–734. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, Z.; Zhang, J. Research on carbon emission differences decomposition and spatial heterogeneity pattern of China’s eight economic regions. Environ. Sci. Pollut. Res. Int. 2022, 29, 29976–29992. [Google Scholar] [CrossRef]
- Banerjee, S. Addressing the carbon emissions embodied in India’s bilateral trade with two eminent Annex-II parties: With input–output and spatial decomposition analysis. Environ. Dev. Sustain. 2020, 23, 5430–5464. [Google Scholar] [CrossRef]
- Taeyoung, J.; Dowon, K. Korean carbon intensity change: Production-theoretical Decomposition Analysis (PDA) and Log Mean Divisia Index (LMDI). Korean Energy Econ. Rev. 2021, 20, 105–138. [Google Scholar]
- Zhang, S. Study on Driving Factors and Reduction Strategies of Greenhouse Gas Emissions for China’s Power Industry. Ph.D. Thesis, Tianjin University, Tianjin, China, 2019. [Google Scholar]
- Shao, L.; Yu, X.; Feng, C. Evaluating the eco-efficiency of China’s industrial sectors: A two-stage network data envelopment analysis. J. Environ. Manag. 2019, 247, 551–560. [Google Scholar] [CrossRef] [PubMed]
- Shephard, R.W.; Fare, R. The law of diminishing returns. Prod. Theory 1974, 99, 287–318. [Google Scholar]
- Färe, R.; Grosskopf, S.; Lovell, C.K.; Pasurka, C. Multilateral productivity comparisons when some outputs are undesirable: A nonparametric approach. Rev. Econ. Stat. 1989, 71, 90–98. [Google Scholar] [CrossRef]
- Farrell, M.J. The measurement of productive efficiencyl. J. R. Soc. Ser. A 1957, 120, 253–290. [Google Scholar] [CrossRef]
- Wang, M.; Feng, C. The impacts of technological gap and scale economy on the low-carbon development of China’s industries: An extended decomposition analysis. Technol. Forecast. Soc. Chang. 2020, 157, 120050. [Google Scholar] [CrossRef]
- Wang, Q.; Hang, Y.; Su, B.; Zhou, P. Contributions to sector-level carbon intensity change: An integrated decomposition analysis. Energy Econ. 2018, 70, 12–25. [Google Scholar] [CrossRef]
- Li, X.; Liao, H.; Du, Y.F.; Wang, C.; Wang, J.W.; Liu, Y. Carbon dioxide emissions from the electricity sector in major countries: A decomposition analysis. Environ. Sci. Pollut. Res. 2018, 25, 6814–6825. [Google Scholar] [CrossRef]
- Xie, B.C.; Tan, X.Y.; Zhang, S.; Wang, H. Decomposing CO2 emission changes in thermal power sector: A modified production-theoretical approach. J. Environ. Manag. 2021, 281, 111887. [Google Scholar] [CrossRef]





| Indicators | Energy Input | Labor | Installed Capacity | Electricity Output | CO2 Emissions |
|---|---|---|---|---|---|
| (104 tce) | (Person) | (104 KW) | (108 KWh) | (104 t) | |
| Maximum | 25,983.68 | 283,000 | 11,135 | 5141.56 | 50,535.26 |
| Minimum | 332.6506 | 19,471 | 3 | 55.63 | 436.6437 |
| Mean | 5648.746 | 117,412.4 | 2717.7 | 1229.527 | 10,042.93 |
| Standard deviation | 5192.419 | 64,939.48 | 2670.228 | 1190.148 | 9292.748 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, H.; Zhan, T.; Yi, Z.; Shuo, W.; Yan, L. A Study on the Drivers of Carbon Emissions in China’s Power Industry Based on an Improved PDA Method. Systems 2023, 11, 495. https://doi.org/10.3390/systems11100495
Wei H, Zhan T, Yi Z, Shuo W, Yan L. A Study on the Drivers of Carbon Emissions in China’s Power Industry Based on an Improved PDA Method. Systems. 2023; 11(10):495. https://doi.org/10.3390/systems11100495
Chicago/Turabian StyleWei, Hu, Tian Zhan, Zhang Yi, Wang Shuo, and Li Yan. 2023. "A Study on the Drivers of Carbon Emissions in China’s Power Industry Based on an Improved PDA Method" Systems 11, no. 10: 495. https://doi.org/10.3390/systems11100495
APA StyleWei, H., Zhan, T., Yi, Z., Shuo, W., & Yan, L. (2023). A Study on the Drivers of Carbon Emissions in China’s Power Industry Based on an Improved PDA Method. Systems, 11(10), 495. https://doi.org/10.3390/systems11100495






