Integrating Subjective–Objective Weights Consideration and a Combined Compromise Solution Method for Handling Supplier Selection Issues

Abstract

The development of artificial intelligence and the recent COVID-19 pandemic as well as the emergence of other diseases has led to dramatic changes in the overall supply chain development. The choice of a suitable supplier will be the key to ensuring sustainable development of the company and the normal operation of the overall supply chain. However, the evaluation data of the supplier selection contains both qualitative and quantitative data simultaneously. In addition, the evaluation information provided by experts often includes some incomplete and hesitant information. These reasons lead to the complexity of supplier selection. Traditional supplier selection calculation methods ignore the objective weight considerations and thus lead to biased assessment results. The main goal of this study is to overcome the limitations of conventional supplier selection methods, fully consider the subjective and objective weights of the evaluation criteria and deal with incomplete information for providing more correct supplier ranking results. A stepwise weight assessment ratio analysis (SWARA) method, the 2-tuple linguistic representation method, and the combined compromise solution (CoCoSo) were applied in this study to solve the problem of supplier selection. To verify the rationality and correctness of the proposed method, the third-party logistics supplier selection was used as the illustrated example in the numerical validation section. The simulation results confirm that the proposed method can effectively deal with supplier selection with unclear information and can provide more reasonable supplier ranking results.

1. Introduction

The key to the successful operation of the supply chain will involve the means to quickly respond to market trend fluctuations and adapt to changes in the business environment. Suppliers are an important part of building a supply chain, choosing the right and suitable supplier will directly affect product quality and competitive advantage. The process of supplier selection is very complicated and difficult, and simultaneously includes multiple experts, multiple evaluation criteria, and both qualitative and quantitative data. The data include the characteristics of benefit and non-benefit criteria, which belong to a multi-expert and multi-criteria decision-making (MCDM) problem.

Handling both qualitative and quantitative data in the supplier selection process is an important issue in supply chain management. Most studies deal with both qualitative and quantitative data using linguistic fuzzy or normalized transformations. Although many MCDM methods integrate qualitative and quantitative data in different ways, there are still some limitations. For example, the subjective and objective weights of evaluation criteria cannot be considered at the same time, and traditional methods cannot deal with the missing or hesitant information. In the process of supplier selection, the weight consideration of the evaluation criteria directly affects the correctness of the evaluation results. The consideration of the evaluation criteria includes subjective weight and objective weight. Subjective weights are subjectively determined by experts based on their professional background, while objective weights are calculated objectively based on the evaluation data. Many studies only consider the subjective weight of the evaluation criteria for processing the MCDM problems, ignoring the objective weight of the evaluation data (e.g., [1,2]). On the contrary, many studies only considered the objective weight of the evaluation data, and ignored the subjective weight determined by the professional experience of experts (e.g., [3,4]). In addition, Pourhejazy et al. [5] used the nested-fuzzy inference system with interactions method to replace the simple weighted average method for solving the product deletion of fast moving consumer goods. Pagone et al. [6] and Saxena et al. [7] proposed the automatic weight distribution method for minimizing subjectivity. The automatic weight distribution method used four weight distributions (uniform, halving, quadratic, and first two) to describe the decision-making space in detail. The advantages of the automatic weight distribution method does not require consultation with decision makers to determine the importance of the evaluation criteria. However, these methods still cannot handle incomplete information and hesitant information provided by experts.

There are many methods for solving the objective weights of the evaluation criteria, such as the statistical variance procedure method [8], entropy method [9], weighted arithmetic average approach [10], criteria importance through the intercriteria correlation (CRITIC) method [11], the stepwise weight assessment ratio analysis (SWARA) method [12], etc. The SWARA method is different from other objective weight calculation methods; the method emphasizes the ratio value of multiple evaluation criteria to calculate the weight of the evaluation criteria.

The combined compromise solution (CoCoSo) approach is a recently newly developed MCDM method. The CoCoSo method was first introduced by Yazdani et al. [13], which combined the simple additive weighted (SAW) method and exponentially weighted product method to propose a compromise solution of combining three different aggregation strategies, then ranking the possible potential alternatives. Since its development, the CoCoSo method has been widely used in many different group decision-making areas, such as the selection of waste clothing recycling channels [14], location selection of the logistics center [15], failure mode and effects analysis [16], and COVID-19 disease drug selection [17]. However, the typical CoCoSo method [13] cannot process the incomplete information and unclear information provided by experts, and it also ignores the consideration of subjective weight and objective weight.

Although many studies use different algorithms to deal with qualitative and quantitative data simultaneously, there still exist some limitations which cannot deal with lost and hesitant information. The main goal of this study is to overcome the limitations of conventional supplier selection methods, fully consider the subjective and objective weights of the evaluation criteria and deal with incomplete information for providing more correct supplier ranking results. A stepwise weight assessment ratio analysis (SWARA) method, the 2-tuple linguistic representation method, and the combined compromise solution (CoCoSo) were applied in this study to solve the problem of supplier selection. The proposed method used the SWARA approach to calculate the objective weight of the evaluation criteria, followed by the subjective and objective integration weights to perform the supplier selection assessment. For the incomplete or unclear information provided by experts, the use of data filling and defuzzification techniques, respectively, fully grasp all of the information provided by the experts.

The rest of this study is organized as follows. Section 2 briefly reviews the relevant literature. Following the discussion on the initial background in the Section 1, in Section 3, the preliminaries are presented, including the SAW method, entropy objective weighting method, SWARA method, CoCoSo method, and the 2-tuple linguistic representation method. Section 4 proposes the integration of the subjective–objective weights consideration and the CoCoSo method as the new supplier selection method. In Section 5, an illustrated example of third-party logistics (3PL) supplier selection is presented and compared with some commonly used supplier selection methods to verify the correctness and rationality of the proposed approach. The Section 6 presents a brief conclusion and future research directions.

2. Literature Review

Supplier selection is a multi-expert and MCDM problem. The evaluation data for the supplier selection contains both qualitative and quantitative data, which will make it more complicated and difficult to find the suitable supplier. Many studies used a different computational logic to combine different qualitative and quantitative data for solving MCDM problems. The summary of the different related studies for the MCDM problem as shown in Table 1.

For the studies on compensatory and non-compensatory measures of MCDM problems, Garcia-Bernabeu et al. [18] used the multi-reference point that was based on weak and strong composite indicators to evaluate the regional innovation performance in Spain. Garcia-Bernabeu et al.’s method can consider the varying degrees of compensability. Bilbao-Terol et al. [19] combined the multiple reference point method and the extended best–worst method to rank the non-life insurance companies in Spain. Bilbao-Terol et al. [19] considered the non-compensatory, partially compensatory, and the fully compensatory operators to obtain aggregated joint performance scores for each company. In terms of considering the non-compensability, partial compensability, and the full compensability, Ruiz and Cabello [20] proposed the multiple reference point partially compensatory indicator to solve the sustainability assessment field decision-making problem.

The consideration of subjective and objective weights of evaluation factors will affect the evaluation results of the MCDM problems. Many studies use the analytic hierarchy process (AHP) method to calculate the subjective weight of the evaluation factors by comparing the evaluation factors with each other (e.g., [21,22,23,24,25]). Extending the concept of the AHP method, Gurbuz and Albayrak [26] used the analytic network process (ANP) method and considered the interdependence of the evaluation factors to calculate the subjective weight of the evaluation factors. According to the subjective confirmation of different experts and the weight of the evaluation criteria, Zeydan and Colpan [27] used the average of the triangular fuzzy numbers to calculate the subjective weight of the evaluation factors.

Many studies have explored the objective weighting of the evaluation criteria by using different calculation methods. For example, Alkan and Kahraman [28] and Krishnan et al. [29] used the criteria importance through the intercriteria correlation (CRITIC) method to calculate the objective weight of the evaluation factors. Irvanizam et al. [30] combined the multi-objective optimization for the basis of the ratio analysis (MOORA) and the trapezoidal fuzzy neutrosophic sets to solve the MCDM problems. Irvanizam et al. [30] used the correlation coefficient and standard deviation method to calculate the objective weight of the evaluation factors. Guo et al. [31] used the concept of entropy to obtain the objective weight of the evaluation factors, then used the technique for order preference by similarity to ideal solution (TOPSIS) method to solve the partner selection problems in the prefabricated construction enterprises.

The SWARA method is different from other objective weight calculation methods; the method emphasizes the ratio value of multiple evaluation criteria to calculate the weight of the evaluation criteria. The SWARA method was first proposed by Keršuliene et al. [32]; the evaluation criteria are graded from the most important weight value to the least important weight value when evaluating possible potential alternatives. Many studies have used the SWARA method to explore the solution to different MCDM problems. For example, Yucenur and Ipekci [33] combined the SWARA and the weighted aggregated sum product assessment to process the location selection of the ocean current power plant. Albawab et al. [34] combined the SWARA method and the additive ratio assessment approach to calculate the performance index of possible potential alternatives, then ranked the different energy storage-related technologies. Currently, the SWARA method has been widely used in different decision-making fields, such as groundwater vulnerability assessment [35], copper exploration [36], groundwater resources assessment [37], maintenance strategy of public buildings [12], and tourist and resident areas of satisfaction for tourism development [38]. Zhou et al. [39] extended the concept of the decision-making trial and evaluation laboratory (DEMATEL) method to obtain the subjective weights of the evaluation factors, and used the entropy method to calculate the objective weight of the evaluation factors. In the processing of the MCDM problem evaluation information, Zhou et al. [39], Chung and Chang [40], and Chang [41] used the hesitant fuzzy linguistic term set to handle the hesitant information that experts provided. However, these methods still cannot handle the incomplete information that experts provided. For the incomplete information process, these methods will directly neglect the incomplete information that causes the loss of valuable information.

Table 1. Summary of the related studies of the MCDM problem (Sources: created by the author).

Authors	MCDM Method											Handling of Lost Information	Handling of Hesitant Information	Weights Consideration
	AHP	ANP	IFS	TOPSIS	NS	MOORA	DEA	CRITIC	SWARA	CoCoSo	MVOWA			Subjective Weight	Objective Weight
Proposed method									V	V		V	V	V	V
Santos et al. [28]	V													V
Rani and Kaushal [29]	V			V										V
Chang et al. [30]	V													V
Pathan et al. [31]	V			V										V
Zhou et al. [32]	V													V
Gurbuz and Albayrak [33]		V												V
Zeydan and Colpan [34]				V			V							V
Alkan and Kahraman [35]			V					V							V
Krishnan et al. [36]								V							V
Irvanizam et al. [37]					V	V									V
Guo et al. [38]				V											V
Zhou et al. [39]	V												V	V	V
Chung and Chang [40]	V						V						V	V
Chang [41]											V		V	V

Note: SWARA: stepwise weight assessment ratio analysis, CoCoSo: combined compromise solution, MVOWA: minimal variance ordered weighted average, HFLTS: hesitant fuzzy linguistic term set, AHP: analytic hierarchy process, TOPSIS: technique for order of preference by similarity to ideal solution, DEA: data envelopment analysis, CRITIC: criteria importance through intercriteria correlation, NS: neutrosophic set, MOORA: optimization method by ratio analysis, ANP: analytic network process, IFS: intuitionistic fuzzy set.

Table 1. Summary of the related studies of the MCDM problem (Sources: created by the author).

Authors	MCDM Method											Handling of Lost Information	Handling of Hesitant Information	Weights Consideration
	AHP	ANP	IFS	TOPSIS	NS	MOORA	DEA	CRITIC	SWARA	CoCoSo	MVOWA			Subjective Weight	Objective Weight
Proposed method									V	V		V	V	V	V
Santos et al. [28]	V													V
Rani and Kaushal [29]	V			V										V
Chang et al. [30]	V													V
Pathan et al. [31]	V			V										V
Zhou et al. [32]	V													V
Gurbuz and Albayrak [33]		V												V
Zeydan and Colpan [34]				V			V							V
Alkan and Kahraman [35]			V					V							V
Krishnan et al. [36]								V							V
Irvanizam et al. [37]					V	V									V
Guo et al. [38]				V											V
Zhou et al. [39]	V												V	V	V
Chung and Chang [40]	V						V						V	V
Chang [41]											V		V	V

Note: SWARA: stepwise weight assessment ratio analysis, CoCoSo: combined compromise solution, MVOWA: minimal variance ordered weighted average, HFLTS: hesitant fuzzy linguistic term set, AHP: analytic hierarchy process, TOPSIS: technique for order of preference by similarity to ideal solution, DEA: data envelopment analysis, CRITIC: criteria importance through intercriteria correlation, NS: neutrosophic set, MOORA: optimization method by ratio analysis, ANP: analytic network process, IFS: intuitionistic fuzzy set.

3. Preliminaries

This section briefly introduces the related definitions and calculation rules of the SAW method, entropy objective weighting method, SWARA method, and the CoCoSo method.

3.1. Simple Additive Weighted Method

The SAW method is one of the most commonly used methods for MCDM problems, and its advantage is the simplicity of calculation. Experts directly decide the weight of each evaluation criterion in the simple weighting method. Then the weight is multiplied by the rating value of the potential alternatives to obtain a simple additive weighted value. Finally, the simple additive weighted value of all potential alternatives ranking from largest to smallest to find the most suitable potential alternative.

The calculation process of the SAW method is as follows [42].

(1)

Establish an initial decision matrix $(x_{ij})$.

$$x_{ij}=\left[\begin{array}{ccc}{x}_{11}& x_{12}& \begin{array}{cc}\dots & x_{1n}\end{array}\\ x_{21}& x_{22}& \begin{array}{cc}\dots & x_{2n}\end{array}\\ \begin{array}{c}⋮\\ x_{m1}\end{array}& \begin{array}{c}⋮\\ x_{m2}\end{array}& \begin{array}{cc}\ddots & ⋮\\ \dots & x_{mn}\end{array}\end{array}\right], i=1, 2, \dots , m, j=1, 2, \dots , n$$

(1)

where $x_{ij}$ is the ith alternative and the jth criterion.

(2)

Normalize the initial decision matrix $(y_{ij})$.

$$y_{ij}=\frac{x_{ij}}{\underset{i}{max} x_{ij}}, \mathrm{for} \mathrm{benefit} \mathrm{criteria}$$

(2)

$$y_{ij}=\frac{\underset{i}{min} x_{ij}}{x_{ij}}, \mathrm{for} \mathrm{non-benefit} \mathrm{criteria}$$

(3)

(3)

Calculate the simple additive weighted value $(SA{W}_i)$.

$$SA{W}_i={{\displaystyle \sum }}_{j=1}^n{w}_j·y_{ij}$$

(4)

3.2. Entropy Objective Weighting Method

The entropy objective weighting method can calculate the relative weight of the evaluation criteria based on the real rating values of each evaluation criterion. The main advantage of the entropy objective weighting method is that it reduces the subjective influence of expert opinions and increases the objectivity of the evaluation results [9].

The calculation process of the entropy objective weighting method is as follows [43].

(1)

Establish an initial decision matrix $(x_{ij})$.

The initial decision matrix $(x_{ij})$ of the entropy objective weighting method is the same as the SAW method, as shown in Equation (1).

(2)

Normalize the initial decision matrix $(y_{ij})$.

The initial decision matrix $(y_{ij})$ of the entropy objective weighting method is normalized and is the same as the SAW method, as shown in Equations (2) and (3).

(3)

Calculate the entropy value of each evaluation criterion.

The formula for calculating the entropy value of the evaluation standard is shown in Equation (5).

$$E_j=-\frac{1}{\ln \left(m\right)}{{\displaystyle \sum }}_{i=1}^m{y}_{ij}·\ln (y_{ij}), j=1, 2, \dots , n$$

(5)

where i is the ith alternative, and j is the jth criterion.

(4)

Calculate the entropy objective weighting of each evaluation criterion.

The formula for calculating the entropy objective weighting of the evaluation standard is shown in Equation (6).

$$w_j=\frac{1-E_j}{{{\displaystyle \sum }}_{j=1}^n\left(1-E_j\right)}$$

(6)

3.3. Stepwise Weight Assessment Ratio Analysis Method

The SWARA method uses the experts’ opinion on the relative importance of the evaluation criteria to gradually calculate the objective weight of the evaluation criteria.

The calculation process of the SWARA method is as follows [44].

(1)

Ranking the comparative importance of the average value $s_j$ in descending order.

(2)

Calculate the coefficient $t_j$.

$$t_j=\left\{\begin{array}{cc}1& j=1\\ s_j+1& j>1\end{array}\right.$$

(7)

(3)

Calculate the recalculated weight $u_j$.

$$u_j=\left\{\begin{array}{cc}1& j=1\\ \frac{u_{j-1}}{t_j}& j>1\end{array}\right.$$

(8)

(4)

Calculate the relative weight of the evaluation criteria.

$$w_j=\frac{u_j}{{{\displaystyle \sum }}_{j=1}^n{u}_j}$$

(9)

where n is the number of evaluation criteria and $w_j$ is the relative weight of evaluation criteria j.

3.4. Combined Compromise Solution Method

The CoCoSo method used the concept of the weighted product method, weighted sum method, and weighted aggregated sum product assessment to rank multiple alternatives of MCDM problems.

The calculation process of the CoCoSo method is as follows [20,45].

(1)

Establish an initial decision matrix $(x_{ij})$.

The initial decision matrix $(x_{ij})$ of the CoCoSo method is the same as that of the SAW method, as shown in Equation (1).

(2)

Normalize the initial decision matrix $(z_{ij})$.

$$z_{ij}=\frac{x_{ij}-\underset{i}{min} x_{ij}}{\underset{i}{max} x_{ij}-\underset{i}{min} x_{ij}}, \mathrm{for} \mathrm{benefit} \mathrm{criteria}$$

(10)

$$z_{ij}=\frac{\underset{i}{max} x_{ij}-x_{ij}}{\underset{i}{max} x_{ij}-\underset{i}{min} x_{ij}}, \mathrm{for} \mathrm{non-benefit} \mathrm{criteria}$$

(11)

where $z_{ij}$ is the ith normalized alternative value for the jth criterion.

(3)

Calculation of the power weight of comparability sequences $(P_i)$ and the total of weighted comparability sequences $(S_i)$ for each alternative.

The $P_i$ value is obtained based on the weighted aggregated sum product assessment multiplicative. The $S_i$ value is obtained based on the gray relational analysis method.

$$P_i={{\displaystyle \sum }}_{j=1}^n{\left(z_{ij}\right)}^{w_j}$$

(12)

$$S_i={{\displaystyle \sum }}_{j=1}^n{w}_j·z_{ij}$$

(13)

(4)

Calculation of the relative weight for each alternative.

$$k_{ia}=\frac{P_i+S_i}{{{\displaystyle \sum }}_{i=1}^m\left(P_i+S_i\right)}$$

(14)

$$k_{ib}=\frac{S_i}{\underset{i}{min} S_i}+\frac{P_i}{\underset{i}{min} P_i}$$

(15)

$$k_{ic}=\frac{\lambda S_i+\left(1-\lambda \right)P_i}{\lambda \underset{i}{max} S_i+\left(1-\lambda \right)\underset{i}{max} P_i}, 0\le \lambda \le 1$$

(16)

$k_{ia}$ is the arithmetic mean of the weighted sum method and the weighted product method. $k_{ib}$ is the sum of the relative scores of the weighted sum method and the weighted product method compared to the optimal value. $k_{ic}$ is the balanced compromise of the weighted sum method and the weighted product method. The λ value is determined by experts. If the experts cannot determine the λ value, it is set to $\lambda =0.5$.

(5)

Ranking of the possible potential alternative.

According to the $k_i$ value, the possible potential alternatives are ranked. A higher $k_i$ value indicates a better possible potential alternative.

$$k_i=\sqrt[3]{k_{ia}{k}_{ib}{k}_{ic}}+\frac{1}{3}\left(k_{ia}+k_{ib}+k_{ic}\right)$$

(17)

3.5. The 2-Tuple Linguistic Representation Method

The 2-tuple linguistic representation method was first introduced by Herrera and Martinez [46]; the method uses the linguistic 2-tuple $\left(s_h, \alpha \right)$ to express the fuzzy linguistic assessment information. The $s_h$ expresses the linguistic variable in the linguistic term set $S=\left\{s_0,s_1,s_2,\dots , s_g\right\}$ and $h=\left[0,g\right]$, $\alpha$ denotes the numerical value of the symbolic translation [47].

Definition 1

([46,48]). Assuming that the $S=\left\{s_0,s_1,s_2,\dots , s_g\right\}$ is an ordered linguistic term set and  $\beta \in \left[0,g\right]$  expresses the results of the symbolic aggregation operation. The linguistic 2-tuple  $\left(s_h, \alpha \right)$ is equal to information  $\beta$, defined as follows.

$$△:\left[0,g\right]\to \mathrm{S}\times \left[-0.5, 0.5\right)$$

(18)

$$△\left(\beta \right)=\left\{\begin{array}{cc}{s}_h,& g=round\left(\beta \right)\\ \alpha =\beta -h,& \alpha \in \left[-0.5, 0.5\right)\end{array}\right.$$

(19)

where α is the distance between the actual and linguistic variable and  $s_h$  expresses the closest linguistic variable.

Definition 2

([46,49]). Assuming that $x=\left\{\left(s_1,{\alpha }_1\right),\left(s_2,{\alpha }_2\right),\dots , \left(s_g,{\alpha }_g\right)\right\}$ is a linguistic 2-tuple set; the 2-tuple arithmetic mean (2-tuple AM) is defined as follows.

$$2 \mathrm{tuple} \mathrm{AM}\left(x\right)=△\left({{\displaystyle \sum }}_{h=1}^g\frac{1}{g}{△}^{-1}\left(s_h,{\alpha }_h\right)\right)=△\left(\frac{1}{g}{{\displaystyle \sum }}_{h=1}^g{\beta }_h\right)$$

(20)

4. Proposed Method

The rapid development of artificial intelligence and the spread of emerging infectious diseases (such as the COVID-19 pandemic) have led to major changes in the composition of supply chain members. Thus, the key to ensuring that the company can pursue profitability and continue to grow steadily now depends on quickly adapting to changes in the environment and consumption patterns and choosing the most suitable supplier. However, the evaluation data of the supplier selection simultaneously includes both qualitative and quantitative data. In addition, the attributes of the assessment data also include benefit and non-benefit attributes. The evaluation data provided by experts simultaneously include clear information, some unclear information, and some hesitant information, all of which increase the difficulty of correctly selecting the most suitable supplier. Moreover, the traditional supplier selection method cannot effectively handle it. To overcome the limitations of traditional supplier selection methods, this paper integrated the subjective–objective weights consideration and the CoCoSo method for handling supplier selection issues. The proposed method used the SWARA method to calculate the objective weight between the evaluation criteria, then combined this objective weight with the subjective weight provided by experts to calculate the integrated weight of the evaluation criteria. For the unclear information and hesitant information provided by experts, data filling and defuzzification techniques, respectively, were used and all of the important information provided by the experts were fully taken into account. Finally, the CoCoSo method was used to rank the possible potential alternative.

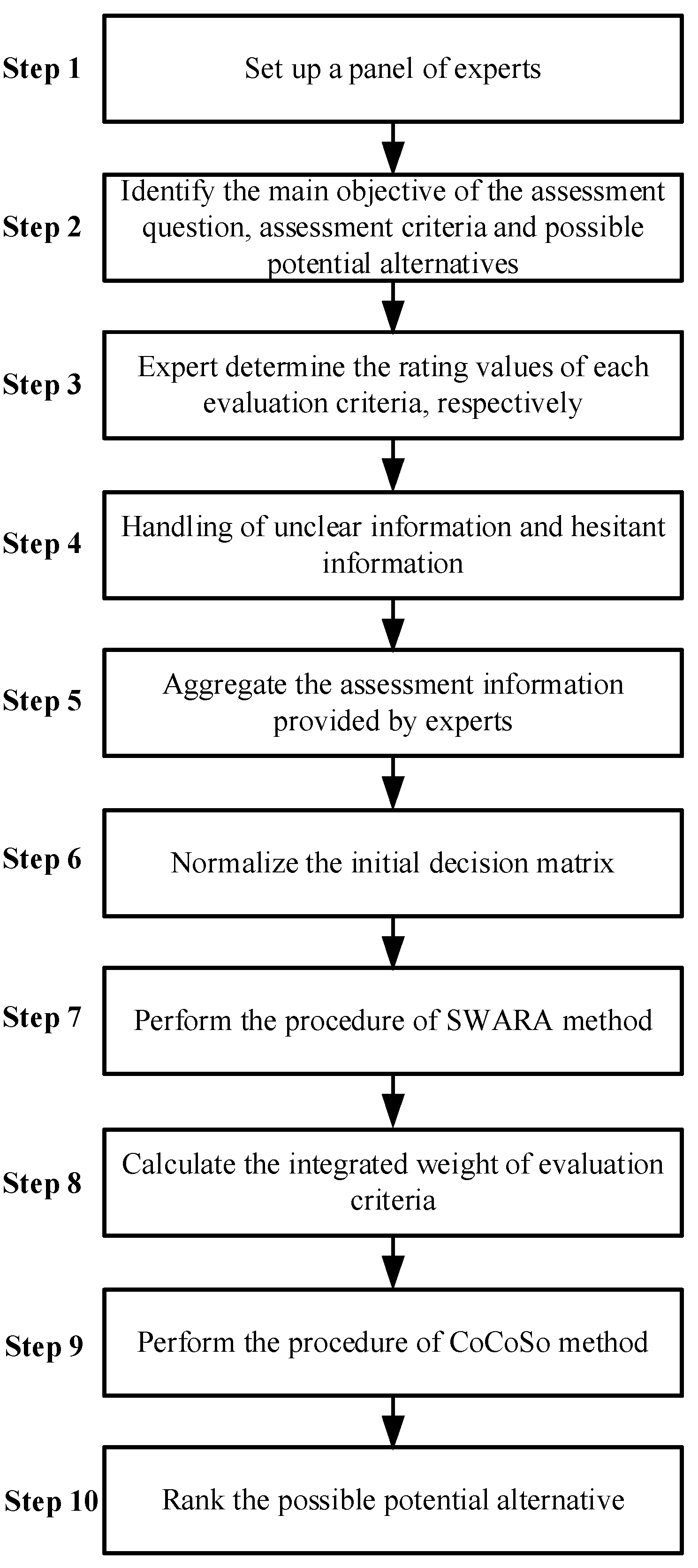
The execution procedure of the proposed method includes the following ten steps, as shown in Figure 1.

Step 1. Set up a panel of experts.

Form a panel of experts and evaluate the supplier selection issues.

Step 2. Identify the main objective of the assessment question, assessment criteria, and possible potential alternatives.

The evaluation team of experts discusses to identify the evaluation question objectives, evaluation criteria, and possible potential alternatives.

Step 3. Determine the rating values of each evaluation criterion, respectively.

Experts, based on their professional background and experience, determine the rating values of each evaluation criterion.

Step 4. Handle unclear information and hesitant information.

For the unclear information, the clear information from other experts was provided to fill in the data. For the hesitant information provided by experts, defuzzification of the value of the interval information using the arithmetic mean (AM) [50,51], as follows.

$$\mathrm{AM}=\frac{l+r}{2}$$

(21)

where l is the left limit value of the interval information and r is the right limit value of the interval information.

Step 5. Aggregate the assessment information provided by experts.

The assessment information provided by experts is aggregated on the selection committee.

Step 6. Normalize the initial decision matrix.

Used Equations (10) and (11) to normalize the initial decision matrix.

Step 7. Perform the procedure of the SWARA method.

Used Equations (7)–(9) to perform the procedure of SWARA.

Step 8. Calculate the integrated weight $(w_j^I$) of the evaluation criteria.

Equation (22) is used to calculate the integrated weight of the evaluation criteria.

$$w_j^I=\beta w_j^S+\left(1-\beta \right)w_j^O, j=1, 2, \dots , n$$

(22)

where $w_j^S$ is the subjective weight of the evaluation criteria, $w_j^O$ is the objective weight of the evaluation criteria, and $\beta$ is the important coefficient of the subjective weight, if the experts cannot determine the $\beta$ value, set $\beta =0.5$.

Step 9. Perform the procedure of the CoCoSo method.

According to the normalized initial decision matrix of Step 5 and the integrated weight of Step 7, Equations (12) and (13) are used to calculate the $P_i$ value and the $S_i$ value, respectively. Then use Equations (14)–(17) to calculate the $k_{ia}$, $k_{ib}$, $k_{ic}$, and the $k_i$ values, respectively.

Step 10. Rank the possible potential alternative.

According to the $k_i$ value of the ranking of the possible potential alternative.

5. Numerical Example

5.1. Case Overview

The continuous advancement of artificial intelligence has led to dramatic changes in the composition of the supply chain. To pursue the sustainable development of the overall supply chain, choosing the right supplier is critical to the successful operation of each enterprise. In this section, the 3PL supplier selection (adapted from [52]) was used as the simulation example to explain and verify the rationality and correctness of the proposed method. The 3PL is different from the traditional logistics method. In the traditional logistics method, enterprises use their own transportation and warehousing equipment to transport and directly deliver the products they sell to customers. In the 3PL, professional logistics service companies are used to complete the logistics operation of products; hence, it is also called logistics outsourcing. The committee of the 3PL provider selection includes three experts (Expert 1, Expert 2, and Expert 3) in the simulation example. The possible alternatives include five possible candidate 3PL providers (PA1, PA2, PA3, PA4, and PA5). The 3PL provider selection consists of five evaluation criteria, the charge (EC1), service delivery (EC2), service quality perceived by customers (EC3), geographic coverage of the European Union (EC4), and flexibility (EC5). Experts decide the weights of the evaluation criteria (EC1, EC2, EC3, EC4, and EC5) to be 0.30, 0.10, 0.25, 0.20, and 0.15, respectively. The evaluation criterion EC1 is the price the company has to pay for the services provided by the 3PL provider to the companies. The evaluation criterion EC2 is the percentage of goods delivered on time by the 3PL provider within the promised time frame. The evaluation criterion EC3 is the service quality perceived by customers, rated on an ordinal scale from s1 to s10, where s1 means the customer perceives the lowest service quality and s10 means the customer perceives the highest service quality. The evaluation criterion EC4 is the percentage of geographic coverage of the European Union by the area served by the 3PL provider. The evaluation criterion EC5 requires the 3PL provider to fit in with the changes in customer needs; this criterion is rated on an ordinal scale from s1 to s10, where s1 means the minimal flexibility and s10 means the maximum flexibility. The evaluation criterion EC1 belongs to the cost criterion, and the evaluation criteria EC2, EC3, EC4, and EC5 belong to the benefit criteria. The rating values of each evaluation criterion for the five possible alternatives is shown in

Table 2. The rating values of each evaluation criterion for the five possible alternatives (the case data adapted from [52]).

Evaluation Criteria	Experts	Possible Alternatives
		PA1	PA2	PA3	PA4	PA5
EC1 (EUR/km)		0.95	0.92	0.99	0.90	1.20
EC2 (%)		99.98	99.95	99.90	98.98	99.97
EC3 (Scale 1–10)	Expert 1	s9	s9	s10	s9	s8
	Expert 2	s9	s10	**	s8	[s8, s9]
	Expert 3	s9	s10	s9	s9	s9
EC4 (%)		88	92	75	85	95
EC5 (Scale 1–10)	Expert 1	s8	s9	s9	s8	s9
	Expert 2	s9	s10	**	s8	[s9, s10]
	Expert 3	s9	s9	s8	s8	s10

** expresses the information that does not exist.

.

5.2. Solution by the Simple Additive Weighted Method

The SAW method [42] is the most commonly used method for supplier selection. The advantage of this method is the simplicity of calculation. However, the SAW method is not able to process the unclear information from experts. In Table 1, Expert 2 provides the evaluation information including partly incomplete information and partly hesitant information; thus, only the evaluation information provided by Expert 1 and Expert 3 can be used in the SAW method. According to the contents of Table 1, Equations (2) and (3) were used to normalize the decision-making matrix and then calculate the simple additive weighted value, the results are shown in

Table 3. The final ranks by the simple additive weighted (SAW) method (Sources: created by the author).

Evaluation Criteria	PA1	PA2	PA3	PA4	PA5	Sum	${\mathit{E}}_{\mathit{j}}$	Weights
EC1 (EUR/km)	−0.051	−0.022	−0.087	0.000	−0.216	−0.375	0.233	0.185
EC2 (%)	0.000	0.000	−0.001	−0.010	0.000	−0.011	0.007	0.239
EC3 (Scale 1–10)	−0.051	0.000	0.000	−0.051	−0.100	−0.202	0.125	0.211
EC4 (%)	−0.071	−0.031	−0.187	−0.100	0.000	−0.388	0.241	0.183
EC5 (Scale 1–10)	−0.100	−0.051	−0.100	−0.145	0.000	−0.395	0.245	0.182

.

5.3. Solution by the Entropy Objective Weighting Method

The entropy objective weighting method [43] can only process clear information from experts. However, the information provided by Expert 2 contains some ambiguous information and some non-existent information in Table 1. Thus, only the evaluation information provided by Experts 1 and 3 can be used in the entropy objective weighting method. According to the contents of Table 1, Equations (2) and (3) were used to normalize the initial decision matrix $(y_{ij})$, the results are shown in Table 2. Both the SAW method and the entropy objective weighting method function the same in this normalized initial decision matrix. Based on the normalized initial decision matrix $(y_{ij})$, Equation (5) was used to calculate the entropy value of five evaluation criteria, and the results are shown in

Table 4. The entropy value of five evaluation criteria (Sources: created by the author).

Evaluation Criteria	PA1	PA2	PA3	PA4	PA5	Sum	${\mathit{E}}_{\mathit{j}}$	Weights
EC1 (EUR/km)	−0.051	−0.022	−0.087	0.000	−0.216	−0.375	0.233	0.185
EC2 (%)	0.000	0.000	−0.001	−0.010	0.000	−0.011	0.007	0.239
EC3 (Scale 1–10)	−0.051	0.000	0.000	−0.051	−0.100	−0.202	0.125	0.211
EC4 (%)	−0.071	−0.031	−0.187	−0.100	0.000	−0.388	0.241	0.183
EC5 (Scale 1–10)	−0.100	−0.051	−0.100	−0.145	0.000	−0.395	0.245	0.182

. The normalized initial decision matrix $(y_{ij})$ was used to multiply the weights to obtain the final rank results by the entropy objective weighting method, the results are shown in

Table 5. The final ranks by the entropy objective weighting method (Sources: created by the author).

Evaluation Criteria	PA1	PA2	PA3	PA4	PA5
EC1 (EUR/km)	0.175	0.181	0.168	0.185	0.139
EC2 (%)	0.239	0.239	0.239	0.237	0.239
EC3 (Scale 1–10)	0.200	0.211	0.211	0.200	0.189
EC4 (%)	0.169	0.177	0.144	0.164	0.183
EC5 (Scale 1–10)	0.163	0.172	0.163	0.153	0.182
Sum	0.947	0.981	0.925	0.939	0.932
Final ranks	2	1	5	3	4

.

5.4. Solution by the Typical Combined Compromise Solution (CoCoSo) Method

The typical CoCoSo method was first proposed by Yazdani et al. [20]; the method uses the concept of exponentially weighted product method, SAW method, and different balanced compromises of the exponentially weighted product method and SAW method to rank the possible multiple potential alternatives. The typical CoCoSo method cannot handle the issues of unclear information and missing information provided from the experts; thus, only the complete and clear information provided by Expert 1 and Expert 3 can be used in the typical CoCoSo method.

As mentioned in Table 2, the evaluation information by Experts 1 and 3 was aggregated and provided as an initial decision matrix, the results are shown in

Table 6. Aggregated information of the evaluation criteria by the typical combined compromise solution (CoCoSo) method (Sources: created by the author).

Evaluation Criteria	PA1	PA2	PA3	PA4	PA5
EC1 (EUR/km)	0.950	0.920	0.990	0.900	1.200
EC2 (%)	99.980	99.950	99.900	98.980	99.970
EC3 (Scale 1–10)	(s9, 0.000)	(s10, −0.500)	(s10, −0.500)	(s9, 0.000)	(s9, −0.500)
EC4 (%)	88.000	92.000	75.000	85.000	95.000
EC5 (Scale 1–10)	(s9, −0.500)	(s9, 0.000)	(s9, −0.500)	(s8, 0.000)	(s10, −0.500)

.

Based on the initial decision matrix of Table 6, Equations (10) and (11) were used to normalize initial decision matrix, the results are shown in

Table 7. Normalize the decision matrix by the typical combined compromise solution (CoCoSo) method (Sources: created by the author).

Evaluation Criteria	PA1	PA2	PA3	PA4	PA5
EC1 (EUR/km)	0.833	0.933	0.700	1.000	0.000
EC2 (%)	1.000	0.970	0.920	0.000	0.990
EC3 (Scale 1–10)	0.500	1.000	1.000	0.500	0.000
EC4 (%)	0.650	0.850	0.000	0.500	1.000
EC5 (Scale 1–10)	0.333	0.667	0.333	0.000	1.000

.

According to the normalized initial decision matrix of Table 7, Equations (12) and (13) were used to calculate the $P_i$ value and the $S_i$ value, respectively, the results are shown in

Table 8. The values of $P_i$ by the typical combined compromise solution (CoCoSo) method (Sources: created by the author).

Evaluation Criteria	PA1	PA2	PA3	PA4	PA5
EC1 (EUR/km)	0.947	0.980	0.899	1.000	0.000
EC2 (%)	1.000	0.997	0.992	0.000	0.999
EC3 (Scale 1–10)	0.841	1.000	1.000	0.841	0.000
EC4 (%)	0.917	0.968	0.000	0.871	1.000
EC5 (Scale 1–10)	0.848	0.941	0.848	0.000	1.000
Pi	4.553	4.885	3.738	2.711	2.999

and

Table 9. The values of $S_i$ by the typical combined compromise solution (CoCoSo) method (Sources: created by the author).

Evaluation Criteria	PA1	PA2	PA3	PA4	PA5
EC1 (EUR/km)	0.250	0.280	0.210	0.300	0.000
EC2 (%)	0.100	0.097	0.092	0.000	0.099
EC3 (Scale 1–10)	0.125	0.250	0.250	0.125	0.000
EC4 (%)	0.130	0.170	0.000	0.100	0.200
EC5 (Scale 1–10)	0.050	0.100	0.050	0.000	0.150
Si	0.655	0.897	0.602	0.525	0.449

.

According to the $P_i$ value of Table 8 and the $S_i$ value of Table 9, use Equations (14)–(17) to calculate the $k_{ia}$, $k_{ib}$, $k_{ic}$, and the $k_i$ values, respectively, the results are shown in

Table 10. The final aggregation ranking of the possible alternatives by the typical combined compromise solution (CoCoSo) method (Sources: created by the author).

	PA1	PA2	PA3	PA4	PA5
ka	0.237	0.263	0.197	0.147	0.157
Ranks	2	1	3	5	4
kb	0.152	0.177	0.163	0.180	0.157
Ranks	5	2	3	1	4
kc	0.901	1.000	0.751	0.560	0.596
Ranks	2	1	3	5	4
ki	0.748	0.840	0.659	0.541	0.548
Final ranks	2	1	3	5	4

.

5.5. Solution by the Proposed Method

The proposed method integrates the subjective–objective weights consideration and the CoCoSo method to deal with the problem of supplier selection under unclear information. The execution procedure of the proposed method includes the following ten steps.

Step 1. Set up a panel of experts.

Form a panel of experts and evaluate the supplier selection issues.

Step 2. Identify the main objective of the assessment question, assessment criteria, and possible potential alternatives.

The main objective of the assessment question is the ranking of the possible potential 3PL supplier. The assessment criteria include charge (EC1), service delivery (EC2), service quality perceived by customers (EC3), geographic coverage of the European Union (EC4), and flexibility (EC5). The possible alternatives include five possible candidate 3PL providers (PA1, PA2, PA3, PA4, and PA5).

Step 3. An expert determines the rating values of each evaluation criterion, respectively.

Based on the different professional background and experience, each expert determines the rating values of each evaluation criterion for the five possible alternatives, respectively; the calculation results are shown in Table 2.

Step 4. Handle unclear information and hesitant information.

As shown in Table 2, Expert 2 provided the rating values of evaluation criteria EC3 and EC5, including some unclear information and hesitant information. Expert 1 and Expert 3 provided clear information to fill the data and Equation (21) was used for the defuzzification of the value of the interval information.

Step 5. Aggregate the assessment information provided by experts.

Aggregation of the assessment information provided by the three experts of the 3PL provider selection committee, the results are shown in

Table 11. Aggregation of the information of the evaluation criteria by experts provided (Sources: created by the author).

Evaluation Criteria	PA1	PA2	PA3	PA4	PA5
EC1 (EUR/km)	0.950	0.920	0.990	0.900	1.200
EC2 (%)	99.980	99.950	99.900	98.980	99.970
EC3 (Scale 1–10)	(s9, 0.000)	(s10, −0.333)	(s10, −0.500)	(s9, 0.333)	(s8, 0.167)
EC4 (%)	88.000	92.000	75.000	85.000	95.000
EC5 (Scale 1–10)	(s9, −0.333)	(s9, 0.333)	(s9, −0.500)	(s9, −0.333)	(s9, 0.167)

.

Step 6. Normalize the initial decision matrix.

Based on the initial decision matrix of Table 11, Equations (10) and (11) were used to normalize the initial decision matrix for the 3PL providers, the results are shown in

Table 12. Normalization of the decision matrix for the 3PL providers (Sources: created by the author).

Evaluation Criteria	PA1	PA2	PA3	PA4	PA5	Sum
EC1 (EUR/km)	0.833	0.933	0.700	1.000	0.000	3.467
EC2 (%)	1.000	0.970	0.920	0.000	0.990	3.880
EC3 (Scale 1–10)	0.556	1.000	0.889	0.778	0.000	3.222
EC4 (%)	0.650	0.850	0.000	0.500	1.000	3.000
EC5 (Scale 1–10)	0.333	1.000	0.167	0.200	0.800	2.200

.

Step 7. Perform the procedure of SWARA.

Equations (7)–(9) were used to perform the procedure of SWARA; the results are shown in

Table 13. The objective weight and integrated weight of the evaluation criteria (Sources: created by the author).

Evaluation Criteria		${\mathit{s}}_{\mathit{j}}$	${\mathit{t}}_{\mathit{j}}$	${\mathit{u}}_{\mathit{j}}$	${\mathit{w}}_{\mathit{j}}$	Subjective Weight	Integrated Weight
EC2 (%)	3.880	–	1.000	1.000	0.333	0.100	0.217
EC1 (EUR/km)	3.467	0.413	1.413	0.708	0.236	0.300	0.268
EC3 (Scale 1–10)	3.222	0.244	1.244	0.569	0.190	0.250	0.220
EC4 (%)	3.000	0.222	1.222	0.465	0.155	0.200	0.178
EC5 (Scale 1–10)	2.200	0.800	1.800	0.258	0.086	0.150	0.118

.

Step 8. Calculate the integrated weight of the evaluation criteria.

According to the subjective weight of the evaluation criteria provided by the experts and the objective weight obtained in Step 7, Equation (22) was used to calculate the integrated weight of evaluation criteria, and the results are shown in Table 13.

Step 9. Perform the procedure of the CoCoSo method.

According to the normalized initial decision matrix of Table 12 and the integrated weight of Table 13, Equations (12) and (13) were used to calculate the $P_i$ value and the $S_i$ value, respectively, the results are shown in

Table 14. The values of $P_i$ by the proposed method (Sources: created by the author).

Evaluation Criteria	PA1	PA2	PA3	PA4	PA5
EC1 (EUR/km)	0.952	0.982	0.909	1.000	0.000
EC2 (%)	1.000	0.993	0.982	0.000	0.998
EC3 (Scale 1–10)	0.879	1.000	0.974	0.946	0.000
EC4 (%)	0.926	0.972	0.000	0.884	1.000
EC5 (Scale 1–10)	0.827	1.000	0.000	0.827	0.974
Pi	4.584	4.947	2.865	3.657	2.972

and

Table 15. The values of $S_i$ by the proposed method (Sources: created by the author).

Evaluation Criteria	PA1	PA2	PA3	PA4	PA5
EC1 (EUR/km)	0.223	0.250	0.188	0.268	0.000
EC2 (%)	0.217	0.210	0.199	0.000	0.215
EC3 (Scale 1–10)	0.122	0.220	0.195	0.171	0.000
EC4 (%)	0.115	0.151	0.000	0.089	0.178
EC5 (Scale 1–10)	0.024	0.118	0.000	0.024	0.094
Si	0.701	0.949	0.582	0.551	0.487

. Then use Equations (14)–(17) to calculate the $k_{ia}$, $k_{ib}$, $k_{ic}$, and the $k_i$ values, respectively, the results are shown in

Table 16. The final aggregation ranking of the possible alternatives (Sources: created by the author).

	PA1	PA2	PA3	PA4	PA5
ka	0.2371	0.2644	0.1546	0.1888	0.1551
Ranks	2	1	5	3	4
kb	0.1594	0.1838	0.1865	0.1591	0.1667
Ranks	4	2	1	5	3
kc	0.8965	1.0000	0.5848	0.7139	0.5866
Ranks	2	1	5	3	4
ki	0.7546	0.8476	0.5651	0.6317	0.5503
Final ranks	2	1	4	3	5

.

Step 10. Rank the possible potential alternative.

According to the $k_i$ value and ranking of the possible 3PL providers, the results are shown in Table 16.

5.6. Comparison and Discussion

In Section 5, the 3PL supplier selection was used to explain the method proposed in this study and to verify the rationality and correctness of the proposed method. The test results were also compared with those of the SAW method [42], entropy objective weighting method [43], and the typical CoCoSo method [20]. The four methods use the same input data (Table 2) for calculation, the main factors were considered and the differences in the ranking results are shown in

Table 17. Differences in the factors considered and ranking results between different calculation methods (Sources: created by the author).

Method	Consideration of the Subjective Weights	Consideration of the Objective Weights	Handling of Lost Information	Handling of Hesitant Information	Rank
SAW method [42]	Yes	No	No	No	PA2 > PA1 = PA4 > PA3 > PA5
Entropy objective weighting method [43]	No	Yes	No	No	PA2 > PA1 > PA4 > PA5 > PA3
Typical CoCoSo method [20]	Yes	No	No	No	PA2 > PA1 > PA3 > PA5 > PA4
Proposed method	Yes	Yes	Yes	Yes	PA2 > PA1 > PA4 > PA3 > PA5

.

According to the contents of Table 2 and Table 17, the main contributions of the proposed method are as follows. First, subjective weights were considered. For the proposed method, SAW method, and the typical CoCoSo method the subjective weights of the different evaluation criteria were considered. However, the entropy objective weighting method does not consider the subjective weights of the different evaluation criteria, which will lead to a bias in the evaluation results.

Second, the objective weights were considered. Both the proposed method and the entropy objective weighting method considered the objective weights of different evaluation criteria, and were able to truly consider the raw data differences of each evaluation criterion for the five possible alternatives. However, both the SAW method and the typical CoCoSo method ignore the consideration of the objective weights between the different evaluation criteria, which will lead to overly subjective assessment results.

The third contribution is the handling of lost information. When the rating values of the evaluation criteria provided by experts contain unclear information, the SAW method, entropy objective weighting method, and the typical CoCoSo method, do not consider all of assessment information provided by this expert, leading to ignoring the consideration of some valuable information. For the handling of lost information, the proposed method used the complete information provided by other experts to fill in the data and fully consider the evaluation information provided by all experts.

The final contribution is the handling of hesitant information. The SAW method, entropy objective weighting method, and the typical CoCoSo method can only deal with clear information and cannot deal with hesitant information provided by experts. If an expert provides some hesitant information, all of the assessment information provided by the expert are not considered in these three methods. The proposed method used Equation (21) for the defuzzification of the value of the interval information and fully considered the professional information provided by all experts; the evaluation results are more accurate and more in line with the actual situation in the real world.

5.7. Sensitivity Analysis

This study used different combinations of subjective weight to perform a sensitivity analysis in the 3PL provider selection case. When the subjective weights of evaluation criteria changed, this study used seven scenarios to determine the ranking results of the possible candidate 3PL providers. In scenario 1, we used the original subjective weights were that provided by experts. The subjective weights of the evaluation criteria (EC1, EC2, EC3, EC4 and EC5) are 0.300, 0.100, 0.250, 0.200 and 0.150, respectively. In scenario 2, we used the equal weight to assign subjective weight to the evaluation criteria. The subjective weights of the evaluation criteria (EC1, EC2, EC3, EC4 and EC5) are 0.200, 0.200, 0.200, 0.200 and 0.200, respectively. In scenario 3, we assume that evaluation criterion EC1 has a greater importance, the subjective weights of the evaluation criteria (EC1, EC2, EC3, EC4 and EC5) are set as 0.400, 0.150, 0.150, 0.150 and 0.150, respectively. In scenario 4, we assume that evaluation criterion EC2 has a greater importance, the subjective weights of the evaluation criteria (EC1, EC2, EC3, EC4 and EC5) are set as 0.150, 0.400, 0.150, 0.150 and 0.150, respectively. In scenario 5, we assume that evaluation criterion EC3 has a greater importance, the subjective weights of the evaluation criteria (EC1, EC2, EC3, EC4 and EC5) are set as 0.150, 0.150, 0.400, 0.150 and 0.150, respectively. In scenario 6, we assume that evaluation criterion EC4 has a greater importance, the subjective weights of the evaluation criteria (EC1, EC2, EC3, EC4, and EC5) are set as 0.150, 0.150, 0.150, 0.400 and 0.150, respectively. In scenario 7, we assume that evaluation criterion EC5 has a greater importance, the subjective weights of the evaluation criteria (EC1, EC2, EC3, EC4 and EC5) are set as 0.150, 0.150, 0.150, 0.150 and 0.400, respectively. The ranking results of different weight combinations are shown in

Table 18. The ranking results of the different weight combinations (Sources: created by the author).

Possible alternatives	Scenario 1		Scenario 2		Scenario 3		Scenario 4
	ki value	Rank	ki value	Rank	ki value	Rank	ki value	Rank
PA1	0.7546	2	0.7532	2	0.7623	2	0.7589	2
PA2	0.8476	1	0.8479	1	0.8471	1	0.8383	1
PA3	0.5651	4	0.5633	5	0.5673	4	0.5669	5
PA4	0.6317	3	0.6124	3	0.6336	3	0.5905	3
PA5	0.5503	5	0.5675	4	0.5501	5	0.5716	4
Possible alternatives	Scenario 5		Scenario 6		Scenario 7
	ki value	Rank	ki value	Rank	ki value	Rank
PA1	0.7487	2	0.7560	2	0.7273	2
PA2	0.8486	1	0.8457	1	0.8469	1
PA3	0.5748	4	0.5493	5	0.5440	5
PA4	0.6227	3	0.6120	3	0.5895	3
PA5	0.5491	5	0.5835	4	0.5692	4

.

According to the results of Table 18, we can find that no matter how the subjective weight of the evaluation criteria is configured, the top three of the possible candidate 3PL providers ranking are PA2, PA1, and PA4, respectively. The ranking of possible alternatives PA3 and PA5 have different ranking results depending on the subjective weight of the evaluation criteria.

5.8. Practical Insights and Management Implications

The choice of a suitable supplier will be the key to ensure the sustainable development of the company and the normal operation of the overall supply chain. However, there are many factors involved in selecting a suitable supplier, such as consideration of the weight of the evaluation factors, consideration of the evaluation information, consideration of both qualitative and quantitative factors, etc.

The advantage of the SAW method is that it is simple to calculate, and it is also the most commonly used method to solve MCDM problems. However, the SAW method has some limitations, it does not consider subjective and objective weights, and cannot deal with unclear information and hesitant information. The proposed method can overcome the limitations of the SAW method by integrating the subjective–objective weights consideration and the CoCoSo method to deal with the problem of supplier selection under unclear information. The proposed method not only can consider subjective and objective weights but also can deal with unclear information and hesitant information. The proposed method calculates the objective weight of the evaluation criteria by using the SWARA method, then uses the integrated weight of the subjective and objective weights and the CoCoSo method to rank the possible potential alternative.

The practical implications of the proposed method can be explained as follows. First, the proposed method can process the incomplete information and unclear information provided by experts in the supplier selection issues. Second, the proposed method can simultaneously take into account both subjective and objective weighting of evaluation criteria. Through the simulation example of the 3PL supplier selection, the findings of this study provide some practical insights and management implications to assist managers in handling supplier selection issues under incomplete information. The consideration of these four factors, the subjective weighting of evaluation criteria, objective weighting of evaluation criteria, handling of missing information, and handling of hesitant information provided by experts, will be the key to correctly rank supplier results.

6. Conclusions

With the development of information technology, the business model of enterprises is constantly changing and improving. Several reasons may cause the disconnection of the original supply chain, such as the COVID-19 pandemic and the emergence of other diseases, acts of war, changes in diplomatic relations, and natural disasters, etc., and lead to the reselection of the appropriate supplier. The selection of the most suitable supplier, will be the key to ensuring the successful functioning of the overall supply chain. To effectively process the supplier selection problems, this study integrated subjective–objective weights consideration and the CoCoSo method for handling supplier selection issues under incomplete information.

The main contributions of the proposed approach are as follows.

(1)

The proposed approach considers the subjective weights of different evaluation criteria;

(2)

The proposed approach considers the objective weights of different evaluation criteria;

(3)

The proposed approach can handle lost information;

(4)

The proposed approach can handle hesitant information.

Although the proposed integrated subjective–objective weights consideration and CoCoSo method is able to deal with the problem of supplier selection under unclear information, the method still cannot account for criteria interactions, distinguishing strict and non-strict decision makers, and special cases, such as veto power. Based on the proposed method, subsequent research can be extended to explore the combination of different calculation methods for subjective weights and objective weights. Follow-up researchers can also use the method proposed in this paper to discuss issues of different fields, such as risk assessment, resource allocation, performance appraisal, construction equipment selection, customer satisfaction assessment, and so on.