A Novel Picture Fuzzy Set-Based Decision Approach for Consumer Trust Project Risk Assessment
Abstract
:1. Introduction
2. Literature Review
2.1. Picture Fuzzy Sets
2.2. Applications of the CRITIC and ARAS Method
3. Preliminaries
3.1. Picture Fuzzy Sets
- (1)
- ;
- (2)
- ;
- (3)
- ;
- (4)
- .
3.2. Prospect Theory
4. The Proposed Picture Fuzzy Decision System Framework
4.1. Phase I: Obtain Picture Fuzzy Decision Matrix (PF-DM)
4.2. Phase II: Determine the Weight of Criteria
4.3. Phase III: Determine Risk Priority and Ranking Order
5. Case Study
5.1. Problem Description and Establishment of Risk Evaluation Model
5.2. Operational Results
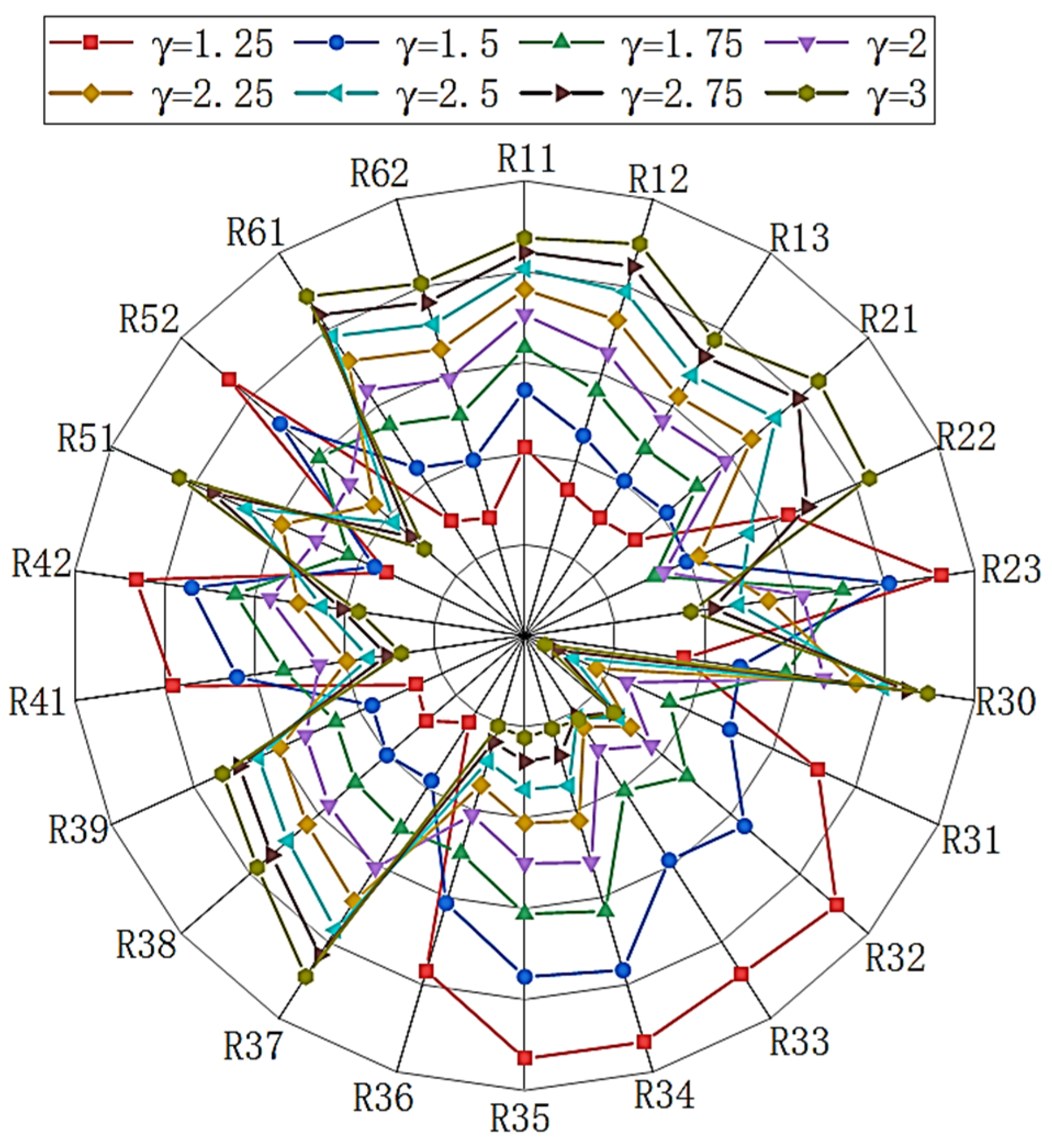
5.3. Sensitivity Analysis
5.4. Comparative Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, Z.; He, Z.; Liu, C. The financing of local government in China: Stimulus loan wanes and shadow banking waxes. J. Financ. Econ. 2020, 137, 42–71. [Google Scholar] [CrossRef]
- Li, J.; Xue, Y. Systemic risk in Chinese shadow banking sector: Risk contagion mechanism, influence and control. J. Quant. Tech. Econ. 2014, 8, 117–130. [Google Scholar] [CrossRef]
- Cui, Z. Risks confronted by trust company in the development of trust business. In Proceedings of the 2010 Third International Conference on Knowledge Discovery and Data Mining, Phuket, Thailand, 9–10 January 2010; pp. 568–571. [Google Scholar] [CrossRef]
- Haisen, H.; Yazdifar, H. Impact of the shadow banking system on monetary policy in China. ICTACT J. Manag. Stud. 2015, 1, 1–12. [Google Scholar] [CrossRef]
- Liu, K. Chinese consumer finance: A primer. Front. Bus. Res. China 2020, 14, 9. [Google Scholar] [CrossRef]
- Gao, L.; Xiao, J.; Wu, W. Big data credit report in credit risk management of consumer finance. Wirel. Commun. Mob. Comput. 2021, 2021, 4811086. [Google Scholar] [CrossRef]
- Liu, F.; Qu, L.; Zhou, X. Research on risk supervision and similarities and differences of demand for consumer finance based on difference in the education level. In Proceedings of the 2019 10th International Conference on E-Business, Management and Economics-ICEME 2019, New York, NY, USA, 15–17 July 2019; pp. 170–174. [Google Scholar] [CrossRef]
- Wang, H.; Tsai, S. Credit risk management of consumer finance based on big data. Mob. Inf. Syst. 2021, 2021, 8189255. [Google Scholar] [CrossRef]
- Gębski, Ł. The impact of the crisis triggered by the COVID-19 pandemic and the actions of regulators on the consumer finance market in poland and other European union countries. Risks 2021, 9, 102. [Google Scholar] [CrossRef]
- Bao, Z.; Huang, D. Shadow Banking in a Crisis: Evidence from Fintech During COVID-19. J. Financ. Quant. Anal. 2021, 56, 2320–2355. [Google Scholar] [CrossRef]
- Min, C.G.; Park, J.K.; Hur, D.; Kim, M.K. A risk evaluation method for ramping capability shortage in power systems. Energy 2016, 113, 1316–1324. [Google Scholar] [CrossRef]
- Wang, L.; Peng, J.; Wang, J. A multi-criteria decision-making framework for risk ranking of energy performance contracting project under picture fuzzy environment. J. Clean. Prod. 2018, 191, 105–118. [Google Scholar] [CrossRef]
- Papapostolou, A.; Karakosta, C.; Nikas, A.; Psarras, J. Exploring opportunities and risks for RES-E deployment under Cooperation Mechanisms between EU and Western Balkans: A multi-criteria assessment. Renew. Sustain. Energy Rev. 2017, 80, 519–530. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, H.; Wang, J.; Li, L. Picture fuzzy normalized projection-based VIKOR method for the risk evaluation of construction project. Appl. Soft Comput. 2018, 64, 216–226. [Google Scholar] [CrossRef]
- Gou, X.; Xu, Z.; Zhou, W.; Herrera-Viedma, E. The risk assessment of construction project investment based on prospect theory with linguistic preference orderings. Econ. Res.-Ekon. Istraživanja 2021, 34, 709–731. [Google Scholar] [CrossRef]
- Zhao, M.; Wei, G.; Wei, C.; Wu, J. Pythagorean Fuzzy TODIM Method Based on the Cumulative Prospect Theory for MAGDM and Its Application on Risk Assessment of Science and Technology Projects. Int. J. Fuzzy Syst. 2021, 23, 1027–1041. [Google Scholar] [CrossRef]
- Wang, R.; Wang, J.; Gao, H.; Wei, G. Methods for MADM with picture fuzzy muirhead mean operators and their application for evaluating the financial investment risk. Symmetry 2019, 11, 6. [Google Scholar] [CrossRef] [Green Version]
- Peng, X.; Huang, H. Fuzzy decision making method based on cocoso with critic for financial risk evaluation. Technol. Econ. Dev. Econ. 2020, 26, 695–724. [Google Scholar] [CrossRef] [Green Version]
- Dahooie, J.H.; Hajiagha, S.H.R.; Farazmehr, S.; Zavadskas, E.K.; Antucheviciene, J. A novel dynamic credit risk evaluation method using data envelopment analysis with common weights and combination of multi-attribute decision-making methods. Comput. Oper. Res. 2021, 129, 105223. [Google Scholar] [CrossRef]
- Du, Y.; Shi, L. Research on financing risk of mining enterprises based on fuzzy comprehensive evaluation. J. Intell. Fuzzy Syst. 2020, 38, 7001–7007. [Google Scholar] [CrossRef]
- Antucheviciene, J.; Kala, Z.; Marzouk, M.; Vaidogas, E.R. Solving Civil Engineering Problems by Means of Fuzzy and Stochastic MCDM Methods: Current State and Future Research. Math. Probl. Eng. 2015, 2015, 362579. [Google Scholar] [CrossRef] [Green Version]
- Wang Chen, H.M.; Chou, S.; Luu, Q.D.; Yu, T.H. A fuzzy MCDM approach for green supplier selection from the economic and environmental aspects. Math. Probl. Eng. 2016, 2016, 8097386. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Wang, W.; Fan, L.; Li, Q.; Chen, X. A novel hybrid MCDM model for machine tool selection using fuzzy DEMATEL, entropy weighting and later defuzzification VIKOR. Appl. Soft Comput. 2020, 91, 106207. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Rostamzadeh, R.; Ghorabaee, M.K.; Govindan, K.; Esmaeili, A.; Nobar, H.B.K. Evaluation of sustainable supply chain risk management using an integrated fuzzy TOPSIS-CRITIC approach. J. Clean. Prod. 2018, 175, 651–669. [Google Scholar] [CrossRef]
- Li, X.; Wang, W.; Zhang, G.; Pan, Q. A risk ranking method based on intuitionistic fuzzy group decision-making model in the process of risk management in equipment projects. In Proceedings of the 2014 Prognostics and System Health Management Conference (PHM-2014 Hunan), Zhangjiajie, China, 24–27 August 2014; pp. 422–426. [Google Scholar] [CrossRef]
- Guo, J. A risk assessment approach for failure mode and effects analysis based on intuitionistic fuzzy sets and evidence theory. J. Intell. Fuzzy Syst. 2016, 30, 869–881. [Google Scholar] [CrossRef]
- Ilbahar, E.; Kahraman, C.; Cebi, S. Risk assessment of renewable energy investments: A modified failure mode and effect analysis based on prospect theory and intuitionistic fuzzy AHP. Energy 2022, 239, 121907. [Google Scholar] [CrossRef]
- Cường, B.C. Picture fuzzy sets. J. Comput. Sci. Cybern. 2014, 30, 5032. [Google Scholar] [CrossRef] [Green Version]
- Meksavang, P.; Shi, H.; Lin, S.; Liu, H. An extended picture fuzzy VIKOR approach for sustainable supplier management and its application in the beef industry. Symmetry 2019, 11, 468. [Google Scholar] [CrossRef] [Green Version]
- Kahneman, D.; Tversky, A. Prospect theory: An analysis of decision under risk. Econometrica 1979, 47, 263–291. [Google Scholar] [CrossRef] [Green Version]
- Cheng, X. A research on the development of artificial intelligence and consumer finance in China. J. Phys. Conf. Ser. 2019, 1176, 042073. [Google Scholar] [CrossRef]
- Xiao, J.J.; Tao, C. Consumer finance/household finance: The definition and scope. China Financ. Rev. Int. 2020, 11, 1–25. [Google Scholar] [CrossRef]
- Xiao, W.; Zhao, Q.; Fei, Q. A comparative study of data mining methods in consumer loans credit scoring management. J. Syst. Sci. Syst. Eng. 2006, 15, 419–435. [Google Scholar] [CrossRef]
- Sun, W.; Chen, M.; Ye, J.; Zhang, Y.; Xu, C.; Zhang, Y.; Wang, Y.; Wu, W.; Zhang, P.; Qu, F. Semi-supervised anti-fraud models for cash pre-loan in internet consumer finance. In Proceedings of the 2019 IEEE International Conference on Industrial Cyber Physical Systems (ICPS), Taipei, Taiwan, 6–9 May 2019; pp. 635–640. [Google Scholar] [CrossRef]
- Carling, K.; Jacobson, T.; Roszbach, K. Dormancy risk and expected profits of consumer loans. J. Bank. Financ. 2001, 25, 717–739. [Google Scholar] [CrossRef]
- Li, S.; Shiue, W.; Huang, M. The evaluation of consumer loans using support vector machines. Expert Syst. Appl. 2006, 30, 772–782. [Google Scholar] [CrossRef]
- Abid, L.; Masmoudi, A.; Zouari-Ghorbel, S. The Consumer Loan’s Payment Default Predictive Model: An Application of the Logistic Regression and the Discriminant Analysis in a Tunisian Commercial Bank. J. Knowl. Econ. 2016, 9, 948–962. [Google Scholar] [CrossRef]
- Zeng, Y.; Yang, Y.; Xu, F.; Zhang, C. Survey of consumer finance research. Syst. Eng.-Theory Pract. 2022, 42, 84–109. [Google Scholar] [CrossRef]
- Rona-Tas, A.; Guseva, A. Consumer credit in comparative perspective. Annu. Rev. Sociol. 2018, 44, 55–75. [Google Scholar] [CrossRef]
- Pope, D.G.; Sydnor, J.R. What’s in a picture?: Evidence of discrimination from Prosper.com. J. Hum. Resour. 2011, 46, 53–92. [Google Scholar] [CrossRef]
- Andreeva, G.; Matuszyk, A. The law of equal opportunities or unintended consequences?: The effect of unisex risk assessment in consumer credit. J. R. Stat. Soc. Ser. A 2019, 182, 1287–1311. [Google Scholar] [CrossRef] [Green Version]
- Herzenstein, M.; Sonenshein, S.; Dholakia, U.M. Tell Me a Good Story and I May Lend you Money: The Role of Narratives in Peer-to-Peer Lending Decisions. J. Mark. Res. 2019, 48, S138–S149. [Google Scholar] [CrossRef] [Green Version]
- Duarte, J.; Siegel, S.; Young, L. Trust and Credit: The Role of Appearance in Peer-to-peer Lending. Rev. Financ. Stud. 2012, 25, 2455–2484. [Google Scholar] [CrossRef]
- Jin, J.; Shang, Q.; Ma, Q. The role of appearance attractiveness and loan amount in peer-to-peer lending: Evidence from event-related potentials. Neurosci. Lett. 2019, 692, 10–15. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, H. Financial literacy, self-efficacy and risky credit behavior among college students: Evidence from online consumer credit. J. Behav. Exp. Financ. 2021, 32, 100569. [Google Scholar] [CrossRef]
- Dorfleitner, G.; Priberny, C.; Schuster, S.; Stoiber, J.; Weber, M.; de Castro, I.; Kammler, J. Description-text related soft information in peer-to-peer lending-Evidence from two leading European platforms. J. Bank. Financ. 2016, 64, 169–187. [Google Scholar] [CrossRef]
- Netzer, O.; Lemaire, A.; Herzenstein, M. When words sweat: Identifying signals for loan default in the text of loan applications. J. Mark. Res. 2019, 56, 960–980. [Google Scholar] [CrossRef]
- Wu, W.; Xu, D.; Zhao, Y.; Liu, X. Do consumer internet behaviours provide incremental information to predict credit default risk? Econ. Political Stud. 2020, 8, 482–499. [Google Scholar] [CrossRef]
- Sztaudynger, M. Macroeconomic factors and consumer loan repayment. Gospod. Nar. 2018, 296, 155–177. [Google Scholar] [CrossRef]
- Kruppa, J.; Schwarz, A.; Arminger, G.; Ziegler, A. Consumer credit risk: Individual probability estimates using machine learning. Expert Syst. Appl. 2013, 40, 5125–5131. [Google Scholar] [CrossRef]
- Bravo, C.; Thomas, L.C.; Weber, R. Improving credit scoring by differentiating defaulter behaviour. J. Oper. Res. Soc. 2017, 66, 771–781. [Google Scholar] [CrossRef] [Green Version]
- Venkiteshwaran, V. Do asset sales affect firm credit risk?—Evidence from credit rating assignments. Manag. Financ. 2014, 40, 903–927. [Google Scholar] [CrossRef]
- Haurin, D.R.; Moulton, S.; Loibl, C.; Brown, J.K. Debt stress and debt illusion: The role of consumer credit, reverse and standard mortgages. J. Gerontol. B Psychol. Sci. Soc. Sci. 2021, 76, 986–995. [Google Scholar] [CrossRef]
- Martens, D.; Baesens, B.; Van Gestel, T.; Vanthienen, J. Comprehensible credit scoring models using rule extraction from support vector machines. Eur. J. Oper. Res. 2007, 183, 1466–1476. [Google Scholar] [CrossRef]
- Oreski, S.; Oreski, D.; Oreski, G. Hybrid system with genetic algorithm and artificial neural networks and its application to retail credit risk assessment. Expert Syst. Appl. 2012, 39, 12605–12617. [Google Scholar] [CrossRef]
- Byanjankar, A. Predicting credit risk in Peer-to-Peer lending with survival analysis. In Proceedings of the 2017 IEEE Symposium Series on Computational Intelligence (SSCI), Honolulu, HI, USA, 27 November–01 December 2017; pp. 1–8. [Google Scholar] [CrossRef]
- Paleologo, G.; Elisseeff, A.; Antonini, G. Subagging for credit scoring models. Eur. J. Oper. Res. 2010, 201, 490–499. [Google Scholar] [CrossRef]
- Khandani, A.E.; Kim, A.J.; Lo, A.W. Consumer credit-risk models via machine-learning algorithms. J. Bank. Financ. 2010, 34, 2767–2787. [Google Scholar] [CrossRef] [Green Version]
- Li, J. Research on enterprise credit risk assessment method based on improved genetic algorithm. In Proceedings of the 2017 9th International Conference on Measuring Technology and Mechatronics Automation (ICMTMA), Changsha, China, 14–15 January 2017; pp. 215–218. [Google Scholar] [CrossRef]
- Li, W.; Ding, S.; Chen, Y.; Wang, H.; Yang, S. Transfer learning-based default prediction model for consumer credit in China. J. Supercomput. 2018, 75, 862–884. [Google Scholar] [CrossRef]
- Pla-Santamaria, D.; Bravo, M.; Reig-Mullor, J.; Salas-Molina, F. A multicriteria approach to manage credit risk under strict uncertainty. Top 2020, 29, 494–523. [Google Scholar] [CrossRef]
- Bao, T.; Xie, X.; Long, P.; Wei, Z. MADM method based on prospect theory and evidential reasoning approach with unknown attribute weights under intuitio67nistic fuzzy environment. Expert Syst. Appl. 2017, 88, 305–317. [Google Scholar] [CrossRef]
- Peng, X. Algorithm for pythagorean fuzzy multi-criteria decision making based on WDBA with new score function. Fundam. Inform. 2019, 165, 99–137. [Google Scholar] [CrossRef]
- Diakoulaki, D.; Mavrotas, G.; Papayannakis, L. Determining objective weights in multiple criteria problems: The critic method. Comput. Oper. Res. 1995, 22, 763–770. [Google Scholar] [CrossRef]
- Zeleny, M. Multiple Criteria Decision Making; McGraw-Hill: New York, NY, USA, 1982. [Google Scholar]
- Peng, X.; Zhang, X.; Luo, Z. Pythagorean fuzzy MCDM method based on CoCoSo and CRITIC with score function for 5G industry evaluation. Artif. Intell. Rev. 2020, 53, 3813–3847. [Google Scholar] [CrossRef]
- Tuş, A.; Adalı, E.A. The new combination with CRITIC and WASPAS methods for the time and attendance software selection problem. Opsearch 2019, 56, 528–538. [Google Scholar] [CrossRef]
- Keshavarz-Ghorabaee, M.; Amiri, M.; Zavadskas, E.K.; Antuchevičienė, J. Assessment of third-party logistics providers using a critic–waspas approach with interval type-2 fuzzy sets. Transport 2017, 32, 66–78. [Google Scholar] [CrossRef] [Green Version]
- Mishra, A.R.; Rani, P. Assessment of sustainable third party reverse logistic provider using the single-valued neutrosophic combined compromise solution framework. Clean. Responsible Consum. 2021, 2, 100011. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R.; Krishankumar, R.; Ravichandran, K.S.; Kar, S. Multi-criteria food waste treatment method selection using single-valued neutrosophic-CRITIC-MULTIMOORA framework. Appl. Soft Comput. 2021, 111, 107657. [Google Scholar] [CrossRef]
- Keshavarz-Ghorabaee, M.; Amiri, M.; Zavadskas, E.K.; Antucheviciene, J. A new hybrid fuzzy MCDM approach for evaluation of construction equipment with sustainability considerations. Arch. Civ. Mech. Eng. 2018, 18, 32–49. [Google Scholar] [CrossRef]
- Wei, G.; Lei, F.; Lin, R.; Wang, R.; Wei, Y.; Wu, J.; Wei, C. Algorithms for probabilistic uncertain linguistic multiple attribute group decision making based on the GRA and CRITIC method: Application to location planning of electric vehicle charging stations. Econ. Res.-Ekon. Istraživanja 2020, 33, 828–846. [Google Scholar] [CrossRef] [Green Version]
- Peng, X.; Krishankumar, R.; Ravichandran, K.S. A novel interval-valued fuzzy soft decision-making method based on CoCoSo and CRITIC for intelligent healthcare management evaluation. Soft Comput. 2021, 25, 4213–4241. [Google Scholar] [CrossRef]
- Rezaei, J. Best-worst multi-criteria decision-making method. Omega 2015, 53, 49–57. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Vilutiene, T. Multiple criteria analysis of foundation instalment alternatives by applying Additive Ratio Assessment (ARAS) method. Arch. Civ. Mech. Eng. 2010, 10, 123–141. [Google Scholar] [CrossRef]
- Mishra, A.R.; Rani, P.; Saha, A. Single-valued neutrosophic similarity measure-based additive ratio assessment framework for optimal site selection of electric vehicle charging station. Int. J. Intell. Syst. 2021, 36, 5573–5604. [Google Scholar] [CrossRef]
- Zamani, M.; Rabbani, A.; Yazdani-Chamzini, A.; Turskis, Z. An Integrated Model for Extending Brand Based on Fuzzy Aras and Anp Methods. J. Bus. Econ. Manag. 2014, 15, 403–423. [Google Scholar] [CrossRef] [Green Version]
- Ghenai, C.; Albawab, M.; Bettayeb, M. Sustainability indicators for renewable energy systems using multi-criteria decision-making model and extended SWARA/ARAS hybrid method. Renew. Energy 2020, 146, 580–597. [Google Scholar] [CrossRef]
- Büyüközkan, G.; Göçer, F. An extension of ARAS methodology under Interval Valued Intuitionistic Fuzzy environment for Digital Supply Chain. Appl. Soft Comput. 2018, 69, 634–654. [Google Scholar] [CrossRef]
- Liu, P.; Cheng, S. An extension of ARAS methodology for multi-criteria group decision-making problems within probability multi-valued neutrosophic sets. Int. J. Fuzzy Syst. 2019, 21, 2472–2489. [Google Scholar] [CrossRef]
- Mishra, A.R.; Rani, P.; Krishankumar, R.; Ravichandran, K.S.; Kar, S. An extended fuzzy decision-making framework using hesitant fuzzy sets for the drug selection to treat the mild symptoms of Coronavirus Disease 2019 (COVID-19). Appl. Soft Comput. 2021, 103, 107155. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, X.; Wang, J.; Li, J.; Li, L. Decision support framework for the risk ranking of agroforestry biomass power generation projects with picture fuzzy information. J. Intell. Fuzzy Syst. 2020, 39, 4631–4650. [Google Scholar] [CrossRef]
- Ashraf, S.; Mahmood, T.; Abdullah, S.; Khan, Q. Different approaches to multi-criteria group decision making problems for picture fuzzy environment. Bull. Braz. Math. Soc. New Ser. 2019, 50, 373–397. [Google Scholar] [CrossRef]
- Peng, X.; Luo, Z. Decision-making model for China’s stock market bubble warning: The CoCoSo with picture fuzzy information. Artif. Intell. Rev. 2021, 54, 5675–5697. [Google Scholar] [CrossRef]
- Wei, G. Picture fuzzy hamacher aggregation operators and their application to multiple attribute decision making. Fundam. Inform. 2018, 157, 271–320. [Google Scholar] [CrossRef]
- Fu, Y. An integrated approach to catering supplier selection using AHP-ARAS-MCGP methodology. J. Air Transp. Manag. 2019, 75, 164–169. [Google Scholar] [CrossRef]
- Naicker, P.; Thopil, G.A. A framework for sustainable utility scale renewable energy selection in South Africa. J. Clean. Prod. 2019, 224, 637–650. [Google Scholar] [CrossRef]
- Deng, X.; Wang, J.; Wei, G.; Lu, M. Models for multiple attribute decision making with some 2-tuple linguistic pythagorean fuzzy hamy mean operators. Mathematics 2018, 6, 236. [Google Scholar] [CrossRef] [Green Version]
- Yu, Y.; Wu, S.; Yu, J.; Xu, Y.; Song, L.; Xu, W. A hybrid multi-criteria decision-making framework for offshore wind turbine selection: A case study in China. Appl. Energy 2022, 328, 120173. [Google Scholar] [CrossRef]
- Li, P.; Liu, J.; Wei, C.; Liu, J. A new EDAS method based on prospect theory for Pythagorean fuzzy set and its application in selecting investment projects for highway. Kybernetes 2021, 51, 2636–2651. [Google Scholar] [CrossRef]
- Zhu, L.; Yang, X. Study on factors of China trust company’s risk. In Proceedings of the ISSGBM International Conference on Social Sciences and Education (ISSGBM-SSE 2016), Windsor, UK, 29–30 September 2016. [Google Scholar]
- Zhu, X. The varying shadow of China’s banking system. J. Comp. Econ. 2021, 49, 135–146. [Google Scholar] [CrossRef]
- Tian, M.; Bi, H.X. The research on the cooperation between banks and trust companies about the shadow banking system. In Proceedings of the 4th International Conference on Financial Risk and Corporate Finance Management, Dalian, China, 7–8 July 2012. [Google Scholar]
- Ebrahimnejad, S.; Mousavi, S.M.; Mojtahedi, S.M.H. A model for risk evaluation in construction projects based on fuzzy MADM. In Proceedings of the 2008 4th IEEE International Conference on Management of Innovation and Technology, Bangkok, Thailand, 21–24 September 2008; pp. 305–310. [Google Scholar] [CrossRef]
- Yazdani-Chamzini, A.; Yakhchali, S.H.; Mahmoodian, M. Risk ranking of tunnel construction projects by using the ELECTRE technique under a fuzzy environment. Int. J. Manag. Sci. Eng. Manag. 2013, 8, 1–14. [Google Scholar] [CrossRef]
- Li, Q.; Zeng, F.e.; Liu, S.; Yang, M.; Xu, F. The effects of China’s sustainable development policy for resource-based cities on local industrial transformation. Resour. Policy 2021, 71, 101940. [Google Scholar] [CrossRef]
- Parkan, C.; Wu, M. Decision-making and performance measurement models with applications to robot selection. Comput. Ind. Eng. 1999, 36, 503–523. [Google Scholar] [CrossRef]

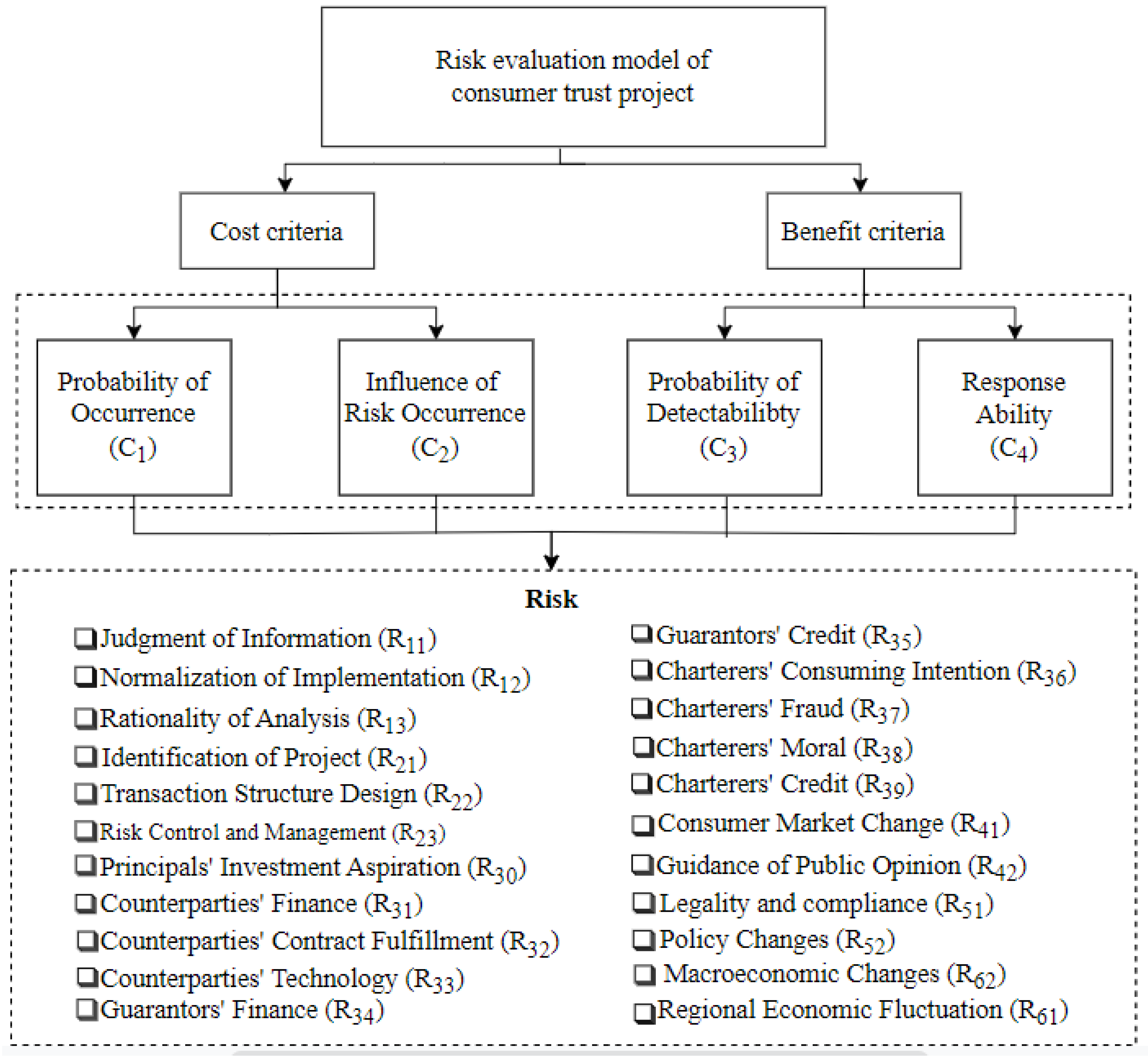

| Dimension | Source | Risk |
|---|---|---|
| Internal risks | Investigation stage (S1) | Judgment of Information (R11) |
| Normalization of Implementation (R12) | ||
| Rationality of Analysis (R13) | ||
| Approval stage (S2) | Identification of Project (R21) | |
| Transaction Structure Design (R22) | ||
| Risk Control and Management (R23) | ||
| Redemption stage (S3) | Principals’ Investment Aspiration (R30) | |
| Counterparties’ Finance (R31) | ||
| Counterparties’ Contract Fulfillment (R32) | ||
| Counterparties’ Technology (R33) | ||
| Guarantors’ Finance (R34) | ||
| Guarantors’ Credit (R35) | ||
| Charterers’ Consuming Intention (R36) | ||
| Charterers’ Fraud (R37) | ||
| Charterers’ Moral (R38) | ||
| Charterers’ Credit (R39) | ||
| External risks | Social aspect (S4) | Consumer Market Change (R41) |
| Guidance of Public Opinion (R42) | ||
| Legal and Policy aspect (S5) | Legality and compliance (R51) | |
| Policy Changes (R52) | ||
| Economic aspect (S6) | Regional Economic Fluctuation (R61) | |
| Macroeconomic Changes (R62) |
| Criteria | Explanation |
|---|---|
| Probability of occurrence | It represents the likelihood of risk occurrence. |
| Risk impact | It means the impact when risk occurs. |
| Risk detectability | It shows the probability to detect risk. |
| Risk responsiveness | It indicates the degree of reaction when risk occurs. |
| Linguistic Scale for Proficiency | Picture Fuzzy Numbers (PFNs) | Linguistic Scale for Rating |
|---|---|---|
| Very Poor (VP) | Very Low (VL) | |
| Poor (P) | Low (L) | |
| Moderately Poor (MP) | Moderately Low (ML) | |
| Fair (F) | Fair (F) | |
| Moderately Good (MG) | Moderately High (MH) | |
| Good (G) | High (H) | |
| Very Good (VG) | Very High (VH) |
| Expert 1 | Expert 2 | Expert 3 | Expert 4 | |
|---|---|---|---|---|
| Linguistic rating | VG | G | MP | MG |
| (PFNs) | ||||
| Weight | 0.31 | 0.28 | 0.19 | 0.22 |
| Internal Risk | C1 | C2 | C3 | C4 |
|---|---|---|---|---|
| R11 | ||||
| R12 | ||||
| R13 | ||||
| R21 | ||||
| R22 | ||||
| R23 | ||||
| R30 | ||||
| R31 | ||||
| R32 | ||||
| R33 | ||||
| R34 | ||||
| R35 | ||||
| R36 | ||||
| R37 | ||||
| R38 | ||||
| R39 |
| External Risk | C1 | C2 | C3 | C4 |
|---|---|---|---|---|
| R41 | ||||
| R42 | ||||
| R51 | ||||
| R52 | ||||
| R61 | ||||
| R62 |
| Internal Risk | C1 | C2 | C3 | C4 |
|---|---|---|---|---|
| R11 | ||||
| R12 | ||||
| R13 | ||||
| R21 | ||||
| R22 | ||||
| R23 | ||||
| R30 | ||||
| R31 | ||||
| R32 | ||||
| R33 | ||||
| R34 | ||||
| R35 | ||||
| R36 | ||||
| R37 | ||||
| R38 | ||||
| R39 |
| External Risk | C1 | C2 | C3 | C4 |
|---|---|---|---|---|
| R41 | ||||
| R42 | ||||
| R51 | ||||
| R52 | ||||
| R61 | ||||
| R62 |
| CRC | SD | Weight | ||||
|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | |||
| C1 | 1.000 | 0.279 | −0.033 | −0.128 | 0.12 | 0.25 |
| C2 | 0.279 | 1.000 | −0.286 | 0.511 | 0.16 | 0.28 |
| C3 | −0.0329 | −0.2864 | 1.0000 | −0.1491 | 0.09 | 0.23 |
| C4 | −0.1275 | 0.5109 | −0.1491 | 1.0000 | 0.12 | 0.24 |
| 22 | 22 | 22 | 22 | 22 | 22 | 22 | 22 | 22 | |
| 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | |
| 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | |
| 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | |
| 11 | 11 | 11 | 11 | 11 | 11 | 12 | 12 | 12 | |
| 16 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | |
| 19 | 19 | 19 | 19 | 18 | 18 | 18 | 18 | 18 | |
| 5 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | |
| 13 | 13 | 12 | 13 | 13 | 13 | 13 | 13 | 13 | |
| 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | |
| 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | 4 | |
| 12 | 12 | 13 | 14 | 14 | 14 | 14 | 14 | 14 | |
| 15 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 17 | |
| 17 | 17 | 17 | 17 | 17 | 17 | 17 | 17 | 16 | |
| 14 | 14 | 14 | 12 | 12 | 12 | 11 | 11 | 11 | |
| 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | |
| 18 | 18 | 18 | 18 | 19 | 19 | 19 | 19 | 19 | |
| 21 | 21 | 21 | 21 | 21 | 21 | 21 | 21 | 21 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 4 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | |
| 6 | 4 | 4 | 3 | 3 | 3 | 3 | 3 | 3 | |
| 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 |
| Ranking | Ranking Difference | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| TH-ARAS (Method1) | PFN-ARAS (Method2) | PWAG (Method3) | TH + MABAC (Method4) | 1 vs. 2 | 1 vs. 3 | 1 vs. 4 | 2 vs. 3 | 2 vs. 4 | 3 vs. 4 |
| 22 | 12 | 12 | 22 | 100 | 100 | 0 | 0 | 100 | 100 |
| 9 | 19 | 19 | 10 | 100 | 100 | 1 | 0 | 81 | 81 |
| 20 | 10 | 10 | 21 | 100 | 100 | 1 | 0 | 121 | 121 |
| 8 | 13 | 14 | 18 | 25 | 36 | 100 | 1 | 25 | 16 |
| 11 | 18 | 18 | 11 | 49 | 49 | 0 | 0 | 49 | 49 |
| 15 | 14 | 13 | 13 | 1 | 4 | 4 | 1 | 1 | 0 |
| 18 | 2 | 2 | 17 | 256 | 256 | 1 | 0 | 225 | 225 |
| 7 | 6 | 5 | 1 | 1 | 4 | 36 | 1 | 25 | 16 |
| 13 | 3 | 3 | 2 | 100 | 100 | 121 | 0 | 1 | 1 |
| 10 | 11 | 11 | 7 | 1 | 1 | 9 | 0 | 16 | 16 |
| 4 | 5 | 6 | 15 | 1 | 4 | 121 | 1 | 100 | 81 |
| 14 | 7 | 7 | 12 | 49 | 49 | 4 | 0 | 25 | 25 |
| 17 | 15 | 15 | 5 | 4 | 4 | 144 | 0 | 100 | 100 |
| 16 | 1 | 1 | 16 | 225 | 225 | 0 | 0 | 225 | 225 |
| 12 | 4 | 4 | 14 | 64 | 64 | 4 | 0 | 100 | 100 |
| 2 | 17 | 17 | 6 | 225 | 225 | 16 | 0 | 121 | 121 |
| 19 | 16 | 16 | 19 | 9 | 9 | 0 | 0 | 9 | 9 |
| 21 | 21 | 21 | 20 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 9 | 9 | 3 | 64 | 64 | 4 | 0 | 36 | 36 |
| 5 | 8 | 8 | 4 | 9 | 9 | 1 | 0 | 16 | 16 |
| 3 | 22 | 22 | 8 | 361 | 361 | 25 | 0 | 196 | 196 |
| 6 | 20 | 20 | 9 | 196 | 196 | 9 | 0 | 121 | 121 |
| RC | 0.095 | 0.106 | 0.682 | 0.998 | 0.043 | 0.065 | |||
| Z | 0.437 | 0.484 | 3.025 | 4.572 | 0.199 | 0.298 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, L.; Fang, H.; Rong, Y.; Min, J.; Xing, Y. A Novel Picture Fuzzy Set-Based Decision Approach for Consumer Trust Project Risk Assessment. Systems 2023, 11, 160. https://doi.org/10.3390/systems11030160
Yu L, Fang H, Rong Y, Min J, Xing Y. A Novel Picture Fuzzy Set-Based Decision Approach for Consumer Trust Project Risk Assessment. Systems. 2023; 11(3):160. https://doi.org/10.3390/systems11030160
Chicago/Turabian StyleYu, Liying, Haijie Fang, Yuan Rong, Jingye Min, and Yuanzhi Xing. 2023. "A Novel Picture Fuzzy Set-Based Decision Approach for Consumer Trust Project Risk Assessment" Systems 11, no. 3: 160. https://doi.org/10.3390/systems11030160
APA StyleYu, L., Fang, H., Rong, Y., Min, J., & Xing, Y. (2023). A Novel Picture Fuzzy Set-Based Decision Approach for Consumer Trust Project Risk Assessment. Systems, 11(3), 160. https://doi.org/10.3390/systems11030160






