Reinforcement Learning for Optimizing Can-Order Policy with the Rolling Horizon Method
Abstract
:1. Introduction
2. Literature Review
3. Optimization Model
3.1. Assumptions and Problem Definition
- The system considers a periodic review COP in which a single buyer orders multiple items;
- When the inventory level of an item drops below the reorder point, that item is replenished along with any other item whose inventory level is below the can-order level. Both the reorder point and COP are assumed to be constant;
- The procurement lead time of each item is a multiple of the inventory review period of a buyer;
- There is a correlation between the items considered in the study;
- The demand for each item follows a specific probability distribution.
Problem Definition
3.2. Mathematical Model
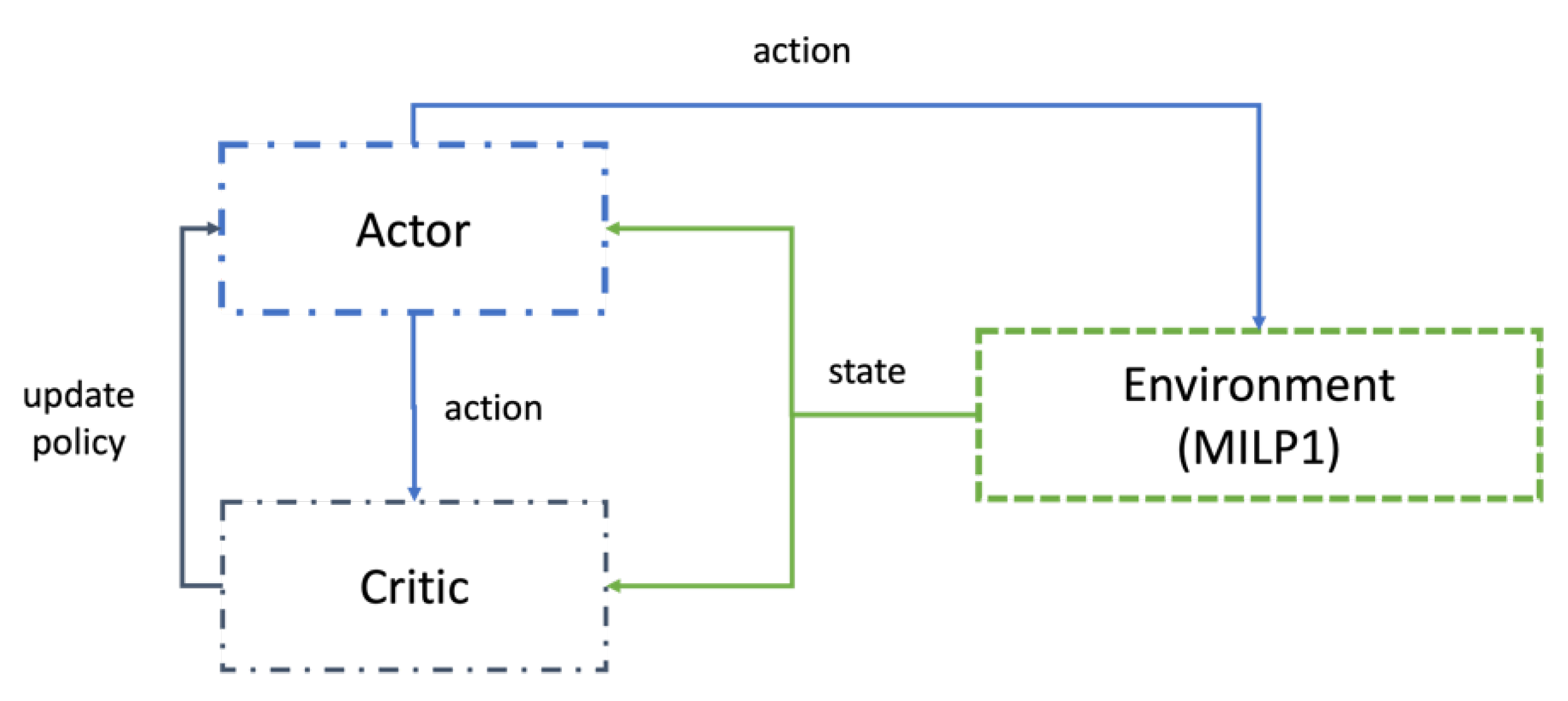
4. Algorithms
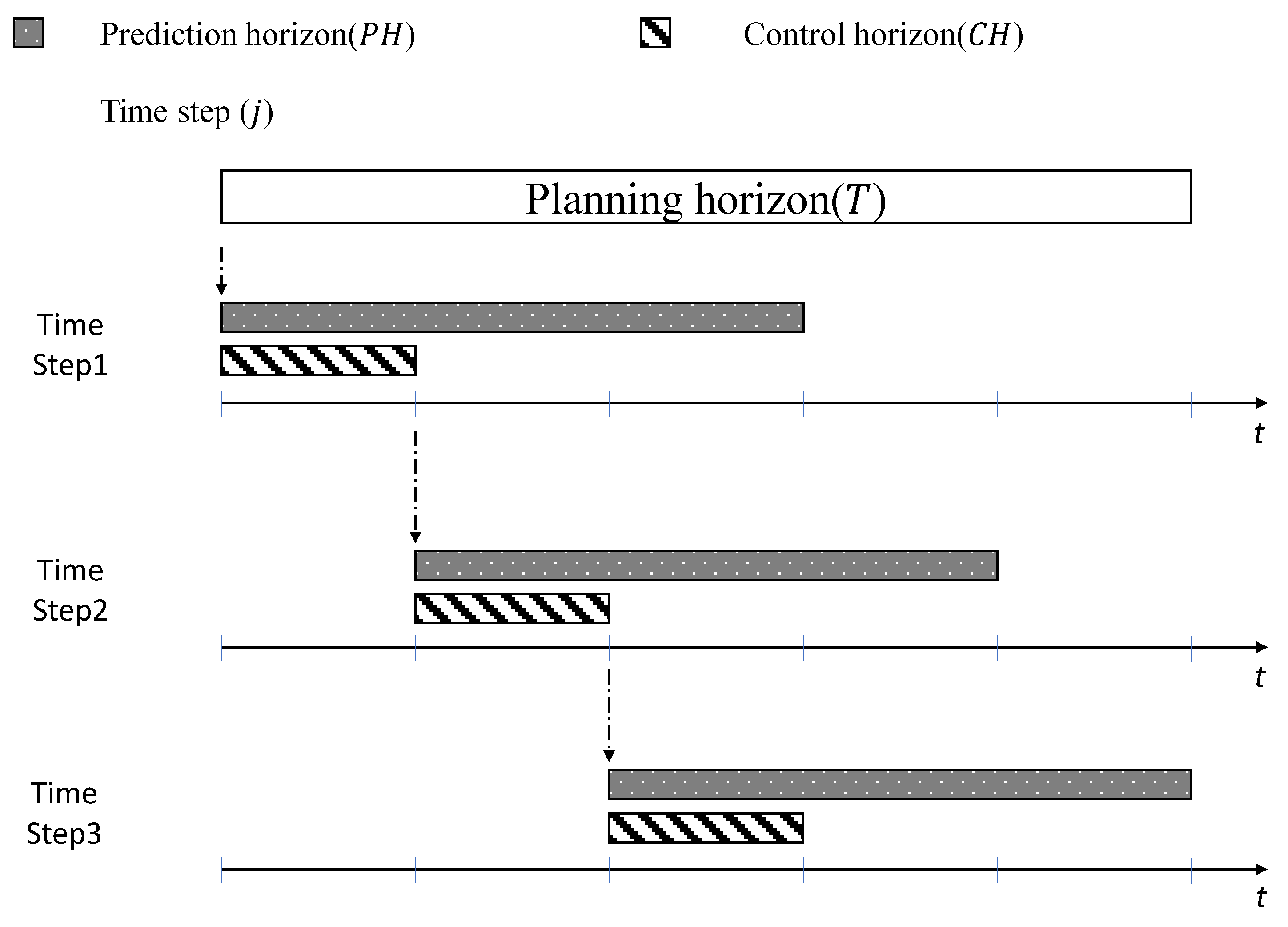
4.1. Rolling Horizon Method
4.2. Dynamic Rolling Horizon Method
5. Numerical Experiments
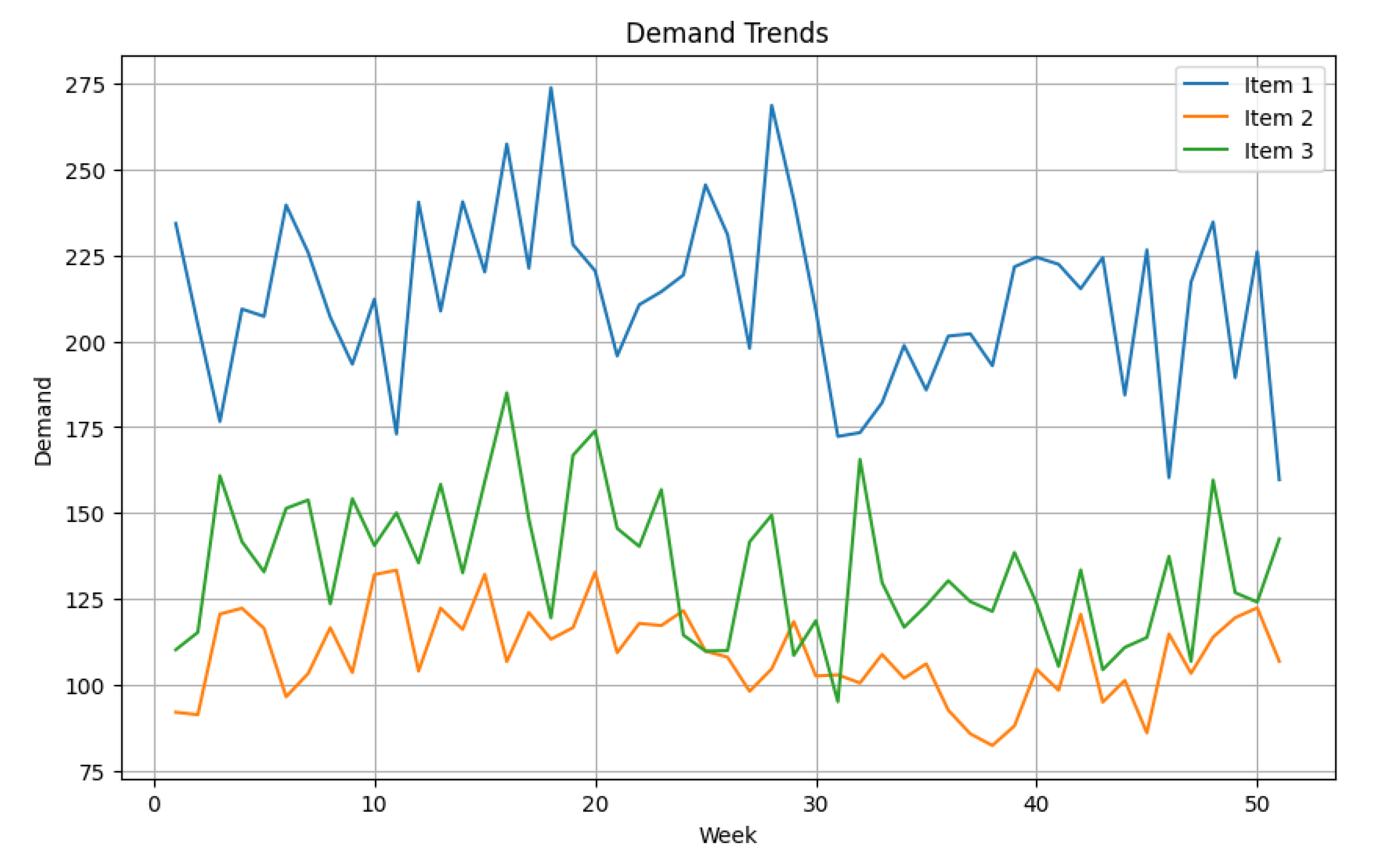
5.1. Experiment Reflecting Situation with Demand Following a Specific Probability Distribution
5.2. Experiment Reflecting Situation with Demand Implying Uncertainty
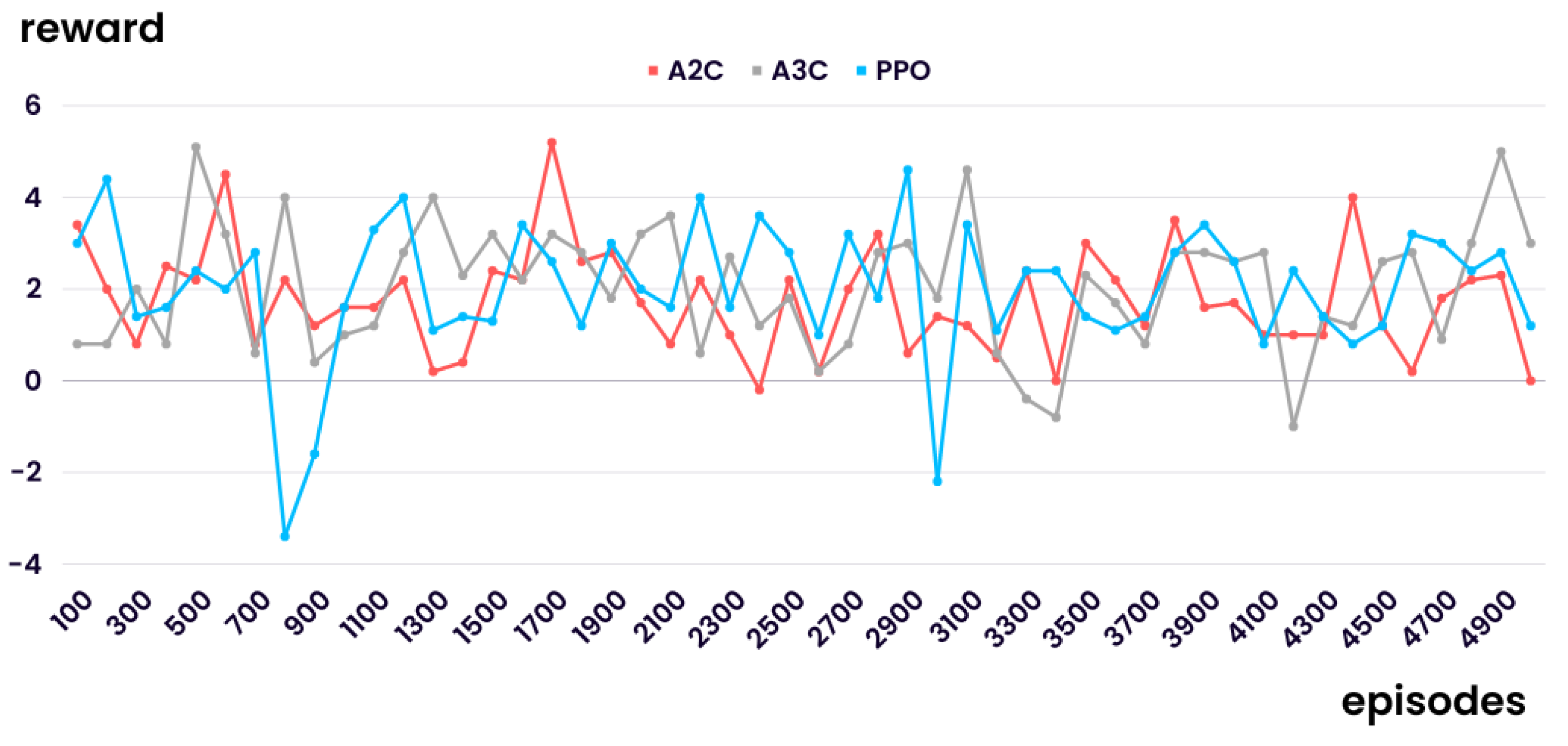
5.3. Comparision Experiment of Dynamic RHM Regarding Interval Length
6. Insights
6.1. Academic Insights
6.2. Managerial Insights
7. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| AI | Artificial Intelligence |
| COP | Can-order Policy |
| MILP | Mixed-integer linear programming |
| RHM | Rolling horizon method |
| RL | Reinforcement learning |
| A2C | Advantage actor–critic |
| A3C | Asynchronous advantage actor–critic |
| PPO | Proximal policy optimization |
| DQN | Deep-Q network |
Appendix A. Notations
| Index | |
| item, | |
| period, | |
| timestep, | |
| Decision variables | |
| Binary variable when an order is confirmed during period | |
| Order-up-to-level of item at period | |
| If drops below , then ; otherwise, | |
| If drops below , then ; otherwise, | |
| If drops below , and at least one item is ordered in period , then ; otherwise, | |
| Prediction horizon at timestep | |
| Variables | |
| Inventory level of item at the end of period | |
| On-hand inventory level of item at the end of period | |
| Backorder inventory level of item at the end of period | |
| Order quantity of item at period | |
| Number of items ordered at period | |
| Parameters of the policy | |
| Hyperparameter in PPO controls the degree of policy update | |
| Parameters | |
| Ordering cost at period | |
| Backorder cost of item at period | |
| Holding cost of item at period | |
| Initial inventory level of item | |
| Replenishment quantity of item , which is ordered before the planning horizon, at period | |
| Forecasted demand of item during period | |
| Real demand of item during period | |
| Can-order level of item | |
| Reorder point of item | |
| Lead time of item | |
| Large number | |
References
- Marilú Destino, J.F.; Müllerklein, D.; Trautwein, V. To Improve Your Supply Chain, Modernize Your Supply-Chain IT. 2022. Available online: https://www.mckinsey.com/capabilities/operations/our-insights/to-improve-your-supply-chain-modernize-your-supply-chain-it (accessed on 12 May 2023).
- AmazonWebServices. Predicting The Future of Demand: How Amazon Is Reinventing Forecasting with Machine Learning. 2021. Available online: https://www.forbes.com/sites/amazonwebservices/2021/12/03/predicting-the-future-of-demand-how-amazon-is-reinventing-forecasting-with-machine-learning/ (accessed on 12 May 2023).
- Mediavilla, M.A.; Dietrich, F.; Palm, D. Review and analysis of artificial intelligence methods for demand forecasting in supply chain management. Procedia CIRP 2022, 107, 1126–1131. [Google Scholar] [CrossRef]
- Boute, R.N.; Gijsbrechts, J.; Van Jaarsveld, W.; Vanvuchelen, N. Deep reinforcement learning for inventory control: A roadmap. Eur. J. Oper. Res. 2022, 298, 401–412. [Google Scholar] [CrossRef]
- Kempf, K.G. Control-oriented approaches to supply chain management in semiconductor manufacturing. In Proceedings of the 2004 American Control Conference, Boston, MA, USA, 30 June–2 July 2004; pp. 4563–4576. [Google Scholar]
- Schwartz, J.D.; Wang, W.; Rivera, D.E. Simulation-based optimization of process control policies for inventory management in supply chains. Automatica 2006, 42, 1311–1320. [Google Scholar] [CrossRef]
- Kayiş, E.; Bilgiç, T.; Karabulut, D. A note on the can-order policy for the two-item stochastic joint-replenishment problem. IIE Trans. 2008, 40, 84–92. [Google Scholar] [CrossRef]
- Nagasawa, K.; Irohara, T.; Matoba, Y.; Liu, S. Applying genetic algorithm for can-order policies in the joint replenishment problem. Ind. Eng. Manag. Syst. 2015, 14, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Noh, J.; Kim, J.S.; Hwang, S.-J. A Multi-Item Replenishment Problem with Carbon Cap-and-Trade under Uncertainty. Sustainability 2020, 12, 4877. [Google Scholar] [CrossRef]
- Tresoldi, E.; Ceselli, A. Rolling-Horizon Heuristics for Capacitated Stochastic Inventory Problems with Forecast Updates. In Advances in Optimization and Decision Science for Society, Services and Enterprises; ODS: Genoa, Italy, 2019; pp. 139–149. [Google Scholar]
- Al-Ameri, T.A.; Shah, N.; Papageorgiou, L.G. Optimization of vendor-managed inventory systems in a rolling horizon framework. Comput. Ind. Eng. 2008, 54, 1019–1047. [Google Scholar] [CrossRef]
- Xie, C.; Wang, L.; Yang, C. Robust inventory management with multiple supply sources. Eur. J. Oper. Res. 2021, 295, 463–474. [Google Scholar] [CrossRef]
- Noh, J.; Hwang, S.-J. Optimization Model for the Energy Supply Chain Management Problem of Supplier Selection in Emergency Procurement. Systems 2023, 11, 48. [Google Scholar] [CrossRef]
- Kara, A.; Dogan, I. Reinforcement learning approaches for specifying ordering policies of perishable inventory systems. Expert Syst. Appl. 2018, 91, 150–158. [Google Scholar] [CrossRef]
- Chen, H.; Chen, Z.; Lin, F.; Zhuang, P. Effective management for blockchain-based agri-food supply chains using deep reinforcement learning. IEEE Access 2021, 9, 36008–36018. [Google Scholar] [CrossRef]
- Chong, J.W.; Kim, W.; Hong, J.S. Optimization of Apparel Supply Chain Using Deep Reinforcement Learning. IEEE Access 2022, 10, 100367–100375. [Google Scholar] [CrossRef]
- Meisheri, H.; Sultana, N.N.; Baranwal, M.; Baniwal, V.; Nath, S.; Verma, S.; Ravindran, B.; Khadilkar, H. Scalable multi-product inventory control with lead time constraints using reinforcement learning. Neural Comput. Appl. 2022, 34, 1735–1757. [Google Scholar] [CrossRef]
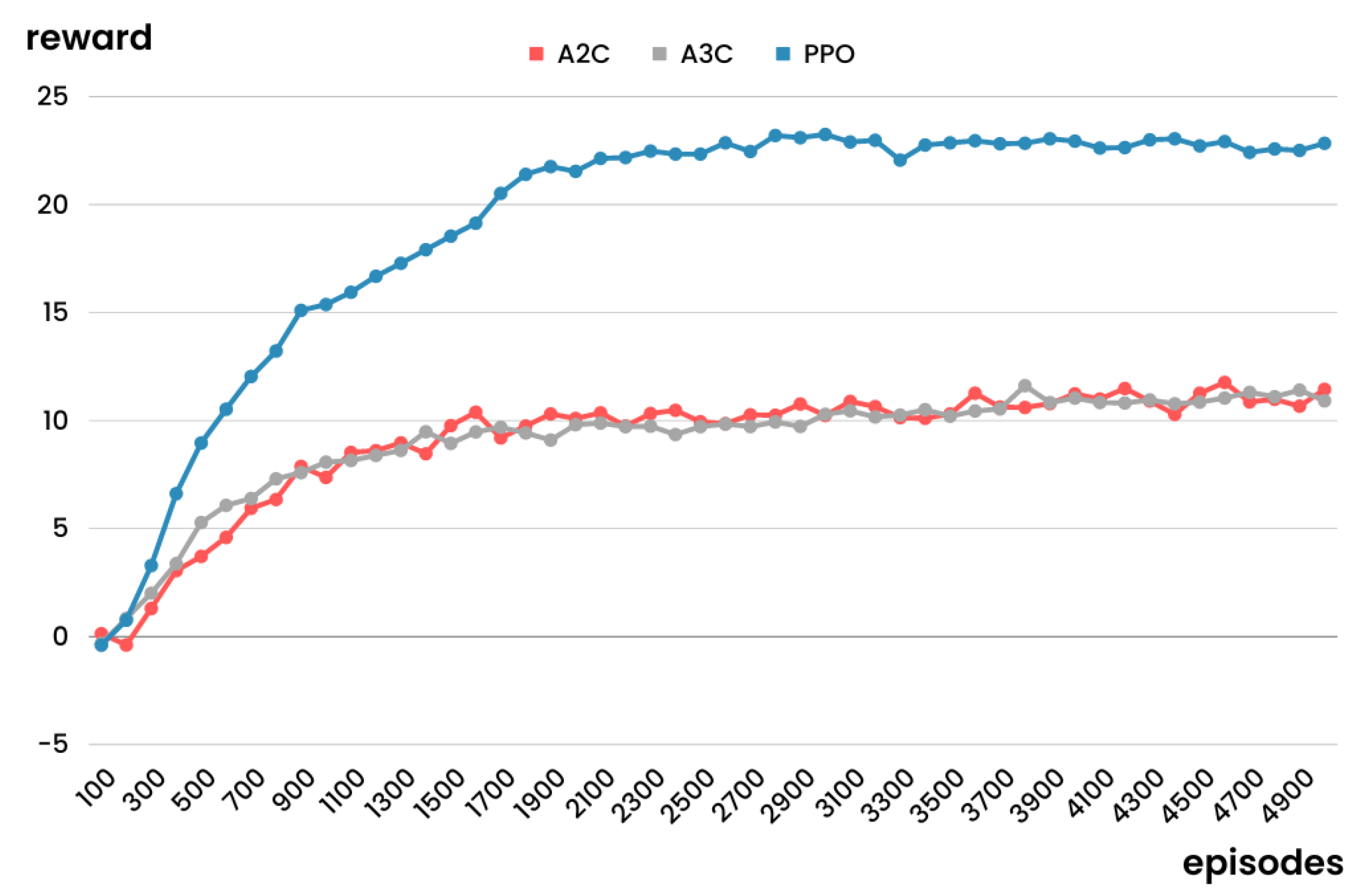
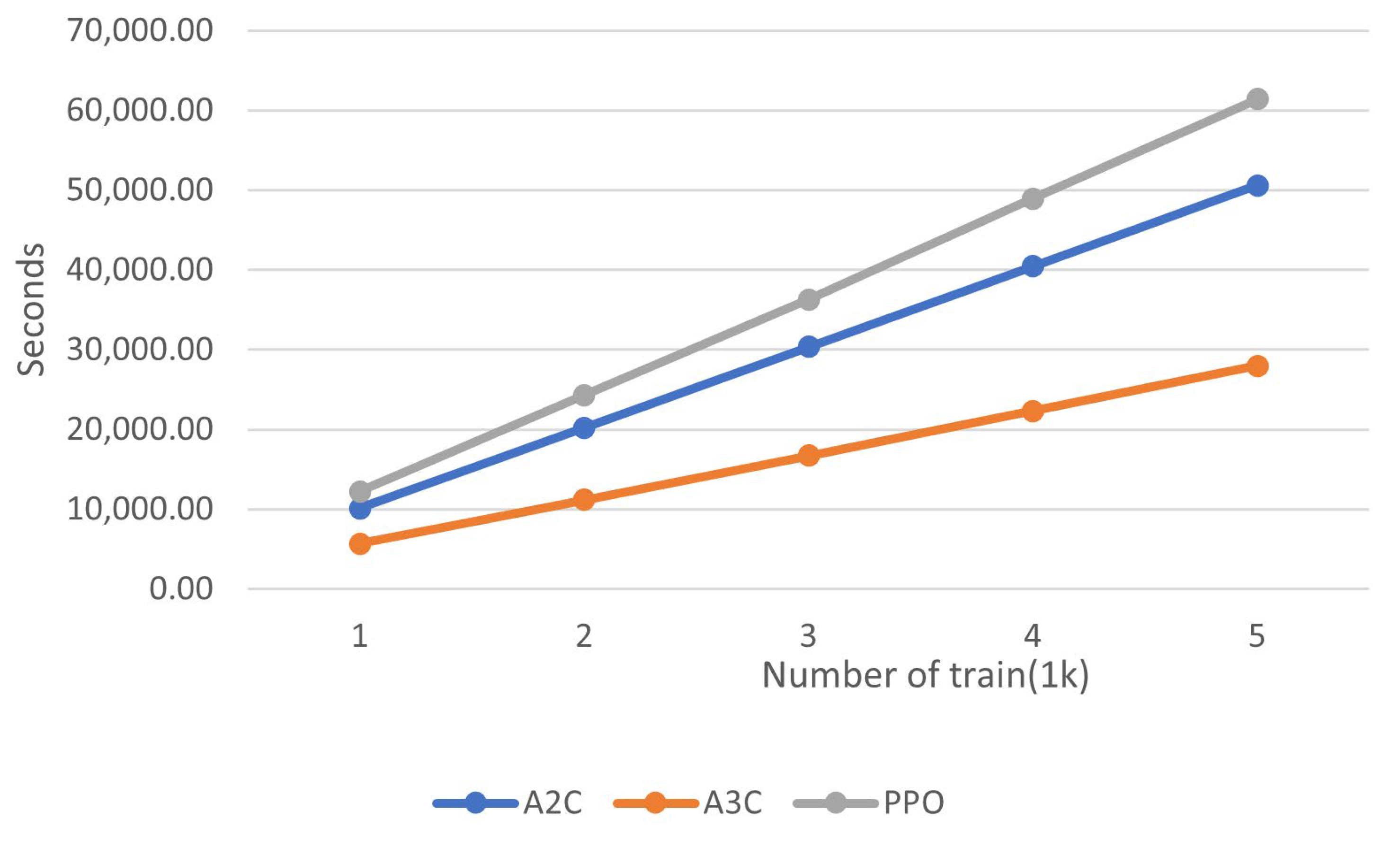
| Hyperparameter | Explanation |
|---|---|
| Number of hidden layers | 2 |
| Number of hidden nodes | 16 |
| Learning rate | 0.00005 |
| Mini-batch size | 128 |
| Item | 1 | 2 | 3 |
|---|---|---|---|
| Demand | |||
| Holding cost | 0.3 | 0.2 | 0.2 |
| Backorder cost | 1.3 | 1.4 | 1.5 |
| Week | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Total Cost |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Algorithm | Interval Length during 10 Weeks | ||||||||||
| A2C | 3 | 3 | 3 | 5 | 3 | 2 | 3 | 6 | 7 | 6 | 4515.50 |
| A3C | 3 | 3 | 3 | 5 | 5 | 3 | 3 | 4 | 2 | 3 | 4359.50 |
| PPO | 3 | 3 | 3 | 4 | 3 | 3 | 3 | 2 | 5 | 3 | 4235.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noh, J. Reinforcement Learning for Optimizing Can-Order Policy with the Rolling Horizon Method. Systems 2023, 11, 350. https://doi.org/10.3390/systems11070350
Noh J. Reinforcement Learning for Optimizing Can-Order Policy with the Rolling Horizon Method. Systems. 2023; 11(7):350. https://doi.org/10.3390/systems11070350
Chicago/Turabian StyleNoh, Jiseong. 2023. "Reinforcement Learning for Optimizing Can-Order Policy with the Rolling Horizon Method" Systems 11, no. 7: 350. https://doi.org/10.3390/systems11070350
APA StyleNoh, J. (2023). Reinforcement Learning for Optimizing Can-Order Policy with the Rolling Horizon Method. Systems, 11(7), 350. https://doi.org/10.3390/systems11070350








