Dynamic Evolutionary Game Approach for Blockchain-Driven Incentive and Restraint Mechanism in Supply Chain Financing
Abstract
:1. Introduction
- (1)
- What dynamic game relationship does the stakeholders in supply chain financing base on BT?
- (2)
- What kind of theoretical model can well characterize the game strategies’ relationship among stakeholders for supply chain financing?
- (3)
- How does BT affect the stakeholders’ strategy choices in supply chain financing?
2. Literature Review
2.1. Supply Chain Financing
2.2. Application of Blockchain Technology
2.3. Application of the Evolutionary Game Theory
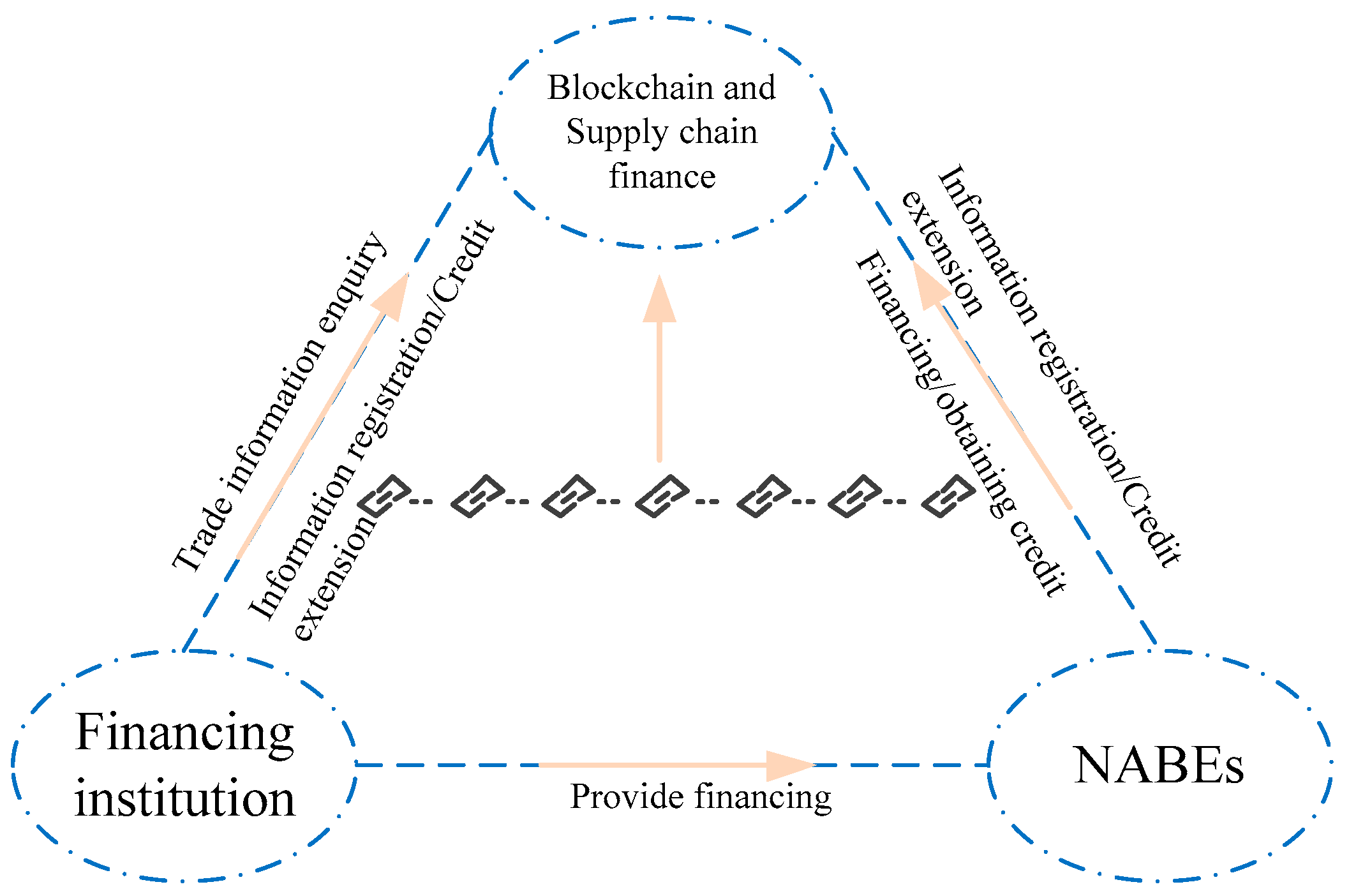
3. Model Formulation
3.1. Assumptions and Parameters for Model
3.2. Construction of the Evolutionary Game Model
3.3. Analysis of the Evolutionary Game Model
3.3.1. The Evolutionary Equilibrium Analysis for FI
3.3.2. The Evolutionary Equilibrium Analysis for NABE
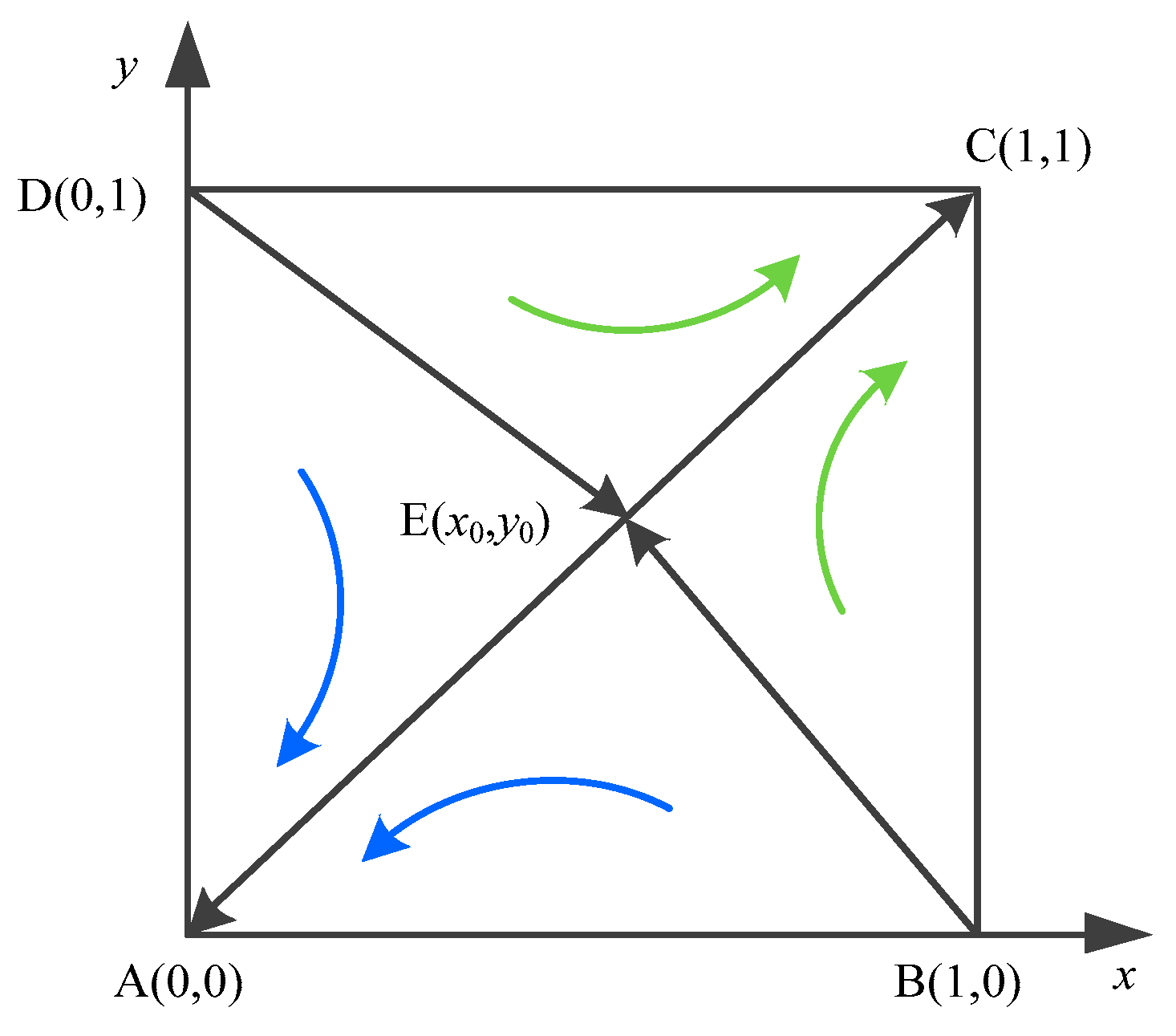
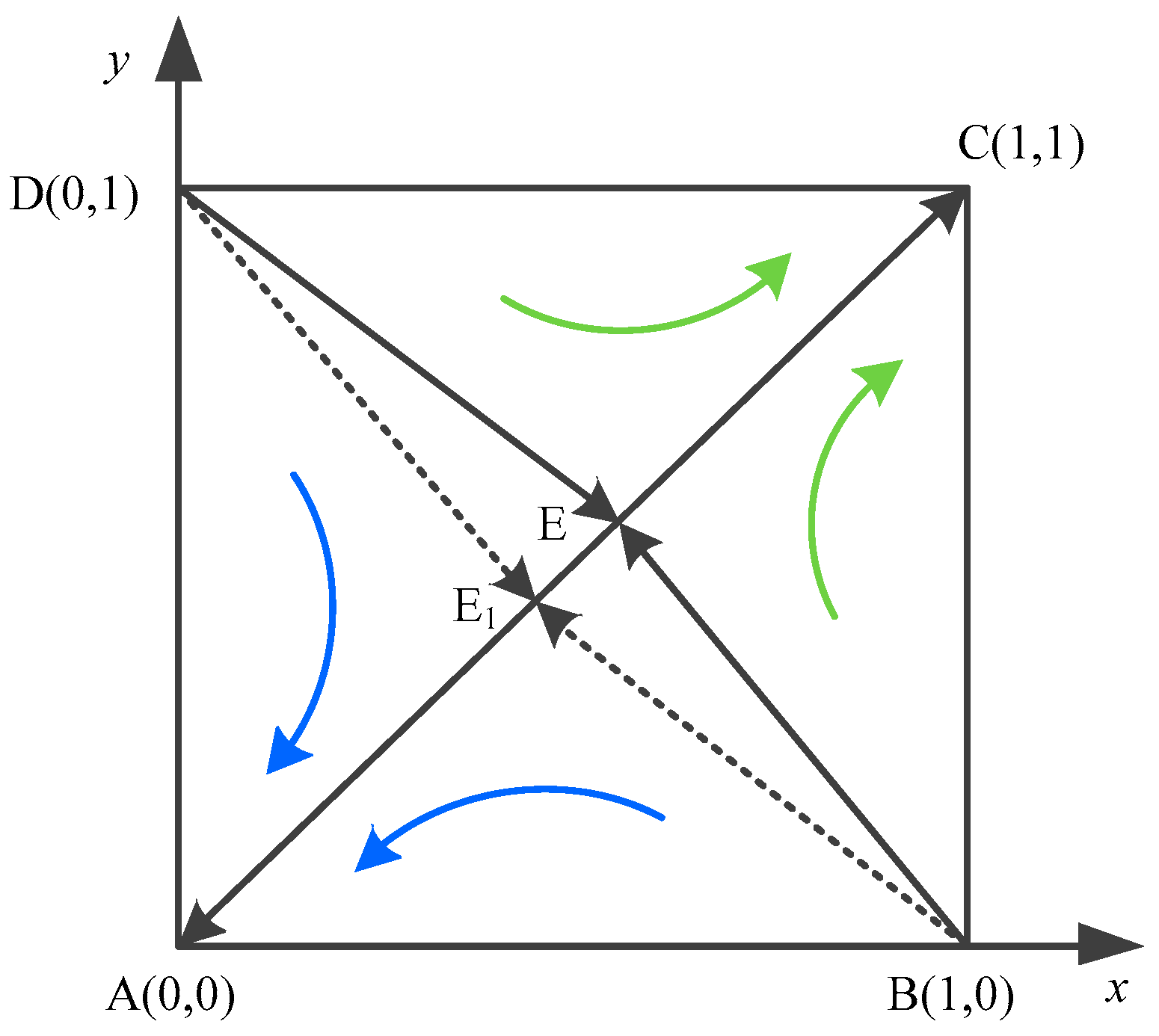
3.3.3. Evolutionary Equilibrium Analysis of Mixed Strategies
4. Simulation Analysis
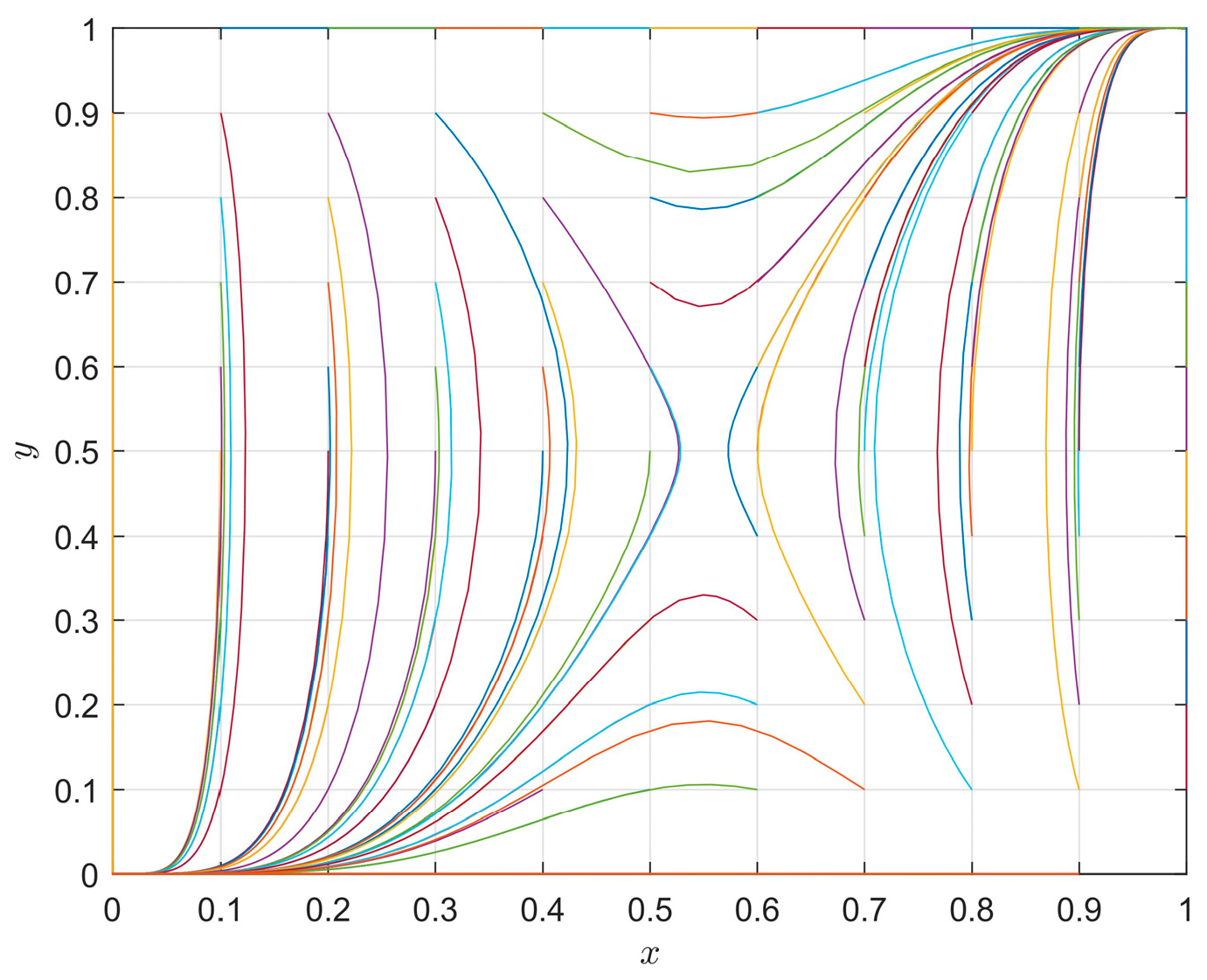
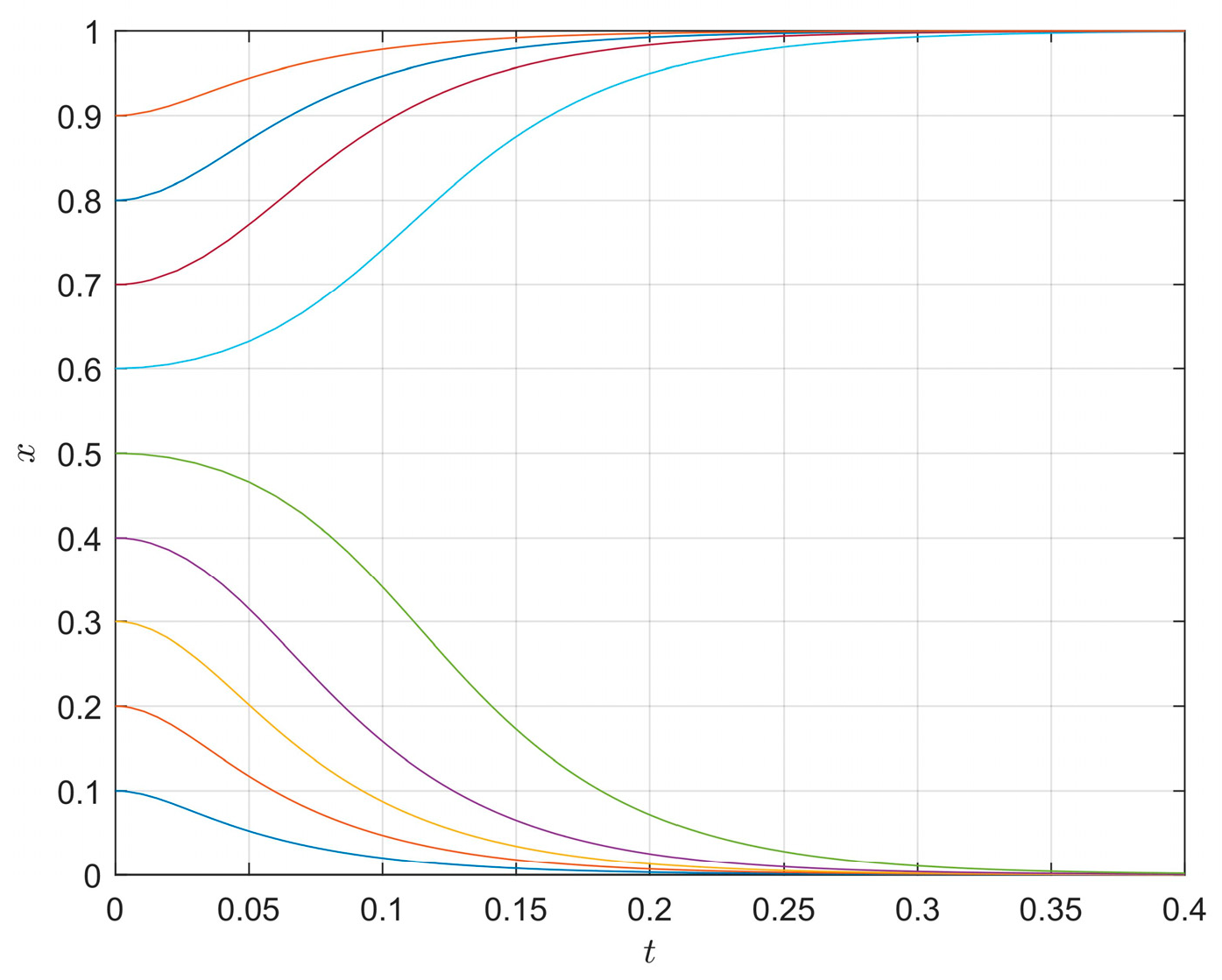
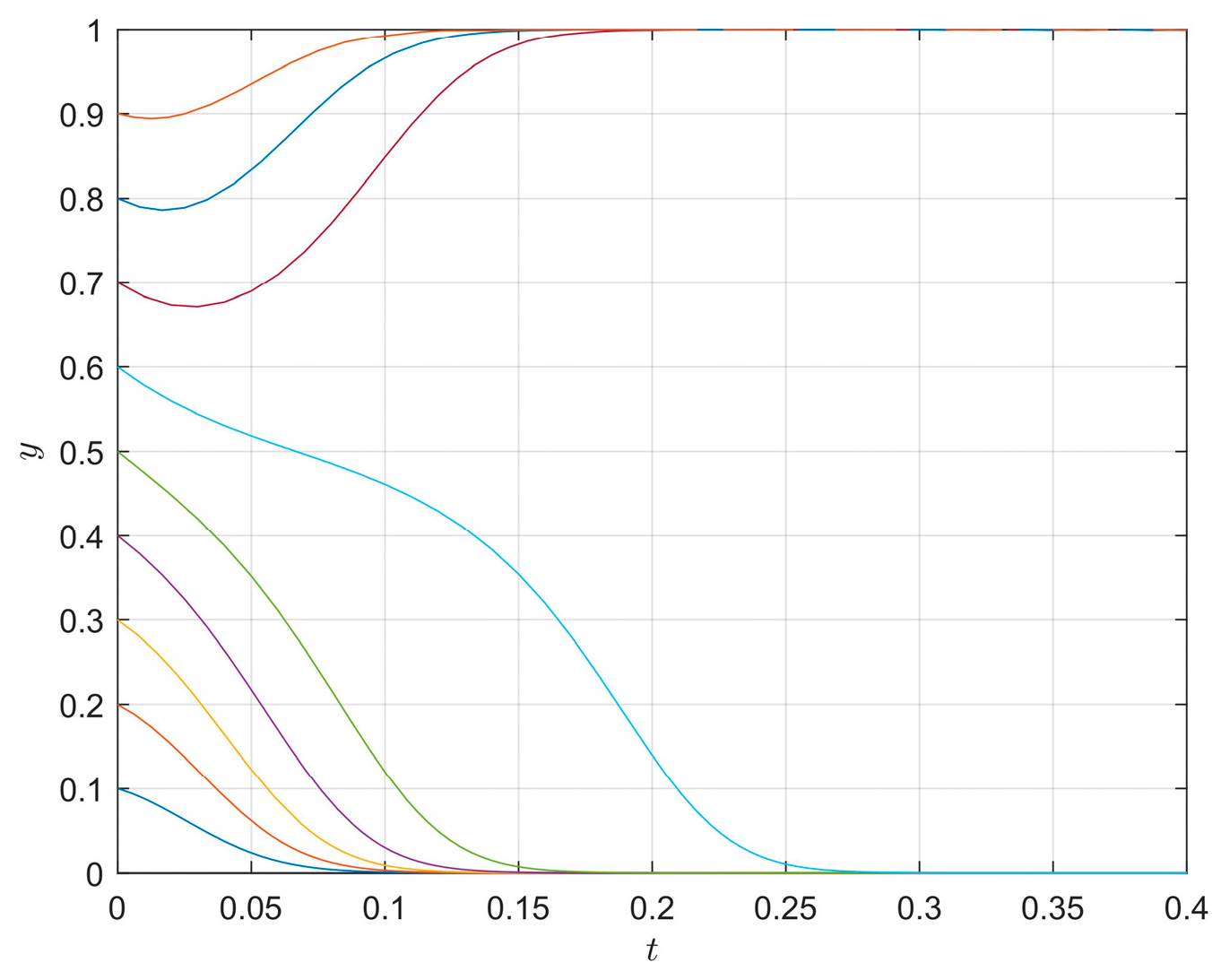
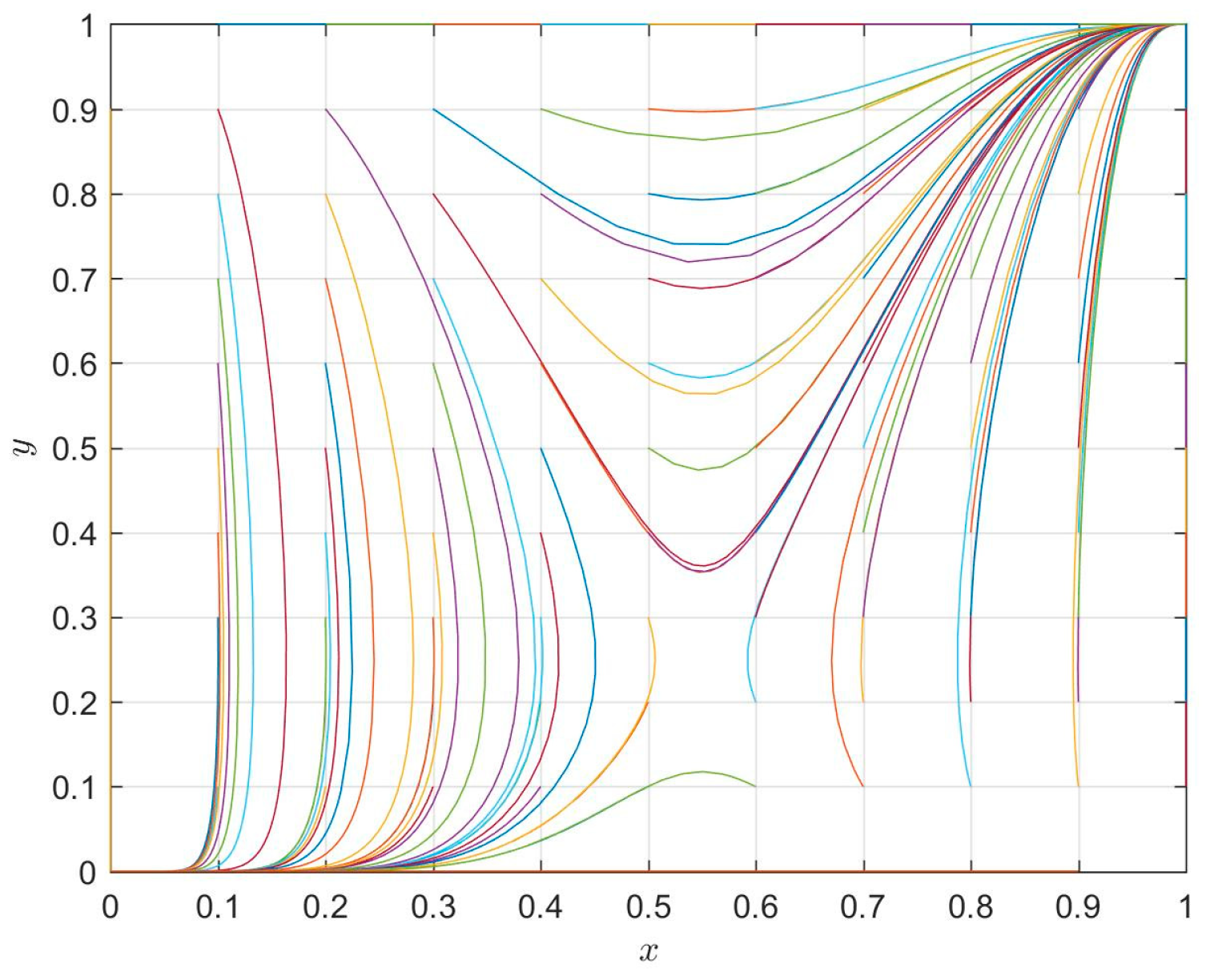
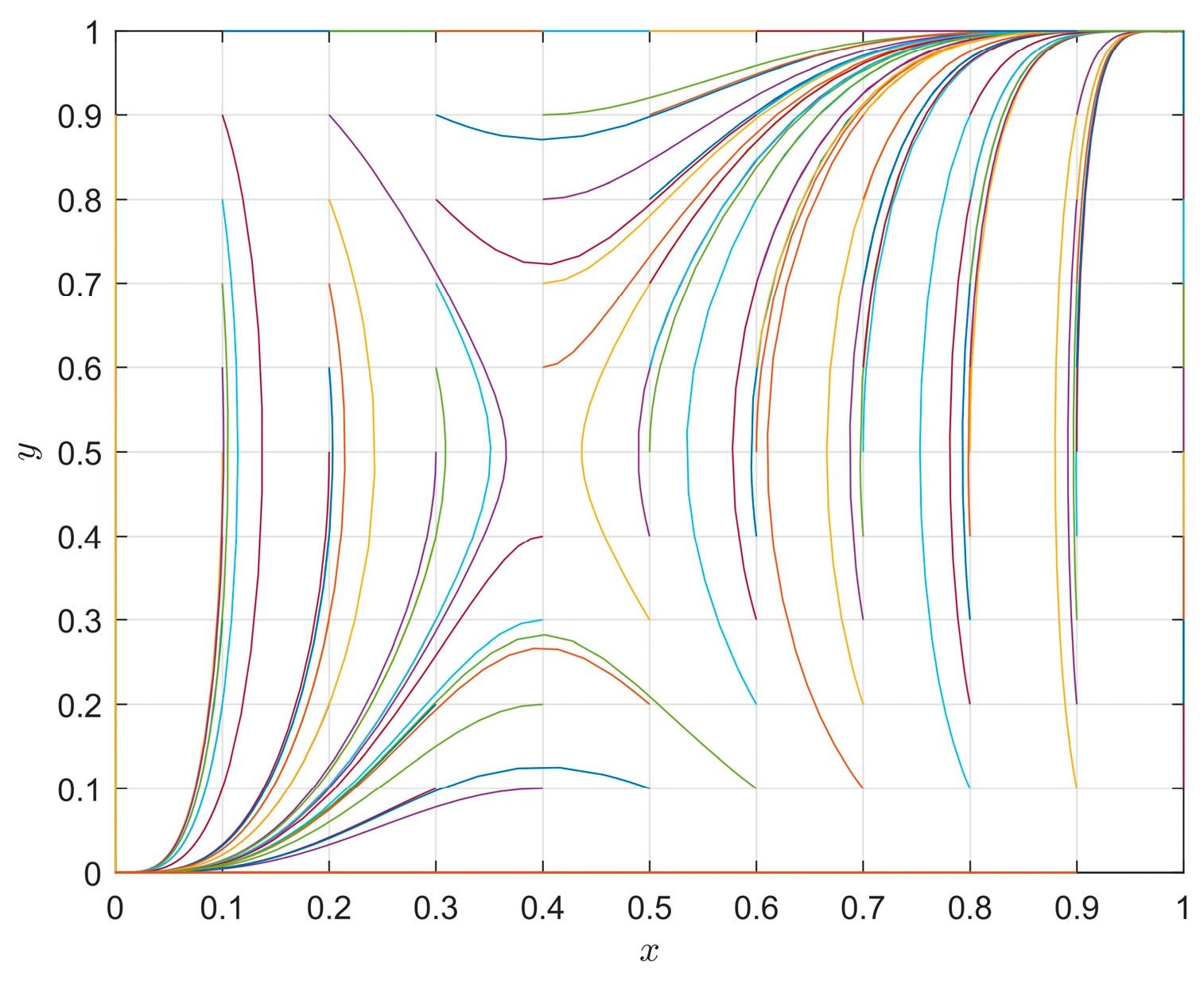
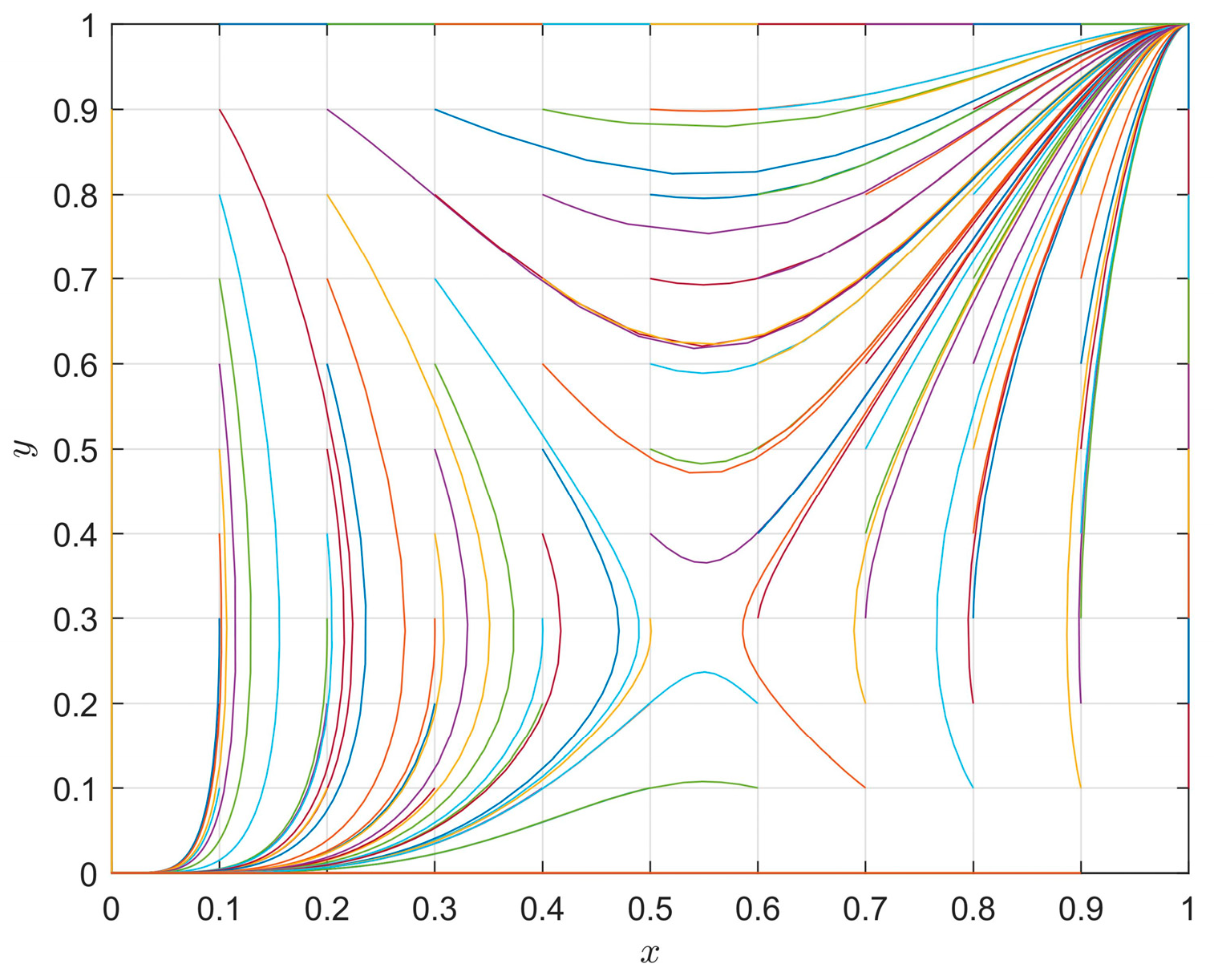
4.1. The Influence of Initial Strategy on the Evolution Path
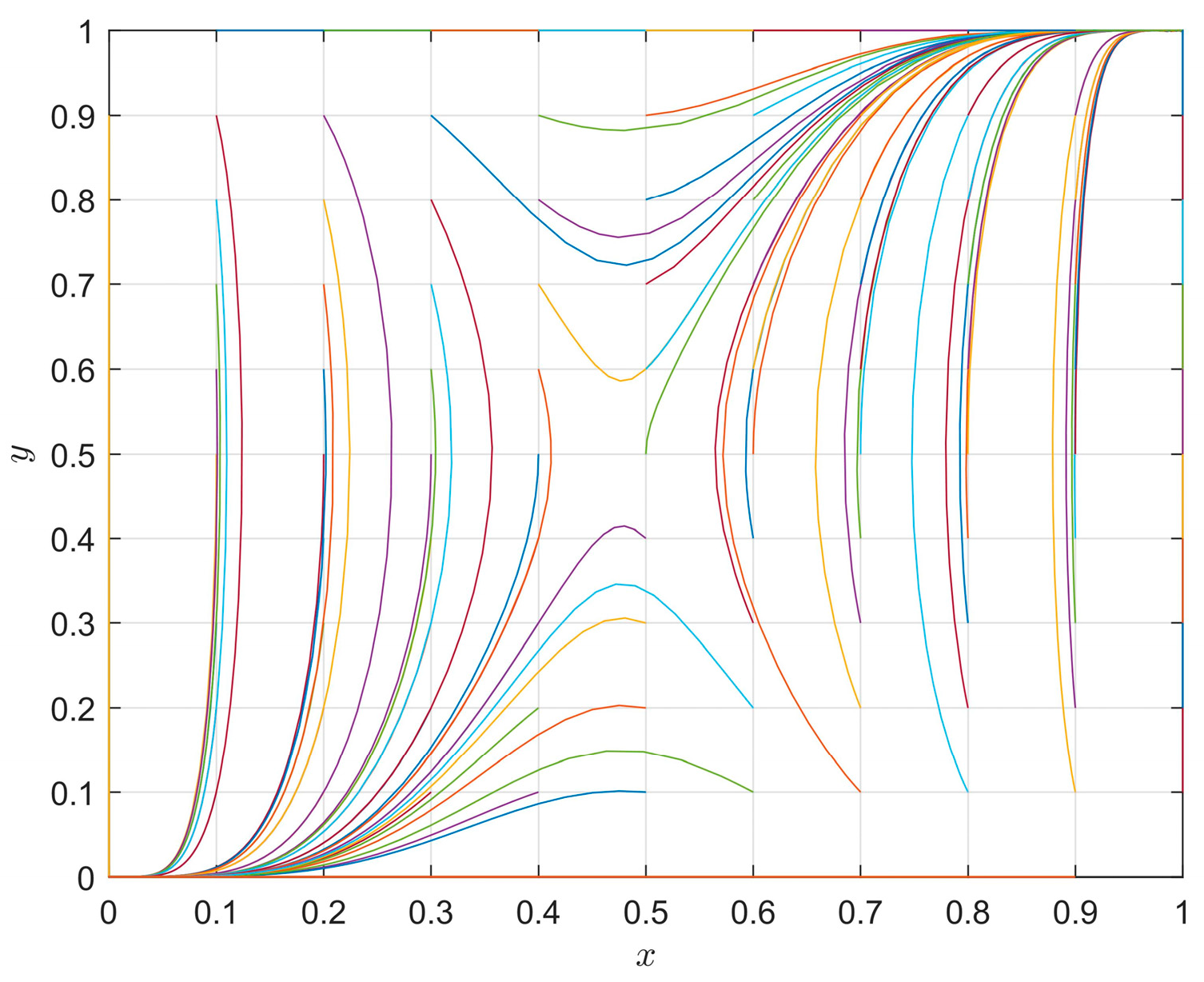
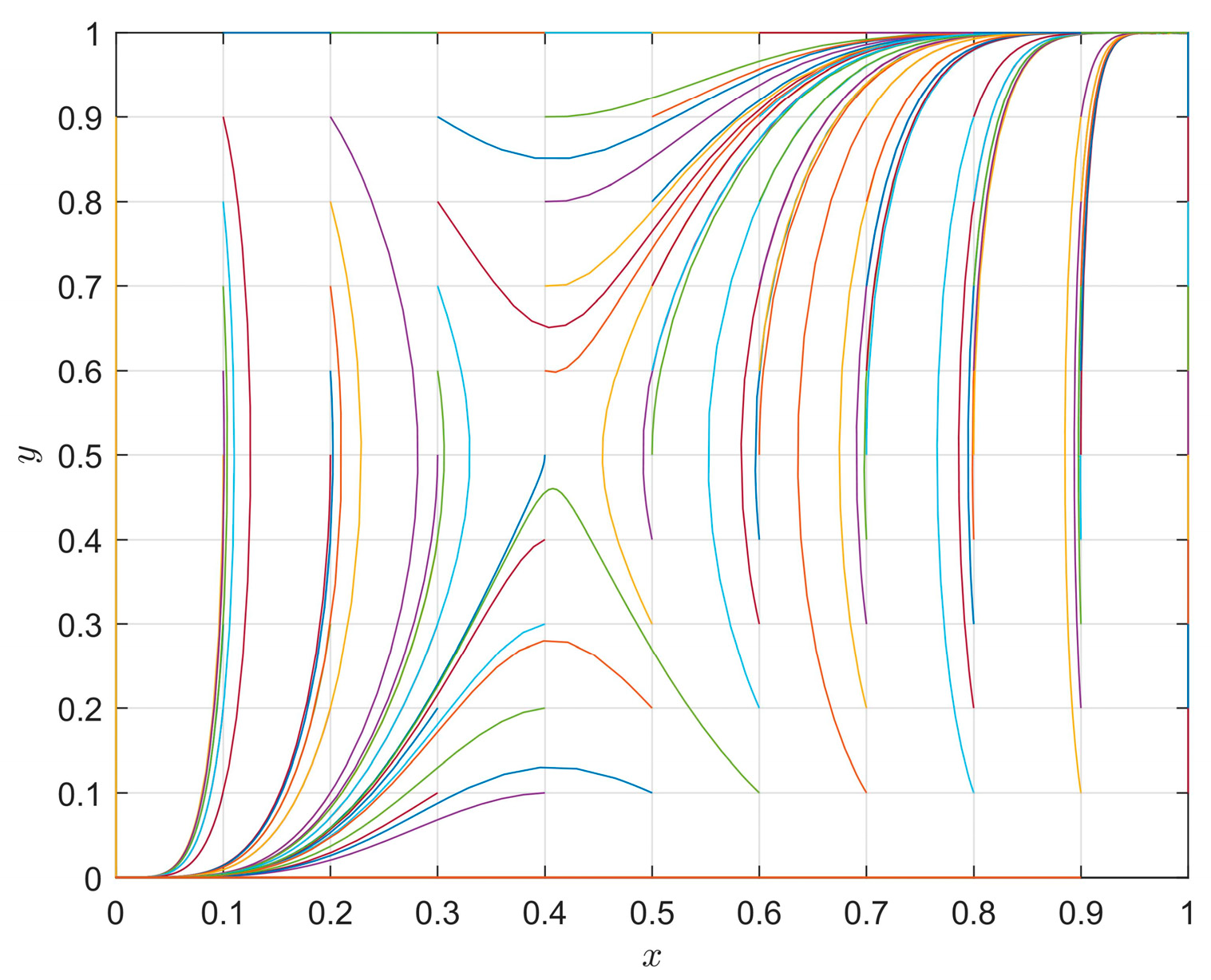
4.2. The Influence of the Different Parameters on Evolution Paths
- (I)
- The influence of the FI’s cost using the BPSM on evolution paths
- (II)
- The influence of the NABE’s interest rate of loans on evolution path
- (III)
- The influence of the FI’s and NABE’s additional benefits on the evolution path
- (IV)
- The influence of the NABE’s default losses on the evolution path
4.3. Discussions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviation
| BT | Blockchain technology |
| FI | Financial institution |
| NABEs | New agricultural business entities |
| SMEs | Small and medium-sized enterprises |
| TSM | Traditional supervised mean |
| BPSM | Blockchain platform supervised mean |
| RDE | Replicated dynamic equation |
Appendix A
- (I)
- If , it can be obtained that and ; then, adopting BPSM is an evolutionary stability strategy for FI. That is, is the evolutionary stable point.
- (II)
- If , it can be obtained that and ; then, adopting TSM is an evolutionary stability strategy for FI. That is, is the evolutionary stable point.
- (III)
- If , an evolutionary stability strategy does not exist for FI since and . That is, no matter what value of is taken, the strategic choice of FI is stable. □
- (I)
- If , it can be obtained that and ; then, adopting repayment is an evolutionary stability strategy for NABE. That is, is the evolutionary stable point.
- (II)
- If , it can be obtained that and ; then, adopting default is an evolutionary stability strategy for NABE. That is, is the evolutionary stable point.
- (III)
- If , an evolutionary stability strategy does not exist for NABE since and . That is, no matter what value of is taken, the strategic choice of NABE is stable. □
References
- Zhang, M.; Zhang, J.; Ma, R.; Chen, X. Quantifying Credit Risk of Supply Chain Finance: A Chinese Automobile Supply Chain Perspective. IEEE Access 2019, 7, 144264–144279. [Google Scholar] [CrossRef]
- Du, M.; Chen, Q.; Xiao, J.; Yang, H.; Ma, X. Supply Chain Finance Innovation Using Blockchain. IEEE Trans. Eng. Manag. 2020, 67, 1045–1058. [Google Scholar] [CrossRef]
- Mou, W.; Wong, W.K.; McAleer, M. Financial Credit Risk Evaluation Based on Core Enterprise Supply Chains. Sustainability 2018, 10, 3699. [Google Scholar] [CrossRef] [Green Version]
- Cheng, L.; Cui, Y.; Duan, K.; Zou, W. The Influence of New Agricultural Business Entities on Farmers’ Employment Decision. Land 2022, 11, 112. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, J.; Li, T.; Chao, J.; Gao, X. Factors Affecting New Agricultural Business Entities’ Adoption of Sustainable Intensification Practices in China: Evidence from the Main Apple-Producing Areas in the Loess Plateau. Agronomy 2021, 11, 2435. [Google Scholar] [CrossRef]
- Kong, X.Z. Status and top level design of new agricultural management entities. Reform 2014, 5, 32–34. [Google Scholar]
- Alchian, A.A.; Demsetz, H. The Property Right Paradigm. J. Econ. Hist. 1973, 33, 16–27. [Google Scholar] [CrossRef] [Green Version]
- Yang, W.; Yan, W. Analysis on Function Orientation and Development Countermeasures of New Agricultural Business Entities. J. Northeast. Agric. Univ. 2016, 23, 82–88. [Google Scholar] [CrossRef]
- Tang, Y.; Yang, M.; Tang, D. Study on the Relieving Mechanism of the Financing Risk of New Agricultural Management Subject. NanJing J. Scoial Sci. 2022, 2, 30–41+101. [Google Scholar]
- Zhu, S.Z.; Chen, Y.T.; Wang, W.W. Risk Assessment of Biological Asset Mortgage Loans of China’s New Agricultural Business Entities. Complexity 2020, 2020, 8865840. [Google Scholar] [CrossRef]
- Shen, K.D. Research on the path of optimizing the financial environment of new agricultural business entities. Agric. Econ. 2022, 3, 102–104. [Google Scholar]
- Saberi, S.; Kouhizadeh, M.; Sarkis, J.; Shen, L. Blockchain technology and its relationships to sustainable supply chain management. Int. J. Prod. Res. 2019, 57, 2117–2135. [Google Scholar] [CrossRef] [Green Version]
- Wu, L.; Lu, W.; Xu, J. Blockchain-based smart contract for smart payment in construction: A focus on the payment freezing and disbursement cycle. Front. Eng. Manag. 2022, 9, 177–195. [Google Scholar] [CrossRef]
- Cagigas, D.; Clifton, J.; Diaz-Fuentes, D.; Fernandez-Gutierrez, M. Blockchain for Public Services: A Systematic Literature Review. IEEE Access 2021, 9, 13904–13921. [Google Scholar] [CrossRef]
- Fan, H. The digital asset value and currency supervision under deep learning and blockchain technology. J. Comput. Appl. Math. 2022, 407, 114061. [Google Scholar] [CrossRef]
- Petroni, B.; Goncalves, R.F.; Ignacio, P.; Reis, J.Z.; Martins, G. Smart contracts applied to a functional architecture for storage and maintenance of digital chain of custody using blockchain. Forensic Sci. Int. Digit. Investig. 2020, 34, 300985. [Google Scholar] [CrossRef]
- Trivedi, S.; Mehta, K.; Sharma, R. Systematic Literature Review on Application of blockchain Technology in E-Finance and Financial Services. J. Technol. Manag. Innov. 2021, 16, 89–102. [Google Scholar] [CrossRef]
- Deepa, N.; Pham, Q.; Nguyen, D.C.; Bhattacharya, S.; Prabadevi, B.; Gadekallu, T.R.; Maddikunta, P.K.R.; Fang, F.; Pathirana, P.N. A survey on blockchain for big data: Approaches, opportunities, and future directions. Future Gener. Comput. Syst. 2022, 131, 209–226. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, J.Z.; He, W.; Li, W. Mitigating information asymmetry in inventory pledge financing through the Internet of things and blockchain. J. Enterp. Inf. Manag. 2021, 34, 1429–1451. [Google Scholar] [CrossRef]
- Jin, W.; Zhang, Q.; Luo, J. Non-collaborative and collaborative financing in a bilateral supply chain with capital constraints. Omega 2018, 88, 210–222. [Google Scholar] [CrossRef]
- Wu, D.D.; Yang, L.P.; Olson, D.L. Green supply chain management under capital constraint. Int. J. Prod. Econ. 2019, 215, 3–10. [Google Scholar] [CrossRef]
- Huo, Y.H.; Lee, C.K.M.; Zhang, S.Z. Trinomial tree based option pricing model in supply chain financing. Ann. Oper. Res. 2021. [Google Scholar] [CrossRef]
- Wang, Z.Q.; Wang, Q.; Lai, Y.; Liang, C.J. Drivers and outcomes of supply chain finance adoption: An empirical investigation in China. Int. J. Prod. Econ. 2020, 220, 107453. [Google Scholar] [CrossRef]
- Yang, J.; Tang, D.; Kong, H.; Boammah, V. Research on financial risk management and control of agricultural products supply chain-A case study of Jiangsu Province of China. Front. Environ. Sci. 2022, 10, 1008716. [Google Scholar] [CrossRef]
- Zhang, Y.; Rehman Khan, S.A. Evolutionary game analysis of green agricultural product supply chain financing system: COVID-19 pandemic. Int. J. Logist. Res. Appl. 2022, 25, 1115–1135. [Google Scholar] [CrossRef]
- Li, Z.; Ju, W.; Kim, S.; Piao, S.; Hu, S.; Lee, J. Study on the Evaluation of Agricultural Supply Chain Finance Model: Focused on Jilin Province China. J. Korea Acad. -Ind. Coop. Soc. 2021, 22, 233–243. [Google Scholar] [CrossRef]
- Yan, B.; Liu, G.; Zhang, Z.; Yan, C. Optimal financing and operation strategy of fresh agricultural supply chain. Aust. J. Agric. Resour. Econ. 2020, 64, 776–794. [Google Scholar] [CrossRef]
- Duan, W.C.; Hu, H.Z.; Zhang, Y.T. What determines the performance of small and medium-sized enterprises supply chain financing? A qualitative comparative analysis of fuzzy sets based on the technology-organization-environment framework. Front. Psychol. 2022, 13, 976218. [Google Scholar] [CrossRef]
- Xu, M.Y.; Ma, S.J.; Wang, G. Differential Game Model of Information Sharing among Supply Chain Finance Based on Blockchain Technology. Sustainability 2022, 14, 7139. [Google Scholar] [CrossRef]
- Wang, Y.; You, J. The Operation Mode of Agricultural Supply Chain Finance Using Blockchain. Comput. Intell. Neurosci. 2022, 2022, 3338030. [Google Scholar] [CrossRef]
- Zhou, Q.; Chen, X.; Li, S. Innovative Financial Approach for Agricultural Sustainability: A Case Study of Alibaba. Sustainbility 2018, 10, 891. [Google Scholar] [CrossRef] [Green Version]
- Zhan, J.; Li, S.; Chen, X. The impact of financing mechanism on supply chain sustainability and efficiency. J. Clean. Prod. 2018, 205, 407–418. [Google Scholar] [CrossRef]
- Cheng, L.; Zou, W.; Duan, K. The Influence of New Agricultural Business Entities on the Economic Welfare of Farmer’s Families. Agriculture 2021, 11, 880. [Google Scholar] [CrossRef]
- Theodore, W.S. Transforming Traditional Agriculture; The University of Chicago Press: Chicago, IL, USA, 1964. [Google Scholar]
- Soto, H.D. Citadels of Dead Capital. Reason 2001, 33, 40–48. [Google Scholar]
- Townsend, R.; Yaron, J. The Credit Risk–Contingency System of an Asian Development Bank. Econ. Perspect. 2001, 25, 31–48. [Google Scholar]
- McCord, M.; Osinde, S. Reducing vulnerability: The supply of health microinsurance in East Africa. J. Int. Dev. 2005, 17, 327–381. [Google Scholar] [CrossRef]
- Zhang, L.; Fan, J. Formal Credit-Assisted New Agricultural Business: A Multifactor Analysis Based on BP Neural Network. Mob. Inf. Syst. 2022, 2022, 7826838. [Google Scholar] [CrossRef]
- Kouhizadeh, M.; Saberi, S.; Sarkis, J. Blockchain technology and the sustainable supply chain: Theoretically exploring adoption barriers. Int. J. Prod. Econ. 2021, 231, 107831. [Google Scholar] [CrossRef]
- Sun, R.; He, D.; Su, H. Evolutionary Game Analysis of Blockchain Technology Preventing Supply Chain Financial Risks. J. Theor. Appl. Electron. Commer. Res. 2021, 16, 2824–2842. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Luong, N.C.; Wang, W.B.; Niyato, D.; Wang, P.; Liang, Y.C.; Kim, D.I. A Survey on Blockchain: A Game Theoretical Perspective. IEEE Access 2019, 7, 47615–47643. [Google Scholar] [CrossRef]
- Yermack, D. Corporate Governance and Blockchains. Rev. Financ. 2017, 21, 7–31. [Google Scholar] [CrossRef] [Green Version]
- Mishkin, F.S.; Strahan, P.E. What will Technology Do to Financial Structure? In National Bureau of Economic Research Working Paper; National Bureau of Economic Research: Cambridge, MA, USA, 1999; p. 6892. Available online: https://ssrn.com/abstract=147163 (accessed on 20 June 2023).
- Song, L.; Luo, Y.; Chang, Z.; Jin, C.; Nicolas, M. Blockchain Adoption in Agricultural Supply Chain for Better Sustainability: A Game Theory Perspective. Sustainability 2022, 14, 1470. [Google Scholar] [CrossRef]
- Niu, B.; Dong, J.; Liu, Y. Incentive alignment for blockchain adoption in medicine supply chains. Transp. Res. Part E-Logist. Transp. Rev. 2021, 152, 102276. [Google Scholar] [CrossRef]
- Shen, L.; Yang, Q.; Hou, Y.; Lin, J. Research on information sharing incentive mechanism of China’s port cold chain logistics enterprises based on blockchain. Ocean. Coast. Manag. 2022, 225, 106229. [Google Scholar] [CrossRef]
- Zhu, Q.; Zong, R.; Xu, M. Three-Party Stochastic Evolutionary Game Analysis of Supply Chain Finance Based on Blockchain Technology. Sustainability 2023, 15, 3084. [Google Scholar] [CrossRef]
- Deng, L.; Li, Y.; Wang, S.; Luo, J. The impact of blockchain on optimal incentive contracts for online supply chain finance. Environ. Sci. Pollut. Res. 2023, 30, 12466–12494. [Google Scholar] [CrossRef]
- Friedman, D. Evolutionary Game in Economics. Econometrica 1991, 59, 637–666. [Google Scholar] [CrossRef] [Green Version]
- Toda, K.; Kuze, N.; Ushio, T. Stability analysis and control of decision-making of miners in blockchain. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2021, E105, 682–688. [Google Scholar] [CrossRef]
- Xu, R.; Guo, T.; Zhao, H. Research on the Path of Policy Financing Guarantee to Promote SMEs’ Green Technology Innovation. Mathematics 2022, 10, 642. [Google Scholar] [CrossRef]
- Kang, K.; Zhao, Y.; Zhang, J.; Qiang, C. Evolutionary game theoretic analysis on low-carbon strategy for supply chain enterprises. J. Clean. Prod. 2019, 230, 981–994. [Google Scholar] [CrossRef]
- Yan, B.; Chen, Z.; Yan, C.; Zhang, Z.; Kang, H. Evolutionary multiplayer game analysis of accounts receivable financing based on supply chain financing. Int. J. Prod. Res. 2021, 1–19. [Google Scholar] [CrossRef]
- Houston, J.F.; Lin, C.; Zhu, Z. The financial implications of supply chain changes. Manag. Sci. 2016, 62, 2520–2542. [Google Scholar] [CrossRef]
- Long, H.Y.; Liu, H.Y.; Li, X.W.; Chen, L.J. An evolutionary game theory study for construction and demolition waste recycling considering green development performance under the Chinese government’s reward-penalty mechanism. Int. J. Environ. Res. Public Health 2020, 17, 6303. [Google Scholar] [CrossRef] [PubMed]
| No. | Research Objective | Methodology | Research Perspective | References |
|---|---|---|---|---|
| 1 | The impact mechanism of supply chain financing | / | Key driving factors for supply chain financing decision-making | [21,23,54] |
| 2 | Incentive mechanism for information sharing among supply chain enterprises | Evolutionary game theory | Encourage participants to use BT | [45,46,47] |
| 3 | The impact of BT on the optimal incentive contract in supply chain finance | Principal-agent model and incentive theory | The impact of BT maturity on participants | [48] |
| 4 | Incentive mechanism for using BT in retailer inventory games | Sequential games | The impact of demand uncertainty on subjects adopting BT | [55] |
| 5 | Incentive and Restraint Mechanism in Supply Chain Financing | Evolutionary game theory | The impact of BT-driven on the behavioral strategies of participants | This paper |
| Parameters | Descriptions | |
|---|---|---|
| Decision variables | The probability using the BPSM for FI | |
| The probability of the repayment on time for the NABE | ||
| The financial income rate for the NABE | ||
| The loan rate from FI | ||
| , | The NABE’s default losses when the FI chooses BPSM and TSM, respectively | |
| The FI’s additional benefits when it chooses the BPSM strategy | ||
| The appraise of collateral for NABE | ||
| The NABE’s additional benefits when it chooses the repayment strategy | ||
| The loan-to-value rate determined by FI | ||
| The FI’s cost choosing the BPSM supervision | ||
| The cost of credit checks when the FI selects TSM supervision | ||
| Strategy | NABE | ||
|---|---|---|---|
| FI | BPSM () | , | , |
| TSM () | , | , | |
| Equilibrium Points | Stability | ||
|---|---|---|---|
| stable | |||
| unstable | |||
| stable | |||
| unstable | |||
| saddle point |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, L.; Cao, Y. Dynamic Evolutionary Game Approach for Blockchain-Driven Incentive and Restraint Mechanism in Supply Chain Financing. Systems 2023, 11, 406. https://doi.org/10.3390/systems11080406
Su L, Cao Y. Dynamic Evolutionary Game Approach for Blockchain-Driven Incentive and Restraint Mechanism in Supply Chain Financing. Systems. 2023; 11(8):406. https://doi.org/10.3390/systems11080406
Chicago/Turabian StyleSu, Limin, and Yongchao Cao. 2023. "Dynamic Evolutionary Game Approach for Blockchain-Driven Incentive and Restraint Mechanism in Supply Chain Financing" Systems 11, no. 8: 406. https://doi.org/10.3390/systems11080406






