Integrated System Design for Post-Disaster Management: Multi-Facility, Multi-Period, and Bi-Objective Optimization Approach
Abstract
1. Introduction
2. Literature Review
3. Problem Description
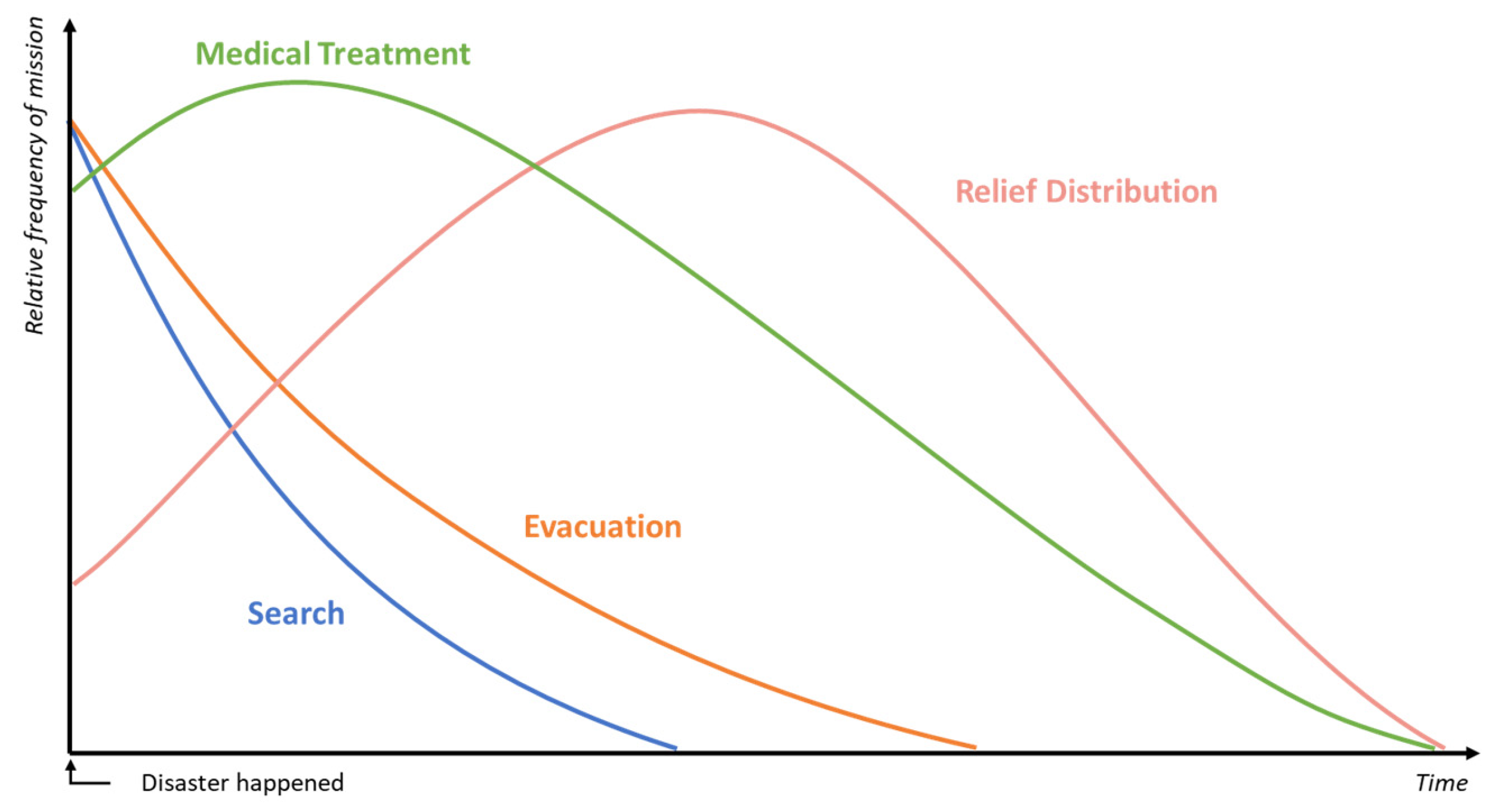
3.1. Multi-Period Missions
3.2. Facility Candidates
3.3. Objectives
4. Mathematical Formulation
4.1. Notations
| I | : | Set of tasks; |
| J | : | Set of candidate sites; |
| K | : | Set of facility types, {S,E,M,R} ∈ K. S, E, M, and R, stand for search, evacuation, medical treatment, and relief distribution, respectively; |
| T | : | Set of periods; |
| ui | : | Set of periods in which task i is defined, ui ⊆ T; |
| mi | : | Type of task i, mi ∈ K; |
| nj | : | Set of available types of candidate facility j, nj ⊆ K; |
| (xi, yi) | : | Location of task I; |
| (xj, yj) | : | Location of candidate infrastructure facility j; |
| Dij | : | Distance between task i and candidate facility j; |
| Tij | : | Travelling time between task i and candidate facility j. Tij is not proportional to Dij; |
| Ait | : | Demand quantity of task i, t ∈ ui. It is equal to 0 for t ∉ ui; |
| Qj,k | : | Capacity of facility j when it is used as type k ∈ nj. It is equal to 0 for k ∉ nj; |
| Cj,kt | : | Operation cost of facility j of type k ∈ nj for period t ∈ T. It is equal to 0 for k ∉ nj; |
| Sj,k | : | Setup cost of candidate j for type k ∈ nj facility; |
| R | : | Service radius of drone station; |
| Smax | : | Maximum allowed transportation time of emergency patients; |
| M | : | A large positive real number; |
| Oj,k | : | Binary setup decision variable. It is equal to 1 if candidate facility j is used for type k ∈ nj facility; |
| Yj,kt | : | Binary location decision variable. It is equal to 1 if candidate facility j of type k ∈ nj is opened for period t; |
| Xi,jt | : | Binary assignment decision variable. It is equal to 1 if task i of k = mi, t ∈ Ui is served by facility j; |
4.2. Formulation
4.3. Estimation of Facility Service Range
5. Approach to Finding Pareto-Optimal Solutions
5.1. Pareto Optimality
5.2. Modified Epsilon-Constraint Algorithm
Subject to F2 < ε
x ∈ D
| Algorithm 1: Modified epsilon-constraint method | |
| 1: | S:= , t = 0 |
| 2: | εt = UB(F2) |
| 3: | While MEC has a feasible solution, do |
| 4: | X* = opt(MEC,εt) |
| 5: | S = S ∪ {X*} |
| 6: | for all s ∈ S |
| 7: | If (X* < s), then S = S-s |
| 8 | end for |
| 9: | ε = F2 (MEC,εt) |
| 10: | t ← t + 1 |
| 11: | end while |
| Output: | Set of Pareto-optimal solutions |
6. Experimental Results
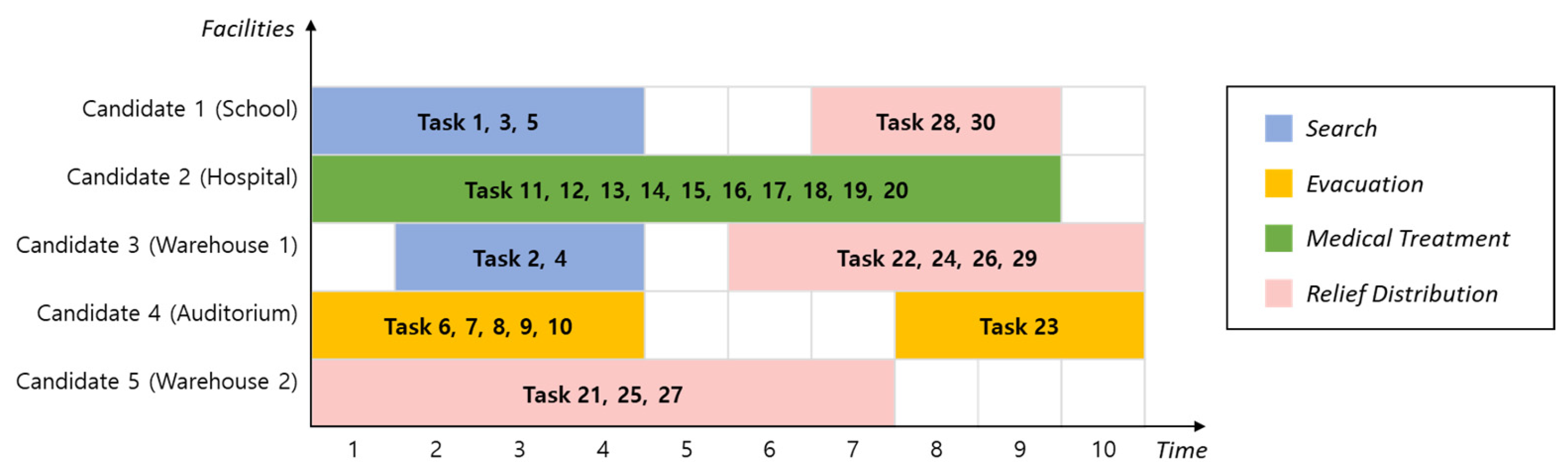
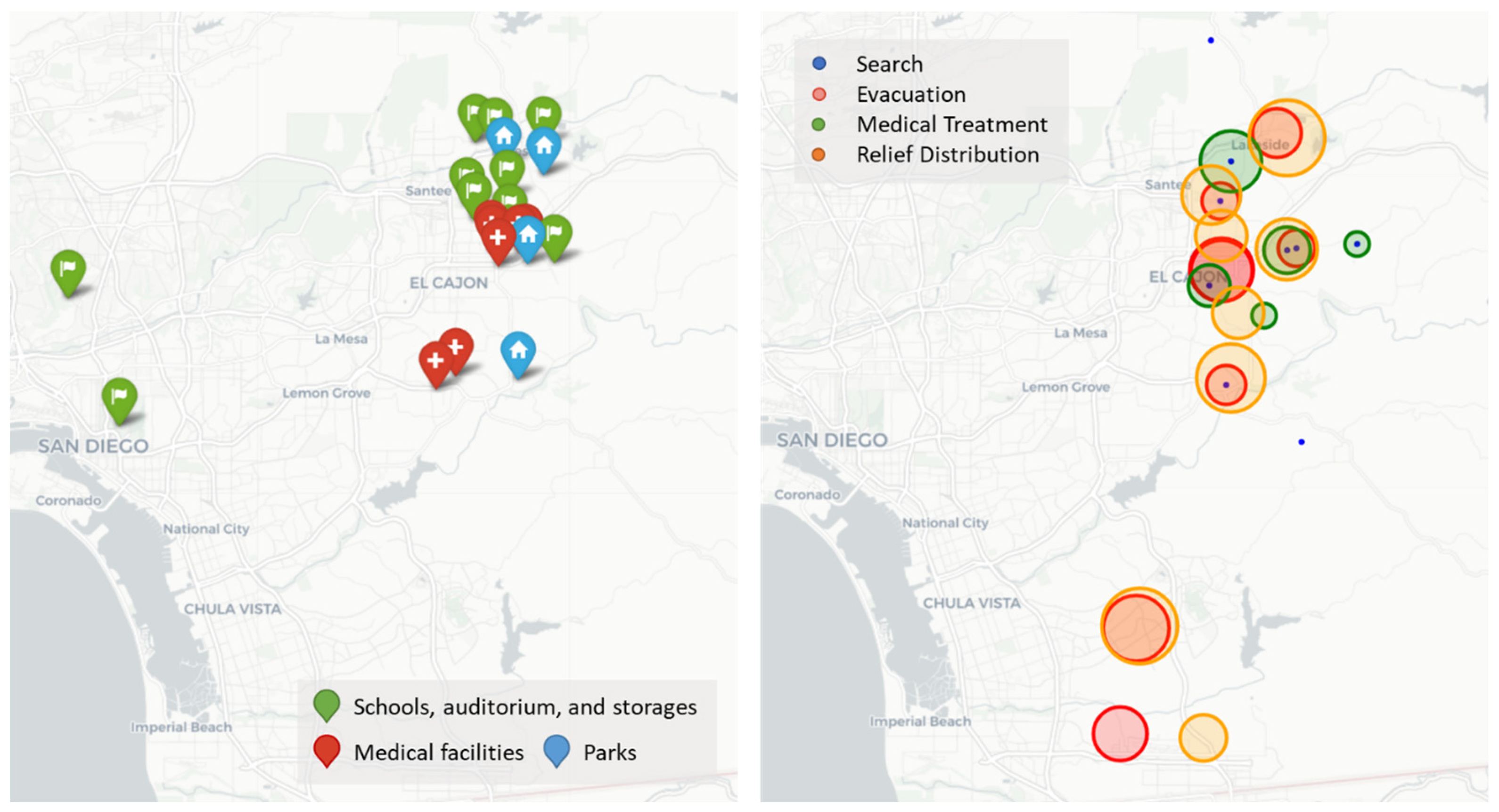
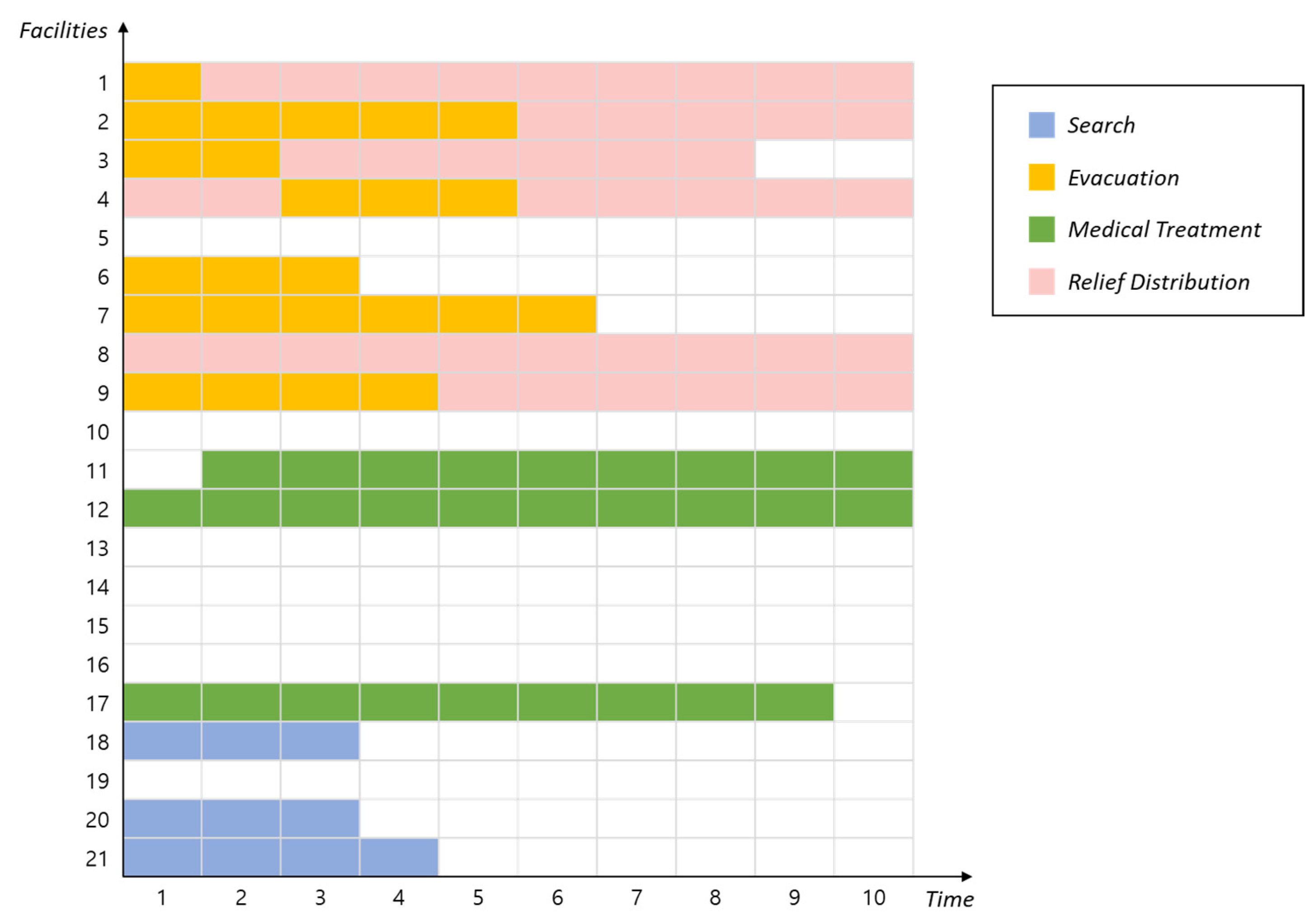
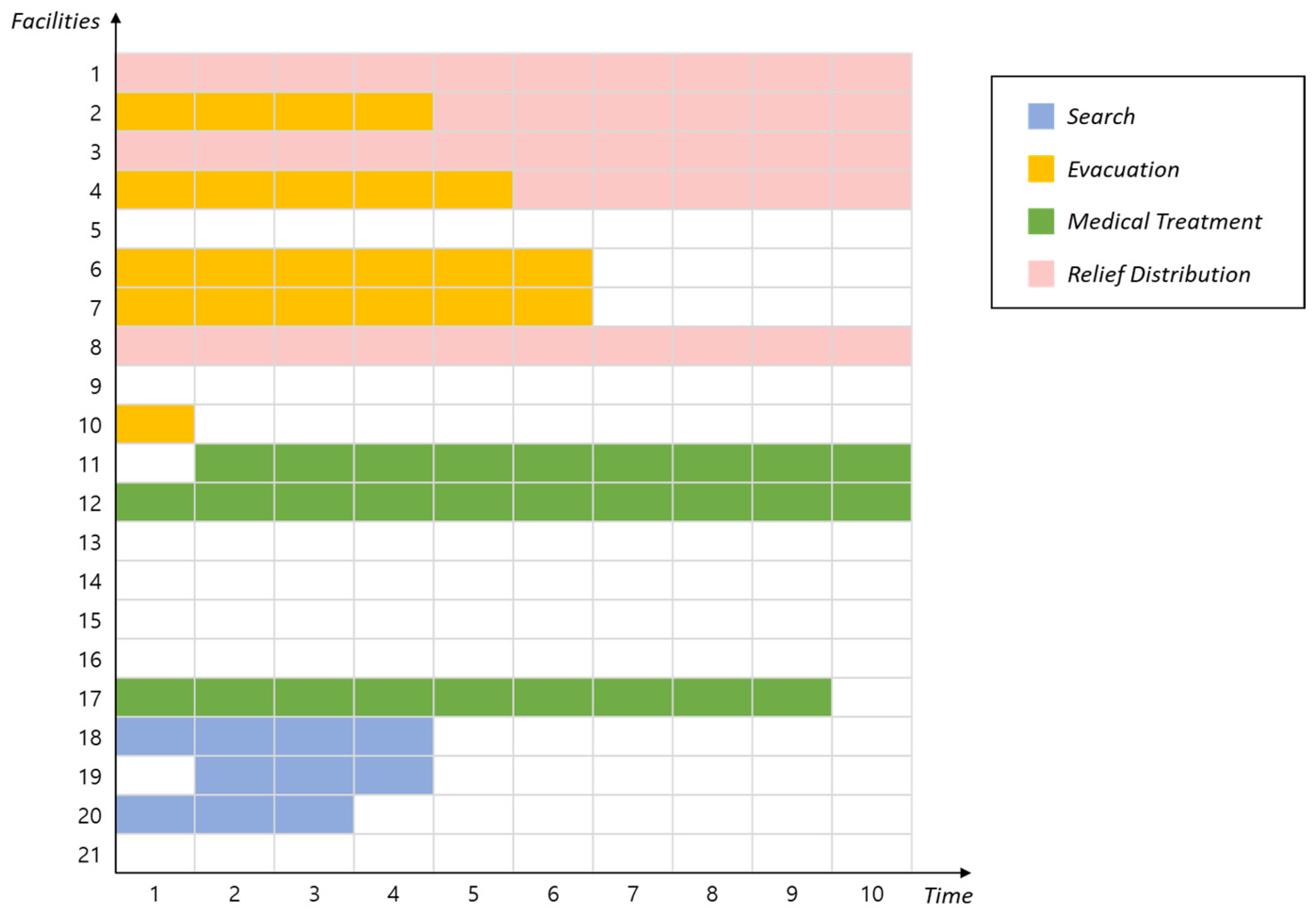
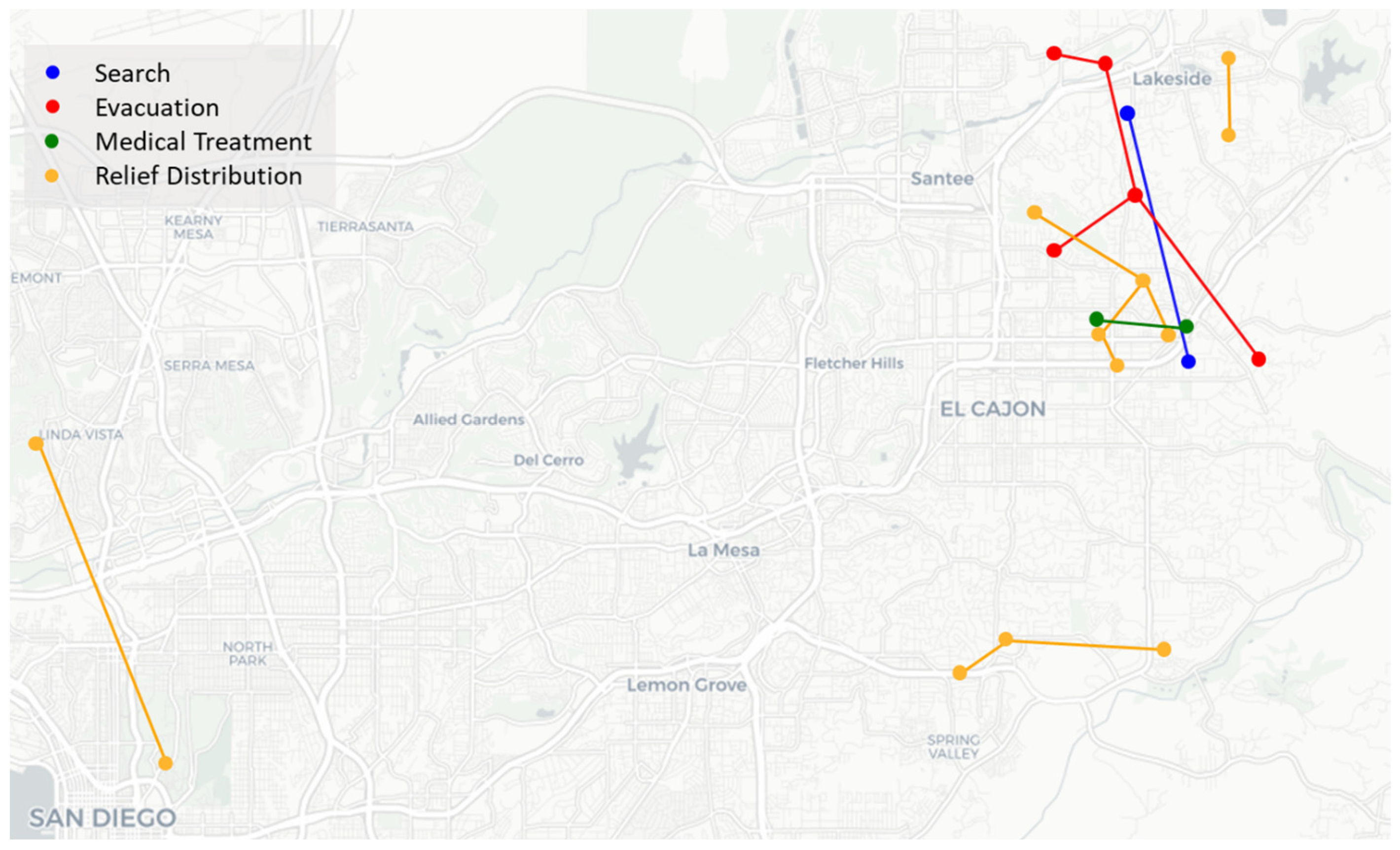
6.1. Illustrative Case Study
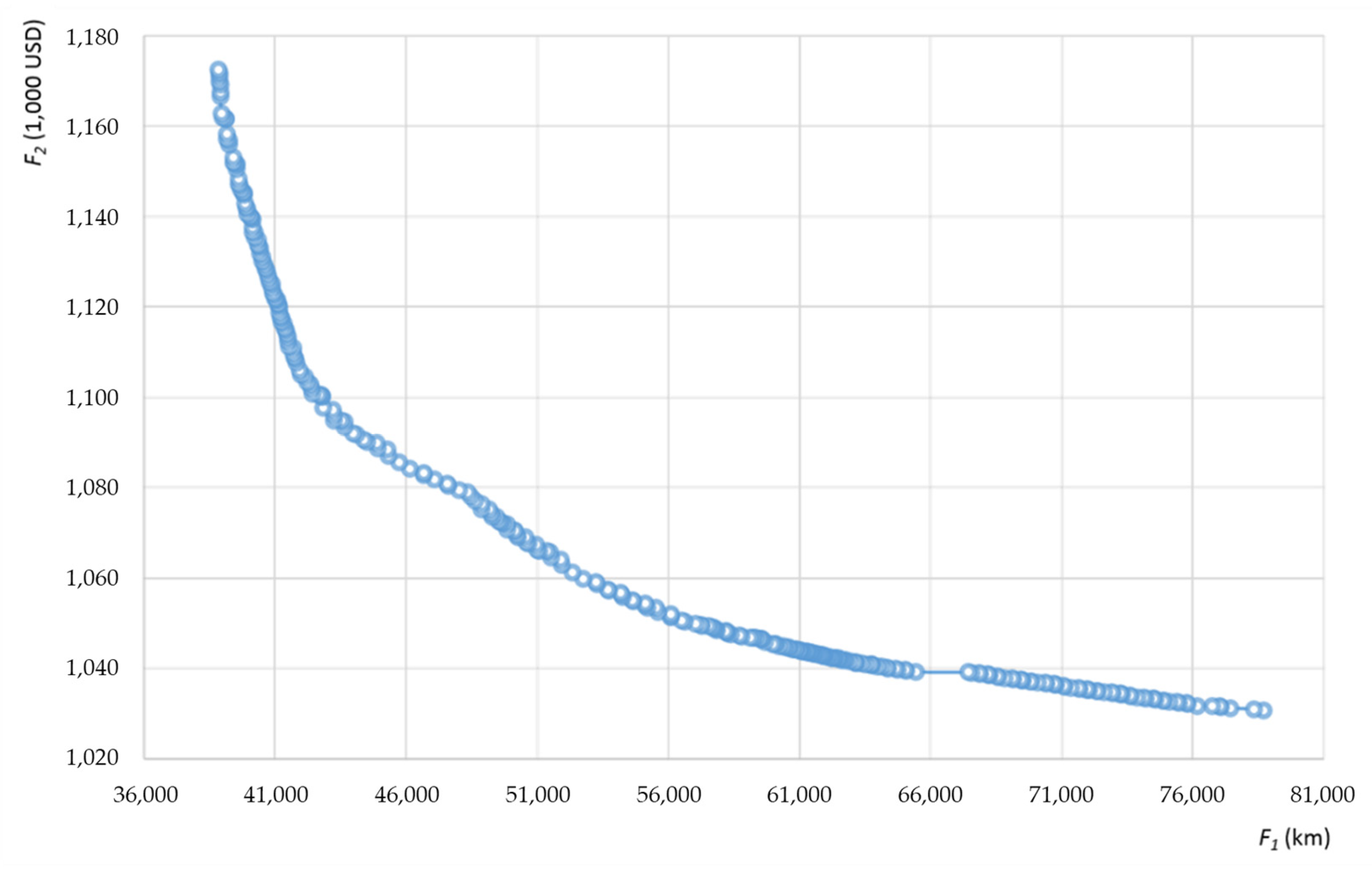
6.2. Results of Large-Sized Experiments
6.3. Connectivity for Complementary Response
7. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Facility Information
| Num | Name | Location (Altitude, Longitude) | nj | Qj,k | Sj,k | Cj,kt | ||||||||||||||
| S | E | M | R | S | E | M | R | S | E | M | R | S | E | M | R | |||||
| 1 | Pepper Drive Elementary School | 32.832 | −116.953 | 1 | 1 | 0 | 1 | 20 | 156 | 0 | 130 | 115 | 1056 | 0 | 1237 | 52 | 562 | 0 | 362 | |
| 2 | Liberty Charter School | 32.825 | −116.949 | 1 | 1 | 0 | 1 | 20 | 150 | 0 | 136 | 103 | 1498 | 0 | 859 | 51 | 627 | 0 | 531 | |
| 3 | St Kieran’s Catholic School | 32.819 | −116.929 | 0 | 1 | 0 | 1 | 20 | 130 | 0 | 190 | 107 | 809 | 0 | 1048 | 91 | 353 | 0 | 629 | |
| 4 | Christian Unified Schools | 32.805 | −116.903 | 0 | 1 | 0 | 1 | 20 | 112 | 0 | 68 | 122 | 667 | 0 | 455 | 52 | 558 | 0 | 258 | |
| 5 | Holy Trinity Catholic School | 32.788 | −117.177 | 0 | 1 | 0 | 1 | 20 | 136 | 0 | 136 | 169 | 712 | 0 | 1209 | 51 | 544 | 0 | 384 | |
| 6 | Winter Gardens Elementary School | 32.835 | −116.931 | 0 | 1 | 0 | 1 | 20 | 190 | 0 | 90 | 182 | 1768 | 0 | 689 | 75 | 921 | 0 | 286 | |
| 7 | Lakeside Middle School | 32.860 | −116.937 | 0 | 1 | 0 | 1 | 20 | 134 | 0 | 44 | 160 | 1131 | 0 | 404 | 54 | 540 | 0 | 148 | |
| 8 | Lakeside Community Center | 32.861 | −116.910 | 1 | 1 | 0 | 1 | 20 | 70 | 0 | 70 | 115 | 615 | 0 | 496 | 79 | 350 | 0 | 237 | |
| 9 | Extra Space Storage | 32.727 | −117.148 | 0 | 1 | 0 | 1 | 0 | 150 | 0 | 336 | 0 | 1129 | 0 | 2264 | 0 | 641 | 0 | 1185 | |
| 10 | A-1 Self Storage | 32.862 | −116.948 | 0 | 1 | 0 | 1 | 0 | 178 | 0 | 250 | 0 | 1285 | 0 | 1402 | 0 | 823 | 0 | 913 | |
| 11 | Granite Hills Healthcare & Wellness Centre | 32.803 | −116.935 | 0 | 0 | 1 | 0 | 0 | 0 | 314 | 0 | 0 | 0 | 1693 | 0 | 0 | 0 | 862 | 0 | |
| 12 | El Cajon Medical Center | 32.810 | −116.920 | 0 | 0 | 1 | 0 | 0 | 0 | 250 | 0 | 0 | 0 | 1410 | 0 | 0 | 0 | 1244 | 0 | |
| 13 | Sharp Rees-Stealy El Cajon | 32.809 | −116.938 | 0 | 0 | 1 | 0 | 0 | 0 | 264 | 0 | 0 | 0 | 1962 | 0 | 0 | 0 | 1114 | 0 | |
| 14 | Kaiser Permanente Bostonia Medical Offices | 32.809 | −116.923 | 0 | 0 | 1 | 0 | 0 | 0 | 196 | 0 | 0 | 0 | 1959 | 0 | 0 | 0 | 717 | 0 | |
| 15 | Scripps Clinic | 32.751 | −116.959 | 0 | 0 | 1 | 0 | 0 | 0 | 198 | 0 | 0 | 0 | 1002 | 0 | 0 | 0 | 963 | 0 | |
| 16 | Audish Hanid DO | 32.745 | −116.970 | 0 | 0 | 1 | 0 | 0 | 0 | 174 | 0 | 0 | 0 | 1170 | 0 | 0 | 0 | 496 | 0 | |
| 17 | Sharp Daniel Hoefer | 32.812 | −116.939 | 0 | 0 | 1 | 0 | 0 | 0 | 150 | 0 | 0 | 0 | 1313 | 0 | 0 | 0 | 489 | 0 | |
| 18 | John F Kennedy Park | 32.804 | −116.918 | 1 | 0 | 0 | 0 | 20 | 0 | 0 | 0 | 170 | 0 | 0 | 0 | 67 | 0 | 0 | 0 | |
| 19 | Lakeside’s River Park Conservancy | 32.846 | −116.910 | 1 | 0 | 0 | 0 | 20 | 0 | 0 | 0 | 132 | 0 | 0 | 0 | 81 | 0 | 0 | 0 | |
| 20 | River View Park | 32.851 | −116.932 | 1 | 0 | 0 | 0 | 20 | 0 | 0 | 0 | 171 | 0 | 0 | 0 | 75 | 0 | 0 | 0 | |
| 21 | Hilton Head County Park | 32.749 | −116.924 | 1 | 0 | 0 | 0 | 20 | 0 | 0 | 0 | 143 | 0 | 0 | 0 | 66 | 0 | 0 | 0 | |
Appendix B. Task Information
| Task | Type | Demand | Location | Ait | Facility (Figure 7) | ||||||||||
| Latitude | Longitude | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||||
| 1 | S | 2 | 32.830 | −116.945 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 20 |
| 2 | S | 5 | 32.743 | −116.941 | 1 | 2 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 21 |
| 3 | S | 5 | 32.808 | −116.902 | 2 | 1 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 18 |
| 4 | S | 4 | 32.716 | −116.899 | 1 | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 21 |
| 5 | S | 2 | 32.807 | −116.907 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 18 |
| 6 | S | 3 | 32.849 | −116.939 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 20 |
| 7 | S | 1 | 32.906 | −116.950 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 20 |
| 8 | S | 4 | 32.810 | −116.868 | 2 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 18 |
| 9 | S | 2 | 32.790 | −116.951 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 18 |
| 10 | E | 335 | 32.798 | −116.944 | 33 | 143 | 94 | 65 | 0 | 0 | 0 | 0 | 0 | 0 | 2, 3, 6 |
| 11 | E | 320 | 32.797 | −116.944 | 94 | 72 | 60 | 49 | 45 | 0 | 0 | 0 | 0 | 0 | 1, 2 |
| 12 | E | 348 | 32.628 | −116.992 | 157 | 84 | 57 | 50 | 0 | 0 | 0 | 0 | 0 | 0 | 6, 9 |
| 13 | E | 284 | 32.578 | −117.001 | 87 | 64 | 53 | 43 | 37 | 0 | 0 | 0 | 0 | 0 | 4, 9 |
| 14 | E | 256 | 32.863 | −116.913 | 75 | 61 | 49 | 37 | 24 | 10 | 0 | 0 | 0 | 0 | 7 |
| 15 | E | 195 | 32.830 | −116.945 | 75 | 54 | 37 | 29 | 0 | 0 | 0 | 0 | 0 | 0 | 2 |
| 16 | E | 201 | 32.743 | −116.941 | 75 | 54 | 37 | 29 | 6 | 0 | 0 | 0 | 0 | 0 | 2, 3, 4 |
| 17 | E | 194 | 32.808 | −116.902 | 72 | 49 | 36 | 24 | 13 | 0 | 0 | 0 | 0 | 0 | 3, 4 |
| 18 | M | 246 | 32.807 | −116.907 | 36 | 61 | 32 | 28 | 26 | 18 | 17 | 13 | 10 | 5 | 12 |
| 19 | M | 315 | 32.849 | −116.939 | 36 | 120 | 35 | 32 | 26 | 22 | 19 | 15 | 10 | 0 | 17 |
| 20 | M | 124 | 32.776 | −116.920 | 0 | 0 | 11 | 29 | 27 | 20 | 15 | 11 | 9 | 2 | 11 |
| 21 | M | 124 | 32.810 | −116.868 | 0 | 0 | 0 | 0 | 12 | 38 | 27 | 22 | 15 | 10 | 12 |
| 22 | M | 215 | 32.790 | −116.951 | 0 | 10 | 22 | 35 | 42 | 40 | 30 | 22 | 14 | 0 | 11 |
| 23 | R | 395 | 32.860 | −116.907 | 15 | 21 | 34 | 42 | 52 | 59 | 64 | 56 | 40 | 12 | 8 |
| 24 | R | 402 | 32.629 | −116.990 | 9 | 25 | 35 | 43 | 52 | 65 | 70 | 48 | 44 | 11 | 1, 3, 4, 9 |
| 25 | R | 356 | 32.747 | −116.939 | 0 | 11 | 41 | 42 | 49 | 65 | 68 | 56 | 24 | 0 | 3, 4 |
| 26 | R | 321 | 32.807 | −116.907 | 0 | 12 | 25 | 32 | 49 | 55 | 61 | 56 | 21 | 10 | 3, 4 |
| 27 | R | 309 | 32.833 | −116.950 | 0 | 21 | 25 | 32 | 49 | 66 | 41 | 32 | 26 | 17 | 1 |
| 28 | R | 245 | 32.576 | −116.954 | 7 | 12 | 25 | 38 | 46 | 53 | 42 | 12 | 10 | 0 | 3, 4, 9 |
| 29 | R | 268 | 32.777 | −116.935 | 13 | 22 | 35 | 42 | 40 | 32 | 29 | 24 | 20 | 11 | 3, 4 |
| 30 | R | 275 | 32.814 | −116.944 | 0 | 0 | 12 | 22 | 35 | 43 | 53 | 61 | 32 | 17 | 2, 3 |
References
- Centre for Research on the Epidemiology of Disaster (CERD). The Economic and Human Impact of Disasters in the Last 10 Years. EM_DAT Database. 2015. Available online: https://www.unisdr.org/files/42862_economichumanimpact20052014unisdr.pdf (accessed on 16 October 2023).
- Waugh, W.L., Jr.; Hy, R.J. Handbook of Emergency Management: Programs and Policies Dealing with Major Hazards and Disasters; Greenwood Press: New York, NY, USA, 1990. [Google Scholar]
- Green, W.G., III. Four Phases of Emergency Management. In Electronic Encyclopedia of Civil Defense and Emergency Management; FEMA: Washington, DC, USA, 2002. [Google Scholar]
- Altay, N.; Green, W.G., III. OR/MS research in disaster operations management. Eur. J. Oper. Res. 2006, 175, 475–493. [Google Scholar] [CrossRef]
- Frost, S. Study Analysing the Current Activities in the Field of Uav. ENTR/2007/065. 2007. Available online: https://ec.europa.eu/docsroom/documents/1706/attachments/1/translations/en/renditions/native (accessed on 26 January 2023).
- Vincenzi, D.A.; Ison, D.C.; Terwilliger, B.A. The role of unmanned aircraft systems (UAS) in disaster response and recovery efforts: Historical, current, and future. In Proceedings of the 2014 Conference on Association for Unmanned Vehicle Systems International, Orlando, FL, USA, 12 May 2014; pp. 12–15. [Google Scholar]
- Song, B.D.; Kim, J.; Morrison, J.R. Rolling Horizon Path Planning of an Autonomous System of UAVs for Persistent Cooperative Service: MILP Formulation and Efficient Heuristics. J. Intell. Robot. Syst. 2016, 84, 241–258. [Google Scholar] [CrossRef]
- Saadatseresht, M.; Mansourian, A.; Taleai, M. Evacuation planning using multiobjective evolutionary optimization approach. Eur. J. Oper. Res. 2009, 198, 305–314. [Google Scholar] [CrossRef]
- Sherali, H.D.; Carter, T.B.; Hobeika, A.G. A location-allocation model and algorithm for evacuation planning under hurricane/flood conditions. Transp. Res. Part B Methodol. 1991, 25, 439–452. [Google Scholar] [CrossRef]
- Kongsomsaksakul, S.; Yang, C.; Chen, A. Shelter location-allocation model for flood evacuation planning. J. East. Asia Soc. Transp. Stud. 2005, 6, 4237–4252. [Google Scholar]
- Kar, B.; Hodgson, M.E. A GIS-based model to determine site suitability of emergency evacuation shelters. Trans. GIS 2008, 12, 227–248. [Google Scholar] [CrossRef]
- Alsalloum, O.I.; Rand, G.K. Extensions to emergency vehicle location models. Comput. Oper. Res. 2006, 33, 2725–2743. [Google Scholar] [CrossRef]
- Rajagopalan, H.K.; Saydam, C.; Xiao, J. A multiperiod set covering location model for dynamic redeployment of ambulances. Comput. Oper. Res. 2008, 35, 814–826. [Google Scholar] [CrossRef]
- Paluzzi, M. Testing a heuristic P-median location allocation model for siting emergency service facilities. In Proceedings of the Annual Meeting of the Association of American Geographers, Philadelphia, PA, USA, 14–19 March 2004. [Google Scholar]
- Jia, H.; Ordóñez, F.; Dessouky, M. A modeling framework for facility location of medical services for large-scale emergencies. IIE Trans. 2007, 39, 41–55. [Google Scholar] [CrossRef]
- Ko, Y.D.; Song, B.D.; Hwang, H. Location, capacity and capability design of emergency medical centers with multiple emergency diseases. Comput. Ind. Eng. 2016, 101, 10–20. [Google Scholar] [CrossRef]
- Fiedrich, F.; Gehbauer, F.; Rickers, U. Optimized resource allocation for emergency response after earthquake disasters. Saf. Sci. 2000, 35, 41–57. [Google Scholar] [CrossRef]
- Fiedrich, F.; Burghardt, P. Agent-based systems for disaster management. Commun. ACM 2007, 50, 41–42. [Google Scholar] [CrossRef]
- Sharma, B.; Ramkumar, M.; Subramanian, N.; Malhotra, B. Dynamic temporary blood facility location-allocation during and post-disaster periods. Ann. Oper. Res. 2019, 283, 705–736. [Google Scholar] [CrossRef]
- Beamon, B.M.; Kotleba, S.A. Inventory modelling for complex emergencies in humanitarian relief operations. Int. J. Logist. Res. Appl. 2006, 9, 1–18. [Google Scholar] [CrossRef]
- Rath, S.; Gutjahr, W.J. A math-heuristic for the warehouse location–routing problem in disaster relief. Comput. Oper. Res. 2014, 42, 25–39. [Google Scholar] [CrossRef]
- Barzinpour, F.; Esmaeili, V. A multi-objective relief chain location distribution model for urban disaster management. Int. J. Adv. Manuf. Technol. 2014, 70, 1291–1302. [Google Scholar] [CrossRef]
- Mete, H.O.; Zabinsky, Z.B. Stochastic optimization of medical supply location and distribution in disaster management. Int. J. Prod. Econ. 2010, 126, 76–84. [Google Scholar] [CrossRef]
- Moshref-Javadi, M.; Lee, S. The latency location-routing problem. Eur. J. Oper. Res. 2016, 255, 604–619. [Google Scholar] [CrossRef]
- Rabiei, P.; Arias-Aranda, D.; Stantchev, V. Introducing a novel multi-objective optimization model for Volunteer as-signment in the post-disaster phase: Combining fuzzy inference systems with NSGA-II and NRGA. Expert Syst. Appl. 2023, 226, 120142. [Google Scholar] [CrossRef]
- Wang, D.; Yang, K.; Yang, L.; Dong, J. Two-stage distributionally robust optimization for disaster relief logistics under option contract and demand ambiguity. Transp. Res. Part E Logist. Transp. Rev. 2023, 170, 103025. [Google Scholar] [CrossRef]
- Apvrille, L.; Tanzi, T.; Dugelay, J.-L. Autonomous drones for assisting rescue services within the context of natural disasters. In Proceedings of the 2014 XXXIth URSI General Assembly and Scientific Symposium (URSI GASS), Beijing, China, 16–23 August 2014; pp. 1–4. [Google Scholar]
- Ezequiel CA, F.; Cua, M.; Libatique, N.C.; Tangonan, G.L.; Alampay, R.; Labuguen, R.T.; Favila, C.M.; Honrado, J.L.E.; Caños, V.; Devaney, C.; et al. UAV aerial imaging applications for post-disaster assessment, environmental management and infrastructure development. In Proceedings of the 2014 International Conference on Unmanned Aircraft Systems (ICUAS), Orlando, FL, USA, 27–30 May 2014; pp. 274–283. [Google Scholar]
- Mersheeva, V.; Friedrich, G. Routing for continuous monitoring by multiple micro UAVs in disaster scenarios. In Proceedings of the 20th European Conference on Artificial Intelligence, Montpellier, France, 27–31 August 2012; IOS Press: Amsterdam, The Netherlands, 2012; pp. 588–593. [Google Scholar]
- Tuna, G.; Nefzi, B.; Conte, G. Unmanned aerial vehicle-aided communications system for disaster recovery. J. Netw. Comput. Appl. 2014, 41, 27–36. [Google Scholar] [CrossRef]
- Kim, J.; Morrison, J.R. On the concerted design and scheduling of multiple resources for persistent UAV operations. J. Intell. Robot. Syst. 2014, 74, 479–498. [Google Scholar] [CrossRef]
- Bor-Yaliniz, R.I.; El-Keyi, A.; Yanikomeroglu, H. Efficient 3-D placement of an aerial base station in next generation cellular networks. In Proceedings of the 2016 IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 22–27 May 2016; pp. 1–5. [Google Scholar]
- Kim, D.; Lee, K.; Moon, I. Stochastic facility location model for drones considering uncertain flight distance. Ann. Oper. Res. 2019, 283, 1283–1302. [Google Scholar] [CrossRef]
- Masroor, R.; Naeem, M.; Ejaz, W. Efficient deployment of UAVs for disaster management: A multi-criterion optimization approach. Comput. Commun. 2021, 177, 185–194. [Google Scholar] [CrossRef]
- Zhang, J.Z.; Srivastava, P.R.; Eachempati, P. Evaluating the effectiveness of drones in emergency situations: A hybrid multi-criteria approach. Ind. Manag. Data Syst. 2023, 123, 302–323. [Google Scholar] [CrossRef]
- Yahyaei, M.; Bozorgi-Amiri, A. Robust reliable humanitarian relief network design: An integration of shelter and supply facility location. Ann. Oper. Res. 2019, 283, 897–916. [Google Scholar] [CrossRef]
- Wallace, W.A.; De Balogh, F. Decision Support Systems for Disaster Management. Public Adm. Rev. 1985, 45, 134. [Google Scholar] [CrossRef]
- Moe, T.L.; Pathranarakul, P. An integrated approach to natural disaster management: Public project management and its critical success factors. Disaster Prev. Manag. Int. J. 2006, 15, 396–413. [Google Scholar]
- Balcik, B.; Beamon, B.M. Facility location in humanitarian relief. Int. J. Logist. Res. Appl. 2008, 11, 101–121. [Google Scholar] [CrossRef]
- Coppola, D.P. Introduction to International Disaster Management; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Nurre, S.G.; Cavdaroglu, B.; Mitchell, J.E.; Sharkey, T.C.; Wallace, W.A. Restoring infrastructure systems: An integrated network design and scheduling (INDS) problem. Eur. J. Oper. Res. 2012, 223, 794–806. [Google Scholar] [CrossRef]
- Lerner, E.B.; Moscati, R.M. The golden hour: Scientific fact or medical “urban legend”? Acad. Emerg. Med. 2001, 8, 758–760. [Google Scholar] [CrossRef]
- Song, B.D.; Park, H.; Park, K. Toward flexible and persistent UAV service: Multi-period and multi-objective system design with task assignment for disaster management. Expert Syst. Appl. 2022, 206, 117855. [Google Scholar] [CrossRef]
- National Highway Traffic Safety Administration. Guide for Interfacility Patient Transfer; National Highway Traffic Safety Administration: Washington, DC, USA, 2006. Available online: https://www.ems.gov/assets/Interfacility_Transfers.pdf (accessed on 18 October 2023).
- Chankong, V.; Haimes, Y.Y. On the characterization of noninferior solutions of the vector optimization problem. Automatica 1982, 18, 697–707. [Google Scholar] [CrossRef]
- Abounacer, R.; Rekik, M.; Renaud, J. An exact solution approach for multi-objective location–transportation problem for disaster response. Comput. Oper. Res. 2014, 41, 83–93. [Google Scholar] [CrossRef]
- Park, K.; Kim, J.; Ko, Y.D.; Song, B.D. Redesign of reverse logistics network with managerial decisions on the minimum quality level and remanufacturing policy. J. Oper. Res. Soc. 2021, 72, 1564–1577. [Google Scholar] [CrossRef]
- Yuan, Z.; Wang, W.; Li, J. A multi-objective risk-constrained approach for capturing and recycling carbon dioxide in multi-energy combined heat and power microgrids. J. Clean. Prod. 2023, 405, 136826. [Google Scholar] [CrossRef]
- Federal Emergency Management Agency (FEMA). Hazus. 2023. Available online: https://www.fema.gov/hazus (accessed on 21 September 2023).
- Peng, F.; Hwang, T.; Ouyang, Y. Formulation and algorithms for discrete minimum-cost group assembly problem. Transp. Res. Rec. J. Transp. Res. Board 2013, 2333, 9–15. [Google Scholar] [CrossRef]


| Facility Type | Facility Candidates |
|---|---|
| Search | School, auditorium, park |
| Evacuation | Stadium, auditorium |
| Medical treatment | Hospital, local clinics |
| Relief distribution | Park, warehouse |
| Parameter | Value(s) |
|---|---|
| Location | San Diego, CA |
| Magnitude | 9.0 |
| Scenario Type | Deterministic and Arbitrary |
| Epicenter | 33.006, −116.906 |
| Attenuation Function | West US. Extensional 2008—Strike Slip |
| Depth and Width | 10 km |
| Fault Type | Strike + Slip |
| |I| ) | |J| | Value of F1 (km) | Value of F2 (1000 USD) | Number of PS | Total CPU Time (s) | CPU Time per PS (s) | ||
|---|---|---|---|---|---|---|---|---|
| Min | Max | Min | Max | |||||
| 30 (174) | 21 | 1030.67 | 1172.46 | 38,862 | 78,684 | 309 | 11,724 | 37.9 |
| |I| ) | |J| | Value of F1 | Value of F2 | Number of PS | Total CPU Time (s) | CPU Time per PS (s) | ||
|---|---|---|---|---|---|---|---|---|
| Min | Max | Min | Max | |||||
| 25 (61) | 10 | 20,894.4 | 32,217.2 | 2651 | 7312 | 27 | 11.61 | 0.43 |
| 20 | 13,284.2 | 37,113.7 | 2332 | 16,700 | 125 | 107.85 | 0.86 | |
| 30 | 10,636.9 | 31,443.1 | 2306 | 25,731 | 204 | 210.04 | 1.03 | |
| 40 | 10,178.8 | 29,411.8 | 2291 | 34,636 | 270 | 309.13 | 1.14 | |
| 50 | 9213.68 | 29,083.1 | 2248 | 42,409 | 316 | 409.60 | 1.30 | |
| 50 (120) | 10 | 41,242.6 | 62,526.6 | 2765 | 7635 | 55 | 28.12 | 0.51 |
| 20 | 24,329.7 | 69,823.7 | 2446 | 17,691 | 270 | 286.68 | 1.06 | |
| 30 | 20,015.6 | 63,905.2 | 2422 | 27,245 | 455 | 655.60 | 1.44 | |
| 40 | 18,924.1 | 58,223.1 | 2407 | 36,569 | 502 | 827.57 | 1.65 | |
| 50 | 17,883.8 | 58,515.0 | 2364 | 44,805 | 629 | 1257.74 | 2.00 | |
| 75 (180) | 10 | 61,708.7 | 92,592.0 | 2765 | 8103 | 110 | 75.58 | 0.69 |
| 20 | 44,396.1 | 102,131.0 | 2446 | 17,324 | 432 | 607.59 | 1.41 | |
| 30 | 39,627.6 | 89,874.4 | 2422 | 26,604 | 515 | 992.71 | 1.93 | |
| 40 | 36,652.0 | 84,114.4 | 2407 | 35,175 | 643 | 1501.30 | 2.33 | |
| 50 | 35,848.2 | 84,413.3 | 2364 | 43,564 | 815 | 2322.84 | 2.85 | |
| 100 (241) | 10 | 80,662.7 | 119,578.0 | 2846 | 8037 | 153 | 107.61 | 0.70 |
| 20 | 48,081.7 | 132,402.0 | 2514 | 17,860 | 685 | 1203.66 | 1.76 | |
| 30 | 39,241.8 | 119,377.0 | 2490 | 27,441 | 1005 | 2699.69 | 2.69 | |
| 40 | 35,816.0 | 111,656.0 | 2470 | 35,746 | 1364 | 4345.28 | 3.19 | |
| 50 | 33,413.0 | 111,836.0 | 2424 | 44,411 | 1576 | 6125.36 | 3.89 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, B.D.; Jun, S.; Lee, S. Integrated System Design for Post-Disaster Management: Multi-Facility, Multi-Period, and Bi-Objective Optimization Approach. Systems 2024, 12, 69. https://doi.org/10.3390/systems12030069
Song BD, Jun S, Lee S. Integrated System Design for Post-Disaster Management: Multi-Facility, Multi-Period, and Bi-Objective Optimization Approach. Systems. 2024; 12(3):69. https://doi.org/10.3390/systems12030069
Chicago/Turabian StyleSong, Byung Duk, Sungbum Jun, and Seokcheon Lee. 2024. "Integrated System Design for Post-Disaster Management: Multi-Facility, Multi-Period, and Bi-Objective Optimization Approach" Systems 12, no. 3: 69. https://doi.org/10.3390/systems12030069
APA StyleSong, B. D., Jun, S., & Lee, S. (2024). Integrated System Design for Post-Disaster Management: Multi-Facility, Multi-Period, and Bi-Objective Optimization Approach. Systems, 12(3), 69. https://doi.org/10.3390/systems12030069






