An SD-LV Calculation Model for the Scale of the Urban Rail Transit Network
Abstract
1. Introduction
2. Literature Review
2.1. The Relationship between the URT and UD
2.2. SD Model
2.3. LV Model
2.4. Literature Review Summary
3. Methodology
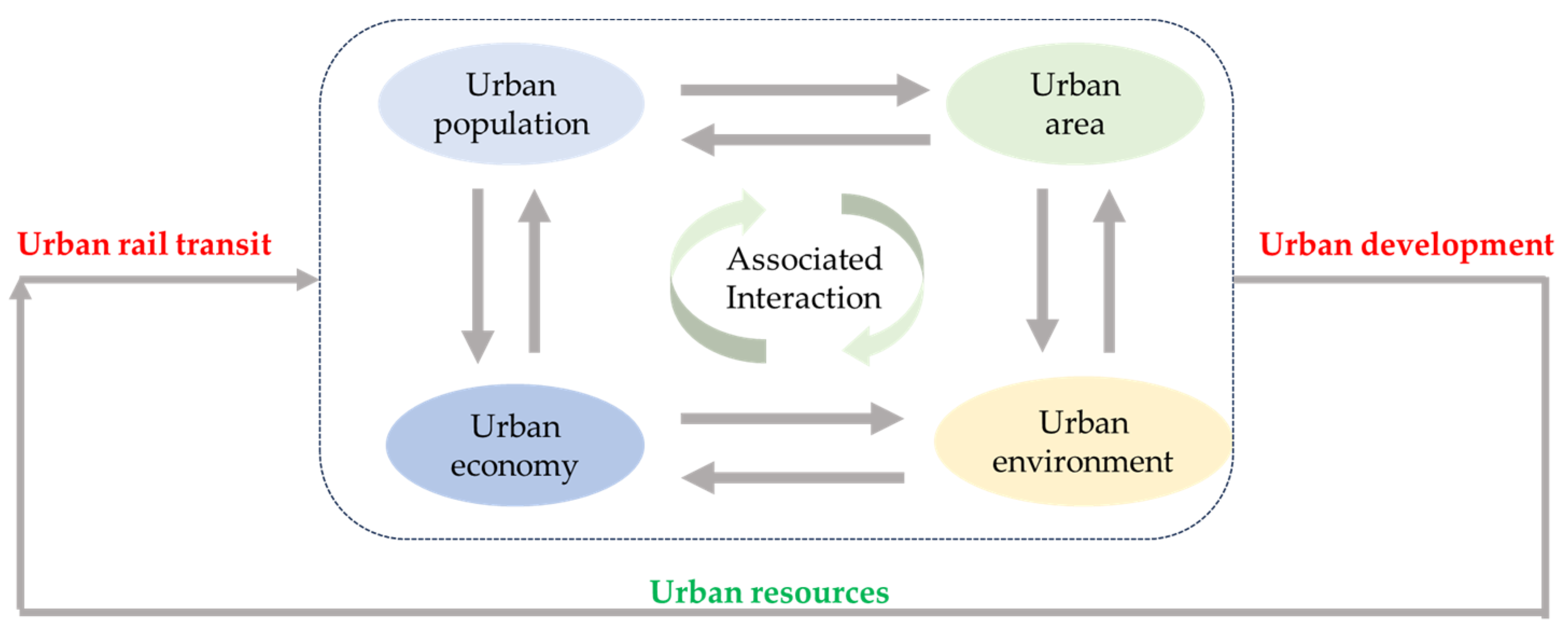
3.1. System Boundary
3.2. Causal Feedback Diagram
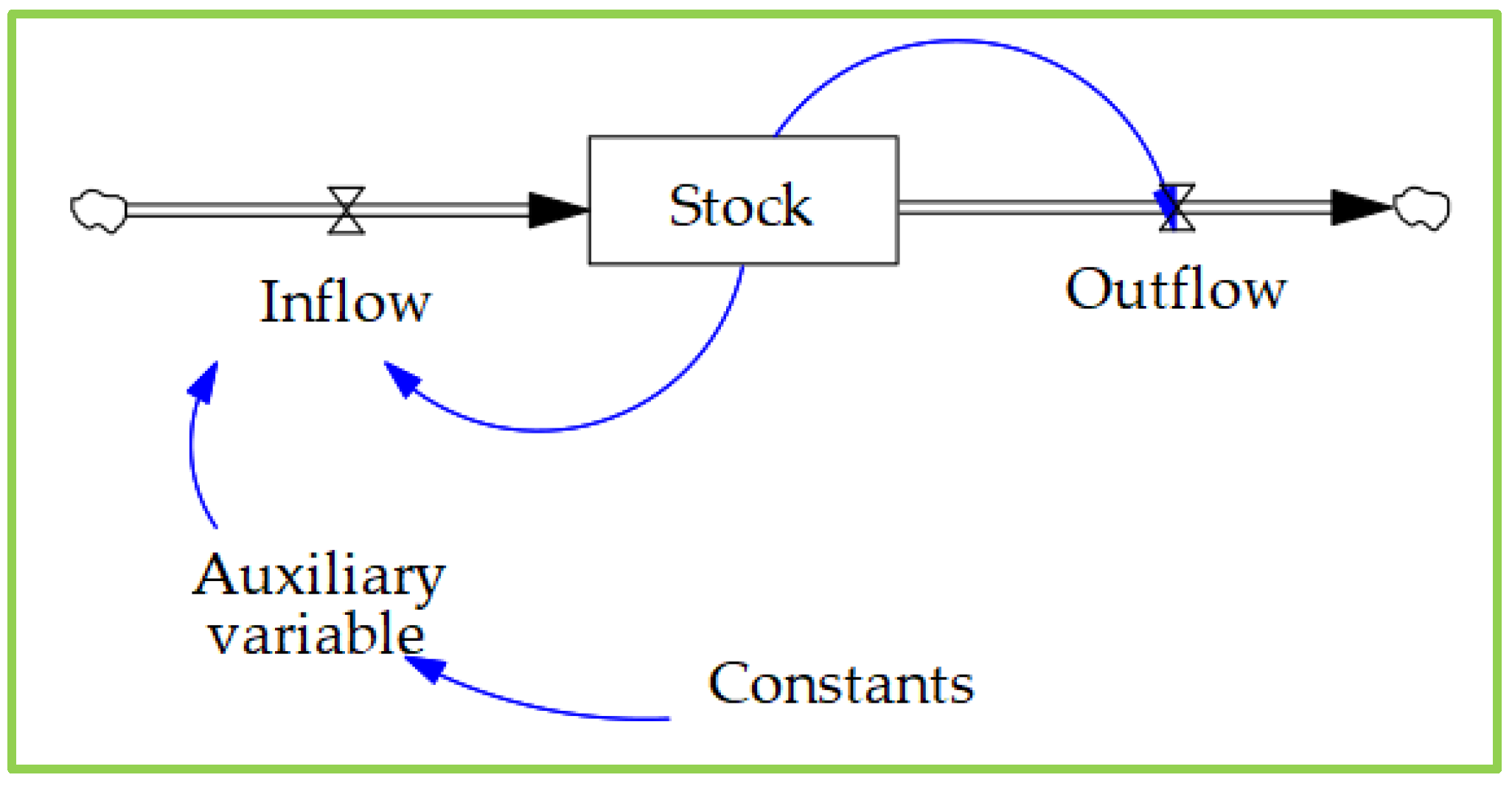
3.3. Stock–Flow Diagram
3.4. SD Equations
3.4.1. LV Mutualism Model
3.4.2. Stability Analysis of the LV Model
3.4.3. SD Equations
4. Case Study
4.1. Data Input
4.2. Model Validation
4.3. Results and Discussion
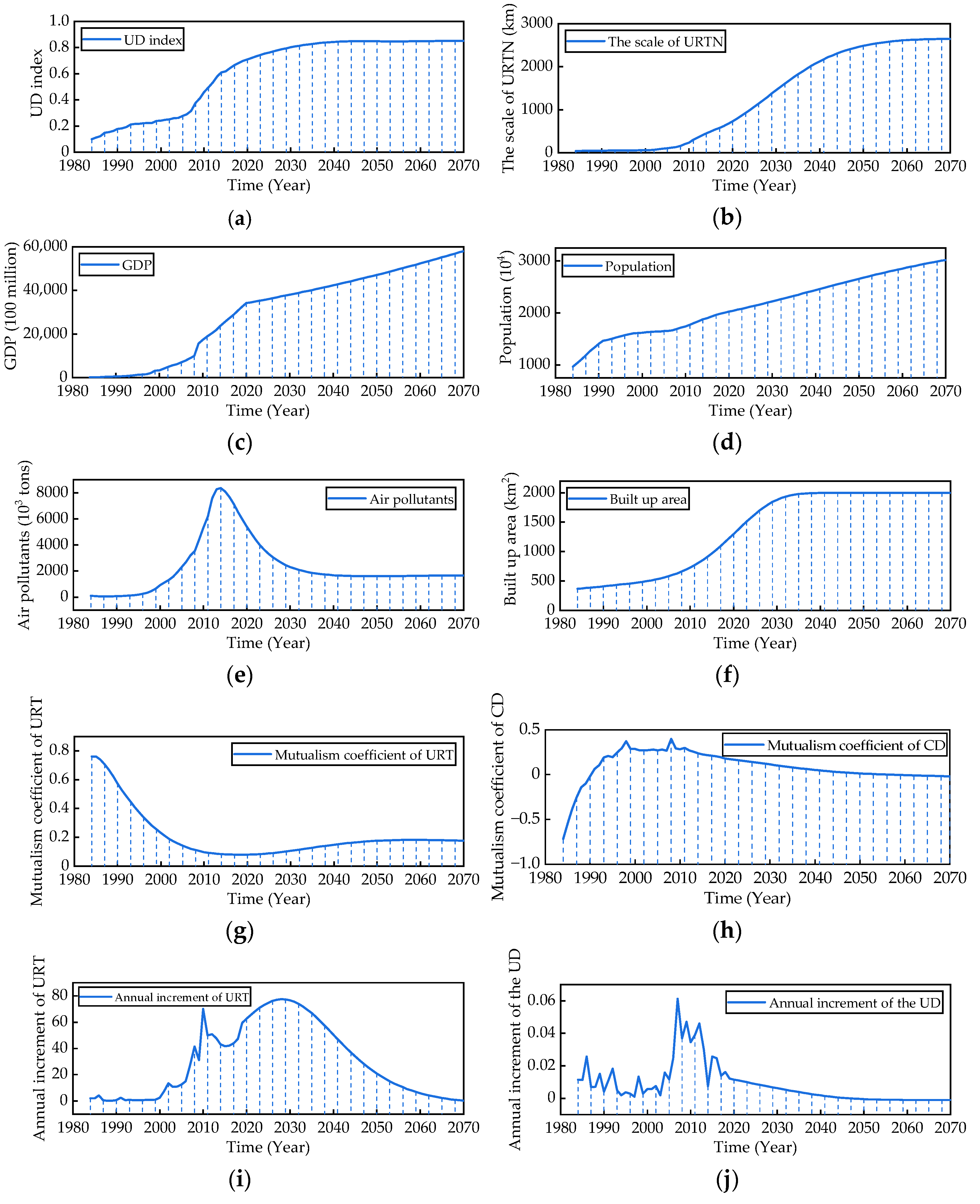
4.3.1. The Simulation Results
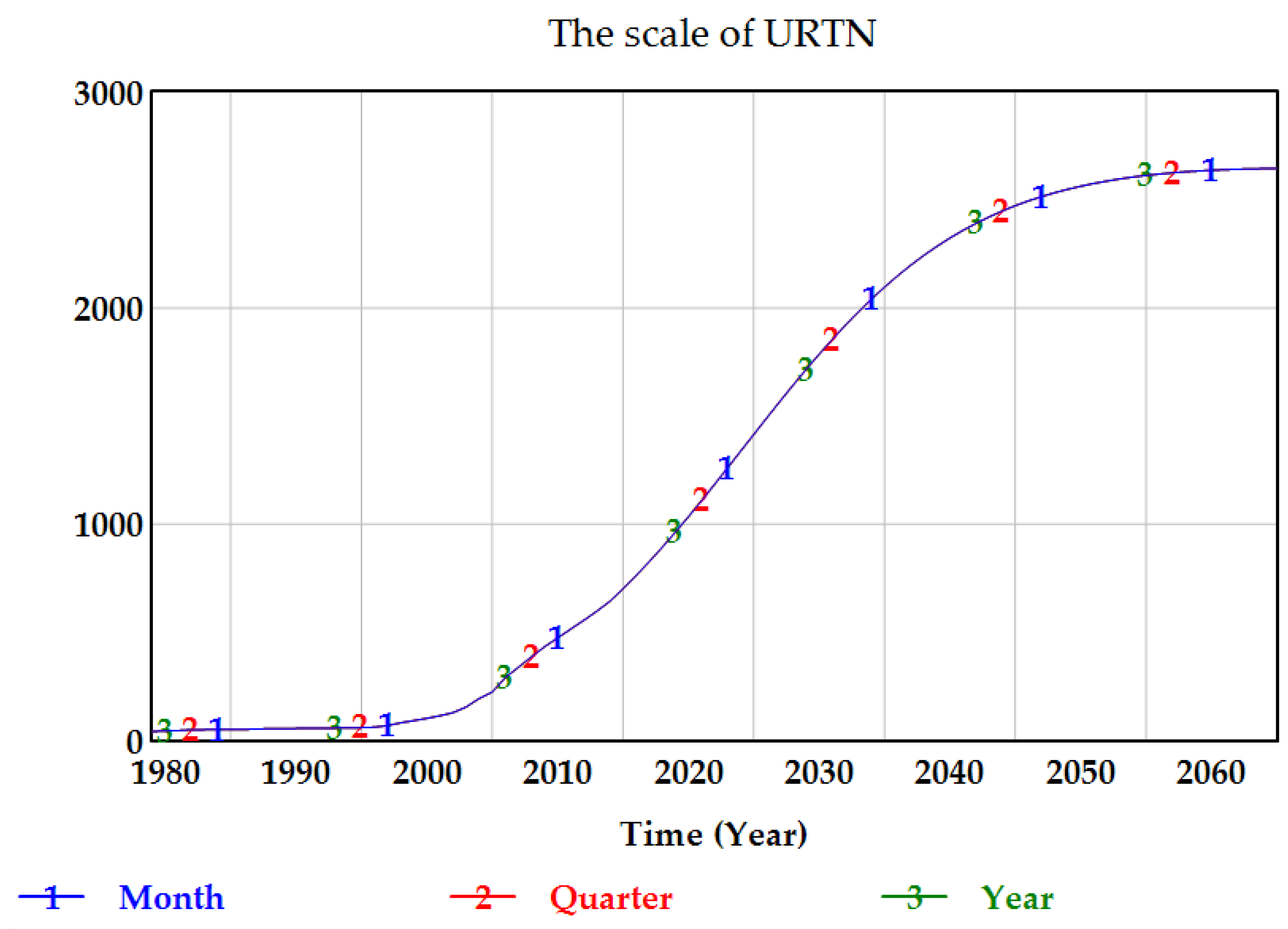
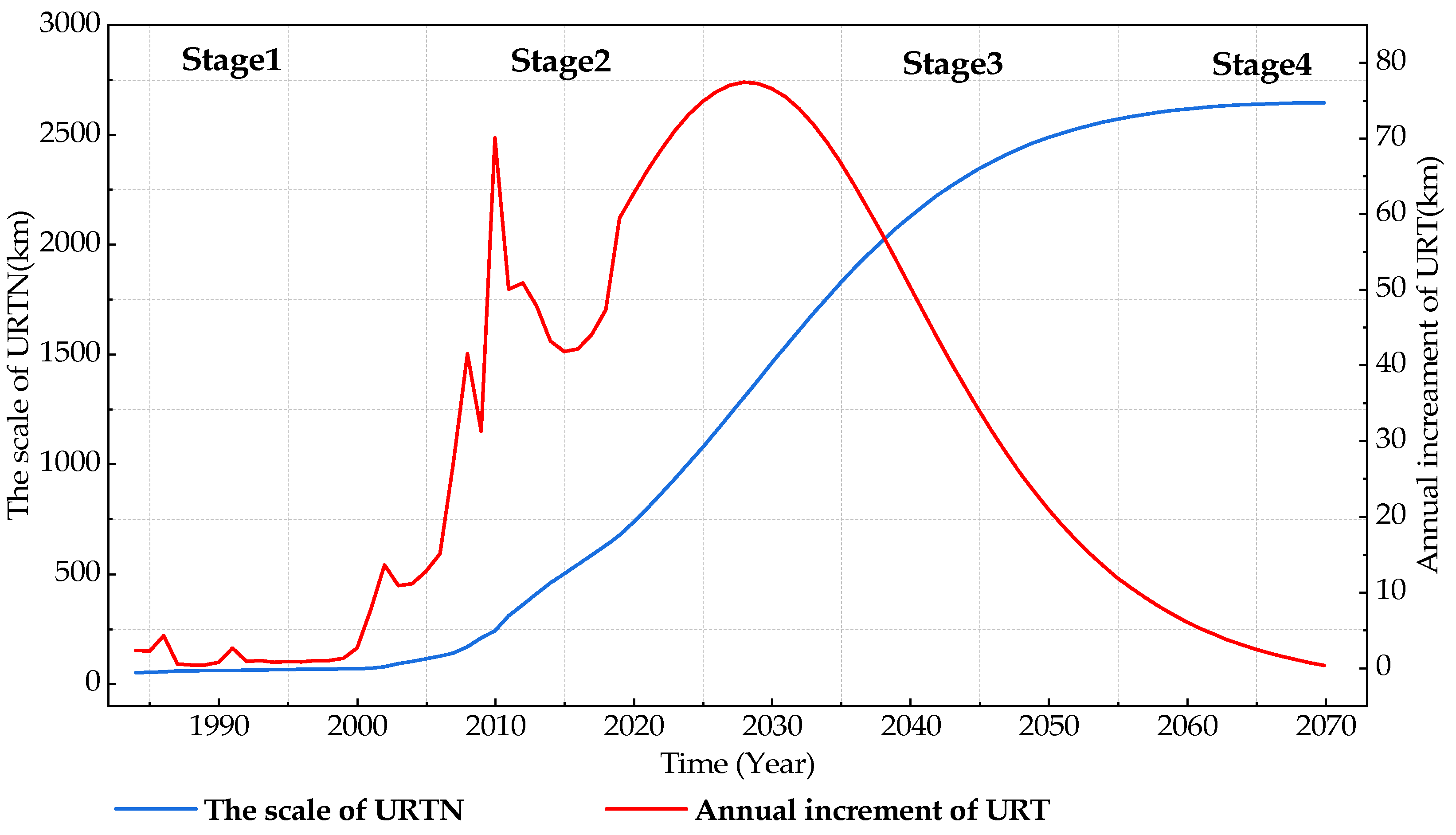
4.3.2. The Scale of URTN
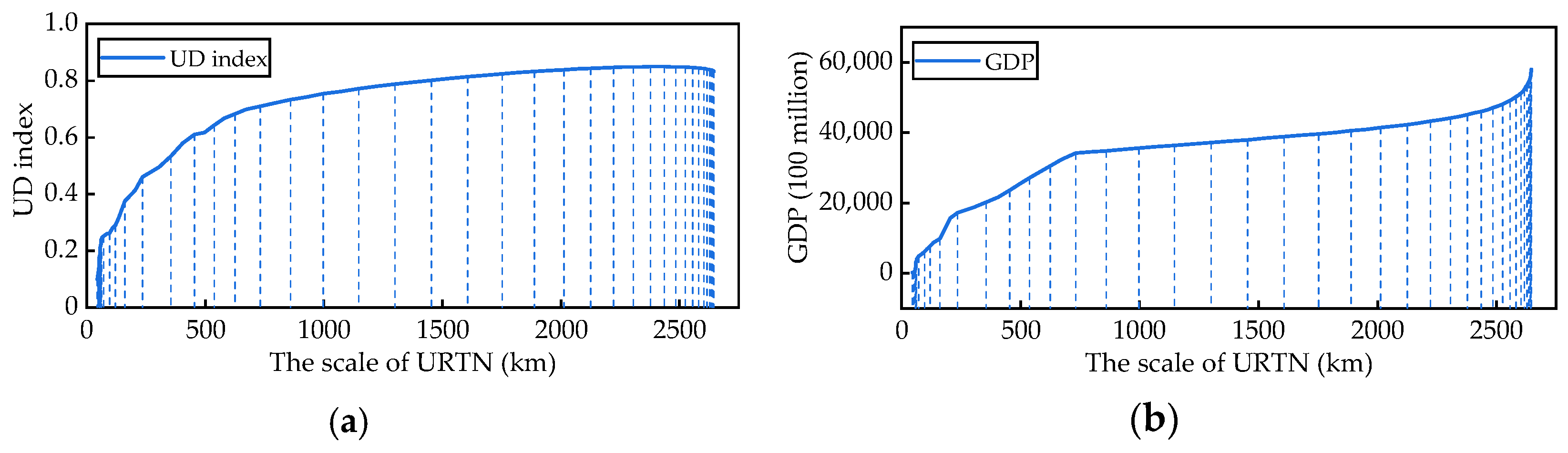
4.3.3. Mutualism Coefficients
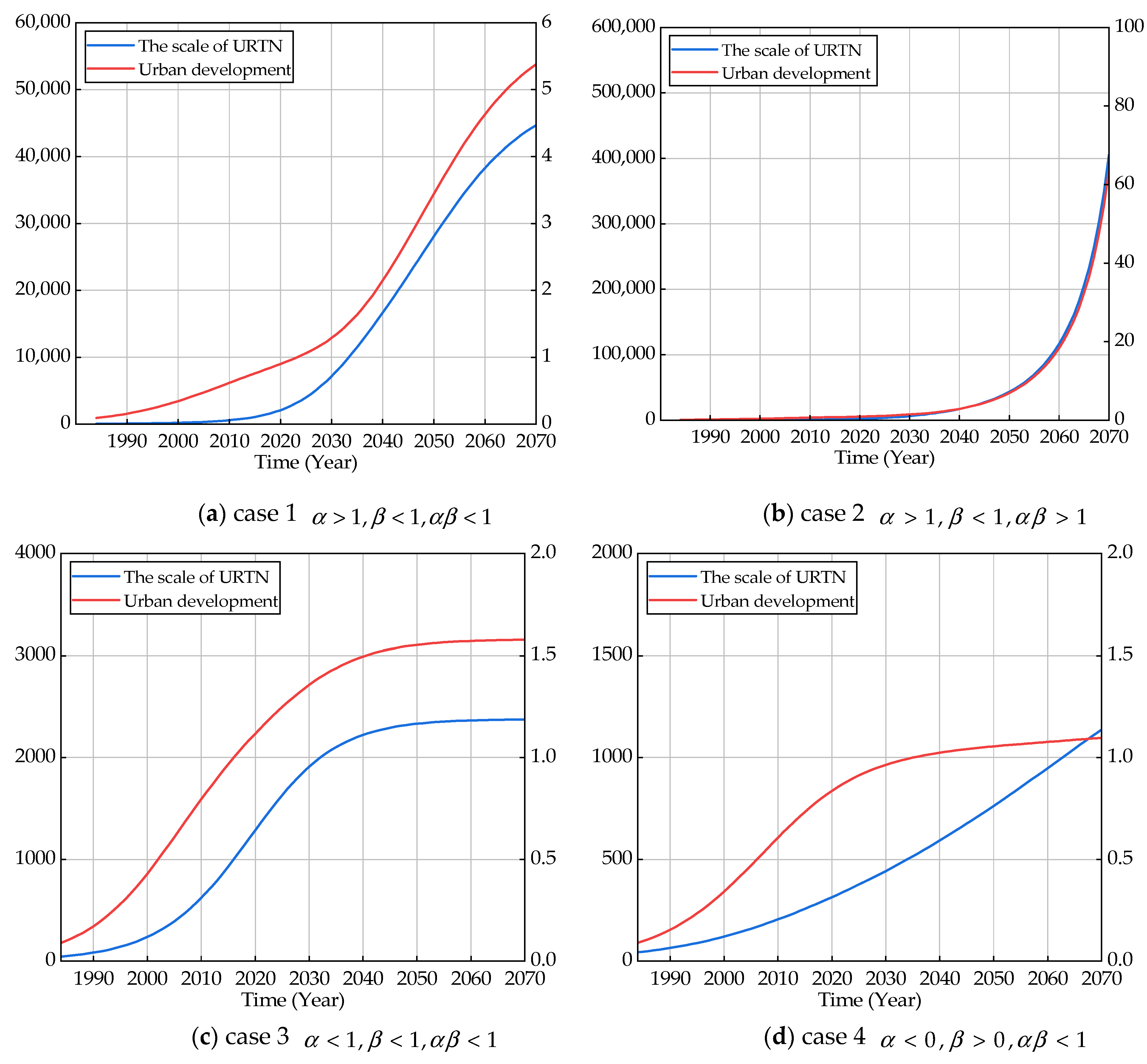
4.3.4. Different Scenarios of Mutualism Coefficient
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Number | Variable Name | Unit | Sample Size | Mean | Standard Error |
|---|---|---|---|---|---|
| 1 | Population | per ten thousand people | 170 | 1471.13 | 704.81 |
| 2 | Urbanization rate | % | 170 | 0.0787 | 0.121 |
| 3 | Built-up area | km2 | 170 | 799.76 | 351.69 |
| 4 | GDP | hundred million | 170 | 10,919.81 | 8022.71 |
| 5 | General public budget revenue | hundred million | 170 | 1549.24 | 1487.99 |
| 6 | Infrastructure investment amount | hundred million | 170 | 1598.36 | 1301.22 |
| 7 | Road length | km | 170 | 5054.62 | 1931.44 |
| 8 | The number of cars | ten thousand vehicles | 170 | 237.84 | 151.11 |
| 9 | The total passenger volume of URT | ten thousand person-times | 170 | 80,385 | 105,944.70 |
| 10 | The total passenger volume of Bus | ten thousand person-times | 170 | 200,503 | 130,822.70 |
| 11 | Urban rail ownership rate | % | 170 | 0.115 | 0.954 |
| Year | Beijing | Tianjin | Shanghai | Guangzhou | Dalian | Wuhan | Chongqing | Shenzhen | Nanjing | Chengdu |
|---|---|---|---|---|---|---|---|---|---|---|
| 2003 | 0.230 | 0.075 | 0.204 | 0.113 | 0.039 | 0.036 | 0.132 | 0.063 | 0.049 | 0.056 |
| 2004 | 0.261 | 0.085 | 0.233 | 0.124 | 0.043 | 0.048 | 0.139 | 0.079 | 0.057 | 0.063 |
| 2005 | 0.280 | 0.099 | 0.262 | 0.137 | 0.048 | 0.058 | 0.153 | 0.099 | 0.073 | 0.072 |
| 2006 | 0.293 | 0.114 | 0.282 | 0.168 | 0.055 | 0.064 | 0.170 | 0.117 | 0.079 | 0.080 |
| 2007 | 0.321 | 0.124 | 0.325 | 0.195 | 0.066 | 0.074 | 0.188 | 0.137 | 0.087 | 0.089 |
| 2008 | 0.391 | 0.141 | 0.359 | 0.213 | 0.08 | 0.093 | 0.205 | 0.150 | 0.095 | 0.102 |
| 2009 | 0.433 | 0.158 | 0.397 | 0.237 | 0.09 | 0.109 | 0.224 | 0.172 | 0.101 | 0.118 |
| 2010 | 0.488 | 0.172 | 0.453 | 0.299 | 0.111 | 0.125 | 0.256 | 0.199 | 0.133 | 0.137 |
| 2011 | 0.528 | 0.194 | 0.478 | 0.368 | 0.131 | 0.138 | 0.297 | 0.253 | 0.150 | 0.160 |
| 2012 | 0.573 | 0.226 | 0.489 | 0.393 | 0.137 | 0.163 | 0.336 | 0.279 | 0.167 | 0.190 |
| 2013 | 0.627 | 0.253 | 0.527 | 0.419 | 0.142 | 0.184 | 0.378 | 0.302 | 0.185 | 0.216 |
| 2014 | 0.663 | 0.272 | 0.559 | 0.441 | 0.143 | 0.209 | 0.414 | 0.326 | 0.223 | 0.249 |
| 2015 | 0.672 | 0.288 | 0.603 | 0.380 | 0.170 | 0.243 | 0.451 | 0.347 | 0.252 | 0.274 |
| Parameter | Estimated Value | Standard Error | p-Value | R2 | Confidence Level |
|---|---|---|---|---|---|
| K | 3028.622 | 34.385 | 0.001 | 0.994 | 95% |
| a | 2488.890 | 568.656 | 0.000 | ||
| b | 0.124 | 0.005 | 0.000 |
References
- Huang, C.; Xia, Y. Study on the Effect of Urban Rail Transit on Regional Economy. Adv. Mater. Res. 2012, 361, 1684–1688. [Google Scholar] [CrossRef]
- Calvo, F.; de Oña, J.; Arán, F. Impact of the Madrid subway on population settlement and land use. Land. Use. Policy 2013, 31, 627–639. [Google Scholar] [CrossRef]
- Sekar, S.P.; Gangopadhyay, D. Impact of rail transit on land use and development: Case study of suburban rail in Chennai. J. Urban. Plan. Dev. 2007, 143, 04016038. [Google Scholar] [CrossRef]
- Jiao, L.; Luo, F.; Wu, F.; Zhang, Y.; Huo, X.; Wu, Y. Exploring the Interactive Coercing Relationship between Urban Rail Transit and the Ecological Environment. Land 2022, 11, 836. [Google Scholar] [CrossRef]
- Shepherd, S.P. A review of system dynamics models applied in transportation. Transp. Metrica B Transp. Dyn. 2014, 2, 83–105. [Google Scholar] [CrossRef]
- Kunc, M.; Mortenson, M.J.; Vidgen, R. A computational literature review of the field of System Dynamics from 1974 to 2017. J. Simul. 2018, 12, 115–127. [Google Scholar] [CrossRef]
- Wangersky, P.J. Lotka-Volterra population models. Ann. Rev. Ecol. Syst. 1978, 9, 189–218. [Google Scholar] [CrossRef]
- Zhang, Z. Mutualism or cooperation among competitors promotes coexistence and competitive ability. Ecol. Model. 2003, 164, 271–282. [Google Scholar] [CrossRef]
- Li, H.; Wang, Z.; Guo, X. Urban rail transit and economic growth—An empirical analysis based on China’s cities panel data. In Proceedings of the 5th International Conference on Industrial Economics System and Industrial Security Engineering (IEIS), Toronto, ON, Canada, 3–6 August 2018; IEEE: Toronto, ON, Canada, 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Lee, E.H.; Shin, H.; Cho, S.H.; Kho, S.-Y.; Kim, D.K. Evaluating the Efficiency of Transit-Oriented Development Using Network Slacks-Based Data Envelopment Analysis. Energies 2019, 12, 3609. [Google Scholar] [CrossRef]
- Wang, Z.; Li, X.; Bobylev, N.; Li, S.; Liu, J. Coupling Coordination of “Urban Rail Transit—Social Economy” Composite System. Infrastructures 2022, 7, 56. [Google Scholar] [CrossRef]
- Liu, D. Analytical forecasting of population distribution over years in a new rail transportation corridor. J. Urban. Plan. Dev. 2016, 142, 04016021. [Google Scholar] [CrossRef]
- Lee, E.H.; Lee, H.; Kho, S.Y.; Kim, D.K. Evaluation of transfer efficiency between bus and subway based on data envelopment analysis using smart card data. KSCE J. Civ. Eng. 2019, 23, 788–799. [Google Scholar] [CrossRef]
- Li, Y. Coordination between Urban Rail Transit Development and Urban Population Change. In Proceedings of the CICTP, Xi’an, China, 14–16 August 2020; pp. 2942–2953. [Google Scholar] [CrossRef]
- Ratner, K.A.; Goetz, A.R. The reshaping of land use and urban form in Denver through transit-oriented development. Cities 2013, 30, 31–46. [Google Scholar] [CrossRef]
- Bhattacharjee, S.; Goetz, A.R. The rail transit system and land use change in the Denver metro region. J. Transp. Geogr. 2016, 54, 440–450. [Google Scholar] [CrossRef]
- Liu, W.; Wang, J. Evaluation of coupling coordination degree between urban rail transit and land use. Int. J. Commun. Syst. 2021, 34, e4015. [Google Scholar] [CrossRef]
- Song, J.; Abuduwayiti, A.; Gou, Z. The role of subway network in urban spatial structure optimization-Wuhan city as an example. Tunn. Undergr. Sp. Tech. 2023, 131, 104842. [Google Scholar]
- Guo, S.; Chen, L. Can urban rail transit systems alleviate air pollution? Empirical evidence from Beijing. Growth Chang. 2019, 50, 130–144. [Google Scholar] [CrossRef]
- Ou, Y.; Zheng, J.; Nam, K.M. Impacts of Urban Rail Transit on On-Road Carbon Emissions: A Structural Equation Modeling Approach. Atmosphere 2022, 13, 1783. [Google Scholar] [CrossRef]
- Ou, Y.; Song, W.; Nam, K.M. Metro-line expansions and local air quality in Shenzhen: Focusing on network effects. Transp. Res. Part D Transp. Environ. 2024, 126, 103991. [Google Scholar] [CrossRef]
- Gendron-Carrier, N.; Gonzalez-Navarro, M.; Polloni, S.; Turner, M.A. Subways and urban air pollution. Am. Econ. J-Appl. Econ. 2022, 14, 164–196. [Google Scholar] [CrossRef]
- Tan, Y.; Jiao, L.; Shuai, C.; Shen, L. A system dynamics model for simulating urban sustainability performance: A China case study. J. Clean. Prod. 2018, 199, 1107–1115. [Google Scholar] [CrossRef]
- Xing, L.; Xue, M.; Hu, M. Dynamic simulation and assessment of the coupling coordination degree of the economy-resource-environment system: Case of Wuhan City in China. J. Environ. Manag. 2019, 230, 474–487. [Google Scholar] [CrossRef]
- Xu, J.; Kang, J. Comparison of ecological risk among different urban patterns based on system dynamics modeling of urban development. J. Urban. Plan. Dev. 2017, 143, 04016034. [Google Scholar] [CrossRef]
- Bach, P.; Tustanovski, E.; Andrew, W.H.; Yung, K.L.; Roblek, V. System dynamics models for the simulation of sustainable urban development: A review and analysis and the stakeholder perspective. Kybernetes 2020, 49, 460–504. [Google Scholar] [CrossRef]
- Su, Y.; Liu, X.; Li, X. Research on traffic congestion based on system dynamics: The case of Chongqing, China. Complexity 2020, 2020, 6123896. [Google Scholar] [CrossRef]
- Yang, H.; Wang, W.; Wei, B. System dynamics for urban traffic jam management in beijing. Environ. Eng. Manag. J. 2015, 14, 1875–1886. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, P.; Ni, S. Assessment of the impacts of urban rail transit on metropolitan regions using system dynamics model. Transp. Res. Procedia 2014, 4, 521–534. [Google Scholar] [CrossRef]
- Chen, Y.; Stasinopoulos, P.; Shiwakoti, N.; Khan, S.K. Using System Dynamics Approach to Explore the Mode Shift between Automated Vehicles, Conventional Vehicles, and Public Transport in Melbourne, Australia. Sensors 2023, 23, 7388. [Google Scholar] [CrossRef]
- Mylonakou, M.; Chassiakos, A.; Karatzas, S.; Liappi, G. System Dynamics Analysis of the Relationship between Urban Transportation and Overall Citizen Satisfaction: A Case Study of Patras City, Greece. Systems 2023, 11, 112. [Google Scholar] [CrossRef]
- Bartuska, L.; Stopka, O.; Luptak, V.; Masek, J. Approach Draft to Evaluate the Transport System State—A Case Study Regarding the Estimation Ratio Model of Transport Supply and Demand. Appl. Sci. 2023, 13, 4638. [Google Scholar] [CrossRef]
- Maheshwari, P.; Khaddar, R.; Kachroo, P.; Shyalan, N. Dynamic model development of performance indices for planning of sustainable transportation systems. In Proceedings of the 15th International IEEE Conference on Intelligent Transportation Systems, Anchorage, AK, USA, 16–19 September 2012. [Google Scholar] [CrossRef]
- Luo, J. Feasibility study on high-speed rail and air cooperation. In Proceedings of the 5th International Conference on Civil Engineering and Transportation, Guangzhou, China, 28–29 November 2015. [Google Scholar] [CrossRef]
- Liang, X.; Meng, X. Investigating the development and interaction of bus-metro based on Lotka-Volterra models: Evidence from seven central cities in China. Mod. Phys. Lett. B. 2021, 35, 2150207. [Google Scholar] [CrossRef]
- Mao, S.; Zhang, Y.; Kang, Y.; Mao, Y. Coopetition analysis in industry upgrade and urban expansion based on fractional derivative gray Lotka-Volterra model. Soft. Comput. 2021, 25, 11485–11507. [Google Scholar] [CrossRef]
- Sun, S.; Wang, W. Analysis on the market evolution of new energy vehicle based on population competition model. Transp. Res. Part D Transp. Environ. 2018, 65, 36–50. [Google Scholar] [CrossRef]
- Yuan, L.; Li, R.; He, W.; Wu, X.; Kong, Y.; Degefu, D.M.; Ramsey, T.S. Coordination of the industrial-ecological economy in the Yangtze River economic belt, China. Front. Environ. Sci. 2022, 10, 882221. [Google Scholar] [CrossRef]
- Liu, K.; Xiong, X.; Xiang, X.; Wu, S.; Shi, D.; Zhang, W.; Zhang, L. Investigating the coordination between ecological and economic systems in China’s green development process: A place-based interdisciplinary evaluation. Ecol. Soc. 2023, 28, 43. [Google Scholar] [CrossRef]
- Yu, S.; Geng, X.; He, J.; Sun, Y. Evolution analysis of product service ecosystem based on interval Pythagorean fuzzy DEMATEL-ISM-SD combination model. J. Clean. Prod. 2023, 421, 138501. [Google Scholar] [CrossRef]
- Kong, H.; Zhang, X.; Zhao, J. How does ridesourcing substitute for public transit? A geospatial perspective in Chengdu, China. J. Transp. Geogr. 2020, 86, 102769. [Google Scholar] [CrossRef]
- Ou, Y.; Bao, Z.; Ng, S.T.; Song, W. Estimating the effect of air quality on bike-sharing usage in Shanghai, China: An instrumental variable approach. Travel. Behav. Soc. 2023, 33, 100626. [Google Scholar] [CrossRef]
- Liang, Y.; Wang, D.; Yang, H.; Yuan, Q.; Yang, L. Examining the causal effects of air pollution on dockless bike-sharing usage using instrumental variables. Transp. Res. Part D Transp. Environ. 2023, 121, 103808. [Google Scholar] [CrossRef]
- Chen, Y. Stage division of urban growth based on logistic model of fractal dimension curves. Res. Phys. 2023, 53, 106940. [Google Scholar] [CrossRef]
- Hu, Z.; Lo, C.P. Modeling urban growth in Atlanta using logistic regression. Comput. Environ. Urban Syst. 2007, 31, 667–688. [Google Scholar] [CrossRef]
- Man, X.; Chen, Y. Fractal-Based Modeling and Spatial Analysis of Urban Form and Growth: A Case Study of Shenzhen in China. ISPRS Int. J. Geo-Inf. 2020, 9, 672. [Google Scholar] [CrossRef]
- Li, S.; Liang, Q.; Han, K.; Wang, H.; Xu, J. A Double-Level Calculation Model for the Construction Schedule Planning of Urban Rail Transit Network. Appl. Sci. 2022, 12, 5268. [Google Scholar] [CrossRef]
- Frédéric, M.; Samir, L.; Louise, M.; Abdelkrim, A. Comprehensive modeling of mat density effect on duckweed (Lemna minor) growth under controlled eutrophication. Water Res. 2006, 40, 2901–2910. [Google Scholar] [CrossRef] [PubMed]
- MacArthur, R.; Levins, R. The limiting similarity, convergence, and divergence of coexisting species. Am. Nat. 1967, 101, 377–385. [Google Scholar] [CrossRef]
- Swain, A.; Chatterjee, S. A new formulation for determination of the competition coefficient in multispecies interaction for Lotka—Volterra type competition models. Curr. Sci. 2017, 112, 1920–1926. [Google Scholar] [CrossRef]
- Beijing Statistical Yearbook. Available online: https://tjj.beijing.gov.cn/tjsj_31433/ (accessed on 28 April 2024).
- Beijing Transport Development Annual Report. Available online: https://www.bjtrc.org.cn/List/index/cid/7.html (accessed on 28 April 2024).
- China Urban Construction Statistical Yearbook. Available online: https://www.mohurd.gov.cn/gongkai/fdzdgknr/sjfb/tjxx/index.html (accessed on 28 April 2024).
- China Urban Statistical Yearbook. Available online: https://www.stats.gov.cn/zs/tjwh/tjkw/tjzl/index.html (accessed on 14 June 2024).
- Hu, W.; Dong, J.; Hwang, B.; Ren, R.; Chen, Y.; Chen, Z. Using system dynamics to analyze the development of urban freight transportation system based on rail transit: A case study of Beijing. Sustain. Cities Soc. 2020, 53, 101923. [Google Scholar] [CrossRef]
- Wang, H.; Wang, Z.; Zhang, K.; Chen, J.; Li, G.; Yang, Y. System dynamics model of taxi management in metropolises: Economic and environmental implications for Beijing. J. Environ. Manag. 2018, 213, 555–565. [Google Scholar] [CrossRef]





| Symbol | Meaning |
|---|---|
 | A and B change in the same direction |
 | A and B change in the opposite direction |
 | Positive feedback loop |
 | Negative feedback loop |
| Equilibrium Point | p | q | Stability Condition |
|---|---|---|---|
| Unstable | |||
| Unstable | |||
| Unstable | |||
| Notation | Meaning | Example |
|---|---|---|
| L | the stocks | denotes the network length of URT. |
| R | the flows | is the annual increment of the network length. |
| A | the rate of change | denotes the growth rate of the network length. |
| Variable Name | Initial Value | Unit |
|---|---|---|
| Scale of URTN | 41 | km |
| Maximum scale of URTN | 3028.66 | km |
| UD index | 0.1 | dimensionless |
| Maximum UD index | 1 | dimensionless |
| GDP | 216 | hundred million |
| Road length | 1436 | km |
| Population | 965 | ten thousand |
| Built-up area | 366 | km2 |
| Air pollutants | 100 | thousand tons |
| Number of private cars | 8.7 | ten thousand |
| Number of taxies | 0.4279 | ten thousand |
| Number of buses | 0.4066 | ten thousand |
| Variable/Year | 2017 | 2018 | 2019 | 2020 | 2021 | |
|---|---|---|---|---|---|---|
| Scale of URTN | Actual value | 587.8 | 636 | 699 | 727 | 783 |
| Simulation Value | 580.24 | 623.51 | 672 | 730.7 | 793.3 | |
| Error | −1.28% | −1.96% | −4.3% | 0.51% | 1.32% | |
| GDP | Actual value | 31,387 | 30,319.97 | 35,371 | 36,103 | 40,269.6 |
| Simulation Value | 29,780.2 | 32,573.8 | 35,500.4 | 38,804.7 | 42,554.1 | |
| Error | −8.01 | 0.78% | −8.19% | 7.48% | 5.67% | |
| Population | Actual value | 2170.8 | 2154.2 | 2153 | 2189 | 2188.6 |
| Simulation Value | 1980.01 | 2001 | 2023 | 2024.11 | 2042.89 | |
| Error | −8.79% | −7.11% | −6.04% | −7.53% | −6.66% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Liang, Q.; Han, K.; Wen, K. An SD-LV Calculation Model for the Scale of the Urban Rail Transit Network. Systems 2024, 12, 233. https://doi.org/10.3390/systems12070233
Li S, Liang Q, Han K, Wen K. An SD-LV Calculation Model for the Scale of the Urban Rail Transit Network. Systems. 2024; 12(7):233. https://doi.org/10.3390/systems12070233
Chicago/Turabian StyleLi, Songsong, Qinghuai Liang, Kuo Han, and Kebing Wen. 2024. "An SD-LV Calculation Model for the Scale of the Urban Rail Transit Network" Systems 12, no. 7: 233. https://doi.org/10.3390/systems12070233
APA StyleLi, S., Liang, Q., Han, K., & Wen, K. (2024). An SD-LV Calculation Model for the Scale of the Urban Rail Transit Network. Systems, 12(7), 233. https://doi.org/10.3390/systems12070233






