Cell Formation Problem with Alternative Routes and Machine Reliability: Review, Analysis, and Future Developments
Abstract
:1. Introduction
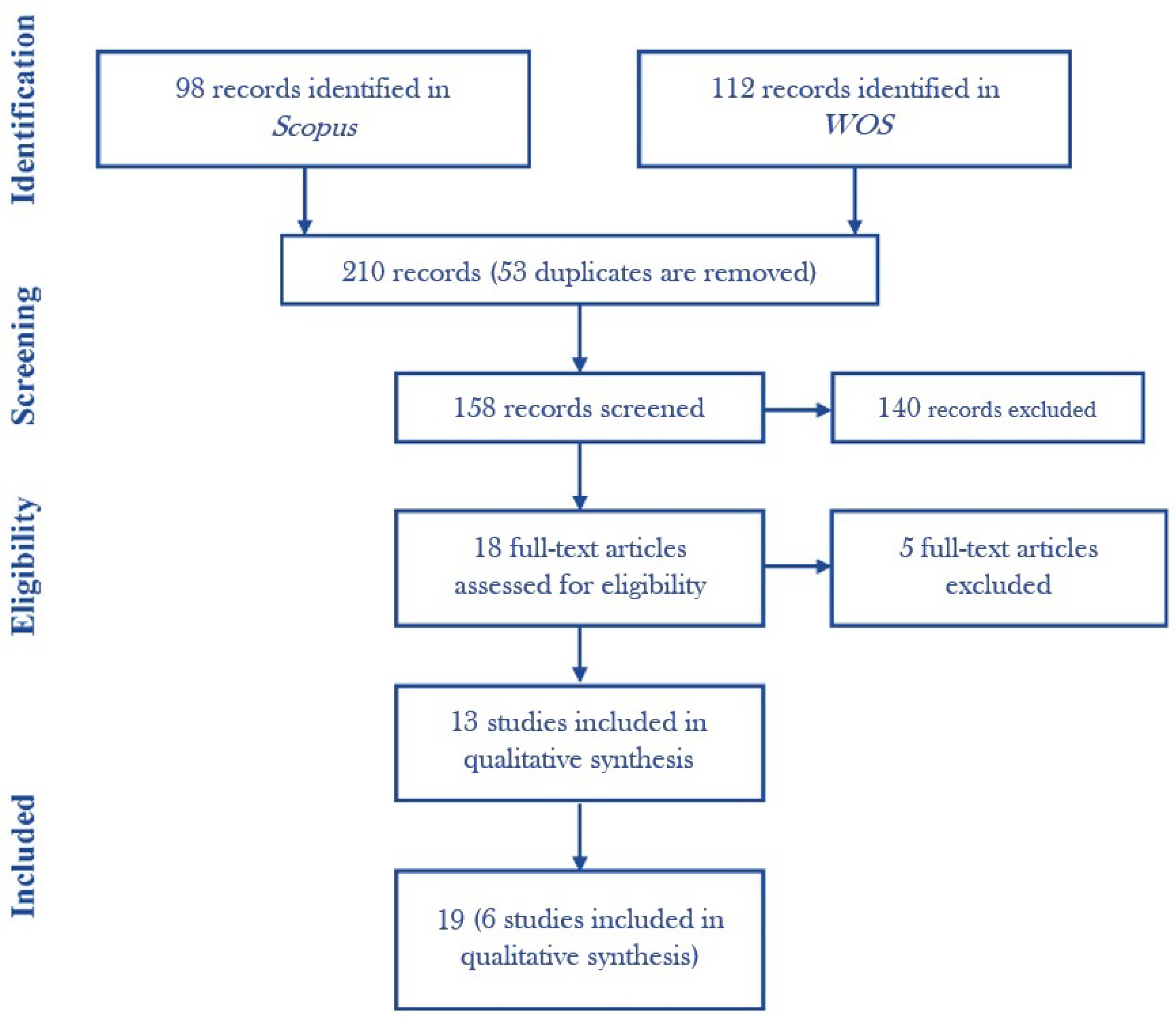
2. Research Method and Article Selection Process
2.1. Research Method
- The recognition of an iterative process;
- Public protocol for systematic reviews;
- Differentiation between conduct and reporting of research;
- Evaluation of the risk of bias at the study and outcome levels;
- The importance of reporting biases in presenting results.
2.2. Article Selection Process
3. Results
3.1. Parameters
| [Ref] | Frequency | Number of Machines | Number of Parts | Number of Cells | Demand per Part/ Production Volume | Number of Routes | Maximum Number of Machines per Cell | Process Time/Operation per Part on One Machine | MTBF/Failure Rate | Intercellular Movement Cost |
|---|---|---|---|---|---|---|---|---|---|---|
| [18]—2023 | 9 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| [19]—2020 | 8 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | |
| [20]—2019 | 9 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| [21]—2019 | 5 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | ||||
| [22]—2019 | 9 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| [23]—2017 | 9 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| [24]—2017 | 9 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| [25]—2016 | 7 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | ||
| [26]—2016 | 9 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| [27]—2016 | 6 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | |||
| [28]—2014 | 9 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| [29]—2011 | 9 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| [30]—2011 | 7 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | ||
| [31]—2011 | 9 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| [32]—2009 | 7 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | ||
| [33]—2008 | 9 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| [34]—2008 | 9 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| [35]—2008 | 9 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| [36]—2007 | 7 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| [Ref] | Minimize Cost | Minimize SRI | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Intercellular Movement Cost | Intracellular Movement Cost | Breakdown (BD) | Machine Operation | Machine Constant | Outsourcing | Refixture/Relocation | Set-Up | LIR/SFR | |
| [18]—2023 | 🗸 | 🗸 | |||||||
| [19]—2020 | 🗸 | 🗸 | 🗸 | 🗸 | |||||
| [20]—2019 | 🗸a | 🗸a | 🗸b | ||||||
| [21]—2019 | |||||||||
| [22]—2019 | 🗸 | 🗸 | 🗸 | 🗸 | |||||
| [23]—2017 | 🗸 | 🗸 | |||||||
| [24]—2017 | 🗸a | 🗸a | 🗸a | 🗸a | 🗸b | ||||
| [25]—2016 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | |||
| [26]—2016 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | ||||
| [27]—2016 | 🗸 | 🗸 | |||||||
| [28]—2014 | 🗸 | 🗸 | 🗸 | 🗸 | |||||
| [29]—2011 | 🗸a | 🗸a | 🗸a | 🗸b | |||||
| [30]—2011 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | |||
| [31]—2011 | 🗸 | 🗸 | |||||||
| [32]—2009 | 🗸a | 🗸a | 🗸a | ||||||
| [33]—2008 | 🗸 | 🗸 | |||||||
| [34]—2008 | 🗸a | 🗸a | 🗸a | ||||||
| [35]—2008 | 🗸 | 🗸 | |||||||
| [36]—2007 | 🗸a | 🗸a | 🗸a | 🗸b | |||||
| Frequency | 18 | 9 | 12 | 5 | 3 | 3 | 5 | 4 | 4 |
| [Ref] | Constraints Used | Only One Route/ Operation per Part | Only One Cell per Machine | Upper Machine Limit per Cell | Lower Machine Limit per Cell | Demand | Machine Capacity | Balance of Machines between Periods | Balance of Processed and Unprocessed Parts/Outsourcing | One Type of Operation per Machine |
|---|---|---|---|---|---|---|---|---|---|---|
| [18]—2023 | 4 | 🗸 | 🗸 | 🗸 | 🗸 | |||||
| [19]—2020 | 3 | 🗸 | 🗸 | 🗸 | ||||||
| [20]—2019 | 2 | 🗸 | 🗸 | |||||||
| [21]—2019 | 2 | 🗸 | 🗸 | |||||||
| [22]—2019 | 4 | 🗸 | 🗸 | 🗸 | 🗸 | |||||
| [23]—2017 | 4 | 🗸 | 🗸 | 🗸 | 🗸 | |||||
| [24]—2017 | 6 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | |||
| [25]—2016 | 6 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | ||||
| [26]—2016 | 7 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸🗸 | 🗸 | |||
| [27]—2016 | 0 | |||||||||
| [28]—2014 | 4 | 🗸 | 🗸 | 🗸 | 🗸 | |||||
| [29]—2011 | 5 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | ||||
| [30]—2011 | 11 | 🗸🗸 | 🗸 | 🗸🗸🗸 | 🗸 | 🗸🗸 | 🗸 | 🗸 | ||
| [31]—2011 | 4 | 🗸 | 🗸 | 🗸 | 🗸 | |||||
| [32]—2009 | 6 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸🗸 | ||||
| [33]—2008 | 4 | 🗸 | 🗸 | 🗸 | 🗸 | |||||
| [34]—2008 | 3 | 🗸 | 🗸 | 🗸 | ||||||
| [35]—2008 | 3 | 🗸 | 🗸 | 🗸 | ||||||
| [36]—2007 | 3 | 🗸 | 🗸 | 🗸 | ||||||
| Frequency | 13 | 15 | 17 | 12 | 4 | 6 | 2 | 4 | 2 | |
| [Ref] | Exact Method | Metaheuristic |
|---|---|---|
| [18]—2023 | Not used | BWO |
| [19]—2020 | Not used | GA |
| [20]—2019 | Not used | GA-KA-RDA |
| [21]—2019 | Not used | NSGA-II |
| [22]—2019 | Not used | CS |
| [23]—2017 | Not used | CSA |
| [24]—2017 | -constraint method | MOICA |
| [25]—2016 | Not used | SA-GA |
| [26]—2016 | RO | Not used |
| [27]—2016 | SCM | Not used |
| [28]—2014 | Not used | SA |
| [29]—2011 | -constraint method | Not used |
| [30]—2011 | Not used | SA-GA |
| [31]—2011 | Not used | TS-GA |
| [32]—2009 | -constraint method | Not used |
| [33]—2008 | Not used | SA-GA-MA |
| [34]—2008 | -constraint method | Not used |
| [35]—2008 | Not used | Not used |
| [36]—2007 | -constraint method | Not used |
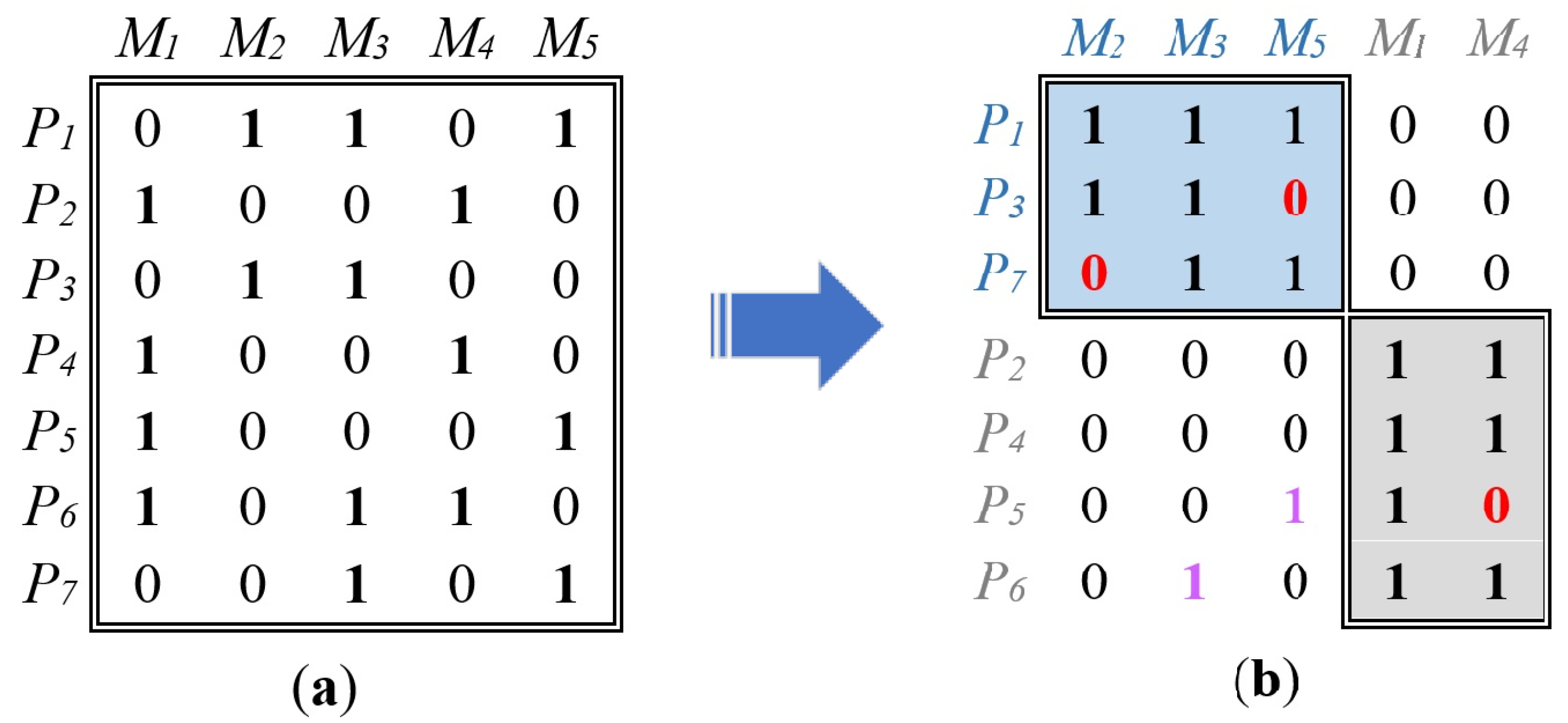
- Number of cells:In most cases, the cells are calculated as part of the model’s objectives, which implies that the calculation begins without knowing the number of cells. Ultimately, the model specifies how many cells are optimal for the case studied.
- Number of routes: This could be because, in certain cases, production routes are not defined with fixed production lines and specific machines. Instead, routes stem from machines’ capability to perform the required operations using a specific part. In this context, multiple machines may be available, but only the one capable of carrying out a necessary production operation for one or several parts is selected.
3.2. Objective Function
3.3. Constraints
- Demand constraints only appear when capacity constraints are also present, indicating that in these studies, demand is dependent on the production capacity of the machines.
- Lower limit constraints only appear when upper limit constraints are present, indicating a priority in avoiding exceeding the capacity of a machine cell.
3.4. Methodology
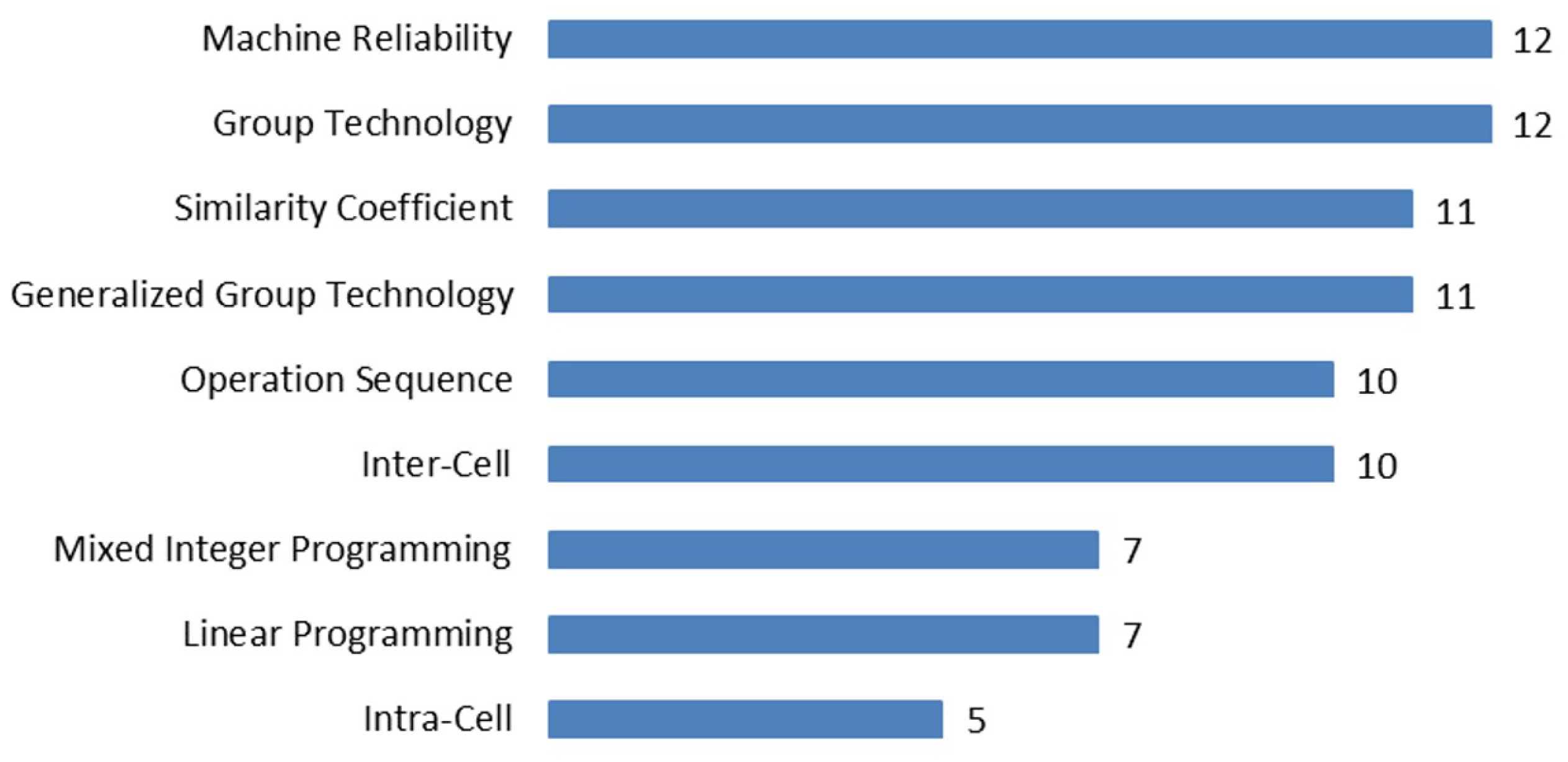
Metaheuristics Used
- Genetic algorithm (1975)—[19,20,25,30,31,33]: As described in [43], a genetic algorithm (GA) is a computational model inspired by biological evolution capable of representing solutions to various problems, game strategies, visual images, or computer programs. Solutions are stored in a computer’s memory and undergo gradual modifications over time, akin to how populations of individuals evolve through natural selection.
- -
- The GA typically commences by initializing a population of random individuals. Subsequently, over a fixed number of generations, the algorithm iterates through the following steps: evaluating the fitness of each individual in the population, selecting parents for reproduction utilizing a selection method (such as roulette wheel or tournament), applying genetic operators like crossover and mutation to generate a new population of offspring, and replacing the old population with the new offspring population. Optionally, the algorithm may incorporate elitism operators or survival selection methods to retain certain individuals from the previous generation in the subsequent one. Moreover, diversification techniques or convergence control methods may be incorporated. Finally, the algorithm yields the best-found individual or the final population.
- Simulated annealing (1983)—[25,28,30,33]: As elucidated in [44], this metaheuristic (SA) emulates the physical process wherein a solid within a heat bath is heated to a maximum value, causing all particles of the solid to arrange in the liquid phase randomly. Subsequently, the cooling process commences by gradually reducing the temperature of the heat bath. Consequently, all particles settle into the fundamental low-energy state of the corresponding lattice, provided the maximum temperature is sufficiently high and the cooling is sufficiently gradual.
- -
- SA initiates with a random or predetermined initial state and specifies an initial temperature and cooling factor. The algorithm iterates until a stopping criterion is satisfied: it generates a new neighboring state by randomly perturbing the current state, calculates the energy difference between the new state and the current state, and then, if the energy difference is negative or less than an acceptance value, accepts the new state as the current state. Otherwise, it computes the probability of accepting the new state based on the energy difference and the current temperature, generates a random number between 0 and 1, and, if the random number is less than the acceptance probability, accepts the new state as the current state. Subsequently, the temperature is reduced according to the cooling factor. Finally, the algorithm returns the best-found state or the final state.
- Tabu search (1986)—[31]: Embedded within problem solving strategies are approaches that merge adaptive memory with responsive exploration [45]. Within this framework, the adaptive memory component of tabu search (TS) facilitates the use of gathered information to direct local choices during the search process. Emphasizing responsive exploration is predicated on the belief that suboptimal strategic decisions often yield more informative outcomes than random selections.
- -
- TS begins with a random or predetermined initial solution and initializes an empty tabu list. The algorithm iterates until a stopping criterion is met: it generates a list of available moves from the current state, applies an aspiration criterion if necessary to permit tabu moves leading to a superior solution, selects the best available move not present in the tabu list, adds the move to the tabu list, applies the move to obtain a new state, updates the best-found solution if the new state surpasses the current best solution, and removes old moves from the tabu list if they have exceeded a certain time or iteration limit. Finally, the algorithm returns the best-found solution.
- Memetic algorithm (1989)—[33]: The MA is a metaheuristic combining elements of genetic algorithms and local search, as outlined by [46]. These algorithms utilize a population of solutions, along with crossover and mutation, akin to genetic algorithms (GAs). However, what sets apart a memetic algorithm is the incorporation of a local improvement phase. Following the application of genetic operators, local search steps are executed on the generated solutions to enhance their quality. This local search aids in refining the solutions and prevents the algorithm from stagnating in suboptimal local optima.
- -
- The MA initializes with a population of random individuals. Subsequently, over a fixed number of generations, the algorithm iterates as follows: for each individual in the population, it applies local improvement operators (such as local search, heuristics, or algorithms), evaluates the fitness of each individual, selects parents for reproduction using a selection method (such as roulette wheel or tournament), applies genetic operators such as crossover and mutation to generate a new population of offspring, and replaces the old population with the new offspring population. Optionally, the algorithm may incorporate elitism operators or survival selection methods to retain certain individuals from the previous generation in the subsequent one. Moreover, diversification techniques or convergence control methods may be employed. Finally, the algorithm returns the best-found individual or the final population.
- Non-Dominated Sorting Genetic Algorithm-II (2002)—[21]: As expounded by [47], the NSGA-II (Non-Dominated Sorting Genetic Algorithm-II) is inspired by the NSGA, a prevalent genetic algorithm based on non-domination for multi-objective optimization. While the NSGA is highly effective, it has been criticized for its computational complexity, lack of elitism, and the necessity to choose the optimal value of its sharing parameter. In response, a modified version was developed—NSGA-II—featuring an improved sorting algorithm, incorporation of elitism, and elimination of the need to preselect the sharing parameter.
- -
- The NSGA-II commences by initializing a population of random individuals. Then, over a fixed number of generations, the algorithm iterates: creating an empty population of offspring, performing parent selection operations (e.g., binary tournament) to choose parents for reproduction, applying crossover and mutation operators to generate offspring, combining the current population with the offspring population to form a combined population, performing non-dominated sorting on the combined population, selecting the best non-dominated individuals until the population is full, applying elitism operators or survival selection methods to maintain diversity, and optionally applying diversification techniques or convergence control. Finally, the algorithm returns the set of non-dominated solutions found.
- Cuckoo search (2009)—[22]: CS is an algorithm inspired by nature and developed based on the breeding behavior of cuckoo birds, as elucidated by [48]. Cuckoos adopt solutions as cuckoo eggs, laying their fertilized eggs in the nests of other cuckoos with the expectation that surrogate parents will nurture their offspring. Upon discovering foreign eggs in their nests, cuckoos either eject them or abandon the nest.
- -
- CS commences by initializing a population of random cuckoo nests. Subsequently, it iterates until a stopping criterion is met: for each cuckoo nest, it evaluates the quality of the nest (solution), generates a new cuckoo nest through a random flight, and assesses if the new nest is superior to the current one. If it is, the current nest is replaced with the new one; otherwise, if a cuckoo discovers a better nest, it abandons its egg (new solution) in the nest, replacing the existing egg (solution) with the new one (new solution). The population of nests is then updated using the Levy flight operator or another random search method, removing less-fit nests and optionally applying diversification techniques or convergence control. Finally, the best nest (solution) found is returned.
- Multi-objective imperialist competitive algorithm (2013)—[24]: As detailed by [49], the MOICA generates potential solutions termed as “countries”. Based on their merits, any country can assume the role of an imperialist or a colony. The most powerful countries are designated as imperialists, forming empires by exerting control over colonies. Subsequently, imperialist competition ensues among these empires, resulting in the dominance of a single empire.
- -
- The MOICA initializes a population comprising both imperialist countries and colonies, all randomly generated. It iterates until a stopping criterion is satisfied. For each imperialist, fitness is computed based on their objectives. Then, for each colony of every imperialist, the fitness of the colony is calculated, and the colony’s position is updated using local search operators. If the colony outperforms its imperialist in fitness, it supersedes the imperialist. The algorithm employs selection operators for both imperialists and colonies, alongside migration operators between them. It updates the positions of each imperialist and colony based on movement operators and applies techniques for diversification or convergence control. Finally, it returns the set of Pareto solutions found.
- Keshtel algorithm (2013)—[20]: This metaheuristic (KA) is inspired by the feeding behavior of Keshtel ducks, scientifically known as “Anas clypeata”, as detailed in [50]. Keshtels, a species of dabbling duck belonging to the Anas family, are commonly found in the northern regions of Iran. Characterized by distinctive large spoon-shaped bills, Keshtels exhibit unique feeding behavior, skimming the water’s surface in shallow lakes. They often form large flocks and migrate seasonally, primarily inhabiting sheltered wetlands or lakes where they feed on seeds and aquatic invertebrates. During foraging, Keshtels efficiently sift through water using their specialized bills equipped with comb-like teeth called lamellae, facilitating food particle filtration. Water is drawn in at the tip of the bill, filtered through the lamellae to capture food, and then expelled at the base.
- -
- The KA begins with an initial population of Keshtels introduced into a virtual lake to explore potential solutions. Keshtels that discover superior food sources upon landing are designated as lucky Keshtels and attract neighboring Keshtels. If a lucky Keshtel finds a superior food source, it and its neighbors relocate. Once local food is depleted, lucky Keshtels disperse, venturing in different directions to seek new sources. Some Keshtels explore uncharted areas, while others migrate to alternative territories or lakes. The positioning of a Keshtel in the lake represents a potential solution, with food source quality indicative of cost minimization in the objective function.
- Red Deer Algorithm (2016)—[20]: This metaheuristic (RDA) is inspired by the mating dynamics of Scottish Red Deer, as outlined in [51]. Red Deer, typically found in woodland and moorland habitats, are selective grazers, feeding on grasses, sedges, heathers, and woody species. Although widely distributed across Scotland, they are absent from certain regions, such as the Northern Isles and much of the central belt and southeast. During the breeding season, male Red Deer engage in loud roaring behavior, with females preferring higher roaring rates associated with greater reproductive success and fighting ability. Female choice may reflect a preference for successful males or those easily located, with competition between males influencing mating patterns.
- -
- The RDA initiates with an initial population of Red Deer, comprising selected individuals as male Red Deer and the remainder termed hinds. After displays of roaring and fighting, harems, groups of hinds, are formed and allocated among male Red Deer based on their abilities, characterized by grace and power. These attributes correspond to the fitness value in genetic algorithms, inversely proportional to roaring abilities, functioning as a means of local search. During fights, two males compete, with the victor selected as the better option at each level. The male Red Deer then redistributes all harems, and the male commanding a harem mates with a percentage of the hinds within it and from other harems. They also mate with the nearest hind, simulating the process of generating new solutions akin to the offspring of Red Deer in a generation.
- Black widow optimizer (2020)—[18]: Developed by [52], this metaheuristic (BWO) operates on a population-based approach and draws inspiration from the mating behavior observed in black widow spiders in their natural environment. During the black widow mating season, the female spider constructs a web and strategically marks specific areas to attract potential mates. Once a male enters the web, it discourages other males from attempting to enter. A noteworthy aspect of black widow mating behavior is the possibility of the female consuming the male, either during or after copulation. Following mating, the female proceeds to deposit eggs into her egg sac. Upon hatching, sibling cannibalism often occurs, with the mother sometimes participating in this process. This phenomenon of cannibalism ultimately promotes the survival of the fittest offspring.
- -
- BWO begins by initializing a population of spiders (representing potential solutions) randomly within the search space. It iterates until a stopping criterion is reached. Each spider’s quality, reflecting its corresponding solution, is evaluated in every iteration. The two best-performing spiders are selected as parents, and they are combined to generate offspring, representing potential solutions. The quality of the offspring is evaluated, and the weaker parent and offspring are removed from the population. Furthermore, a certain number of spiders undergo mutation to prevent local optima, and the quality of the mutated spiders is assessed. Finally, the new population is selected from the surviving spiders (including the stronger parent, offspring, and mutated spiders) based on their quality. This process continues iteratively until the stopping criterion is met, ultimately returning the best solution found.
4. Main Insights Collected
4.1. Line Stoppage after Machine Downtime
4.2. MTTR
4.3. Multiple Periods in the Models
4.4. Most Commonly Used Model
4.4.1. Model Assumptions
- The total number of cells is defined;
- The lower limit of machines per cell is known;
- The upper limit of machines per cell is known;
- Each part has at least one process route, but only a single route can be selected;
- Each route has different operations with ordered sequences, and machines perform these operations. The sequence must be taken into account, as it will help determine when a part passes from one cell to another, in addition to collaborating with the calculation of material handling costs;
- Each type of part has its time of operation (or processing) in each machine;
- Multiple identical machines were not considered;
- The production demand of each part is known and said demand is also deterministic;
- The Mean Time Between Failures (MTBFs) was used for the machine reliability calculation.
4.4.2. Parameters
| m: | Quantity of machines; |
| n: | Quantity of parts; |
| c: | Quantity of cells; |
| r: | Total quantity of routes; |
| : | Part i production volume; |
| : | Quantity of routes per part i; |
| : | Lower limit of the quantity of machines in cell l; |
| : | Upper limit of the quantity of machines in cell l; |
| : | Quantity of machines in route j of part i; |
| , ,…, : | Machines index of route j of part i; |
| : | Duration required for processing a part i on machine k; |
| : | Cost associated with machine k breakdown; |
| : | Cost associated with intercellular movement for part i in route j; |
| : | Mean time between failure of machine k. |
4.4.3. Variables
4.4.4. Mathematical Model
4.5. Lower Limit of Machines per Cell
4.6. Metaheuristics as a Resolution Method for the GCFP
4.7. The Lack of Applicability in Real Industrial Environments
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sarin, S.; Jain, P.K. A review on the developments of machine-cell formation problem in cellular manufacturing systems. Benchmarking Int. J. 2018, 25, 172–194. [Google Scholar]
- Albadawi, A.; Salman, A.; Essam, D. A comprehensive review of cell formation techniques in cellular manufacturing. Int. J. Adv. Manuf. Technol. 2019, 100, 1–24. [Google Scholar]
- Surynek, P. Compact representations of cooperative path-finding as SAT based on matchings in bipartite graphs. In Proceedings of the 2014 IEEE 26th International Conference on Tools with Artificial Intelligence, Limassol, Cyprus, 10–12 November 2014; pp. 875–882. [Google Scholar]
- Kumar, P.; Pant, M. A review on machine cell formation techniques for cellular manufacturing systems. Procedia Manuf. 2017, 11, 1675–1686. [Google Scholar]
- Gen, M.; Cheng, R.; Lin, L. A survey of cellular manufacturing systems. Int. J. Prod. Res. 2019, 572, 604–626. [Google Scholar]
- Henriques, A.; Richardson, J. The Triple Bottom Line: Does It All Add Up; Routledge: Abingdon, UK, 2013. [Google Scholar]
- Gupta, S.; Verma, R.; Agrawal, R. A Review on Recent Developments in Cellular Manufacturing Systems. Mater. Today Proc. 2020, 33, 1076–1081. [Google Scholar]
- Kusiak, A. The generalized group technology concept. Int. J. Prod. Res. 1987, 25, 561–569. [Google Scholar] [CrossRef]
- Kapur, K.C.; Pecht, M. Reliability Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Blache, K.M.; Shrivastava, A.B. Defining failure of manufacturing machinery and equipment. In Proceedings of the Annual Reliability and Maintainability Symposium (RAMS), Anaheim, CA, USA, 24–27 January 1994; pp. 69–75. [Google Scholar]
- Moher, D.; Liberati, A.; Tetzlaff, J.; Altman, D.G.; Group, P. Preferred reporting items for systematic reviews and meta-analyses: The PRISMA statement. Int. J. Surg. 2010, 8, 336–341. [Google Scholar] [CrossRef] [PubMed]
- Dekkers, R. Group technology: Amalgamation with design of organisational structures. Int. J. Prod. Econ. 2018, 200, 262–277. [Google Scholar] [CrossRef]
- del Pozo-Antúnez, J.J.; Fernández-Navarro, F.; Molina-Sánchez, H.; Ariza-Montes, A.; Carbonero-Ruz, M. The machine-part cell formation problem with non-binary values: A milp model and a case of study in the accounting profession. Mathematics 2021, 9, 1768. [Google Scholar] [CrossRef]
- Liu, C.; Wang, J.; Leung, J.Y.T. Integrated bacteria foraging algorithm for cellular manufacturing in supply chain considering facility transfer and production planning. Appl. Soft Comput. 2018, 62, 602–618. [Google Scholar] [CrossRef]
- Rostami, A.; Paydar, M.M.; Asadi-Gangraj, E. A hybrid genetic algorithm for integrating virtual cellular manufacturing with supply chain management considering new product development. Comput. Ind. Eng. 2020, 145, 106565. [Google Scholar] [CrossRef]
- Salimpour, S.; Pourvaziri, H.; Azab, A. Semi-robust layout design for cellular manufacturing in a dynamic environment. Comput. Oper. Res. 2021, 133, 105367. [Google Scholar] [CrossRef]
- Bazaraa, M.S.; Jarvis, J.J.; Sherali, H.D. Linear Programming and Network Flows; John Wiley and Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Figueroa-Torrez, P.; Durán, O.; Crawford, B.; Cisternas-Caneo, F. A Binary Black Widow Optimization Algorithm for Addressing the Cell Formation Problem Involving Alternative Routes and Machine Reliability. Mathematics 2023, 11, 3475. [Google Scholar] [CrossRef]
- Rafiee, M.; Mohamaditalab, A. Investigation into skill leveled operators in a multi-period cellular manufacturing system with the existence of multi-functional machines. Sci. Iran. 2020, 27, 3219–3232. [Google Scholar] [CrossRef]
- Golmohammadi, A.M.; Honarvar, M.; Guangdong, G.; Hosseini-Nasab, H. A new mathematical model for integration of cell formation with machine layout and cell layout by considering alternative process routing reliability; A novel hybrid metaheuristic. Int. J. Ind. Eng. Prod. Res. 2019, 30, 405–427. [Google Scholar]
- Souier, M.; Dahane, M.; Maliki, F. An NSGA-II-based multiobjective approach for real-time routing selection in a flexible manufacturing system under uncertainty and reliability constraints. Int. J. Adv. Manuf. Technol. 2019, 100, 2813–2829. [Google Scholar] [CrossRef]
- Karoum, B.; Elbenani, Y.B. Optimization of the material handling costs and the machine reliability in cellular manufacturing system using cuckoo search algorithm. Neural Comput. Appl. 2019, 31, 3743–3757. [Google Scholar] [CrossRef]
- Karoum, B.; Elbenani, Y.B. A clonal selection algorithm for the generalized cell formation problem considering machine reliability and alternative routings. Prod. Eng. 2017, 11, 545–556. [Google Scholar] [CrossRef]
- Shirzadi, S.; Tavakkoli-Moghaddam, R.; Kia, R.; Mohammadi, M. A multi-objective imperialist competitive algorithm for integrating intra-cell layout and processing route reliability in a cellular manufacturing system. Int. J. Comput. Integr. Manuf. 2017, 30, 839–855. [Google Scholar] [CrossRef]
- Deep, K.; Singh, P.K. Dynamic cellular manufacturing system design considering alternative routing and part operation tradeoff using simulated annealing based genetic algorithm. Sādhanā 2016, 41, 1063–1079. [Google Scholar] [CrossRef]
- Sakhaii, M.; Tavakkoli-Moghaddam, R.; Bagheri, M.; Vatani, B. A robust optimization approach for an integrated dynamic cellular manufacturing system and production planning with unreliable machines. Appl. Math. Model. 2016, 40, 169–191. [Google Scholar] [CrossRef]
- Alhourani, F. Cellular manufacturing system design considering machines reliability and parts alternative process routings. Int. J. Prod. Res. 2016, 54, 846–863. [Google Scholar] [CrossRef]
- Jouzdani, J.; Barzinpour, F.; Shafia, M.A.; Fathian, M. Applying simulated annealing to a generalized cell formation problem considering alternative routings and machine reliability. Asia-Pac. J. Oper. Res. 2014, 31, 1450021. [Google Scholar] [CrossRef]
- Das, K.; Abdul-Kader, W. Consideration of dynamic changes in machine reliability and part demand: A cellular manufacturing systems design model. Int. J. Prod. Res. 2011, 49, 2123–2142. [Google Scholar] [CrossRef]
- Saxena, L.K.; Jain, P.K. Dynamic cellular manufacturing systems design—A comprehensive model. Int. J. Adv. Manuf. Technol. 2011, 53, 11–34. [Google Scholar] [CrossRef]
- Chung, S.H.; Wu, T.H.; Chang, C.C. An efficient tabu search algorithm to the cell formation problem with alternative routings and machine reliability considerations. Comput. Ind. Eng. 2011, 60, 7–15. [Google Scholar] [CrossRef]
- Safaei, N.; Tavakkoli-Moghaddam, R.; Sassani, F. A series—Parallel redundant reliability system for cellular manufacturing design. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2009, 223, 233–250. [Google Scholar] [CrossRef]
- Jabalameli, M.S.; Arkat, J.; Sakri, M.S. Applying metaheuristics in the generalized cell formation problem considering machine reliability. J. Chin. Inst. Ind. Eng. 2008, 25, 261–274. [Google Scholar] [CrossRef]
- Jabal Ameli, M.S.; Arkat, J.; Barzinpour, F. Modelling the effects of machine breakdowns in the generalized cell formation problem. Int. J. Adv. Manuf. Technol. 2008, 39, 838–850. [Google Scholar] [CrossRef]
- Saeed Jabal Ameli, M.; Arkat, J. Cell formation with alternative process routings and machine reliability consideration. Int. J. Adv. Manuf. Technol. 2008, 35, 761–768. [Google Scholar] [CrossRef]
- Das, K.; Lashkari, R.S.; Sengupta, S. Reliability consideration in the design and analysis of cellular manufacturing systems. Int. J. Prod. Econ. 2007, 105, 243–262. [Google Scholar] [CrossRef]
- Winston, W.L. Operations Research: Applications and Algorithm; Thomson Learning, Inc.: Chicago, IN, USA, 2004. [Google Scholar]
- Taha, H.A. Operations Research: An Introduction; Pearson Education India: Hoboken, NJ, USA, 2013. [Google Scholar]
- Jaccard, T.J. Étude comparative de la distribution florale dans une portion des Alpes et des Jura. Bull. Société Vaudoise Sci. Nat. 1901, 37, 547–579. [Google Scholar]
- Jourdan, L.; Basseur, M.; Talbi, E.G. Hybridizing exact methods and metaheuristics: A taxonomy. Eur. J. Oper. Res. 2009, 199, 620–629. [Google Scholar] [CrossRef]
- Gogna, A.; Tayal, A. Metaheuristics: Review and application. J. Exp. Theor. Artif. Intell. 2013, 25, 503–526. [Google Scholar] [CrossRef]
- Laumanns, M.; Thiele, L.; Zitzler, E. An efficient, adaptive parameter variation scheme for metaheuristics based on the epsilon-constraint method. Eur. J. Oper. Res. 2006, 169, 932–942. [Google Scholar] [CrossRef]
- Forrest, S. Genetic Algorithms; ACM: New York, NY, USA, 1996; pp. 77–80. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Glover, F.; Laguna, M.; Marti, R. Principles of tabu search. Approx. Algorithms Metaheuristics 2007, 23, 1–12. [Google Scholar]
- Chen, T.; Ning, Q.; Wang, H. A review of memetic algorithms. J. Bionic Eng. 2013, 10, 406–419. [Google Scholar]
- Seshadri, A. A fast elitist multiobjective genetic algorithm: NSGA-II. MATLAB Cent. 2006, 182, 182–197. [Google Scholar]
- Yang, X.S.; Deb, S. Cuckoo search via Lévy flights. In Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar]
- Enayatifar, R.; Yousefi, M.; Abdullah, A.H.; Darus, A.N. MOICA: A novel multi-objective approach based on imperialist competitive algorithm. Appl. Math. Comput. 2013, 219, 8829–8841. [Google Scholar] [CrossRef]
- Hajiaghaei-Keshteli, M.; Aminnayeri, M. Solving the integrated scheduling of production and rail transportation problem by Keshtel algorithm. Appl. Soft Comput. 2014, 25, 184–203. [Google Scholar] [CrossRef]
- Fard, A.F.; Hajiaghaei-Keshteli, M. Red Deer Algorithm (RDA); a new optimization algorithm inspired by Red Deers’ mating. In Proceedings of the International Conference on Industrial Engineering, Chelyabinsk, Russia, 19–20 May 2016; pp. 331–342. [Google Scholar]
- Hayyolalam, V.; Kazem, A.A.P. Black widow optimization algorithm: A novel meta-heuristic approach for solving engineering optimization problems. Eng. Appl. Artif. Intell. 2020, 87, 103249. [Google Scholar] [CrossRef]
- Grover, W.D.; Sack, A. High availability survivable networks: When is reducing MTTR better than adding protection capacity? In Proceedings of the 6th International Workshop on Design and Reliable Communication Networks, La Rochelle, France, 7–10 October 2007; pp. 1–7. [Google Scholar]
- Luan, F.; Li, R.; Liu, S.Q.; Tang, B.; Li, S.; Masoud, M. An improved sparrow search algorithm for solving the energy-saving flexible job shop scheduling problem. Machines 2022, 10, 847. [Google Scholar] [CrossRef]
- Chang, J.; Yu, D.; Zhou, Z.; He, W.; Zhang, L. Hierarchical reinforcement learning for multi-objective real-time flexible scheduling in a smart shop floor. Machines 2022, 10, 1195. [Google Scholar] [CrossRef]
- Ballakur, A.; Steudel, H.J. A within-cell utilization based heuristic for designing cellular manufacturing systems. Int. J. Prod. Res. 1987, 25, 639–665. [Google Scholar] [CrossRef]
- Talbi, E.G. Metaheuristics: From Design to Implementation; John Wiley and Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Du-Harpur, X.; Watt, F.; Luscombe, N.; Lynch, M. What is AI? Applications of artificial intelligence to dermatology. Br. J. Dermatol. 2020, 183, 423–430. [Google Scholar] [CrossRef] [PubMed]
- Buruk Sahin, Y.; Alpay, S. Integrated cell formation and part scheduling: A new mathematical model along with two meta-heuristics and a case study for truck industry. Sci. Iran. 2024, 31, 888–905. [Google Scholar] [CrossRef]
- Mahmoodian, V.; Jabbarzadeh, A.; Rezazadeh, H.; Barzinpour, F. A novel intelligent particle swarm optimization algorithm for solving cell formation problem. Neural Comput. Appl. 2019, 31, 801–815. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Figueroa-Torrez, P.; Durán, O.; Sellitto, M. Cell Formation Problem with Alternative Routes and Machine Reliability: Review, Analysis, and Future Developments. Systems 2024, 12, 288. https://doi.org/10.3390/systems12080288
Figueroa-Torrez P, Durán O, Sellitto M. Cell Formation Problem with Alternative Routes and Machine Reliability: Review, Analysis, and Future Developments. Systems. 2024; 12(8):288. https://doi.org/10.3390/systems12080288
Chicago/Turabian StyleFigueroa-Torrez, Paulo, Orlando Durán, and Miguel Sellitto. 2024. "Cell Formation Problem with Alternative Routes and Machine Reliability: Review, Analysis, and Future Developments" Systems 12, no. 8: 288. https://doi.org/10.3390/systems12080288
APA StyleFigueroa-Torrez, P., Durán, O., & Sellitto, M. (2024). Cell Formation Problem with Alternative Routes and Machine Reliability: Review, Analysis, and Future Developments. Systems, 12(8), 288. https://doi.org/10.3390/systems12080288








