An Integrated Optimization Framework for Connected and Automated Vehicles and Traffic Signals in Urban Networks
Abstract
:1. Introduction
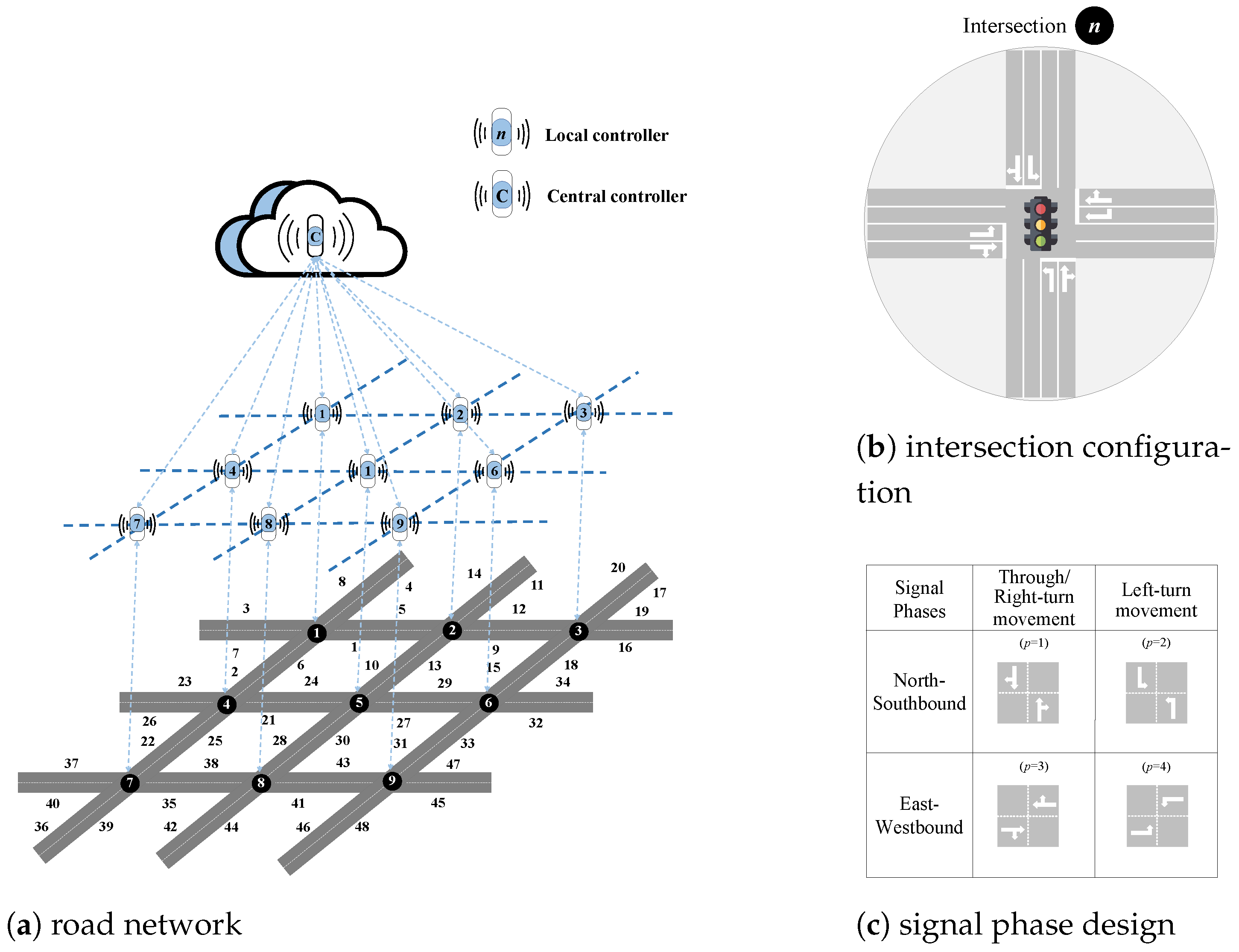
2. Problem Description
3. Model Formulation
3.1. The Route Guidance Module
3.1.1. Constraints
3.1.2. Objective Function
3.2. The Signal Optimization Module
3.2.1. Constraints
3.2.2. Objective Function
3.3. The Trajectory Planning Module
3.3.1. Control and State Variables
3.3.2. Constraints
3.3.3. Objective Function
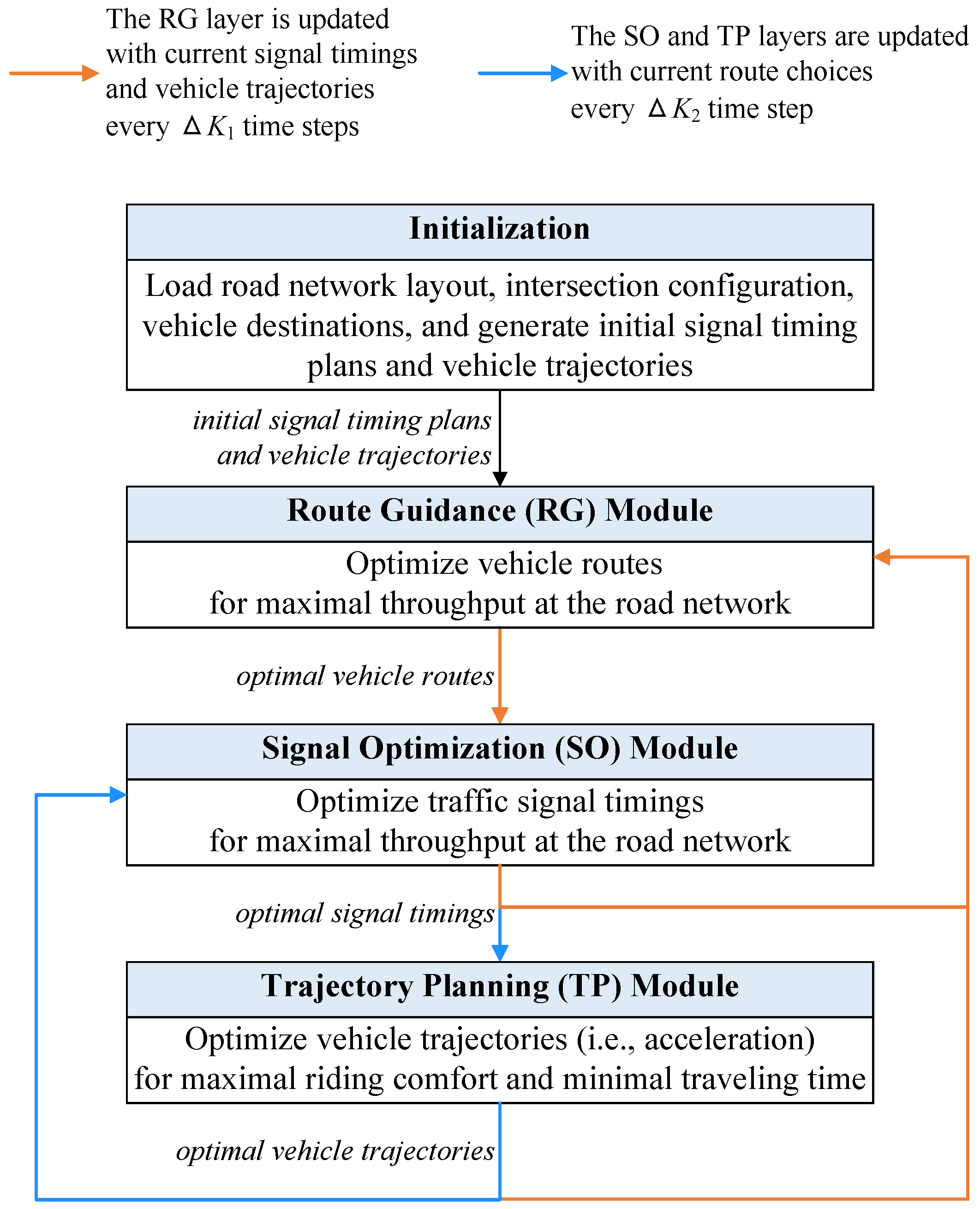
4. Solution Approach
4.1. Description of the Three-Level Framework
4.2. Dijkstra Algorithm for the Route Guidance Module
- Initialization: Set tentative link lengths for all intersections. The tentative link length of the source intersection is set to zero, while the tentative link lengths from the source intersection to other inaccessible intersections are set to infinity. Meanwhile, sort all intersections by tentative link length.
- Selection of the shortest distance intersection: The intersection with the shortest tentative link length is selected and marked as the shortest link.
- Relaxation: Calculate the lane lengths from the selected intersection to each adjacent intersection for all adjacent intersections. If the length of this link is less than the tentative link length of the adjacent intersection currently recorded, update the tentative link length of the adjacent intersection and record them by length.
- Repetition: Steps 2 and 3 are repeated until all shortest links are determined or all intersections are considered.
- Completion: The algorithm ends when all reachable intersections find their shortest routes. The shortest routes are therefore found by tracing the predecessor intersections.
4.3. Dynamic Programming for the Signal Optimization Module
| Algorithm 1 Dynamic programming to solve the signal optimization module. |
| Require: current vehicle condition and signal plan |
| Ensure: |
| for each vehicle do |
| calculate the shortest arrival time at the downstream intersection |
| identify platoons according to the space gaps |
| for each platoon do |
| record the arrival times of the leader and tail vehicles in the platoon |
| end for |
| end for |
| for each phase p do |
| initialize the signal plan using the arrival times of the leader and tail vehicles in the platoon |
| while do not satisfy all constraints of Equations (15)–(17) do |
| forward recursion |
| obtain the feasible solutions that satisfy all constraints |
| calculate the values of the objective function Equation (18) using the feasible solutions |
| backward recursion |
| retrieve the optimal solution |
| end while |
| update the signal parameters and for phase p |
| end for |
4.4. Linear Programming for the Trajectory Planning Module
4.4.1. Linearization
4.4.2. Distribution
4.5. Solution Framework
5. Simulation Results and Discussions
5.1. Experiment Design
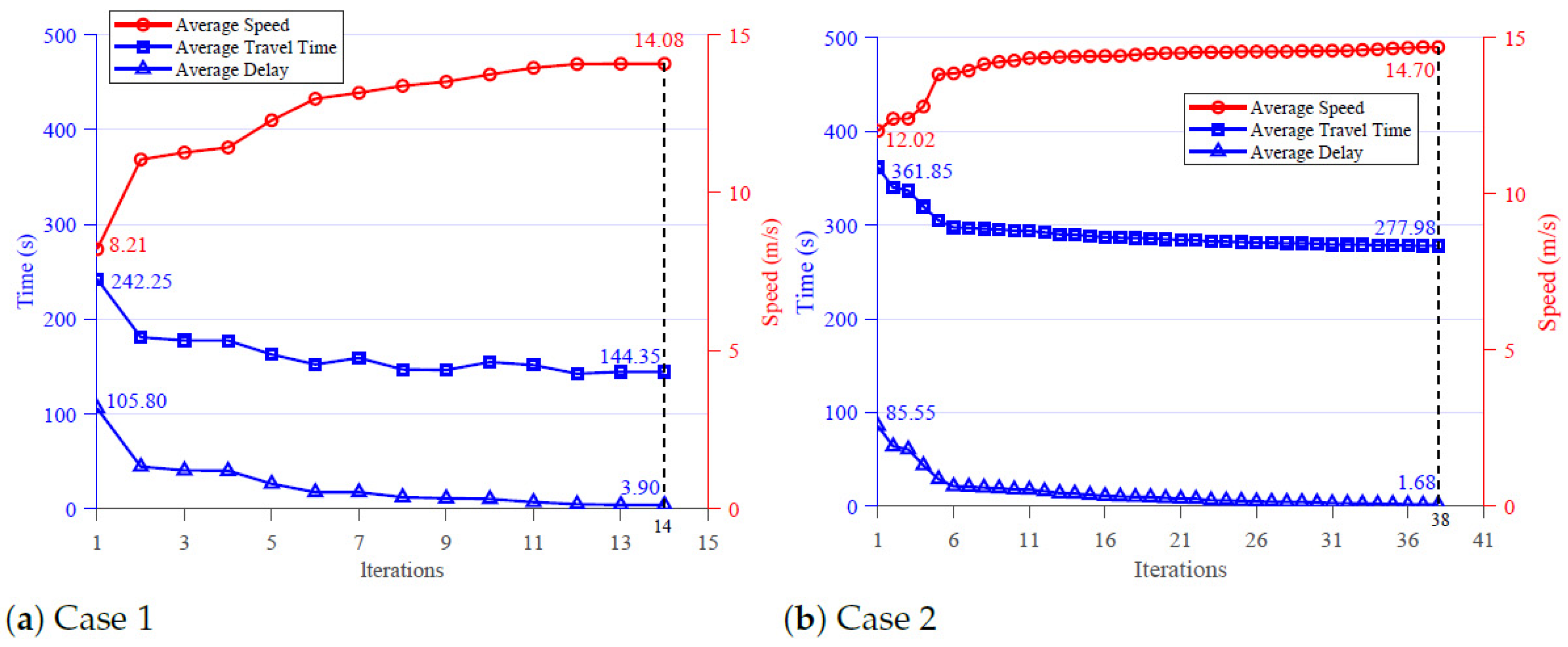
5.2. Performance Analysis
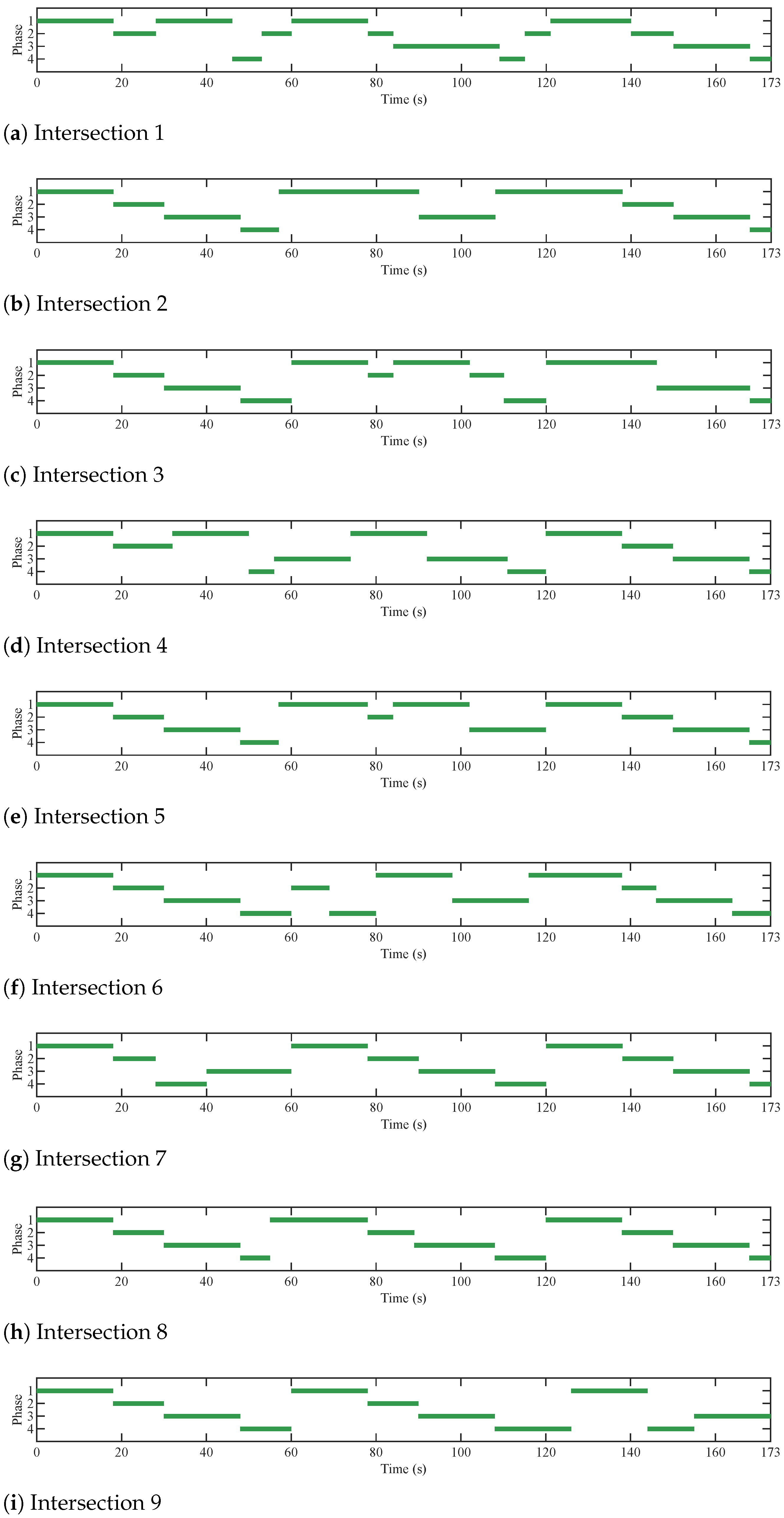
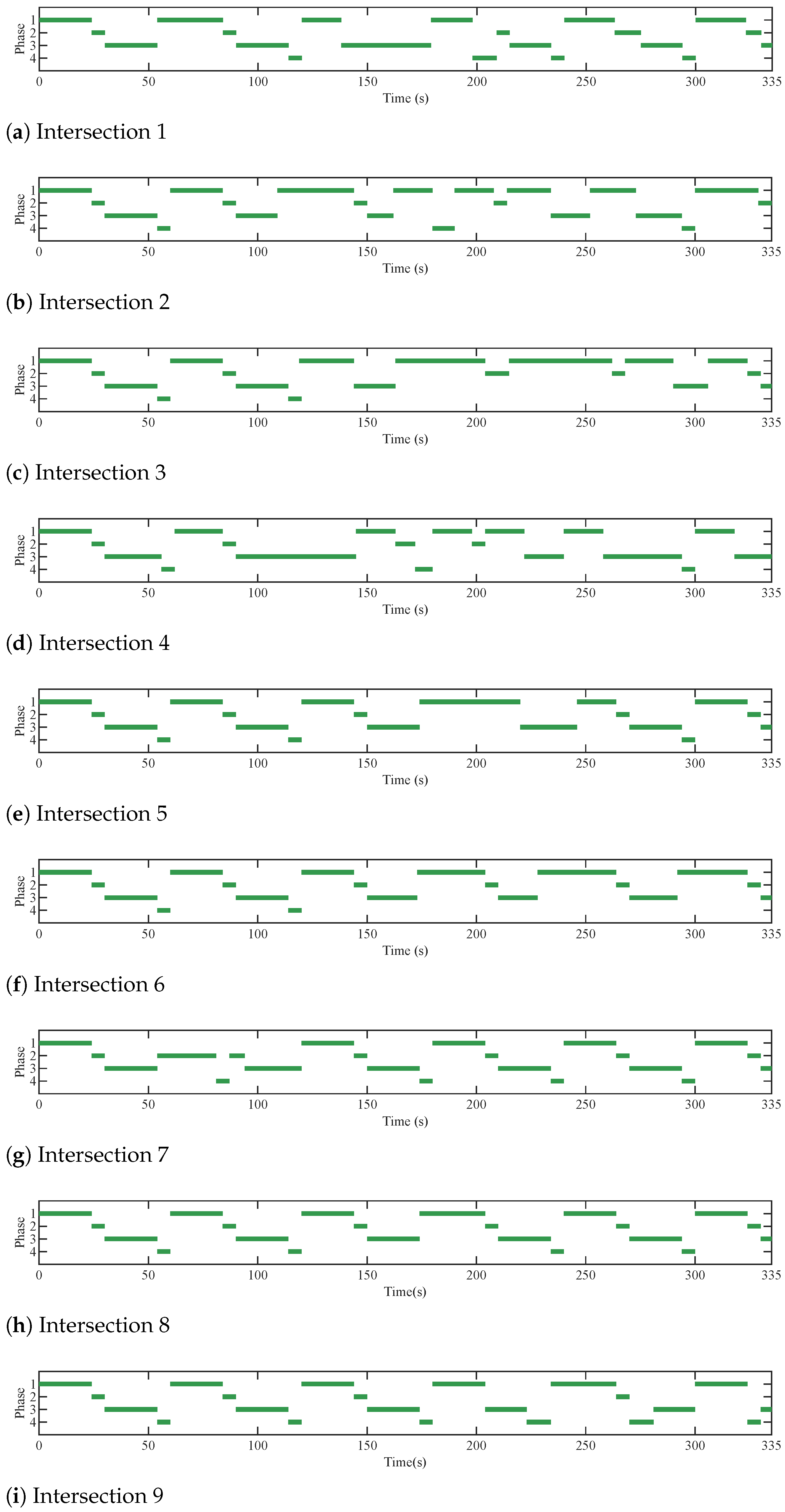
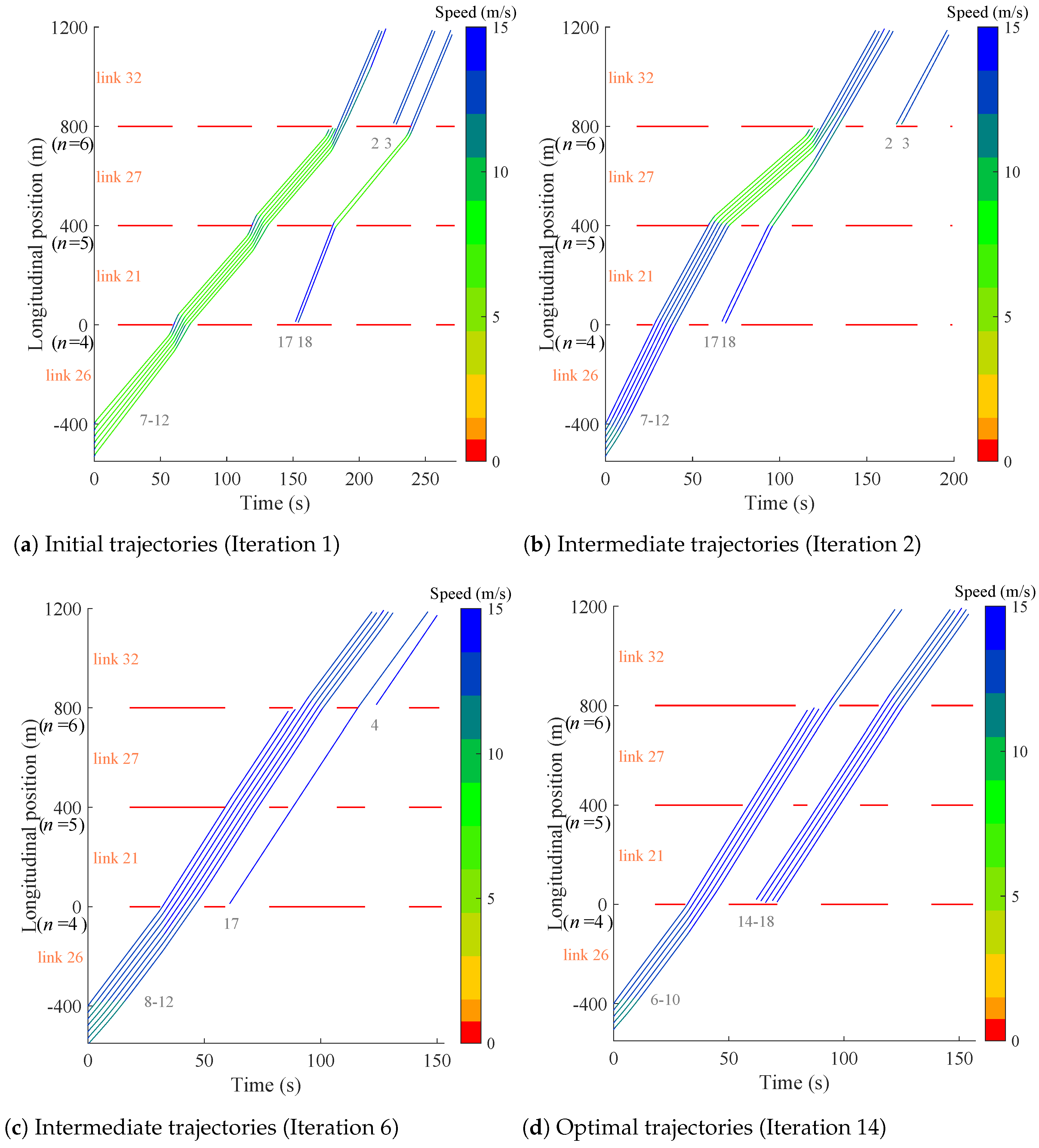
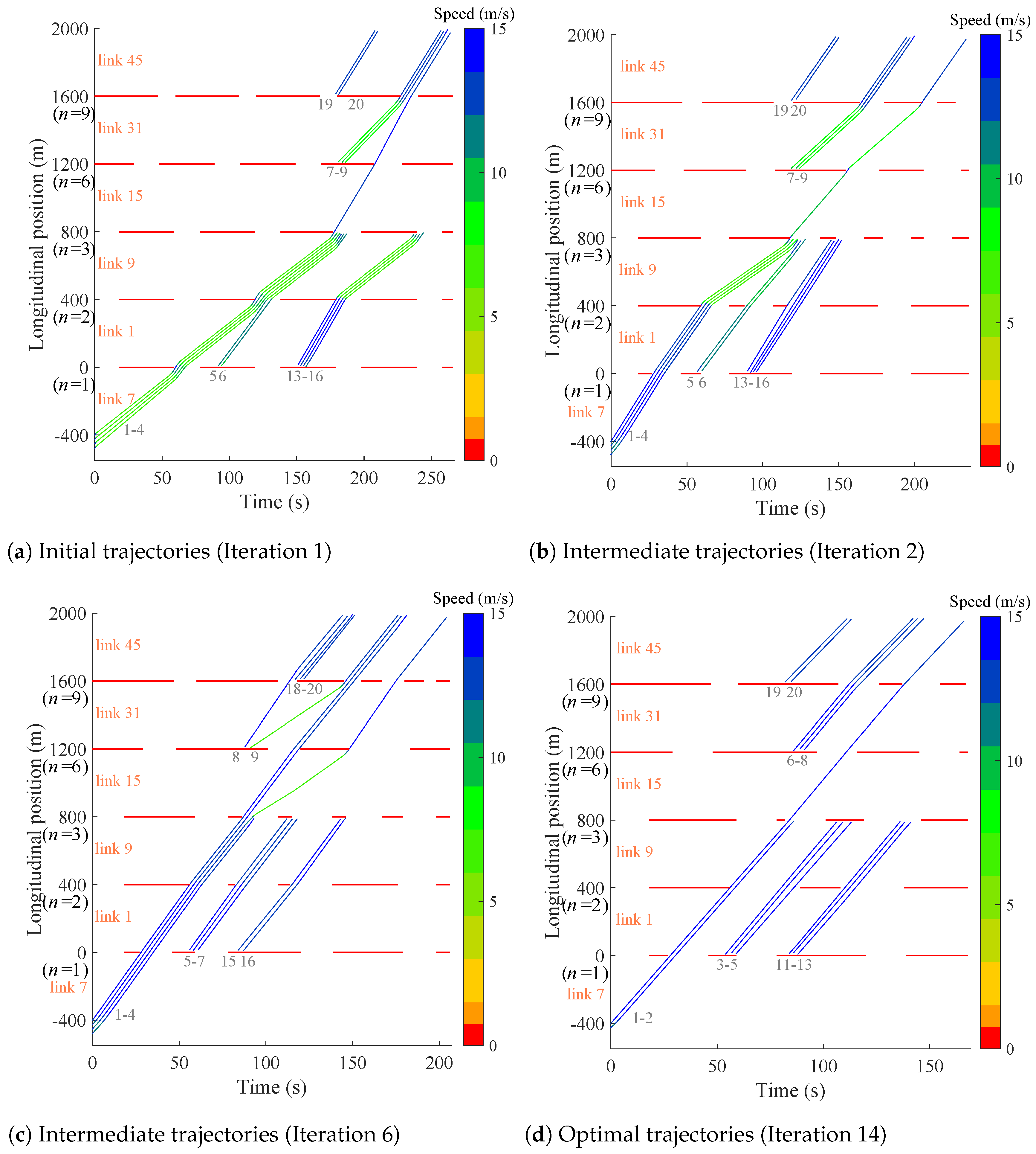
5.2.1. Operational Performance
- A.
- Route Guidance Module
- B.
- Signal Optimization Module
- C.
- Trajectory Planning Module
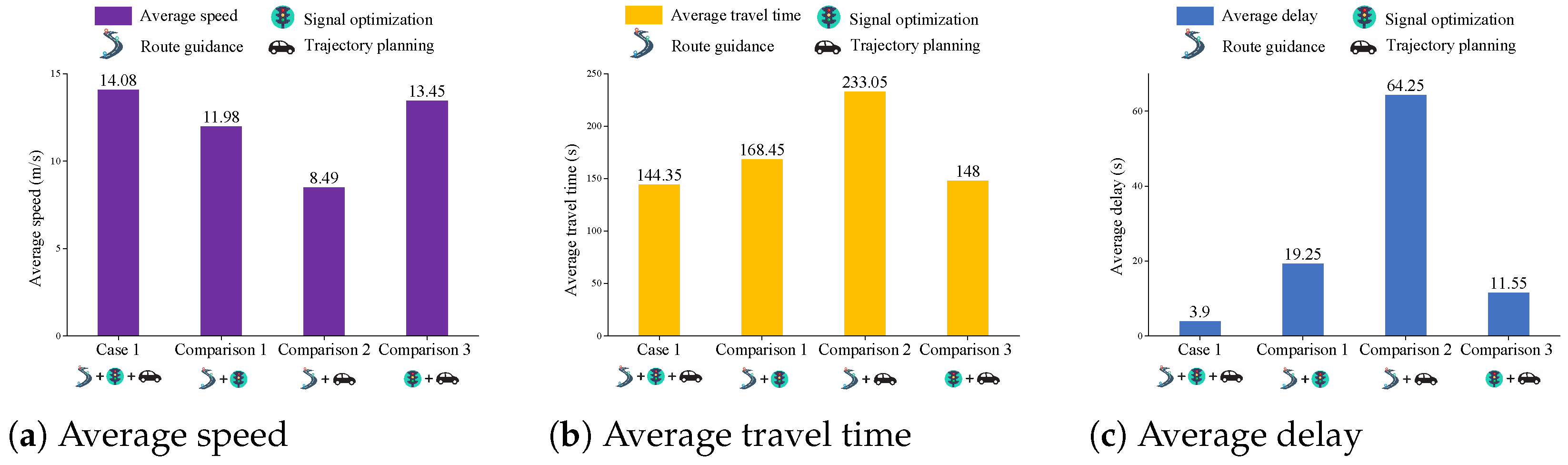
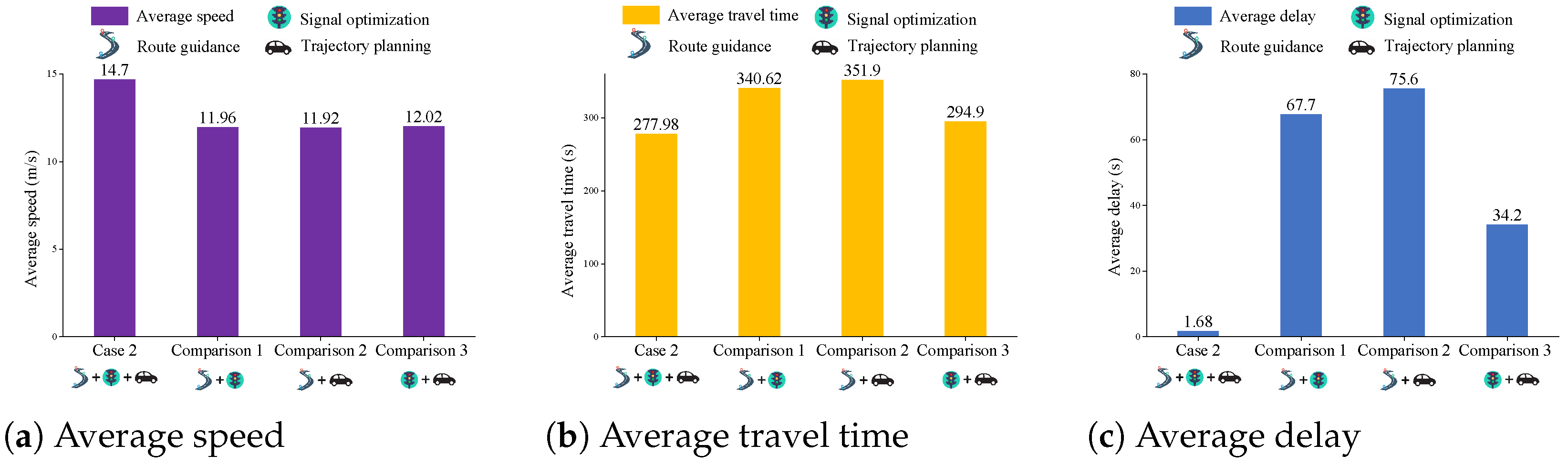
5.2.2. Comparative Performance
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, L.; Zhang, Z.; Jiang, H.; Zhou, B.; Yu, H.; Ren, Y. Deep Reinforcement Learning with Fuzzy Feature Fusion for Cooperative Control in Traffic Light and Connected Autonomous Vehicles. IEEE Trans. Fuzzy Syst. 2024, 33, 377–391. [Google Scholar] [CrossRef]
- Wolniak, R.; Gajdzik, B.; Grebski, M.; Danel, R.; Grebski, W.W. Business models used in smart cities—Theoretical approach with examples of smart cities. Smart Cities 2024, 7, 1626–1669. [Google Scholar] [CrossRef]
- Feng, Y.; Head, K.L.; Khoshmagham, S.; Zamanipour, M. A real-time adaptive signal control in a connected vehicle environment. Transp. Res. Part C Emerg. Technol. 2015, 55, 460–473. [Google Scholar] [CrossRef]
- Mohebifard, R.; Hajbabaie, A. Optimal network-level traffic signal control: A benders decomposition-based solution algorithm. Transp. Res. Part B Methodol. 2019, 121, 252–274. [Google Scholar] [CrossRef]
- Miller-Hooks, E.D.; Mahmassani, H.S. Least expected time paths in stochastic, time-varying transportation networks. Transp. Sci 2000, 34, 198–215. [Google Scholar] [CrossRef]
- Wu, X. Study on mean-standard deviation shortest path problem in stochastic and time-dependent networks: A stochastic dominance based approach. Transp. Res. Part B Methodol. 2015, 80, 275–290. [Google Scholar] [CrossRef]
- Stebbins, S.; Hickman, M.; Kim, J.; Vu, H.L. Characterising green light optimal speed advisory trajectories for platoon-based optimisation. Transp. Res. Part C Emerg. Technol. 2017, 82, 43–62. [Google Scholar] [CrossRef]
- Nguyen, C.H.; Hoang, N.H.; Lee, S.; Vu, H.L. A system optimal speed advisory framework for a network of connected and autonomous vehicles. IEEE Trans. Intell. Transp. Syst. 2021, 23, 5727–5739. [Google Scholar] [CrossRef]
- Liu, M.; Hoogendoorn, S.; Wang, M. Receding Horizon Cooperative Platoon Trajectory Planning on Corridors with Dynamic Traffic Signal. Transp. Res. Rec. 2020, 2674, 324–338. [Google Scholar] [CrossRef]
- Li, J.; Zhao, W. Trajectory Generation of Ultra-Low-Frequency Travel Routes in Large-Scale Complex Road Networks. Systems 2023, 11, 61. [Google Scholar] [CrossRef]
- Pitre, R.R.; Li, X.R.; Delbalzo, R. UAV route planning for joint search and track missions—An information-value approach. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 2551–2565. [Google Scholar] [CrossRef]
- Coutinho, W.P.; Fliege, J.; Battarra, M. Glider routing and trajectory optimisation in disaster assessment. Eur. J. Oper. Res. 2019, 274, 1138–1154. [Google Scholar] [CrossRef]
- Li, P.; Mirchandani, P.; Zhou, X. Solving simultaneous route guidance and traffic signal optimization problem using space-phase-time hypernetwork. Transp. Res. Part B Methodol. 2015, 81, 103–130. [Google Scholar] [CrossRef]
- Li, P.T.; Zhou, X. Recasting and optimizing intersection automation as a connected-and-automated-vehicle (CAV) scheduling problem: A sequential branch-and-bound search approach in phase-time-traffic hypernetwork. Transp. Res. Part B Methodol. 2017, 105, 479–506. [Google Scholar] [CrossRef]
- Chen, L.W.; Hu, T.Y. Flow equilibrium under dynamic traffic assignment and signal control—An illustration of pretimed and actuated signal control policies. IEEE Trans. Intell. Transp. Syst. 2012, 13, 1266–1276. [Google Scholar] [CrossRef]
- Liu, R.; Smith, M. Route choice and traffic signal control: A study of the stability and instability of a new dynamical model of route choice and traffic signal control. Transp. Res. Part B Methodol. 2015, 77, 123–145. [Google Scholar] [CrossRef]
- Chai, H.; Zhang, H.M.; Ghosal, D.; Chuah, C.N. Dynamic traffic routing in a network with adaptive signal control. Transp. Res. Part C Emerg. Technol. 2017, 85, 64–85. [Google Scholar] [CrossRef]
- Chen, H.; Qiu, T.Z. Distributed dynamic route guidance and signal control for mobile edge computing-enhanced connected vehicle environment. IEEE Trans. Intell. Transp. Syst. 2021, 23, 12251–12262. [Google Scholar] [CrossRef]
- Niroumand, R.; Tajalli, M.; Hajibabai, L.; Hajbabaie, A. Joint optimization of vehicle-group trajectory and signal timing: Introducing the white phase for mixed-autonomy traffic stream. Transp. Res. Part C Emerg. Technol. 2020, 116, 102659. [Google Scholar] [CrossRef]
- Yang, Z.; Feng, Y.; Liu, H.X. A cooperative driving framework for urban arterials in mixed traffic conditions. Transp. Res. Part C Emerg. Technol. 2021, 124, 102918. [Google Scholar] [CrossRef]
- Liu, M.; Zhao, J.; Hoogendoorn, S.; Wang, M. An optimal control approach of integrating traffic signals and cooperative vehicle trajectories at intersections. Transp. B 2022, 10, 971–987. [Google Scholar] [CrossRef]
- Liu, H.; Flores, C.E.; Spring, J.; Shladover, S.E.; Lu, X.Y. Field assessment of intersection performance enhanced by traffic signal optimization and vehicle trajectory planning. IEEE Trans. Intell. Transp. Syst. 2021, 23, 11549–11561. [Google Scholar] [CrossRef]
- Ma, W.; Li, J.; Yu, C. Shared-phase-dedicated-lane based intersection control with mixed traffic of human-driven vehicles and connected and automated vehicles. Transp. Res. Part C Emerg. Technol. 2022, 135, 103509. [Google Scholar] [CrossRef]
- Niroumand, R.; Hajibabai, L.; Hajbabaie, A. White phase intersection control through distributed coordination: A mobile controller paradigm in a mixed traffic stream. IEEE Trans. Intell. Transp. Syst. 2023, 24, 2993–3007. [Google Scholar] [CrossRef]
- Li, M.; Wu, X.; He, X.; Yu, G.; Wang, Y. An eco-driving system for electric vehicles with signal control under V2X environment. Transp. Res. Part C Emerg. Technol. 2018, 93, 335–350. [Google Scholar] [CrossRef]
- Dong, H.; Zhuang, W.; Chen, B.; Lu, Y.; Liu, S.; Xu, L.; Pi, D.; Yin, G. Predictive energy-efficient driving strategy design of connected electric vehicle among multiple signalized intersections. Transp. Res. Part C Emerg. Technol. 2022, 137, 103595. [Google Scholar] [CrossRef]
- Tajalli, M.; Hajbabaie, A. Distributed optimization and coordination algorithms for dynamic speed optimization of connected and autonomous vehicles in urban street networks. Transp. Res. Part C Emerg. Technol. 2018, 95, 497–515. [Google Scholar] [CrossRef]
- Tajalli, M.; Mehrabipour, M.; Hajbabaie, A. Network-level coordinated speed optimization and traffic light control for connected and automated vehicles. IEEE Trans. Intell. Transp. Syst. 2020, 22, 6748–6759. [Google Scholar] [CrossRef]
- Nguyen, C.H.; Hoang, N.H.; Vu, H.L. A joint trajectory planning and signal control framework for a network of connected and autonomous vehicles. IEEE Trans. Intell. Transp. Syst. 2023, 24, 5052–5068. [Google Scholar] [CrossRef]
- Sundarraj, S.; Reddy, R.V.K.; Basam, M.B.; Lokesh, G.H.; Flammini, F.; Natarajan, R. Route planning for an autonomous robotic vehicle employing a weight-controlled particle swarm-optimized Dijkstra algorithm. IEEE Access 2023, 11, 92433–92442. [Google Scholar] [CrossRef]
- Liu, M.; Zhao, J.; Hoogendoorn, S.; Wang, M. A single-layer approach for joint optimization of traffic signals and cooperative vehicle trajectories at isolated intersections. Transp. Res. Part C Emerg. Technol. 2022, 134, 103459. [Google Scholar] [CrossRef]

| Parameter | Description | Value (Unit) |
|---|---|---|
| Length of each link in Case 1 and 2, respectively, | 400 m, 800 m | |
| Link saturation flow rate | 1800 veh/h/ln | |
| - | Jam density | 0.3 veh/m |
| - | Lane number | 2 |
| , | Maximum green time for through or right-turn movements (p = 1, 3) at intersection n | 60 s |
| , | Minimum green time for through or right-turn movements (p = 1, 3) at intersection n | 18 s |
| , | Maximum green time for left-turn movement (p = 2, 4) at intersection n | 24 s |
| , | Minimum green time for left-turn movement (p = 2, 4) at intersection n | 6 s |
| - | Initial vehicle speed | 13 m/s |
| - | Initial space gap | 31 m |
| Vehicle length | 3 m | |
| Minimum space gap at standstill conditions | 2 m | |
| Allowable maximum acceleration | 2 m/s2 | |
| Allowable minimum acceleration | −5 m/s2 | |
| Maximum speed | 15 m/s | |
| Minimum safe car-following time gap | 2 s | |
| Cost weight | 10 s | |
| Cost weight | 1 | |
| I | Controller vehicle numbers in Cases 1 and 2 | 20, 40 |
| Vehicle Index | Initial Routes | Optimal Routes |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 | ||
| 11 | ||
| 12 | ||
| 13 | ||
| 14 | ||
| 15 | ||
| 16 | ||
| 17 | ||
| 18 | ||
| 19 | ||
| 20 |
| Vehicle Index | Iteration 29 | Iteration 31 | Optimal Routes |
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| 6 | |||
| 7 | |||
| 8 | |||
| 9 | |||
| 10 | |||
| 11 | |||
| 12 | |||
| 13 | |||
| 14 | |||
| 15 | |||
| 16 | |||
| 17 | |||
| 18 | |||
| 19 | |||
| 20 | |||
| 21 | |||
| 22 | |||
| 23 | |||
| 24 | |||
| 25 | |||
| 26 | |||
| 27 | |||
| 28 | |||
| 29 | |||
| 30 | |||
| 31 | |||
| 32 | |||
| 33 | |||
| 34 | |||
| 35 | |||
| 36 | |||
| 37 | |||
| 38 | |||
| 39 | |||
| 40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Li, Y.; Liu, X.; Chen, Y.; Hao, R. An Integrated Optimization Framework for Connected and Automated Vehicles and Traffic Signals in Urban Networks. Systems 2025, 13, 224. https://doi.org/10.3390/systems13040224
Liu M, Li Y, Liu X, Chen Y, Hao R. An Integrated Optimization Framework for Connected and Automated Vehicles and Traffic Signals in Urban Networks. Systems. 2025; 13(4):224. https://doi.org/10.3390/systems13040224
Chicago/Turabian StyleLiu, Meiqi, Yalan Li, Xiaofei Liu, Yang Chen, and Ruochen Hao. 2025. "An Integrated Optimization Framework for Connected and Automated Vehicles and Traffic Signals in Urban Networks" Systems 13, no. 4: 224. https://doi.org/10.3390/systems13040224
APA StyleLiu, M., Li, Y., Liu, X., Chen, Y., & Hao, R. (2025). An Integrated Optimization Framework for Connected and Automated Vehicles and Traffic Signals in Urban Networks. Systems, 13(4), 224. https://doi.org/10.3390/systems13040224








