Mesoscopic Monitoring of Human Skin Explants Viscoelastic Properties

Abstract

The investigation of the mechanical properties of skin is of great interest for monitoring physiological and pathological changes in the cutaneous barrier function for dermatological and cosmetic issues. Skin constitutes a complex tissue because of its multi-layered organisation. From a rheological point of view, it can be considered to be a soft tissue with viscoelastic properties. In order to characterise ex vivo mechanical properties of skin on the mesoscopic scale, a biosensor including a thickness shear mode transducer (TSM) in contact with a skin explant was used. A specific experimental set-up was developed to monitor continuously and in real-time human skin explants, including the dermis and the epidermis. These were kept alive for up to 8 days. Skin viscoelastic evolutions can be quantified with a multi-frequency impedance measurement (from 5 MHz to 45 MHz) combined with a dedicated fractional calculus model. Two relevant parameters for the non-destructive mesoscopic characterisation of skin explants were extracted: the structural parameter ${\alpha }_{app}$ and the apparent viscosity ${\eta }_{app}$. In this study, the validity of the biosensor, including repeatability and viability, was controlled. A typical signature of the viscoelastic evolutions of the different cutaneous layers was identified. Finally, monitoring was carried out on stripped explants mimicking a weakened barrier function.

1. Introduction

Skin constitutes a complex multi-layered tissue that protects the organism against physical, chemical, and biological external aggressions. This protection is referred to as the barrier function [1,2,3]. Skin also regulates body hydration and temperature through several exchange processes (water equilibrium, exogenous molecules absorption, and elimination through perspiration). Cutaneous mechanical properties are closely related to the barrier function [4], hydration [5,6,7] and external skin appearance. They depend on age, phenotype, and biological sex [8,9,10].

Knowledge about skin properties and their evolution mechanisms is essential for dermatological and cosmetic issues. Many ex vivo and in vivo macroscopic experimental tests have been carried out to characterise the mechanical properties of skin based on indentation, torsion, tension or suction [11,12,13,14,15,16,17,18]. On the mesoscopic and microscopic scales, several tomography and elastography techniques are commonly used [19,20,21,22,23,24,25,26,27,28,29]. These studies are especially relevant for dermatological diagnosis [30,31] and wound healing improvement [32,33]. The usual macroscopic scale tests focus on tissue properties, while the microscopic scale studies address cellular or molecular properties. However, it remains challenging to track mesoscopic modifications (tissue properties at the characteristic length of 1–10 µm) of the different skin layers using a suitable alternative technique to animal or clinical studies.

In this context, using three-dimensional ex vivo skin models is promising since they present the main mechanical and biological characteristics of native tissue [34,35]. As in vivo skin, their mechanical properties are related to the thickness of the layers and the interactions between the dermis and the epidermis. At the macroscopic scale, these two layers can be approximated by a viscoelastic fluid and an elastic solid, respectively [18,36,37]. On a smaller scale, both cutaneous layers exhibit specific mechanical behaviour as a result of their internal composition and structure [18,38].

The dermis is a 1–4 mm thick connective tissue. Its dominant constitutive cells are fibroblasts that synthesise the extracellular matrix. The latter is made of a fibrous structure immersed in a ground substance. The fibrous structure includes elastin and collagen, which are responsible for the elastic and tensile properties of the skin, respectively. Collagen has a high tensile strength (traction-resistance), and elastin is responsible for the ability of the skin to recoil (elasticity) [30]. Two areas can be distinguished: the reticular dermis and the papillary dermis. The first one is thick and close to the hypodermis. The second is thinner and extends into the epidermis to create a strong bond at the dermal-epidermal junction (DEJ). The epidermis is a 50 μm to 1.5 mm thick epithelial tissue. It mainly consists of keratinocytes that differentiate by migrating outward, forming several distinct sublayers. The outermost sublayer of the epidermis, the stratum corneum (SC), plays a crucial role in the skin barrier function. The keratinocytes in this upper layer are flat, anucleate, filled with keratin, and are called corneocytes. This protein content enables SC extension, while a cornified cell envelope and tight junctions (corneodesmosomes) ensure its mechanical strength. Finally, SC is covered by a hydrolipidic film containing sebum that reduces the friction coefficient at the skin surface. Epidermal homeostasis is based on the balance between cell renewal and the desquamation process.

This paper presents an ultrasonic set-up based on a thickness shear mode (TSM) quartz crystal transducer to monitor the viscoelastic properties of skin explants, consisting of human ex vivo tissue samples obtained from surgical residues, including the dermis and the epidermis. This transducer was used to study the viscoelasticity of organic and inorganic soft materials [39,40,41,42,43,44]. Moreover, measurements on thawed explants demonstrated over several hours the instrumental system ability to perform accurate monitoring of this kind of samples [45], and preliminary results on fresh skin explants have already been presented [46]. This biosensor enables continuous and non-destructive ex vivo monitoring on the mesoscopic scale. In order to target the different cutaneous layers, multi-frequency measurements were carried out.

The present study aims to validate the method and demonstrate the capability of the instrumental device to characterise the cutaneous barrier function through viscoelastic parameters on the mesoscopic scale. In total, 18 abdominal skin explants from 23-year-old to 57-year-old donors were monitored for up to 8 days. Furthermore, four stripped explants mimicking a weakened barrier function were monitored to investigate the relation between viscoelastic properties and barrier function.

2. Materials and Methods

Following the inverse problem approach, this part shows what material is studied, i.e., the ex vivo human skin explants. Then, the characterisation means are presented: what physical principle was used and how. A non-destructive technique which generates shear waves by piezoelectricity was used in the experiment. The biological conditions needed to ensure the explants survival are highlighted. Finally, the way to retrieve relevant mechanical parameters to characterise the cutaneous tissues is discussed. Monitoring the electrical impedance of the transducer/explant coupled system, combined with a dedicated rheological model based on fractional calculus, gives access to two apparent quantities: the mesoscopic structural parameter and the apparent viscosity.

2.1. Ex Vivo Skin Samples

Human skin explants were supplied by the BIO-EC Laboratory [47]. A total of 18 explants were monitored using the TSM sensor. They were prepared from the abdominoplasty of 11 female donors from 23 years old to 57 years old. After its preparation, a skin explant innately deteriorates. At the end of the monitoring, the explants viability was controlled by BIO-EC using histological assessments and was compared to an equivalent explant cultured in normal conditions. Viability criteria were based on tissue morphology and cell survival. The duration of the monitoring varied from 4 to 8 days to evaluate its influence on viability. The donor age, the duration of monitoring, and the final survival condition are summarised in

Table 1. Donor information and final survival condition of the panel of 18 skin explants. All skin explants were from female donors of phototype 1 or 2, except n°16 which was of phototype 5. The final survival condition was unknown for explants 5, 6 & 7 because of the failure of the histological test.

N° of Sample	Donor Age	Day of Histological Characterisation	Final Survival Condition
1	57	4	Quite good
2	57	6	Quite good
3	48	6	Mildly altered
4	44	4	Mildly altered
5	23	8	Unknown
6	23	4	Unknown
7	23	6	Unknown
8	45	6	Moderately altered
9	50	8	Quite altered
10	44	4	Good
11	44	6	Moderately altered
12	34	6	Altered
13	34	6	Moderately altered
14	34	6	Quite altered
15	34	6	Altered
16	36	6	Moderately altered
17	45	5	Quite good
18	40	3	Good

. The thickness of the different cutaneous layers was also measured. The 38 mm diameter cutaneous samples comprised a dermis with a thickness of 2.7 mm and an epidermis with a thickness of 35 µm with a standard deviation of 0.8 mm and 7 µm.

2.2. Weakened Barrier Function Skin Model

In addition, a skin model mimicking a weakened barrier function was studied in order to evaluate the capability of the ultrasonic monitoring set-up to sense skin surface modifications. Tape stripping involves the application of successive adhesives to remove part of the superficial skin layers in order to mimic a weakened barrier. Four explants were prepared from abdominoplasty that had been stripped five times with an adhesive tape layer [48,49,50,51]. Their final survival condition and the measurement duration are given in

Table 2. Donor information and final survival condition of the 4 stripped skin explants. S1 and S2 were from female donors of phototype 5 while S3 and S4 were from ones of phototype 1–2.

N° of Sample	Donor Age	Day of Histological Characterisation	Final Survival Condition
S1	36	6	Mildly altered
S2	36	6	Good
S3	44	4	Quite good
S4	44	6	Mildly altered

. Supplementary histological analyses based on Mowry colouration were carried out.

2.3. Experimental Set-Up for Rheological Mesoscopic Ex Vivo Skin Monitoring

Skin viscoelasticity estimation was performed by monitoring the impedance of an ultrasonic transducer generating shear waves. An AT-cut quartz substrate covered with gold electrodes (Qsense QSX-301) was used as the TSM transducer. Indeed, because of its piezoelectric properties, an electric field excitation between the electrodes generates a shear wave at odd-numbered resonant harmonics with a standing wave displacement. Its first resonance frequency occurs at 5 MHz [52,53,54]. The transducer frequency response is modified when loaded with a complex material [55]. 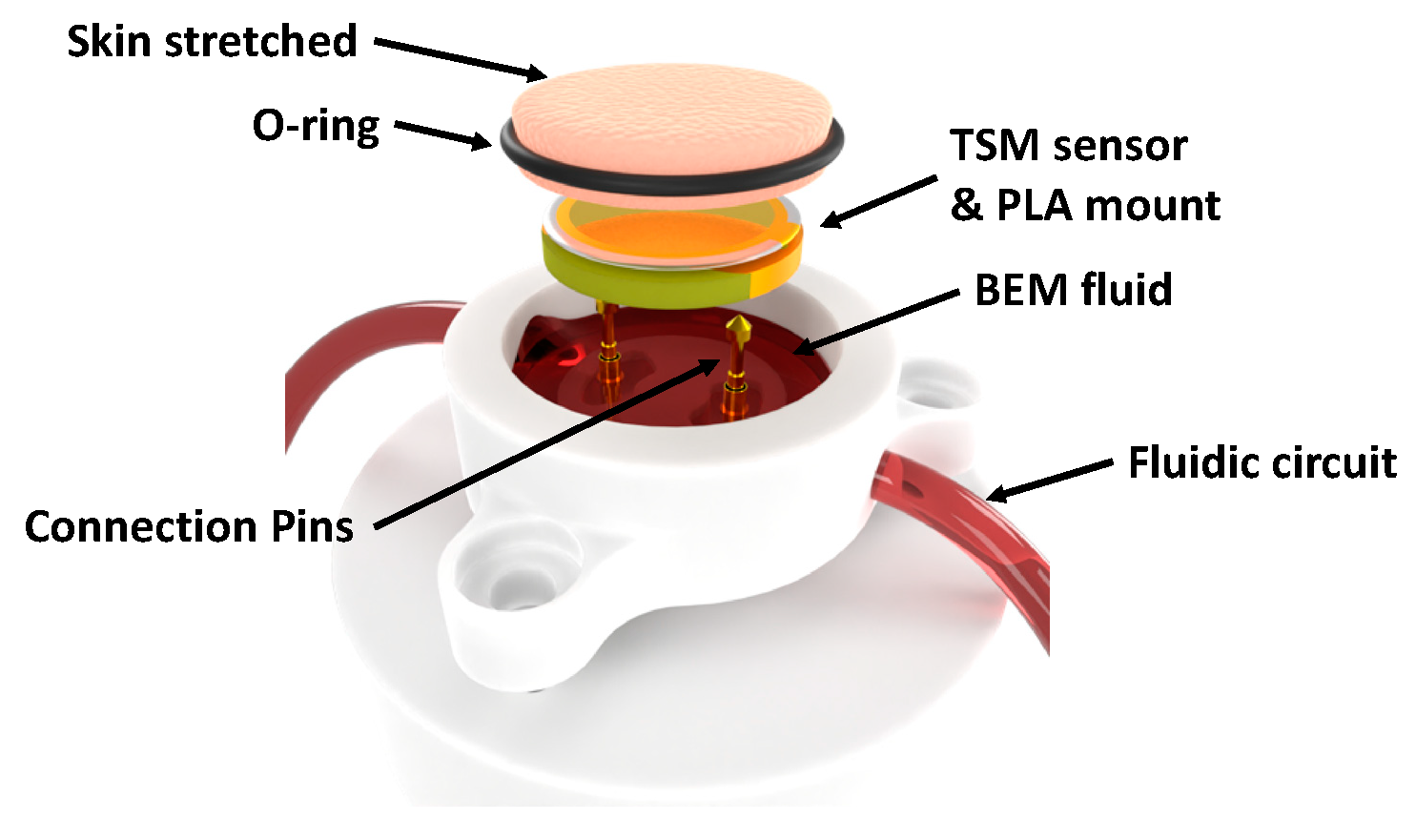In the current study, the loading material was a skin explant, whose dermis was immersed in a nutritive fluid called BIO-EC’s Explants Medium (BEM). The sample was deposited on the TSM sensor upper electrode. In order to monitor the living skin explant during the measurement, the dedicated experimental set-up required the following two conditions: close contact between the dermis and the sensor and proper irrigation of the dermis by the nutritional fluid. Therefore, the skin explant preparation on the sensor was critical. Thus, a dedicated fluidic system integrating the TSM transducer was designed to supply the explant, kept in tension, with the nutritive liquid BEM (Figure 1).

The design of the whole biosensor is presented in a dedicated article [46]. However, the following details are given to understand the experimental system better. The transducer diameter was 14 mm. The skin explant was bound to a PLA mount using a toric joint to ensure controlled tension and dermis-to-sensor contact. As the PLA mount external diameter measured 19 mm, the usable area of the cutaneous tissue was 20 mm. The fluidic circuit was connected to an external BEM tank to continuously renew the nutritive fluid in a PEEK well. The renewal was ensured by peristaltic pumps (Boxer 9000—24 V, 33 RPM, 3 rollers) with a flow of $1.5 \pm 0.1 {\mathrm{cm}}^3{·\min }^{-1}$ in “standard laboratory conditions”. As the edges of the explant soaked in BEM, the entire dermis was supplied by capillarity. The fluidic system and the external BEM tanks were introduced inside a controlled atmosphere incubator (Binder CB170) whose temperature, CO₂ and humidity were fixed at 37 °C, 5%, and 80%, respectively. Special attention was paid to keeping the environment sterile. Finally, all materials were biocompatible (PLA, PEEK, polydimethylsiloxane seals).

2.4. Viscoelastic Parameters Measurements

An impedance analyser (Keysight E5061B) controlled the excitation wave and measured the TSM sensor response near the harmonic resonances by reflectometry. In order to perform a multi-scale characterisation, measurements were carried out at the first five harmonics (near 5, 15, 25, 35 and 45 MHz). According to the constitutive equations and the boundary conditions, the sensor can be modelled by two electrical models. The three-port Mason’s transmission line describes the ultrasonic propagation effects, while a lumped element circuit (modified Butterworth-Van-Dyke, BVD) gives the impedance response near the resonance frequencies [55,56]. Conforming to these two models, an impedance analysis of the loaded sensor enabled the computation of the complex fluid viscoelasticity (e.g., due to chemical cross-linking), the fluid viscosity and the mass effect of a liquid or a rigid layer [57,58,59,60,61]. As the BEM fluid is a low-viscous liquid, the load was assimilated to a bilayer medium made of the BEM and the skin explant in contact with the TSM. Therefore, two additional impedances were added in series in the motional branch: one for the BEM ($Z_{BEM}$) and one for the skin explant, including the dermis and the epidermis ($Z_{skin}$) (Figure 2) [62,63]. The lumped elements of the modified BVD model are presented in Figure 2, and the TSM parameters and electrical components are summarised in

Table 3. BVD Lumped elements and intrinsic characteristics of unloaded TSM sensor [55,56].

TSM Parameters and Electrical Components	Typical Value	Description
${\epsilon }_q$	3.982 × 10−20 A2·s4·g−1·cm−3	Permittivity of quartz
${\eta }_q$	3.5 × 10−3 g·s−1·cm−1	Viscosity of quartz
${\mu }_q$	2.947 × 1012 Pa	Shear elastic constant of quartz
${\rho }_q$	2.651 × g·cm−3	Quartz density
$K_0^2$	≈8 × 10−3	Electromechanical coupling factor
$R_0$	10 × kΩ	Static equivalent resistance at 5 MHz
$C_0$	4 × pF	Static equivalent capacitance at 5 MHz
$R_1$	10 × Ω	Motional equivalent resistance at 5 MHz
$L_1$	30 × mH	Motional equivalent inductance at 5 MHz
$C_1$	10 × fF	Motional equivalent capacitance at 5 MHz

.

From a mechanical point of view, these two additional impedances are related to the mechanical impedance ($Z_m$) changes in each layer of the skin, including the nutritional liquid effects at the surface of the TSM sensor ($Z_{BEM}$). These changes impact the shear wave propagation. Under linear conditions (small deformations) and according to the viscoelastic constitutive laws, the mechanical impedance, in which real and imaginary parts are denoted $R\left(\omega \right)$ and $X\left(\omega \right)$, respectively, can be expressed as in Equation (1) [64].

$$Z_m\left(\omega \right)=R\left(\omega \right)+jX\left(\omega \right)=\sqrt{\rho G^{*}\left(\omega \right)},$$

(1)

where $\rho$ is the density of the loaded material and $j=\sqrt{-1}$. $G^{*}$ is the complex shear modulus at the resonant frequency of $\omega /2\pi$. It is representative of the behaviour (mechanical stress $\tilde{\sigma }$) of the loaded material at a given harmonic frequency when the latter is subjected to a strain $\tilde{\gamma }$, as shown in Equation (2).

$$\tilde{\sigma }\left(t,\omega \right)=G^{*}\left(\omega \right) \tilde{\gamma }\left(t,\omega \right).$$

(2)

A multifrequency study can then give access to a multi-scale characterisation.

2.5. A Mesoscopic Model for Rheological Skin Explant Characterisation

In order to take into account the complexity of the dermis and the epidermis, their mesoscopic mechanical behaviour can be optimally modelled through rheological equations by incorporating the fractional derivative element referred to as the spring-pot model [65]. The skin is then seen as a non-Newtonian complex fluid described by a non-linear frequency-dependent power law (Equation (3)). This behaviour introduces two suitable independent apparent parameters related to viscoelastic changes on the investigated scale:

$$G^{*}\left(\omega \right)={\eta }_0{\tau }^{{\alpha }_{app}-1}{\left(j\omega \right)}^{{\alpha }_{app}}={\eta }_{app}{\left(j\omega \right)}^{{\alpha }_{app}}.$$

(3)

The quasi-static viscosity ${\eta }_0$ and the relaxation time constant $\tau$ on the investigated scale defines the apparent dynamic viscosity ${\eta }_{app}$. It represents the resistance to deformation of the characteristic probed volume, in other words, its “thickness”. As explained in the introduction, skin constitutes a complex tissue because of its multi-layered organisation. From a mechanical point of view, it is made of more or less solid elements, , including the dermis 3D fibrous network and the epidermis keratin, as well as fluid elements such as the ground substance of the dermis. The power law parameter ${\alpha }_{app}$ depends on the cross-linking state of the internal structure on the investigated scale. According to the spring-pot dynamic constitutive relationships, the structural parameter ${\alpha }_{app}$ is null in the case of a pure elastic medium (solid state), equal to 1 for a Newtonian fluid [39,66,67,68], and comprised between 0 and 1 for complex fluids, polymers, and gels [39,69,70]. Since the dermis is the majority layer of skin explants and can be seen as a viscoelastic fluid [26], the parameter ${\alpha }_{app}$ of skin explants should be between 0 and 1.

Assuming that a shear wave can be locally approximated by a uniform plane wave when it propagates into the skin [71], the complex propagation constant $k^{*}\left(\omega \right)$ is connected to the complex shear modulus $G^{*}$ as follows [68,72,73]:

$$k^{*}\left(\omega \right)=k^{\prime }\left(\omega \right)-j{k}^{″}\left(\omega \right)={\omega }^{{\alpha }_{app}}{\left(\frac{\rho }{G^{*}}\right)}^{\frac{1}{2}},$$

(4)

where $k^{\prime }\left(\omega \right)$ and $k^{″}\left(\omega \right)$ are the phase constant and the attenuation constant of the propagating shear wave, respectively. Considering the skin explant as a complex fluid, the wavelength $\lambda$ of a shear wave can be approximated by:

$$\lambda =\frac{2\pi }{k^{\prime }\left(\omega \right)}\approx 2\pi \sqrt{\frac{{\eta }_{app}}{\rho {\omega }^{{\alpha }_{app}}}}.$$

(5)

Given a significant wavelength regarding the characteristic size of the compounds of interest, the complex shear modulus, ${\alpha }_{app}$ and ${\eta }_{app}$ can be easily calculated from the added mechanical impedance of the TSM sensor in contact with the skin. Indeed, the investigation scale is determined by the wavelength, and is related to the operating frequency. Here, the skin is probed on the mesoscopic scale because of the ultrasonic operating range. Using Equations (1) and (3), skin changes can be monitored from Equation (6):

$$Z_m\left(\omega \right)=\sqrt{\rho {\eta }_{app}{\omega }^{{\alpha }_{app}}} e^{j\frac{\pi }{4}{\alpha }_{app}},$$

(6)

Finally, the complex shear modulus $G^{*}$ can be separated in Equations (7) and (8).

$$G^{\prime }\left(\omega \right)={\eta }_{app}{\omega }^{{\alpha }_{app}}\cos \left(\frac{\pi }{2}{\alpha }_{app}\right),$$

(7)

$$G^{″}\left(\omega \right)={\eta }_{app}{\omega }^{{\alpha }_{app}}\sin \left(\frac{\pi }{2}{\alpha }_{app}\right).$$

(8)

3. Results and Discussion

This section validates the experimental methodology by testing the measurement reproducibility, repeatability, and representativeness. The results for a Newtonian liquid are compared to monitoring curves for cutaneous tissue. In addition, the ability of the biosensor to distinguish the behaviour of the dermis and the whole tissue based on wave penetration is discussed. From these validations, the results are discussed with regard to how the sensor response explains biological phenomena on the mesoscopic scale: the impact of the sample age and condition, including skin barrier impairment.

3.1. Nutritional Liquid Mechanical Characterisation

It is necessary to evaluate the repeatability and the reproducibility of the experimental set-up for standard products such as Newtonian fluids to prove the validity of the methodology. The nutritive fluid used to ensure the explant survival is supposed to be one of this kind.

In order to extract $Z_{BEM}$, the TSM sensor was only loaded with the nutritive fluid in the first step. Before positioning each skin explant, the BEM mechanical impedance was measured for a few hours. From Equations (1) and (3), the structure parameter ${\alpha }_{app}$ was calculated at each harmonic frequency. The statistical study of the real ($R$) and imaginary ($X$) parts of $Z_{BEM}$, as well as ${\alpha }_{app}$, was performed from the time evolution of the 18 measurements [74].

Table 4. Statistical mean and standard deviation (SD) values of measured mechanical impedance for BEM loading. The values are averaged over 18 measurements.

Frequency (MHz)	R (Pa·s·m−1)		X (Pa·s·m−1)		αapp
	Mean	SD	Mean	SD	Mean	SD
5	3364	170	3356	167	0.994	0.014
15	5388	270	5390	270	0.997	0.008
25	8812	440	8814	440	0.998	0.004
35	11,681	580	11,680	584	0.998	0.004
45	14,746	740	14,741	737	0.999	0.002

presents a synthesis at each probed frequency.

As expected with Equation (3), the real and imaginary parts of the complex shear modulus increase as a function of the probed frequencies. Considering the standard deviation, the real and the imaginary parts of the mechanical impedance were equal within 5% of each other. In addition, the statistical average of the BEM structure parameter ${\alpha }_{app}$ robustly converged to 1. The relative error is principally due to the surface rugosity of the TSM transducer and the induced mass effect [61,75,76,77]. These results confirm that the BEM can be considered to be a stable Newtonian liquid. Furthermore, the repeatability and consistency of the measurement should also enable the differentiation of the rheological evolution of skin from BEM one. Assuming the bilayer condition, $Z_{BEM}$will be considered constant during the skin explant monitoring.

3.2. Typical Kinetic of Ex Vivo Skin Explants on a Mesoscopic Scale

A second step of validation was to check that the measurements are different for a complex material from those of a Newtonian fluid and are consistent with the expected material behaviour.

Following the nutritive liquid characterisation, the skin explants viscoelastic evolution on the mesoscopic scale can be measured. The final survival condition assessed by histology is given in Table 1. The viability quality of explants kept alive in the measurement apparatus up to 4 days is comparable to the equivalent explants grown in normal tissue culture conditions. From 4 days of survival, the alterations are slightly more pronounced when the explants are on the sensor. However, the viability was still satisfactory for the explants monitored for up to 6 days of measurement.

A multilayer characterisation of the skin explant was proposed using the multifrequency analysis [44]. In order to study the structural parameter ${\alpha }_{app}$ and the apparent viscosity ${\eta }_{app}$ on the corresponding mesoscopic investigation scales, monitoring was performed from 5 to 45 MHz harmonics. For all skin explants, similar signatures were obtained. The kinetic evolutions of ${\alpha }_{app}$and ${\eta }_{app}$ are presented in Figure 3 for the explants 9 and 15 of Table 1. These two samples were prepared from donors of 50 and 34 years old, respectively, and are representative of all the samples.

The structural parameter ${\alpha }_{app}$ and the apparent viscosity ${\eta }_{app}$ decrease and increase over time for all frequencies, respectively. These evolutions are consistent with the rigidification of the explants and the thickening of the epidermis during survival. Two phases can be identified. At the beginning of monitoring, for about one day for the 34-year-old sample and half a day for the 50-year-old sample, there was a substantial decrease of ${\alpha }_{app}$ while ${\eta }_{app}$ increased significantly. Since the explants were tensioned, in contact with the sensor and a nutritive fluid, and inside a moisture-saturated environment, their viscoelastic properties were strongly modified. After this adaptation phase, in the case of the 34-year-old sample, both parameters continued to evolve, with a slower slope, linearly and with the same direction of change. This corresponds to the normal survival and degradation phase of the explant. These evolutions are observed at all frequencies, suggesting an overall dehydration process in the different cutaneous layers. For the 50-year-old sample, similar conclusions can be drawn for the first frequency, while upper harmonics remain stable after the adaptation phase. This observation can be explained by wave penetration, which will be detailed in Section 3.3.

Regarding the absolute values, both apparent mesoscopic parameters exhibit different values as a function of donor age and frequency (e.g., investigation scale). The structural parameter and the apparent viscosity were lower and higher, respectively, for the 34-year-old sample than for the 50-year-old one. The evolutions of these parameters were similar for all frequencies, even if the amplitudes are different. ${\alpha }_{app}$ rises by 0.25 while ${\eta }_{app}$ drops by 1 mPa·s at 5 MHz. This observation was also made, to a lesser extent, for other frequencies.

It is also possible to monitor the complex shear modulus on the mesoscopic scale using Equations (7) and (8). The complex shear modulus real part $G^{\prime }$ and imaginary part $G^{″}$ are given in Figure 4 for the same samples.

On the investigated scales, $G^{\prime }$ and $G^{″}$ had the same order of magnitude. There was a more substantial growth for $G^{\prime }$ and $G^{″}$ from the third day of monitoring (Figure 4a) of the 34-year-old sample. A slope change around the third day could also be observed for this sample in Figure 3. This phenomenon seems to be related to premature stiffening (generally announcing a prompt expiry of the explant life).

3.3. Wavelength and Investigation Scale

Since the measurements were carried out at the first five harmonics of the TSM sensor, a multifrequency study was possible, and each harmonic gave access to a different characterisation volume. In order to interpret the rheological measurements on the skin explants, regarding the biological changes in the dermis and the epidermis, the typical wavelength $\lambda$ can be calculated using Equation (5) and compared to the typical dermis thickness. The latter reaches 2.7 ± 1.0 mm with a confidence interval of 97.5% according to the histological characterisation carried out by BIO-EC after each study.

The penetration lengths that were computed for each shear wave frequency are given Figure 5. A time frame from day 1 to day 3 was used so that the wavelength is representative of the natural skin living condition (the adaptation phase was thus excluded and, according to Table 1, a good condition of the explants was ensured).

The deepest shear wave penetration occurred at 5 MHz for all donor ages. In addition, the shear wave wavelength decreased as a function of the donor’s age. The probability that the most superficial layers were included is thus higher for skin under 40 years old. For these samples, waves can generally reach the papillary dermis and the epidermal layer if the dermis does not exceed 1.8 mm. In contrast, in the case of the highest harmonics (from 15 to 45 MHz) only the reticular dermis can be studied as $\lambda$ < 1 mm, regardless of age.

In conclusion, the multi-frequency analysis makes it possible to study the skin explants independently on different scales: either a volume limited to the reticular dermis with the highest harmonics (from 15 to 45 MHz), or a volume that can reach the and includes the papillary dermis at least, at 5 MHz.

3.4. Mesoscopic Apparent Rheology and Structural Age-Related Changes

As the experimental device is sensitive to explant natural degradation and can distinguish the evolution of the dermis from the whole tissue, the following discussion deals with the impact of skin structural changes on mesoscopic apparent rheological parameters.

Human skin ageing is a complex biological phenomenon involving two kinds of processes. Intrinsic ageing is genetically determined, and is chronological. Extrinsic ageing is related to environmental influence, mainly ultraviolet radiation from sun exposure, pollution and smoking [79,80,81,82]. In the epidermis, cutaneous ageing leads to a modification of the cells shape and size and a change in the lipidic content [83,84,85]. The barrier function is consequently altered. In the dermis, fibroblasts tend to atrophy and the extracellular matrix is remodelled, implying a degradation of both collagen and elastin. Moreover, the dermal-epidermal junction (DEJ) flattens, reducing the surface between the dermis and epidermis because of the degradation of the fibre network [86]. The DEJ structural integrity and mechanical stability are affected, impeding the transfer of nutrients from the dermis to the epidermis. However, modifications in the lipidic content may be compensated by SC flattening [84,85,86]. Finally, a decreased epidermis hydration occurs because of reduced water movement from the dermis to the epidermis. Depending on the anatomic site, there can be a slight decrease in the trans-epidermal loss, a parameter often assessed to evaluate the barrier function. The modification of water transport in the epidermis is linked to a reduced hyaluronan concentration (HA) and an abnormal glycosaminoglycan (GAG) content. These two molecules are indeed implied in the retention of water [87,88].

From a rheological point of view, skin ageing is correlated to a global loss of skin elasticity and structural degradation [8,29,89,90]. The loss of elasticity and global moisture can be monitored separately in the reticular and papillary dermis with the multifrequency analysis of ${\alpha }_{app}$and ${\eta }_{app}$. The structural parameter ${\alpha }_{app}$ and the apparent viscosity ${\eta }_{app}$ averaged on a time frame between day 1 to day 3 are presented as a function of age for all probed frequencies in Figure 6.

According to Figure 6a, for upper harmonics, the value of the structural parameter is around 0.7 to 0.75. This value agrees with Zimm’s theory and with the ultrasonic studies that were carried out on gels [39,91]. Thus, the dominant component of the dermis, seen on the mesoscopic scale, seems to be the ground substance. Consequently, the very low values for skin samples under 40 years old at 5 MHz (${\alpha }_{app}$ from 0.3 to 0.5) are consistent with a well-structured elastin and collagen fibres network providing skin strength and elasticity. In addition, ${\alpha }_{app}$ increases as a function of the donor’s age. The dermis fibres network degradation and the DEJ flattening that both arise with cutaneous ageing can explain this observation.

Regarding the apparent viscosity (Figure 6b), there is a strong decrease of ${\eta }_{app}$ as a function of age (from 7 mPa.s to 1 mPa.s at 5 MHz). This evolution can be related to two effects. On the one hand, the degradation of the elastic fibre network in the dermis, related to cutaneous ageing, leads to an increase in the apparent fluid content mobility. The lower values of ${\eta }_{app}$ (approximately 1.2 mPa·s) measured for frequencies from 15 to 45 MHz are consistent with the high-water content in the dermis [92]. On the other hand, the SC higher dryness and the decreased TEWL imply a water retention phenomenon in the reticular dermis. The exponential decay of ${\eta }_{app}$ at 5 MHz suggests that the technique can sense SC barrier function modification related to ageing, which occurs here at around 40 years old.

3.5. Barrier Function Monitoring

Since the biosensor seems to sense the skin structural changes, the question is whether it is sensitive to skin surface modification. Removal of the SC superficial layers leads to an impairment of the barrier function [51,93]. Stripped skin explants from 2 donors (a 36-year-old with phototype 5 donor and a 44-year-old with phototype 1–2 donor) were studied to confirm the relation between the cutaneous barrier function and the viscoelastic properties. This study also aims to validate the ability of mesoscopic rheology to monitor SC barrier function modifications. For 36-year-old abdominoplasty, the experiment consisted of 6-day-long rheological monitoring of tape-stripped skin explants, compared to a non-stripped one (noted “C.”). For 44-year-old abdominoplasty, one of the explants was removed on the fourth day of measurement to check its viability.

The structural parameter and apparent viscosity evolutions of stripped explants compared to a non-stripped control explant are given in Figure 7. Only the measurement at 5 and 45 MHz are presented so that the viscoelastic properties can be discussed on a scale located in the dermis and a scale taking into account all the cutaneous layers, respectively. It shows the effects of weakened barrier function on structural and viscoelastic evolutions on the mesoscopic scale.

For the 36-year-old sample (Figure 7a), the ${\alpha }_{app}$ value at 5 MHz is higher for the stripped explants than for the control (0.5 for S2 vs. 0.35 for the control at day 3). This result highlights the importance of the SC in the mechanical integrity of the epidermal layer. The result for skin explants prepared from an older donor (Figure 7c) is different as a low ${\alpha }_{app}$ value has been measured at 5 MHz regardless of the SC layer integrity. A poor hydration condition for those explants could be the reason. It would agree with well-known effects: an initial well-hydrated SC increases the skin flexibility, while lower hydration and thickness variations due to intrinsic cutaneous ageing lead to a very stiff layer [84,94].

Regarding kinetics, there is a more substantial decrease in ${\alpha }_{app}$ during the monitoring for stripped explants than for the controls. This evolution confirms a continuous stiffening process due to the water loss of the explant. For the 36-year-old samples at 5 MHz, the slopes of ${\eta }_{app}$ are more pronounced after the third day of monitoring (more so for S1 and less so for S2). For the 44-year-old samples (S3 and S4), the slope growths occur whether focusing on the dermis (45 MHz) or on the whole skin (5 MHz). Especially for S4 at 45 MHz, this starts from the beginning of the monitoring. The accelerated explant degradation related to the stripping occurs first at the epidermis level and then at the dermis level. This gradual degradation makes sense because the monitored explant is irrigated with the nutritional liquid from the dermis. Depending on the initial hydration and barrier function quality, the explants degradation can be prematurely accelerated. In this case, the apparent viscosity drastically increases due to the rapid dehydration and the resulting stiffening of the epidermis. This result agrees with the histological viability results, which highlight an altered final skin.

In addition to the viability reported in Table 2, a Mowry staining method analysis showed that the glycosaminoglycan level in the dermis is lower for stripped explants than for the control. Since glycosaminoglycans are involved in water retention in the dermis layer, these results are consistent with the fact that tape-stripping induces a more significant water loss.

4. Conclusions

The viscoelastic properties of skin explants were successfully characterised by a real-time and non-destructive technique based on a TSM ultrasonic transducer. The repeatability of the sensor was checked using the measurement on the nutritive fluid. Even if explants have been monitored for up to 8 days, the viability seems to be satisfactory for up to 6 days. Then, human skin explants can be kept alive and monitored for up to 8 days. An appropriate fractional derivative model and a multi-frequency analysis were used to characterise the mesoscopic viscoelastic behaviour of both the dermis and the epidermis during the lifetime of ex vivo skin explants. By carrying out a multi-frequency monitoring of skin explants using the TSM sensor, it was thus possible to interpret the structural evolutions at the level of the different cutaneous skin layers. The study on 22 skin explants from donors between 23 and 57 years old and its validation with various previous skin studies proved the relevance of the two following mesoscopic parameters: the mesoscopic structural parameter ${\alpha }_{app}$ and apparent viscosity ${\eta }_{app}$. Using their kinetics, it becomes possible to carry out non-destructive monitoring of the loss of the fibre network in the dermis, hydration and the impact of the SC barrier function. However, developing such a multi-frequency measurement set-up requires maintaining the skin explant in constant tension and ensuring adequate contact with the transducer to preserve a steady supply of BEM. More reliable results could be obtained using reconstructed skin with controlled biological variability, such as known layer thicknesses, and by improving the experimental device. For instance, the skin tension must be better controlled.

In the future, the practical usefulness of this system is to gather qualitative and quantitative information regarding human skin water balance. Consequently, this non-destructive ex vivo technique is a promising tool for the assessment of the mechanical properties of skin as an alternative to animal or clinical studies. It could help for research regarding product-to-skin interactions for safety and efficacy testing. It would be particularly interesting to measure the effect of ingredients acting on mechanical properties (caffeine, retinoic derivatives, moisturizers, etc.). With regard to the efficiency of the technique to characterise complex materials, a study of reconstructed skin with known layers thicknesses, should lead to a better multi-scale characterisation.