The Method of Studying Cosmetic Creams Based on the Principles of Systems Theory and Mathematical Modeling Techniques
Abstract
:1. Introduction
- -
- Analytical or theoretical models based on knowledge of physico-chemical laws, as well as physico-chemical processes that govern the state and evolution of the studied system. When determining these types of models, a series of simplifying assumptions are adopted, logically justified by the particular analysis system. Here, the model is determined after laborious procedures and is usually characterized by complex systems of higher order matrix equations.
- -
- Experimental or statistical models based on the correlation of experimental data.
- -
- Using these data, equations that describe the relationships between the output variables and the input variables are determined based on the principles of mathematical statistics and regression analysis. These dependencies are usually expressed by polynomial equations of different orders. Mathematical expressions amenable to automatic calculation are used directly in practical applications as well as in experimental research.
- -
- Mixed or analytical-experimental models derived from both the existing dependence relationships between the output and the input variables, as well as through the statistical processing of the experimental data. Most of the time, these mathematical models are much simpler; however, they show lower precision in relation to the real system.
- -
- Due to the fact that the studied cosmetic emulsion (Figure 1) has an increased number of in/out variables, the f function of the theoretical model has high complexity, and we used experimental-computational mathematical modeling techniques. The other reason for using this mathematical model is to reduce the cost of raw materials.
- -
- According to Figure 1, there are multiple subsystems and initially three distinct and different phases: oily, aqueous, and solid. After the homogenations process and obtaining the actual emulsion, the result will be a homogeneous mixture, characterized by the output variables values. These output variables are in fact quality indicators that influence the final result of a performant cosmetic emulsion.
- -
- Considering the above mentioned mathematical modeling techniques, in this paper we studied using the principles of Systems Theory [1,2,3,4] a series of emulsions/creams prepared according to our own recipes (E1–E4), as well as the “Remineralizing antiwrinkle cream” (E5) produced (and released on the market) by Virago Beauty SRL, Faget, Romania.
2. Materials and Methods
2.1. Materials
2.2. The Emulsions Preparation
- -
- The aqueous phase contains: water, glycerin, sodium benzoate;
- -
- The oily phase contains: coco-caprylate/caprate, cetearyl olivate, sorbitan olivate, Vitis vinifera (grape) seed oil, Helianthus annuus (sunflower) seed oil, Glycine soja (soybean) oil, Olea europaea (olive) fruit oil, Butyrospermum parkii butter, Theobroma cacao seed butter, cetearyl alcohol, benzyl alcohol, chlorphenesin;
- -
- The third phase contains the active ingredients: Saccharomyces/zinc ferment, Saccharomyces/copper ferment, Saccharomyces/magnesium ferment, Saccharomyces/iron ferment, Saccharomyces/silicon ferment, Lactobacillus ferment lysate, Camellia sinensis leaf extract, Punica granatum extract, caffeine, vegetable collagen, Imperata cylindrica root extract, sodium hyaluronate;
- -
- The fourth phase contains the perfume.
2.3. Methodology Used to Determine Experimental-Computational Mathematical Models
- -
- Obtaining experimental databases by measuring the following quality indicators values: evaporation residue RE, total number of germs NTG, pH, relative density d, evaporation loss PE;
- -
- The processing of experimental data obtained in the laboratory was carried out with the software Statistica 14.0, version with multiple linear regression method and Microsoft Excel, version with nonlinear regression method. Thus, both 3D and 2D graphical representations and the corresponding mathematical equations and the values of adequacy indicators were obtained.
- -
- The experimental-computational mathematical models were tested based on the calculated adequacy indicator values: dispersion σ2, standard deviation σ, model accuracy indicator R2 and root mean square error RMSE [24];
- -
- Authenticity of the model was checked with the classical method of calculating the absolute error E [5].
3. Results
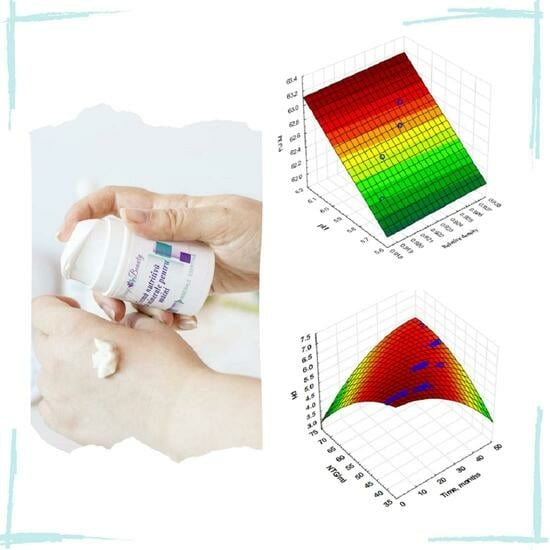
3.1. Dependence of Evaporation Residue (RE) on Total Number of Germs (NTG) and pH for the Emulsions E1–E4, Followed for 4 Years
3.2. Dependence of the Evaporation Loss (PE) on pH and Relative Density (d) for Emulsion E5 (“Remineralizing Anti-Wrinkle Cream” Virago Beauty), at 40 °C and 4 °C
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cristea, M.; Agachi, Ș. Elements of Systems Theory; Editura Risoprint: Cluj-Napoca, Romania, 2002; pp. 2–20. (In Romanian) [Google Scholar]
- Dragomir, T.L. Elements of Systems Theory; Editura Politehnica: Timișoara, Romania, 2004; pp. 15–28. (In Romanian) [Google Scholar]
- Manea, A.E.; Perju, M.D.; Tămaș, A. Systems theory and the study of cosmetic products. J. Eng. Sci. Innov. (JESI) 2022, 7, 45–58. [Google Scholar] [CrossRef]
- Todinca, T.; Geantă, M. Modeling and Simulation of Chemical Processes. Applications in Matlab; Editura Politehnic: Timişoara, Romania, 1999; pp. 7–8, 53–55, 163–175. (In Romanian) [Google Scholar]
- Manea, E.A.; Perju, M.D.; Tămaș, A. Contributions to the study of cosmetic emulsions using analytical-experimental mathematical models. Stud. UBB Chem. 2022, 67, 97–112. [Google Scholar] [CrossRef]
- Available online: www.viragobeauty.com (accessed on 11 June 2023).
- Available online: https://ec.europa.eu/growth/tools-databases/cosing (accessed on 22 May 2023).
- Mank, V.; Polonska, T. Use of natural oils as bioactive ingredients of cosmetic products. Ukr. Food J. 2016, 5, 281–289. [Google Scholar] [CrossRef]
- Gunstone, F. The Chemistry of Oils and Fats; Blackwell Publishing Ltd.: Hoboken, NJ, USA, 2004; pp. 1–30. [Google Scholar]
- Kunik, O.; Saribekova, D.; Lazzara, G.; Cavallaro, G. Emulsions based on fatty acid from vegetable oils for cosmetics. Ind. Crops Prod. 2022, 189, 115776. [Google Scholar] [CrossRef]
- IFSCC. Cosmetic Raw Material Analysis and Quality; Micelle Press: Weymouth, UK, 1994; Volume 1, pp. 33–72. [Google Scholar]
- Kulkarni, V.S.; Shaw, C. Essential Chemistry for Formulators of Semisolid and Liquid Dosages, 1st ed.; Academic Press: Cambridge, MA, USA, 2016; pp. 29–41. [Google Scholar]
- Available online: https://www.lorealparisusa.com/ingredient-library/sodium-lauryl-sulfate (accessed on 6 July 2023).
- Ud-Din, S.; McGeorge, D.; Bayat, A. Topical management of striae distensae (stretch marks): Prevention and therapy of striae rubrae and albae. J. Eur. Acad. Dermatol. Venereol. 2016, 30, 211–222. [Google Scholar] [CrossRef]
- Available online: https://www.healthline.com/health/beauty-skin-care/cocoa-butter-benefits (accessed on 7 July 2023).
- Vaseline Skin Moisturizing Cream. China Patent CN104188832A, 10 December 2014.
- Petry, T.; Bury, D.; Fautz, R.; Hauser, M.; Huber, B.; Markowetz, A.; Mishra, S.; Rettinger, K.; Schuh, W.; Teichert, T. Review of data on the dermal penetration of mineral oils and waxes used in cosmetic applications. Toxicol. Lett. 2017, 280, 70–78. [Google Scholar] [CrossRef] [PubMed]
- IFSCC Monograph Number 4. Introduction to Cosmetic Emulsions and Emulsification; Micelle Press: Weymouth, UK, 1997; pp. 7–38. [Google Scholar]
- Popovici, I.; Lupuleasa, D. Pharmaceutical Technology; Editura Polirom: Iaşi, Romania, 2017; Volume 2, pp. 154–265. (In Romanian) [Google Scholar]
- Romanian Pharmacopoeia, 10th ed.; Editura Medicală: Bucureşti, Romania, 1993; pp. 387–388, 982–1163. (In Romanian)
- Sakamoto, K.; Lochhead, R.Y.; Maibach, H.I.; Yamashita, Y. Cosmetic Science and Technology: Theoretical Principles and Applications, 1st ed.; Elsevier Science Publishing Co. Inc.: Amsterdam, The Netherlands, 2017; pp. 489–505. [Google Scholar]
- Manea, A.; Tămaș, A.; Nițu, S.; Perju, D. The study of the rheological behavior and the oxidation stability of some cosmetic emulsions. Stud. UBB Chem. 2021, 66, 283–295. [Google Scholar] [CrossRef]
- European Pharmacopoeia, 8th ed.; Council of Europe: Strasbourg, France, 2014; Volume I, pp. 11–227, 551–793.
- Bețianu, C.S.; Cozma, P.; Roșca, M.; Comăniță-Ungureanu, E.D.; Mămăligă, I.; Gavrilescu, M. Sorption of organic pollutants onto soils: Surface diffusion mechanism of Congo red azo dye. Processes 2020, 8, 1639. [Google Scholar] [CrossRef]








| Ingredients | Functions | Reference |
|---|---|---|
| Stearic acid | Surfactant, emulsifying, emollient, emulsion stabilizing | [7,8,9,10,11] |
| Cetyl alcohol | Surfactant, emulsifying, emollient, emulsion stabilizing, viscosity controlling | [7,11] |
| Cetearyl alcohol | Surfactant, emulsifying, emollient, emulsion stabilizing, viscosity controlling, opacifying | [7,11,12] |
| Cetyl palmitate/Cetaceum | Skin conditioning—emollient | [7,11] |
| Cetearyl olivate | Skin conditioning—emollient, emulsifying, emulsion stabilizing | [7] |
| Sorbitan olivate | Surfactant—emulsifying | [7] |
| Sodium lauryl sulfate | Surfactant—cleansing, emulsifier, foaming agent | [7,11,13] |
| Theobroma Cacao Seed Butter | Skin conditioning agent—miscellaneous, skin protecting, emollient and moisturizer, anti-inflammatory properties | [7,9,11,14,15] |
| Butyrospermum Parkii Butter | Skin conditioning, skin protecting, emollient and moisturizer | [7,11] |
| Petrolatum/Vaseline | Skin conditioning—emollient, moisturizer | [7,11,16] |
| Paraffinum liquidum /Paraffin oil | Skin protecting, fortifying the natural moisture barrier (occlusive emollient) | [7,11,17] |
| Coco-caprylate caprate | Skin conditioning—emollient | [7] |
| Vitis vinifera seed oil | Skin conditioning—emollient | [7] |
| Helianthus annuus seed oil | Skin conditioning—emollient, skin conditioning—miscellaneous, skin conditioning—occlusive, solvent | [7] |
| Glycine soja oil | Skin conditioning—emollient | [7] |
| Olea europaea fruit oil | Skin conditioning | [7] |
| Glycerin | Humectant, skin conditioning—miscellaneous, skin protecting, solvent, viscosity controlling | [7,11] |
| Methylparaben/Methyl 4-hydroxybenzoate | Preservative | [7] |
| Benzyl alcohol | Preservative | [7] |
| Chlorphenisin | Antimicrobial, preservative | [7] |
| Sodium benzoate | Preservative | [7] |
| Water/aqua | Solvent | [7] |
| Saccharomyces/copper ferment | Skin conditioning | [7] |
| Saccharomyces/iron ferment | Skin conditioning | [7] |
| Saccharomyces/silicon ferment | Skin conditioning | [7] |
| Saccharomyces/zinc ferment | Skin conditioning | [7] |
| Saccharomyces/magnesium ferment | Skin conditioning | [7] |
| Lactobacillus ferment lysate | Skin conditioning | [7] |
| Camellia Sinensis leaf extract | Antioxidant, skin conditioning—emollient, skin protecting, humectant, antimicrobial, tonic | [7] |
| Punica Granatum extract | Astringent, tonic | [7] |
| Caffeine | Skin conditioning | [7] |
| Vegetable collagen | Moisturizing, skin conditioning | [7] |
| Imperata Cylindrica root extract | Skin conditioning | [7] |
| Sodium hyaluronate | Humectant, skin conditioning | [7] |
| Spirulina | Antioxidant | [7] |
| Honey | Humectant, skin conditioning | [7] |
| Tocopherol | Antioxidant | [7] |
| Retinyl palmitate | Skin conditioning | [7] |
| Type of Emulsion | Equation |
|---|---|
| E1 | |
| E2 | |
| E3 | |
| E4 |
| Type of Emulsion | Dispersion σ2 | Standard Deviation σ | Model Accuracy Indicator R2 | Root Mean Square Error RMSE |
|---|---|---|---|---|
| E1 | 0.2696 | 0.5193 | 0.7646 | 0.0726 |
| E2 | 0.0362 | 0.1903 | 0.8189 | 0.0266 |
| E3 | 0.3485 | 0.5903 | 0.9113 | 0.0825 |
| E4 | 0.9174 | 0.9578 | 0.8730 | 0.1338 |
| Type of Emulsion | TimeT, [Months] | Experimental RE, [%] | Calculated RE, [%] | Absolute Error Value, [%] |
|---|---|---|---|---|
| E1 | 1 | 43.66 | 42.26 | 3.31 |
| 48 | 39.18 | 39.46 | 0.70 | |
| E2 | 1 | 39.92 | 39.43 | 1.24 |
| 48 | 38.30 | 37.90 | 1.05 | |
| E3 | 1 | 34.20 | 32.52 | 5.17 |
| 48 | 27.83 | 26.57 | 4.74 | |
| E4 | 1 | 32.83 | 31.42 | 10.35 |
| 48 | 24.98 | 23.86 | 4.69 |
| Type of Emulsion | Equation | Model Accuracy Indicator R2 | Root Mean Square Error RMSE |
|---|---|---|---|
| E1 | 0.9241 | 0.0412 | |
| E2 | 0.9583 | 0.0146 | |
| E3 | 0.9921 | 0.0248 | |
| E4 | 0.9900 | 0.038 |
| Temperature, °C | Equation |
|---|---|
| 40 | |
| 4 |
| Temperature, °C | Dispersion σ2 | Standard Deviation, σ | Model Accuracy Indicator, R2 | Root Mean Square Error RMSE |
|---|---|---|---|---|
| 40 | 0.00563 | 0.0750 | 0.9713 | 0.0214 |
| 4 | 0.00134 | 0.0366 | 0.9971 | 0.0105 |
| Temperature, °C | Time T, [Days] | Experimental PE, [%] | Calculated PE, [%] | Absolute Error Value, [%] |
|---|---|---|---|---|
| 40 | 0 | 62.92 | 62.99 | 0.11 |
| 8 | 61.99 | 62.95 | 1.52 | |
| 4 | 0 | 62.92 | 62.89 | 0.04 |
| 8 | 61.42 | 61.43 | 0.02 |
| Quality Indicators | Equations of the Mathematical Models | Model Accuracy Indicator, R2 | Root Mean Square Error RMSE |
|---|---|---|---|
| Evaporation loss at 40 ± 2 °C, % | 0.9994 | 0.0058 | |
| Evaporation loss at 4 ± 2 °C, % | 0.9934 | 0.0490 | |
| pH at 40 ± 2 °C | 0.9843 | 0.0080 | |
| pH at 4 ± 2 °C | 0.9577 | 0.0148 | |
| Relative density at 40 ± 2 °C | 0.9942 | 0.00032 | |
| Relative density at 4 ± 2 °C | 0.9934 | 0.00113 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manea, A.; Perju, D.; Tămaș, A. The Method of Studying Cosmetic Creams Based on the Principles of Systems Theory and Mathematical Modeling Techniques. Cosmetics 2023, 10, 118. https://doi.org/10.3390/cosmetics10050118
Manea A, Perju D, Tămaș A. The Method of Studying Cosmetic Creams Based on the Principles of Systems Theory and Mathematical Modeling Techniques. Cosmetics. 2023; 10(5):118. https://doi.org/10.3390/cosmetics10050118
Chicago/Turabian StyleManea, Adela, Delia Perju, and Andra Tămaș. 2023. "The Method of Studying Cosmetic Creams Based on the Principles of Systems Theory and Mathematical Modeling Techniques" Cosmetics 10, no. 5: 118. https://doi.org/10.3390/cosmetics10050118
APA StyleManea, A., Perju, D., & Tămaș, A. (2023). The Method of Studying Cosmetic Creams Based on the Principles of Systems Theory and Mathematical Modeling Techniques. Cosmetics, 10(5), 118. https://doi.org/10.3390/cosmetics10050118