An Improved Fault Diagnosis Using 1D-Convolutional Neural Network Model
Abstract
:1. Introduction
2. Structure of 1D-CNN Model
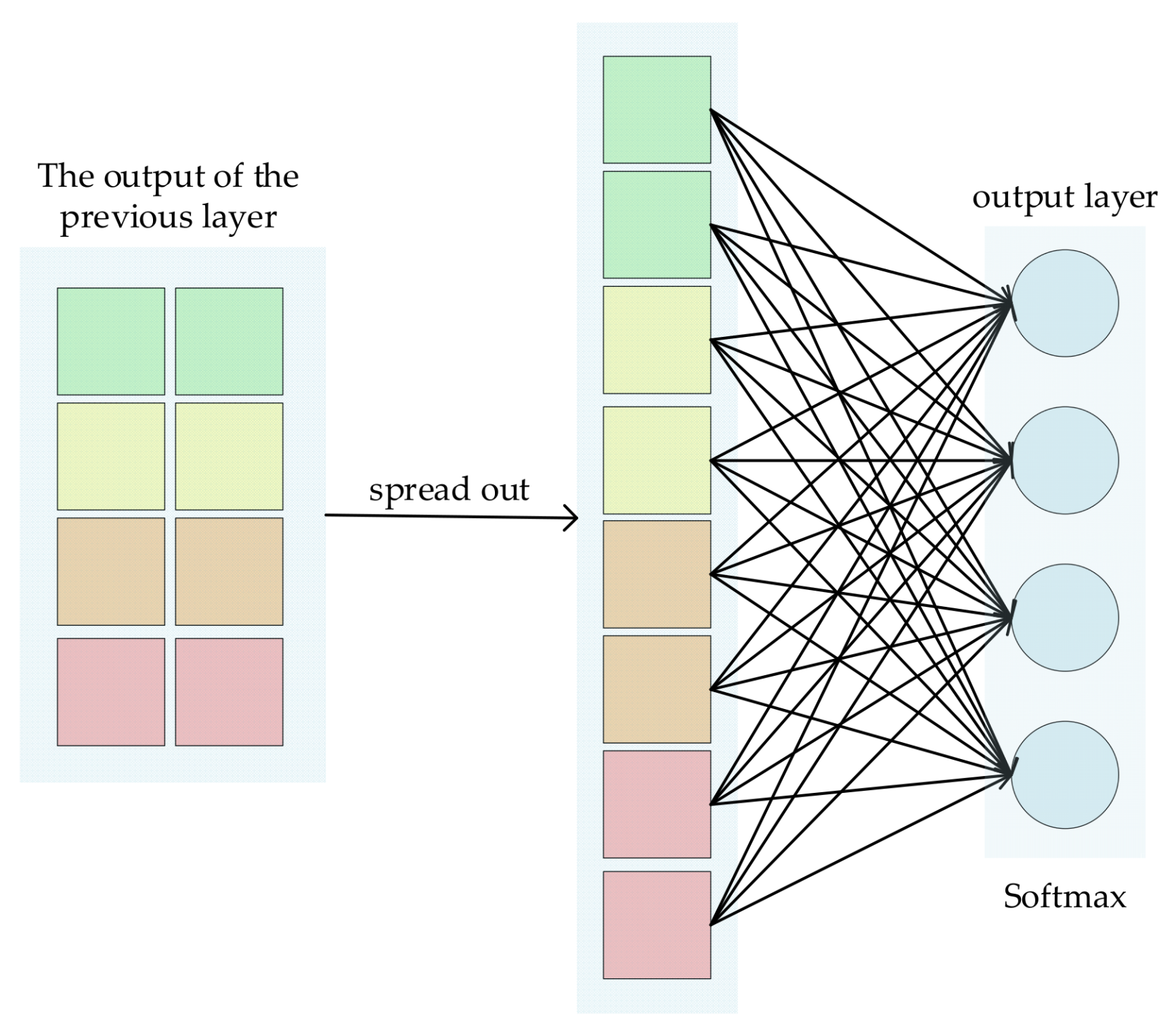
2.1. A Brief Introduction to Convolutional Neural Networks
2.2. Fault Diagnosis Process Based on 1D-CNN
- (1)
- A sensor is installed on the corresponding position of the rolling bearing.
- (2)
- The one-dimensional vibration signal is first collected as the raw data, and then the signal data is divided into training, validation, and test sets.
- (3)
- The training set is used as the input of 1D-CNN network. The model is trained, the validation set is used in order to verify the model performance, and appropriate network model parameters are selected.
- (4)
- The test set is put to the trained model, and the performance of the model is evaluated.
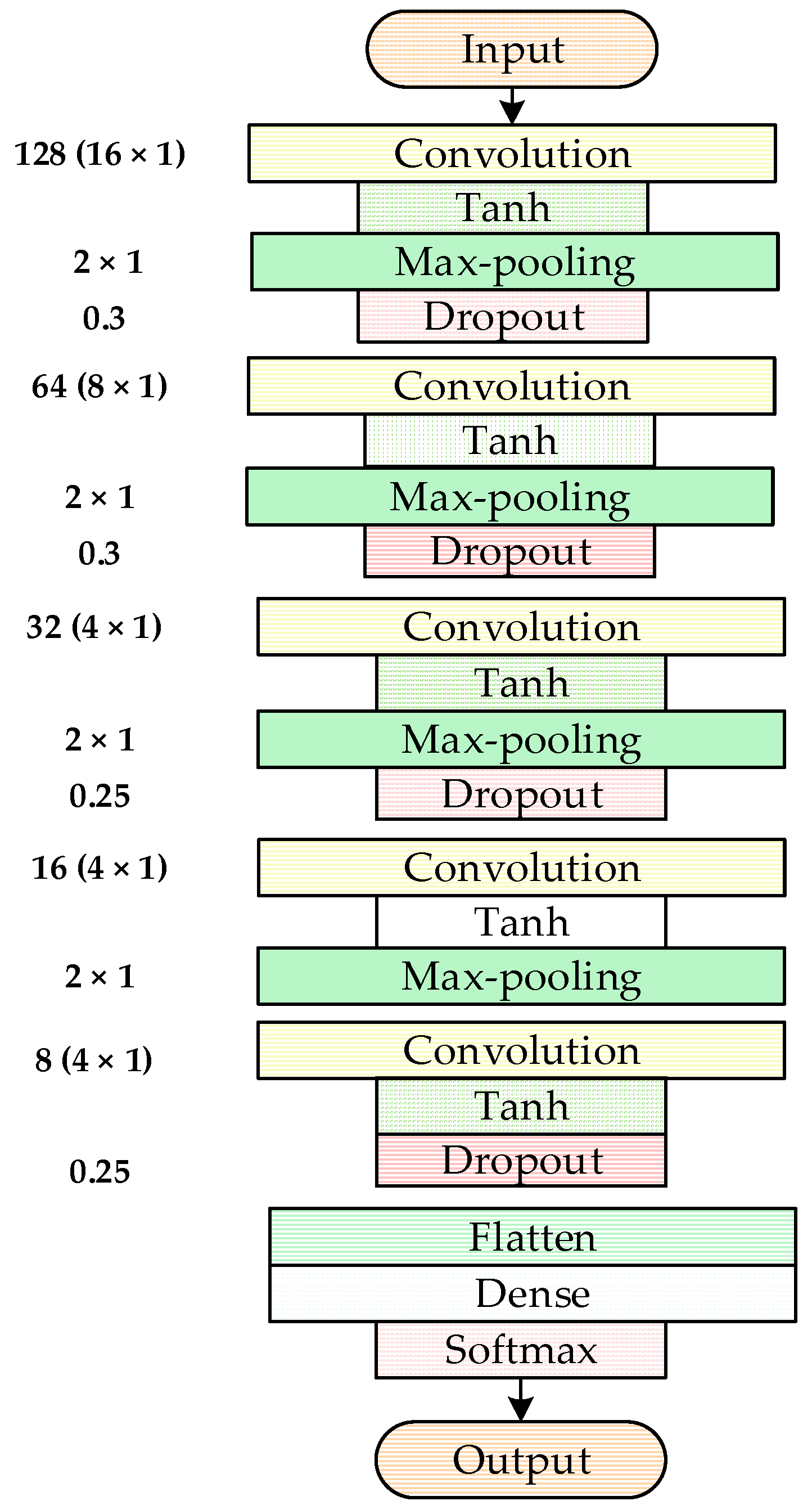
2.3. 1D-CNN Structure
3. Data Set Description and Model Parameter Selection
3.1. Data Set Description
3.2. 1D-CNN Model Parameter Selection
3.3. The Specific Parameters of Six Models
- (1)
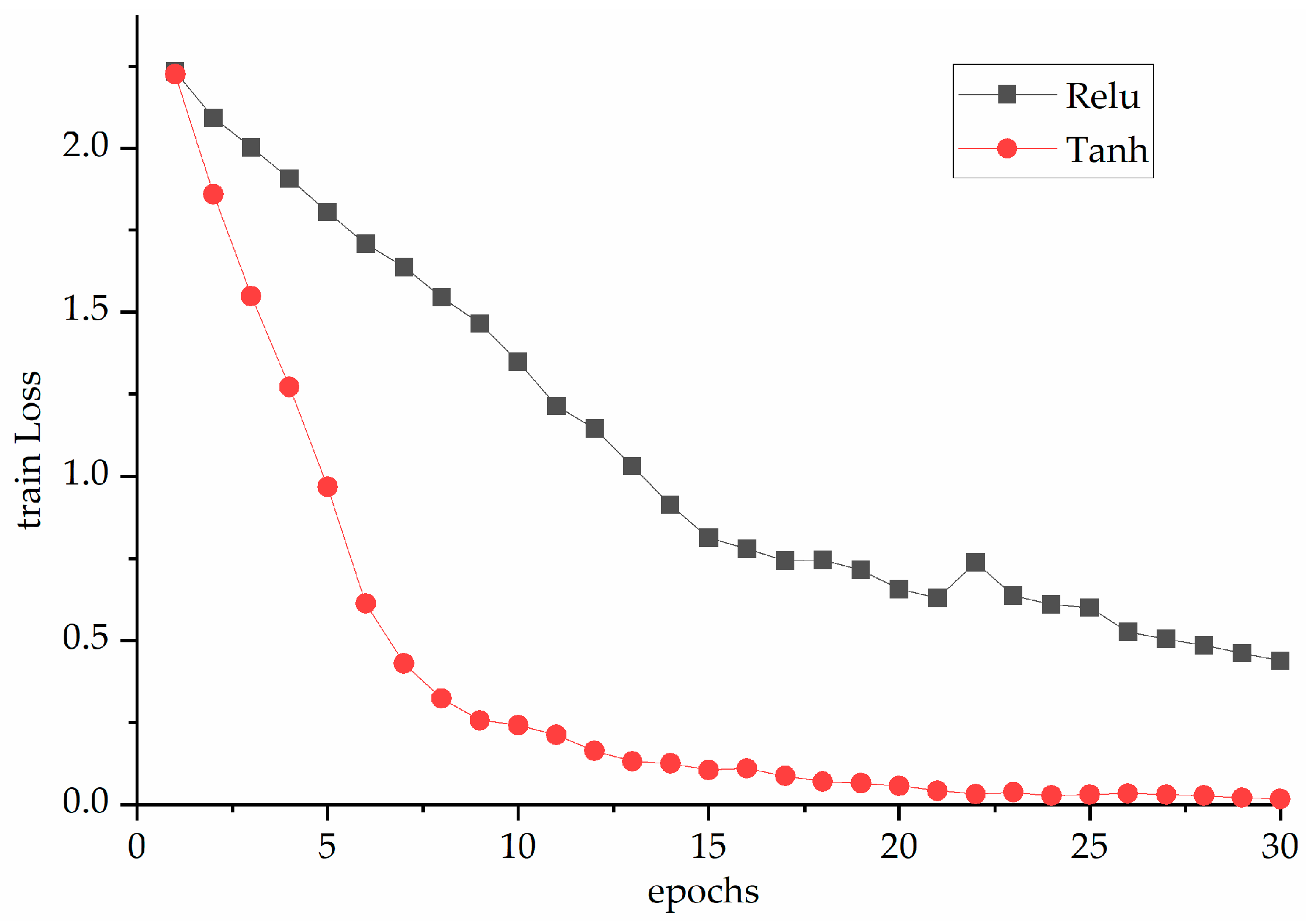
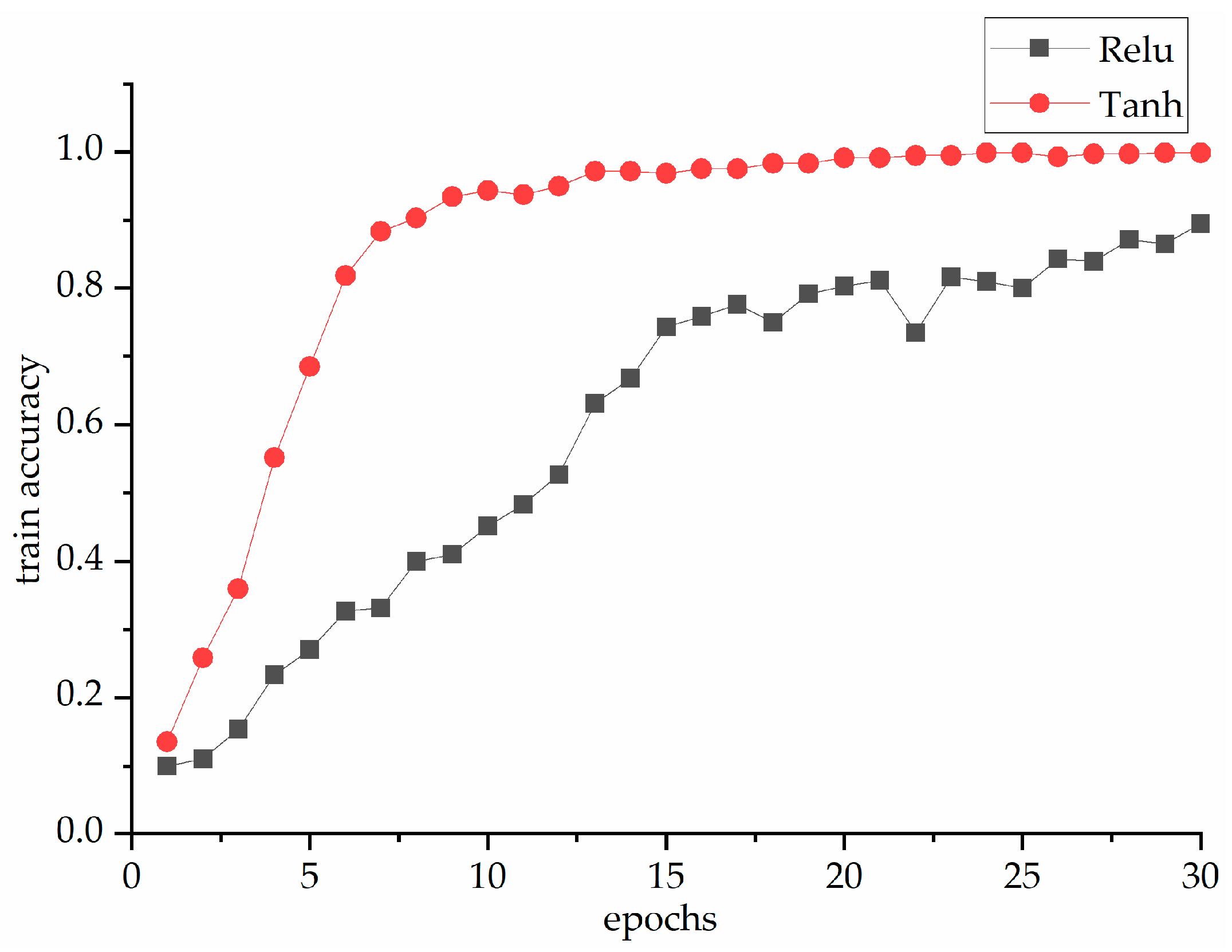
- 1D-CNN modelThe learning ratio was set to 0.001 and the activation function is set to Tanh. The optimizer was Adam, which combines the advantages of Adagrad and RMSprop algorithm and it has high computing efficiency and low memory requirement. The loss function is categorical_crossentrop, the batch-size was set to 64, and the iteration time was 30.
- (2)
- LSTM modelThe first layer of the LSTM had 32 neurons with Tanh as the activation function. The second layer had 32 neurons in the full connection layer with Relu as the activation function. The third layer had 10 neurons and it was classified by Softmax. The learning ratio was set to 0.001 and the optimizer is Adam. The loss function was categorical_crossentropy. The batch- size was 32 and iteration time was 30.
- (3)
- MLP modelThe first, second, third, and fourth layers were the whole connective layer with 300, 400, 200 and 100 neurons, respectively. The activation function was Relu. Dropout operations were adopted with a probability of 0.4 in each full connection layer. The fifth layer was the output layer with 10 neurons and it was classified by Softmax. The learning ratio was set to 0.002 and the optimizer is Adam. The loss function wascategorical_crossentropy. The batch- size was 32 and the iteration time was 40.
- (4)
- SVM modelThe GridSearchCV (10-fold cross verification parameters) is adopted. Gaussian kernel (RBF) is selected as the kernel function of SVM. The penalty factor C is determined to be 128, and gamma (controls the width of gaussian kernel and it determines the distribution of data mapped to the new feature space) is 0.002.
- (5)
- RandomForest modelThe GridSearchCV (10-fold cross verification parameters) is adopted. Three-hundred decision trees were used in order to construct the random forest model. The maximum depth of the random forest tree is 16, and the minimum number of tree splits was 5.
- (6)
- KNN modelThe GridSearchCV (10-fold cross verification parameters) is used for the KNN model in order to determine the best K value of 1.
4. Experimental Results and Analysis
4.1. Compared with Other Model Experiments
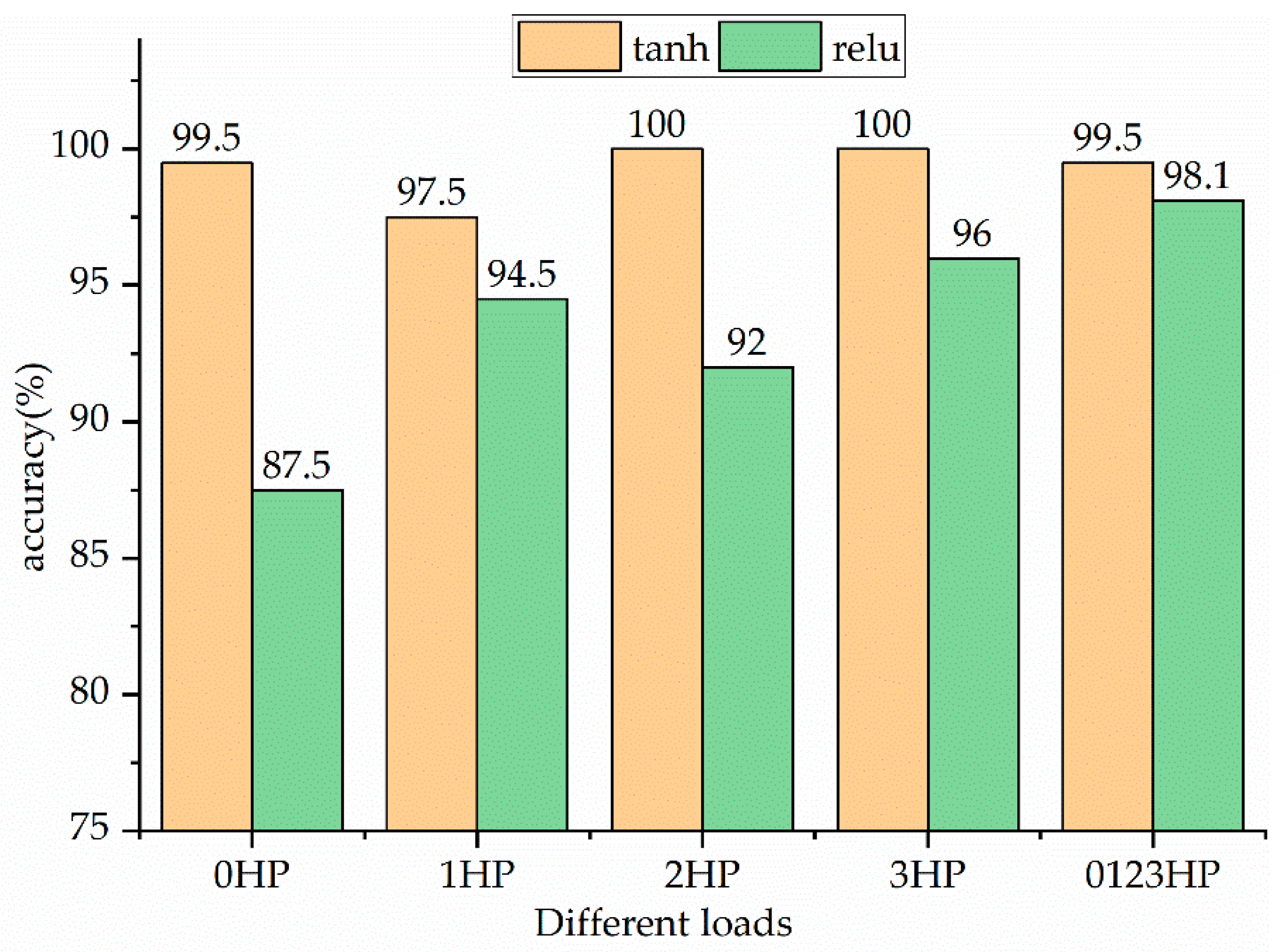
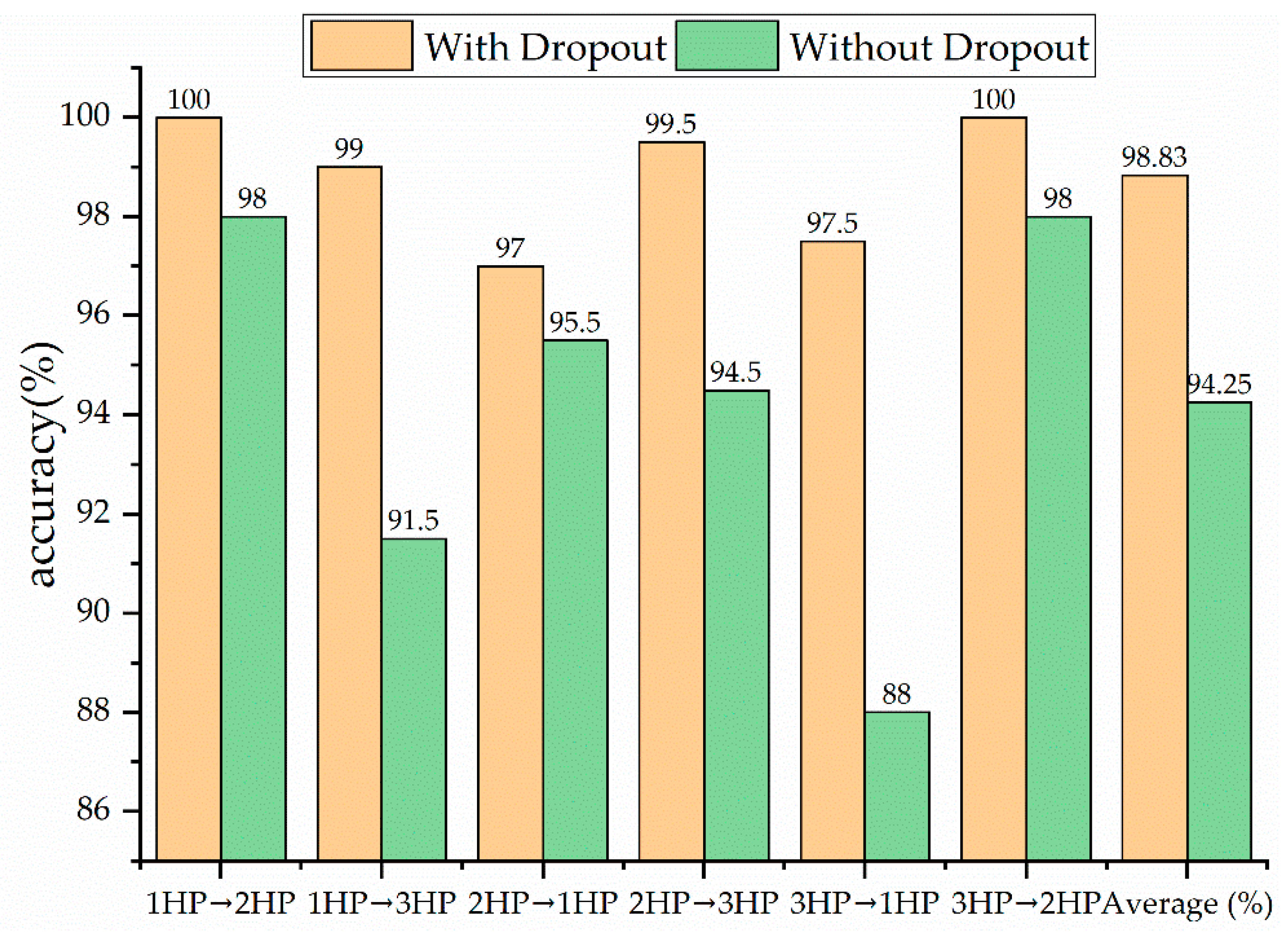
4.2. Performances under Different Loads
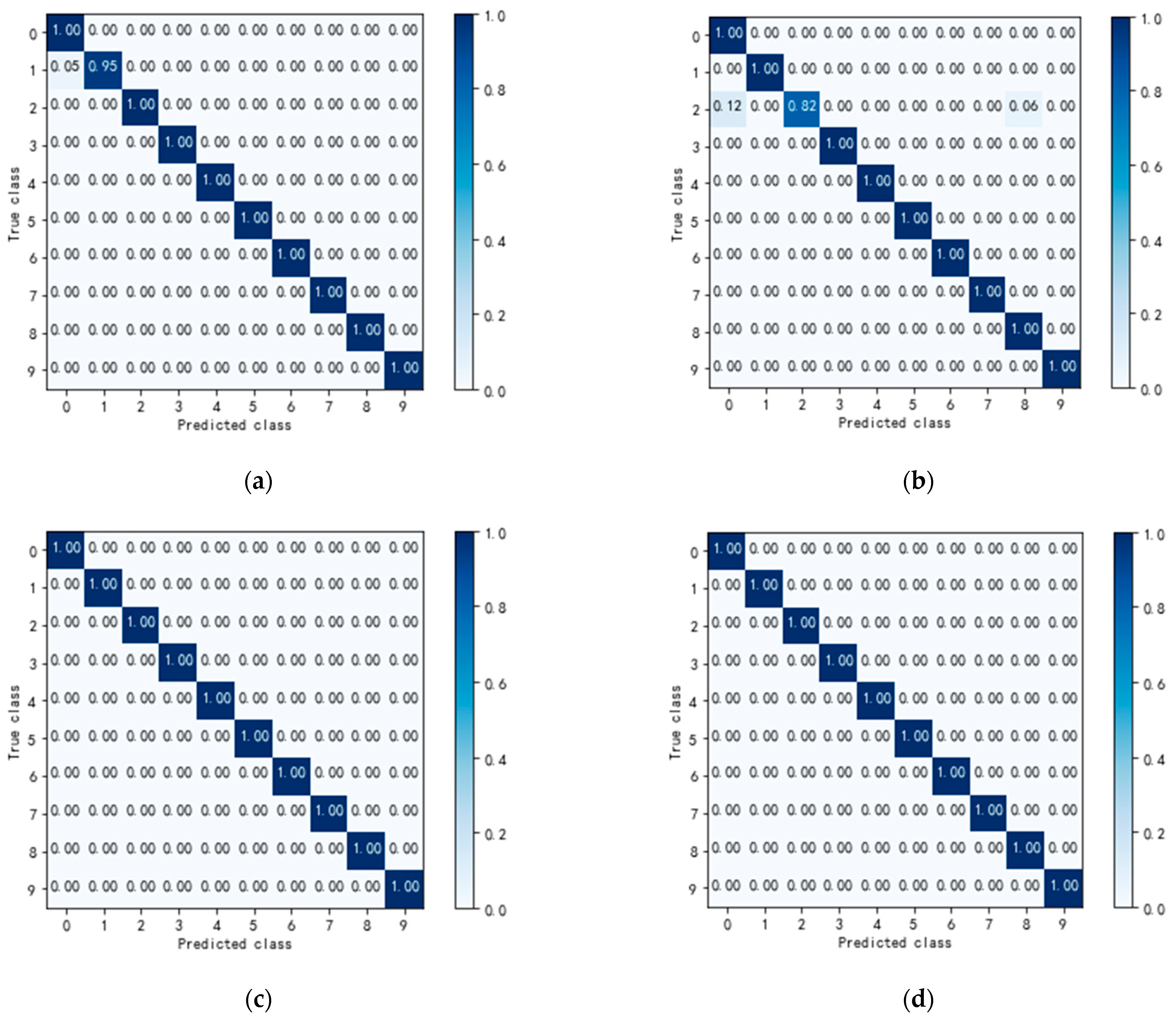
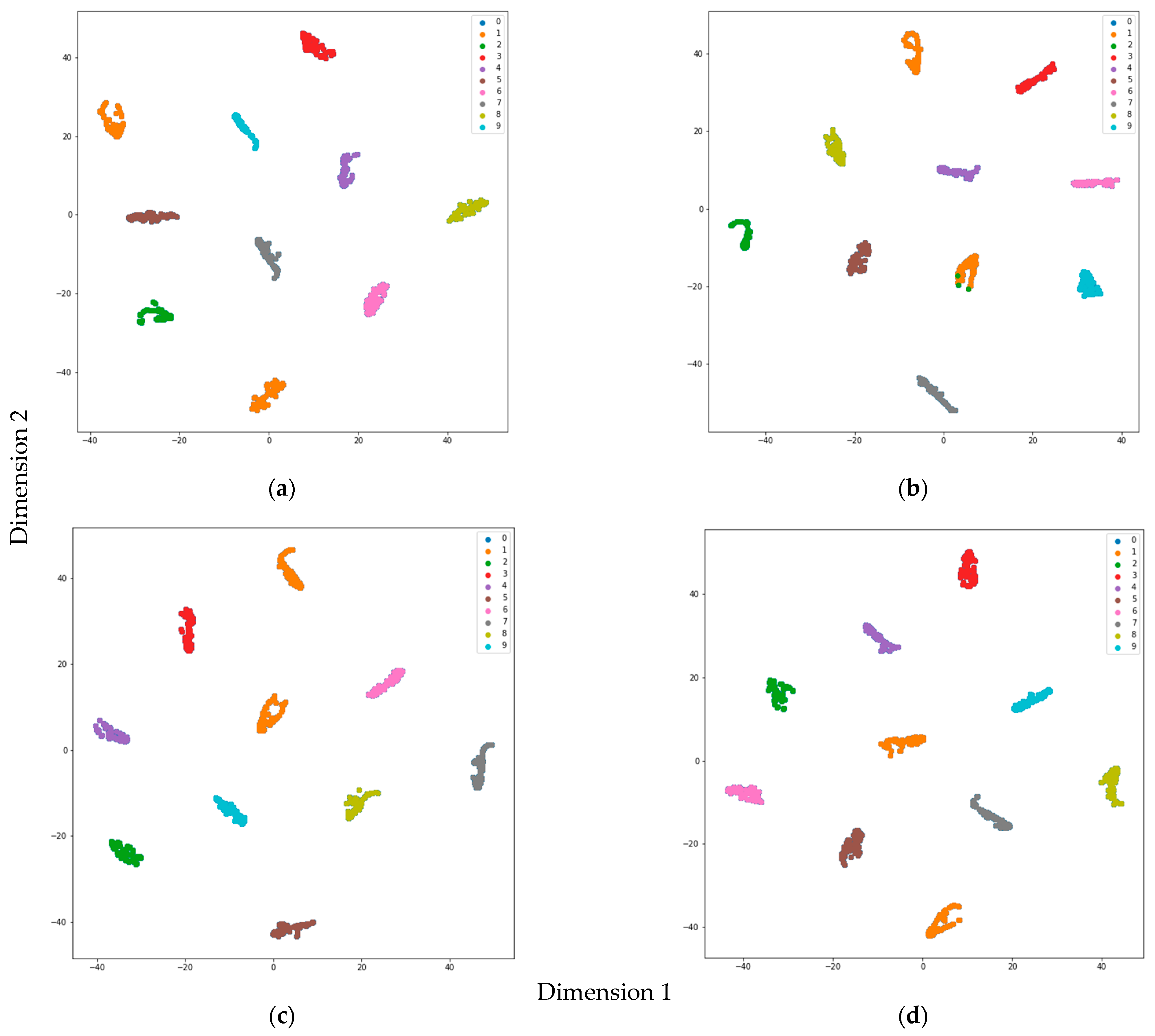
4.3. Visual Analysis of Validity of 1D-CNN Model
5. Conclusions
- (1)
- The method that is proposed in this paper shows an average accuracy of 99.2% under a single load and 98.83% across different loads. Moreover, the original vibration data of the bearings are directly used without preprocessing.
- (2)
- In this paper, we propose a 1D-CNN network structure, in which the number of convolution kernels decreases with the reduction of the size of the convolution kernel, and that network structure effectively improves the accuracy of bearing fault diagnosis.
- (3)
- The 1D-CNN model has great advantages for analyzing complex and non-stationary signals when compared with traditional machine learning methods.
- (4)
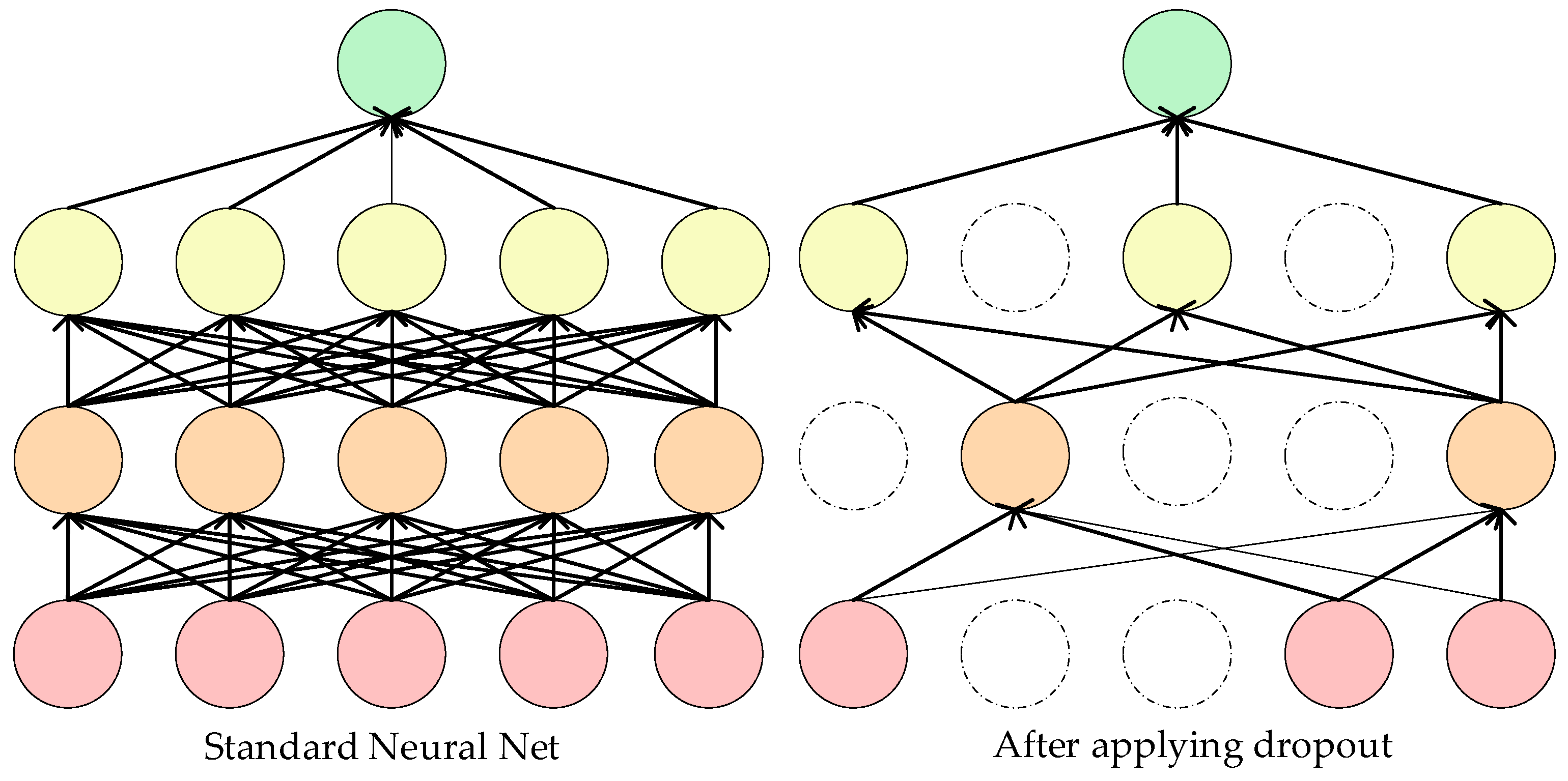
- The Dropout layer added to the 1D-CNN model effectively improves the accuracy of cross-load training and it enhances the generalization ability of the model.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nandi, S.; Toliyat, H.A.; Li, X. Condition Monitoring and Fault Diagnosis of Electrical Motors—A Review. IEEE Trans. Energy Convers. 2005, 20, 719–729. [Google Scholar] [CrossRef]
- Lei, Y.; Lin, J.; Zuo, M.J.; He, Z. Condition monitoring and fault diagnosis of planetary gearboxes: A review. Measurement 2014, 48, 292–305. [Google Scholar] [CrossRef]
- Fan, L.; Wang, S.; Wang, X.; Han, F.; Lyu, H. Nonlinear dynamic modeling of a helicopter planetary gear train for carrier plate crack fault diagnosis. Chin. J. Aeronaut. 2016, 29, 675–687. [Google Scholar] [CrossRef] [Green Version]
- Gao, Z.; Cecati, C.; Ding, S.X. A Survey of Fault Diagnosis and Fault-Tolerant Techniques—Part I: Fault Diagnosis With Model-Based and Signal-Based Approaches. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar] [CrossRef] [Green Version]
- Li, D.Z.; Wang, W.; Ismail, F. An Enhanced Bispectrum Technique with Auxiliary Frequency Injection for Induction Motor Health Condition Monitoring. IEEE Trans. Ind. Electron. 2015, 64, 2679–2687. [Google Scholar] [CrossRef]
- Filippetti, F.; Bellini, A.; Capolino, G. Condition monitoring and diagnosis of rotor faults in induction machines: State of art and future perspectives. In Proceedings of the 2013 IEEE Workshop on Electrical Machines Design, Control and Diagnosis (WEMDCD), Paris, France, 11–12 March 2013; pp. 196–209. [Google Scholar]
- Kral, C.; Habetler, T.G.; Harley, R.G. Detection of mechanical imbalances of induction machines without spectral analysis of time-domain signals. IEEE Trans. Ind. Appl. 2004, 40, 1101–1106. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Z.; Wang, J.; Wang, J. Time–frequency analysis for bearing fault diagnosis using multiple Q-factor Gabor wavelets. ISA Trans. 2019, 87, 225–234. [Google Scholar] [CrossRef]
- Gao, H.; Liang, L.; Chen, X.; Xu, G. Feature extraction and recognition for rolling element bearing fault utilizing short-time Fourier transform and non-negative matrix factorization. Chin. J. Mech. Eng. 2015, 28, 96–105. [Google Scholar] [CrossRef]
- Li, Y.; Xu, M.; Huang, W.; Zuo, M.J.; Liu, L. An improved EMD method for fault diagnosis of rolling bearing. In Proceedings of the 2016 Prognostics and System Health Management Conference (PHM-Chengdu), Chengdu, China, 19–21 October 2016; pp. 1–5. [Google Scholar]
- Li, H.; Liu, T.; Wu, X.; Chen, Q. Research on bearing fault feature extraction based on singular value decomposition and optimized frequency band entropy. Mech. Syst. Signal Process. 2019, 118, 477–502. [Google Scholar] [CrossRef]
- Battineni, G.; Sagaro, G.G.; Chinatalapudi, N.; Amenta, F. Applications of Machine Learning Predictive Models in the Chronic Disease Diagnosis. JPM 2020, 10, 21. [Google Scholar] [CrossRef] [Green Version]
- Chen, R.; Huang, D.; Zhao, L. Fault Diagnosis of Rolling Bearing Based on EEMD Information Entropy and Improved SVM. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 4961–4966. [Google Scholar]
- Appana, D.K.; Islam, M.R.; Kim, J.-M. Reliable Fault Diagnosis of Bearings Using Distance and Density Similarity on an Enhanced k-NN. In Proceedings of the 3rd Artificial Life and Computational Intelligence, Geelong, VIC, Australia, 31 January–2 February 2017; pp. 193–203. [Google Scholar]
- Wang, X.; Zheng, Y.; Zhao, Z.; Wang, J. Bearing Fault Diagnosis Based on Statistical Locally Linear Embedding. Sensors 2015, 15, 16225–16247. [Google Scholar] [CrossRef] [PubMed]
- Georgoulas, G.; Karvelis, P.; Loutas, T.; Stylios, C.D. Rolling element bearings diagnostics using the Symbolic Aggregate approXimation. Mech. Syst. Signal Process. 2015, 60–61, 229–242. [Google Scholar] [CrossRef]
- Yin, A.; Lu, J.; Dai, Z.; Li, J.; Ouyang, Q. Isomap and Deep Belief Network-Based Machine Health Combined Assessment Model. SV-JME 2016, 62, 740–750. [Google Scholar] [CrossRef]
- Liu, H.; Li, L.; Ma, J. Rolling Bearing Fault Diagnosis Based on STFT-Deep Learning and Sound Signals. Shock Vib. 2016. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Zhou, J.; Zheng, Y.; Jiang, W.; Zhang, Y. Fault diagnosis of rolling bearings with recurrent neural network-based autoencoders. ISA Trans. 2018, 77, 167–178. [Google Scholar] [CrossRef] [PubMed]
- Qu, J.; Gao, F.; Tian, Y. A Novel Hierarchical Algorithm for Bearing Fault Diagnosis Based on Stacked LSTM. Shock Vib. 2019. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Ince, T.; Kiranyaz, S.; Eren, L.; Askar, M.; Gabbouj, M. Real-Time Motor Fault Detection by 1-D Convolutional Neural Networks. IEEE Trans. Ind. Electron. 2016, 63, 7067–7075. [Google Scholar] [CrossRef]
- Eren, L.; Ince, T.; Kiranyaz, S. A Generic Intelligent Bearing Fault Diagnosis System Using Compact Adaptive 1D CNN Classifier. J. Signal Process. Syst. 2019, 91, 179–189. [Google Scholar] [CrossRef]
- Zhang, W.; Li, C.; Peng, G.; Chen, Y.; Zhang, Z. A deep convolutional neural network with new training methods for bearing fault diagnosis under noisy environment and different working load. Mech. Syst. Signal Process. 2018, 100, 439–453. [Google Scholar] [CrossRef]
- Ma, S.; Cai, W.; Liu, W.; Shang, Z.; Liu, G. A Lighted Deep Convolutional Neural Network Based Fault Diagnosis of Rotating Machinery. Sensors 2019, 19, 2381. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, X.; Mao, D.; Li, X. Bearing fault diagnosis based on vibro-acoustic data fusion and 1D-CNN network. Measurement 2020, 108518. [Google Scholar] [CrossRef]
- Shenfield, A.; Howarth, M. A Novel Deep Learning Model for the Detection and Identification of Rolling Element-Bearing Faults. Sensors 2020, 20, 5112. [Google Scholar] [CrossRef]
- Yuan, L.; Lian, D.; Kang, X.; Chen, Y.; Zhai, K. Rolling Bearing Fault Diagnosis Based on Convolutional Neural Network and Support Vector Machine. IEEE Access 2020, 8, 137395–137406. [Google Scholar] [CrossRef]
- Han, T.; Tian, Z.; Yin, Z.; Tan, A.C.C. Bearing fault identification based on convolutional neural network by different input modes. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 474. [Google Scholar] [CrossRef]
- Hubel, D.H.; Wiesel, T.N. Receptive fields of single neurones in the cat’s striate cortex. J. Physiol. 1959, 148, 574–591. [Google Scholar] [CrossRef] [PubMed]
- Lawrence, S.; Giles, C.L.; Tsoi, A.C.; Back, A.D. Face recognition: A convolutional neural-network approach. IEEE Trans. Neural Netw. 1997, 8, 98–113. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, N.; Hinton, G.; Krizhevsky, A. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar] [CrossRef]
- Smith, W.A.; Randall, R.B. Rolling element bearing diagnostics using the Case Western Reserve University data: A benchmark study. Mech. Syst. Signal Process. 2015, 64–65, 100–131. [Google Scholar] [CrossRef]
- Liu, H.; Yao, D.; Yang, J.; Li, X. Lightweight Convolutional Neural Network and Its Application in Rolling Bearing Fault Diagnosis under Variable Working Conditions. Sensors 2019, 19, 4827. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Sun, Y.; Guo, L.; Gao, H.; Hong, X.; Song, H. A new bearing fault diagnosis method based on modified convolutional neural networks. Chin. J. Aeronaut. 2020, 33, 439–447. [Google Scholar] [CrossRef]
- Zhu, X.; Luo, X.; Zhao, J.; Hou, D.; Han, Z.; Wang, Y. Research on deep feature learning and condition recognition method for bearing vibration. Appl. Acoust. 2020, 168, 107435. [Google Scholar] [CrossRef]
- Maaten, L.; Van der Hinton, G. Visualizing Data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]


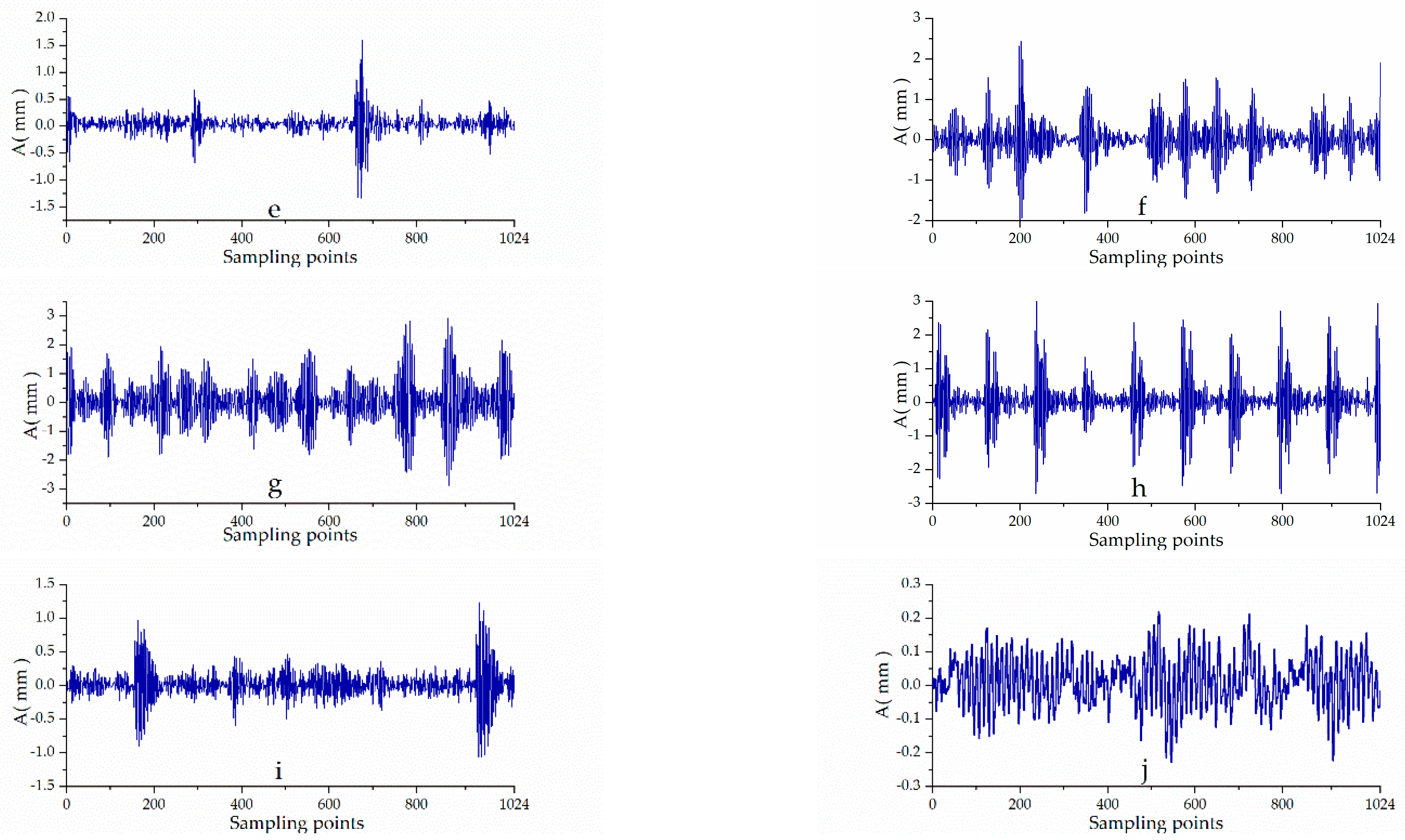



| Fault Type | Fault Diameter (mm) | Fault Orientation | Number of Samples | ||||
|---|---|---|---|---|---|---|---|
| 0 HP | 1 HP | 2 HP | 3 HP | 0123 HP | |||
| Ball (a) | 0.0028 | / | 100 | 100 | 100 | 100 | 400 |
| Ball (b) | 0.0056 | / | 100 | 100 | 100 | 100 | 400 |
| Ball (c) | 0.0112 | / | 100 | 100 | 100 | 100 | 400 |
| Inner-race (d) | 0.0028 | / | 100 | 100 | 100 | 100 | 400 |
| Inner-race (e) | 0.0056 | / | 100 | 100 | 100 | 100 | 400 |
| Inner-race (f) | 0.0112 | / | 100 | 100 | 100 | 100 | 400 |
| Outer-race (g) | 0.0028 | @3:00 | 100 | 100 | 100 | 100 | 400 |
| Outer-race (h) | 0.0028 | @6:00 | 100 | 100 | 100 | 100 | 400 |
| Outer-race (i) | 0.0028 | @12:00 | 100 | 100 | 100 | 100 | 400 |
| Normal (j) | 0 | / | 100 | 100 | 100 | 100 | 400 |
| Network Layer | Output Characteristic | Specific Settings |
|---|---|---|
| Input layer | 1024 × 1 | 1024 pieces of vibration data |
| Conv1 layer | 1009 × 128 | 128 @ 16 × 1, stride = 1 |
| Pool1 layer | 504 × 128 | pool size is 2 × 1, stride = 2 |
| Conv2 layer | 497 × 64 | 64 @ 8 × 1, stride = 1 |
| Pool2 layer | 248 × 64 | pool size is 2 × 1, stride = 2 |
| Conv3 layer | 245 × 32 | 32 @ 4 × 1, stride = 1 |
| Pool3 layer | 122 × 32 | pool size is 2 × 1, stride = 2 |
| Conv4 layer | 119 × 16 | 16 @ 4 × 1, stride = 1 |
| Pool4 layer | 59 × 16 | pool size is 2 × 1, stride = 2 |
| Conv5 layer | 56 × 8 | 8 @ 4 × 1, stride = 1 |
| Flatten | 1 × 448 | 448 neurons |
| Dense | 1 × 10 | 10 neurons |
| Method | Highest Accuracy (%) | Lowest Accuracy (%) | Mean (%) |
|---|---|---|---|
| 1D-CNN | 99.9 | 97.6 | 99.2 |
| LSTM | 94.35 | 79.6 | 86.79 |
| MLP | 86.83 | 71.9 | 78.59 |
| SVM | 75.63 | 65 | 71.05 |
| RandomForst | 74.57 | 64.53 | 68.38 |
| KNN | 39.2 | 28.6 | 33.26 |
| Method | 0HP | 1HP | 2HP | 3HP | 0123HP | |
|---|---|---|---|---|---|---|
| 1D-CNN | Accuracy (%) | 99.3 | 97.6 | 99.5 | 99.9 | 99.68 |
| Std (%) | 0.82 | |||||
| LSTM | Accuracy (%) | 90.7 | 79.6 | 84.9 | 84.4 | 94.35 |
| Std (%) | 5.17 | |||||
| MLP | Accuracy (%) | 76.8 | 71.9 | 82.9 | 74.5 | 86.83 |
| Std (%) | 5.50 | |||||
| SVM | Accuracy (%) | 73.3 | 65 | 70.2 | 71.1 | 75.63 |
| Std (%) | 3.56 | |||||
| RandomForst | Accuracy (%) | 64.53 | 64.8 | 71.87 | 66.13 | 74.57 |
| Std (%) | 4.08 | |||||
| KNN | Accuracy (%) | 36.2 | 31.9 | 28.6 | 39.2 | 30.38 |
| Std (%) | 3.89 | |||||
| 1D-CNN | ShufflenetV2 [34] | MobileNet [34] | ICN [34] | DFCNN [35] | PFC-CNN [36] | |
|---|---|---|---|---|---|---|
| Highest accuracy (%) | 100 | 99.4 | 98.4 | 99.8 | / | 97 |
| Lowest accuracy (%) | 97 | 96.3 | 90 | 94.17 | / | 90 |
| Average (%) | 98.3 | 97.36 | 94.38 | 97.07 | 90.05 | 93.31 |
| Bearing State | Ball 0.0028 | Ball 0.0056 | Ball 0.0112 | Inner 0.0028 | Inner 0.0056 | Inner 0.0112 | Outer @3 0.0028 | Outer @6 0.0028 | Outer @12 0.0028 | Normal 0 |
|---|---|---|---|---|---|---|---|---|---|---|
| ID | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.-C.; Liu, Z.; Yang, G.; Wu, C.-C.; Ye, Q. An Improved Fault Diagnosis Using 1D-Convolutional Neural Network Model. Electronics 2021, 10, 59. https://doi.org/10.3390/electronics10010059
Chen C-C, Liu Z, Yang G, Wu C-C, Ye Q. An Improved Fault Diagnosis Using 1D-Convolutional Neural Network Model. Electronics. 2021; 10(1):59. https://doi.org/10.3390/electronics10010059
Chicago/Turabian StyleChen, Chih-Cheng, Zhen Liu, Guangsong Yang, Chia-Chun Wu, and Qiubo Ye. 2021. "An Improved Fault Diagnosis Using 1D-Convolutional Neural Network Model" Electronics 10, no. 1: 59. https://doi.org/10.3390/electronics10010059
APA StyleChen, C.-C., Liu, Z., Yang, G., Wu, C.-C., & Ye, Q. (2021). An Improved Fault Diagnosis Using 1D-Convolutional Neural Network Model. Electronics, 10(1), 59. https://doi.org/10.3390/electronics10010059









