1. Introduction
In wireless communication, the contribution of automatic modulation classification (AMC) has grown dramatically because of its convenience in a wide range of applications [
1]. The AMC technique reduces the overhead caused by sharing modulation scheme between transmitter and receiver [
2]. For example, many military applications demand automatic detection of modulation schemes utilized by the signal from adversaries [
3,
4]. This type of application also incorporates signal jamming and interception. As a result, AMC plays an essential role in civilian and military applications regarding the recognition of received signals. For instance, digital modulation classification (MC) methods have had a paradigm shift from manual operational systems to automatic systems because of their several advantages. Manual modulation clarification (MMC) requires manual measurement of parameters of intercepted signals to recognize modulation types. In MMC, four types of information, namely, intermediate frequency time waveform, average and instantaneous spectra of signal, sound and signal, and instantaneous amplitude, are available for the search operator. Manual analysis becomes problematic and inaccurate when the number of intercepted modulation types increases. This method also requires experienced analyzers and does not guarantee reliable classification results. However, these shortcomings can be addressed via AMC. AMC is more powerful than MMC because it integrates an automatic modulation recognizer into an electronic receiver.
In prior works, two traditional processes have been executed to identify the modulation type of the received signal [
5,
6,
7]. They are maximum likelihood- and feature extraction-based modulation identification. The maximum likelihood-based classification method executes the likelihood function on the received signal [
8]. Examples of systems that use this approach are (i) faster maximum likelihood function-based MC [
9], (ii) expectation conditional maximization algorithm [
10], and (iii) sparse coefficient-based expectation maximization algorithm [
11].
Although the maximum likelihood-based classification method provides an optimal solution in AMC, it suffers from substantial computational complexity issues. It also demands the prior information of the transmitter. On the contrary, the feature-based AMC (FB-AMC) method has less computation time and does not require prior information about the transmitter. It relies on two significant processes, namely, feature extraction and classification [
7]. The higher-order statistics (HOS) features present in the time domain were considered by authors in [
12,
13] for MC. The authors in [
14] introduced compressive sensing aided FB-AMC, in which the cyclic feature was extracted to classify the modulation type of the signal.
Machine learning (ML)-based feature classification methods such as support vector machine (SVM), K-nearest neighbor (KNN), neural networks, and so on have been studied in many preceding papers associated with AMC. The authors in [
15] utilized the long short-term memory (LSTM) algorithm to classify the modulation type of the given signal. The deep hierarchical network-based algorithm was exploited in [
16] to perform effective MC. The extreme learning machine algorithm was utilized to classify the modulation type of the given signal in [
17]. Reference [
18] used a linear discriminant analysis (LDA) classifier to detect the accurate modulation type of the signal acquired from the transmitter.
From the detailed literature review (discussed in
Section 2), it can be seen that FB-AMC still faces drawbacks in the detection of accurate modulation type of the given signal. The reasons are as follows:
Significant preprocessing steps, such as blind equalization and sampling, are not considered before MC.
The lack of consideration of significant features, such as time and frequency, during the feature extraction process leads to a reduction in accuracy in feature extraction and classification.
Most FB-AMC methods cannot achieve high accuracy at low signal-to-noise ratio (SNR) rate due to the lack of concentration in enhancing the performance of ML-based classification algorithms.
AMC has gained much interest owing to its wide range of applications, such as electronic surveillance and electromagnetic signal monitoring. Nevertheless, it faces many difficulties during modulation detection [
19] because it does not utilize any prior knowledge, such as channel state information, signal-to-noise ratio (SNR), and noise characteristics. In the literature, many works have concentrated on feature-based MC. However, they did not consider effective preprocessing mechanisms to enhance the quality of the received signal [
20]. Likewise, ML-based feature extraction and classification have been exploited in many AMC-related works. Still, they are insufficient in enhancing accuracy in high and low SNR rates. Furthermore, ML-based algorithms introduce complexity into MC [
21]. Here, the machine learning algorithm uses high-order cumulant features with standard decision criteria. This issue has been resolved by a few works in FB-AMC. To address these downsides in current AMC studies, a new AMC, called AMC by using two-layer capsule network (TL-CapsNet) (AMC2N), is proposed. It has the following objectives:
To increase the quality of the received signal, before the MC process;
To increase the accuracy in feature extraction, even at a low SNR rate;
To enhance the performance of ML-based MC;
To enhance the accuracy, during classification for low and high SNR rates.
To achieve improved performance in MC, our AMC2N method contributes the following processes:
This work presents a novel TL-CapsNet model for the accurate classification of modulation schemes. The proposed TL-CapsNet differs from existing works by analyzing the real and imaginary parts of received signals.
Firstly, the AMC2N enhances received signal quality using a trilevel preprocessing method. This work executes three processes, namely, blind equalization, sampling, and quantization. The binary constant modulus algorithm (BCMA) is employed for the blind equalization, which evades the intersymbol interference (ISI) of the signal. Furthermore, sampling and quantization are performed to reduce aliasing effects and the bits necessary to represent the given signal. This proposed preprocessing method can enhance AMC accuracy.
Secondly, a novel TL-CapsNet is introduced to process the preprocessed signal. The TL-CapsNet has three major responsibilities, i.e., (i) feature extraction, in which the TL-CapsNet extracts all important features from the real and imaginary parts of the signal in parallel; (ii) feature clustering, in which all extracted features are clustered based on feature similarity factors in the TL-CapsNet to boost the classification process; and (iii) modulation classification.
Finally, the performance of the AMC2N method is evaluated using five validation metrics, including accuracy, precision, recall, F-Score, and computation time. The simulation results are compared with those of existing methods.
The rest of this paper is organized as follows: In
Section 2, we review prior works related to FB-AMC; in
Section 3, we provide a signal model of the proposed AMC2N method; in
Section 4, we explain the proposed AMC2N method with the proposed algorithms; in
Section 5, we elucidate the experimental evaluation of the proposed AMC2N method; and in
Section 6, we conclude the contribution of this study and discusses future directions.
3. Automatic Modulation Classification Signal
In wireless communication systems, a digitally modulated signal is represented as [
43]:
where
represents the inphase component,
represents the quadrature component,
represents the carrier frequency,
denotes the carrier frequency offset, and
represents the phase offset.
= 0 for ASK and FSK. Carrier frequency varies in FSK. The amplitude of the modulated signal is static, and the phase is variable for PSK modulation scheme. Hence,
and
components are changeable when
is constant in PSK modulation. QAM is the integration of ASK and PSK modulations, in which amplitude and phase are changeable.
Figure 2 depicts the communication system model of the AMC process at the receiver. In general, the deficiencies of the transmitter and receiver of the system introduce noise during signal transmission. Among numerous noises, Rayleigh fading and additive white Gaussian noise (AWGN) are the most common ones. AWGN does not cause phase offset and amplitude attenuation on the transmitted signal. Hence, the received signal is expressed as:
where
represents the additive white noise, which obeys the zero mean Gaussian distribution. This model is effective to portray the propagation of wired and communication frequency signals.
Rayleigh fading elucidates the Doppler shift and amplitude attenuation caused by refraction, reflection, and relative motion between the transmitter and receiver in the promulgation of a wireless signal. The received signal under this type of noisy environment is represented as:
where
denotes the path gain of the transmitted path ‘l’ and
represents the path gain of ‘l’ delay.
This study focuses on the classification of six modulation schemes, namely, ASK, FSK, QPSK, BPSK, 16-QAM, and 64-QAM. These modulation schemes are considered because they are widely utilized in civilian- and military-related applications [
43].
4. Proposed AMC Using a Feature Clustering-Based Two-Lane Capsule Network (AMC2N)
The design of the proposed AMC2N method is discussed in this section. This section is further segregated into multiple subsections for enhanced understanding of the proposed concept.
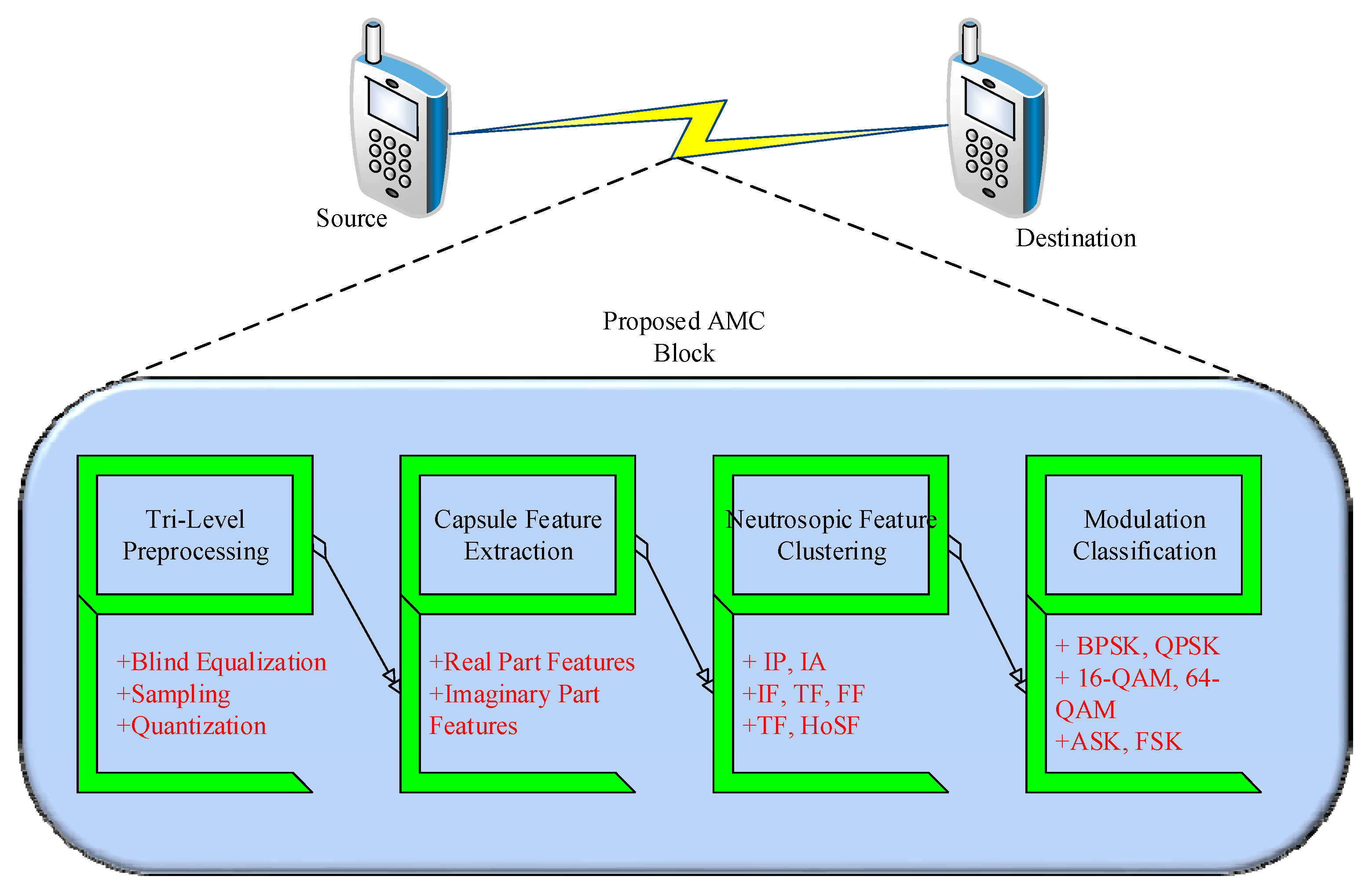
4.1. Conceptual Overview
The aim of this study is to design a robust AMC method to provide improved results under low and high SNR rates. To achieve this goal, AMC2N formulates four sequential stages, namely, trilevel preprocessing, capsule-based feature extraction, feature clustering, and classification, as depicted in
Figure 3.
In the first stage, three successive preprocessing steps, namely, blind equalization, sampling, and quantization, are applied. This stage is specifically designed to enhance the quality of the received signal. It executes the binary constant modulus algorithm (BCMA) to perform blind equalization, which evades the ISI of the signal. Sampling and quantization processes are performed to reduce the aliasing effects and bits required to represent the given signal.
In the second stage, the TL-CapsNet is used to improve feature extraction. To the best of our knowledge, no existing AMC utilizes a TL-CapsNet in FB-AMC. The TL-CapsNet algorithm is employed because it demonstrates satisfactory performance under low and high SNR rates. The preprocessed signal and estimated SNR value of the given signal are provided as input in the proposed TL-CapsNet. Seven essential features, namely, instantaneous amplitude, instantaneous phase, instantaneous frequency, time-domain features, frequency-domain features, transformation-domain features, and HOS features (cumulant and moment) are extracted. The features are extracted from the real and imaginary parts of the preprocessed signal to obtain enhanced results in the modulation recognition process. The TL-CapsNet uses two lanes to extract the features in parallel. Next, the extracted features are clustered based on feature similarity. The neutrosophic c-means (NCM) algorithm clusters the features from the real and imaginary parts of the signal. In general, the real part of a signal has a group of data, that is, the real-valued function, whereas the imaginary part contains zero. It can be determined by using complex Fourier transform [
44] on the received signal. In terms of the real and imaginary parts, the signal can be represented as:
where
represents the real part and
represents the imaginary part. In addition,
. Thus, implementing the MC process is easy, because NCM reduces the vast feature set of the signal. If a vast number of features are processed in the classifier, then, the performance of the classifier will degrade owing to the considerable amount of data processing. This work concentrates on six modulation schemes, specifically, QPSK, BPSK, ASK, FSK, 16-QAM, and 64-QAM. Subsequently, the performance of the proposed method is evaluated using six performance metrics, namely, feature extraction accuracy, classification accuracy, precision, recall, F-score, and computation time.
4.2. Trilevel Preprocessing
In FB-AMC scheme, preprocessing, plays a vital role because signal transmitted from the transmitter contains interference and noise, and thus degrades the performance of the FB-AMC system. Accordingly, the proposed AMC2N starts the process by improving the signal quality via trilevel preprocessing procedures, namely, blind equalization, sampling, and quantisation.
4.2.1. Blind Equalization
The main objective of blind equalization is to remove the ISI of the received signal, for example, in wireless communications systems, ISI occurs frequently because of limited bandwidth and multipath propagation [
45]. The BCMA method is used to perform equalization in the AMC2N method. BCMA is chosen because it has been proven to perform better than the existing CMA method [
46].
The BCMA method develops a new cost function and its iterative formula to eradicate the errors introduced by traditional CMA, such as excess and steady-state errors.
A received signal is expressed as [
46]:
where
represents the channel impulse response,
represents the transmitted data sequence, and
represents the noise.
To remove ISI, an equalizer is imposed on the received signal. The output acquired from the proposed blind equalizer is approximated as follows:
where
signifies the input signal vector of the equalizer. The vector
denotes the blind equalizer tap coefficient. The blind equalizer order is denoted as
. For each modulus value
, the respective attained samples are expressed as follows:
where
signifies the discriminate threshold, and
represents the partial discriminate value between
and the residual modulus values.
The cost function generated using the BCMA method is represented as:
where
and
are the modulus values of the constellation points.
The proposed BCMA method updates the cost functions by using the following equation:
where
denotes the step size and the sample
represented in Equation (8) belongs to the upcoming set:
where
signifies the group of utilized samples at the
iteration process.
All of the above-mentioned processes and equations are utilized in the blind equalization process. The received signal is firstly processed with the blind equalization process by using a blind equalizer before the decision-making process is performed to remove the ISI from the received signal.
4.2.2. Sampling
Sampling is performed to reduce the aliasing effect of the given signal. The sampling signal provides the discrete time signal from the continuous time signal [
47]. The notation
signifies the time interval amongst the samples, then, the moment at which the samples obtained are provided as
, where
. Hence, the discrete time signal
related to the continuous time signal is denoted as [
47]:
If a single sample occurs in each
second, then, the sampling frequency
is defined as:
The sampling frequency can also be defined in terms of the radians denoted by
as:
From these processes, the sampling of the received signal is conducted, in which the discrete time signal is converted into a continuous signal. The values of the continuous function for every second are also measured.
4.2.3. Quantization
Quantization is a significant process in modulation recognition [
48]. It produces a received signal that has a range of discrete finite values. This study focuses on performing nonuniform quantization because it provides less quantization error as compared with the uniform quantization process [
49]. We consider fixed signal
and utilize fixed positive integer
. The Lloyd-Max quantizer [
50] is adopted; it exploits two sets of parameters, as shown as follows:
Bin boundaries with min
Replacement values
The quantization function changes
values present in the bin (i.e., represented as (
)) with the value of
, which is expressed as [
49]:
The main goal of the Lloyd-Max quantizer is to reduce the quantization error, which is achieved via the following equation:
with these processes, the proposed Lloyd-Max quantizer algorithm quantizes the received signal, approximates the original signal, and separates the original signal from the added noise. It eases the further feature extraction and classification processes.
Figure 4 depicts the trilevel preprocessing steps. Briefly, blind equalization removes unwanted ISI from the signal. Next, sampling and quantization are performed to reduce aliasing and approximate the original signal. With the aid of these preprocessing procedures, the proposed AMC2N can improve the quality of received signals and enhance MC performance.
4.3. Two-Layer Capsule Network (TL-CapsNet)-Based AMC
Feature extraction and classification play a vital role in the MC of a given system. Most previous studies have concentrated on exploiting the CNN algorithm to extract features from a signal. Nonetheless, CNN loses the spatial information of a given signal during feature extraction, which leads to an inaccurate result in MC [
51]. To solve this issue in conventional CNN, this study proposes a TL-CapsNet.
The TL-CapsNet is a recent deep learning algorithm that functions better than conventional CNN in feature extraction and classification [
52]. We improve a TL-CapsNet by designing a novel TL-CapsNet architecture, as our work requires processing the real and imaginary parts of a signal. The proposed TL-CapsNet architecture is shown in
Figure 5.
As shown in the figure, the input signal (modulated signal) is fed into our TL-CapsNet model. In the proposed model, the real and imaginary parts of the signal are processed in two separate lanes, that is, the real lane and imaginary lane. Consideration of the real and imaginary parts of the signal improves the robustness of the work in low SNR scenarios. Each lane consists of a convolutional (Conv) layer, a convolutional capsule layer (with PrimaryCaps), and a hidden caps layer (DigitCaps). The proposed TL-CapsNet performs the following major processes:
Feature extraction;
Feature clustering;
Classification.
4.3.1. Feature Extraction
Unlike conventional CNN, the TL-CapsNet considers spatial information during feature extraction, which can lead to an improvement in feature extraction accuracy during AMC. The dynamic routing process of the TL-CapsNet assists in feature extraction. In general, dynamic routing is performed in the DigitCaps layer. As shown in
Figure 5, the real and imaginary parts and SNR of the signal are fed into the convolution layer of the TL-CapsNet. Next, a conventional integer encoding method is used for encoding. Encoding is the process of converting each input signal into codes. Each input signal is mapped into integer values. Next, the features in the signal are extracted in the primary caps, which match the ultimate caps in the DigitCaps layer. Ultimate high-level features can be extracted from the signal (real and imaginary parts) by processing the signal in the primary caps and DigitCaps. From the DigitCaps, we extract the features used in the NCM clustering.
Figure 3 illustrates the proposed TL-CapsNet for feature extraction. To the best of our knowledge, this study is the first to exploit a TL-CapsNet in FB-AMC. The proposed TL-CapsNet performs better than existing CNNs by producing an effective feature extraction process, which does not lose any spatial-related information of the signal [
53]. The convolutional layer comprises 256 × 9 convolutional kernels and a rectified linear unit (ReLU) activation function with stride 1. It primarily performs a convolutional operation to extract low-level features from the real and imaginary parts of a signal. After the low-level features are extracted, the output of the convolutional network is fed into two layers, namely, the primary cap and digit cap. The primary capsule refers to multidimensional entities at the lowest level and comprises the convolutional capsule layer incorporating 32 8D capsule channels individually for each primary capsule. The digit cap layer comprises 16D capsules for every digit class with 10 vectors.
It also requires less training time and data requirements to train the network. Furthermore, the TL-CapsNet can work under a new or unseen variation of a given input class without being trained with the data. This capability is essential in the proposed MC, because the received signal has large SNR rate variations (i.e., changes between low and high SNR rates). Thus, the proposed AMC2N can extract features under different SNR variations. The SNR is computed by considering the signal power (
) and noise power (
) extracted from the received signal as (
). For the SNR calculation, this work uses a conventional method, namely, split-symbol moment estimation, which is discussed in [
54]. The SNR is estimated through the following formulation:
where
is the average total power and
is the average power of the signal, which can be represented as:
The SNR is estimated for number of samples and . To extract features, the proposed TL-CapsNet considers input such as the preprocessed signal and estimated SNR of the given signal. SNR information is given as input to the TL-CapsNet to extract features under different SNR variations and increase the robustness of the proposed AMC2N to work within large SNR variations.
The TL-CapsNet considers the real () and imaginary () parts of the preprocessed signal. The real and imaginary parts of the signal are considered, because modulated signals change in phase and amplitude information with respect to the shape of the constellation diagram. This variation affects the imaginary and real parts of a complex signal. Thus, the proposed technique can work properly in such varied conditions by considering both parts. In the TL-CapNet, the dynamic routing procedure assists in the feature extraction. Feature extraction is performed by the PrimaryCaps. Furthermore, the features are matched in the hidden caps layer through the dynamic routing process. The dynamic routing process assists in providing the output of the primary capsules to the hidden capsules. The routing agreement works on the ability of the hidden capsules to predict the parent’s output.
Dynamic routing is performed between the two successive capsule layers (i.e., the primary cap and digit cap). It is exploited to resolve the issue in which a high-rate capsule transfers the output value of a low-rate capsule. All routing logits denoted as
are initialised as 0. The routing logits are updated by increasing the iteration level. The formula for updating the routing logits is given in [
51] as:
where:
where
represents the predicted vectors from the capsule layer
in the network,
represents the output from the capsule layer, and
represents the weighted matrix.
The total input in the first layer of the capsule is expressed as:
where
signifies the coupling coefficient obtained during the iterative process using the following equation:
The pseudocode for the proposed TL-CapsNet-based feature extraction is given as follows:
Pseudocode 1 depicts the processes involved in the capsule-based feature extraction and initializes the input and output nodes of the network. The aforementioned processes are used to extract features from the real and imaginary parts of the signal. Seven features, namely, instantaneous amplitude, instantaneous frequency, instantaneous phase, time-domain features, frequency-domain features, transformation-domain features, and HOS features are extracted from the received signal using the TL-CapsNet. HOS features play a vital role in MC, because they are robust under different SNR rates, thereby, increasing the efficacy of the proposed capsule-based feature extraction. Likewise, the extracted instantaneous features are highly significant in MC, because they provide the accurate condition of the received signal. On the basis of five primary features, this study further introduces 15 subfeatures. These features are considered to attain enhanced results in the classification process. Features are important to attain high accuracy during the classification process. The considered features are indicated in
Table 2.
| Pseudocode 1. Dynamic routing-based feature extraction in TL-CapsNet. |
Require:, SNR
Ensure: Extracted Features |
Initialize nodes (input and output);
Add Edges of nodes using broadcasting;
Design two-lanes
Divide into
Compute SNR
For each lane
//Routing------------
For all capsule in layer and capsule in layer ():
For (each iteration ) do
Computesoftmax function for all capsule in layer ;
Computesoftmax function for all capsule in layer
;
Updateweight using Equation (15);
End for
Emit (); |
4.3.2. Feature Clustering
Once the features are extracted in the primary caps and mapped in the DigitCaps, the features are clustered by computing similarity in the concatenate layer. In this stage, the NCM clustering process is proposed to restructure and reorganize the extracted features to improve the accuracy of the proposed AMC. If raw extracted features are directly given to the classification, then, the SoftMax layer must process the raw features on its own. Its performance could degrade if the features are affected by noises. Thus, clustering the features can help in grouping them into predetermined groups. In addition, this process can group noises into one specific group. By providing substantial systematically processed features, classification is believed to improve the classification of modulation schemes. As previously mentioned, a limited number of works have focused on reducing the difficulty faced by the classification module during modulation detection. In the present work, the AMC2N concentrates on reducing AMC difficulties via the feature clustering process. The clustering of feature vectors from real and imaginary parts is achieved by implementing the NCM algorithm. The proposed NCM clustering method is chosen, because it has been proven to demonstrate better performance than the fuzzy c-means clustering algorithm in terms of avoiding inaccurate results [
24].
Pseudocode 2 describes the procedures involved in the feature clustering process using the NCM algorithm. It requires three membership functions, namely, the truth set
, indeterminate set
, and false set
. It initially estimates the cluster center by using the following equation [
24]:
where
represents the weight vector and
denotes the constant value.
| Pseudocode 2. Feature clustering in TL-CapsNet. |
Require:
Ensure: Clustered features |
Initialize;
For (each feature do
EstimateCluster center () vector using Equation (22);
Estimate using Equation (23);
Update, , using Equations (25)–(27) respectively;
, , ;
If
Assign;
End If
If (
StopClustering Process;
Else
Continue estimation;
End If
End for |
The proposed NCM algorithm formulates the objective function to form clusters. The function is given as:
where
is estimated with respect to the indices of the first and second largest values of
obtained via comparison using the following equation:
where
and
are cluster members.
The first part of Equation (23) signifies the degree with respect to the main clusters, whilst the second part of the equation represents the degree with respect to the cluster boundary. The third part of the equation denotes the outlier or noise of the clusters.
The three membership functions are then updated using the following expressions:
where
signifies the constant parameter in the NCM clustering process.
With the aid of these processes, the proposed NCM algorithm clusters the features from the real and imaginary parts. It initially estimates the cluster center, and then formulates the objective function to cluster the features extracted from the real and imaginary parts of the signal. This study reduces the considerable feature set processing during classification through clustering.
In
Figure 6, NCM cluster-based feature clustering is depicted. The features extracted from each signal are clearly clustered into seven clusters. In the testing phase, comparing the features with the cluster centers instead of comparing each feature is possible.
4.3.3. Modulation Classification at Softmax Layer
After the feature clustering process in the concatenate layer, the signal is classified in the SoftMax layer. The output vector of the capsule is constructed using the squash function, which is expressed as:
where
represents the vector output of the capsule layer
. It is expressed in a probability manner; thus, it is adjustable between the values [0, 1]. Based on the squash function, the SoftMax layer determines the output-proposed modulation. The output is delivered by the fully connected dense layer with 128 units. For each class, margin loss is computed. For class
, the margin loss is given as:
where
is 1 if a sample is presented for class
and 0 otherwise. All other variables are the upper and lower bounds set in the range of [0, 1]. In this work, we consider
as 0.9 and
as 0.1. In the decoder unit, the features are reconstructed, and reconstruction loss is computed as follows:
Reconstruction loss is computed in terms of the mean squared error between the original signal
and reconstructed signal
. In our proposed TL-CapsNet, the current extracted features are compared with the cluster centroid, which is computed in the concatenate layer to produce the final classification output. Involvement of the feature clustering process in the TL-CapsNet minimizes classification time by reducing comparisons made among features. In
Figure 7, we provide the detailed pipeline architecture of the proposed work. When two nodes communicate with each other, the proposed AMC block is executed at the destination to identify the modulation scheme accurately.
In summary, the proposed AMC2N technique firstly performs trilevel preprocessing, namely, blind equalization, sampling, and quantization. ISI, aliasing, and noise in the received signal are removed to ease the proceeding processes. The proposed AMC2N technique extracts features from the real and imaginary parts of the signal using a TL-CapsNet, thereby, making the proposed AMC2N the first AMC technique to utilize a TL-CapsNet in three aspects. Firstly, features are extracted in parallel through two lanes for the real and imaginary parts. Secondly, the extracted features are clustered in the concatenate layer to boost the classification process. Lastly, the SoftMax layer classifies the benefits of the algorithms included in the proposed AMC2N, which are summarized in
Table 3.
5. Result and Discussion
This section is dedicated to a description of the investigation of the performance of the proposed AMC2N method by using the simulation results. To characterize the efficacy of the proposed AMC2N method, this section is further divided into three subtopics, namely, experimental setup, result analysis, and research summary.
5.1. Experimental Setup
In this subsection, the simulation scenario of the proposed AMC2N method is discussed. For evaluation purposes, this study generates simulated training and test signals with 1024 samples for MC by using the parameters presented in
Table 4. Signals with six modulation schemes, namely, QPSK, BPSK, ASK, FSK, 16-QAM, and 64-QAM are generated. In
Table 5, the value of all parameters proposed method are included.
The generated signals are incorporated with AWGN for SNR rates between −10 and 10 dB. The objective of incorporating AWGN is to evaluate the capability of the proposed AMC2N to work under a noisy environment.
To validate the performance of the proposed AMC2N approach, five performance metrics, namely, accuracy, precision, recall, F-score, and computation time, are considered.
Accuracy (
) is the most instinctual metric to measure the system performance. It is measured by computing the ratio of the correctly estimated modulation scheme to the original modulation scheme of the received signal. It can be approximated as follows:
where
represents the true positive,
represents the true negative,
represents the false positive, and
represents the false negative. As the work is about multi-class classification, we construct confusion matrix by considering actual class and predicted class for all classes. Then, we compute the metrics from the confusion matrix.
Precision (
) is one of the crucial metrics to measure the exactness of the AMC2N approach. It is measured by estimating the ratio of the relevant MC result to the total obtained modulation result. It is expressed as follows:
Recall (
) is a significant metric to measure the completeness of the proposed AMC2N approach. It is estimated by calculating the total amount of the relevant MC results that are actually retrieved. It is expressed in mathematical form as follows:
F-score (
) validation is used to measure the accuracy of the test results. It is defined as the joint evaluation of the precision and recall parameters. It is expressed as follows:
Computation time is essential to validate the efficacy of the proposed AMC2N approach in terms of providing computational processing time that is as low as possible. It is measured by considering time elapsed to complete the MC process.
5.2. Result Analysis
The simulation results of the proposed AMC2N are compared with those of existing methods, in particular, CNN [
38], R-CNN [
39], CL [
40], and LBP [
41]. The reason behind selecting these methods for comparison is that the contributions of these methods are similar to the contributions, i.e., preprocessing, feature extraction, and classification of the proposed method.
Table 6 describes the comparison of the existing methods with their core intention, modulation scheme considered, performance under SNR variations, and downsides. The notations of × and √ signify the poor and moderate performance, respectively, of the existing methods under SNR variations.
All parameters are tested under two scenarios, as follows:
Scenario 1 (with varying SNR rates): In this scenario, the SNR range is varied, and the number of samples is fixed. This scenario is considered to prove the efficacy of our proposed work in varying SNR ranges, that is, low and high SNR scenarios from −10 dB to 10 dB with an increasing step of 2 dB.
Scenario 2 (with varying sample numbers): In this scenario, the SNR value is fixed, and the number of samples is varied. In this scenario, the efficacy of the proposed TL-CapsNet is tested using low and high numbers of samples from 25 to 200 with an increasing step of 25.
5.2.1. Effect of Accuracy
Accuracy is examined in both scenarios to evaluate the efficacy of our proposed work. Feature extraction and classification accuracy is determined in both scenarios. The accuracy of the proposed method is compared with that of existing methods, such as CNN, R-CNN, CL, and LBP.
Figure 8 and
Figure 9 present the results of the percentage accuracy of the feature extraction process for Scenarios 1 and 2.
As presented in
Figure 8, the proposed AMC2N approach demonstrates better performance than the existing methods in Scenario 1. The results show that the proposed TL-CapsNet demonstrates a high performance of more than 95% under low and high SNR rates. The introduction of the real and imaginary parts of a given signal assists the proposed AMC2N to extract accurate features, which enhances the feature extraction performance. In general, in prior works, feature extraction is performed by neglecting the imaginary parts of a signal, which is the reason behind low accuracy. In addition, we compute the SNR as a feature and include it in the feature extraction process to improve accuracy. As a result, performance is enhanced from 80% to 90% for −10 dB to −2 dB values and up to more than 90% subsequently. The analysis shows that accuracy increases as the SNR range increases. Similarly, when the SNR is reduced to lower than −10 dB, accuracy will degrade. However, variation in the accuracy range is 16% for SNR variations. Thus, the proposed AMC2N can maintain accuracy better than the existing methods even in low SNR ranges. Moreover, the feature extraction performance of the other methods is poor. This result can be attributed to their inefficiency in extracting features under low SNR rates (i.e., feature extraction accuracy is less than 50% for an SNR from −10 dB to −2 dB). On the basis of the results, the proposed method can successfully increase accuracy to a maximum of 58% under low SNR rates and to 20% in high SNR rates as compared with the other methods.
In
Figure 9, the accuracy of the proposed and existing methods is compared in Scenario 2, that is, based on varying sample sizes. The sample size denotes the number of samples considered for classification. The proposed method achieves better accuracy than the existing methods. This result also supports the advantage of the proposed work processes for the real and imaginary parts of the signal. Moreover, the proposed model can learn more features than the existing methods. Thus, the proposed method achieves improved accuracy up to 70% even with small sample sizes. Furthermore, the proposed work can achieve feature extraction accuracy of over 45%, which is greater than that of the existing CNN, R-CNN, CL, and LBP models at 25 samples.
In
Figure 10, classification accuracy is compared in Scenario 1, and as expected, the proposed AMC2N is the best AMC method. It can successfully demonstrate accuracy of more than 95% for all SNR rates. This result is observed, because feature extraction is a significant classification process. Moreover, the proposed work attains superior accuracy in feature extraction in both scenarios, which indicates that classification accuracy is likewise improved. Feature clustering reduces classification complexity and helps improve the performance of the proposed AMC2N. CNN, R-CNN, and CL demonstrate a classification accuracy of only more than 75% for 8 dB and 10 dB SNR rates. The LBP method produces the worst classification rate, in which classification accuracy for 8 dB and 10 dB tested SNR rates is less than 72%. The existing methods demonstrate poor classification accuracy as compared with the proposed AMC2N approach, especially under low SNR rates (i.e., accuracy of less than 50% from −10 dB to −2 dB SNR rates). These methods use raw extracted features, which are large in number. This condition leads to an increment in the model complexity of the existing methods, which affects their classification accuracy. The main issue to note is that the proposed AMC2N method achieves accuracy of up to 95%. The analysis shows that the proposed work achieves the objective of accurate classification in low SNR scenarios. This result is obtained, because the proposed AMC2N initially augments the received signal through optimum preprocessing steps. Next, the noiseless signal is obtained and further processed for classification. In the classification, the proposed TL-CapsNet classifier considers the SNR range of the current signal as input. In addition, the separation of the real and imaginary parts of the signal for feature extraction improves accuracy. In general, the proposed AMC2N method successfully increases the accuracy percentage by up to 59% under low SNR rates and up to 18% under high SNR rates as compared with the existing methods.
In
Figure 11, classification accuracy is verified based on varying sample sizes. When the sample size is small, the existing methods (i.e., CNN, R-CNN, and so on) demonstrate accuracy, as they require enormous amounts of samples for effective classification. In real time, a signal is affected by noises, which are not processed in prior works. However, the proposed work demonstrates accuracy higher than 65%, even with 25 samples, owing to the involvement of optimum feature learning and feature clustering processes.
In
Figure 12, the accuracy confusion matrix for the proposed AMC2N is presented. Most of the different types of modulation signals are classified correctly, which is above 90%. This result shows that the proposed AMC2N demonstrates high capability in classifying different types of modulation signals.
5.2.2. Effect of Precision
Precision is measured in both scenarios to evaluate the efficacy of our proposed work. The precision performance of the proposed AMC2N method is compared with that of the existing methods.
Figure 13 and
Figure 14 present the results of the precision percentage.
Figure 13 and
Figure 14 show that the performance of the proposed AMC2N method is better than that of the existing methods in both scenarios. This superiority is achieved via our proposed mechanisms before the MC process. Our work initially improves the quality of the received signal through trilevel preprocessing. Three preprocessing steps, namely, blind equalization, sampling, and quantization, are performed to enhance the quality of the received signal. The three processes remove ISI, aliasing, and noise from the signal. If these deficiencies are removed from the received signal, then, signal quality is improved. This process of enhancing received signal quality provides improved feature extraction and classification results. Thus, performance is enhanced under the proposed work even for signals with low SNR rates. Moreover, we achieve improved results with small sample amounts.
The existing methods perform poorly as compared with our proposed work. In addition, they lack effective preprocessing steps, such as blind equalization, sampling, and quantization. Thus, the precision measure is affected during the evaluation process. CNN, R-CNN, and CL achieve high precision of more than 80%, and LBP has a precision rate of less than 80% at an SNR of 10 dB. These state-of-the-art methods achieve less than 30% at −10 dB and less than 85% at 10 dB. By contrast, our proposed method increases accuracy by up to a maximum of 58% at −10 dB and a minimum of 20% at 10 dB as compared with the existing methods. Furthermore, our proposed work achieves accuracy higher than 65% with 25 samples.
5.2.3. Effect of Recall
The recall validation metric is measured by varying the sample size and SNR range to prove the efficacy of the proposed work. The recall metric of the proposed method is compared with that of the existing methods.
Figure 15 and
Figure 16 show that the recall performance of the proposed method is better than that of the other methods, with varying SNR ranges and sample sizes. Substantial features are required to achieve an improved recall result in AMC. Hence, our proposed AMC2N method extracts features from real and imaginary parts of the signal. Six different features, namely, instantaneous features (amplitude, frequency and phase), time-domain features, frequency-domain features, transformation-domain features, and HOS features are extracted. These features play a vital role in the classification of modulation schemes. Among them, HOS features are robust to SNR variations, and thus can enhance classification performance.
The existing methods provide poor results in recall performance as compared with the proposed work owing to their inefficiency in extracting effective features in the feature extraction process. CNN, R-CNN, CL, and LBP achieve recall lower than 30% when the sample size is small and 50% under low SNR rates. In the worst scenario, the proposed work demonstrates better performance than the existing works.
5.2.4. Effect of F-Score
The F-score measure is evaluated in the two scenarios. The F-score metric of the proposed method is compared with that of the existing methods.
Figure 17 and
Figure 18 show that the performance of the proposed work, in terms of the F-score measure, is better than that of the existing methods. This superiority is attributed to our proposed similar feature clustering-based modulation scheme classification process. Clustering extracted features reduces the difficulty of the ML-based classifier. We provide input as the center value of each cluster feature, and thus avoid substantial feature processing in the ML-based classifier. Hence, our work enhances F-score performance during MC.
The existing methods demonstrate poor F-score performance as compared with the proposed work owing to their poor performance in handling the substantial number of features extracted from the given signal. They achieve less than 83% at an SNR of −10 dB and more than 95% at an SNR of 10 dB. Moreover, they achieve more than 60% with low sample amounts and 96% with high sample amounts. The proposed method increases F-score performance by up to a maximum of 26% at 10 dB and a minimum of 58% at −10 dB as compared with the existing methods.
5.2.5. Effect of Computation Time
Computation time is measured by increasing the sample size considered in the classification. The computation time of the proposed method is compared with that of the existing methods.
As shown in
Figure 19, the proposed method requires less computation time than the existing methods. Our proposed TL-CapsNet performs fast and reduces training time. Furthermore, involvement of the feature clustering process reduces the time needed to classify the modulation scheme of the given signal. Our proposed model processes only cluster center feature values, and thus requires less time as compared with vast feature processing. Hence, our method reduces computation time as compared with the existing methods.
The existing methods require considerable computation time to implement the FB-AMC. They require 112 ms for 25 samples and 312 ms for 200 samples. Specifically, CL and LBP need more than 500 ms for 200 samples. By contrast, our proposed method reduces computation time to a maximum of 255 ms for 200 samples and a minimum of 72 ms for 25 samples as compared with the existing methods.
5.2.6. Impact of TL-CapsNet in Results
This research introduces a new capsule-based feature extraction procedure to boost AMC accuracy. The results show that the proposed method achieves improved accuracy and performs well even in low SNR scenarios. In this section, we compare the results of our proposed work with those of the existing methods.
In the absence of a TL-CapsNet, that is, with CapsNet, accuracy is low, specifically, lower than 75%. By incorporating a TL-CapsNet, accuracy can be improved by up to 96%. In
Table 7, we compare the proposed work with the base algorithms. At the same time, the absence of NCM clustering directly affects feature extraction accuracy by up to 88%. This accuracy level is achieved with the help of a TL-CapsNet with reconstruction mechanisms. Classification accuracy is also affected, as it relies on extracted features. In addition, the feature clustering process directly affects computation time, that is, the proposed method with a feature clustering process reduces computation time by up to 50 ms, which is 12 ms less than that of the base algorithms. Overall, the proposed work achieves improved performance in terms of accuracy and time consumption.
5.2.7. Complexity Analysis
In this subsection, we analyse the complexity of the proposed AMC approach and compare the complexity with the existing works. The comparison is summarized in
Table 8.
The analysis summarizes the complexity of proposed and existing works. It can be seen that the complexity of proposed approach is lower than the existing works. The complexity of the proposed work includes computations needed by preprocessing () and classification ). Thus, the proposed approach achieves promising outcomes with lower complexity.
6. Conclusions
The contributions of AMC to digital wireless communication systems have increased dramatically. This study aims to achieve improved MC accuracy under low and high SNR rates. In this regard, a robust AMC method, namely, the AMC2N, is proposed. The AMC2N executes four significant processes to achieve enhanced performance. Moreover, preprocessing is executed to enhance the quality of the received signal by applying three sequential processes, namely, blind equalization, sampling, and quantization. We design a novel TL-CapsNet that performs feature extraction, feature clustering, and classification. Seven sets of significant features are extracted from the imaginary and real parts of the signal, which are clustered to boost the classification. Finally, classification is performed in the SoftMax layer with a modified loss function. It considers six modulation schemes for classification, specifically, QPSK, BPSK, ASK, FSK, 16-QAM, and 64-QAM. The experiment results show that the proposed AMC method demonstrates superior performance. The fusion of four important phases in the proposed work supports the improved efficiency. The acquired results are compared with those of existing methods (i.e., CNN, R-CNN, CL, and LBP) in terms of accuracy, precision, recall, F-score, and computation time. The results prove that the proposed AMC2N method outperforms the existing methods in all the metrics.