Reliability and Economic Efficiency Analysis of 4-Leg Inverter Compared with 3-Leg Inverters
Abstract
:1. Introduction
2. Three-Phase 3-Leg and 4-Leg Inverter
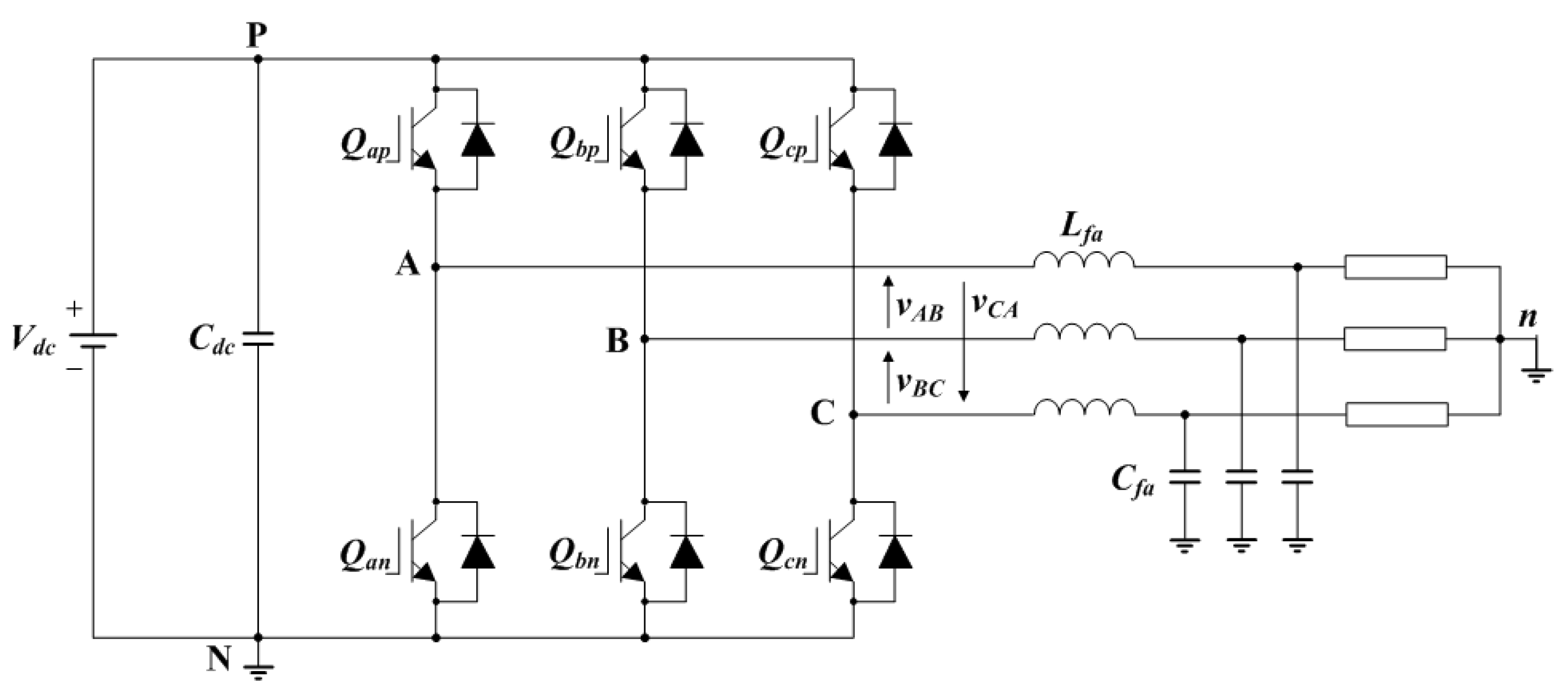
2.1. 3-Leg Inverter
2.2. 3-Leg Inverter Employing Split DC-Link Capacitor
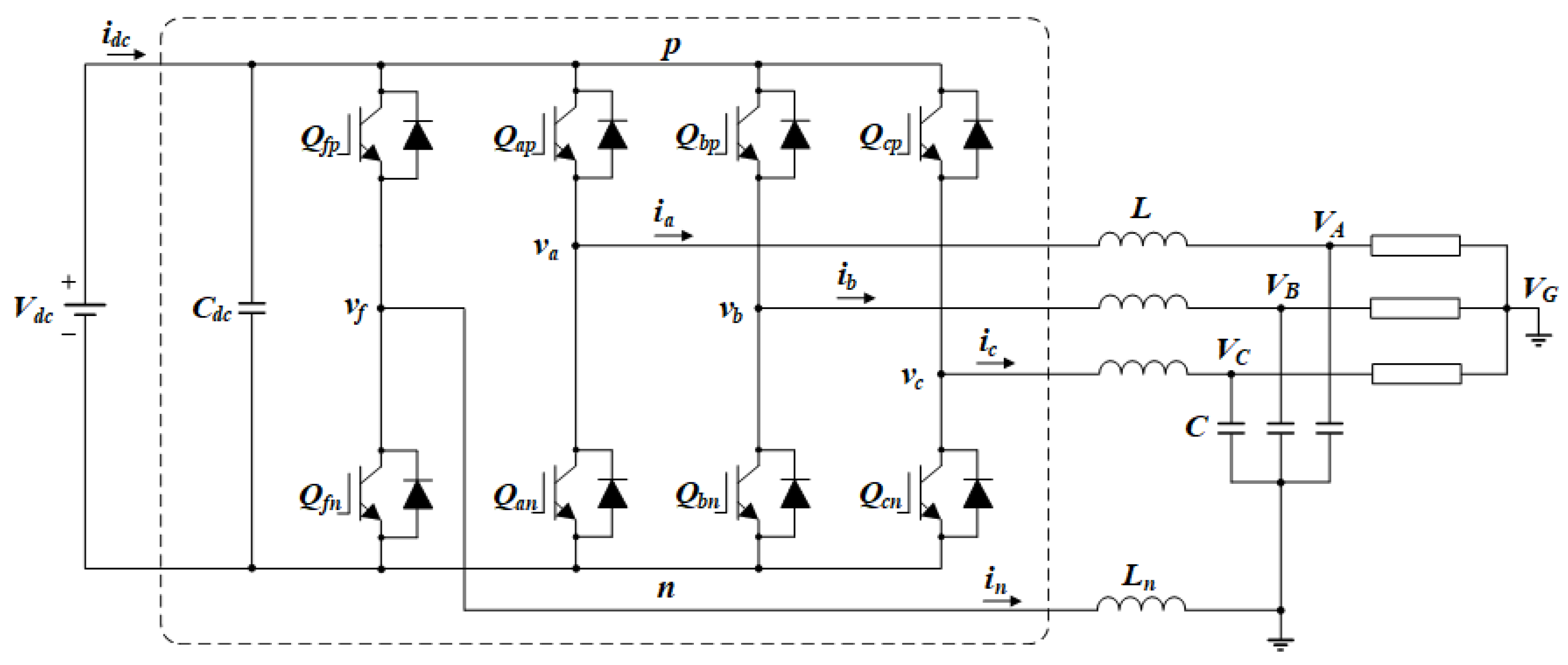
2.3. 4-Leg Inverter
3. Reliability Analysis of Inverters
3.1. Calculation of Part Failure Rate by MIL-HDBK-217F
3.1.1. Failure Rate of IGBT
3.1.2. Failure Rate of DC-Link Capacitor
3.1.3. Failure Rate of Filter Capacitor
3.1.4. Failure Rate of Filter Inductor
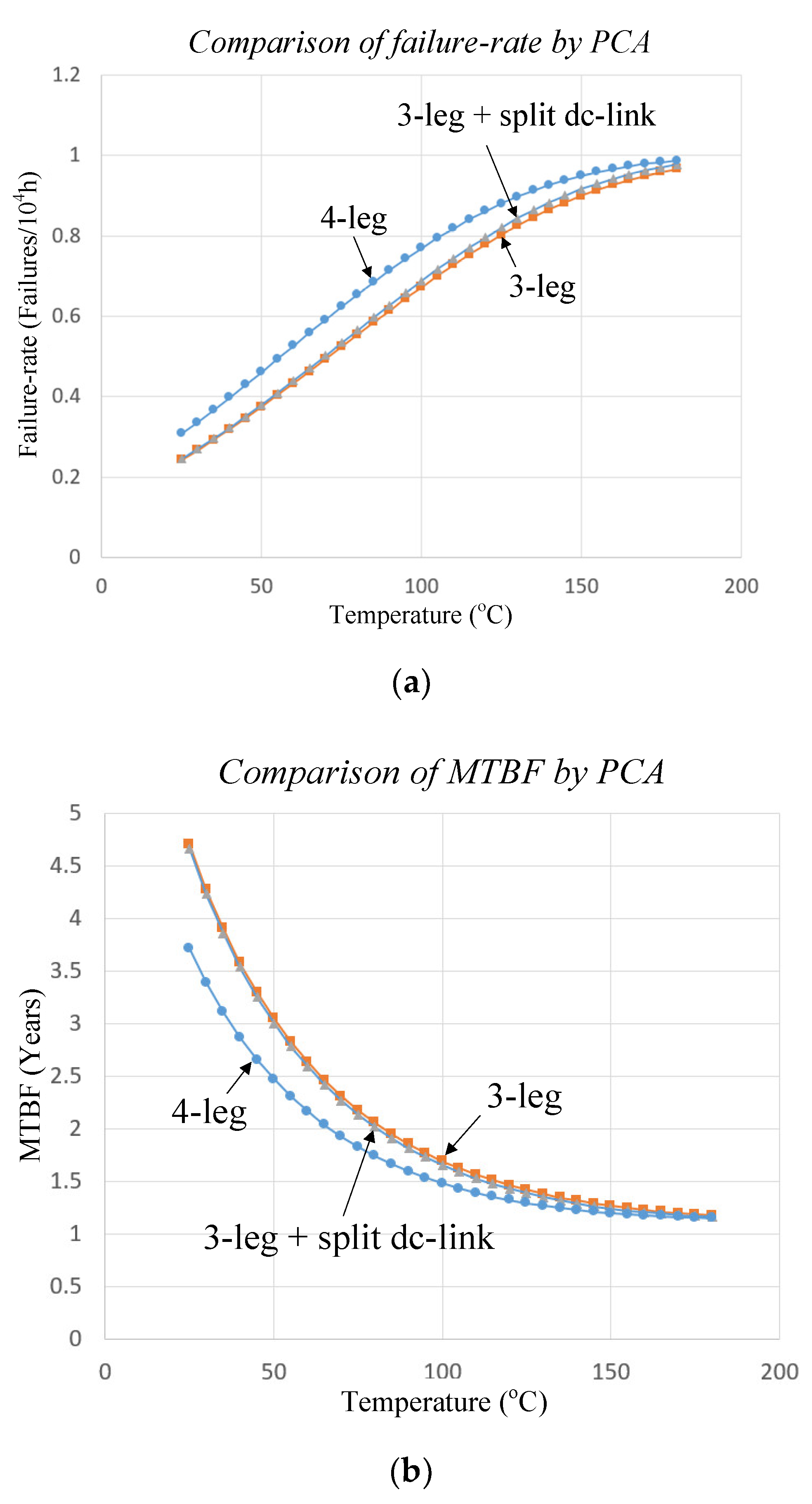
3.2. Failure Rate by Part Count Failure Analysis (PCA)
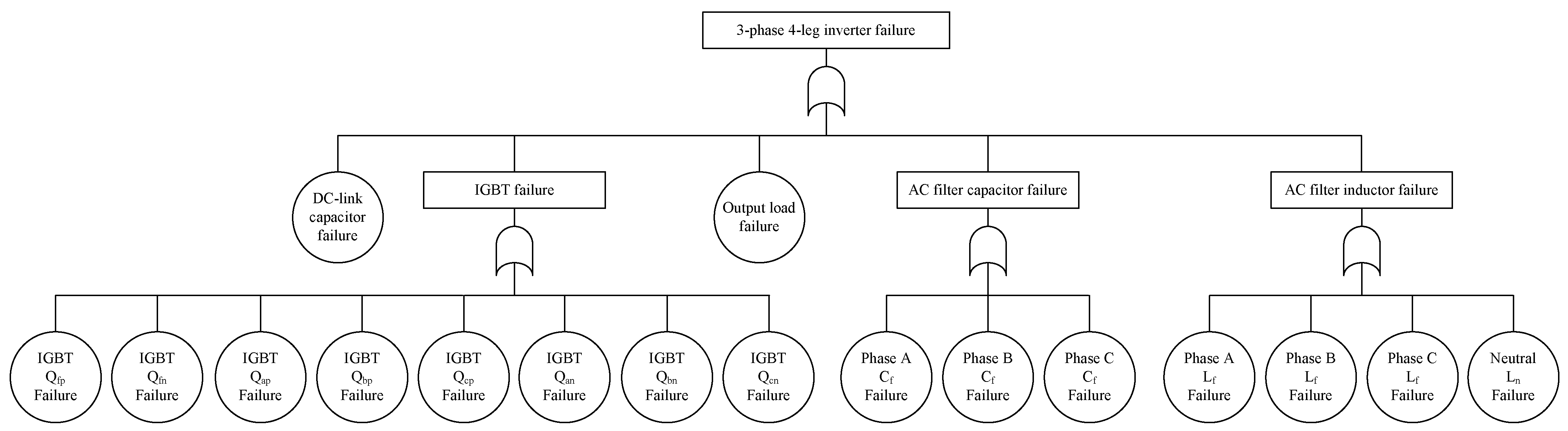
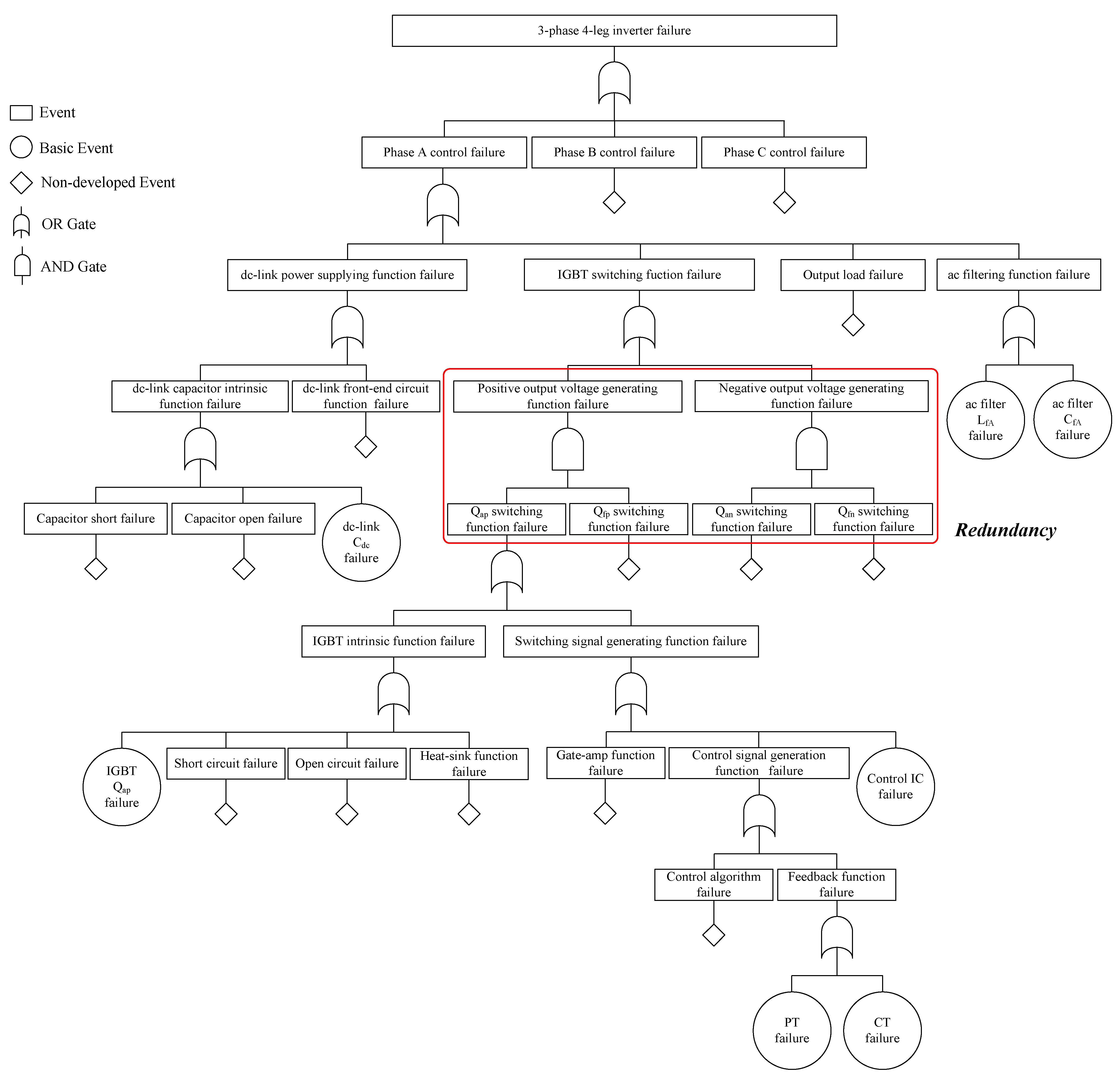
3.3. Failure Rate by Fault-Tree Analysis (FTA)
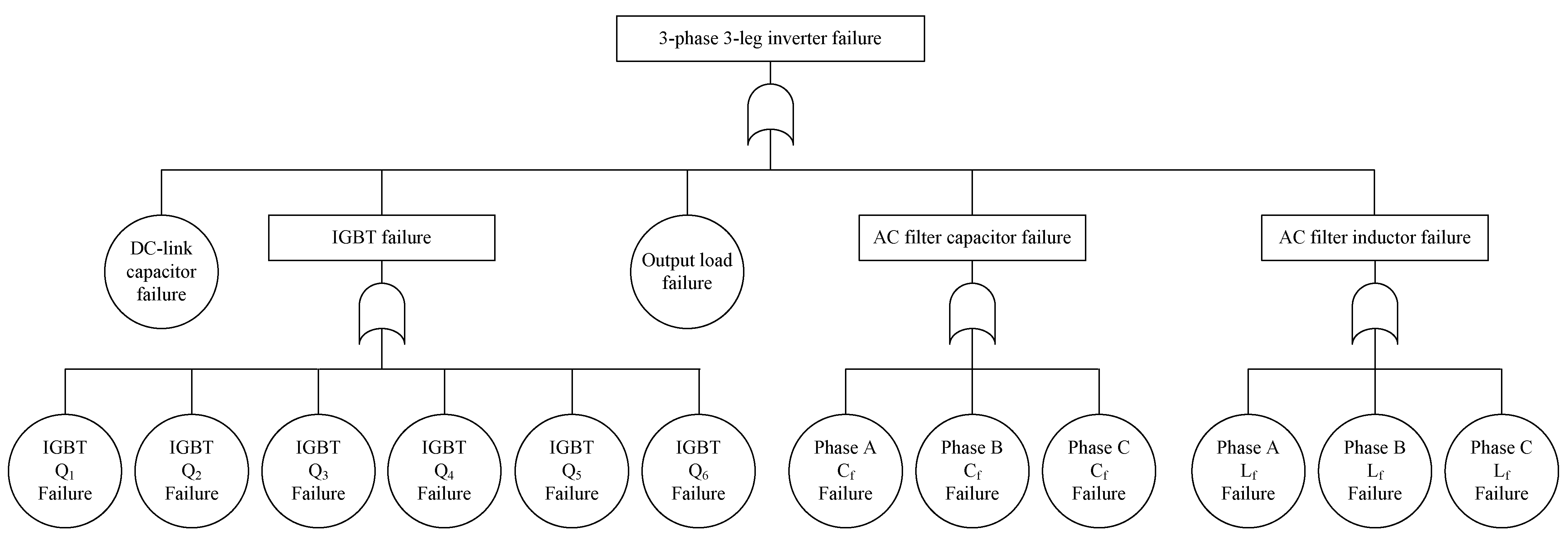
3.3.1. Fault-Tree Design of 3-Leg Inverter
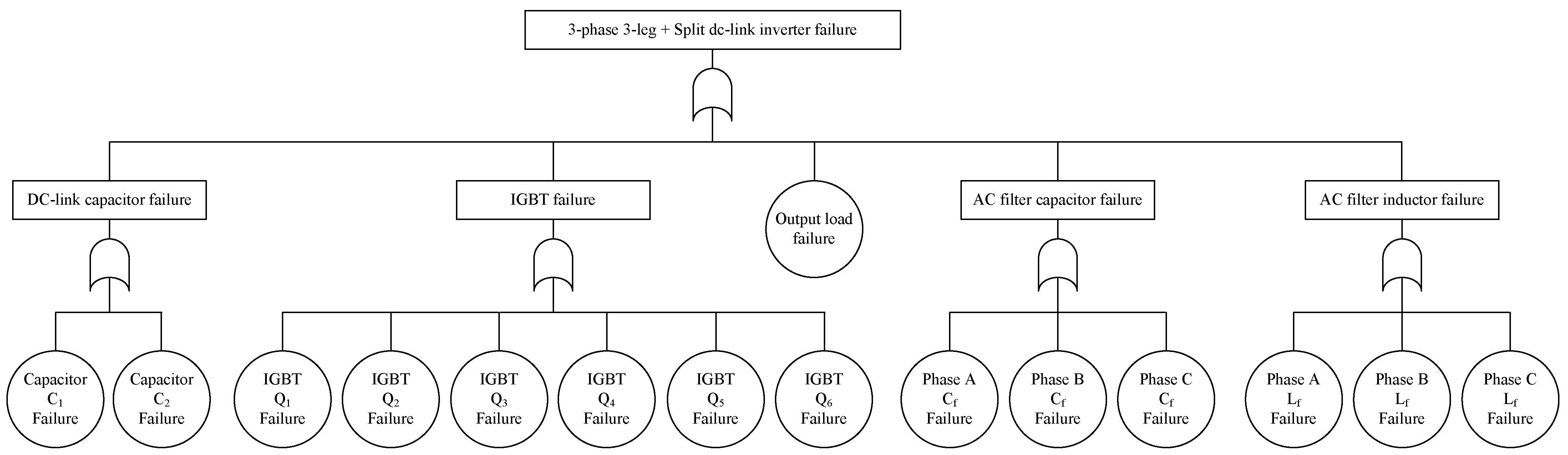
3.3.2. Fault-Tree Design of 3-Leg Inverter Employing Split DC-Link Capacitors
3.3.3. Fault-Tree Design of 4-Leg Inverter
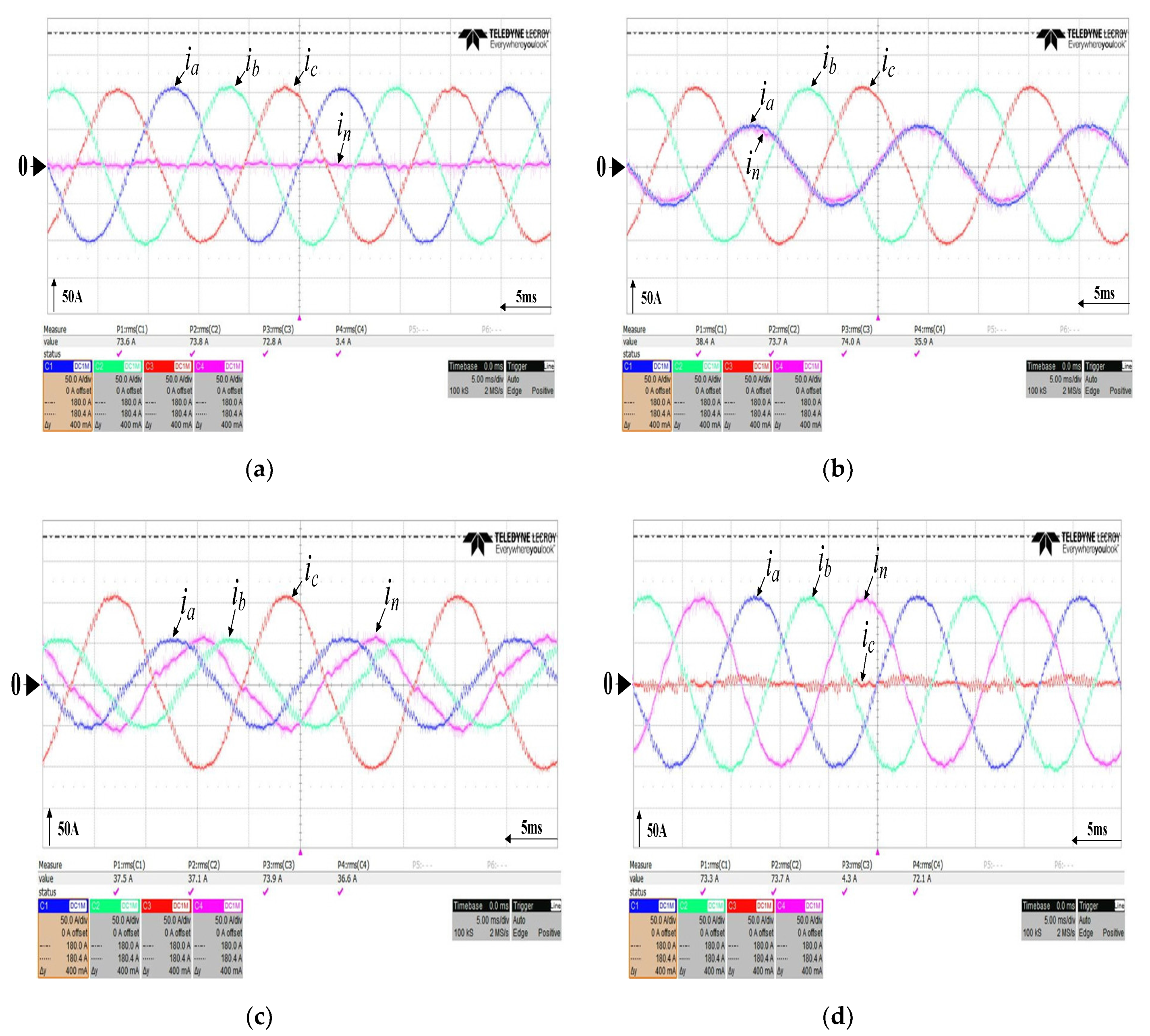
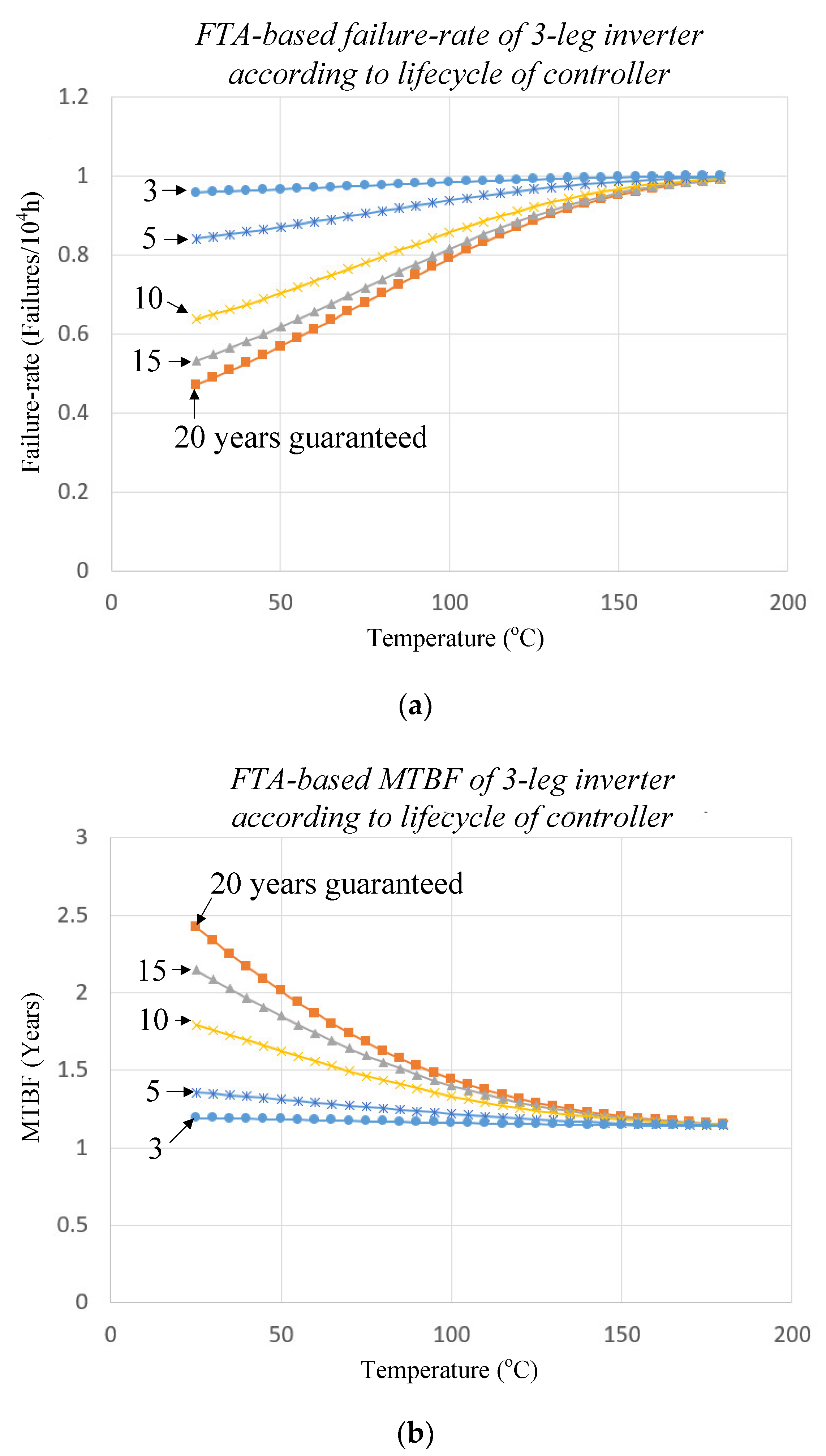
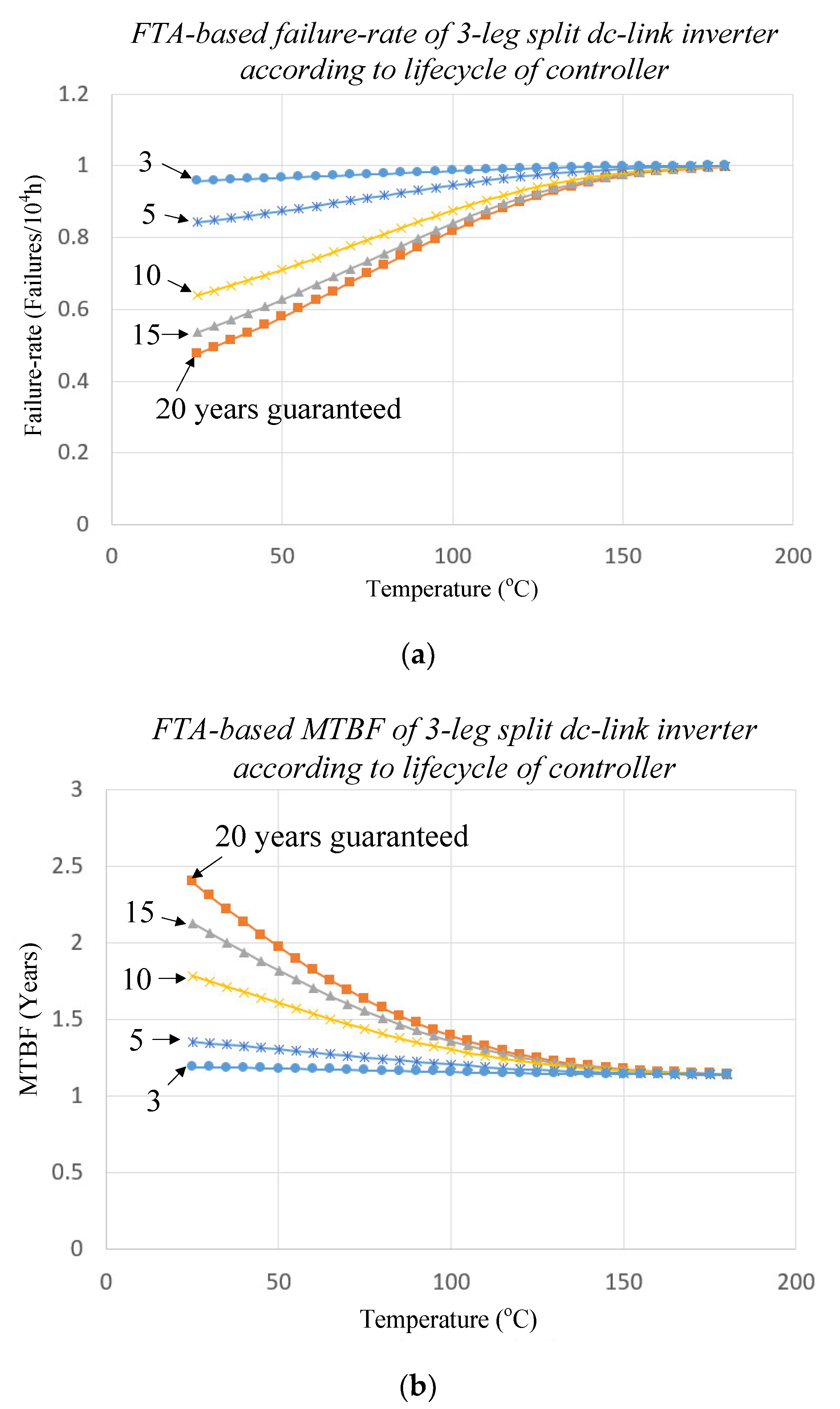
3.4. Failure Rate of the Three-Phase Inverter According to the Reliability of the Controller
4. Economic Efficiency Analysis of Inverter
4.1. Cost Model of IGBT
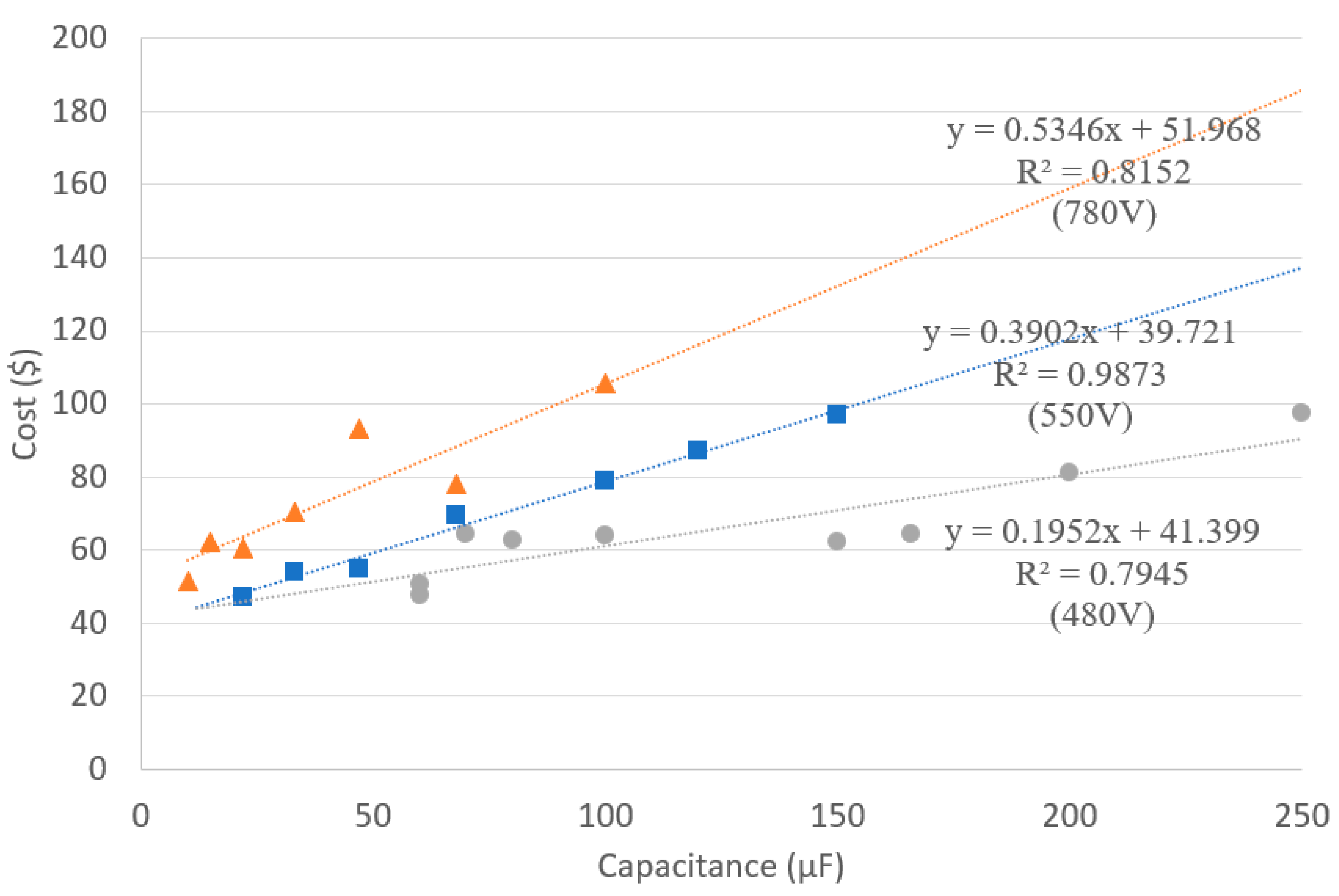
4.2. Cost Model of Capacitor
4.2.1. Cost Model of DC-Link Capacitor
4.2.2. Cost Model of Filter Capacitor
4.3. Cost Model of Filter Inductor
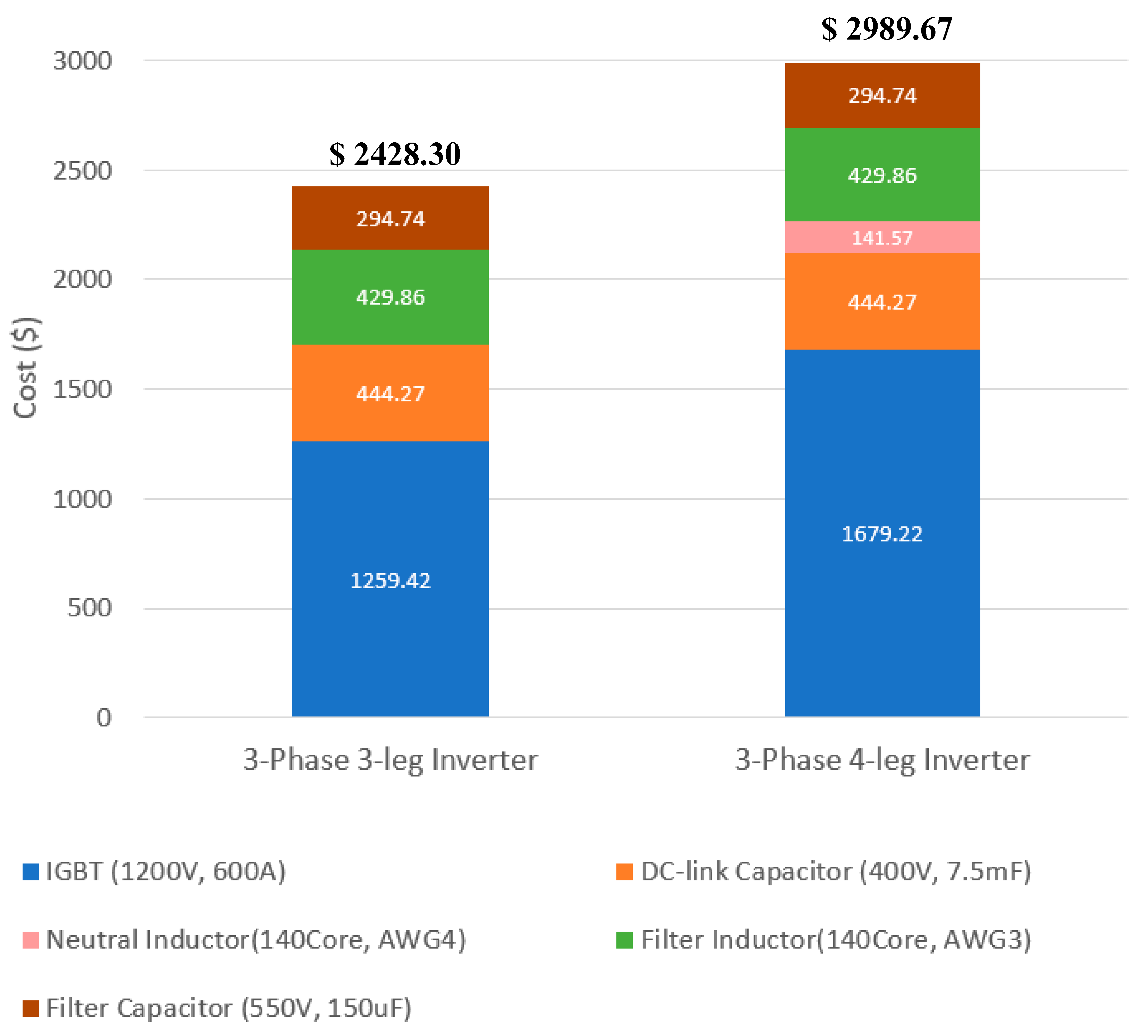
4.4. Cost Comparison of the Inverter Using the Part Cost Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Douglass, P.J.; Trintis, I.; Munk-Nielsen, S. Voltage unbalance compensation with smart three-phase loads. In Proceedings of the Power Systems Computation Conference, PSCC 2016, Genoa, Italy, 20–24 June 2016; pp. 1–7. [Google Scholar]
- Hu, J.; Fu, X.; Liao, T.; Chen, X.; Ji, K.; Sheng, H.; Zhao, W. Low Voltage Distribution Network Line Loss Calculation Based on The Theory of Three-phase Unbalanced Load. In Proceedings of the 3rd International Conference on Intelligent Energy and Power Systems, IEPS 2017, Hangzhou, China, 10 October 2017; pp. 65–71. [Google Scholar]
- Lin, F.; Tan, K.; Lai, Y.; Luo, W. Intelligent PV Power System with Unbalanced Current Compensation Using CFNN-AMF. IEEE Trans. Power Electron. 2019, 34, 8588–8598. [Google Scholar] [CrossRef]
- Han, J.; Oh, Y.S.; Gwon, G.H.; Kim, D.U.; Noh, C.H.; Jung, T.H.; Lee, S.J.; Kim, C.H. Modeling and Analysis of a Low-Voltage DC Distribution System. Resources 2015, 4, 713–735. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Konikkara, D.D.; Monti, A. A generalized approach for harmonics and unbalanced current compensation through inverter interfaced distributed generator. In Proceedings of the IEEE 5th International Symposium on Power Electronics for Distributed Generation Systems, PEDG 2014, Galway, Ireland, 24–27 June 2014; pp. 1–8. [Google Scholar]
- Bifaretti, S.; Lidozzi, A.; Solero, L.; Crescimbini, F. Comparison of modulation techniques for active split dc-bus three-phase four-leg inverters. In Proceedings of the IEEE Energy Conversion Congress and Exposition, ECCE 2014, Pittsburgh, PA, USA, 14–18 September 2014; pp. 14–18. [Google Scholar]
- Lin, Z.; Ruan, X.; Jia, L.; Zhao, W.; Liu, H.; Rao, P. Optimized Design of the Neutral Inductor and Filter Inductors in Three-Phase Four-Wire Inverter With Split DC-Link Capacitors. IEEE Trans. Power Electron. 2019, 34, 247–262. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, J.; Li, J. Modeling, Analysis, and Mitigation of Load Neutral Point Voltage for Three-Phase Four-Leg Inverter. IEEE Trans. Ind. Electron. 2013, 60, 2010–2021. [Google Scholar] [CrossRef]
- Hadidian Moghaddam, M.J.; Kalam, A.; Miveh, M.R.; Naderipour, A.; Gandoman, F.H.; Ghadimi, A.A.; Abdul-Malek, Z. Improved Voltage Unbalance and Harmonics Compensation Control Strategy for an Isolated Microgrid. Energies 2018, 11, 2688–2714. [Google Scholar] [CrossRef] [Green Version]
- Chee, S.J.; Kim, H.S.; Sul, S.K.; Ko, S. Common-Mode Voltage Reduction of Three-Level Four-Leg PWM Converter. IEEE Trans. Ind. Appl. 2015, 51, 4006–4016. [Google Scholar] [CrossRef]
- Zhang, R.; Prasad, V.H.; Boroyevich, D.; Lee, F.C. Three-dimensional space vector modulation for four leg voltage source converters. IEEE Trans. Power Electron. 2002, 17, 314–326. [Google Scholar] [CrossRef]
- Aissani, M.; Aliouane, K. Three-dimensional space vector modulation for four-leg voltage-source converter used as an active compensator. In Proceedings of the International Symposium on Power Electronics, Electrical Drives, Automation and Motion, SPEEDAM 2010, Pisa, Italy, 14–16 June 2010; pp. 1416–1421. [Google Scholar]
- Golwala, H.; Chudamani, R. New Three-Dimensional Space Vector-Based Switching Signal Generation Technique without Null Vectors and With Reduced Switching Losses for a Grid-Connected Four-Leg Inverter. IEEE Trans. Power Electron. 2016, 31, 1026–1035. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, P.; Zhao, S.; Gao, J.; Sun, X. Research on a discontinuous three-dimensional space vector modulation strategy for the three-phase four-leg inverter. In Proceedings of the IEEE 8th International Power Electronics and Motion Control Conference, IPEMC-ECCE Asia 2016, Hefei, China, 22–26 May 2016; pp. 575–580. [Google Scholar]
- Llonch-Masachs, M.; Heredero-Peris, D.; Montesinos-Miracle, D.; Rull-Duran, J. Understanding the three and four-leg inverter Space Vector. In Proceedings of the 18th European Conference on Power Electronics and Applications, EPE ECCE Europe 2016, Karlsruhe, Germany, 5–9 September 2016; pp. 1–10. [Google Scholar]
- Kim, J.H.; Sul, S.K. A carrier-based PWM method for three-phase four-leg voltage source converters. IEEE Trans. Power Electron. 2004, 19, 66–75. [Google Scholar] [CrossRef]
- Kim, J.H.; Sul, S.K.; Kim, H.; Ji, J.K. A PWM strategy for four-leg voltage source converters and applications to a novel line interactive UPS in a three phase four wire system. In Proceedings of the 39th IEEE Industry Applications Conference, IAS 2004, Seattle, WA, USA, 3–7 October 2004; pp. 2202–2209. [Google Scholar]
- Kim, S.Y.; Song, S.G.; Park, S.J. Minimum Loss Discontinuous Pulse-Width Modulation Per Phase Method for Three-Phase Four-Leg Inverter. IEEE Access 2020, 8, 122923–122935. [Google Scholar] [CrossRef]
- Gamini Jayasinghe, S.D.; Mahinda Vilathgamuwa, D.; Madawala, U.K. A Dual Inverter-Based Supercapacitor Direct Integration Scheme for Wind Energy Conversion Systems. IEEE Trans. Ind. Appl. 2013, 49, 1023–1030. [Google Scholar] [CrossRef]
- Reliability prediction of electric equipment. In Rep. MIL-HDBK-217F; Department of Defense, Washington DC, Tech.: Washington, DC, USA, 1991; Available online: http://everyspec.com/MIL-HDBK/MIL-HDBK-0200-0299/MIL-HDBK-217F_14591 (accessed on 3 January 2021).
- Choudhary, K.; Sidharthan, P. Reliability Prediction of Electronic Power Conditioner (EPC) using MIL-HDBK-217 based Parts Count Method. In Proceedings of the International Conference on Computer, Communication and Control, IC4 2015, Indore, India, 10–12 September 2015. [Google Scholar]
- Mou, H.; Hu, W.; Sun, Y.; Zhao, G. A Comparison and Case Studies of Electronic Product Reliability Prediction Methods Based on Handbooks. In Proceedings of the International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering, QR2MSE 2013, Chengdu, China, 15–18 July 2013; pp. 112–115. [Google Scholar]
- Jones, J.; Hayes, J. A comparison of electronic-reliability prediction models. IEEE Trans. Reliab. 1999, 48, 127–134. [Google Scholar] [CrossRef]
- Yeo, S.C.; Kang, F.S. Fault-Tree Based Failure-Rate Analysis for Boost Converter and Interleaved Boost Converter. J. Electr. Eng. Technol. 2019, 14, 2375–2387. [Google Scholar] [CrossRef]
- Kang, F.S.; Song, S.G. Fault-Tree Based Failure-Rate Analysis for Clamped-double Submodule employing dc-short current protecting function. J. Electr. Eng. Technol. 2020, in press. [Google Scholar] [CrossRef]
- Khalil, M.; Soulatiantork, P. Reliability assessment of PV inverters. In Proceedings of the 14th IMEKO TC10 Workshop Technical Diagnostics, New Perspectives in Measurements, Tools and Techniques for System’s Reliability, Maintainability and Safety 2016, Milan, Italy, 27–28 June 2016; pp. 389–393. [Google Scholar]
- Shoults, L.W. Implementation of Design Failure Modes and Effects Analysis for Hybrid Vehicle Systems. Master’s Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, May 2016. [Google Scholar]
- Basu, J.B. Failure Modes and Effects Analysis (FMEA) of a Rooftop PV System. Int. J. Sci. Eng. Res. 2015, 3, 51–55. [Google Scholar]
- MIL-STD-1629A, Procedures for Performing a Failure Mode, Effects and Criticality Analysis, November 1980. Available online: https://www.fmea-fmeca.com/milstd1629.pdf (accessed on 3 January 2021).
- IEC-60182, Analysis Techniques for System Reliability-Procedure for Failure Mode and Effects Analysis (FMEA). 2006. Available online: https://webstore.iec.ch/preview/info_iec60812%7Bed2.0%7Den_d.pdf (accessed on 3 January 2021).
- Burkart, R.; Kolar, J.W. Component cost models for multi-objective optimizations of switched-mode power converters. In Proceedings of the IEEE Energy Conversion Congress and Exposition ECCE 2013, Denver, CO, USA, 15–19 September 2013; pp. 2139–2146. [Google Scholar]
- Domingues-Olavarría, G.; Fyhr, P.; Reinap, A.; Andersson, M.; Alaküla, M. From Chip to Converter: A Complete Cost Model for Power Electronics Converters. IEEE Trans. Power Electron. 2017, 32, 8681–8692. [Google Scholar] [CrossRef]
- Valchev, V.C.; Bossche, A.V. Inductors and Transformers for Power Electronics, 1st ed.; CRC Press: Boca Raton, FL, USA, 2005; pp. 33–42. [Google Scholar]









| Item | Values |
|---|---|
| Output power | 100 kW |
| Output voltage (line-to-neutral) | 380 V, 60 Hz |
| DC-link voltage | 600 V |
| DC-link capacitance | 15.5 mF |
| Switching device | IGBT CM600HA-24H |
| ac filter for A, B, C phase legs | 660 μH |
| ac filter inductor for neutral leg | 330 μH |
| ac filter capacitor for each phase | 150 μH |
| MTBF (Year) | MTBF (Day) | MTBF (h) | Failure Rate (Failures/104h) |
|---|---|---|---|
| 3 | 1095 | 26,280 | 0.380517504 |
| 5 | 1825 | 43,800 | 0.228310502 |
| 10 | 3650 | 87,600 | 0.114155251 |
| 15 | 5475 | 131,400 | 0.076103501 |
| 20 | 7300 | 175,200 | 0.057077626 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kwak, Y.-g.; Heo, D.-h.; Kim, S.-P.; Song, S.-G.; Park, S.-J.; Kang, F.-s. Reliability and Economic Efficiency Analysis of 4-Leg Inverter Compared with 3-Leg Inverters. Electronics 2021, 10, 87. https://doi.org/10.3390/electronics10010087
Kwak Y-g, Heo D-h, Kim S-P, Song S-G, Park S-J, Kang F-s. Reliability and Economic Efficiency Analysis of 4-Leg Inverter Compared with 3-Leg Inverters. Electronics. 2021; 10(1):87. https://doi.org/10.3390/electronics10010087
Chicago/Turabian StyleKwak, Yun-gi, Dae-ho Heo, Sun-Pil Kim, Sung-Geun Song, Sung-Jun Park, and Feel-soon Kang. 2021. "Reliability and Economic Efficiency Analysis of 4-Leg Inverter Compared with 3-Leg Inverters" Electronics 10, no. 1: 87. https://doi.org/10.3390/electronics10010087
APA StyleKwak, Y.-g., Heo, D.-h., Kim, S.-P., Song, S.-G., Park, S.-J., & Kang, F.-s. (2021). Reliability and Economic Efficiency Analysis of 4-Leg Inverter Compared with 3-Leg Inverters. Electronics, 10(1), 87. https://doi.org/10.3390/electronics10010087







