Sub-THz and THz SiGe HBT Electrical Compact Modeling
Abstract
:1. Introduction
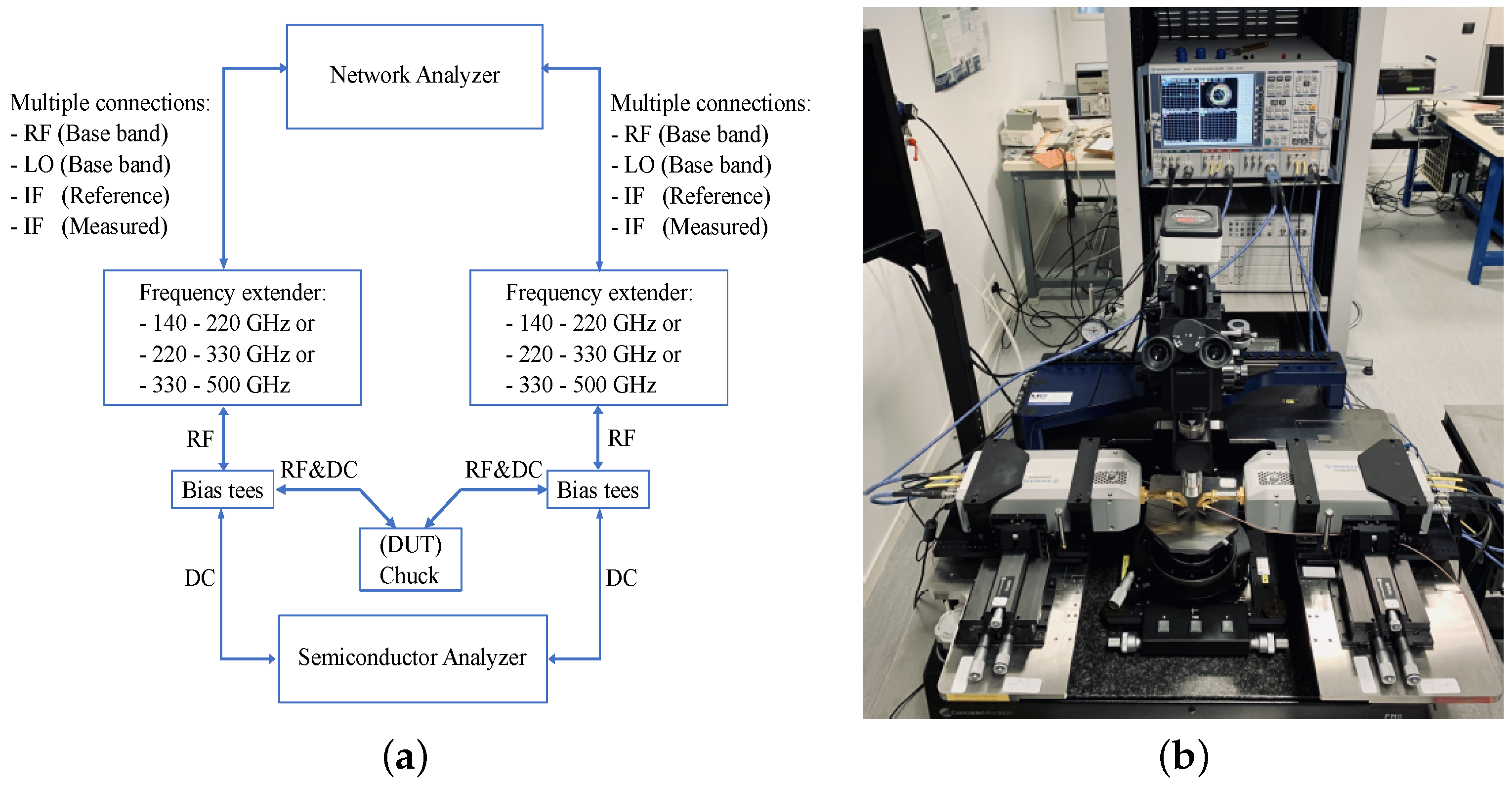
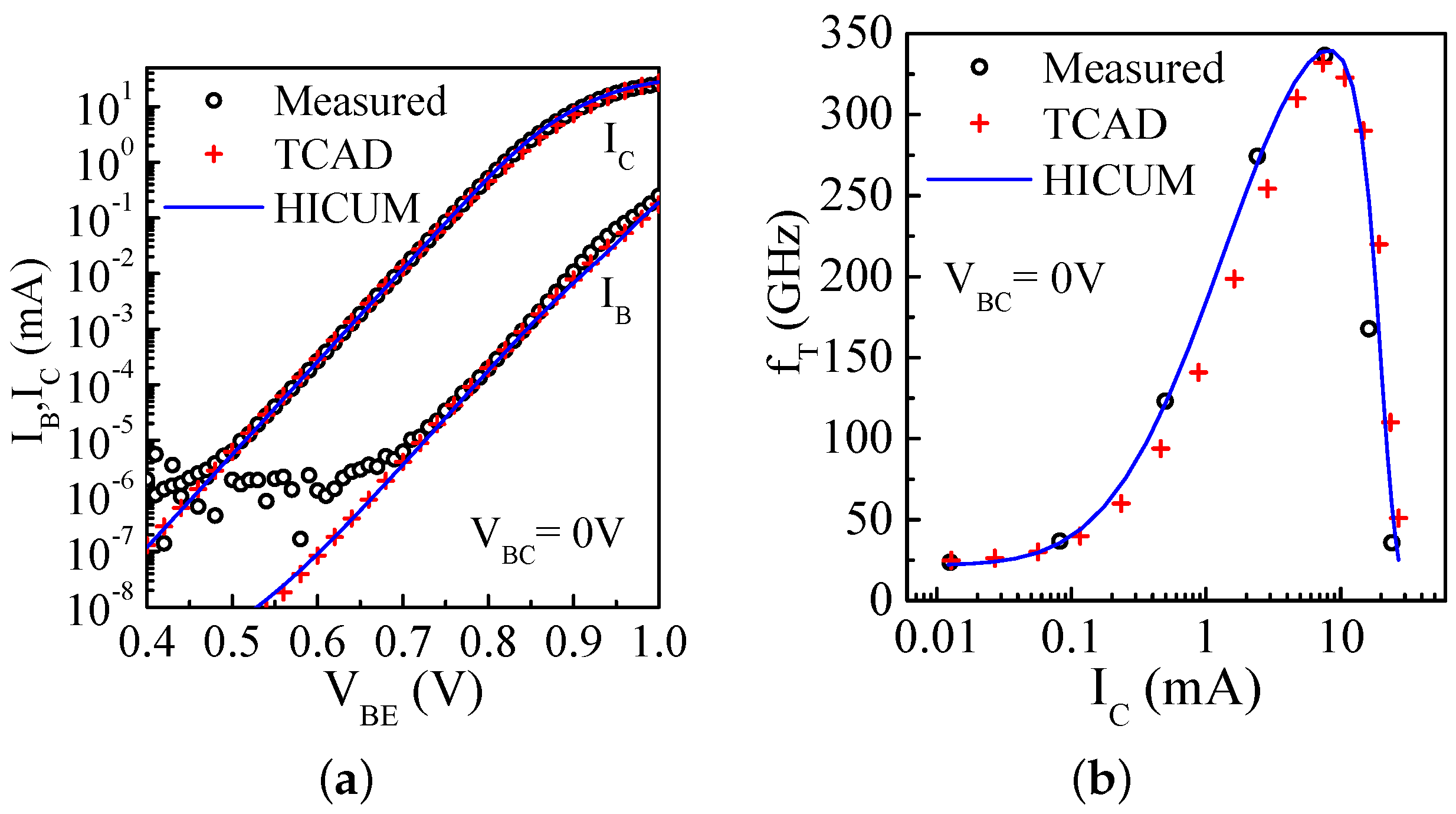
2. Measurement Setup, TCAD Calibration and Quasi-Static Modeling
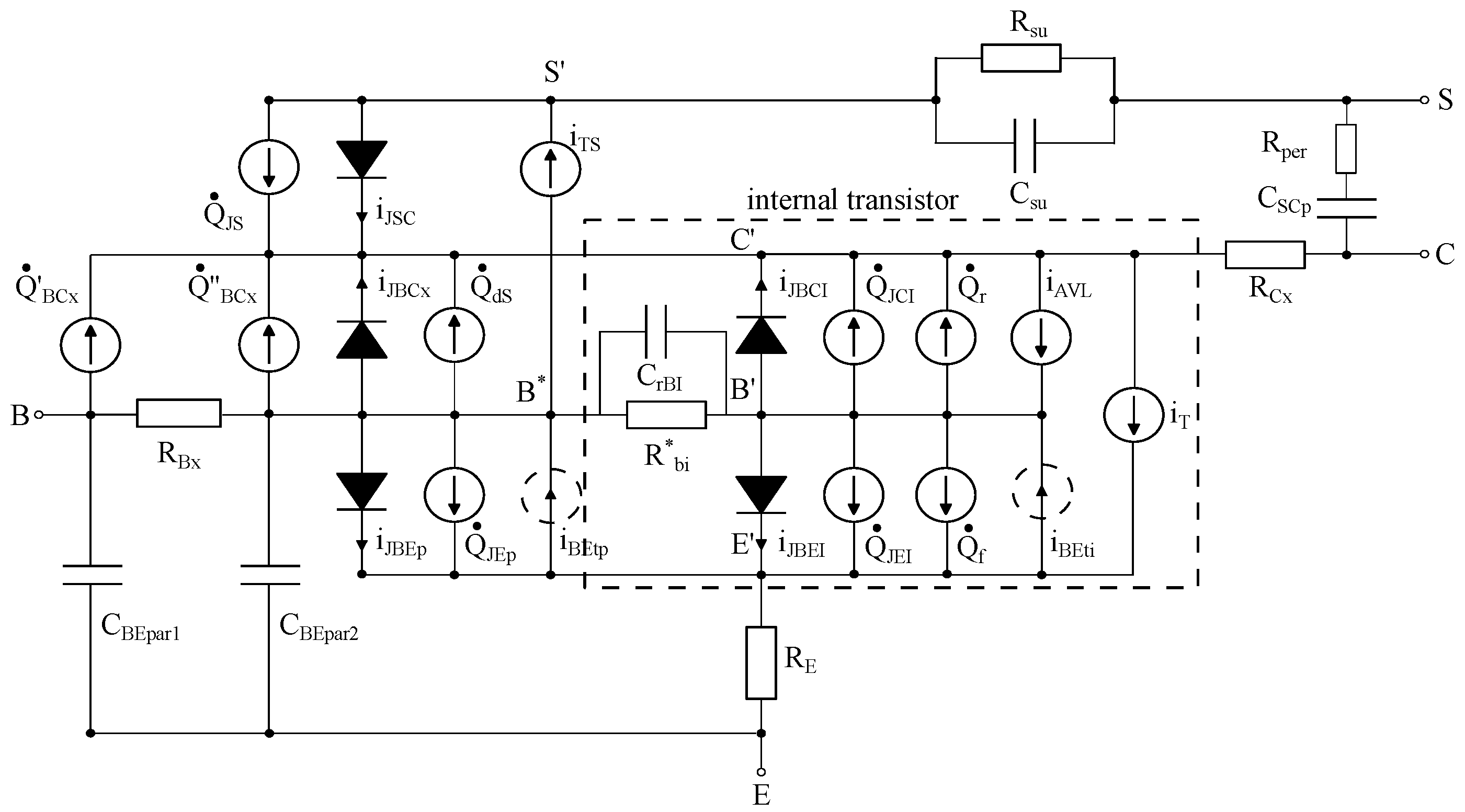
3. High-Frequency Model Parameter Estimation
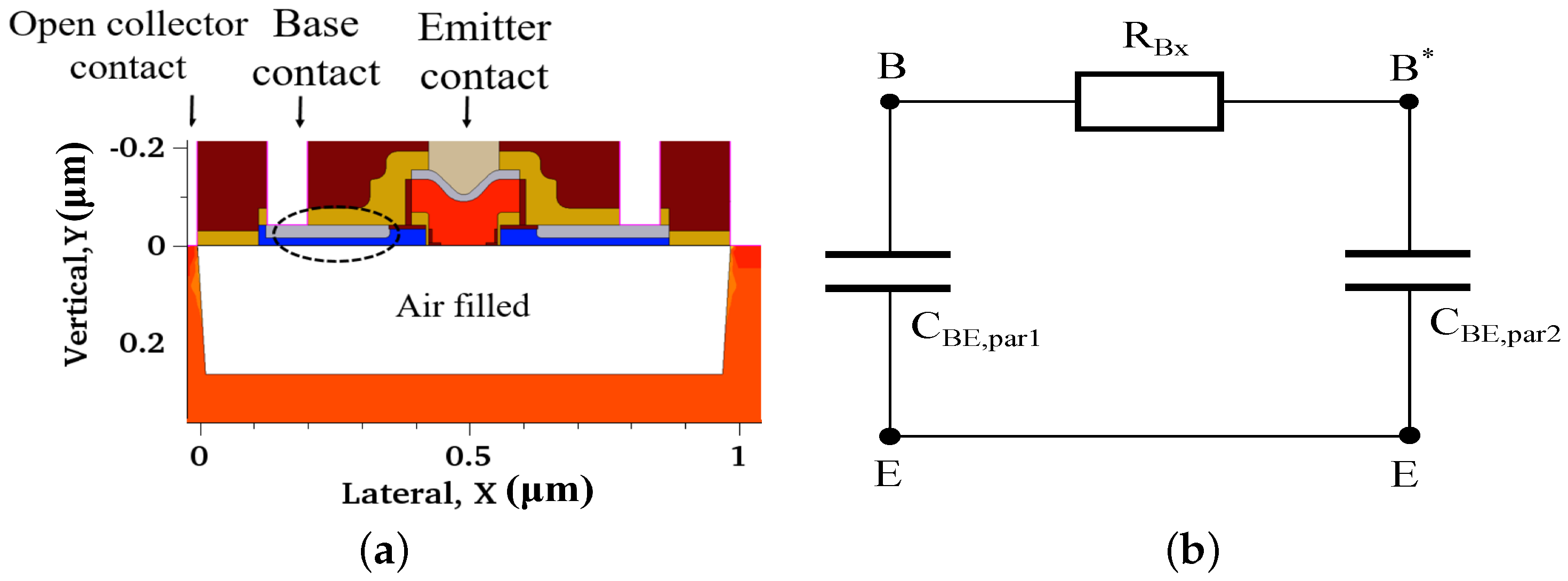
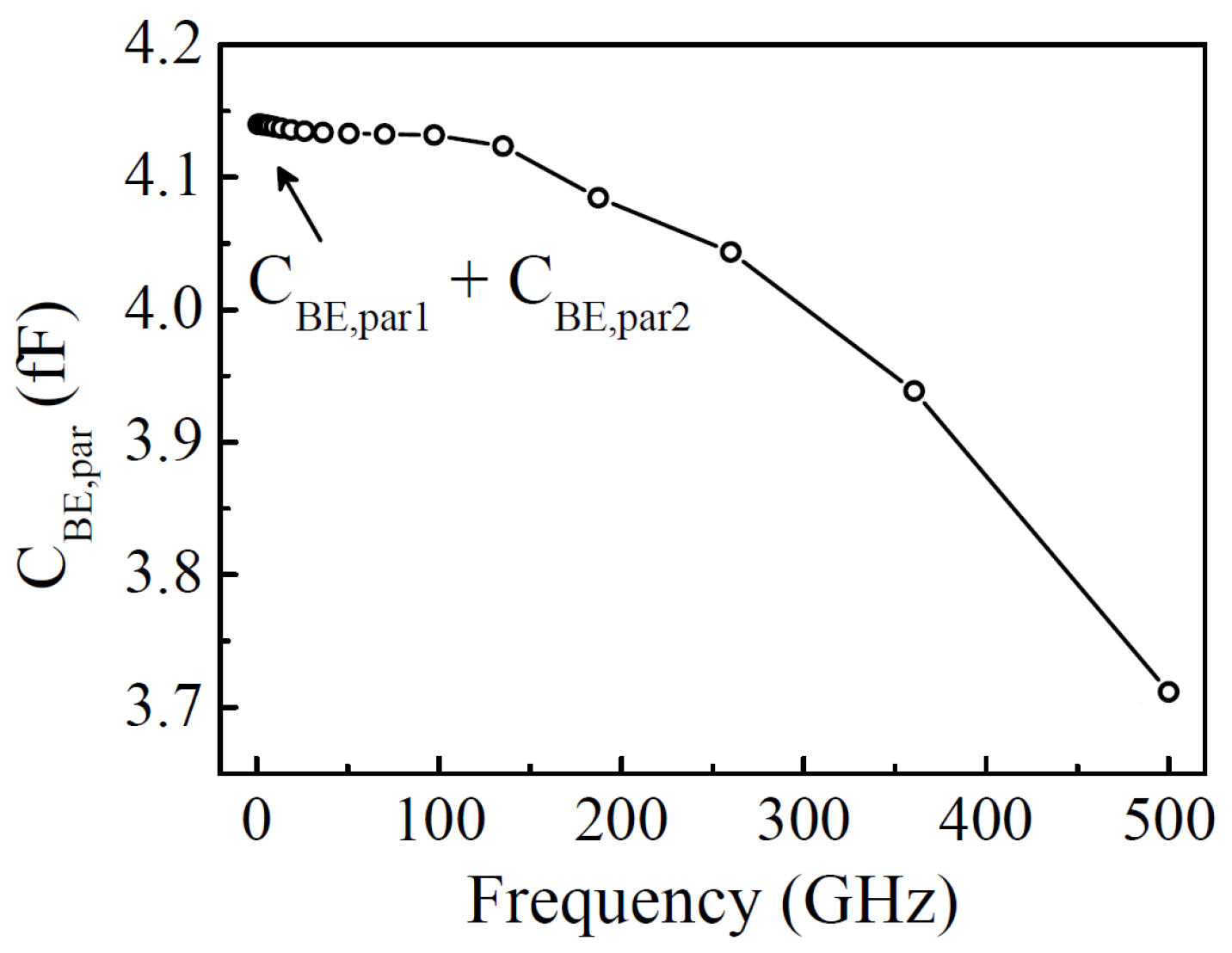
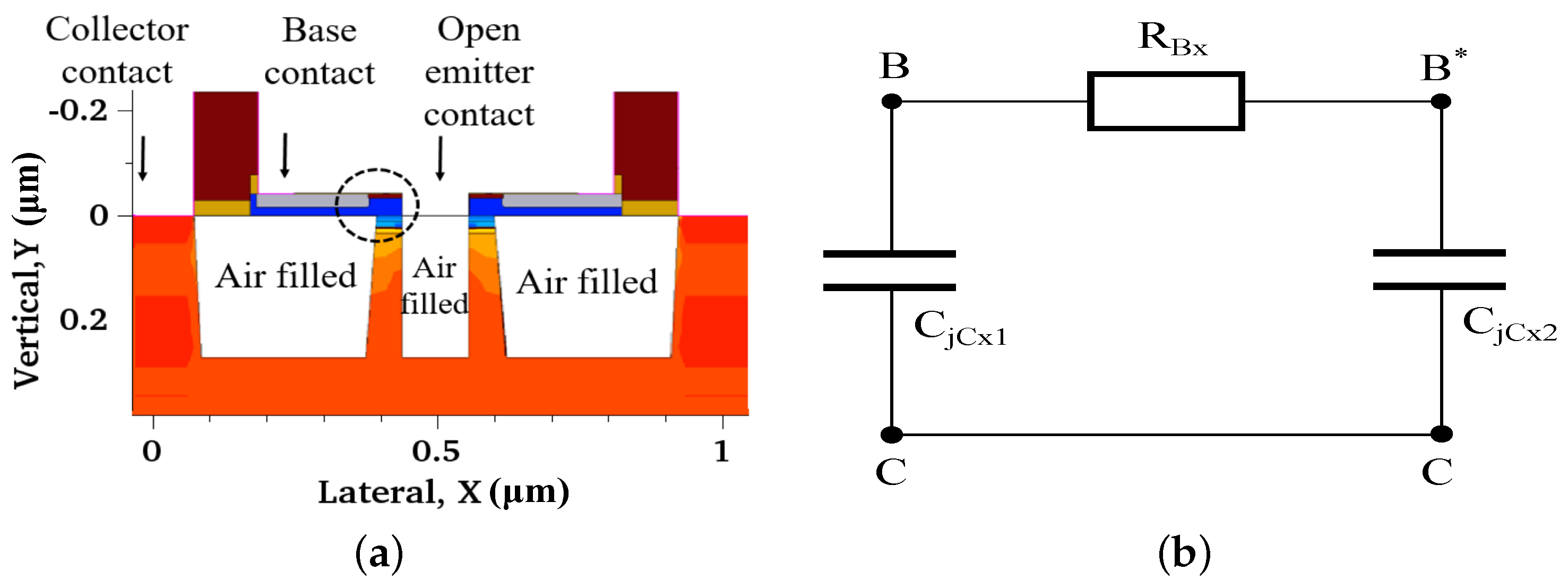
3.1. Parasitic Capacitance Parameters
3.2. Sensitivity Analysis for HF Parameters
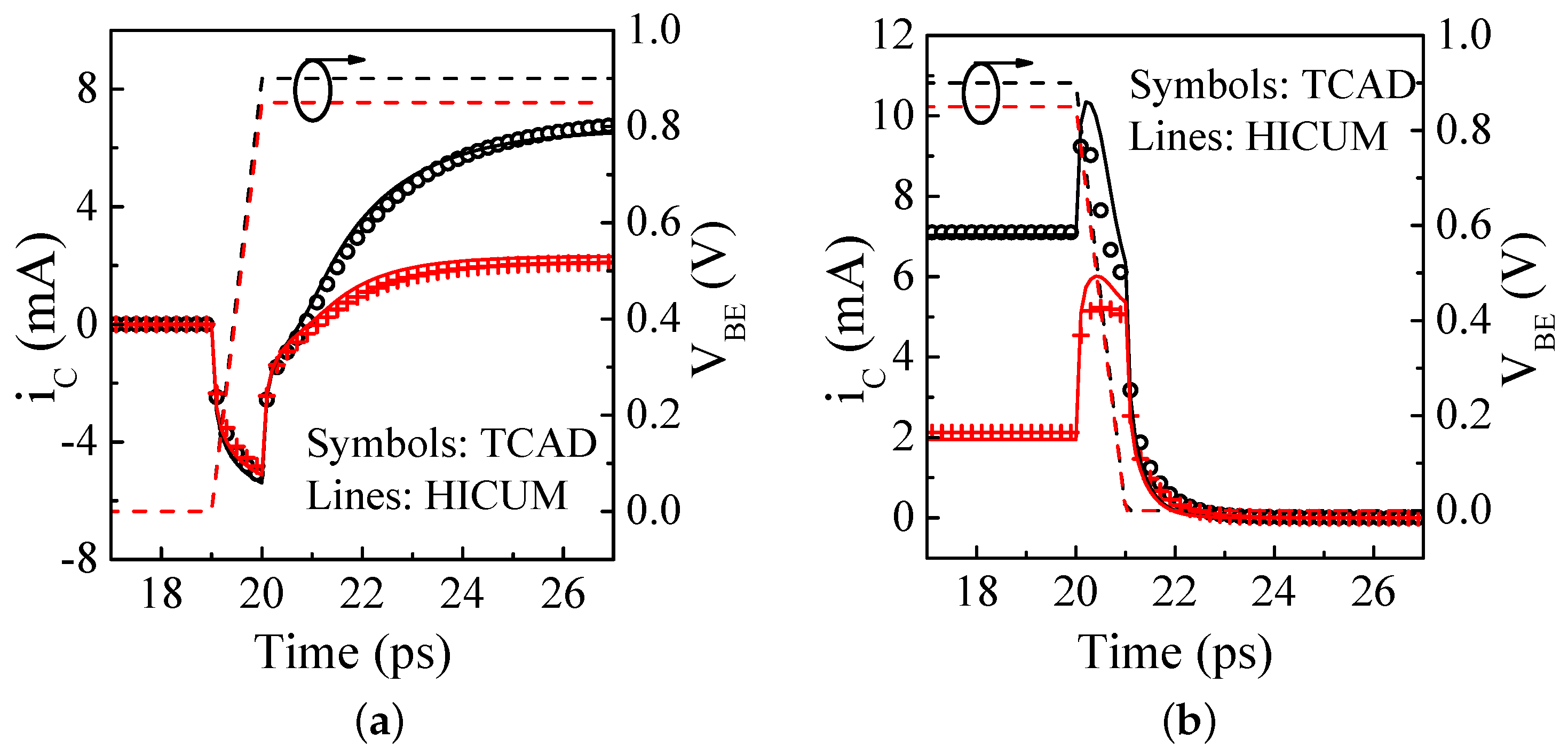
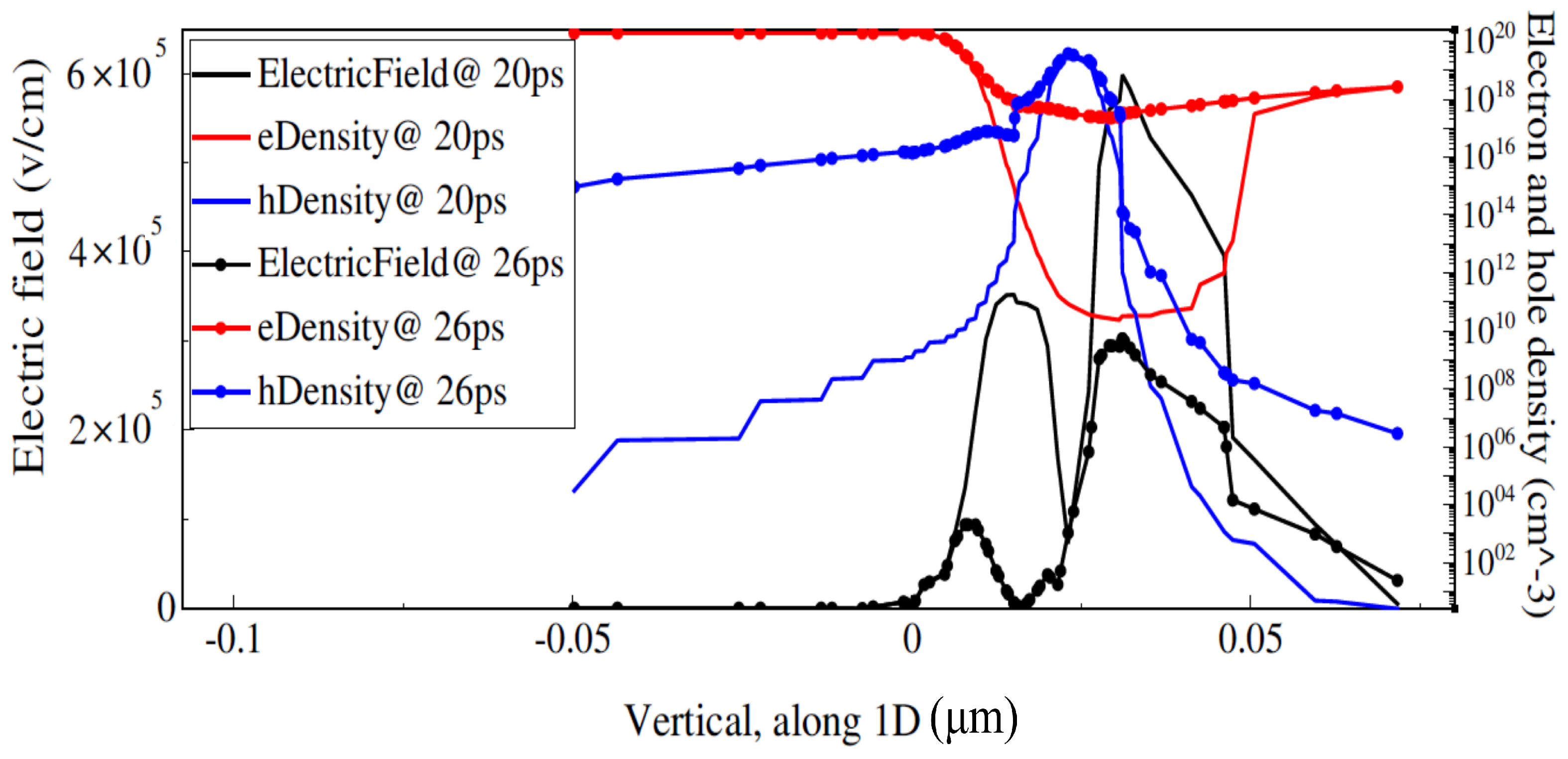
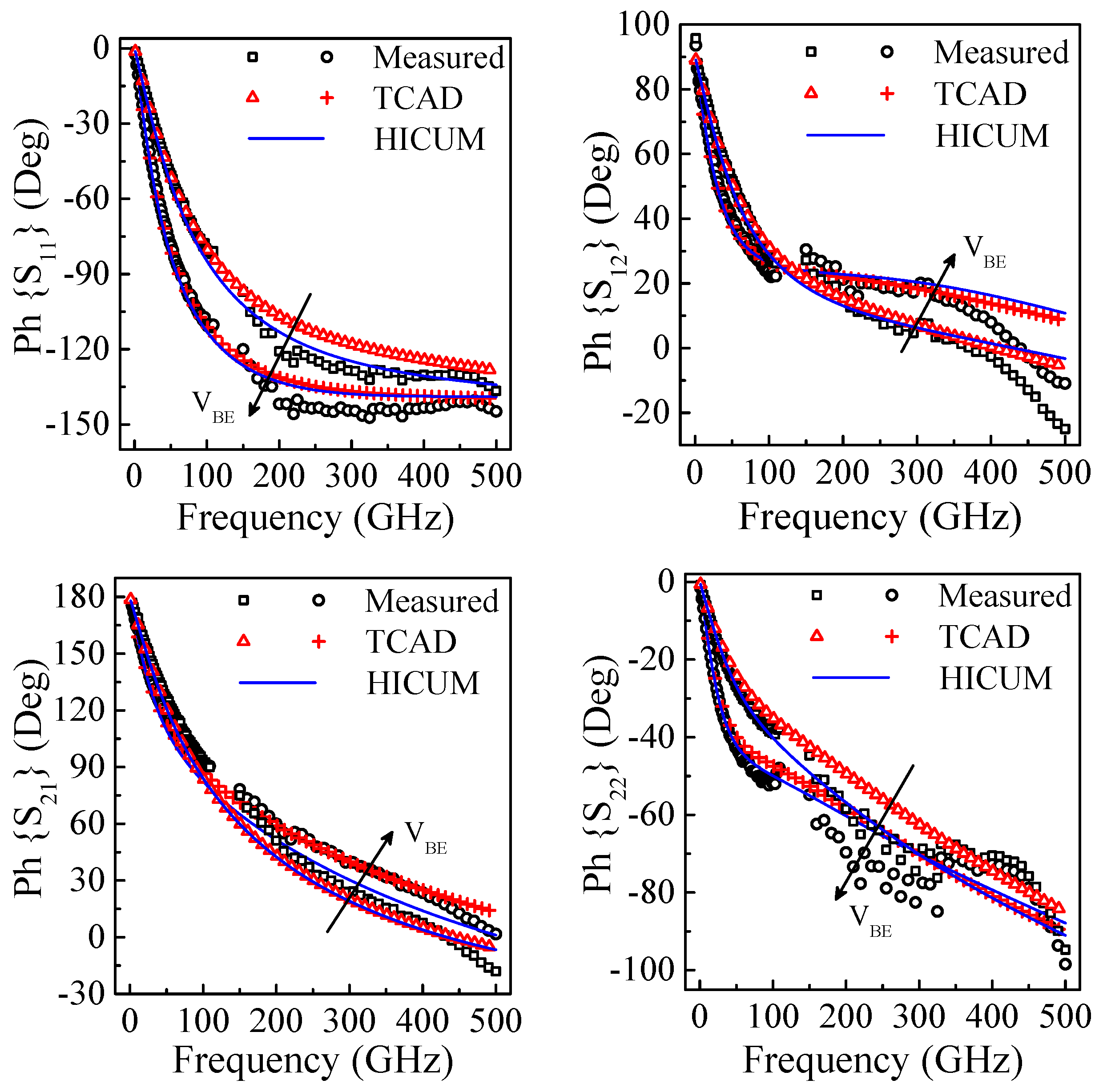
4. High Frequency Compact Model Evaluation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Harame, D.; Larson, L.; Case, M.; Kovacic, S.; Voinigescu, S.; Tewksbury, T.; Nguyen-Ngoc, D.; Stein, K.; Cressler, J.; Jeng, S.; et al. SiGe HBT technology: Device and application issues. In Proceedings of the International Electron Devices Meeting, Washington, DC, USA, 10–13 December 1995; pp. 731–734. [Google Scholar] [CrossRef]
- Cressler, J.D. SiGe HBT technology: A new contender for Si-based RF and microwave circuit applications. IEEE Trans. Microw. Theory Tech. 1998, 46, 572–589. [Google Scholar] [CrossRef]
- Rappaport, T.S.; Xing, Y.; Kanhere, O.; Ju, S.; Madanayake, A.; Mandal, S.; Alkhateeb, A.; Trichopoulos, G.C. Wireless Communications and Applications above 100 GHz: Opportunities and Challenges for 6G and beyond. IEEE Access 2019, 7, 78729–78757. [Google Scholar] [CrossRef]
- Heinemann, B.; Rücker, H.; Barth, R.; Bärwolf, F.; Drews, J.; Fischer, G.G.; Fox, A.; Fursenko, O.; Grabolla, T.; Herzel, F.; et al. SiGe HBT with fx/fmax of 505 GHz/720 GHz. In Proceedings of the 2016 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 3–7 December 2016; pp. 3.1.1–3.1.4. [Google Scholar] [CrossRef]
- Chevalier, P.; Avenier, G.; Ribes, G.; Montagné, A.; Canderle, E.; Céli, D.; Derrier, N.; Deglise, C.; Durand, C.; Quémerais, T.; et al. A 55 nm triple gate oxide 9 metal layers SiGe BiCMOS technology featuring 320 GHz fT/370 GHz fMAX HBT and high-Q millimeter-wave passives. In Proceedings of the 2014 IEEE International Electron Devices Meeting, San Francisco, CA, USA, 15–17 December 2014; pp. 3.9.1–3.9.3. [Google Scholar] [CrossRef]
- Schröter, M.; Rosenbaum, T.; Chevalier, P.; Heinemann, B.; Voinigescu, S.P.; Preisler, E.; Böck, J.; Mukherjee, A. SiGe HBT Technology: Future Trends and TCAD-Based Roadmap. Proc. IEEE 2017, 105, 1068–1086. [Google Scholar] [CrossRef]
- Schroter, M.; Wedel, G.; Heinemann, B.; Jungemann, C.; Krause, J.; Chevalier, P.; Chantre, A. Physical and Electrical Performance Limits of High-Speed SiGeC HBTs—Part I: Vertical Scaling. IEEE Trans. Electron Devices 2011, 58, 3687–3696. [Google Scholar] [CrossRef]
- Schroter, M.; Pawlak, A.; Mukherjee, A. HICUM/L2: A Geometry Scalable Physics-Based Compact Bipolar Transistor Model. August 2013. Available online: https://www.iee.et.tu-dresden.de/iee/eb/forsch/Hicum_PD/Hicum23/hicum_L2V2p32_manual.pdf (accessed on 12 May 2021).
- Koldehoff, A.; Schröter, M.; Rein, H.M. A compact bipolar transistor model for very-high-frequency applications with special regard to narrow emitter stripes and high current densities. Solid-State Electron. 1993, 36, 1035–1048. [Google Scholar] [CrossRef]
- Schroter, M.; Mukherjee, A.; Chakravorty, A. HICUM-Productization and Support Update. October CMC Meeting, Boston. October 2007. Available online: https://www.iee.et.tu-dresden.de/iee/eb/forsch/AK-Bipo/2007/AKB2007_04_Schroeter_Oct07_HICUM_update.pdf (accessed on 12 May 2021).
- Pritchard, R.L. Two-Dimensional Current Flow in Junction Transistors at High Frequencies. Proc. IRE 1958, 46, 1152–1160. [Google Scholar] [CrossRef]
- Schröter, M.; Krattenmacher, M. Modeling distributed dynamic lateral large-signal switching effects in bipolar transistors. In Proceedings of the 2019 IEEE 19th Topical Meeting on Silicon Monolithic Integrated Circuits in RF Systems (SiRF), Orlando, FL, USA, 20–23 January 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Yadav, S.; Chakravorty, A.; Schroter, M. Modeling of the Lateral Emitter-Current Crowding Effect in SiGe HBTs. IEEE Trans. Electron Devices 2016, 63, 4160–4166. [Google Scholar] [CrossRef]
- Williams, D.F.; Marks, R.B. Transmission line capacitance measurement. IEEE Microw. Guid. Wave Lett. 1991, 1, 243–245. [Google Scholar] [CrossRef]
- Fregonese, S.; Deng, M.; De Matos, M.; Yadav, C.; Joly, S.; Plano, B.; Raya, C.; Ardouin, B.; Zimmer, T. Comparison of On-Wafer TRL Calibration to ISS SOLT Calibration With Open-Short De-Embedding up to 500 GHz. IEEE Trans. Terahertz Sci. Technol. 2019, 9, 89–97. [Google Scholar] [CrossRef]
- Cabbia, M.; Deng, M.; Fregonese, S.; Matos, M.D.; Céli, D.; Zimmer, T. In-Situ Calibration and De-Embedding Test Structure Design for SiGe HBT On-Wafer Characterization up to 500 GHz. In Proceedings of the 2020 94th ARFTG Microwave Measurement Symposium (ARFTG), San Antonio, TX, USA, 26–29 January 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Cabbia, M. Sub-Millimeter Wave On-Wafer Calibration and Device Characterization. Ph.D. Thesis, University of Bordeaux, Bordeaux, France, January 2021. [Google Scholar]
- Saha, B.; Frégonese, S.; Panda, S.R.; Chakravorty, A.; Céli, D.; Zimmer, T. Collector-substrate modeling of SiGe HBTs up to THz range. In Proceedings of the 2019 IEEE BiCMOS and Compound semiconductor Integrated Circuits and Technology Symposium (BCICTS), Nashville, TN, USA, 3–6 November 2019; pp. 1–4. [Google Scholar] [CrossRef]
- VU, V.T.; Celi, D.; Zimmer, T.; Fregonese, S.; Chevalier, P. TCAD Calibration of High-Speed Si/SiGe HBTs in 55-nm BiCMOS. ECS Trans. 2016, 75, 113–119. [Google Scholar] [CrossRef]
- Panda, S.R.; Fregonese, S.; Chakravorty, A.; Zimmer, T. TCAD simulation and assessment of anomalous deflection in measured S-parameters of SiGe HBTs in THz range. In Proceedings of the 2019 IEEE BiCMOS and Compound semiconductor Integrated Circuits and Technology Symposium (BCICTS), Nashville, TN, USA, 3–6 November 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Raya, C. Modélisation et Optimisation de Transistors Bipolaires à Hétérojonction Si/SiGeC Ultra Rapides Pour Applications Millimétriques. Ph.D. Thesis, University of Bordeaux, Bordeaux, France, July 2008. [Google Scholar]
- Raya, C.; Schwartzmann, T.; Chevalier, P.; Pourchon, F.; Celi, D.; Zimmer, T. New Method for Oxide Capacitance Extraction. In Proceedings of the 2007 IEEE Bipolar/BiCMOS Circuits and Technology Meeting, Boston, MA, USA, 30 September–2 October 2007; pp. 188–191. [Google Scholar] [CrossRef]
- Ardouin, B.; Zimmer, T.; Mnif, H.; Fouillat, P. Direct method for bipolar base-emitter and base-collector capacitance splitting using high frequency measurements. In Proceedings of the 2001 BIPOLAR/BiCMOS Circuits and Technology Meeting (Cat. No.01CH37212), Minneapolis, MN, USA, 2 October 2001; pp. 114–117. [Google Scholar] [CrossRef]
- Schröter, M.; Pawlak, A. A Geometry Scalable Physics-Based Compact Bipolar Transistor Model. Chair for Electron Devices and Integrated Circuits and Dept. of Electrical and Computer Engineering. March 2017. Available online: https://www.iee.et.tu-dresden.de/iee/eb/forsch/Hicum_PD/Hicum23/hicum_L2V2p4p0_manual.pdf (accessed on 12 May 2021).
- Fregonese, S.; Lehmann, S.; Zimmer, T.; Schroter, M.; Celi, D.; Ardouin, B.; Beckrich, H.; Brenner, P.; Kraus, W. A computationally efficient physics-based compact bipolar transistor model for circuit Design-part II: Parameter extraction and experimental results. IEEE Trans. Electron Devices 2006, 53, 287–295. [Google Scholar] [CrossRef]
- Wakimoto, T.; Akazawa, Y. A low-power wide-band amplifier using a new parasitic capacitance compensation technique. IEEE J. Solid-State Circuits 1990, 25, 200–206. [Google Scholar] [CrossRef]
- Voinigescu, S.P.; Dacquay, E.; Adinolfi, V.; Sarkas, I.; Balteanu, A.; Tomkins, A.; Celi, D.; Chevalier, P. Characterization and Modeling of an SiGe HBT Technology for Transceiver Applications in the 100–300-GHz Range. IEEE Trans. Microw. Theory Tech. 2012, 60, 4024–4034. [Google Scholar] [CrossRef]
- Galatro, L.; Pawlak, A.; Schroter, M.; Spirito, M. Capacitively Loaded Inverted CPWs for Distributed TRL-Based De-Embedding at (Sub) mm-Waves. IEEE Trans. Microw. Theory Tech. 2017, 65, 4914–4924. [Google Scholar] [CrossRef]
- Fregonese, S.; Cabbia, M.; Yadav, C.; Deng, M.; Panda, S.R.; De Matos, M.; Céli, D.; Chakravorty, A.; Zimmer, T. Analysis of High-Frequency Measurement of Transistors Along With Electromagnetic and SPICE Cosimulation. IEEE Trans. Electron Devices 2020, 67, 4770–4776. [Google Scholar] [CrossRef]
- Panda, S.R.; Fregonese, S.; Deng, M.; Chakravorty, A.; Zimmer, T. TCAD and EM co-simulation method to verify SiGe HBT measurements up to 500 GHz. Solid-State Electron. 2020, 174, 107915. [Google Scholar] [CrossRef]



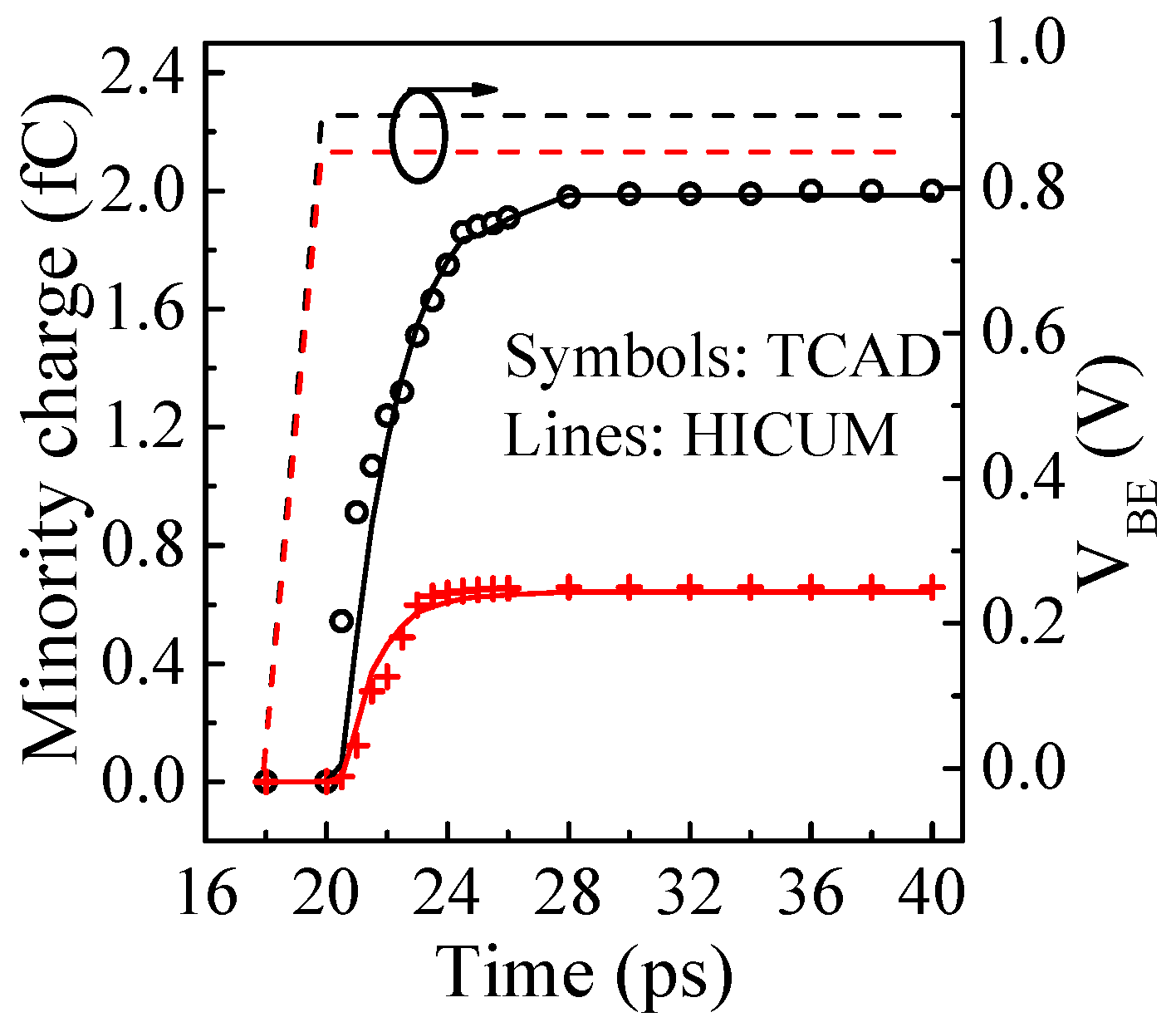

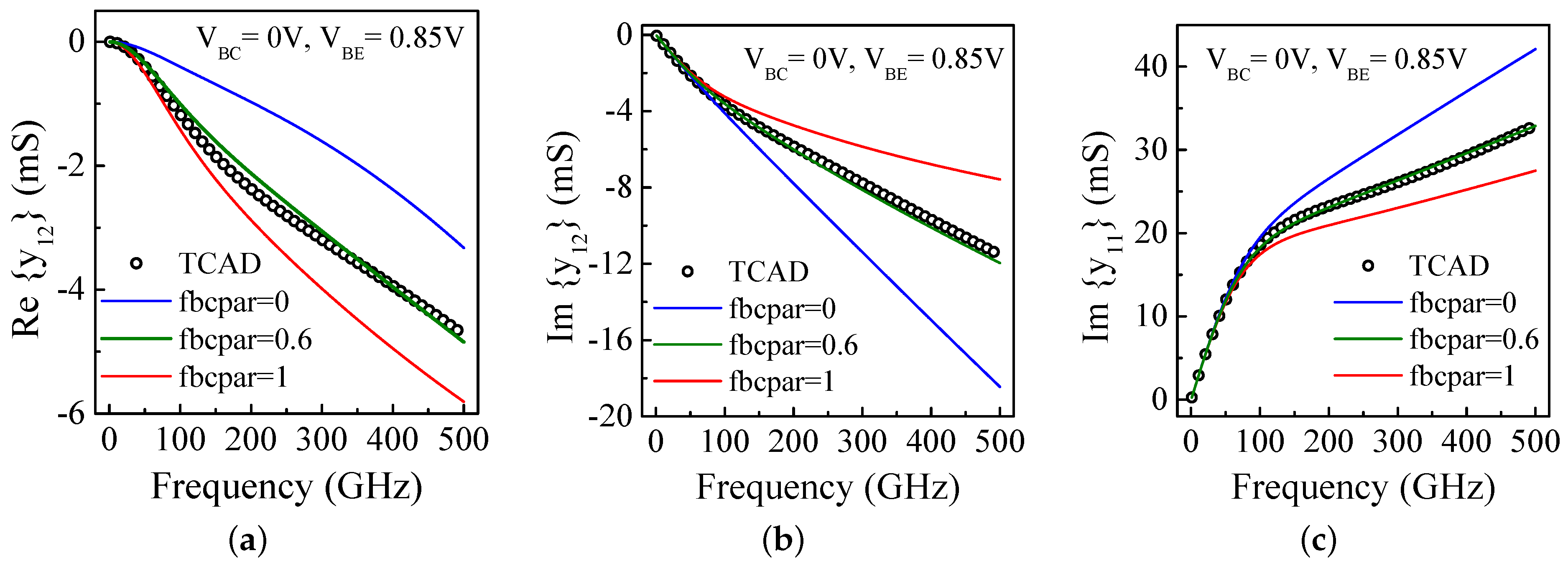
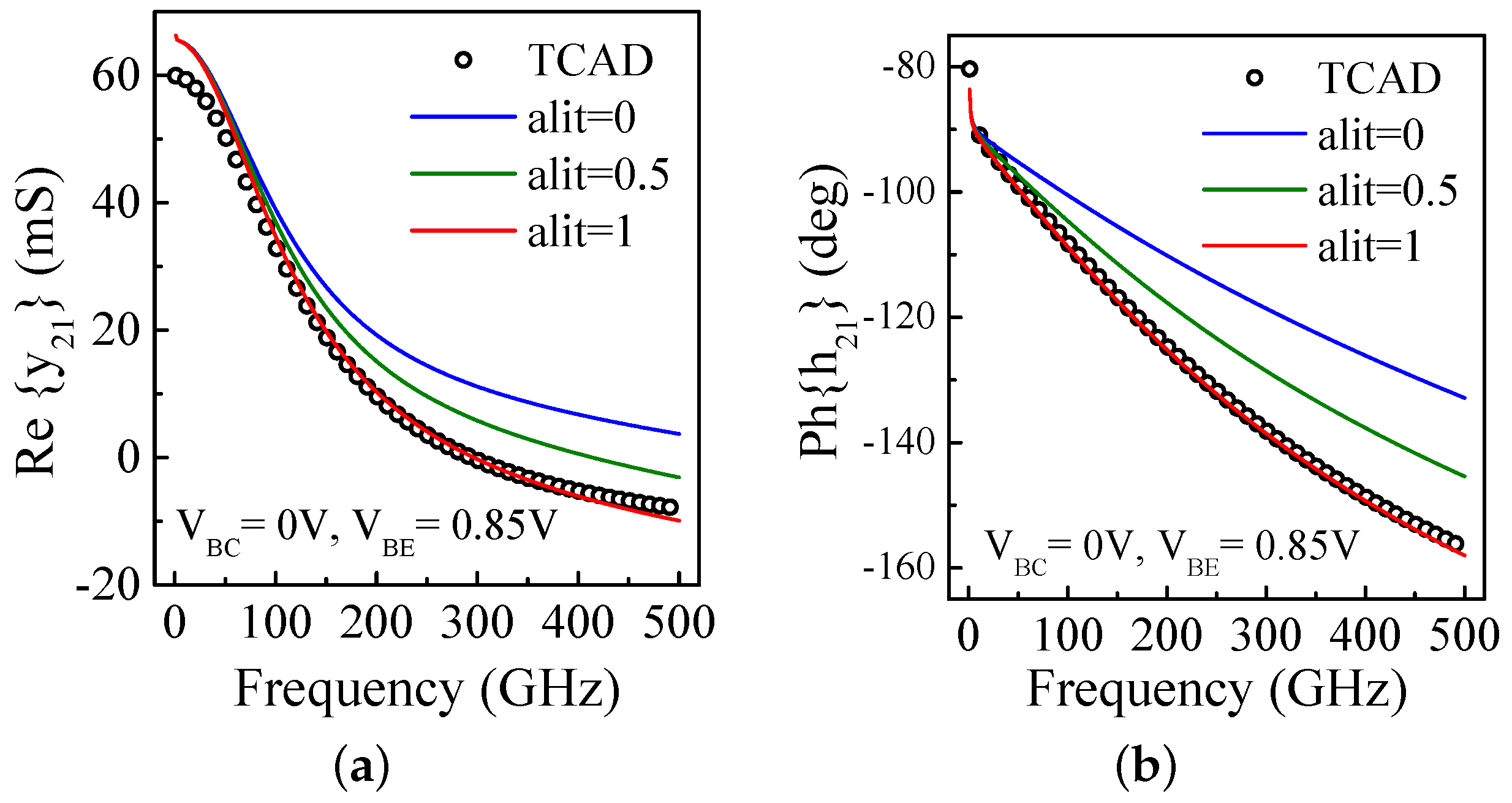
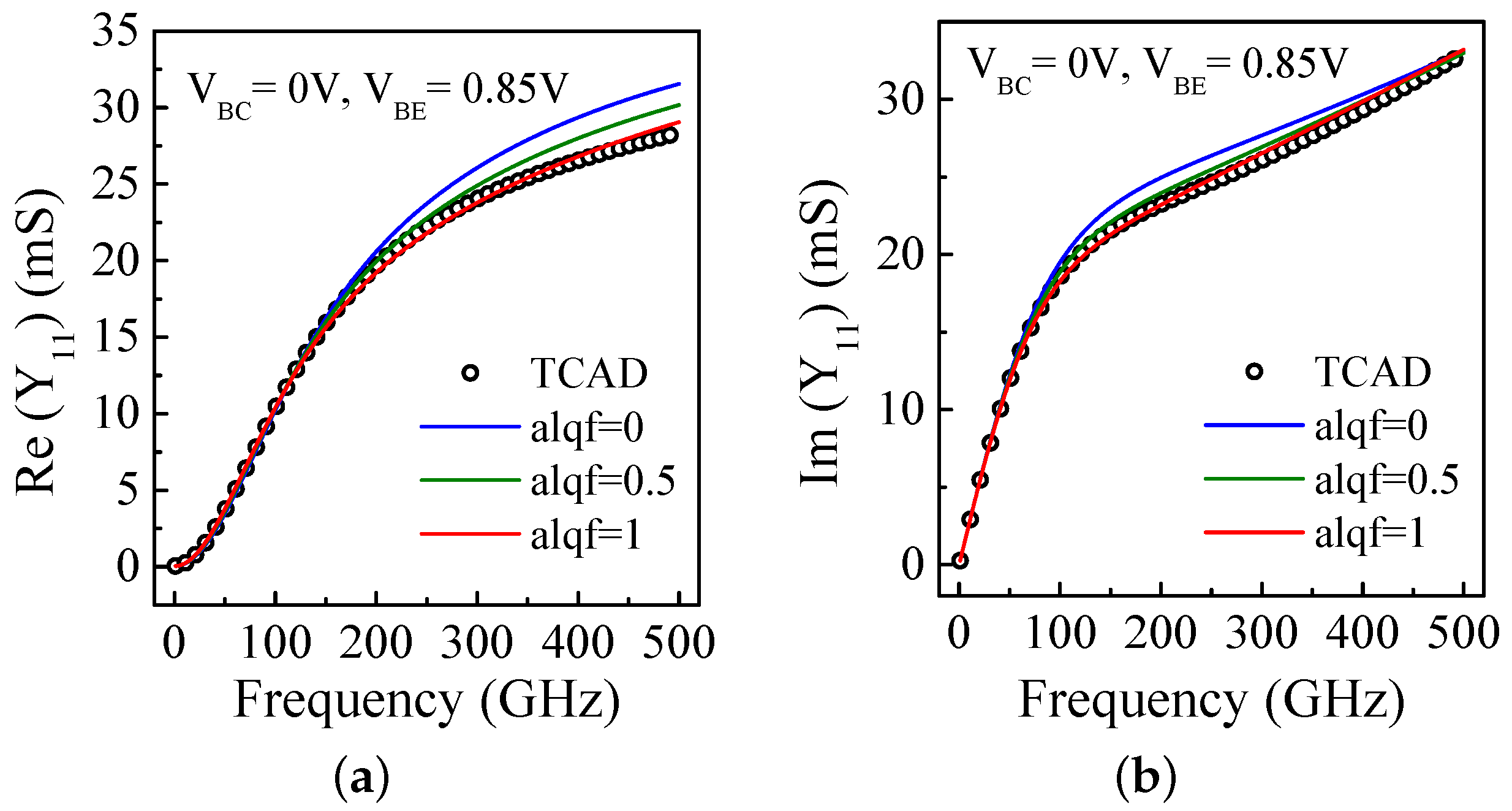


| Structural Parameters | Values |
|---|---|
| Layout width (W) | 2.78 µm |
| Layout length (L) | 5.12 µm |
| Width of deep trench | 0.42 µm |
| Depth of deep trench | 3.5 µm |
| Depth access | 1 µm |
| Substrate contact from DT | 0.8 µm |
| Width of substrate contact | 0.1 µm |
| N | 1.5 × 10 cm |
| N | 4.5 × 10 cm |
| N | 5 × 10 cm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saha, B.; Fregonese, S.; Chakravorty, A.; Panda, S.R.; Zimmer, T. Sub-THz and THz SiGe HBT Electrical Compact Modeling. Electronics 2021, 10, 1397. https://doi.org/10.3390/electronics10121397
Saha B, Fregonese S, Chakravorty A, Panda SR, Zimmer T. Sub-THz and THz SiGe HBT Electrical Compact Modeling. Electronics. 2021; 10(12):1397. https://doi.org/10.3390/electronics10121397
Chicago/Turabian StyleSaha, Bishwadeep, Sebastien Fregonese, Anjan Chakravorty, Soumya Ranjan Panda, and Thomas Zimmer. 2021. "Sub-THz and THz SiGe HBT Electrical Compact Modeling" Electronics 10, no. 12: 1397. https://doi.org/10.3390/electronics10121397
APA StyleSaha, B., Fregonese, S., Chakravorty, A., Panda, S. R., & Zimmer, T. (2021). Sub-THz and THz SiGe HBT Electrical Compact Modeling. Electronics, 10(12), 1397. https://doi.org/10.3390/electronics10121397







