Multiple Instance Learning with Differential Evolutionary Pooling
Abstract
:1. Introduction
2. Multiple Instance Learning
3. Differential Evolution
3.1. Operations in Differential Evolution
3.1.1. Initialization
3.1.2. Mutation
3.1.3. Crossover
3.1.4. Selection
3.2. SaDE
3.3. jDE
3.4. JADE
3.5. SHADE
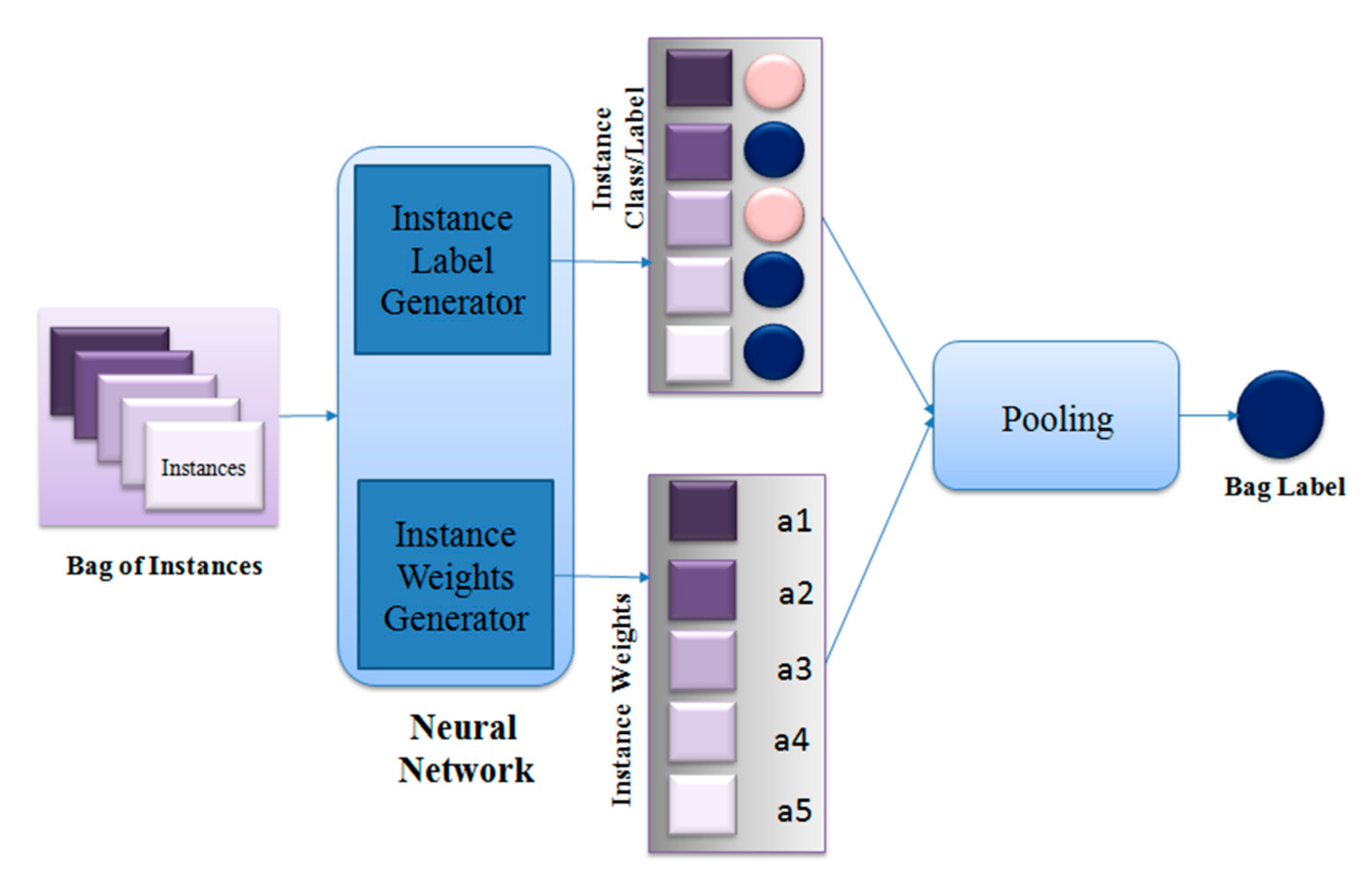
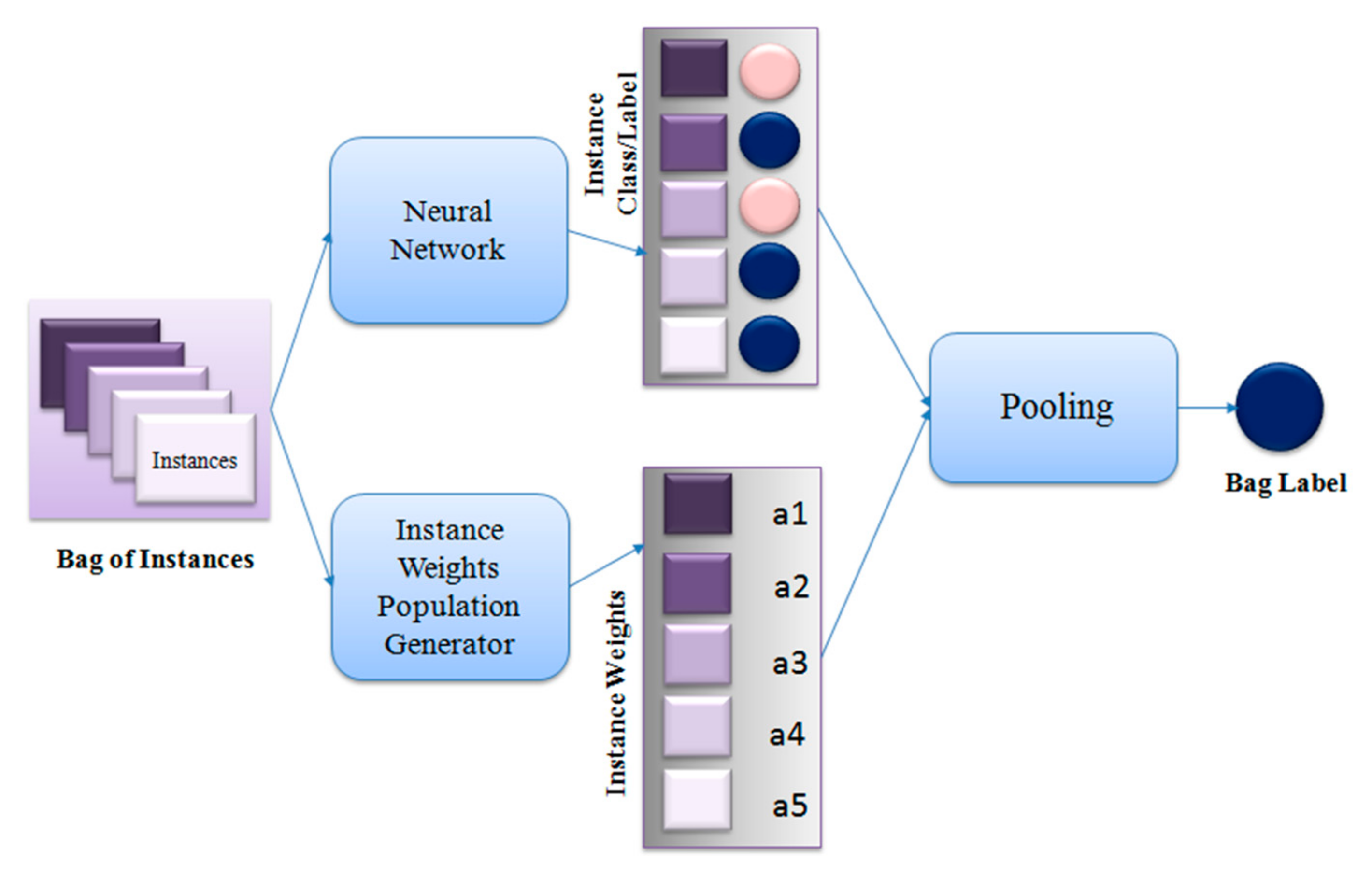
4. Proposed Method
| Algorithm 1. MIL Pooling Function using DE |
| ● Set scaling factor F, crossover probability CR, Number of individuals in a population NP ● Set individual index, i = 1 ● Set maximum iteration number max_iter ● Set iteration number, iter = 1 ● Set number of bags P according to dataset ● Set bag number, p = 1 ● Initialize population of instance weights for each bag with NP individuals ● While iter<= max_iter ○ While p <= P ■ While i<= NP ● Run feed-forward pass on neural network to generate instance labels ● Calculate bag label, ● Calculate loss for ● Generate 3 random numbers in [0,NP] – j1, j2, j3 where j1 ≠ j2 ≠ j3 ≠i ● Calculate mutant ● dim = dimension of ● for d = 1:dim ○ Generate random number r in [0, 1] and random number in [1,dim] ○ if r <= CR or = d ■ ○ else ■ ● Calculate bag label for , ● Calculate loss for ● If ○ |
5. Results and Discussion
5.1. Experimental Setup
5.2. Results Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cheplygina, V.; de Bruijne, M.; Pluim, J.P.W. Not-so-supervised: A survey of semi-supervised, multi-instance, and transfer learning in medical image analysis. Med. Image Anal. 2019, 54, 280–296. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Quellec, G.; Cazuguel, G.; Cochener, B.; Lamard, M. Multiple-Instance Learning for Medical Image and Video Analysis. IEEE Rev. Biomed. Eng. 2017, 10, 213–234. [Google Scholar] [CrossRef] [PubMed]
- Dietterich, T.G.; Lathrop, R.H.; Lozano-Pérez, T. Solving the multiple instance problem with axis-parallel rectangles. Artif. Intell. 1997, 89, 31–71. [Google Scholar] [CrossRef] [Green Version]
- Ramon, J.; De Raedt, L. Multi instance neural networks. In Proceedings of the ICML-2000 Workshop on Attribute-Value and Relational Learning, Stanford, CA, USA, 2 July 2000; pp. 53–60. [Google Scholar]
- Ilse, M.; Tomczak, J.M.; Welling, M. Attention-Based Deep Multiple Instance Learning. In Proceedings of the 35th International Conference on Machine Learning, Proceedings of Machine Learning Research (PMLR), Stockholm, Sweden, 10–15 July 2018; pp. 2127–2136. [Google Scholar]
- Yan, Y.; Wang, X.; Fang, J.; Liu, W.; Huang, J.; Zhu, J.; Takeuchi, I. Deep Multi-instance Learning with Dynamic Pooling. In Proceedings of the Asian Conference on Machine Learning, Beijing, China, 14–16 November 2018; pp. 1–16. [Google Scholar]
- Liu, D.; Zhou, Y.; Sun, X.; Zha, Z.; Zeng, W. Adaptive Pooling in Multi-instance Learning for Web Video Annotation. In Proceedings of the 2017 IEEE International Conference on Computer Vision Workshops (ICCVW), Venice, Italy, 22–29 October 2017; pp. 318–327. [Google Scholar]
- Bhattacharjee, K.; Pant, M.; Zhang, Y.D.; Satapathy, S.C. Multiple Instance Learning with Genetic Pooling for medical data analysis. Pattern Recognit. Lett. 2020, 133, 247–255. [Google Scholar] [CrossRef]
- Wang, X.; Yan, Y.; Tang, P.; Bai, X.; Liu, W. Revisiting multiple instance neural networks. Pattern Recognit. 2018, 74, 15–24. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Poon, J.; Sun, S.; Poon, S. Attention-based Multi-instance Neural Network for Medical Diagnosis from Incomplete and Low Quality Data. In Proceedings of the International Joint Conference on Neural Networks, Budapest, Hungary, 14–19 July 2019. [Google Scholar]
- Wang, Z.; Poon, J.; Poon, S. AMI-Net+: A Novel Multi-Instance Neural Network for Medical Diagnosis from Incomplete and Imbalanced Data. arXiv 2019, arXiv:1907.01734. [Google Scholar]
- Bhattacharjee, K.; Tiwari, A.; Pant, M.; Ahn, C.W. A Pooling Function based on Differential Evolution for Multiple Instance Learning. In Proceedings of the 9th International Conference on Smart Media and Applications (SMA 2020), Jeju, Korea, 17–19 September 2020. [Google Scholar]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Qin, A.K.; Suganthan, P.N. Self-adaptive differential evolution algorithm for numerical optimization. In Proceedings of the 2005 IEEE Congress on Evolutionary Computation, IEEE CEC 2005, Edinburgh, UK, 2–5 September 2005; Volume 2, pp. 1785–1791. [Google Scholar]
- Brest, J.; Greiner, S.; Bošković, B.; Mernik, M.; Zumer, V. Self-adapting control parameters in differential evolution: A comparative study on numerical benchmark problems. IEEE Trans. Evol. Comput. 2006, 10, 646–657. [Google Scholar] [CrossRef]
- Zhang, J.; Sanderson, A.C. JADE: Adaptive differential evolution with optional external archive. IEEE Trans. Evol. Comput. 2009, 13, 945–958. [Google Scholar] [CrossRef]
- Tanabe, R.; Fukunaga, A. Success-history based parameter adaptation for Differential Evolution. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, CEC 2013, Cancun, Mexico, 20–23 June 2013; pp. 71–78. [Google Scholar]
- Carbonneau, M.-A.; Cheplygina, V.; Granger, E.; Gagnon, G. Multiple instance learning: A survey of problem characteristics and applications. Pattern Recognit. 2018, 77, 329–353. [Google Scholar] [CrossRef] [Green Version]
- Amores, J. Multiple instance classification: Review, taxonomy and comparative study. Artif. Intell. 2013, 201, 81–105. [Google Scholar] [CrossRef]
- Wang, S.; Zhu, Y.; Yu, L.; Chen, H.; Lin, H.; Wan, X.; Fan, X.; Heng, P.A. RMDL: Recalibrated multi-instance deep learning for whole slide gastric image classification. Med. Image Anal. 2019, 58, 101549. [Google Scholar] [CrossRef]
- Yousefi, M.; Krzyżak, A.; Suen, C.Y. Mass detection in digital breast tomosynthesis data using convolutional neural networks and multiple instance learning. Comput. Biol. Med. 2018, 96, 283–293. [Google Scholar] [CrossRef]
- Cao, P.; Ren, F.; Wan, C.; Yang, J.; Zaiane, O. Efficient multi-kernel multi-instance learning using weakly supervised and imbalanced data for diabetic retinopathy diagnosis. Comput. Med. Imaging Graph. 2018, 69, 112–124. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, J.; Adeli, E.; Shen, D. Landmark-based deep multi-instance learning for brain disease diagnosis. Med. Image Anal. 2018, 43, 157–168. [Google Scholar] [CrossRef]
- Yao, J.; Zhu, X.; Jonnagaddala, J.; Hawkins, N.; Huang, J. Whole Slide Images based Cancer Survival Prediction using Attention Guided Deep Multiple Instance Learning Networks. Med. Image Anal. 2020, 65, 101789. [Google Scholar] [CrossRef]
- Bilal; Pant, M.; Zaheer, H.; Garcia-Hernandez, L.; Abraham, A. Differential Evolution: A review of more than two decades of research. Eng. Appl. Artif. Intell. 2020, 90, 103479. [Google Scholar] [CrossRef]
- Caraffini, F.; Kononova, A.V.; Corne, D. Infeasibility and structural bias in differential evolution. Inf. Sci. 2019, 496, 161–179. [Google Scholar] [CrossRef] [Green Version]
- Stanovov, V.; Akhmedova, S.; Semenkin, E. LSHADE Algorithm with Rank-Based Selective Pressure Strategy for Solving CEC 2017 Benchmark Problems. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation, CEC 2018, Rio de Janeiro, Brazil, 8–13 July 2018. [Google Scholar]
- Awad, N.H.; Ali, M.Z.; Suganthan, P.N. Ensemble sinusoidal differential covariance matrix adaptation with Euclidean neighborhood for solving CEC2017 benchmark problems. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation, CEC 2017, Donostia, Spain, 5–8 June 2017; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2017; pp. 372–379. [Google Scholar]
- Awad, N.H.; Ali, M.Z.; Suganthan, P.N.; Reynolds, R.G. An ensemble sinusoidal parameter adaptation incorporated with L-SHADE for solving CEC2014 benchmark problems. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation, CEC 2016, Vancouver, BC, Canada, 24–29 July 2016; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2016; pp. 2958–2965. [Google Scholar]
- Yeh, J.F.; Chen, T.Y.; Chiang, T.C. Modified L-SHADE for Single Objective Real-Parameter Optimization. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation, CEC 2019, Wellington, New Zealand, 10–13 June 2019; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2019; pp. 381–386. [Google Scholar]
- Zhang, S.X.; Chan, W.S.; Tang, K.S.; Zheng, S.Y. Adaptive strategy in differential evolution via explicit exploitation and exploration controls. Appl. Soft Comput. 2021, 107, 107494. [Google Scholar] [CrossRef]
- Zeng, Z.; Zhang, M.; Chen, T.; Hong, Z. A new selection operator for differential evolution algorithm. Knowl. Based Syst. 2021, 226, 107150. [Google Scholar] [CrossRef]
- Salgotra, R.; Singh, U.; Saha, S.; Nagar, A. New Improved SALSHADE-cnEpSin Algorithm with Adaptive Parameters. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation, CEC 2019, Wellington, New Zealand, 10–13 June 2019; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2019; pp. 3150–3156. [Google Scholar]
- Han, G.; Chen, X. A Bi-level Differential Evolutionary Algorithm for Constrained Optimization. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation, CEC 2019, Wellington, New Zealand, 10–13 June 2019; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2019; pp. 1628–1633. [Google Scholar]
- Yang, Z.; Qiu, H.; Gao, L.; Jiang, C.; Chen, L.; Cai, X. A Novel Surrogate-assisted Differential Evolution for Expensive Optimization Problems with both Equality and Inequality Constraints. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation, CEC 2019, Wellington, New Zealand, 10–13 June 2019; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2019; pp. 1688–1695. [Google Scholar]
- Zheng, X.; Lei, Y.; Qin, A.K.; Zhou, D.; Shi, J.; Gong, M. Differential Evolutionary Multi-task Optimization. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation, CEC 2019, Wellington, New Zealand, 10–13 June 2019; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2019; pp. 1914–1921. [Google Scholar]
- Mousavirad, S.J.; Rahnamayan, S. A Novel Center-based Differential Evolution Algorithm. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation, CEC 2020, Glasgow, UK, 19–24 July 2020; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2020. [Google Scholar]
- Pant, M.; Vig, G. Clustering based Adaptive Differential Evolution for Numerical Optimization. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation, CEC 2020, Glasgow, UK, 19–24 July 2020; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2020. [Google Scholar]
- Kizilay, D.; Tasgetiren, M.F.; Oztop, H.; Kandiller, L.; Suganthan, P.N. A Differential Evolution Algorithm with Q-Learning for Solving Engineering Design Problems. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation, CEC 2020, Glasgow, UK, 19–24 July 2020; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2020. [Google Scholar]
- Jou, Y.C.; Wang, S.Y.; Yeh, J.F.; Chiang, T.C. Multi-population Modified L-SHADE for Single Objective Bound Constrained optimization. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation, CEC 2020, Glasgow, UK, 19–24 July 2020; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2020. [Google Scholar]
- Vaswani, A.; Brain, G.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5998–6008. [Google Scholar]
- Ba, J.L.; Kiros, J.R.; Hinton, G.E. Layer Normalization. arXiv 2016, arXiv:1607.06450. [Google Scholar]
- Hegerty, B.; Hung, C.-C.; Kasprak, K. A Comparative Study on Differential Evolution and Genetic Algorithms for Some Combinatorial Problems. In Proceedings of the 8th Mexican International Conference on Artificial Intelligence, Guanajuato, Mexico, 9–13November 2009. [Google Scholar]
- Caraffini, F.; Iacca, G. The SOS platform: Designing, tuning and statistically benchmarking optimisation algorithms. Mathematics 2020, 8, 785. [Google Scholar] [CrossRef]





| MIL Pooling | AUC | AP | Accuracy | Balanced Accuracy | NPV | Specificity | Zero One Loss | Hamming Loss |
|---|---|---|---|---|---|---|---|---|
| Max pooling | 0.7283375 | 0.1879182 | 0.9377546 | 0.5026506 | 0.9427535 | 0.9943237 | 0.0622454 | 0.0622454 |
| Mean pooling | 0.7521901 | 0.2006572 | 0.9418427 | 0.5091218 | 0.9435413 | 0.9979871 | 0.0581573 | 0.0581573 |
| Sum pooling | 0.5755536 | 0.1003711 | 0.9201445 | 0.5401024 | 0.9472548 | 0.9697003 | 0.0798555 | 0.0798555 |
| Log-sum-exp pooling | 0.7359605 | 0.1830831 | 0.9405848 | 0.5107879 | 0.9437524 | 0.9963193 | 0.0594152 | 0.0594152 |
| Gated Attention pooling | 0.7544704 | 0.1958218 | 0.9424716 | 0.5023977 | 0.9427499 | 0.9996672 | 0.0575284 | 0.0575284 |
| Genetic pooling | 0.8862781 | 0.3782898 | 0.9424716 | 0.5023977 | 0.9427499 | 0.9996672 | 0.0575284 | 0.0575284 |
| DE pooling | 0.9838043 | 0.8429034 | 0.9537898 | 0.5983575 | 0.9532767 | 1 | 0.0462101 | 0.0462101 |
| Ranks | ||||
|---|---|---|---|---|
| Algorithm | N | Mean Rank | Sum of Ranks | |
| AUC | GA | 5 | 3.00 | 15.00 |
| DE | 5 | 8.00 | 40.00 | |
| Total | 10 | |||
| Accuracy | GA | 5 | 5.10 | 25.50 |
| DE | 5 | 5.90 | 29.50 | |
| Total | 10 | |||
| BalancedAccuracy | GA | 5 | 3.50 | 17.50 |
| DE | 5 | 7.50 | 37.50 | |
| Total | 10 | |||
| NPV | GA | 5 | 5.00 | 25.00 |
| DE | 5 | 6.00 | 30.00 | |
| Total | 10 | |||
| ZeroOneLoss | GA | 5 | 5.90 | 29.50 |
| DE | 5 | 5.10 | 25.50 | |
| Total | 10 | |||
| Test Statistics a | |||||
|---|---|---|---|---|---|
| AUC | Accuracy | BalancedAccuracy | NPV | ZeroOneLoss | |
| Mann–Whitney U | 0.000 | 10.500 | 2.500 | 10.000 | 10.500 |
| Wilcoxon W | 15.000 | 25.500 | 17.500 | 25.000 | 25.500 |
| Z | −2.611 | −0.419 | −2.155 | −0.522 | −0.419 |
| Asymp. Sig. (2-tailed) | 0.009 | 0.675 | 0.031 | 0.602 | 0.675 |
| Exact Sig. [2x(1-tailed Sig.)] | 0.008 b | 0.690 b | 0.032 b | 0.690 b | 0.690 b |
| Variant | AUC | AP | Accuracy | Balanced Accuracy | NPV | Specificity | Zero One Loss | Hamming Loss |
|---|---|---|---|---|---|---|---|---|
| DE | 0.6883591 | 0.1278299 | 0.9424716 | 0.5 | 0.9424716 | 1 | 0.0575284 | 0.0575284 |
| SaDE | 0.6794218 | 0.1435111 | 0.9405858 | 0.5051259 | 0.9429468 | 0.9973487 | 0.0594142 | 0.0594142 |
| jDE | 0.7101309 | 0.1285298 | 0.9512579 | 0.5074733 | 0.9426030 | 0.9866064 | 0.0691636 | 0.0691636 |
| JADE | 0.6956148 | 0.1277994 | 0.9449686 | 0.5 | 0.9424716 | 1 | 0.0575284 | 0.0575284 |
| SHADE | 0.7292417 | 0.1323776 | 0.9512579 | 0.5 | 0.9424716 | 1 | 0.0575284 | 0.0575284 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhattacharjee, K.; Tiwari, A.; Pant, M.; Ahn, C.W.; Oh, S. Multiple Instance Learning with Differential Evolutionary Pooling. Electronics 2021, 10, 1403. https://doi.org/10.3390/electronics10121403
Bhattacharjee K, Tiwari A, Pant M, Ahn CW, Oh S. Multiple Instance Learning with Differential Evolutionary Pooling. Electronics. 2021; 10(12):1403. https://doi.org/10.3390/electronics10121403
Chicago/Turabian StyleBhattacharjee, Kamanasish, Arti Tiwari, Millie Pant, Chang Wook Ahn, and Sanghoun Oh. 2021. "Multiple Instance Learning with Differential Evolutionary Pooling" Electronics 10, no. 12: 1403. https://doi.org/10.3390/electronics10121403
APA StyleBhattacharjee, K., Tiwari, A., Pant, M., Ahn, C. W., & Oh, S. (2021). Multiple Instance Learning with Differential Evolutionary Pooling. Electronics, 10(12), 1403. https://doi.org/10.3390/electronics10121403







