SOGI-FLL Grid Frequency Monitoring with an Error-Based Algorithm for a Better Response in Face of Voltage Sag and Swell Faults
Abstract
:1. Introduction
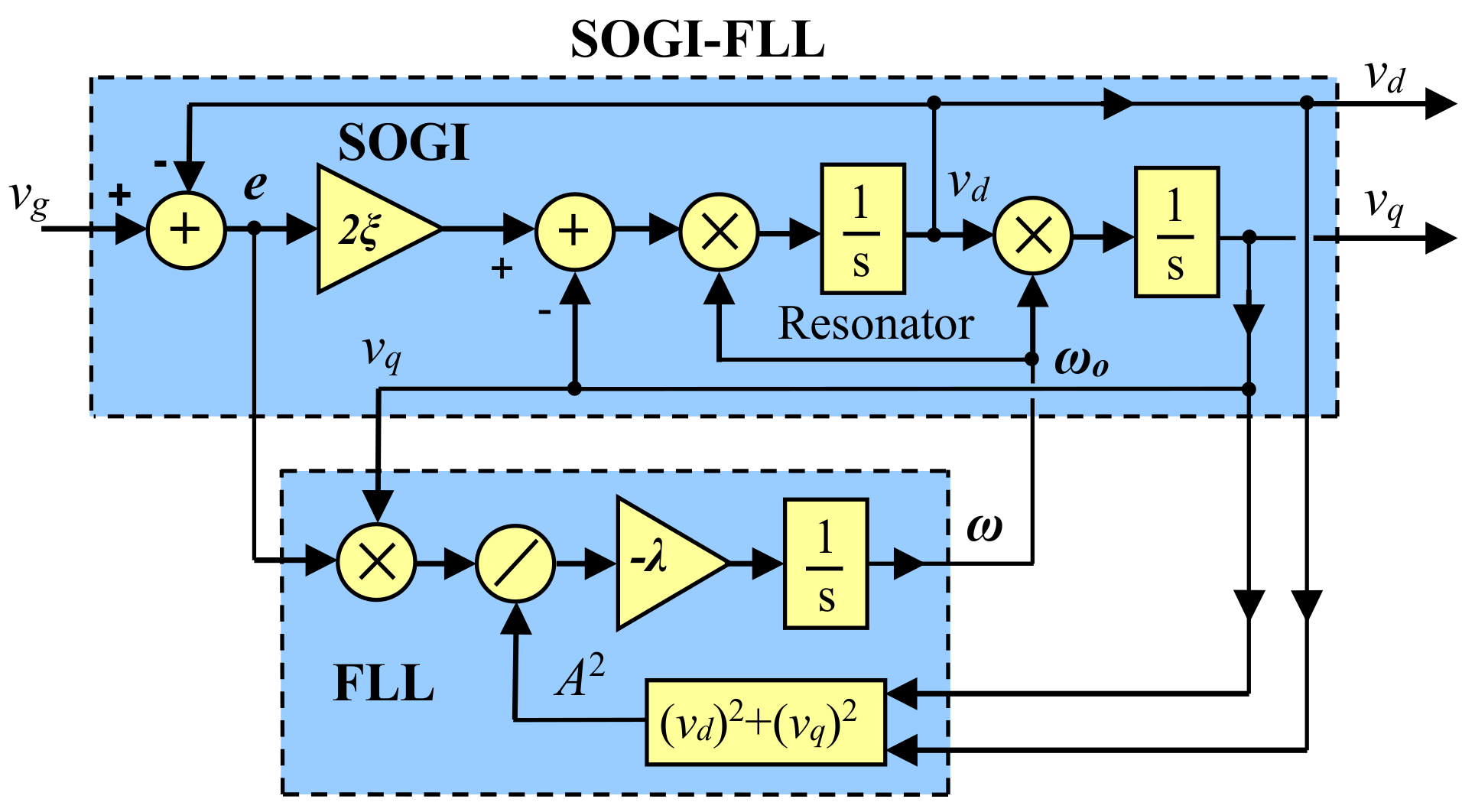
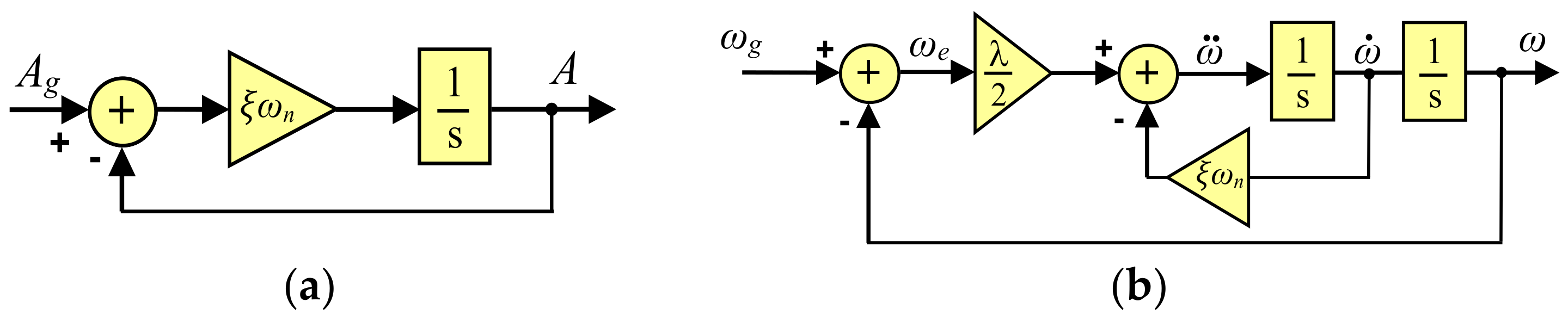
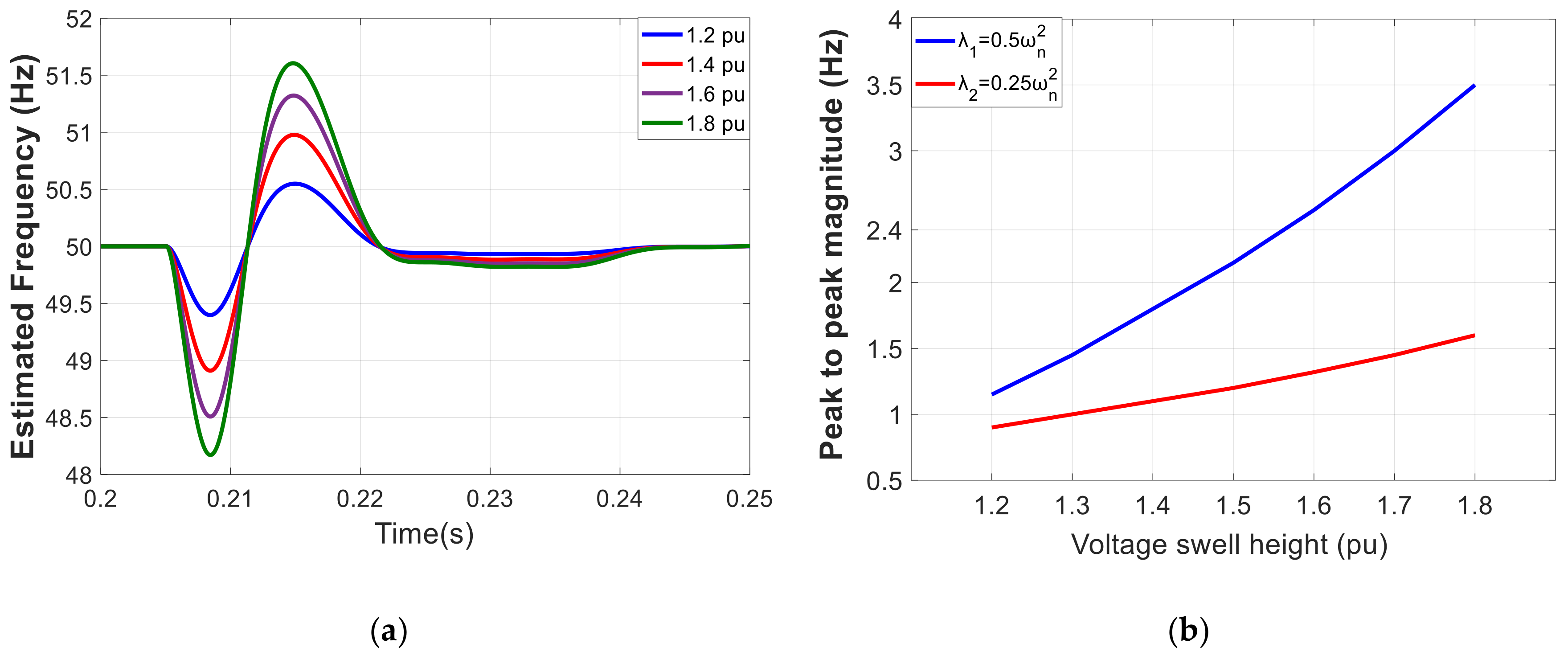
2. SOGI-FLL Response to Voltage Sags and Swells
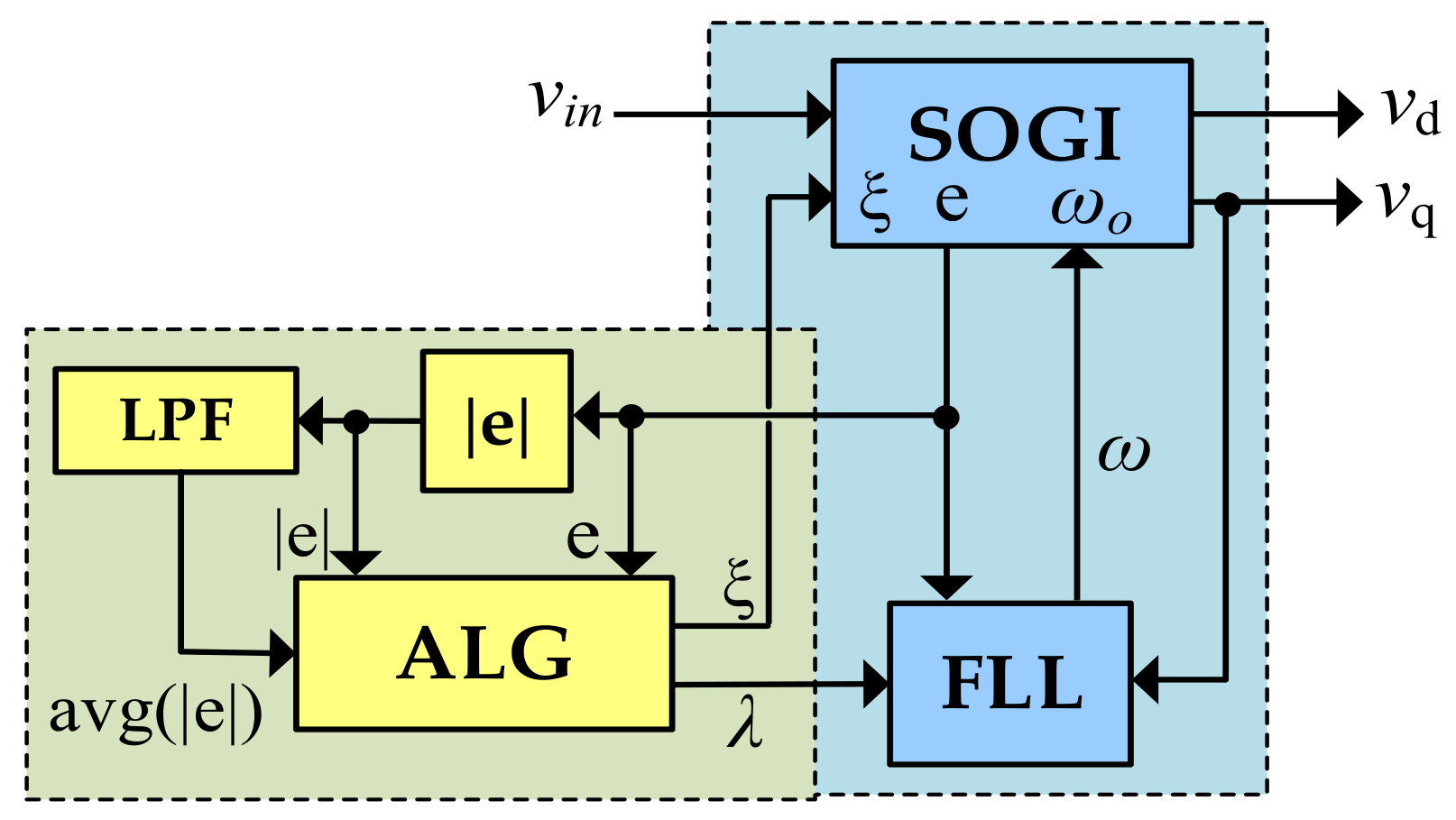
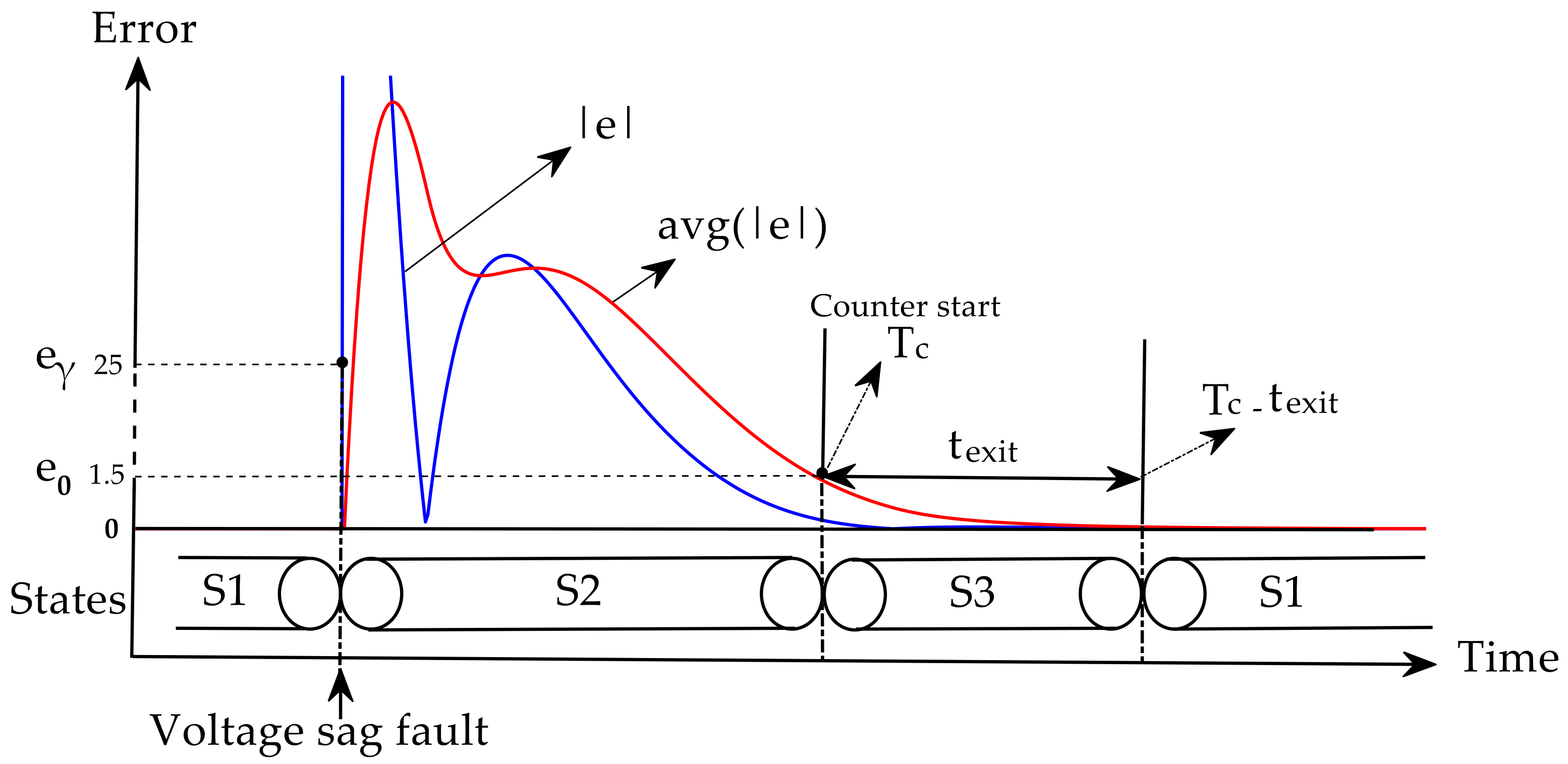
3. Reducing the Perturbation Impact by Means of a SOGI’s Error-Based Algorithm
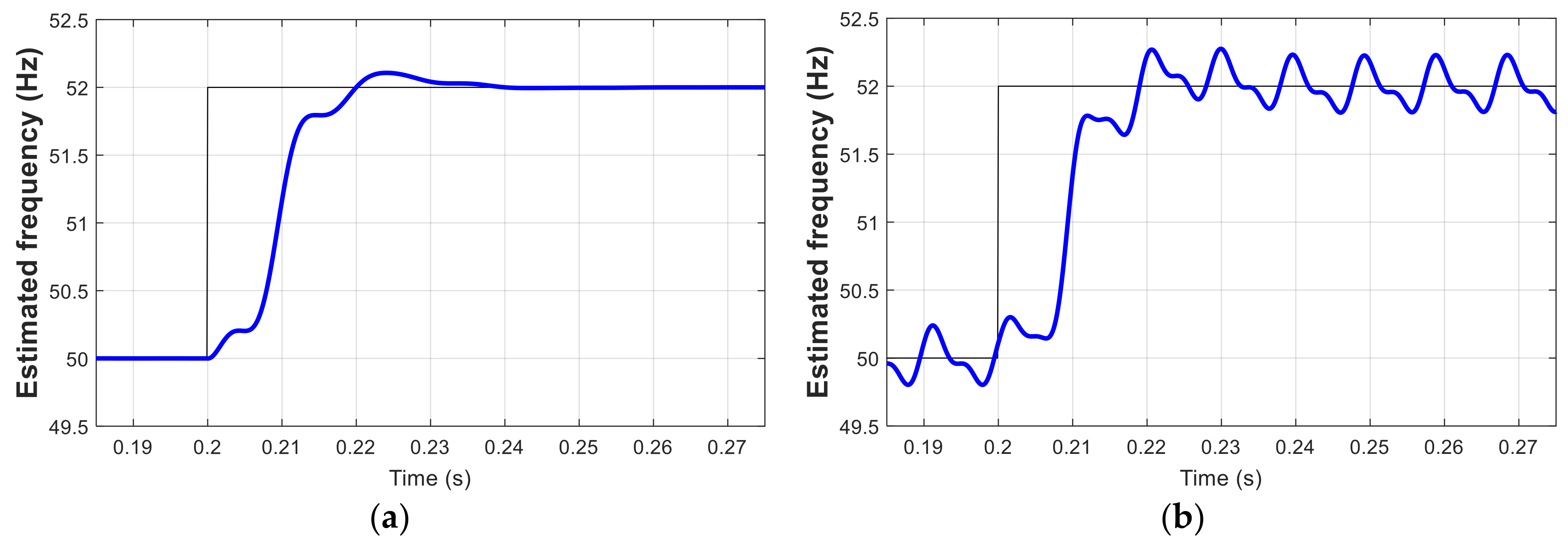
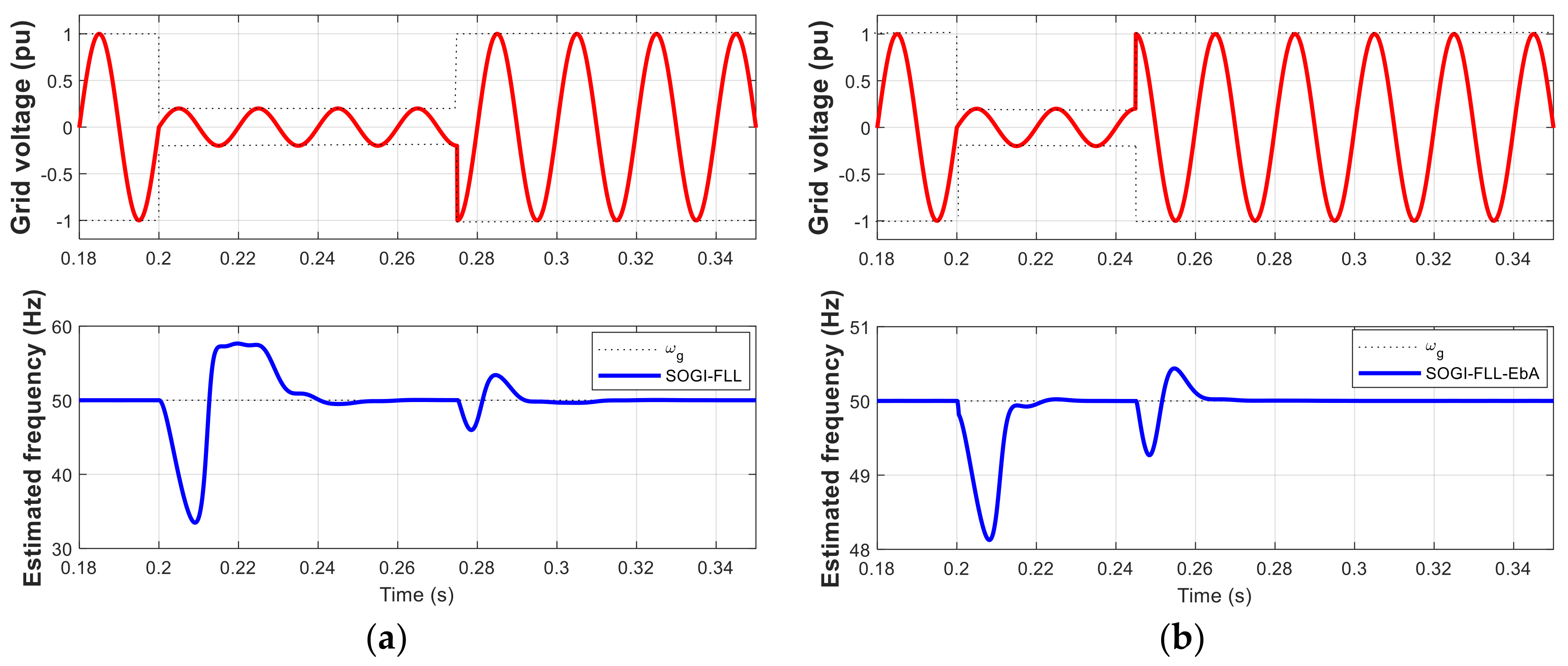
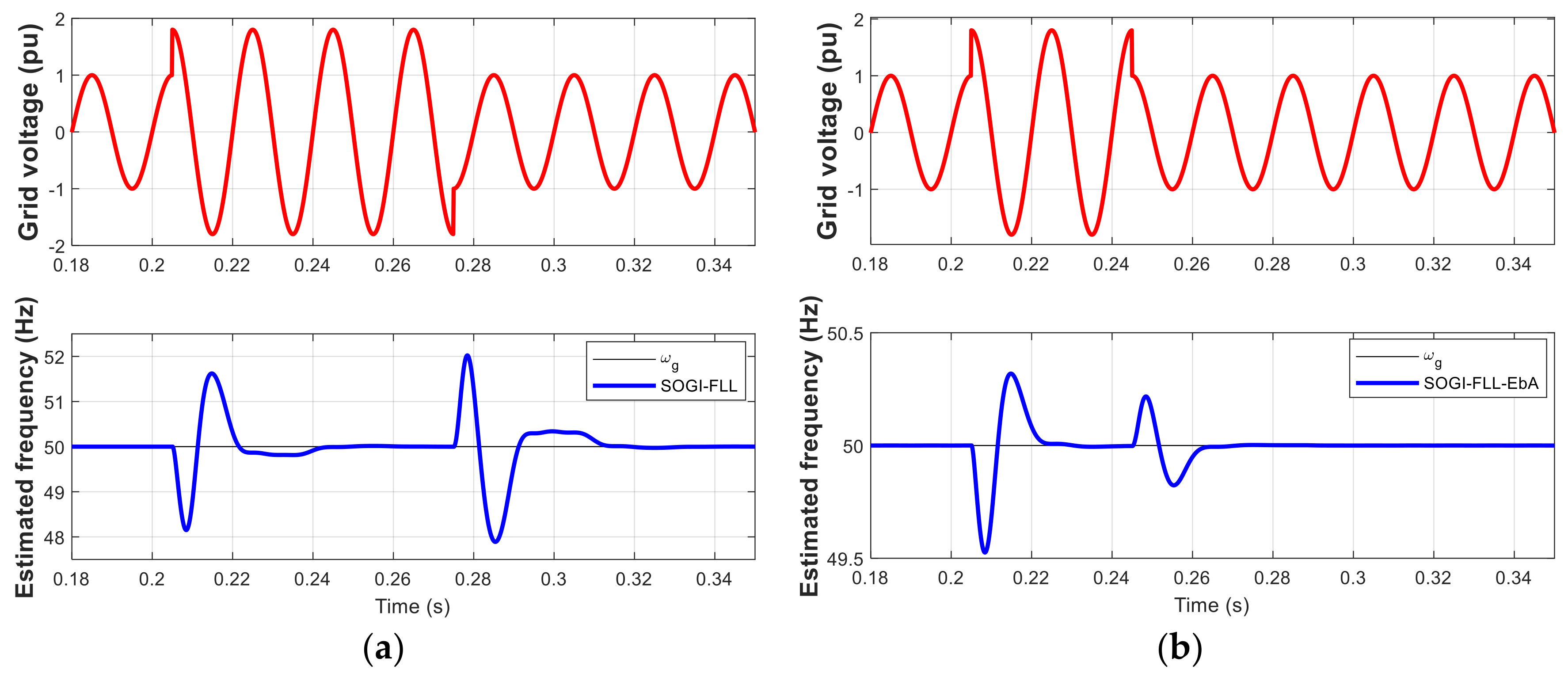
4. Simulation and HIL Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ogata, K.; Brewer, J.W. Modern Control Engineering, 4th ed.; Prentice-Hall: Hoboken, NJ, USA, 2002. [Google Scholar]
- Dugan, R.C.; Mcgranaghan, M.F.; Santoso, S.; Beaty, H.W. Electrical Power Systems Quality, 3rd ed.; McGraw-Hill: New York, NY, USA, 2002. [Google Scholar]
- Kusko, A.; Thompson, M.C. Power Quality in Electrical Systems; McGraw-Hill: New York, NY, USA, 2007. [Google Scholar]
- Teodorescu, R.; Liserre, M.; Rodríguez, P. Grid Converters for Photovoltaic and Wind Power Systems; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 29. [Google Scholar]
- IEEE Recommended Practices and Requirements for Harmonic Control in Electric Power Systems; IEEE Std 519-1992; IEEE: Piscataway, NJ, USA, 1993; pp. 519–1992.
- Matas, J.; Castilla, M.; Miret, J.; De Vicuna, L.G.; Guzman, R. An Adaptive Prefiltering Method to Improve the Speed/Accuracy Tradeoff of Voltage Sequence Detection Methods Under Adverse Grid Conditions. IEEE Trans. Ind. Electron. 2014, 61, 2139–2151. [Google Scholar] [CrossRef]
- Naidoo, R.; Pillay, P. A New Method of Voltage Sag and Swell Detection. IEEE Trans. Power Deliv. 2007, 22, 1056–1063. [Google Scholar] [CrossRef]
- Yunus, A.S.; Masoum, M.A.; Abu-Siada, A. Application of SMES to enhance the dynamic performance of DFIG during voltage sag and swell. IEEE Trans. Appl. Supercond. 2012, 22, 5702009. [Google Scholar] [CrossRef]
- Popavath, L.N.; Kaliannan, P. Photovoltaic-STATCOM with low voltage ride through strategy and power quality enhancement in a grid integrated wind-PV system. Electronics 2018, 7, 51. [Google Scholar] [CrossRef] [Green Version]
- Rey-Boué, A.B.; Guerrero-Rodríguez, N.F.; Stöckl, J.; Strasser, T.I. Modeling and Design of the Vector Control for a Three-Phase Single-Stage Grid-Connected PV System with LVRT Capability according to the Spanish Grid Code. Energies 2019, 12, 2899. [Google Scholar] [CrossRef] [Green Version]
- Safdarian, A.; Fotuhi-Firuzabad, M.; Lehtonen, M. A General Framework for Voltage Sag Performance Analysis of Distribution Networks. Energies 2019, 12, 2824. [Google Scholar] [CrossRef] [Green Version]
- Pu, Y.; Yang, H.; Ma, X.; Sun, X. Recognition of Voltage Sag Sources Based on Phase Space Reconstruction and Improved VGG Transfer Learning. Entropy 2019, 21, 999. [Google Scholar] [CrossRef] [Green Version]
- Li, D.; Mei, F.; Zhang, C.; Sha, H.; Zheng, J. Self-Supervised Voltage Sag Source Identification Method Based on CNN. Energies 2019, 12, 1059. [Google Scholar] [CrossRef] [Green Version]
- Serrano-Fontova, A.; Torrens, P.C.; Bosch, R. Power Quality Disturbances Assessment during Unintentional Islanding Scenarios. A Contribution to Voltage Sag Studies. Energies 2019, 12, 3198. [Google Scholar] [CrossRef] [Green Version]
- Chamchuen, S.; Siritaratiwat, A.; Fuangfoo, P.; Suthisopapan, P.; Khunkitti, P. High-Accuracy Power Quality Disturbance Classification Using the Adaptive ABC-PSO as Optimal Feature Selection Algorithm. Energies 2021, 14, 1238. [Google Scholar] [CrossRef]
- Doget, T.; Etien, E.; Rambault, L.; Cauet, S. A PLL-Based Online Estimation of Induction Motor Consumption Without Electrical Measurement. Electronics 2019, 8, 469. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; De Jong, E.C.W.; Wang, X.; Yang, D.; Blaabjerg, F.; Cuk, V.; Cobben, J.F.G. The Impact of PLL Dynamics on the Low Inertia Power Grid: A Case Study of Bonaire Island Power System. Energies 2019, 12, 1259. [Google Scholar] [CrossRef] [Green Version]
- Du, H.; Sun, Q.; Cheng, Q.; Ma, D.; Wang, X. An Adaptive Frequency Phase-Locked Loop Based on a Third Order Generalized Integrator. Energies 2019, 12, 309. [Google Scholar] [CrossRef] [Green Version]
- Filipovic, F.; Petronijevic, M.; Mitrovic, N.; Bankovic, B.; Kostic, V. A Novel Repetitive Control Enhanced Phase-Locked Loop for Synchronization of Three-Phase Grid-Connected Converters. Energies 2020, 13, 135. [Google Scholar] [CrossRef] [Green Version]
- Rodríguez, P.; Luna, A.; Candela, I.; Mujal, R.; Teodorescu, R.; Blaabjerg, F. Multiresonant Frequency-Locked Loop for Grid Synchronization of Power Converters Under Distorted Grid Conditions. IEEE Trans. Ind. Electron. 2010, 58, 127–138. [Google Scholar] [CrossRef] [Green Version]
- Park, S.J.; Nguyen, T.H.; Lee, D.-C. Advanced SOGI-FLL scheme based on fuzzy logic for single-phase grid-connected con-verters. J. Power Electron. 2014, 14, 598–607. [Google Scholar] [CrossRef] [Green Version]
- Kang, J.W.; Shin, K.W.; Lee, H.; Kang, K.M.; Kim, J.; Won, C.Y. A Study on Stability Control of Grid Connected DC Distribution System Based on Second Order Generalized Integrator-Frequency Locked Loop (SOGI-FLL). Appl. Sci. 2018, 8, 1387. [Google Scholar] [CrossRef] [Green Version]
- Matas, J.; Martin, H.; de la Hoz, J.; Abusorrah, A.; Al-Turki, Y.A.; Al-Hindawi, M. A family of gradient descent grid frequency estimators for the SOGI filter. IEEE Trans. Power Electron. 2018, 33, 5796–5810. [Google Scholar] [CrossRef]
- Golestan, S.; Ebrahimzadeh, E.; Guerrero, J.M.; Vasquez, J.C. An Adaptive Resonant Regulator for Single-Phase Grid-Tied VSCs. IEEE Trans. Power Electron. 2018, 33, 1867–1873. [Google Scholar] [CrossRef]
- Matas, J.; Martin, H.; Elmariachet, J.; Abusorrah, A.; Al-Turki, Y. A New LPF-Based Grid Frequency Estimation for the SOGI Filter with Improved Harmonic Rejection. Renew. Energy Power Qual. J. 2018, 1, 716–721. [Google Scholar] [CrossRef]
- Golestan, S.; Guerrero, J.M.; Vasquez, J.C.; Abusorrah, A.M.; Al-Turki, Y. Modeling, Tuning, and Performance Comparison of Second-Order-Generalized-Integrator-Based FLLs. IEEE Trans. Power Electron. 2018, 33, 10229–10239. [Google Scholar] [CrossRef] [Green Version]
- Ye, S. Fuzzy sliding mode observer with dual SOGI-FLL in sensorless control of PMSM drives. ISA Trans. 2019, 85, 161–176. [Google Scholar] [CrossRef]
- El Mariachet, J.; Matas, J.; Martín, H.; Li, M.; Guan, Y.; Guerrero, J.M. A Power Calculation Algorithm for Single-Phase Droop-Operated-Inverters Considering Linear and Nonlinear Loads HIL-Assessed. Electronics 2019, 8, 1366. [Google Scholar] [CrossRef] [Green Version]
- Cao, W.; Liu, K.; Kang, H.; Wang, S.; Fan, D.; Zhao, J. Resonance Detection Strategy for Multi-Parallel Inverter-Based Grid-Connected Renewable Power System Using Cascaded SOGI-FLL. Sustainability 2019, 11, 4839. [Google Scholar] [CrossRef] [Green Version]
- Matas, J.; Martin, H.; De La Hoz, J.; Abusorrah, A.; Al-Turki, Y.A.; Alshaeikh, H. A New THD Measurement Method with Small Computational Burden Using a SOGI-FLL Grid Monitoring System. IEEE Trans. Power Electron. 2019, 35, 5797–5811. [Google Scholar] [CrossRef]
- Kim, D.-H.; Kim, M.-S.; Kim, H.-J. Frequency-Tracking Algorithm Based on SOGI-FLL for Wireless Power Transfer System to Operate ZPA Region. Electronics 2020, 9, 1303. [Google Scholar] [CrossRef]
- Nejad, S.A.; Matas, J.; Martín, H.; De La Hoz, J.; Al-Turki, Y.A. New SOGI-FLL Grid Frequency Monitoring with a Finite State Machine Approach for Better Response in the Face of Voltage Sag and Swell Faults. Electronics 2020, 9, 612. [Google Scholar] [CrossRef] [Green Version]
- Golestan, S.; Guerrero, J.M.; Vasquez, J.C.; Abusorrah, A.M.; Al-Turki, Y.A. Standard SOGI-FLL and Its Close Variants: Precise Modeling in LTP Framework and Determining Stability Region/Robustness Metrics. IEEE Trans. Power Electron. 2020, 36, 409–422. [Google Scholar] [CrossRef]
- Golestan, S.; Guerrero, J.M.; Musavi, F.; Vasquez, J.C. Single-Phase Frequency-Locked Loops: A Comprehensive Review. IEEE Trans. Power Electron. 2019, 34, 11791–11812. [Google Scholar] [CrossRef]
- Typhoon HIL. Hil 4/6 Series Hardware User Guide; Typhoon HIL Inc.: Somerville, MA, USA, 2021; Available online: https://www.typhoon-hil.com/documentation/typhoon-hil-hardware-manual/hil4-6_series_user_guide/topics/hil4-6_abstract.html (accessed on 10 June 2021).




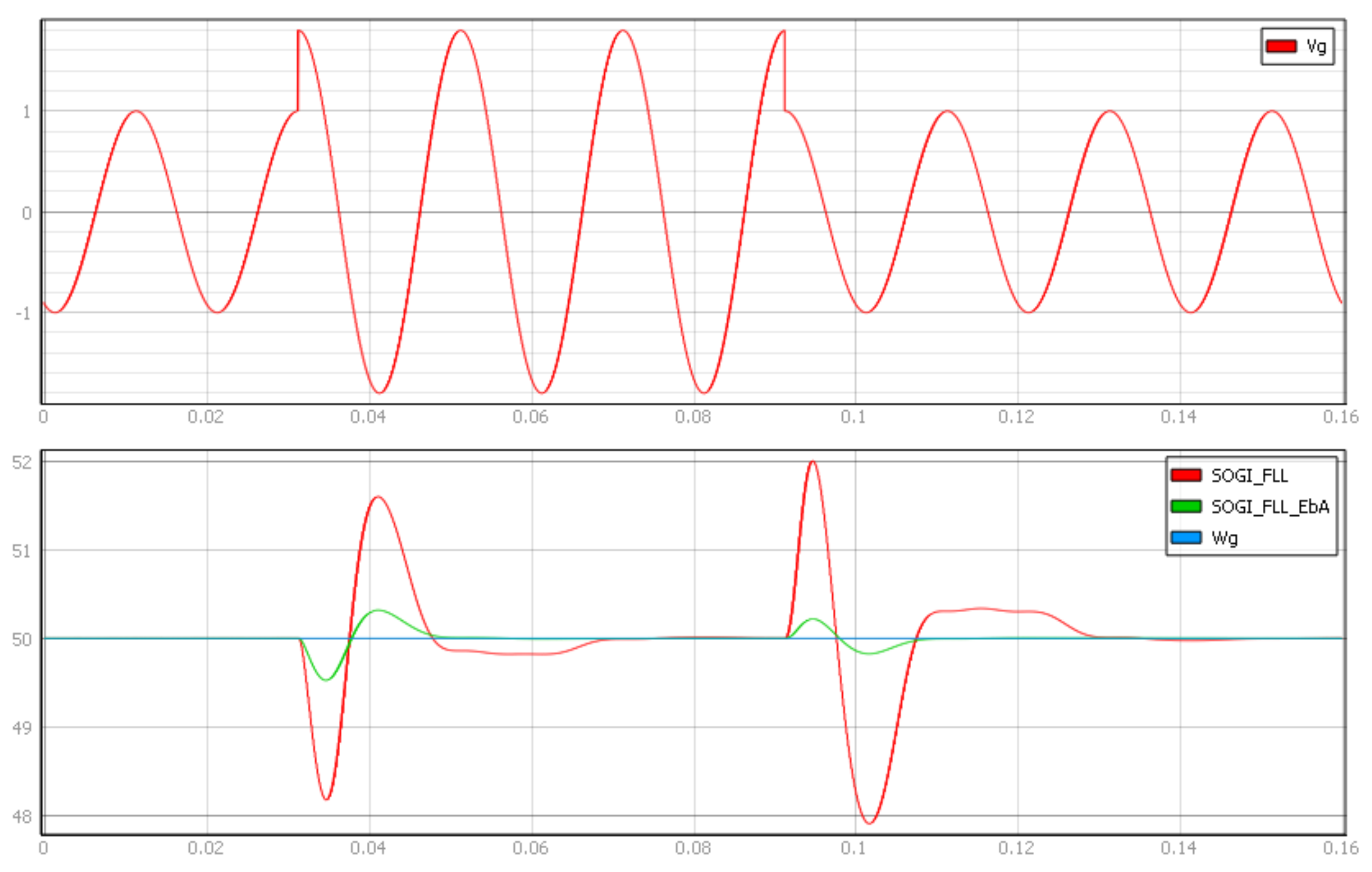
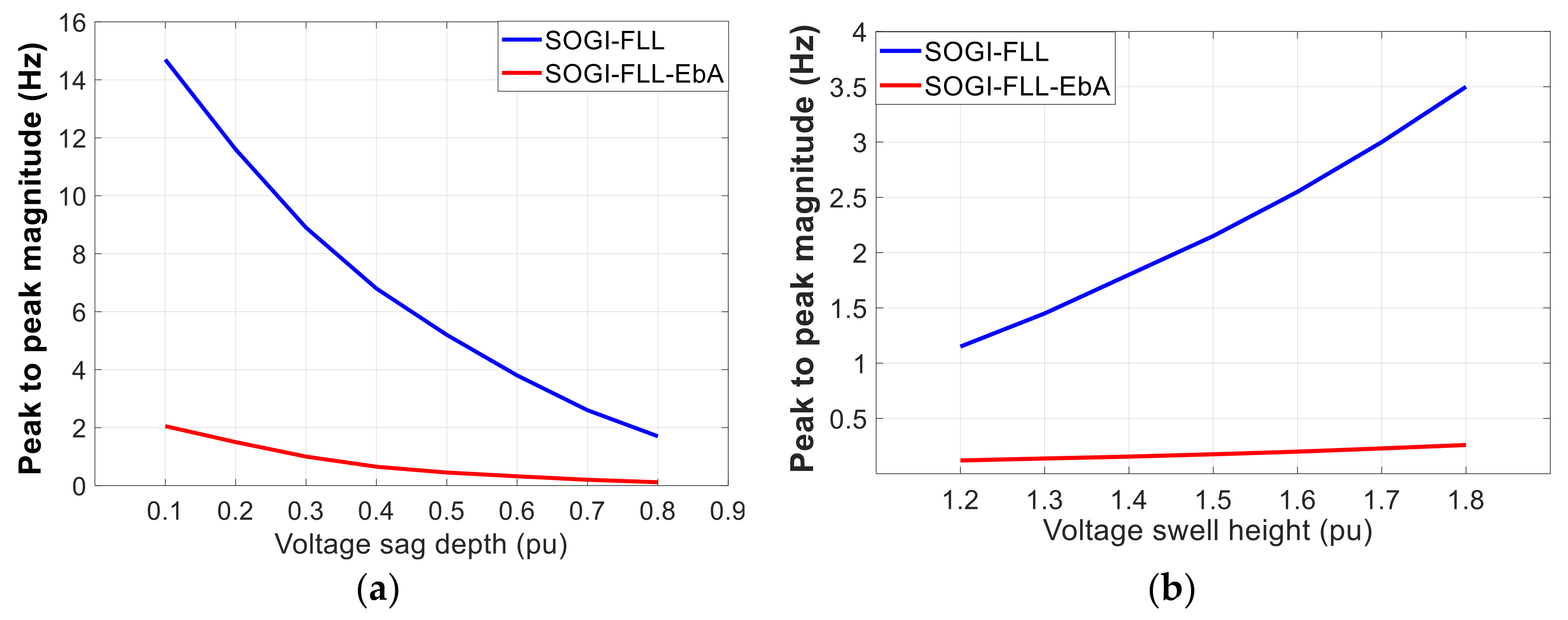
| Parameter | Mp | State | |
|---|---|---|---|
| S1 | S2–S3 | ||
| 4.32% | |||
| 0% | |||
| Parameter | Value | ||
| Fault-type | Sag | Swell | |
| 25 V | 25 V | ||
| 1.5 V | 7 V | ||
| 8.5 ms | 12 ms | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdali Nejad, S.; Matas, J.; Elmariachet, J.; Martín, H.; de la Hoz, J. SOGI-FLL Grid Frequency Monitoring with an Error-Based Algorithm for a Better Response in Face of Voltage Sag and Swell Faults. Electronics 2021, 10, 1414. https://doi.org/10.3390/electronics10121414
Abdali Nejad S, Matas J, Elmariachet J, Martín H, de la Hoz J. SOGI-FLL Grid Frequency Monitoring with an Error-Based Algorithm for a Better Response in Face of Voltage Sag and Swell Faults. Electronics. 2021; 10(12):1414. https://doi.org/10.3390/electronics10121414
Chicago/Turabian StyleAbdali Nejad, Sajad, José Matas, Jordi Elmariachet, Helena Martín, and Jordi de la Hoz. 2021. "SOGI-FLL Grid Frequency Monitoring with an Error-Based Algorithm for a Better Response in Face of Voltage Sag and Swell Faults" Electronics 10, no. 12: 1414. https://doi.org/10.3390/electronics10121414






