Analysis and Performance Assessment of a Real-Time Correction Pseudo-Correlation Microwave Radiometer for Medical Applications
Abstract
:1. Introduction
2. Background Overview of MWR Systems for Medical Applications
3. Microwave Receiver Analysis
3.1. 180 Hybrid Coupler Pseudo-Correlation Configuration
3.2. Noise Analysis
3.3. Receiver Analysis
4. Receiver Design and Results
4.1. System Design
4.2. Performance Results
4.3. Receiver Calibration Procedure and Application
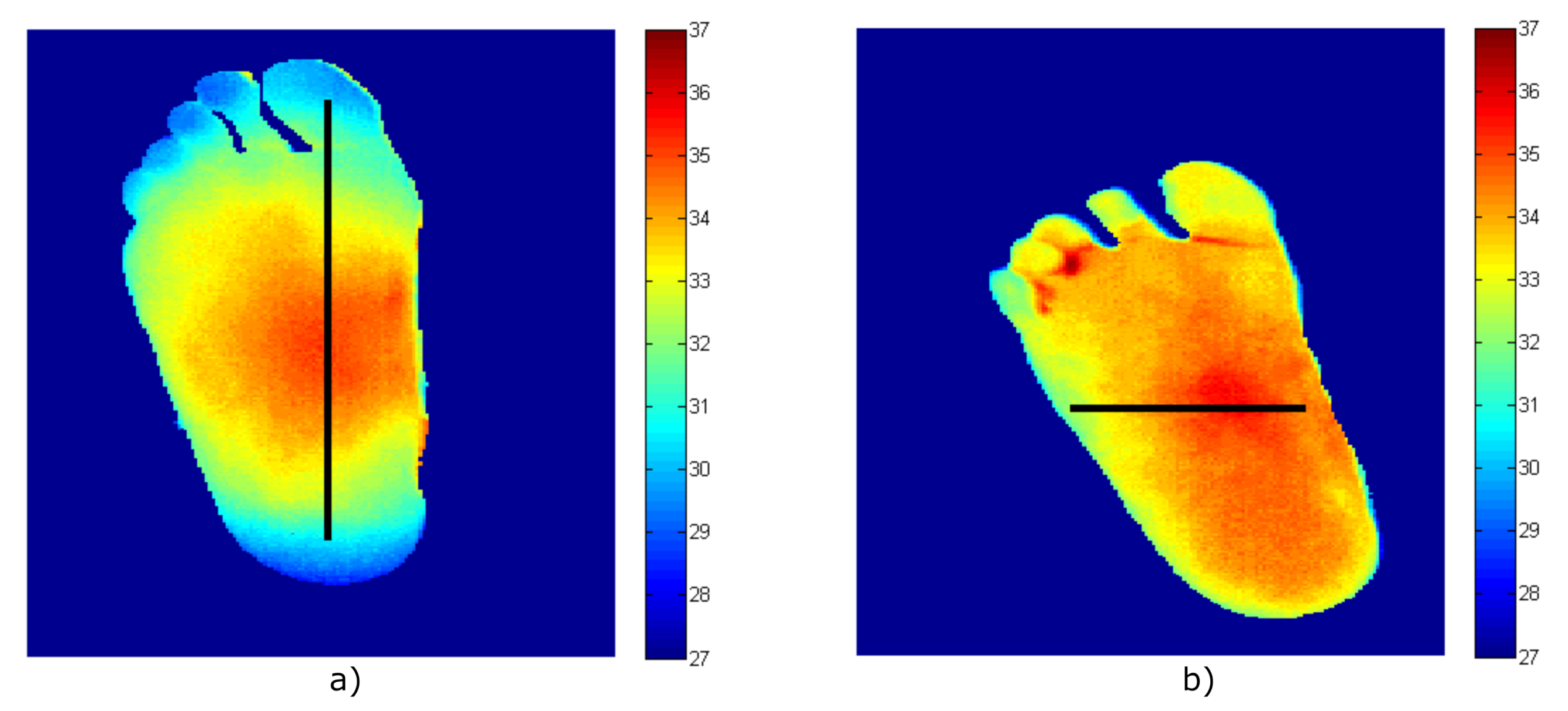
4.4. Validation of the Measurement Procedure Employing the Foot’s Temperature Patterns
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Webber, J.C.; Pospieszalski, M.W. Microwave instrumentation for radio astronomy. IEEE Trans. Microw. Theory Tech. 2002, 50, 986–995. [Google Scholar] [CrossRef]
- Carr, K.L. Microwave radiometry: Its importance to the detection of cancer. IEEE Trans. Microw. Theory Tech. 1989, 37, 1862–1869. [Google Scholar] [CrossRef]
- Goryanin, I.; Karbainov, S.; Shevelev, O.; Tarakanov, A.; Redpath, K.; Vesnin, S.; Ivanov, Y. Passive microwave radiometry in biomedical studies. Drug Discov. Today 2020, 25, 757–763. [Google Scholar] [CrossRef] [PubMed]
- Vesnin, S.; Sedankin, M.; Ovchinnikov, L. Microwave radiometer for medical application. In Proceedings of the 29th Annual Meeting of the European Society for Hyptherthermic Oncology, Torina, Italy, 11–14 June 2014. [Google Scholar]
- Baltag, O.; Banarescu, A.; Costandache, D.; Rau, M.; Ojica, S. Microwaves and infrared thermography–applications in early breast cancer detection. In Proceedings of the International Conference on Advancements of Medicine and Health Care through Technology, Cluj-Napoca, Romania, 23–26 September 2009; pp. 195–198. [Google Scholar]
- Ring, E.F.J.; Hartmann, J.; Ammer, K.; Thomas, R.; Land, D.; Hand, J.W. Infrared and microwave medical thermometry. In Experimental Methods in the Physical Sciences; Elsevier: Amsterdam, The Netherlands, 2010; Volume 43, pp. 393–448. [Google Scholar]
- Scheeler, R.P. A Microwave Radiometer for Internal Body Temperature Measurement. Ph.D. Thesis, University of Colorado at Boulder, Boulder, CO, USA, 2013. [Google Scholar]
- Eshraghi, Y.; Nasr, V.; Parra-Sanchez, I.; Van Duren, A.; Botham, M.; Santoscoy, T.; Sessler, D.I. An evaluation of a zero-heat-flux cutaneous thermometer in cardiac surgical patients. Anesth. Analg. 2014, 119, 543–549. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Momenroodaki, P.; Haines, W.; Fromandi, M.; Popovic, Z. Noninvasive internal body temperature tracking with near-field microwave radiometry. IEEE Trans. Microw. Theory Tech. 2018, 66, 2535–2545. [Google Scholar] [CrossRef]
- Aldhaeebi, M.A.; Alzoubi, K.; Almoneef, T.S.; Bamatraf, S.M.; Attia, H.; M Ramahi, O. Review of Microwaves Techniques for Breast Cancer Detection. Sensors 2020, 20, 2390. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Islam, M.; Mahmud, M.; Islam, M.T.; Kibria, S.; Samsuzzaman, M. A low cost and portable microwave imaging system for breast tumor detection using UWB directional antenna array. Sci. Rep. 2019, 9, 1–13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bocquet, B.; Van de Velde, J.; Mamouni, A.; Leroy, Y.; Giaux, G.; Delannoy, J.; Delvalee, D. Microwave radiometric imaging at 3 GHz for the exploration of breast tumors. IEEE Trans. Microw. Theory Tech. 1990, 38, 791–793. [Google Scholar] [CrossRef]
- Casu, M.R.; Vacca, M.; Tobon, J.A.; Pulimeno, A.; Sarwar, I.; Solimene, R.; Vipiana, F. A COTS-Based Microwave Imaging System for Breast-Cancer Detection. IEEE Trans. Biomed. Circuits Syst. 2017, 11, 804–814. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Drakopoulou, M.; Moldovan, C.; Toutouzas, K.; Tousoulis, D. The role of microwave radiometry in carotid artery disease. Diagnostic and clinical prospective. Curr. Opin. Pharmacol. 2018, 39, 99–104. [Google Scholar] [CrossRef] [PubMed]
- Toutouzas, K.; Grassos, C.; Drakopoulou, M.; Synetos, A.; Tsiamis, E.; Aggeli, C.; Stathogiannis, K.; Klettas, D.; Kavantzas, N.; Agrogiannis, G.; et al. First in vivo application of microwave radiometry in human carotids: A new noninvasive method for detection of local inflammatory activation. J. Am. Coll. Cardiol. 2012, 59, 1645–1653. [Google Scholar] [CrossRef] [Green Version]
- Spiliopoulos, S.; Theodosiadou, V.; Barampoutis, N.; Katsanos, K.; Davlouros, P.; Reppas, L.; Kitrou, P.; Palialexis, K.; Konstantos, C.; Siores, E.; et al. Multi-center feasibility study of microwave radiometry thermometry for non-invasive differential diagnosis of arterial disease in diabetic patients with suspected critical limb ischemia. J. Diabetes Its Complicat. 2017, 31, 1109–1114. [Google Scholar] [CrossRef]
- Hand, J.; Van Leeuwen, G.; Mizushina, S.; Van de Kamer, J.; Maruyama, K.; Sugiura, T.; Azzopardi, D.; Edwards, A. Monitoring of deep brain temperature in infants using multi-frequency microwave radiometry and thermal modelling. Phys. Med. Biol. 2001, 46, 1885. [Google Scholar] [CrossRef] [Green Version]
- Maruyma, K.; Mizushina, S.; Sugiura, T.; Van Leeuwen, G.; Hand, J.; Marrocco, G.; Bardati, F.; Edwards, A.; Azzopardi, D.; Land, D. Feasibility of noninvasive measurement of deep brain temperature in newborn infants by multifrequency microwave radiometry. IEEE Trans. Microw. Theory Tech. 2000, 48, 2141–2147. [Google Scholar]
- Zinovyev, S. New medical technology–functional microwave thermography: Experimental study. KnE Energy 2018, 3, 547–555. [Google Scholar] [CrossRef]
- Galiana, G.; Branca, R.T.; Jenista, E.R.; Warren, W.S. Accurate temperature imaging based on intermolecular coherences in magnetic resonance. Science 2008, 322, 421–424. [Google Scholar] [CrossRef] [Green Version]
- Childs, C.; Harrison, R.; Hodkinson, C. Tympanic membrane temperature as a measure of core temperature. Arch. Dis. Child. 1999, 80, 262–266. [Google Scholar] [CrossRef] [Green Version]
- Land, D. Medical microwave radiometry and its clinical applications. In Proceedings of the IEE Colloquium on Application of Microwaves in Medicine, London, UK, 28 February 1995. [Google Scholar]
- Barrett, A.H.; Myers, P.C.; Sadowsky, N. Microwave thermography in the detection of breast cancer. Am. J. Roentgenol. 1980, 134, 365–368. [Google Scholar] [CrossRef] [Green Version]
- Momenroodaki, P.; Haines, W.; Popović, Z. Non-invasive microwave thermometry of multilayer human tissues. In Proceedings of the 2017 IEEE MTT-S International Microwave Symposium (IMS), Honololu, HI, USA, 4–9 June 2017; pp. 1387–1390. [Google Scholar]
- Momenroodaki, P.; Popovic, Z.; Scheeler, R. A 1.4-GHz radiometer for internal body temperature measurements. In Proceedings of the 2015 European Microwave Conference (EuMC), Paris, France, 7–10 September 2015; pp. 694–697.
- Park, W.; Jeong, J. Total Power Radiometer for Medical Sensor Applications Using Matched and Mismatched Noise Sources. Sensors 2017, 17, 2105. [Google Scholar] [CrossRef] [Green Version]
- Klemetsen, ∅; Jacobsen, S. Improved radiometric performance attained by an elliptical microwave antenna with suction. IEEE Trans. Biomed. Eng. 2012, 59, 263–271. [Google Scholar] [CrossRef] [Green Version]
- Klemetsen, ∅; Birkelund, Y.; Jacobsen, S.K.; Maccarini, P.F.; Stauffer, P.R. Design of medical radiometer front-end for improved performance. Prog. Electromagn. Res. B Pier B 2011, 27, 289. [Google Scholar] [CrossRef] [Green Version]
- Ravi, V.M.; Akki, R.S.; Sugumar, S.; Venkata, K.C.; Arunachalam, K. Design and evaluation of medical microwave radiometer for measuring tissue temperature. In Proceedings of the 2019 URSI Asia-Pacific Radio Science Conference (AP-RASC), New Delhi, India, 9–15 March 2019; pp. 1–3. [Google Scholar]
- Land, D. An efficient, accurate and robust radiometer configuration for microwave temperature measurement for industrial and medical applications. J. Microw. Power Electromagn. Energy 2001, 36, 139–153. [Google Scholar] [CrossRef]
- Livanos, N.A.; Hammal, S.; Nikolopoulos, C.D.; Baklezos, A.T.; Capsalis, C.N.; Koulouras, G.E.; Charamis, P.I.; Vardiambasis, I.O.; Nassiopoulos, A.; Kostopoulos, S.A.; et al. Design and interdisciplinary simulations of a hand-held device for internal-body temperature sensing using microwave radiometry. IEEE Sens. J. 2018, 18, 2421–2433. [Google Scholar] [CrossRef]
- Vesnin, S.G.; Sedankin, M.K.; Ovchinnikov, L.M.; Gudkov, A.G.; Leushin, V.Y.; Sidorov, I.A.; Goryanin, I.I. Portable microwave radiometer for wearable devices. Sens. Actuators A Phys. 2021, 318, 112506. [Google Scholar] [CrossRef]
- Villa, E.; Arteaga-Marrero, N.; León, G.; Herrán, L.; Mateos, I.; Ruiz-Alzola, J. A 3.5-GHz pseudo-correlation type radiometer for biomedical applications. AEU Int. J. Electron. Commun. 2021, 130, 153558. [Google Scholar] [CrossRef]
- Tiuri, M. Radio astronomy receivers. IEEE Trans. Mil. Electron. 1964, 8, 264–272. [Google Scholar] [CrossRef]
- Jarosik, N.; Bennett, C.; Halpern, M.; Hinshaw, G.; Kogut, A.; Limon, M.; Meyer, S.; Page, L.; Pospieszalski, M.; Spergel, D.; et al. Design, implementation, and testing of the microwave anisotropy probe radiometers. Astrophys. J. Suppl. Ser. 2003, 145, 413. [Google Scholar] [CrossRef]
- Aja, B.; Artal, E.; de la Fuente, L.; Pascual, J.P.; Mediavilla, A.; Roddis, N.; Kettle, D.; Winder, W.F.; Cara, L.P.; de Paco, P. Very low-noise differential radiometer at 30 GHz for the PLANCK LFI. IEEE Trans. Microw. Theory Tech. 2005, 53, 2050–2062. [Google Scholar] [CrossRef] [Green Version]
- Harris, A.; Zonak, S.; Watts, G.; Norrod, R. Design Considerations for Correlation Radiometers. Available online: http://library.nrao.edu/public/memos/gbt/GBT_254.pdf (accessed on 22 October 2007).
- Villa, E.; Arteaga-Marrero, N.; Ruiz-Alzola, J. Performance Assessment of Low-Cost Thermal Cameras for Medical Applications. Sensors 2020, 20, 1321. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Arteaga-Marrero, N.; Hernández, A.; Villa, E.; González-Pérez, S.; Luque, C.; Ruiz-Alzola, J. Segmentation Approaches for Diabetic Foot Disorders. Sensors 2021, 21, 934. [Google Scholar] [CrossRef] [PubMed]
- González-Pérez, S.; Perea Ström, D.; Arteaga-Marrero, N.; Luque, C.; Sidrach-Cardona, I.; Villa, E.; Ruiz-Alzola, J. Assessment of Registration Methods for Thermal Infrared and Visible Images for Diabetic Foot Monitoring. Sensors 2021, 21, 2264. [Google Scholar] [CrossRef] [PubMed]
- Bait-Suwailam, M.M.; Bahadur, I. Non-Invasive Microwave CSRR-Based Sensor for Diabetic Foot Ulcers Detection. In Proceedings of the 2021 18th International Multi-Conference on Systems, Signals & Devices (SSD), Monastir, Tunisia, 22–25 March 2021; pp. 1237–1240. [Google Scholar]
- Osmonov, B.; Ovchinnikov, L.; Galazis, C.; Emilov, B.; Karaibragimov, M.; Seitov, M.; Vesnin, S.; Losev, A.; Levshinskii, V.; Popov, I.; et al. Passive Microwave Radiometry for the Diagnosis of Coronavirus Disease 2019 Lung Complications in Kyrgyzstan. Diagnostics 2021, 11, 259. [Google Scholar] [CrossRef] [PubMed]
- Lavery, L.A.; Higgins, K.R.; Lanctot, D.R.; Constantinides, G.P.; Zamorano, R.G.; Athanasiou, K.A.; Armstrong, D.G.; Agrawal, C.M. Preventing diabetic foot ulcer recurrence in high-risk patients: Use of temperature monitoring as a self-assessment tool. Diabetes Care 2007, 30, 14–20. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Microwave Remote Sensing: Active and Passive. Volume 1—Microwave Remote Sensing Fundamentals and Radiometry; Artech House, Inc.: Norwood, MA, USA, 1981; Volume 1. [Google Scholar]
- Fujimoto, K. On the correlation radiometer technique. IEEE Trans. Microw. Theory Tech. 1964, 12, 203–212. [Google Scholar] [CrossRef]
- Kraus, J.D.; Tiuri, M.; Räisänen, A.V.; Carr, T.D. Radio Astronomy; Cygnus-Quasar Books: Powell, OH, USA, 1986; Volume 69. [Google Scholar]
- Faris, J.J. Sensitivity of a correlation radiometer. J. Res. Natl. Bur. Stand. C 1967, 71, 153–170. [Google Scholar] [CrossRef]
- Kerr, A. On the noise properties of balanced amplifiers. IEEE Microw. Guid. Wave Lett. 1998, 8, 390–392. [Google Scholar] [CrossRef]
- Aja, B.; de la Fuente, L.; Artal, E.; Villa, E.; Cano-de Diego, J.L.; Mediavilla, A. 10-to 19.5-GHz microwave receiver of an electro-optical interferometer for radio astronomy. J. Astron. Telesc. Instruments Syst. 2019, 5, 035007. [Google Scholar] [CrossRef]
- Note, A.A. Noise Figure Measurement Accuracy—The Y-Factor Method; Agilent Technology: Palo Alto, CA, USA, 2001. [Google Scholar]
- Mini-Circuits. Technical Datasheet Low Noise Amplifier TAMP-362GLN+. 2018. Available online: https://www.minicircuits.com/pdfs/TAMP-362GLN+.pdf (accessed on 1 May 2021).
- Mini-Circuits. Technical Datasheet Bandpass Filter BFCN-3600+. 2018. Available online: https://www.minicircuits.com/pdfs/BFCN-3600+.pdf (accessed on 1 May 2021).
- Pozar, D.M. Microwave Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Mini-Circuits. Typical Performance Data Amplifier TAMP-362GLN+. 2018. Available online: https://www.minicircuits.com/pages/s-params/TAMP-362GLN+_VIEW.pdf (accessed on 1 May 2021).




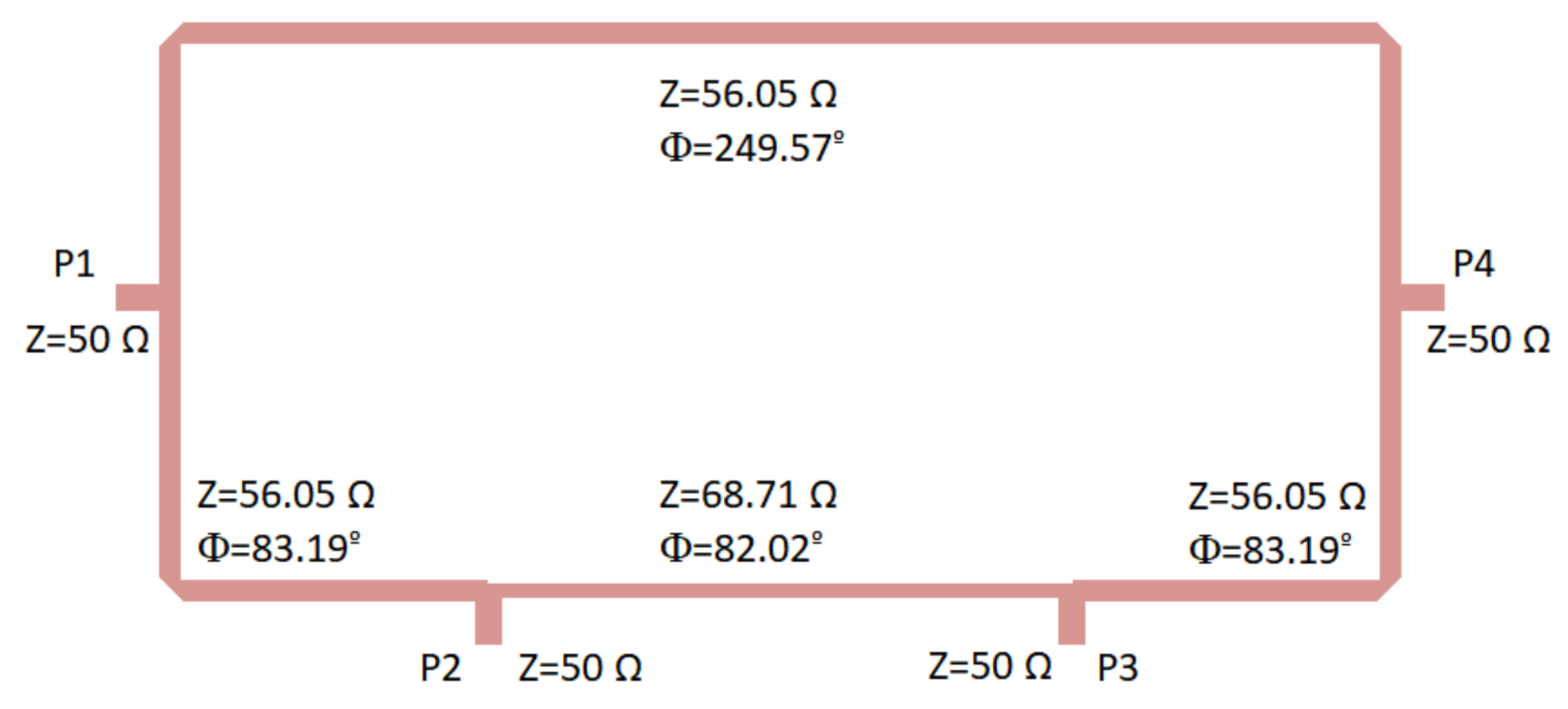

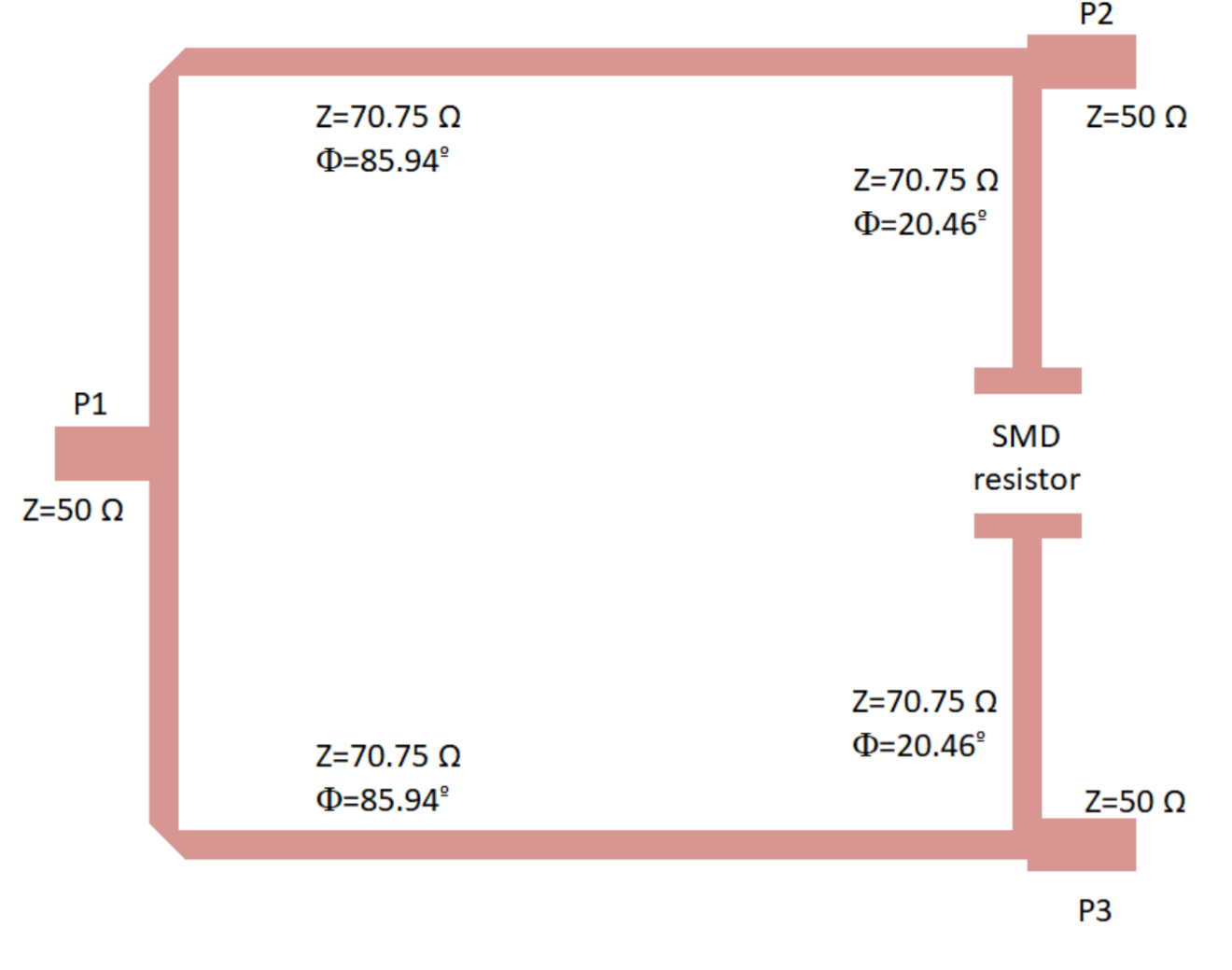
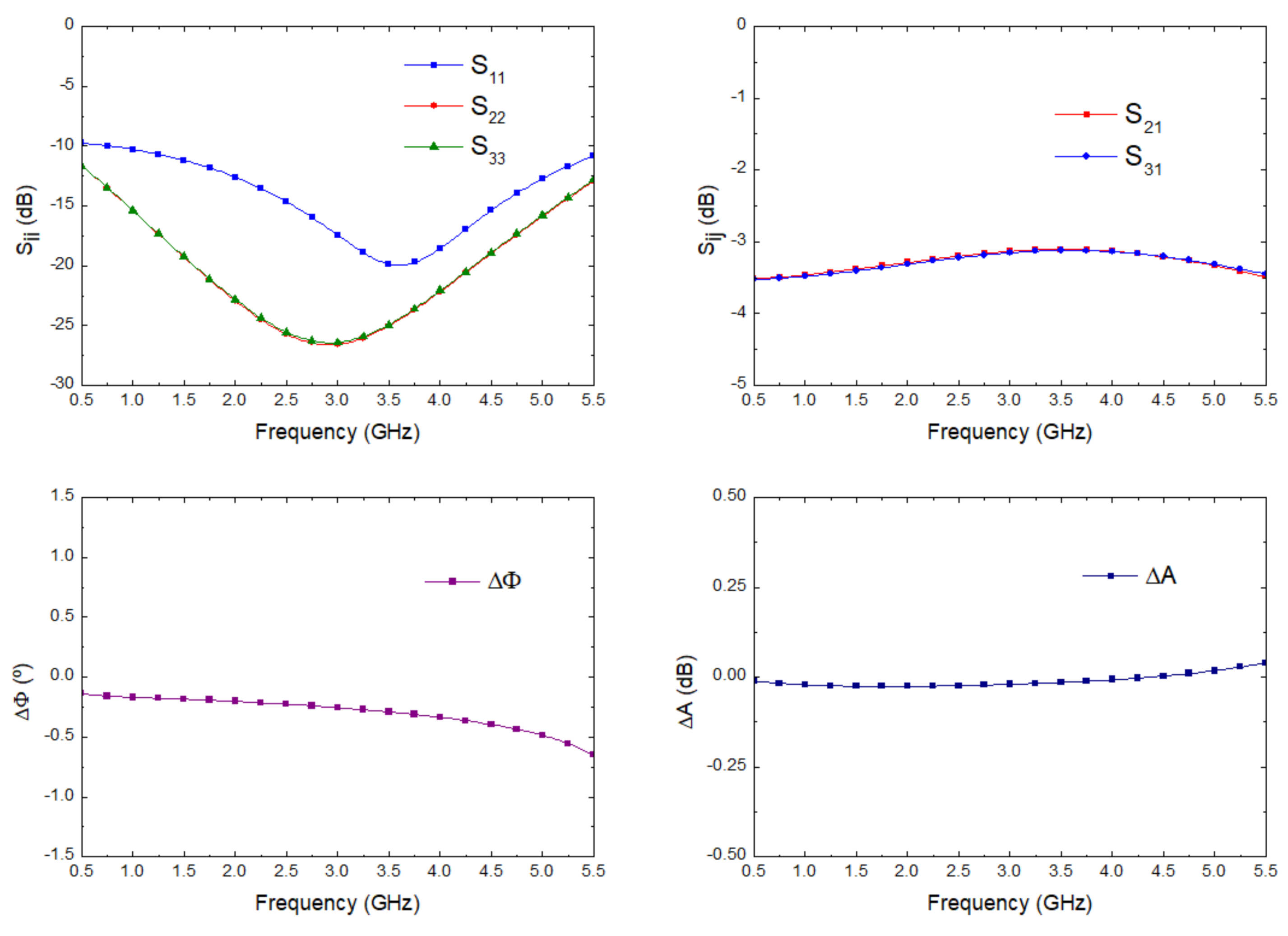
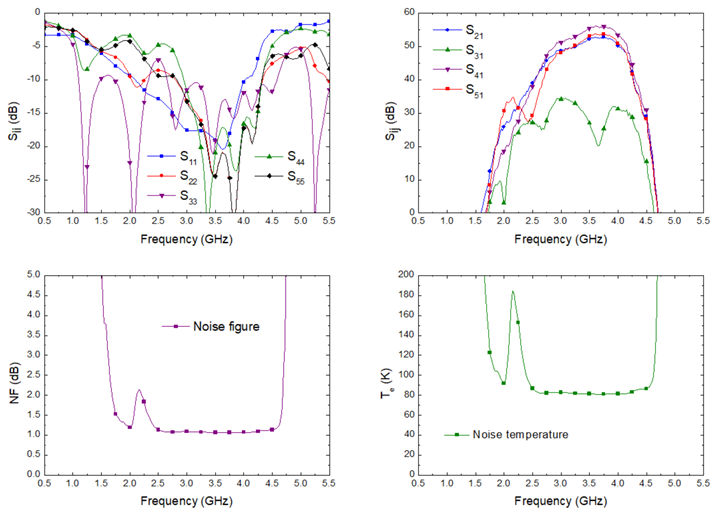
| Reference | Configuration | Operation Frequency (GHz) | Bandwidth (GHz) | Noise Temperature (K) |
|---|---|---|---|---|
| [9] | Dicke switched | 1.4 | ≈0.03 | 127.30 |
| [26] | Switched | 3 | 0.23 | >148.94 |
| [27] | Dicke switched | 3.5 | 0.66 | 217.20 |
| [29] | Dicke switched | 1.3 | 0.33 | <288.60 |
| [33] | Pseudo-correlation | 3.5 | 1.33 | 140.26 |
| This work | Pseudo-correlation | 3.5 | 1.26 | 82.57 |
| Subsystem | Output Signal |
|---|---|
| Low-noise Amplifier LNA#k1 | voak1 = gak1·(Sink + nak1)·e; Sin1 = Sant, Sin2 = Sref |
| Hybrid 180 H#1 | voH11 = (1/)·aH1·[(voa11 + nH11)·e−(voa21 + nH12)·e] voH12 = (1/)·aH1·[(voa11 + nH11)·e+(voa21 + nH12)·e] |
| Low-noise Amplifier LNA#k2 + Band-pass Filter BPF#k | voafk = gafk·(voH1k + nafk)·e |
| Power Splitters S#k | voski = (1/)·ask·(voafk+nsk)·e with i = 1, 2 |
| Hybrid 180 H#2 | voH21 = (1/)·aH2·[(vos12 + nH21)·e−(vos21 + nH22)·e] voH22 = (1/)·aH2·[(vos12 + nH21)·e+(vos21 + nH22)·e] |
| Tant = 400 K | Tant = 500 K | Tant = 310 K | Theoretical Temperature | |
|---|---|---|---|---|
| Tref = 100 K | Tref = 250 K | Tref = 290 K | ||
| Predetection Point in Figure 2 | Temperature(K) | Temperature(K) | Temperature(K) | Temperature(K) |
| (2) | 124.96 | 187.44 | 149.96 | · (Tant + Tref) |
| (3) | 49.98 | 124.96 | 144.96 | ·Tref |
| (4) | 199.94 | 249.93 | 154.95 | ·Tant |
| (5) | 124.96 | 187.44 | 149.96 | · (Tant + Tref) |
| Device | Part Number | Technical Features |
|---|---|---|
| Low-noise Amplifier (LNA) | TAMP-362GLN+ (MiniCircuits) | 3.3–3.6 GHz, 20 dB gain, 0.9 dB noise figure |
| Band-pass Filter (BPF) | BFCN-3600+ (MiniCircuits) | 3.3–3.9 GHz, 1.3 dB insertion loss |
| Schottky diode detector | ACSP-2643NZC3 (Aeroflex) | Zero bias, 1000 mV/mW sensitivity, −46 dBm tangential sensitivity |
| Predetection Point in Figure 2 | Power (dBm) |
|---|---|
| (2) | −27.17 |
| (3) | −27.56 |
| (4) | −27.31 |
| (5) | −27.22 |
| ENR = 3 dB | ENR = 6 dB | ENR = 9 dB | ENR = 12 dB | ENR = 15 dB | |
|---|---|---|---|---|---|
| Predetection Point | Power (dBm) | Power (dBm) | Power (dBm) | Power (dBm) | Power (dBm) |
| (2) | −24.60 | −22.95 | −20.84 | −18.35 | −15.64 |
| (3) | −27.52 | −27.47 | −27.39 | −27.21 | −26.89 |
| (4) | −23.35 | −21.26 | −18.81 | −16.11 | −13.27 |
| (5) | −24.82 | −23.24 | −21.18 | −18.74 | −16.05 |
| Parameter | Output | |||
|---|---|---|---|---|
| k = 1 | k = 2 | k = 3 | k = 4 | |
| Ak | = 0.509 | = 0.007 | = 1.008 | = 0.564 |
| Rk | = 0.550 | 1 | = 0.007 | = 0.507 |
| Nk | 2 · = 1.053 | 1 | = 1.008 | 2 · = 1.064 |
| Volunteer #1 | Volunteer #2 | ||
|---|---|---|---|
| Treal-1 (K) | Tant-1 (K) | Treal-2 (K) | Tant-2 (K) |
| 303.46 | 303.43 | 305.23 | 305.20 |
| 305.11 | 305.08 | 306.65 | 306.62 |
| 308.19 | 308.16 | 308.67 | 308.64 |
| 306.30 | 306.27 | 308.07 | 308.04 |
| 302.39 | 302.36 | 307.72 | 307.69 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Villa, E.; Aja, B.; de la Fuente, L.; Artal, E.; Arteaga-Marrero, N.; González-Pérez, S.; Ruiz-Alzola, J. Analysis and Performance Assessment of a Real-Time Correction Pseudo-Correlation Microwave Radiometer for Medical Applications. Electronics 2021, 10, 1427. https://doi.org/10.3390/electronics10121427
Villa E, Aja B, de la Fuente L, Artal E, Arteaga-Marrero N, González-Pérez S, Ruiz-Alzola J. Analysis and Performance Assessment of a Real-Time Correction Pseudo-Correlation Microwave Radiometer for Medical Applications. Electronics. 2021; 10(12):1427. https://doi.org/10.3390/electronics10121427
Chicago/Turabian StyleVilla, Enrique, Beatriz Aja, Luisa de la Fuente, Eduardo Artal, Natalia Arteaga-Marrero, Sara González-Pérez, and Juan Ruiz-Alzola. 2021. "Analysis and Performance Assessment of a Real-Time Correction Pseudo-Correlation Microwave Radiometer for Medical Applications" Electronics 10, no. 12: 1427. https://doi.org/10.3390/electronics10121427
APA StyleVilla, E., Aja, B., de la Fuente, L., Artal, E., Arteaga-Marrero, N., González-Pérez, S., & Ruiz-Alzola, J. (2021). Analysis and Performance Assessment of a Real-Time Correction Pseudo-Correlation Microwave Radiometer for Medical Applications. Electronics, 10(12), 1427. https://doi.org/10.3390/electronics10121427







