Robust Model Predictive Controller Using Recurrent Neural Networks for Input–Output Linear Parameter Varying Systems
Abstract
:1. Introduction
- An RNN-based optimization algorithm is developed to offer global convergence and lower the online computational load.
- Free control moves are added to the constant control gain to maintain the closed-loop stability when facing bounded disturbances.
- Concerning previous studies for MPC with LPV, the proposed method inherently enjoys a shrunken conservatism degree as a result of finding the larger possible terminal region, using free control moves, and the global solution of the optimization problem.
2. Problem Statement
3. Robust Model Predictive Controller
3.1. Offline Controller
- for And .
- If then
- .
3.2. Online Controller
- .
- is an RPI set of the system (1) with .
- for ,,
4. Real-Time Optimization Problem Using RNN
- The value of and model ;
- Specify K using (12) and using (15);
- Repeat the procedure of finding by solving Equations (38)–(40).
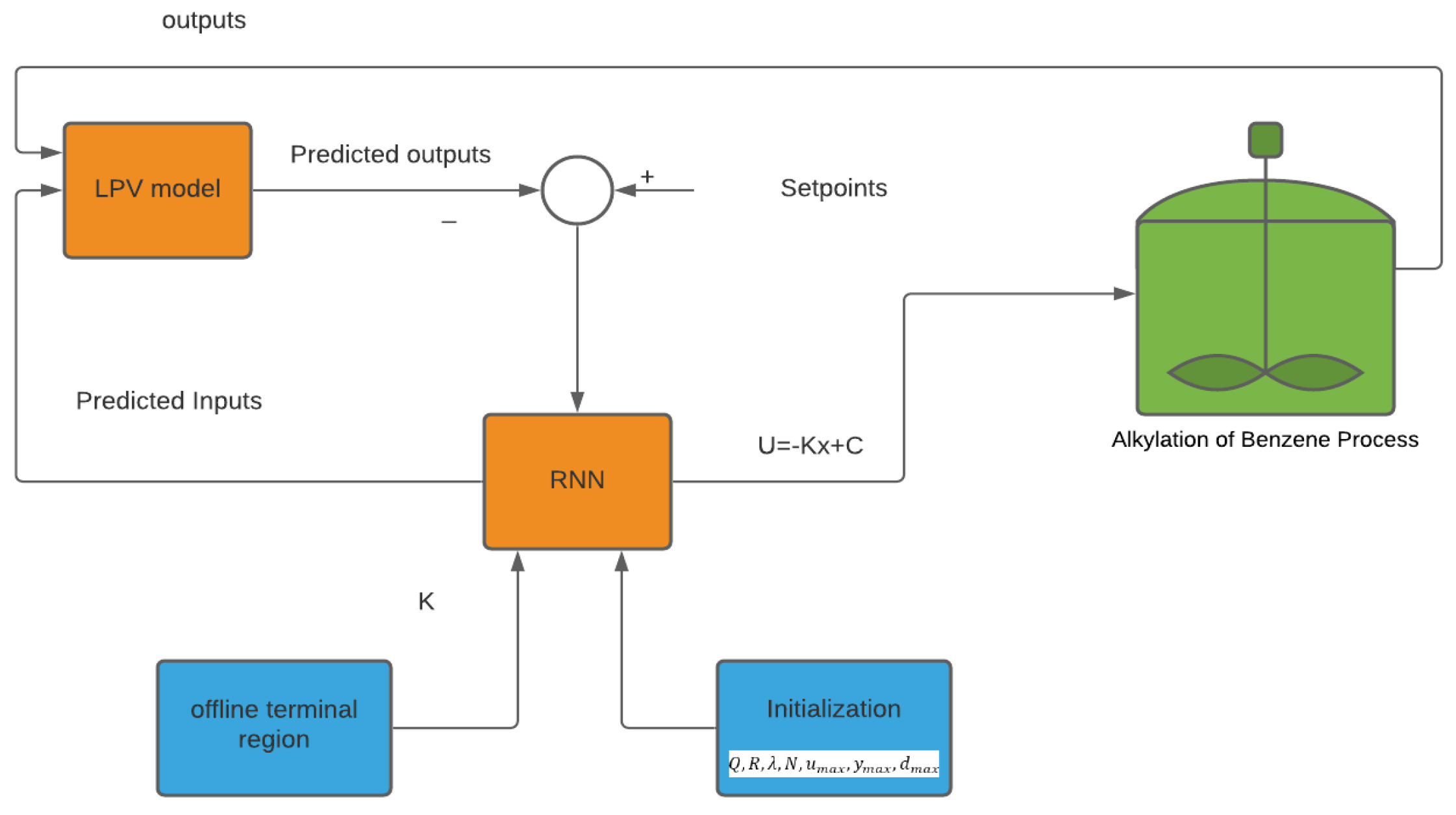
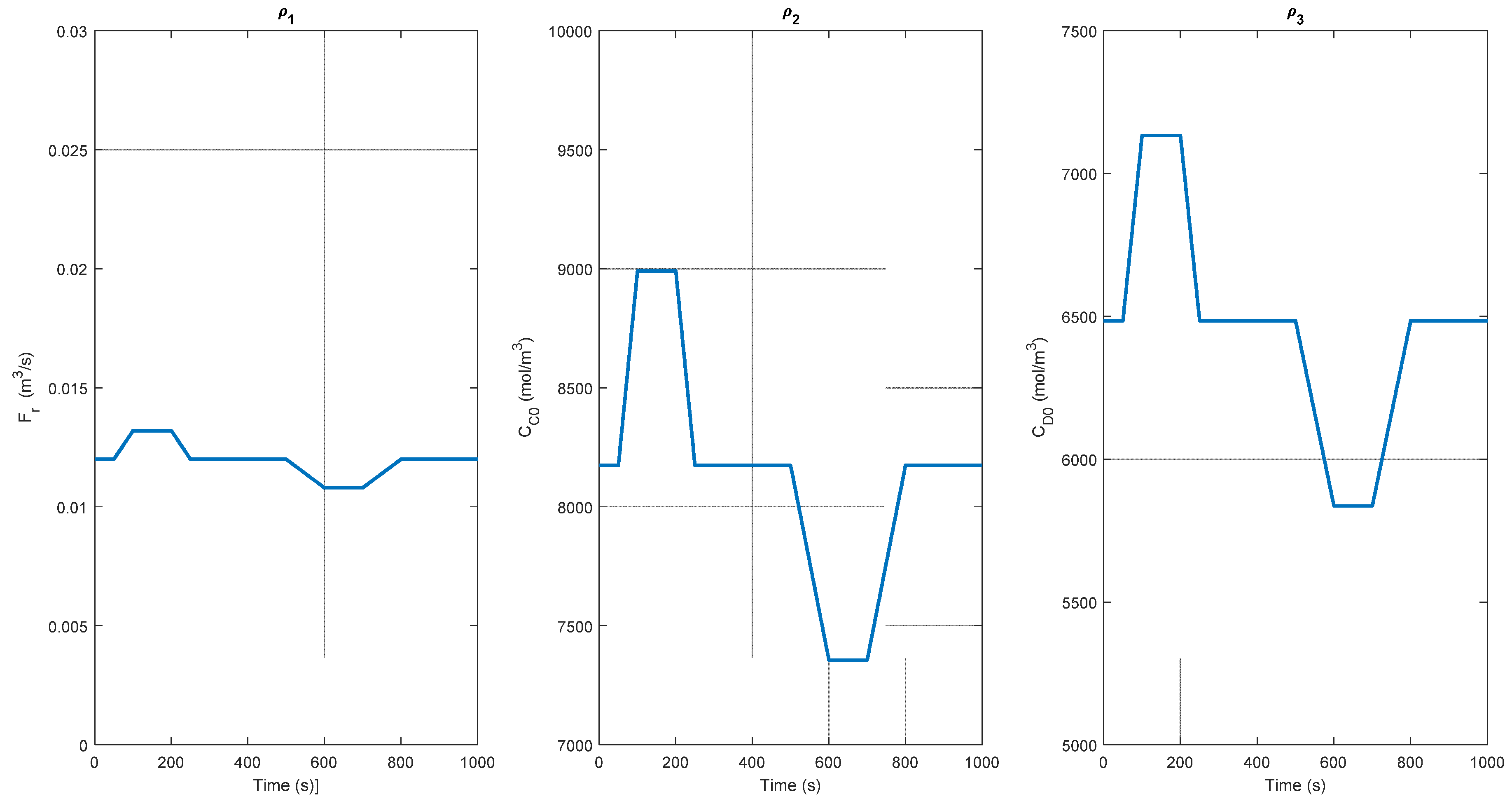
5. Case Study
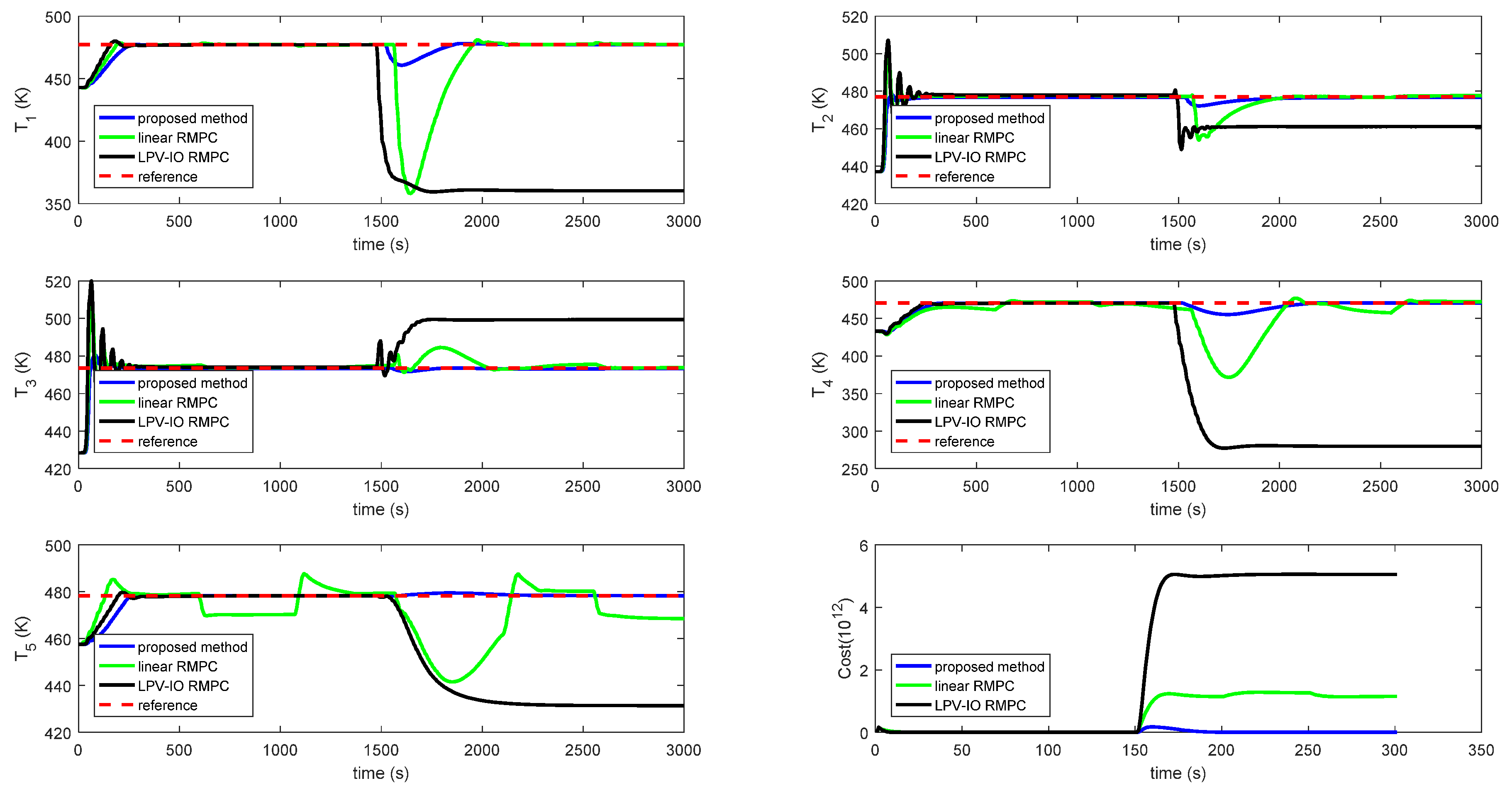
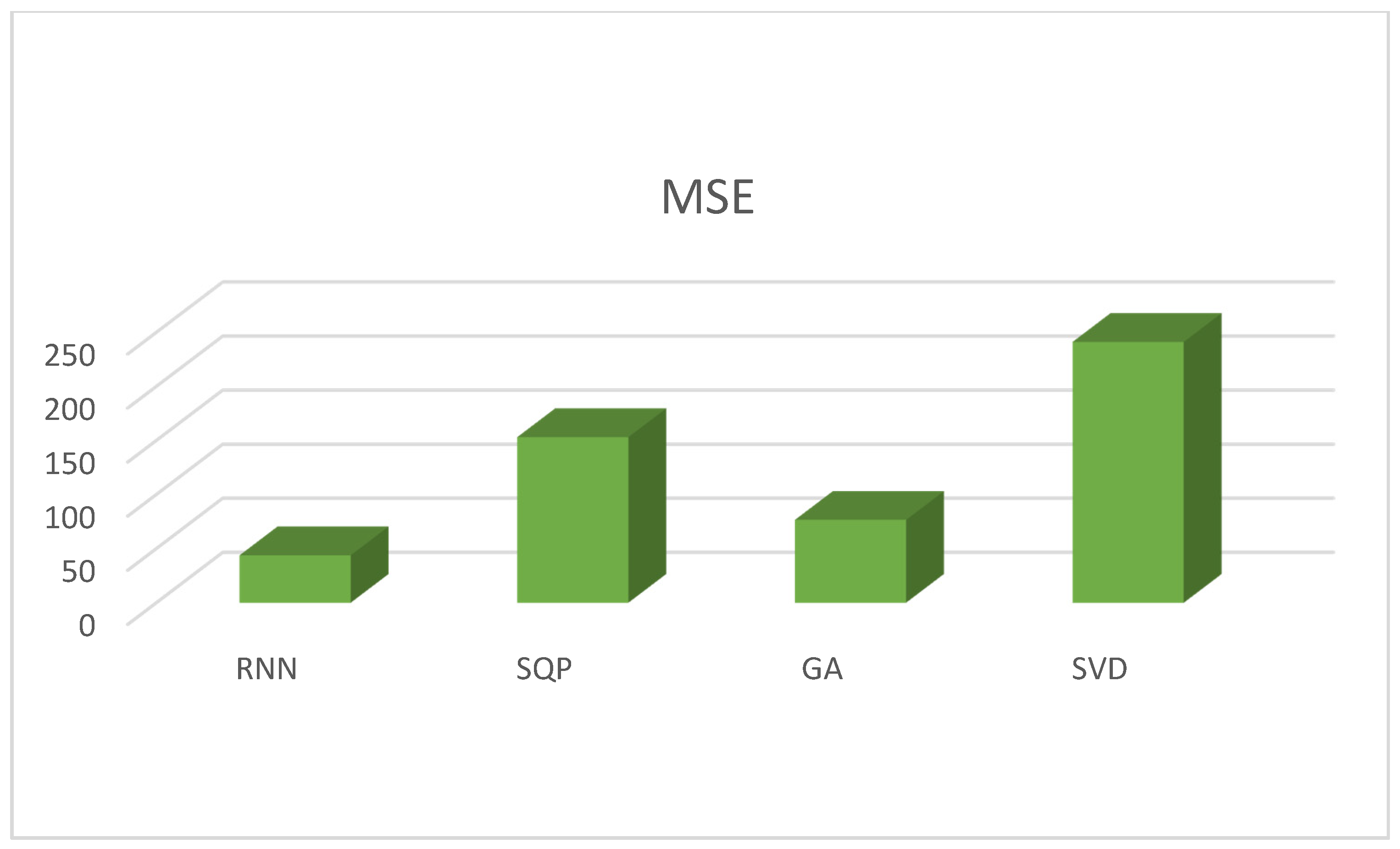
6. Results and Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Camacho, E.F.; Alba, C.B. Model Predictive Control; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Yaramasu, V.; Wu, B. Model Predictive Control of Wind Energy Conversion Systems; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Raković, S.V.; Levine, W.S. Handbook of Model Predictive Control; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Zhang, R.; Xue, A.; Gao, F. Model Predictive Control; Springer Science and Business Media LLC: Berlin, Germany, 2019. [Google Scholar]
- Morato, M.M.; Normey-Rico, J.E.; Sename, O. Model predictive control design for linear parameter varying systems: A survey. Annu. Rev. Control. 2020, 49, 64–80. [Google Scholar] [CrossRef]
- Yu, S.; Böhm, C.; Chen, H.; Allgöwer, F. Model predictive control of constrained LPV systems. Int. J. Control 2012, 85, 671–683. [Google Scholar] [CrossRef]
- Yang, Y.; Ding, B. Model predictive control for LPV models with maximal stabilizable model range. Asian J. Control 2020, 22, 1940–1950. [Google Scholar] [CrossRef]
- Hu, C.; Wei, X.; Ren, Y. Passive fault-tolerant control based on weighted LPV tube-MPC for air-breathing hypersonic vehicles. Int. J. Control Autom. Syst. 2019, 17, 1957–1970. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, X.; Yang, X. Delay-dependent robust dissipative control for singular LPV systems with multiple input delays. Int. J. Control Autom. Syst. 2019, 17, 327–335. [Google Scholar] [CrossRef]
- Abbas, H.S.; Toth, R.; Meskin, N.; Mohammadpour, J.; Hanema, J. A robust MPC for input-output LPV Models. IEEE Trans. Autom. Control 2016, 61, 4183–4188. [Google Scholar] [CrossRef]
- Ding, B.; Wang, P.; Hu, J. Dynamic output feedback robust MPC with one free control move for LPV model with bounded disturbance. Asian J. Control 2017, 20, 755–767. [Google Scholar] [CrossRef]
- Hu, J.; Ding, B. One-step ahead robust MPC for LPV model with bounded disturbance. Eur. J. Control 2020, 52, 59–66. [Google Scholar] [CrossRef]
- Alcalá, E.; Puig, V.; Quevedo, J.; Rosolia, U. Autonomous racing using linear parameter varying-model predictive control (LPV-MPC). Control Eng. Pract. 2020, 95, 104270. [Google Scholar] [CrossRef]
- Li, D.; Xi, Y. The feedback robust MPC for LPV systems with bounded rates of parameter changes. IEEE Trans. Autom. Control 2010, 55, 503–507. [Google Scholar]
- Xu, Z.; Zhao, J.; Qian, J.; Zhu, Y. Nonlinear MPC using an identified LPV model. Ind. Eng. Chem. Res. 2009, 48, 3043–3051. [Google Scholar] [CrossRef]
- Calderón, H.M.; Cisneros, P.S.; Werner, H. qLPV predictive control-A benchmark study on state space vs input-output approach. IFAC-Pap. 2019, 52, 146–151. [Google Scholar] [CrossRef]
- Abbas, H.S.; Hanema, J.; Tóth, R.; Mohammadpour, J.; Meskin, N. An improved robust model predictive control for linear parameter-varying input-output models. Int. J. Robust Nonlinear Control 2018, 28, 859–880. [Google Scholar] [CrossRef]
- Cisneros, P.S.G.; Werner, H. Stabilizing model predictive control for nonlinear systems in input-output quasi-LPV form. In Proceedings of the 2019 American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019; pp. 1002–1007. [Google Scholar]
- Bouzerdoum, A.; Pattison, T. Neural network for quadratic optimization with bound constraints. IEEE Trans. Neural Netw. 1993, 4, 293–304. [Google Scholar] [CrossRef]
- Tan, K.C.; Tang, H.; Yi, Z. Global exponential stability of discrete-time neural networks for constrained quadratic optimization. Neurocomputing 2004, 56, 399–406. [Google Scholar] [CrossRef]
- Xia, Y.; Wang, J. A recurrent neural network for nonlinear convex optimization subject to nonlinear inequality constraints. IEEE Trans. Circuits Syst. I Regul. Pap. 2004, 51, 1385–1394. [Google Scholar] [CrossRef]
- Xia, Y.; Feng, G.; Wang, J. A novel recurrent neural network for solving nonlinear optimization problems with inequality constraints. IEEE Trans. Neural Netw. 2008, 19, 1340–1353. [Google Scholar] [PubMed]
- Xia, Y.; Wang, J. A general projection neural network for solving monotone variational inequalities and related optimization problems. IEEE Trans. Neural Netw. 2004, 15, 318–328. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, L.V.; Qin, X. Some Results on Strongly Pseudomonotone Quasi-Variational Inequalities. Set-Valued Var. Anal. 2019, 28, 239–257. [Google Scholar] [CrossRef]
- Pan, Y.; Wang, J. Model predictive control for nonlinear affine systems based on the simplified dual neural network. In Proceedings of the 2009 IEEE International Conference on Control Applications, St. Petersburg, Russia, 8–10 July 2009; pp. 683–688. [Google Scholar]
- Wu, Z.; Christofides, P.D. Optimizing process economics and operational safety via economic MPC using barrier functions and recurrent neural network models. Chem. Eng. Res. Des. 2019, 152, 455–465. [Google Scholar] [CrossRef]
- Lanzetti, N.; Lian, Y.Z.; Cortinovis, A.; Dominguez, L.; Mercangoz, M.; Jones, C. Recurrent neural network based MPC for process industries. In Proceedings of the 2019 18th European Control Conference (ECC), Naples, Italy, 25–28 June 2019; pp. 1005–1010. [Google Scholar]
- Wollnack, S.; Werner, H. LPV-IO controller design: An LMI approach. In Proceedings of the 2016 American Control Conference (ACC); Institute of Electrical and Electronics Engineers (IEEE), Boston, MA, USA, 6–8 July 2016; pp. 4617–4622. [Google Scholar]
- Morato, M.M.; Normey-Rico, J.E.; Sename, O. Novel qLPV MPC Design with Least-Squares Scheduling Prediction. IFAC Pap. 2019, 52, 158–163. [Google Scholar] [CrossRef]
- Zhang, S.; Dai, L.; Xia, Y. Adaptive MPC for constrained systems with parameter uncertainty and additive disturbance. IET Control Theory Appl. 2019, 13, 2500–2506. [Google Scholar] [CrossRef]
- Pan, Y.; Wang, J. A neurodynamic optimization approach to nonlinear model predictive control. In Proceedings of the 2010 IEEE International Conference on Systems, Man and Cybernetics; Institute of Electrical and Electronics Engineers (IEEE), Istanbul, Turkey, 10–13 October 2010; pp. 1597–1602. [Google Scholar]
- Salahshoor, K.; Hadian, M. A decentralized event-based model predictive controller design method for large-scale systems. Autom. Control. Inf. Sci. 2014, 2, 26–31. [Google Scholar]
- Liu, J.; Chen, X.; De La Pena, D.M.; Christofides, P.D. Sequential and iterative architectures for distributed model predictive control of nonlinear process systems. Part I: Theory. AIChE J. 2010, 56, 3148–3155. [Google Scholar]
- Kayacan, E.; Ramon, H.; Saeys, W. Distributed nonlinear model predictive control of an autonomous tractor–trailer system. Mechatronics 2014, 24, 926–933. [Google Scholar] [CrossRef]
- Hu, J.; Ding, B. Output feedback robust MPC for linear systems with norm-bounded model uncertainty and disturbance. Automatica 2019, 108, 108489. [Google Scholar] [CrossRef]
- Moradmand, A.; Dorostian, M.; Shafai, B. Energy scheduling for residential distributed energy resources with uncertainties using model-based predictive control. JEPE 2021, 132, 107074. [Google Scholar]
- Dorostian, M.; Moradmand, A. Hierarchical Robust Model-based Predictive Control in Supply Chain Management under Demand Uncertainty and Time-delay. In Proceedings of the 2021 7th International Conference on Control, Instrumentation and Automation (ICCIA), Tabriz, Iran, 23–24 February 2021; pp. 1–6. [Google Scholar]



| Variables | Definition |
|---|---|
| Concentrations of A, B, C, D in CSTR-1 | |
| Concentrations of A, B, C, D in CSTR-2 | |
| Concentrations of A, B, C, D in CSTR-3 | |
| Concentrations of A, B, C, D in Separator | |
| Concentrations of A, B, C, D in CSTR-1 | |
| Concentrations of A, B, C, D in | |
| Temperatures in each vessel | |
| Reference temperature | |
| Effluent flow rates from each vessel | |
| Feed flow rates to each vessel | |
| Recycle flow rates | |
| Enthalpies of vaporization of A, B, C, D | |
| Enthalpies of A, B, C, D at | |
| Heat of reactions 1, 2, and 3 | |
| Volume of each vessel | |
| External heat/coolant inputs to each vessel | |
| Heat capacity of A, B, C, D at liquid phase | |
| Relative volatilities of A, B, C, D | |
| Molar densities of pure A, B, C, D | |
| Feed temperatures of pure A, B, D | |
| Fraction of overhead flow recycled to the reactors | |
| Concentrations of A, B, C, D in CSTR-1 | |
| Concentrations of A, B, C, D in CSTR-2 | |
| Concentrations of A, B, C, D in CSTR-3 | |
| Concentrations of A, B, C, D in Separator | |
| Concentrations of A, B, C, D in CSTR-1 | |
| Concentrations of A, B, C, D in | |
| Temperatures in each vessel | |
| Reference temperature | |
| Effluent flow rates from each vessel | |
| Feed flow rates to each vessel | |
| Recycle flow rates | |
| Enthalpies of vaporization of A, B, C, D | |
| Enthalpies of A, B, C, D at | |
| Heat of reactions 1, 2, and 3 | |
| Volume of each vessel | |
| External heat/coolant inputs to each vessel | |
| Heat capacity of A, B, C, D at liquid phase | |
| Relative volatilities of A, B, C, D | |
| Molar densities of pure A, B, C, D |
| Steady-State Temperatures of Vessels (K) | Steady-State Inputs (J/K) | Initial Temperatures of Vessels (K) |
|---|---|---|
| Method | Total | |||||
|---|---|---|---|---|---|---|
| LRMPC | 391.40 | 387.25 | 346.72 | 331.76 | 408.73 | 347.56 |
| LPV-RMPC | ||||||
| Proposed method | 67.32 | 65.30 | 52.34 | 60.00 | 76.45 | 43.84 |
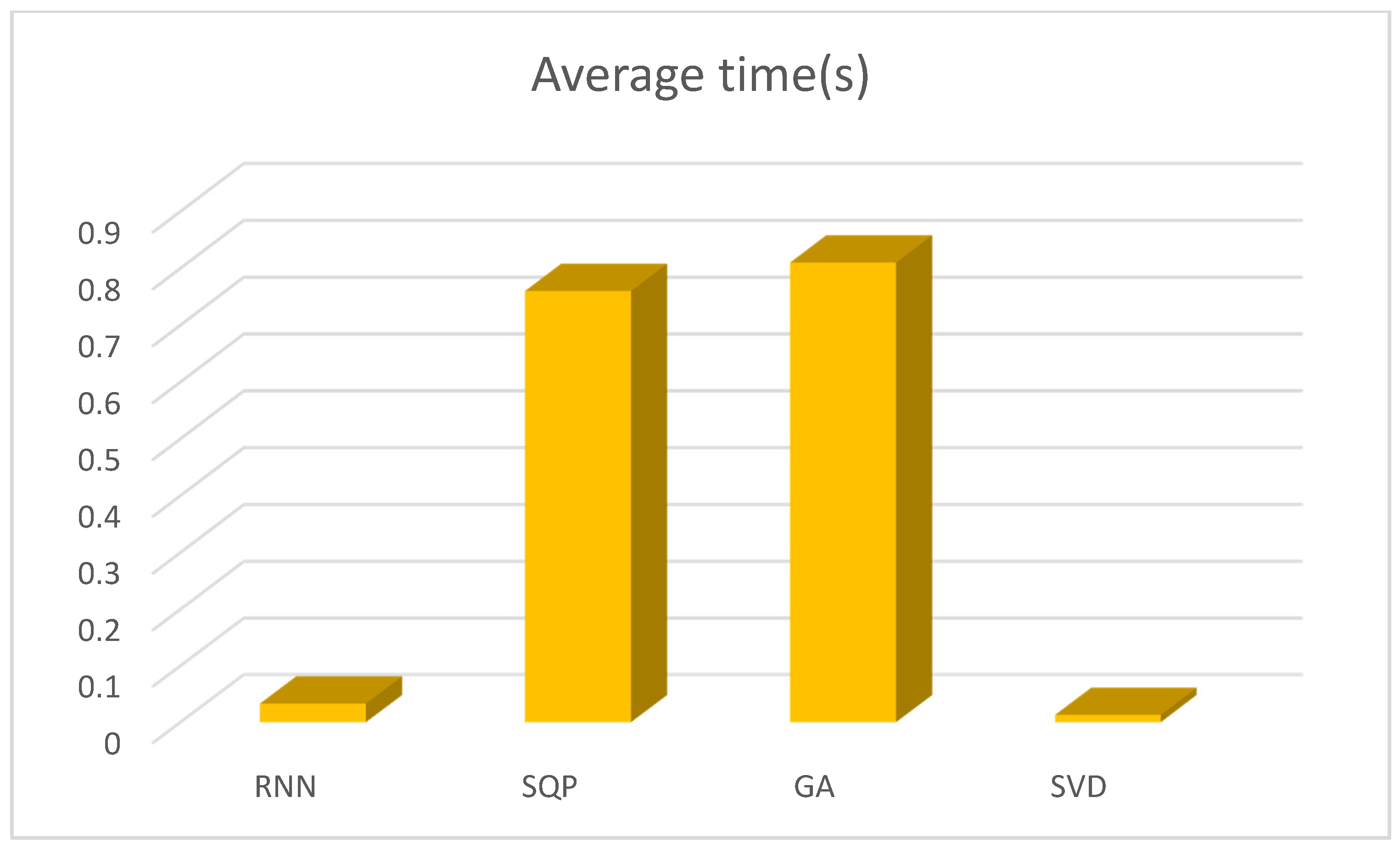
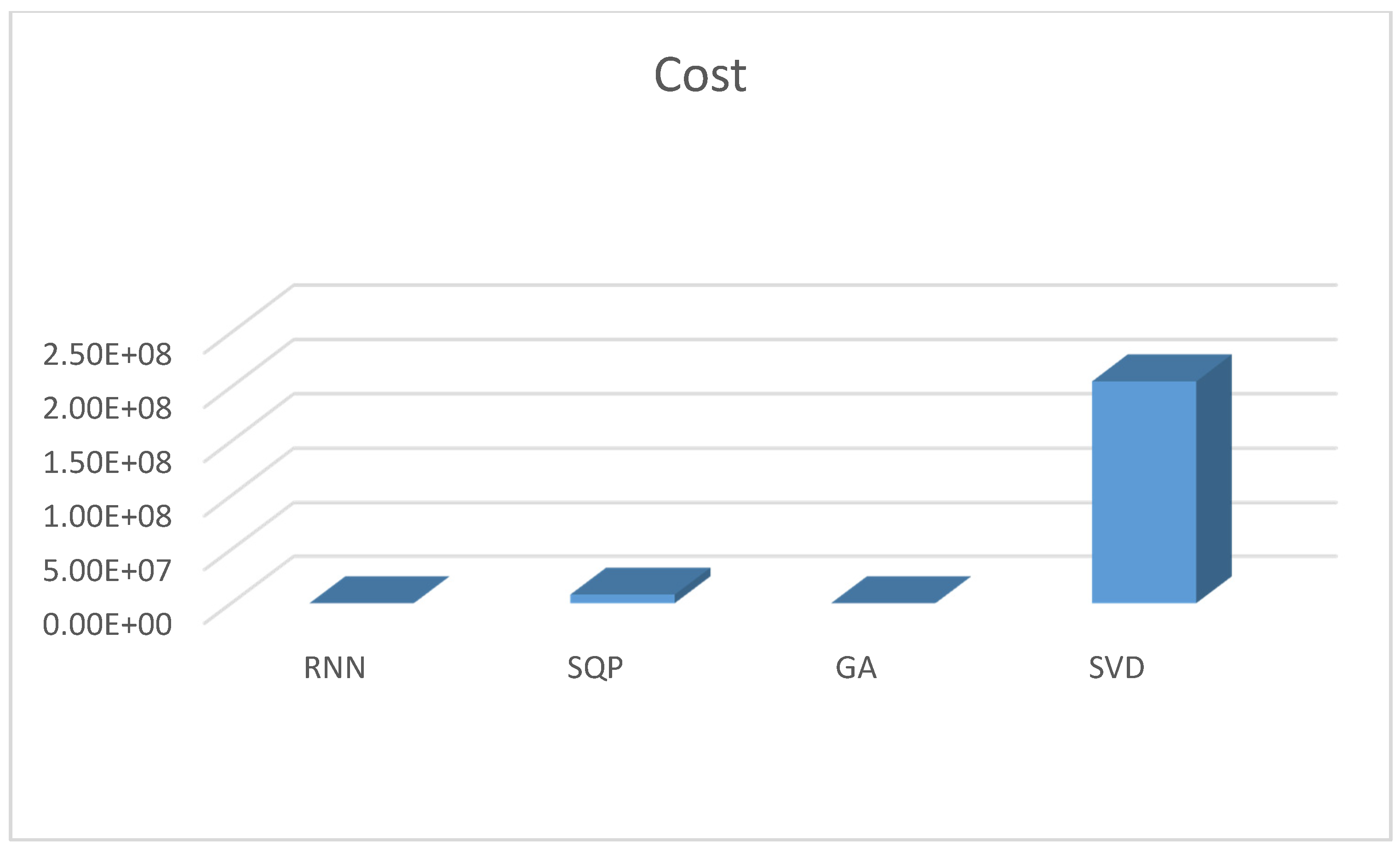
| Optimization Algorithm | MSE | Average Time | Cost |
|---|---|---|---|
| RNN | 43.84 | 0.033 | |
| SQP | 153.12 | 0.76 | |
| GA | 76.55 | 0.81 | |
| SVD | 241.22 | 0.013 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hadian, M.; Ramezani, A.; Zhang, W. Robust Model Predictive Controller Using Recurrent Neural Networks for Input–Output Linear Parameter Varying Systems. Electronics 2021, 10, 1557. https://doi.org/10.3390/electronics10131557
Hadian M, Ramezani A, Zhang W. Robust Model Predictive Controller Using Recurrent Neural Networks for Input–Output Linear Parameter Varying Systems. Electronics. 2021; 10(13):1557. https://doi.org/10.3390/electronics10131557
Chicago/Turabian StyleHadian, Mohsen, Amin Ramezani, and Wenjun Zhang. 2021. "Robust Model Predictive Controller Using Recurrent Neural Networks for Input–Output Linear Parameter Varying Systems" Electronics 10, no. 13: 1557. https://doi.org/10.3390/electronics10131557
APA StyleHadian, M., Ramezani, A., & Zhang, W. (2021). Robust Model Predictive Controller Using Recurrent Neural Networks for Input–Output Linear Parameter Varying Systems. Electronics, 10(13), 1557. https://doi.org/10.3390/electronics10131557







