Categorization and SEU Fault Simulations of Radiation-Hardened-by-Design Flip-Flops
Abstract
1. Introduction
2. Conventional Transmission Gate Flip-Flop (TGFF)
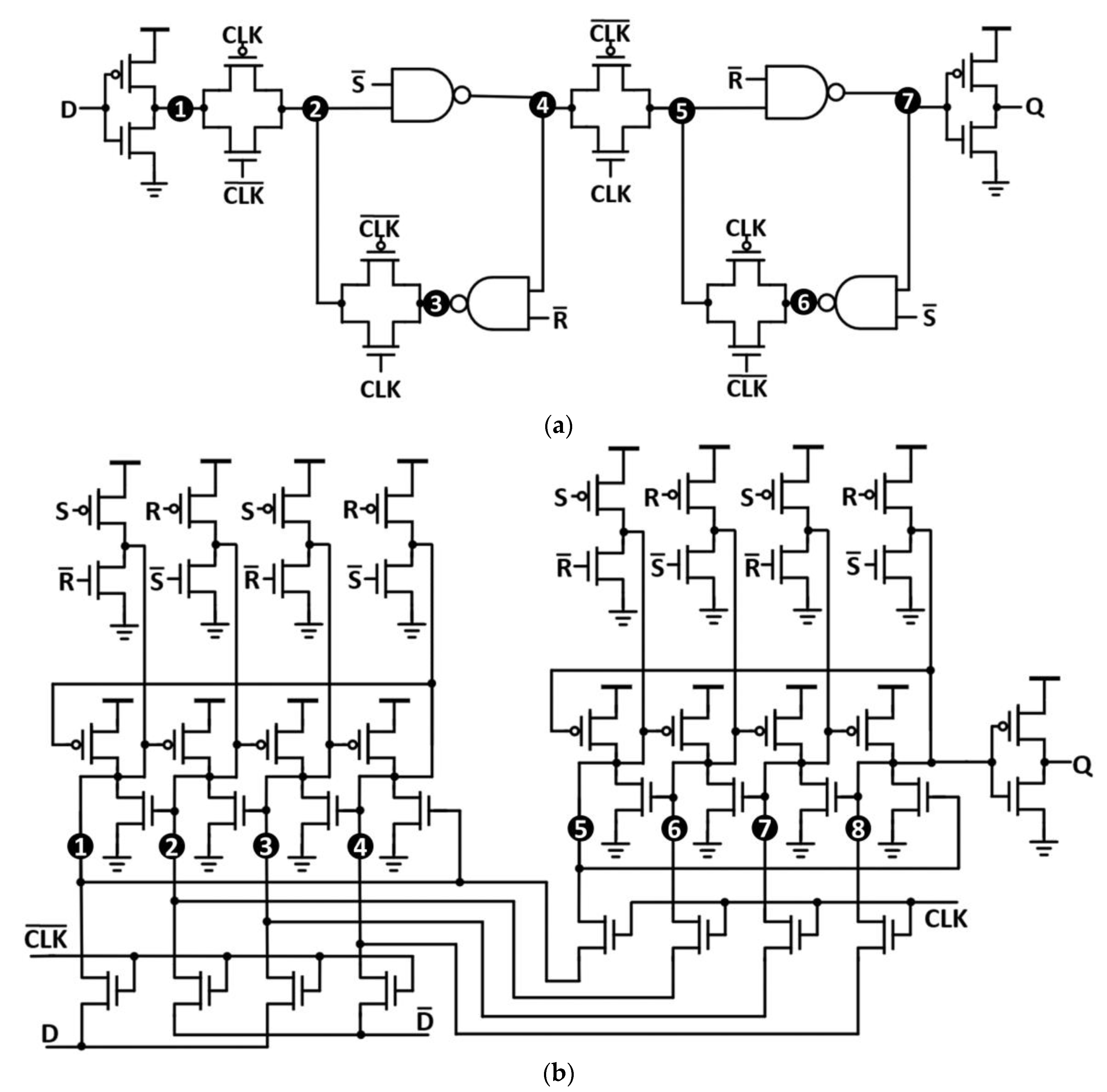
3. Radiation-Hardened-by-Design Flip-Flops (RHBD FF)
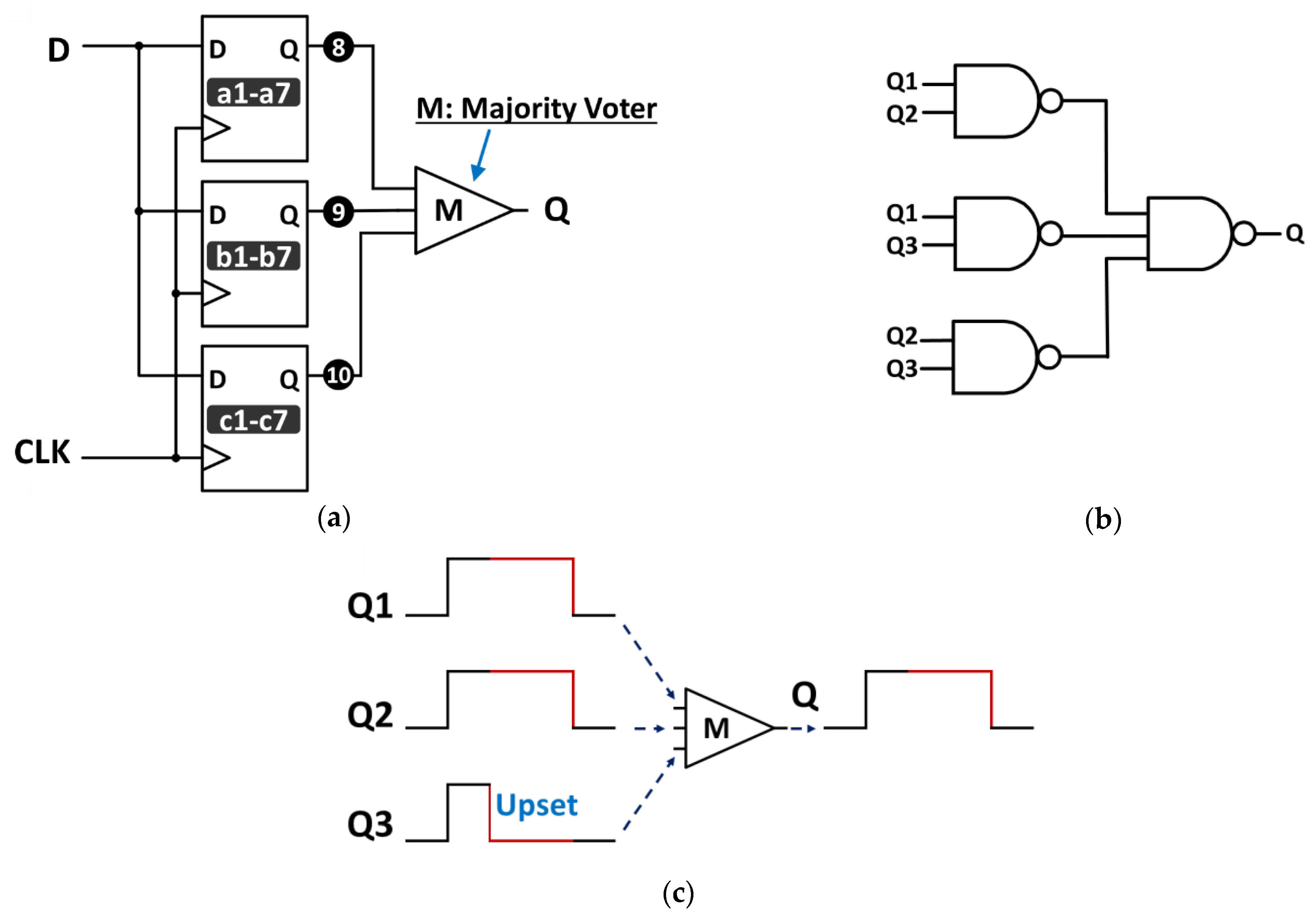
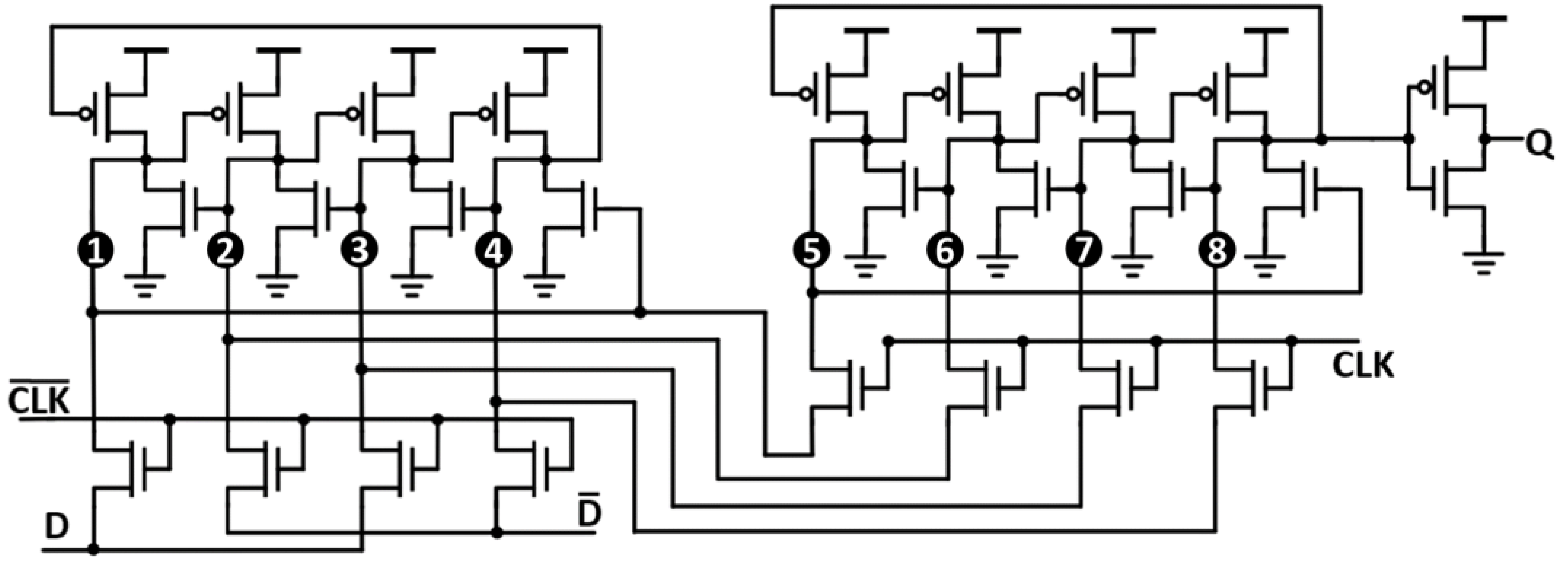
3.1. Spatial Redundancy FF
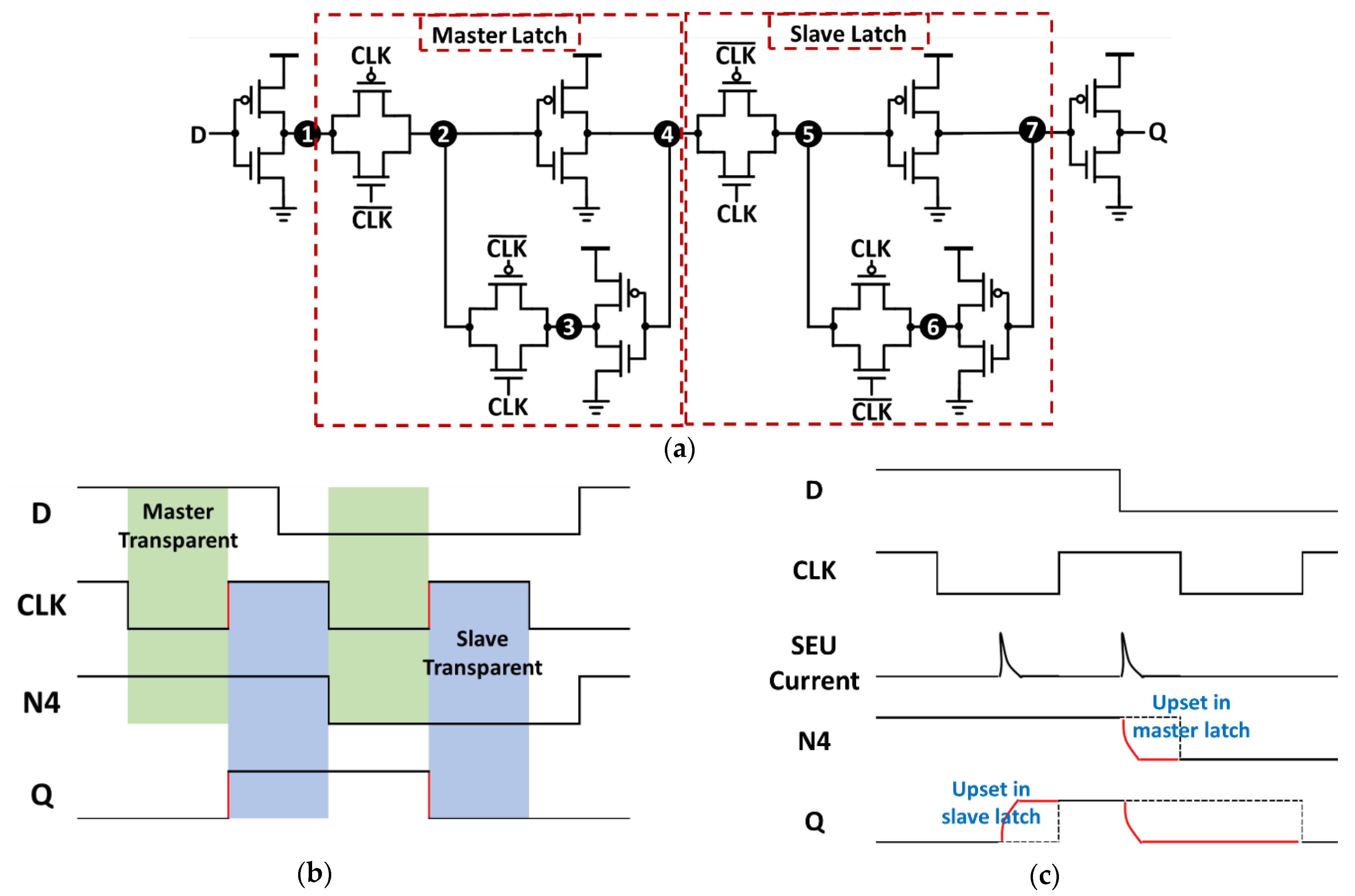
3.2. Temporal Redundancy FF
3.3. Node Hardened FF
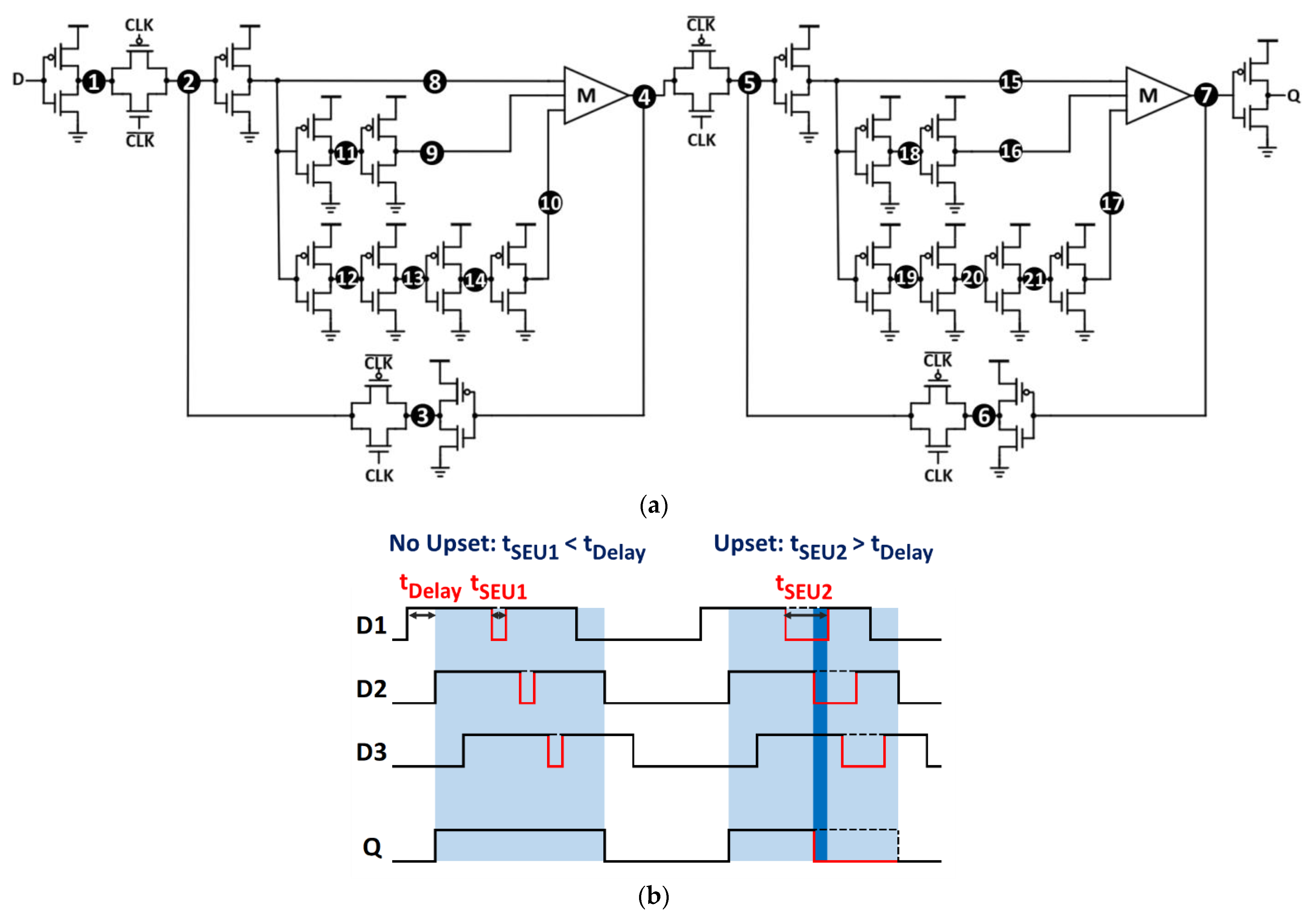
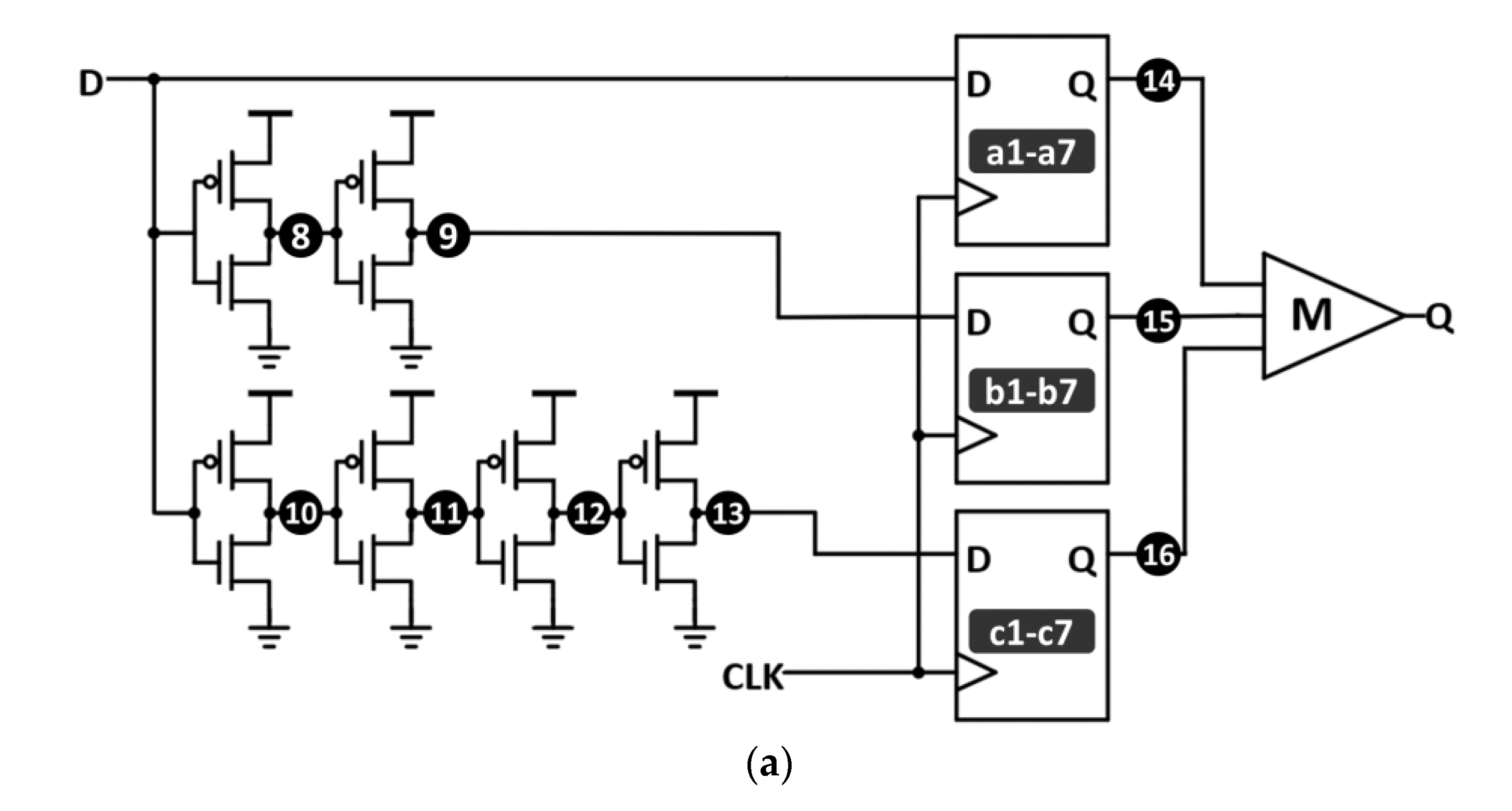
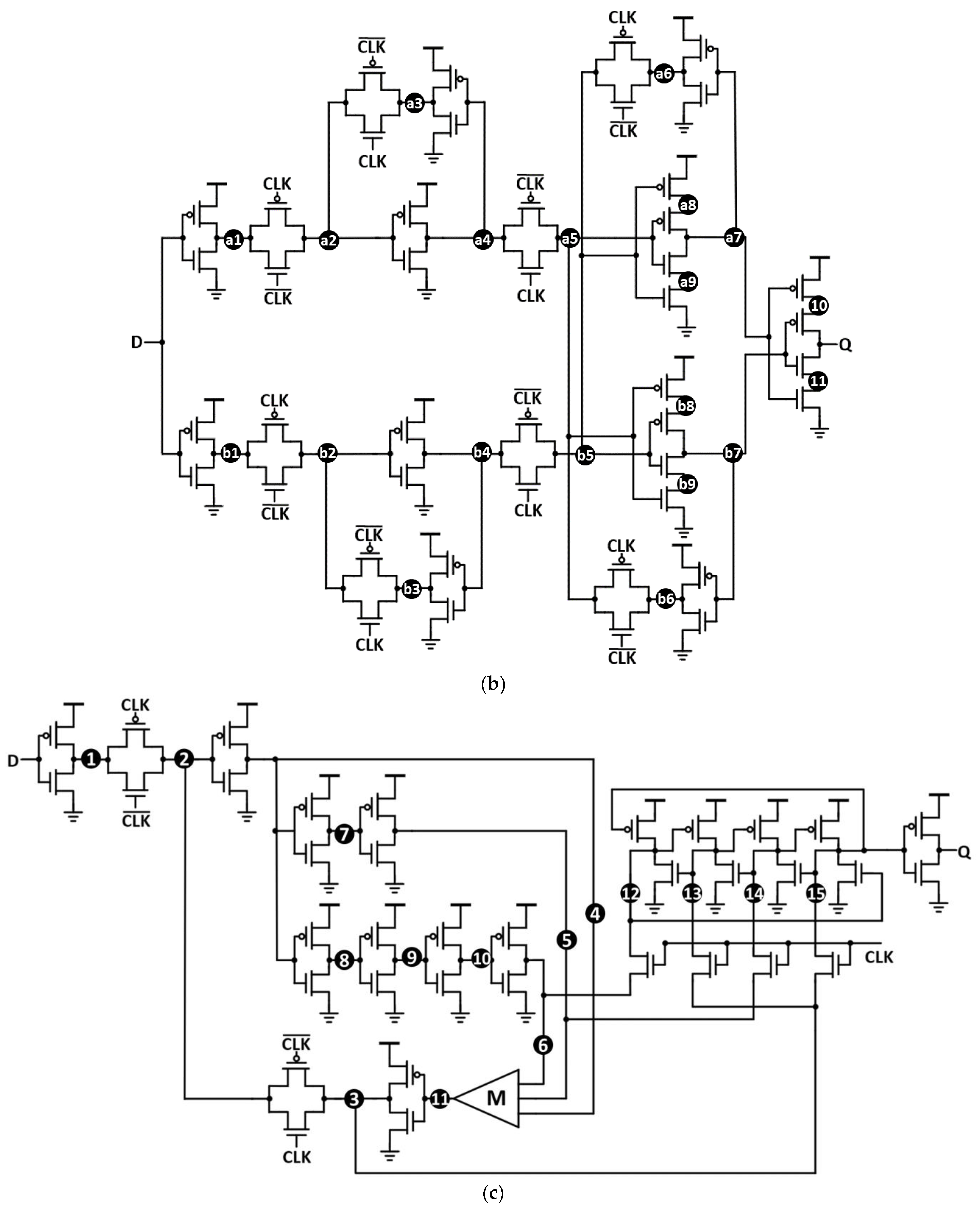
3.4. Hybrid Hardened FF
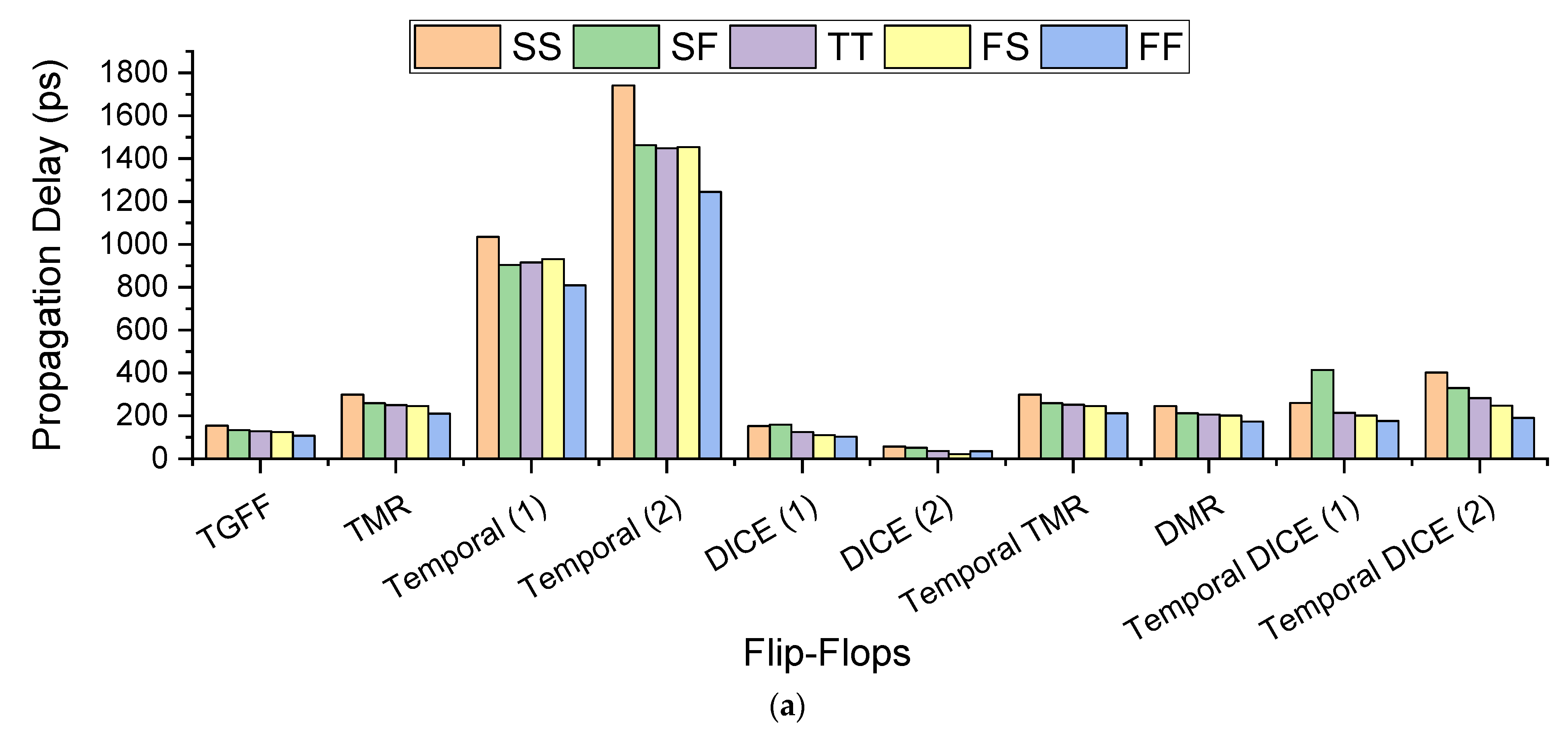
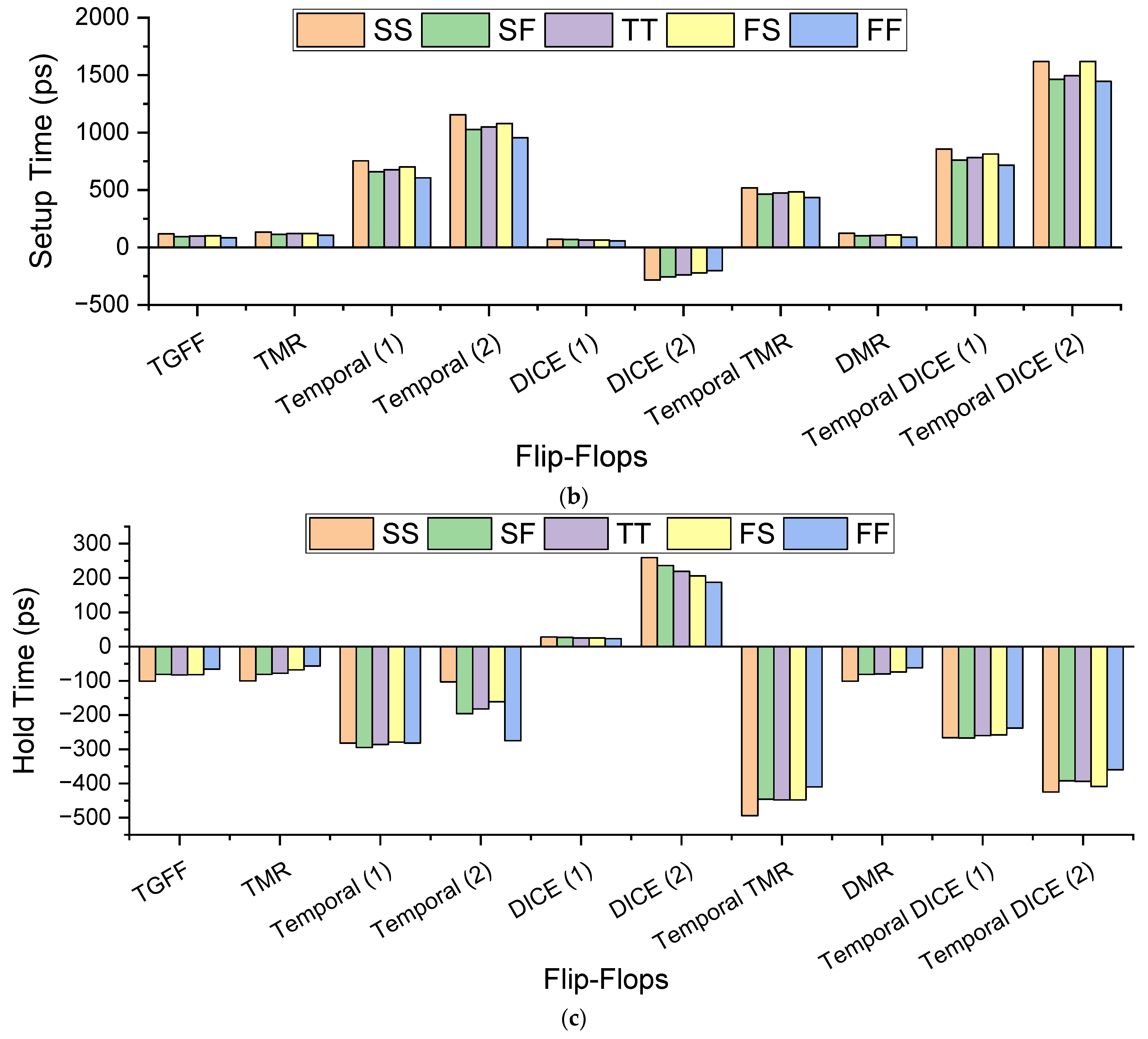
4. Results and Measurements
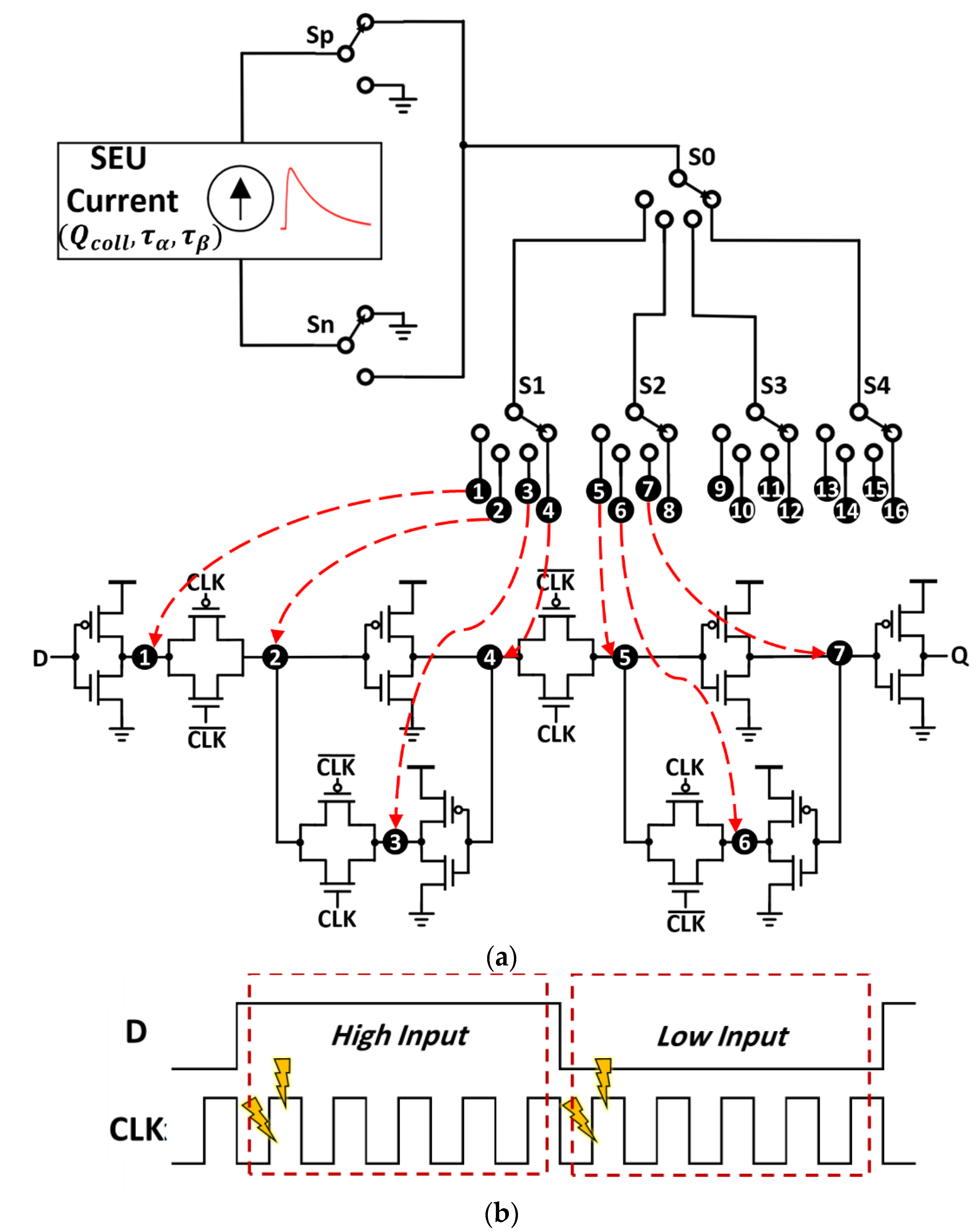
4.1. The SEU Testbench
- Both positive and negative SEU spikes are tested, by changing both Sp and Sn switches simultaneously in Figure 6a.
- SEU current is injected at the two cases of input D; high input (D = 1) and low input (D = 0) as shown in Figure 6b.
- For each input case, SEU current is timed at the positive edge of the clock and when the clock level is stable as shown in Figure 6b by the yellow thunder symbols.
- A wide range of clock frequencies is applied (100 MHz, 250 MHz, 500 MHz, 1 GHz, 2 GHz).
- An extended range of the deposited charge (Qcoll) is used (1 fC to 2.16 pC).
4.2. Transistors Sizing and Area
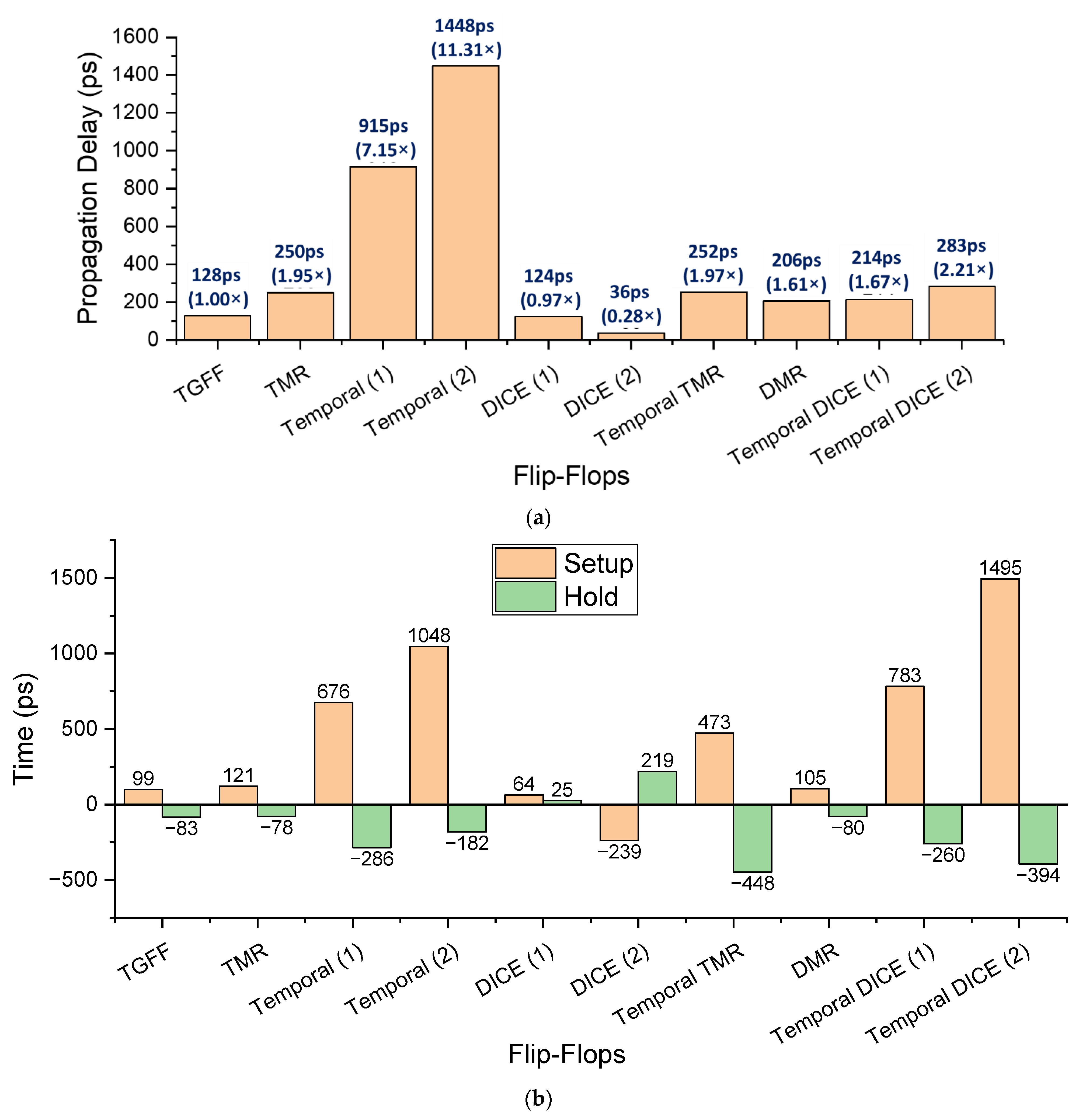
4.3. The Simulation Results
4.4. Critical Nodes
4.5. Process Corners Simulations
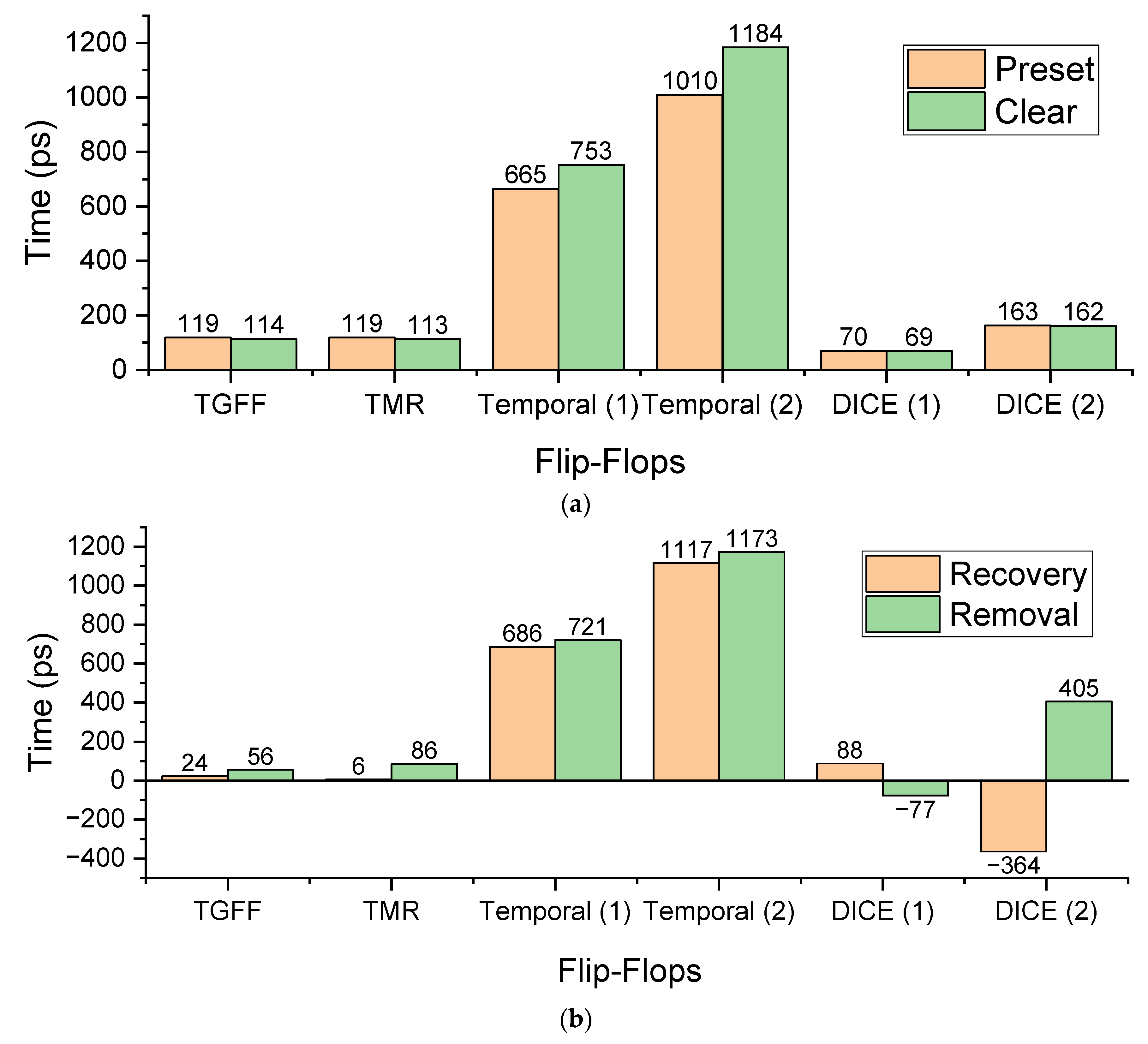
4.6. Asynchronous Preset/Clear
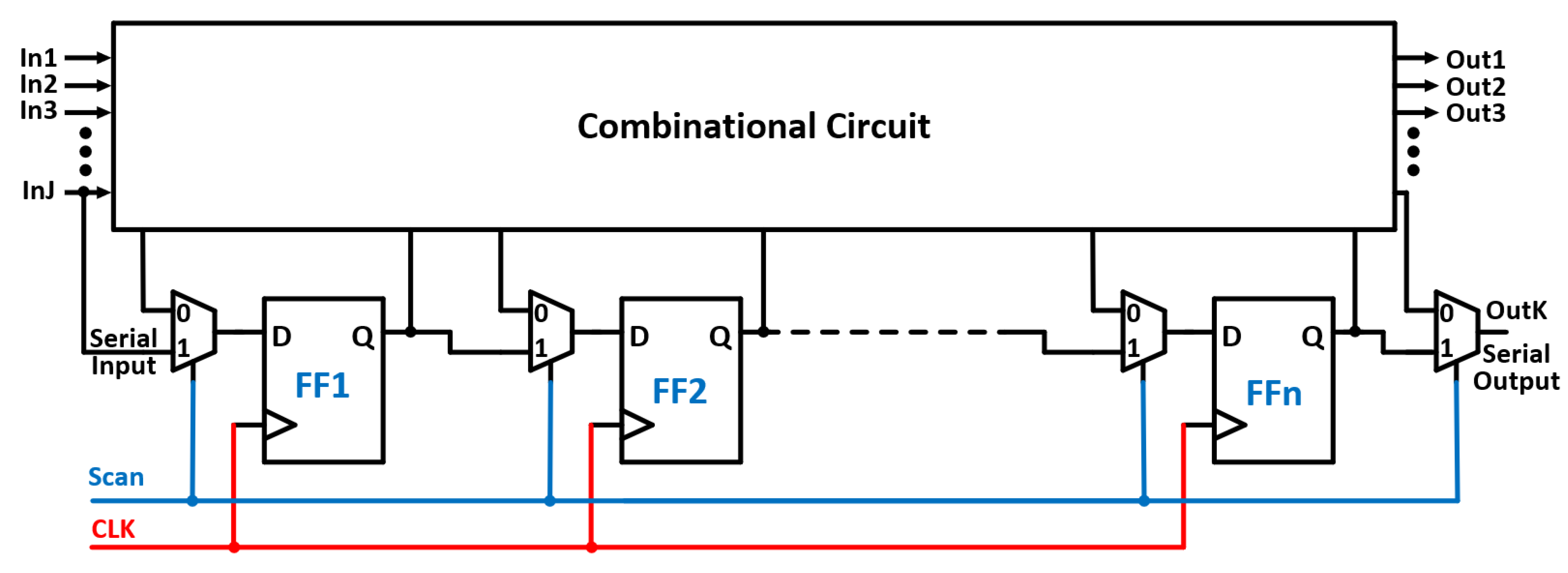
4.7. Design for Testability
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Teifel, J. Self-Voting Dual-Modular-Redundancy Circuits for Single-Event-Transient Mitigation. IEEE Trans. Nucl. Sci. 2008, 55, 3435–3439. [Google Scholar] [CrossRef]
- Gaillard, R.; Nicolaidis, M. Soft Errors in Modern Electronic Systems. In Single Event Effects: Mechanisms and Classification; Springer: Boston, MA, USA, 2011; pp. 27–54. [Google Scholar]
- Jain, A.; Gupta, A.; Garg, S.; Veggetti, A.; Castelnovo, A.; Crippa, D.; Gerardin, S.; Bagatin, M.; Cazzaniga, C. A Low Cost Robust Radiation Hardened Flip-Flop Circuit. In Proceedings of the IEEE Region 10 International Conference TENCON, Penang, Malaysia, 5–8 November 2017. [Google Scholar]
- Alidash, H.K.; Oklobdzija, V.G. Low-Power Soft Error Hardened Latch. J. Low Power Electron. 2010, 6, 218–226. [Google Scholar] [CrossRef]
- Sajjade, F.M.; Goyal, N.K.; Varaprasad, B.; Moogina, R. Radiation hardened by design latches—A review and SEU fault simulations. Microelectron. Reliab. 2018, 83, 127–135. [Google Scholar] [CrossRef]
- He, Y.; Chen, S. Comparison of heavy-ion induced SEU for D- and TMR-flip-flop designs in 65-nm bulk CMOS technology. Sci. China Inf. Sci. 2014, 57, 1–7. [Google Scholar] [CrossRef][Green Version]
- Petrovic, V.; Krstic, M. Design Flow for Radhard TMR Flip-Flops. In Proceedings of the IEEE 18th International Symposium on Design and Diagnostics of Electronic Circuits & Systems, Belgrade, Serbia, 22–24 April 2015. [Google Scholar]
- Li, J.; Xiao, L.-Y.; Li, H.-C.; Qi, C.-H. A Low-Overhead Radiation Hardened Flip-Flop Design for Soft Error Detection. In Proceedings of the 14th IEEE International Conference on Solid-State and Integrated Circuit Technology (ICSICT), Qingdao, China, 31 October–3 November 2018. [Google Scholar]
- Zhang, J.; Li, Y.; Han, T.; Li, J. Radiation Hardened Design Based on TMR_5DFF for ASIC. In Proceedings of the IEEE 5th International Conference on Computer and Communications (ICCC), Chengdu, China, 6–9 December 2019. [Google Scholar]
- Mavis, D.; Eaton, P. Soft error rate mitigation techniques for modern microcircuits. In Proceedings of the IEEE International Reliability Physics Symposium. Proceedings. 40th Annual (Cat. No. 02CH37320), Dallas, TX, USA, 7–11 April 2002. [Google Scholar]
- Shuler, R.; Kouba, C.; O’Neill, P. SEU performance of TAG based flip-flops. IEEE Trans. Nucl. Sci. 2005, 52, 2550–2553. [Google Scholar] [CrossRef]
- Asli, R.N.; Shirinzadeh, S. High Efficiency Time Redundant Hardened Latch for Reliable Circuit Design. J. Electron. Test. 2013, 29, 537–544. [Google Scholar] [CrossRef]
- Xuan, S.; Li, N.; Tong, J. SEU Hardened Flip-Flop Based on Dynamic Logic. IEEE Trans. Nucl. Sci. 2013, 60, 3932–3936. [Google Scholar] [CrossRef]
- Adapur, R.S.; Kumar, S.S. A SEU Hardened Dual Dynamic Node Pulsed Hybrid Flip-Flop with an Embedded Logic Module. In Soft Computing Systems (ICSCS); Springer: Berlin, Germany, 2018. [Google Scholar]
- Calin, T.; Nicolaidis, M.; Velazco, R. Upset hardened memory design for submicron CMOS technology. IEEE Trans. Nucl. Sci. 1996, 43, 2874–2878. [Google Scholar] [CrossRef]
- Monnier, F.R.G.C.T. Flip-Flop Hardening for Space Applications. In Proceedings of the International Workshop on Memory Technology Design and Testing (Cat. No.98TB100236), San Jose, CA, USA, 25 August 1998. [Google Scholar]
- Jagannathan, S.; Loveless, T.D.; Bhuva, B.L.; Wen, S.-J.; Wong, R.; Sachdev, M.; Rennie, D.; Massengill, L.W. Single-Event Tolerant Flip-Flop Design in 40-nm Bulk CMOS Technology. IEEE Trans. Nucl. Sci. 2011, 58, 3033–3037. [Google Scholar] [CrossRef]
- Furuta, J.; Yamaguchi, J.; Kobayashi, K. A Radiation-Hardened Non-Redundant Flip-Flop, Stacked Leveling Critical Charge Flip-Flop in a 65 nm Thin BOX FD-SOI Process. IEEE Trans. Nucl. Sci. 2016, 63, 2080–2086. [Google Scholar] [CrossRef]
- Yamada, K.; Maruoka, H.; Furuta, J.; Kobayashi, K. Radiation-Hardened Flip-Flops with Low Delay Overheads Using PMOS Pass-Transistors to Suppress a SET Pulse in a 65 nm FDSOI Process. IEEE Trans. Nucl. Sci. 2018, 65, 1814–1822. [Google Scholar] [CrossRef]
- Maruoka, H.; Hifumi, M.; Furuta, J. Kobayashi, K. A Low-Power Radiation-Hardened Flip-Flop with Stacked Transistors in a 65 nm FDSOI Process. IEICE Trans. Electron. 2018, 101, 273–280. [Google Scholar] [CrossRef]
- Zhang, M.; Guo, Z.; Xu, W. An Adaptive Single Event Upset (SEU)-Hardened Flip-Flop Design. In Proceedings of the IEEE International Conference on Electron Devices and Solid-State Circuits (EDSSC), Xi’an, China, 12–14 June 2019. [Google Scholar]
- Ebara, M.; Yamada, K.; Furuta, J.; Kobayashi, K. Comparison of Radiation Hardness of Stacked Transmission-Gate Flip Flop and Stacked Tristate-Inverter Flip Flop in a 65 nm Thin BOX FDSOI Process. In Proceedings of the IEEE 25th International Symposium on On-Line Testing and Robust System Design (IOLTS), Rhodes, Greece, 1–3 July 2019. [Google Scholar]
- Jaya, G.L.; Chen, S.; Liter, S. A dual redundancy radiation-hardened Flip-Flop based on C-element in 65nm process. In Proceedings of the International Symposium on Integrated Circuits (ISIC), Singapore, 12–14 December 2016. [Google Scholar]
- Wang, Q.; Jin, L. A radiation hardened scan flip-flop design with built-in soft error resilience. In Proceedings of the 12th IEEE International Conference on Solid-State and Integrated Circuit Technology (ICSICT), Guilin, China, 28–31 October 2014. [Google Scholar]
- Kobayashi, K.; Furuta, J.; Maruoka, H.; Hifumi, M.; Kumashiro, S.; Kato, T.; Kohri, S. A 16 nm FinFET radiation-hardened flip-flop, bistable cross-coupled dual-modular-redundancy FF for terrestrial and outer-space highly-reliable systems. In Proceedings of the IEEE International Reliability Physics Symposium (IRPS), Monterey, CA, USA, 2–6 April 2017. [Google Scholar]
- Yamamoto, R.; Hamanaka, C.; Furuta, J.; Kobayashi, K.; Onodera, H. An Area-Efficient 65 nm Radiation-Hard Dual-Modular Flip-Flop to Avoid Multiple Cell Upsets. IEEE Trans. Nucl. Sci. 2011, 58, 3053–3059. [Google Scholar] [CrossRef]
- Knudsen, J.E.; Clark, L.T. An Area and Power Efficient Radiation Hardened by Design Flip-Flop. IEEE Trans. Nucl. Sci. 2006, 53, 3392–3399. [Google Scholar] [CrossRef]
- Kobayashi, K.; Kubota, K.; Masuda, M.; Manzawa, Y.; Furuta, J.; Kanda, S.; Onodera, H. A Low-Power and Area-Efficient Radiation-Hard Redundant Flip-Flop, DICE ACFF, in a 65 nm Thin-BOX FD-SOI. IEEE Trans. Nucl. Sci. 2014, 61, 1881–1888. [Google Scholar] [CrossRef]
- Gerosa, G.; Gary, S.; Dietz, C.; Pham, D.; Hoover, K.; Alvarez, J.; Sanchez, H.; Ippolito, P.; Litch, S.; Eno, J.; et al. A 2.2 w, 80 mhz superscalar risc microprocessor. IEEE J. Solid-State Circuits 1994, 29, 1440–1454. [Google Scholar] [CrossRef]
- Alioto, M.; Consoli, E.; Palumbo, G. Flip-Flop Design in Nanometer CMOS; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Markovic, D.; Nikolic, B.; Brodersen, R. Analysis and design of low-energy flip-flops. In Proceedings of the 2001 International Symposium on Low Power Electronics and Design, Huntington Beach, CA, USA, 6–7 August 2001. [Google Scholar]
- Tsukita, Y.; Ebara, M.; Furuta, J.; Kobayashi, K. Soft-Error Tolerance Depending on Supply Voltage by Heavy Ions on Radiation-Hardened Flip Flops in a 65 nm Bulk Process. In Proceedings of the IEEE 13th International Conference on ASIC (ASICON), Chongqing, China, 29 October–1 November 2019. [Google Scholar]
- Nsengiyumva, P. Investigating the Effects of Single-Event Upsets in Static and Dynamic Registers. Master’s Thesis, University of New Hampshire, Durham, NH, USA, 2014. [Google Scholar]
- Nagpal, C.; Garg, R.; Khatri, S.P. A Delay-efficient Radiation-hard Digital Design Approach Using CWSP Elements. In Proceedings of the 2008 Design, Automation and Test in Europe, Munich, Germany, 10–14 March 2008. [Google Scholar]
- Zhou, Q.; Mohanram, K. Gate sizing to radiation harden combinational logic. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2006, 25, 155–166. [Google Scholar] [CrossRef]
- Hass, K.; Ambles, J. Single event transients in deep submicron CMOS. In Proceedings of the 42nd Midwest Symposium on Circuits and Systems, Las Cruces, NM, USA, 8–11 August 1999. [Google Scholar]
- Ukey, S.; Rathkanthiwar, S.; Kakde, S. VLSI implementation of low power scan based testing. In Proceedings of the International Conference on Communication and Signal Processing (ICCSP), Melmaruvathur, India, 6–8 April 2016. [Google Scholar]
- Hamed, E.; Lee, I. Data for RHBD-FF.xlsx. Figshare. Dataset. 2021. Available online: https://figshare.com/articles/dataset/Data_for_RHBD-FF_xlsx/14879697 (accessed on 30 June 2021).



| A | B | Out |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | Float |
| 1 | 0 | Float |
| 1 | 1 | 1 |
| Flip-Flop | TGFF | TMR FF | Temporal FF | DICE FF | Temporal TMR FF | DMR FF | Temporal DICE FF | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (1) | (2) | (1) | (2) 3 | ||||||
| # Transistors | All | 20 | 78 | 80 | 28 | 90 | 44 | 54 | 74 | ||
| W1, L2 | 20 | 78 | 56 | 28 | 20 | 78 | 44 | 42 | 58 | ||
| 4W, 4L | - | - | 24 | - | - | - | 12 | - | 12 | - | |
| 4W, 6L | - | - | - | 24 | - | - | - | - | - | 12 | |
| 23W, L | - | - | - | - | - | 8 | - | - | - | 4 | |
| Flip-Flop | TGFF | TMR FF | Temporal FF | DICE FF | Temporal TMR FF | DMR FF | Temporal DICE FF | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (1) | (2) | (1) | (2) | ||||||
| Nodes tested | 7 | 24 | 21 | 8 | 30 | 20 | 15 | ||||
| Critical node | 2 | - | 5 | All | 8 | 9 | 2 | 2, 5 | |||
| Qcritical (fC) | 100 MHz | 18 | FI 1 | 91 | 171 | 5 2 | FI 1 | FI 1 | 16 2 | 58 | 234 |
| 250 MHz | 18 | 60 | 51 | 5 2 | 16 2 | 58 | 40 | ||||
| 500 MHz | 18 | 32 | NF 3 | 5 2 | 16 2 | 31 | NF 3 | ||||
| 1 GHz | 18 | NF 3 | 5 | 175 | 13 | 16 | NF 3 | ||||
| 2 GHz | 18 | 5 | 39 | NF 3 | 16 | ||||||
| Flip-Flop | TGFF | TMR FF | Temporal FF | DICE FF | Temporal TMR FF | DMR FF | Temporal DICE FF | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (1) | (2) | (1) | (2) | ||||||
| Qcritical (fC) 100 MHz | SS | 16 | FI 1 | 83 | 159 | 4 2 | FI 1 | FI 1 | 14 2 | 55 | 197 |
| SF | 18 | 78 | 177 | 4 2 | 16 2 | 57 | 234 | ||||
| TT | 18 | 91 | 171 | 5 2 | 16 2 | 58 | 234 | ||||
| FS | 18 | 106 | 166 | 5 2 | 16 2 | 65 | 233 | ||||
| FF | 21 | 97 | 186 | 5 2 | 19 2 | 61 | 294 | ||||
| Qcritical (fC) 250 MHz | SS | 16 | 47 | 41 | 4 2 | 14 2 | 55 | 38 | |||
| SF | 18 | 56 | 50 | 4 2 | 16 2 | 57 | 40 | ||||
| TT | 18 | 60 | 51 | 5 2 | 16 2 | 58 | 40 | ||||
| FS | 18 | 63 | 51 | 5 2 | 16 2 | 65 | 38 | ||||
| FF | 21 | 80 | 62 | 5 2 | 19 2 | 61 | 44 | ||||
| Qcritical (fC) 500 MHz | SS | 16 | 22 | NF 3 | 4 2 | 14 2 | 24 | NF 3 | |||
| SF | 18 | 33 | 4 2 | 16 2 | 30 | ||||||
| TT | 18 | 32 | 5 2 | 16 2 | 31 | ||||||
| FS | 18 | 31 | 5 2 | 16 2 | 31 | ||||||
| FF | 21 | 43 | 5 2 | 19 2 | 32 | ||||||
| Qcritical (fC) 1 GHz | SS | 16 | NF 3 | 4 | 135 | 7 | 14 | NF 3 | |||
| SF | 18 | 4 | 188 | 13 | 16 | ||||||
| TT | 18 | 5 | 175 | 13 | 16 | ||||||
| FS | 18 | 5 | 162 | 13 | 16 | ||||||
| FF | 21 | 5 | 233 | 17 | 19 | ||||||
| Qcritical (fC) 2 GHz | SS | 15 | 4 | 26 | NF 3 | 13 | |||||
| SF | 18 | 4 | 55 | 16 | |||||||
| TT | 18 | 5 | 39 | 16 | |||||||
| FS | 18 | 5 | 35 | 16 | |||||||
| FF | 21 | 5 | 61 | 19 | |||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamed, E.A.; Lee, I. Categorization and SEU Fault Simulations of Radiation-Hardened-by-Design Flip-Flops. Electronics 2021, 10, 1572. https://doi.org/10.3390/electronics10131572
Hamed EA, Lee I. Categorization and SEU Fault Simulations of Radiation-Hardened-by-Design Flip-Flops. Electronics. 2021; 10(13):1572. https://doi.org/10.3390/electronics10131572
Chicago/Turabian StyleHamed, Ehab A., and Inhee Lee. 2021. "Categorization and SEU Fault Simulations of Radiation-Hardened-by-Design Flip-Flops" Electronics 10, no. 13: 1572. https://doi.org/10.3390/electronics10131572
APA StyleHamed, E. A., & Lee, I. (2021). Categorization and SEU Fault Simulations of Radiation-Hardened-by-Design Flip-Flops. Electronics, 10(13), 1572. https://doi.org/10.3390/electronics10131572







