Estimation of Lithium-Ion Batteries State-Condition in Electric Vehicle Applications: Issues and State of the Art
Abstract
:1. Introduction
- Production and distribution of electric energy (stationary application);
- Portable tools and devices (on-board application);
- Electric vehicles (EVs).
The Lithium-Ion Battery Characteristics
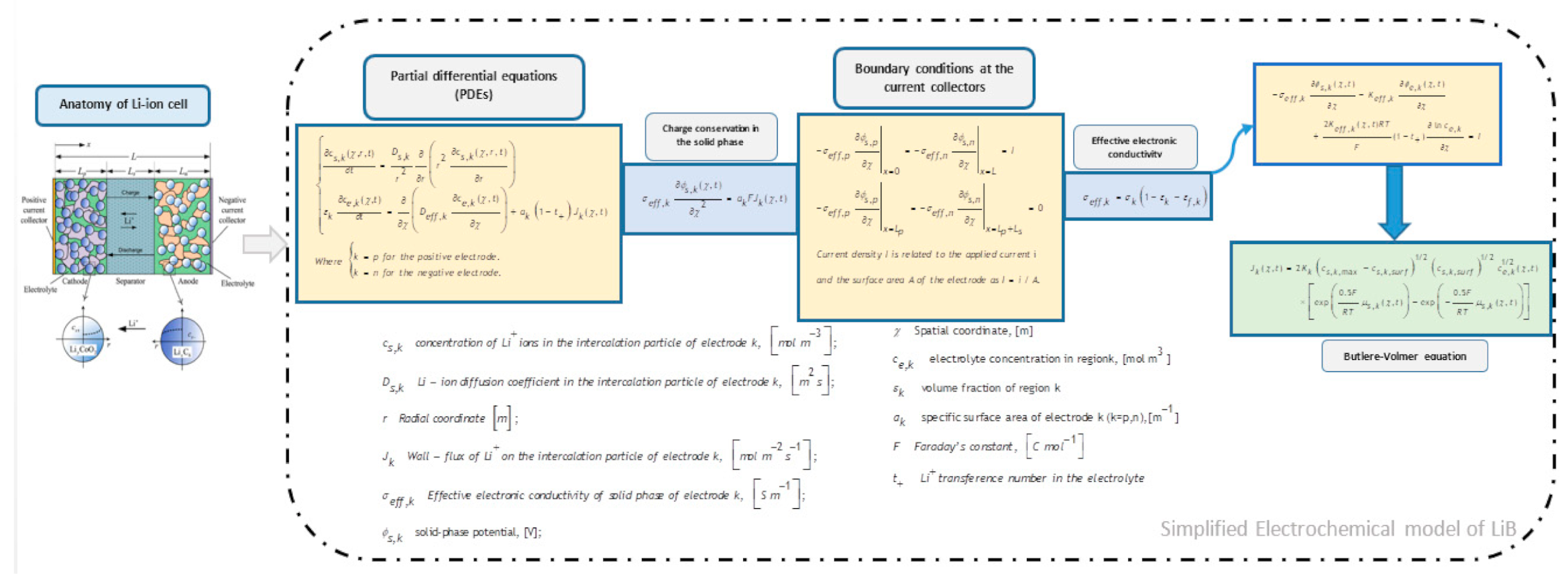
2. Modelling of LiBs
2.1. Electrochemical Modelling of LiBs
2.2. Equivalent Circuit Models for LiBs
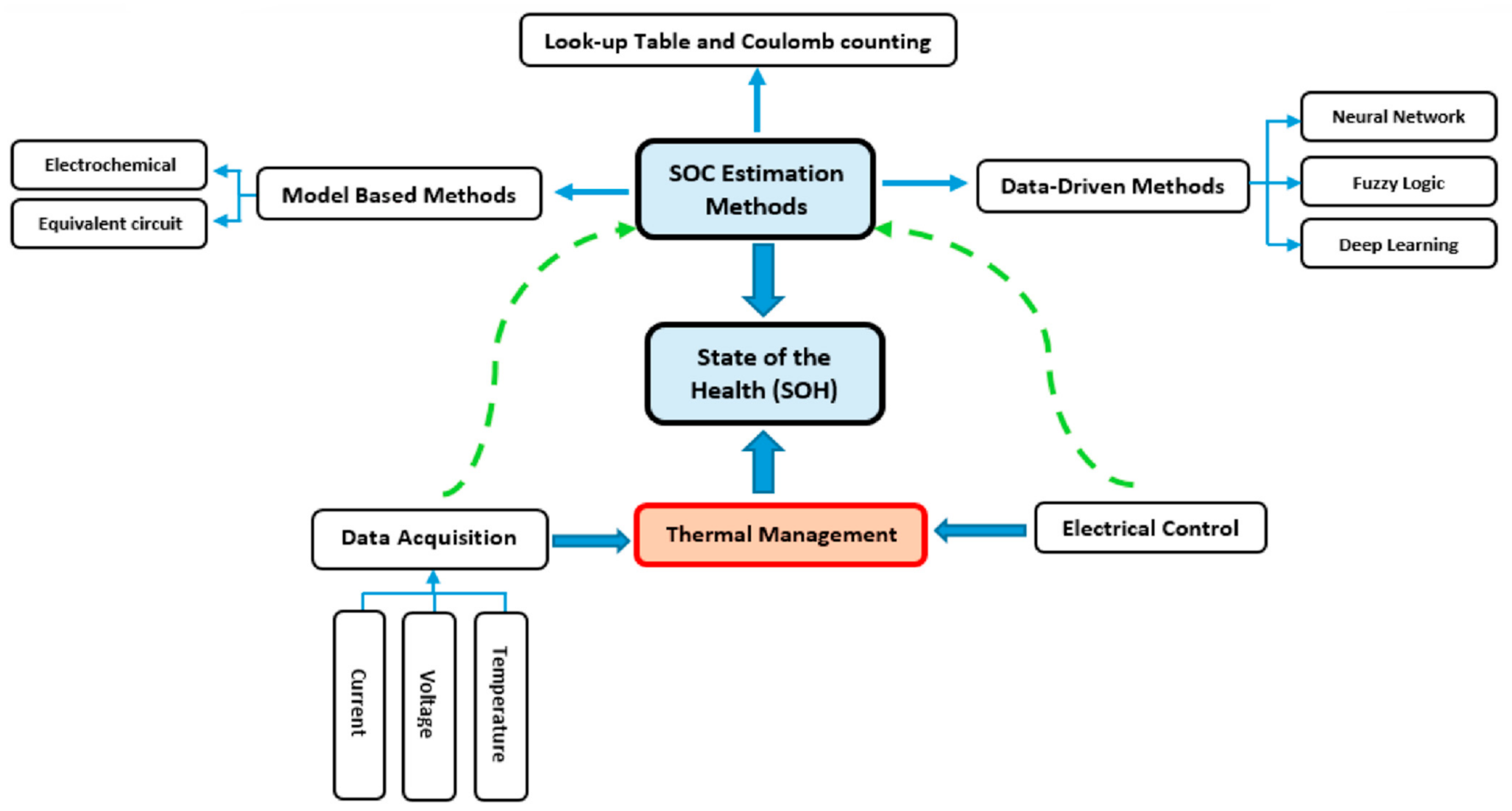
3. Battery State Estimation Methods
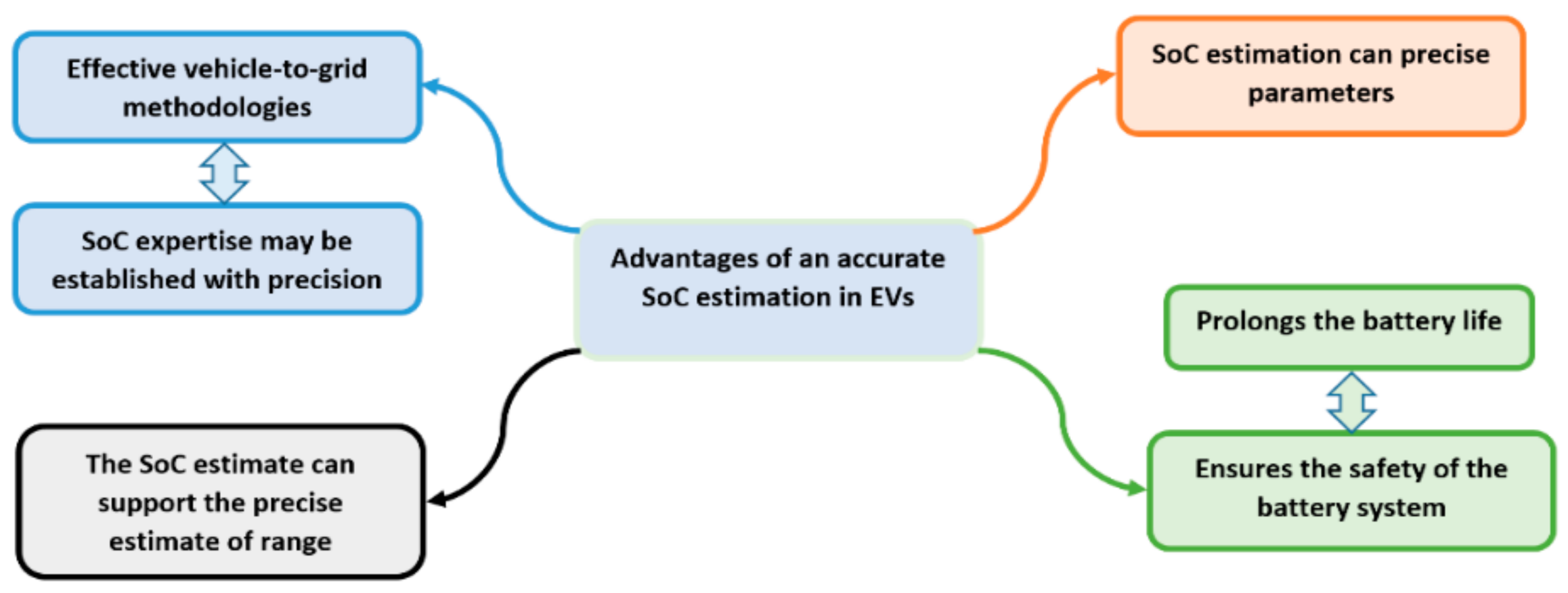
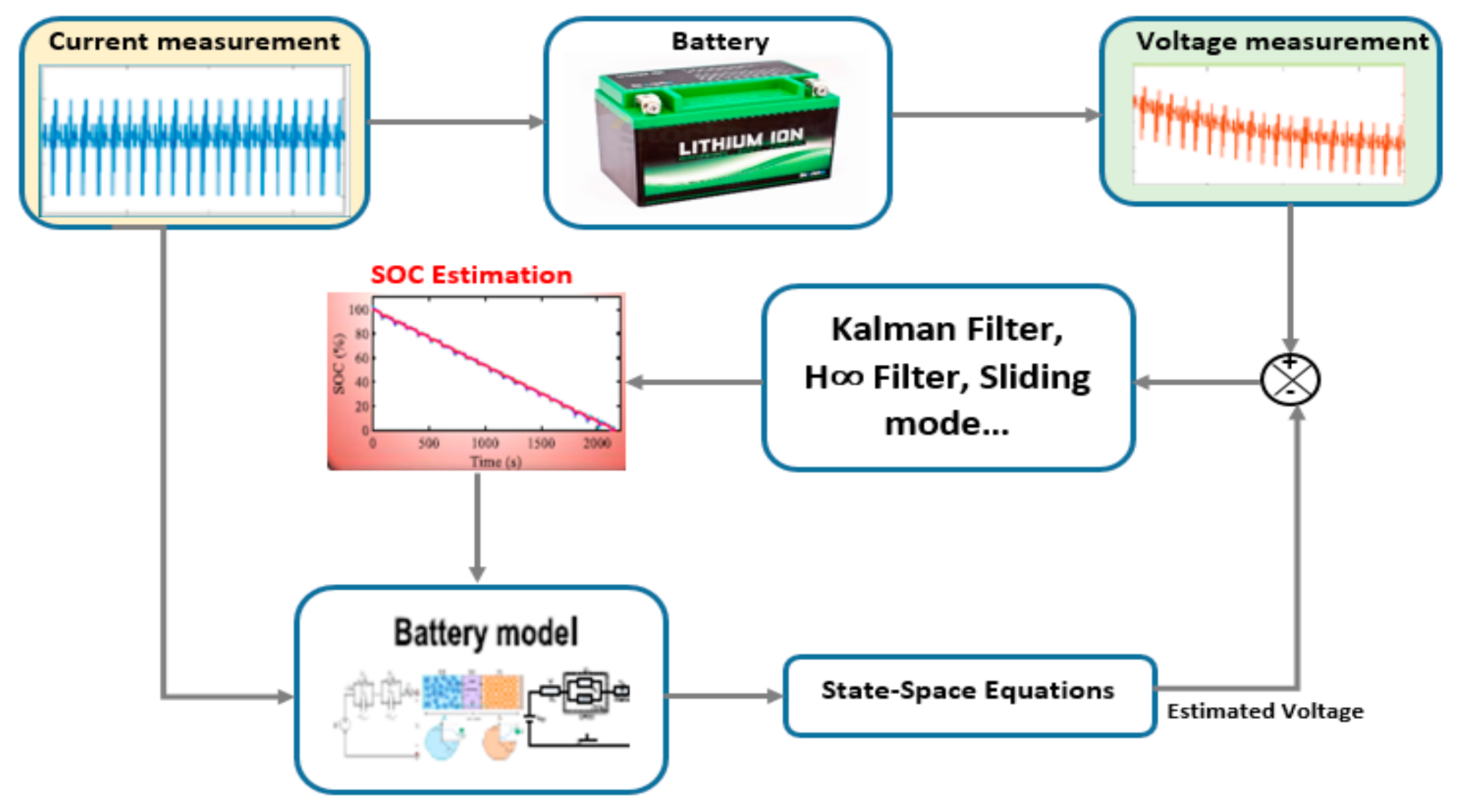
3.1. The SoC Estimation Method
- The change in impedance is not sensitive to variations in SoC for a certain range of SoCs, and there may be a non-monotonic relationship between impedance and SoCs;
- The impedance may change over time due to historical and current working conditions [138];
- Online impedance measurement will contain contact impedance;
- It is difficult to assess the change in the impedance between LiB cells [143].
3.1.1. Model-Based Estimation Method
- The UKF was more reliable than the EKF and the partial filter when the SoC was properly configured;
- The UKF was more robust to initial values of SoC;
- At the beginning of the SoC calculation, the PF demonstrated a quicker convergence potential than the UKF and the EKF;
- The EKF and the UKF have become more computationally effective than the PF;
- All proposed algorithms were able to estimate the SoC of the aged battery.
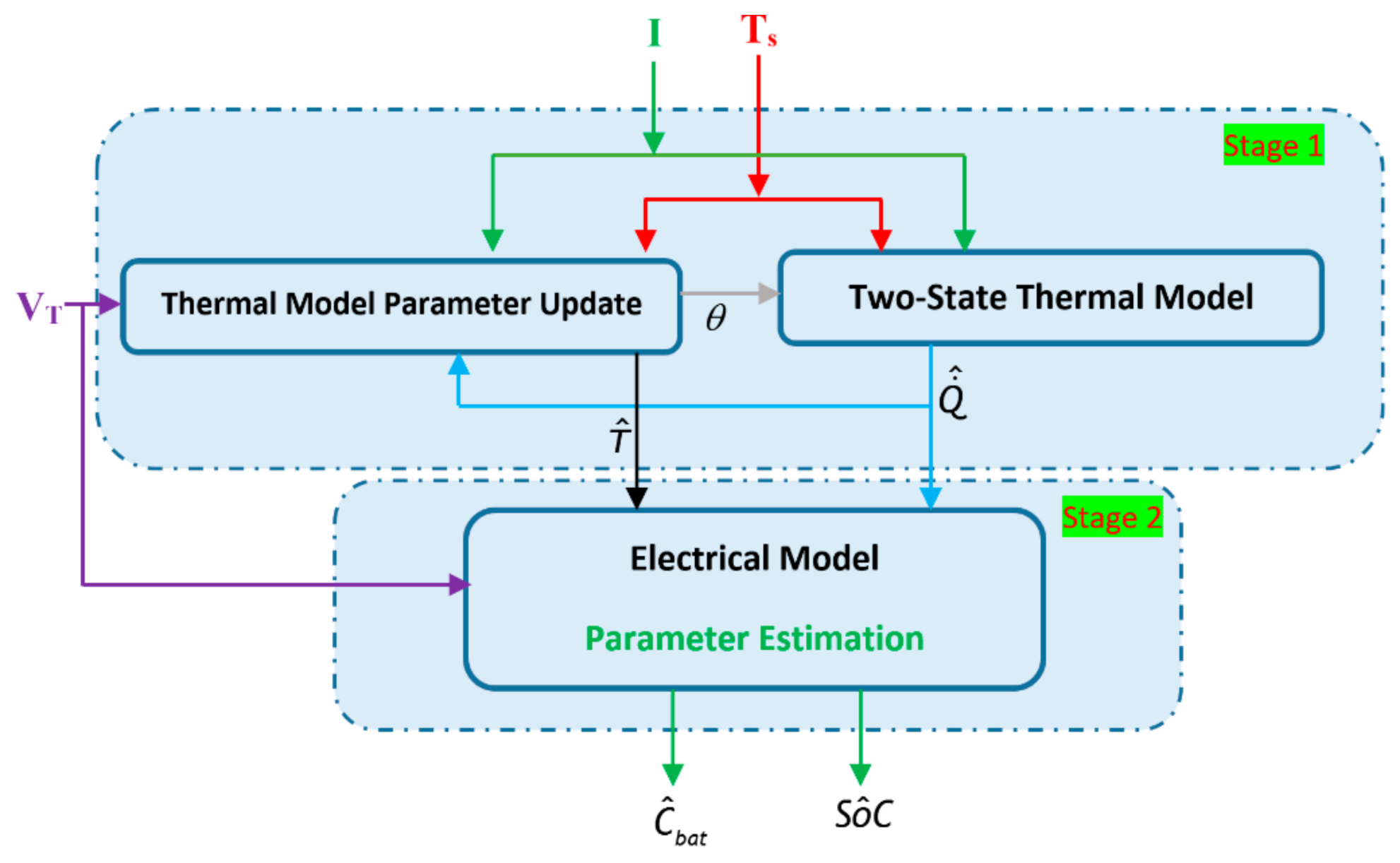
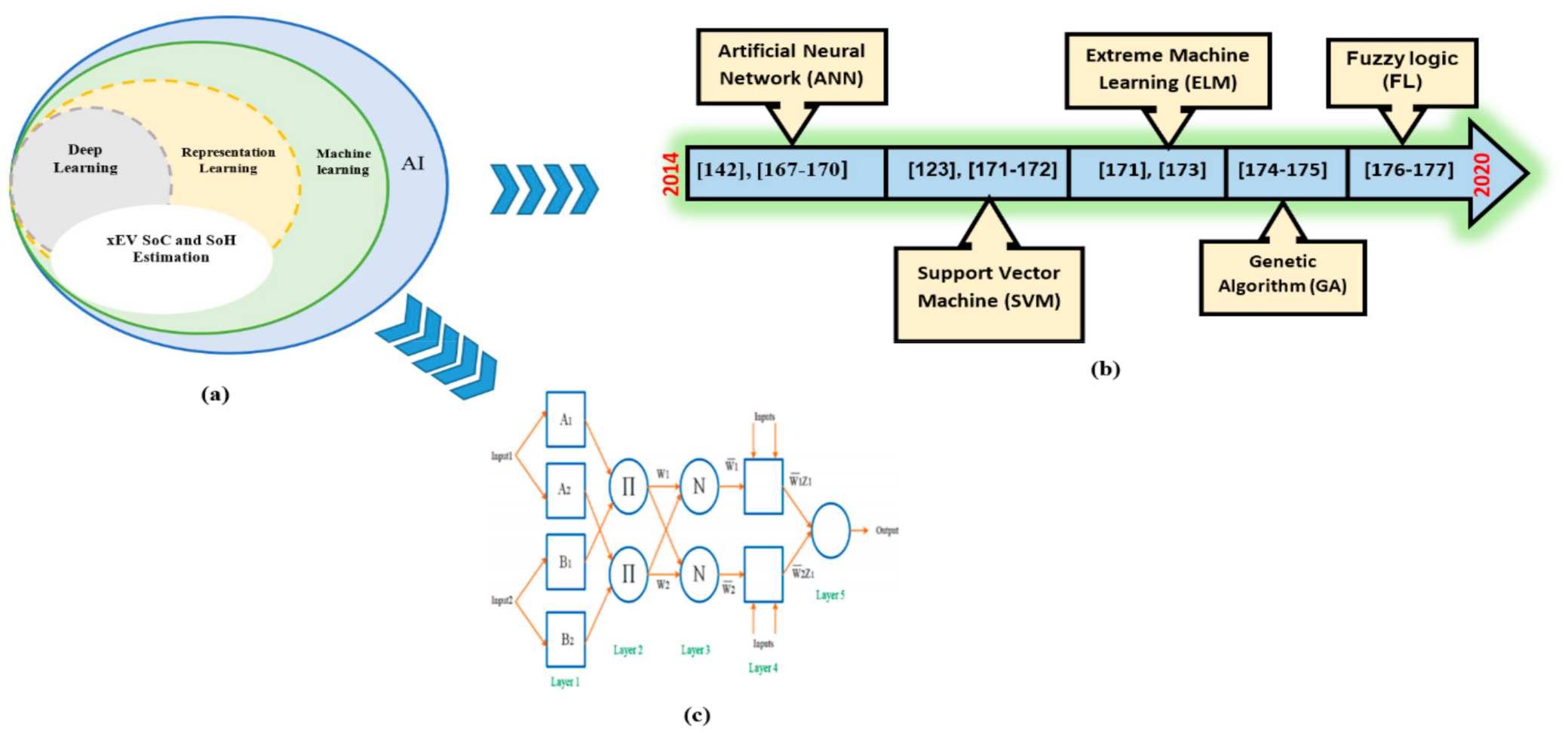
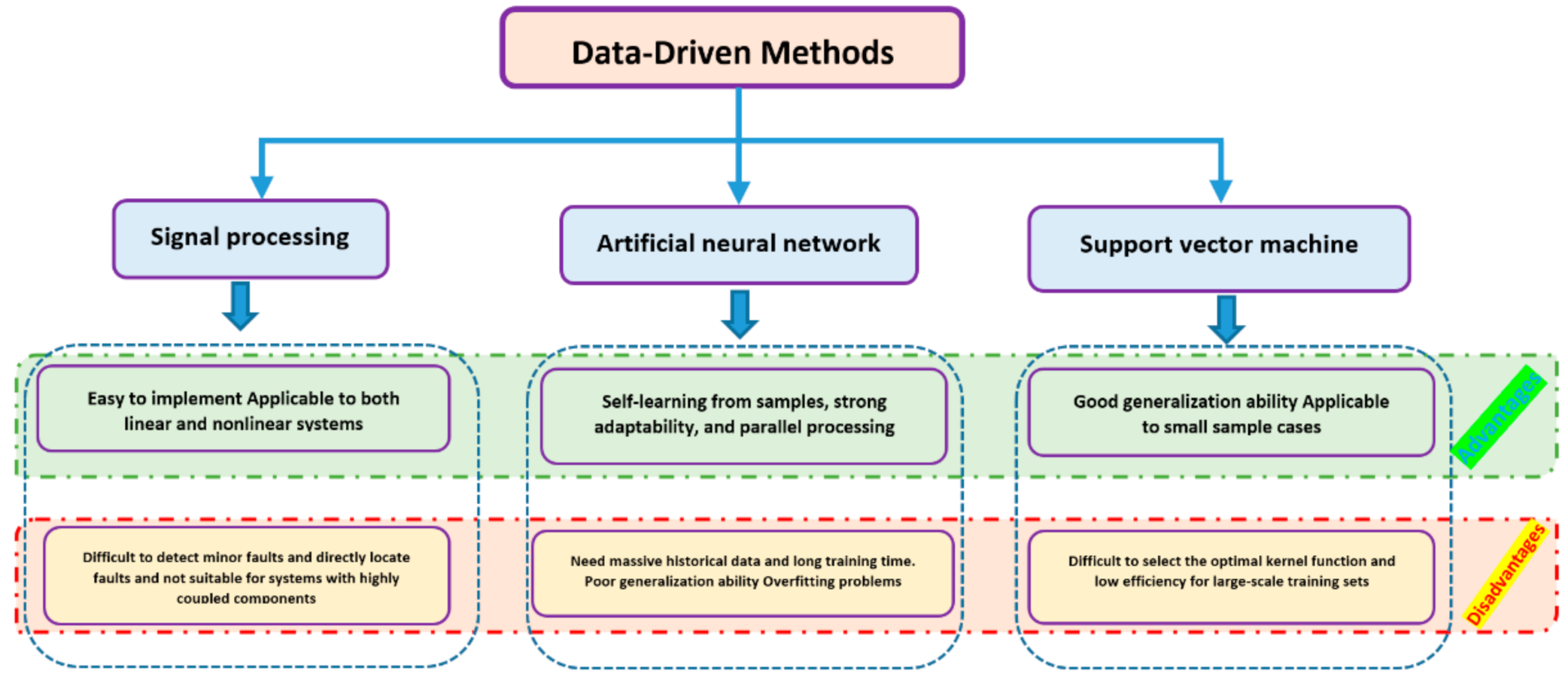
3.1.2. Data-Driven Based Estimation Methods

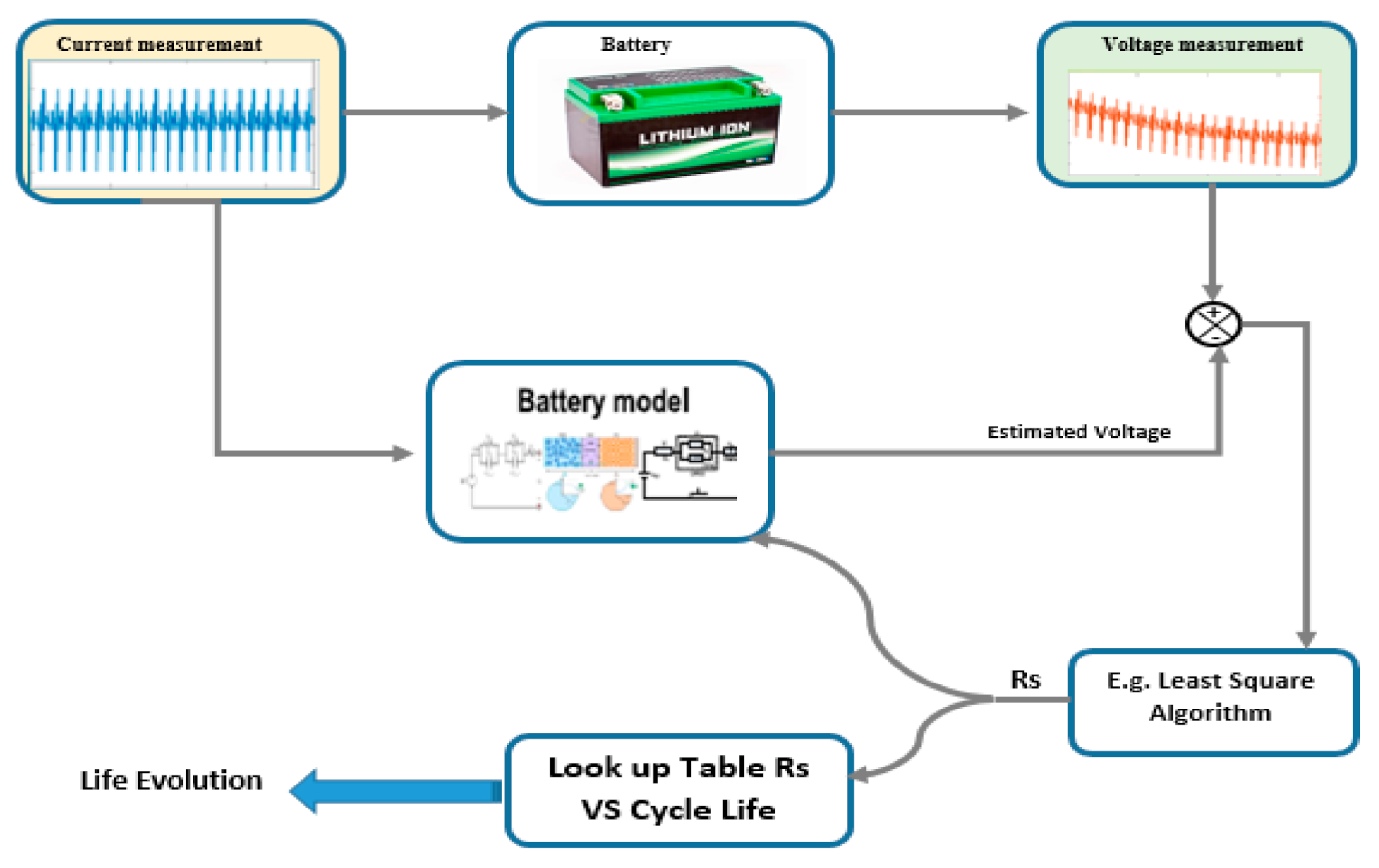
3.2. The Internal Resistance Estimation Method
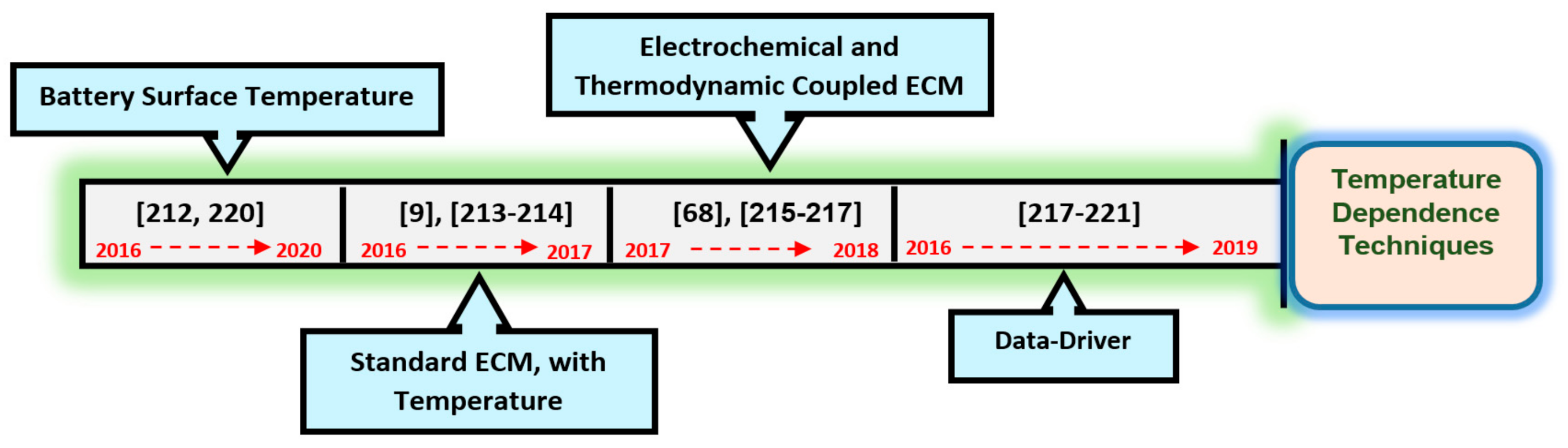
4. The Aging of LiB and Temperature Dependence
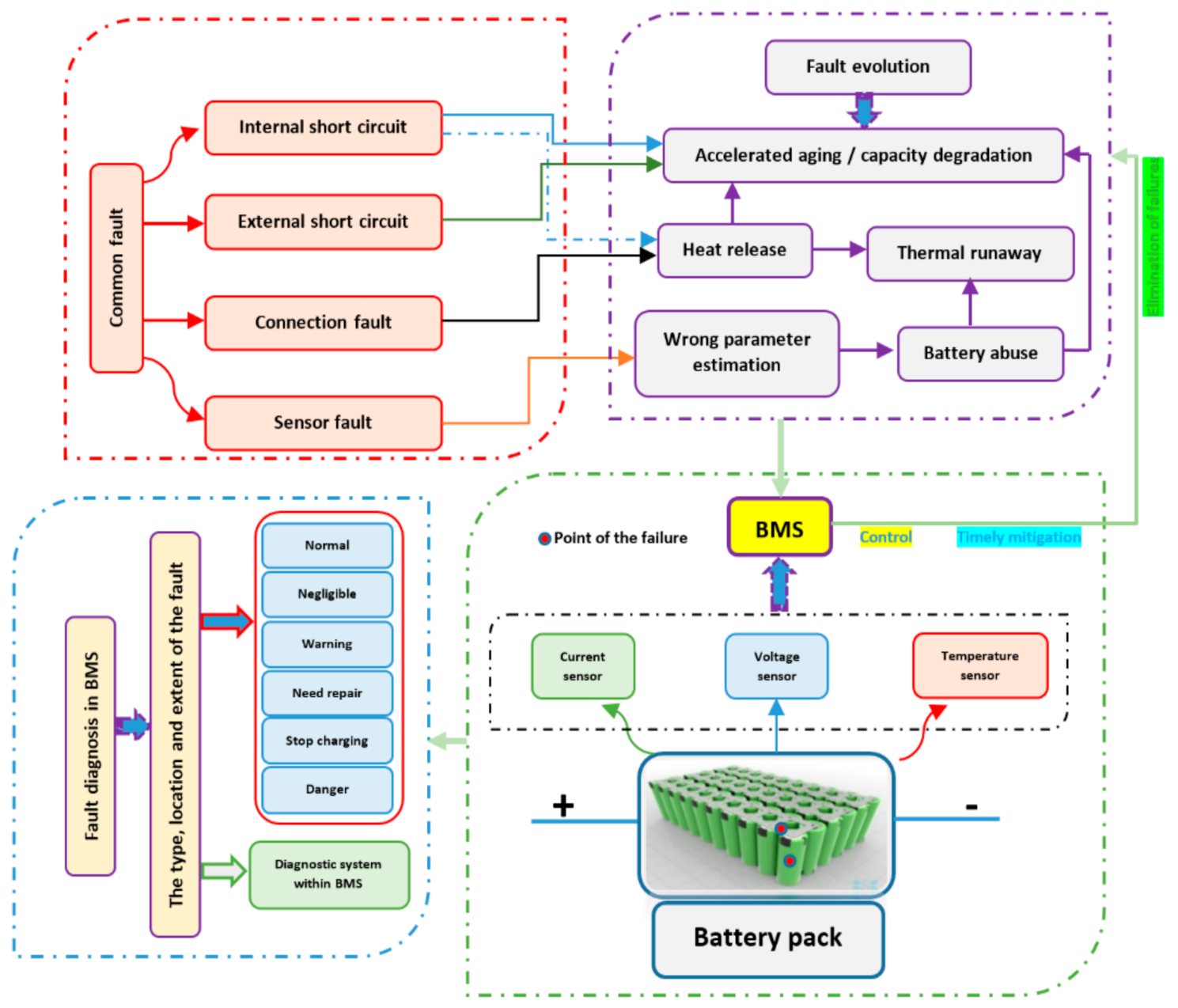
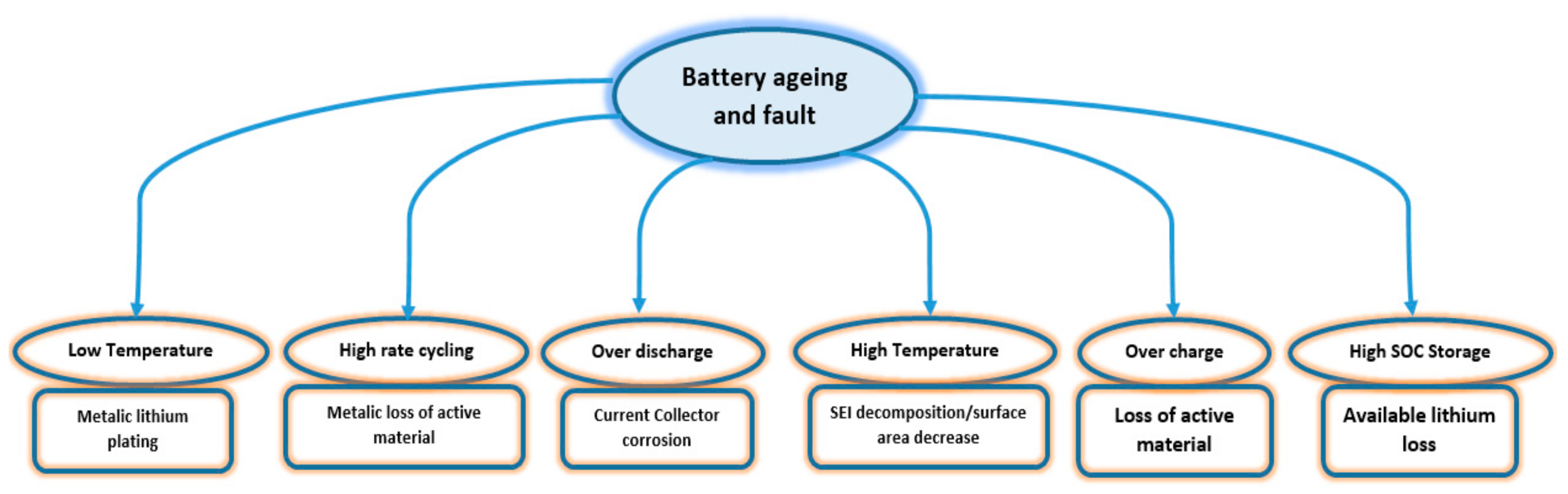
- The energy of the battery is very much affected, and influenced, by its OCV;
- OCV model must take the temperature into account;
- The total energy of the battery is influenced by the ambient temperature and load current;
- The errors caused by current or voltage measurement noises have to be considered.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sulaiman, N.; Hannan, M.A.; Mohamed, A.; Majlan, E.H.; Daud, W.R.W. A review on energy management system for fuel cell hybrid electric vehicle: Issues and challenges. Renew. Sustain. Energy Rev. 2015, 52, 802–814. [Google Scholar] [CrossRef]
- Essl, C.; Seifert, L.; Rabe, M.; Fuchs, A. Early Detection of Failing Automotive Batteries Using Gas Sensors. Batteries 2021, 7, 25. [Google Scholar] [CrossRef]
- Ibrahim, A.; Jiang, F. The electric vehicle energy management: An overview of the energy system and related modeling and simulation. Renew. Sustain. Energy Rev. 2021, 144, 111049. [Google Scholar] [CrossRef]
- Gabbar, H.A.; Othman, A.M.; Abdussami, M.R. Review of Battery Management Systems (BMS) Development and Industrial Standards. Technologies 2021, 9, 28. [Google Scholar] [CrossRef]
- Xing, Y.; Ma, E.W.M.; Tsui, K.L.; Pecht, M. Battery management systems in electric and hybrid vehicles. Energies 2011, 4, 1840–1857. [Google Scholar] [CrossRef]
- Eichi, H.R.; Ojha, U.; Baronti, F.; Chow, M.Y. Battery management system: An overview of its application in the smart grid and electric vehicles. IEEE Ind. Electron. Mag. 2013, 7, 4–15. [Google Scholar] [CrossRef]
- Zou, C.; Manzie, C.; Nešić, D.; Kallapur, A.G. Multi-time-scale observer design for state-of-charge and state-of-health of a lithium-ion battery. J. Power Sources 2016, 335, 121–130. [Google Scholar] [CrossRef]
- Dong, G.; Chen, Z.; Wei, J.; Zhang, C.; Wang, P. An online model-based method for state of energy estimation of lithium-ion batteries using dual filters. J. Power Sources 2016, 301, 277–286. [Google Scholar] [CrossRef]
- He, H.; Zhang, Y.; Xiong, R.; Wang, C. A novel Gaussian model based battery state estimation approach: State-of-Energy. Appl. Energy 2015, 151, 41–48. [Google Scholar] [CrossRef]
- Zhai, G.; Liu, S.; Wang, Z.; Zhang, W.; Ma, Z. State of Energy Estimation of Lithium Titanate Battery for Rail Transit Application. Energy Procedia 2017, 105, 3146–3151. [Google Scholar] [CrossRef]
- Li, Y.; Chattopadhyay, P.; Ray, A.; Rahn, C.D. Identification of the battery state-of-health parameter from input-output pairs of time series data. J. Power Sources 2015, 285, 235–246. [Google Scholar] [CrossRef]
- Feng, T.; Yang, L.; Zhao, X.; Zhang, H.; Qiang, J. Online identification of lithium-ion battery parameters based on an improved equivalent-circuit model and its implementation on battery state-of-power prediction. J. Power Sources 2015, 281, 192–203. [Google Scholar] [CrossRef]
- Beck, D.; Dechent, P.; Junker, M.; Sauer, D.U.; Dubarry, M. Inhomogeneities and Cell-to-Cell Variations in Lithium-Ion Batteries, a Review. Energies 2021, 14, 3276. [Google Scholar] [CrossRef]
- Zheng, Y.; Ouyang, M.; Han, X.; Lu, L.; Li, J. Investigating the error sources of the online state of charge estimation methods for lithium-ion batteries in electric vehicles. J. Power Sources 2018, 377, 161–188. [Google Scholar] [CrossRef]
- Yang, K.; Tang, Y.; Zhang, Z. Parameter Identification and State-of-Charge Estimation for Lithium-Ion Batteries Using Separated Time Scales and Extended Kalman Filter. Energies 2021, 14, 1054. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Peng, H.; Sun, F. Robustness analysis of State-of-Charge estimation methods for two types of Li-ion batteries. J. Power Sources 2012, 217, 209–219. [Google Scholar] [CrossRef]
- Lim, K.; Bastawrous, H.A.; Duong, V.-H.; See, K.W.; Zhang, P.; Dou, S.X. Fading Kalman filter-based real-time state of charge estimation in LiFePO4 battery-powered electric vehicles. Appl. Energy 2016, 169, 40–48. [Google Scholar] [CrossRef]
- Gao, Z.C.; Chin, C.S.; Toh, W.D.; Chiew, J.; Jia, J. State-of-charge estimation and active cell pack balancing design of lithium battery power system for smart electric vehicle. J. Adv. Transp. 2017, 2017, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Jia, J.; Lin, P.; Chin, C.S.; Toh, W.D.; Gao, Z.; Lyu, H.; Cham, Y.T.; Mesbahi, E. Multirate strong tracking extended Kalman filter and its implementation on lithium iron phosphate (LiFePO4) battery system. In Proceedings of the IEEE International Conference on Power Electronics and Drive Systems, Sydney, NSW, Australia, 9–12 June 2015; pp. 640–645. [Google Scholar]
- Tang, X.; Liu, B.; Gao, F.; Lv, Z. State-of-charge estimation for Li-Ion power batteries based on a tuning free observer. Energies 2016, 9, 675. [Google Scholar] [CrossRef] [Green Version]
- Torai, S.; Nakagomi, M.; Yoshitake, S.; Yamaguchi, S.; Oyama, N. State-of-health estimation of LiFePO4/graphite batteries based on a model using differential capacity. J. Power Sources 2016, 306, 62–69. [Google Scholar] [CrossRef]
- Ning, B.; Xu, J.; Cao, B.; Wang, B.; Xu, G. A sliding mode observer SOC estimation method based on parameter adaptive battery model. Energy Procedia 2016, 88, 619–626. [Google Scholar] [CrossRef] [Green Version]
- Zhong, Q.; Zhong, F.; Cheng, J.; Li, H.; Zhong, S. State of charge estimation of lithium-ion batteries using fractional order sliding mode observer. ISA Trans. 2017, 66, 448–459. [Google Scholar] [CrossRef]
- Kim, I.S. The novel state of charge estimation method for lithium battery using sliding mode observer. J. Power Sources 2006, 163, 584–590. [Google Scholar] [CrossRef]
- Ma, Y.; Li, B.; Xie, Y.; Chen, H. Estimating the State of Charge of Lithium-ion Battery based on Sliding Mode Observer. IFAC Papers Online 2016, 49, 54–61. [Google Scholar] [CrossRef]
- Zhang, F.; Liu, G.; Fang, L. A battery state of charge estimation method using sliding mode observer. In Proceedings of the 2008 World Congress on Intelligent Control and Automation, Chongqing, China, 25–27 June 2008; pp. 989–994. [Google Scholar]
- Du, J.; Liu, Z.; Wang, Y.; Wen, C. An adaptive sliding mode observer for lithium-ion battery state of charge and state of health estimation in electric vehicles. Control Eng. Pract. 2016, 54, 81–90. [Google Scholar] [CrossRef]
- Lin, C.; Mu, H.; Xiong, R.; Shen, W. A novel multi-model probability battery state of charge estimation approach for electric vehicles using H-infinity algorithm. Appl. Energy 2016, 166, 76–87. [Google Scholar] [CrossRef]
- Mu, H.; Xiong, R.; Sun, F. A novel multi-model probability based battery state-of-charge fusion estimation approach. Energy Procedia 2016, 88, 840–846. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Q.; Xiong, N.; Yang, M.-L.; Huang, R.-S.; Hu, G.-D. State of Charge Estimation for Lithium-Ion Battery Based on Nonlinear Observer: An H∞ Method. Energies 2017, 10, 679. [Google Scholar] [CrossRef] [Green Version]
- Chen, N.; Zhang, P.; Dai, J.; Gui, W. Estimating the State-of-Charge of Lithium-Ion Battery Using an H-Infinity Observer Based on Electrochemical Impedance Model. IEEE Access 2020, 8, 26872–26884. [Google Scholar] [CrossRef]
- Hu, X.; Sun, F.; Zou, Y. Estimation of State of Charge of a Lithium-Ion Battery Pack for Electric Vehicles Using an Adaptive Luenberger Observer. Energies 2010, 3, 1586–1603. [Google Scholar] [CrossRef]
- Bartlett, A.; Marcicki, J.; Onori, S.; Rizzoni, G.; Yang, X.G.; Miller, T. Electrochemical model-based state of charge and capacity estimation for a composite electrode lithium-ion battery. IEEE Trans. Control Syst. Technol. 2016, 24, 384–399. [Google Scholar] [CrossRef]
- Moura, J.N.; Chaturvedi, N.A.; Krstić, M. Adaptive partial differential equation observer for battery state-of-charge/state-of-health estimation via an electrochemical model. J. Dyn. Syst. Meas. Control 2014, 136, 11–15. [Google Scholar] [CrossRef]
- Klass, V.; Behm, M.; Lindbergh, G. Evaluating real-life performance of lithium-ion battery packs in electric vehicles. J. Electrochem. Soc. 2012, 159, 1856–1860. [Google Scholar] [CrossRef]
- Charkhgard, M.; Zarif, M.H. Design of adaptive H∞ filter for implementing on state-of-charge estimation based on battery state-of-charge-varying modelling. Power Electron. IET 2015, 8, 1825–1833. [Google Scholar] [CrossRef]
- Xia, B.; Chen, Z.; Mi, C. External Short Circuit Fault Diagnosis for Lithium-Ion Batteries. In Proceedings of the IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 15–18 June 2014; pp. 1–7. [Google Scholar]
- Chiu, K.; Lin, C.; Yeh, S.; Lin, Y.; Chen, K. An electrochemical modeling of lithium-ion battery nail penetration. J. Power Sources 2014, 251, 254–263. [Google Scholar] [CrossRef]
- Kalawoun, J.; Biletska, K.; Suard, F.; Montaru, M. From a novel classification of the battery state of charge estimators toward a conception of an ideal one. J. Power Sources 2015, 279, 694–706. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Klee Barillas, J.; Guenther, C.; Danzer, M.A. A comparative study of state of charge estimation algorithms for LiFePO4 batteries used in electric vehicles. J. Power Sources 2013, 230, 244–250. [Google Scholar] [CrossRef]
- Burgos, C.; Sáez, D.; Orchard, M.E.; Cárdenas, R. Fuzzy modelling for the state-of-charge estimation of lead-acid batteries. J. Power Sources 2015, 274, 355–366. [Google Scholar] [CrossRef]
- Oh, K.-Y.; Samad, N.A.; Kim, Y.; Siegel, J.B.; Stefanopoulou, A.G.; Epureanu, B.I. A novel phenomenological multi-physics model of Li-ion battery cells. J. Power Sources 2016, 326, 447–458. [Google Scholar] [CrossRef] [Green Version]
- Zhang, M.; Fan, X. Review on the State of Charge Estimation Methods for Electric Vehicle Battery. World Electr. Veh. J. 2020, 11, 23. [Google Scholar] [CrossRef] [Green Version]
- Nejad, S.; Gladwin, D.T.; Stone, D.A. A systematic review of lumped-parameter equivalent circuit models for real-time estimation of lithium-ion battery states. J. Power Sources 2016, 316, 183–196. [Google Scholar] [CrossRef] [Green Version]
- Zhang, R.; Xia, B.; Li, B.; Cao, L.; Lai, Y.; Zheng, W.; Wang, H.; Wang, W. State of the Art of Lithium-Ion Battery SOC Estimation for Electrical Vehicles. Energies 2018, 11, 1820. [Google Scholar] [CrossRef] [Green Version]
- Tsang, K.M.; Sun, L.; Chan, W.L. Identification and modelling of Lithium ion battery. Energy Conver. Manag. 2010, 51, 2857–2862. [Google Scholar] [CrossRef]
- Saariluoma, H.; Piiroinen, A.; Unt, A.; Hakanen, J.; Rautava, T.; Salminen, A. Overview of Optical Digital Measuring Challenges and Technologies in Laser Welded Components in EV Battery Module Design and Manufacturing. Batteries 2020, 6, 47. [Google Scholar] [CrossRef]
- Saw, L.H.; Ye, Y.; Tay, A.A. Integration issues of lithium-ion battery into electric vehicles battery pack. J. Clean. Prod. 2016, 113, 1032–1045. [Google Scholar] [CrossRef]
- Al-Turjman, F.; Malekloo, A. Smart parking in IoT-enabled cities: A survey. Sustain. Cities Soc. 2019, 49, 101608. [Google Scholar] [CrossRef]
- Oswal, M.; Paul, J.; Zhao, R. A Comparative Study of Lithium-Ion Batteries; Tech. Rep. AME 578 Project; University of Southern California: Los Angeles, CA, USA, 2010. [Google Scholar]
- Pramanik, P.; Sinhababu, N.; Mukherjee, B.; Padmanaban, S.; Maity, A.; Upadhyaya, B.; Holm-Nielsen, J.; Choudhury, P. Power Consumption Analysis, Measurement, Management, and Issues: A State-of-the-Art Review of Smartphone Battery and Energy Usage. IEEE Access 2019, 7, 182113–182172. [Google Scholar] [CrossRef]
- Arora, S.; Shen, W.; Kapoor, A. Review of mechanical design and strategic placement technique of a robust battery pack for electric vehicles. Renew. Sustain. Energy Rev. 2016, 60, 1319–1331. [Google Scholar] [CrossRef]
- Pizarro-Carmona, V.; Cortés-Carmona, M.; Palma-Behnke, R.; Calderón-Muñoz, W.; Orchard, M.E.; Estévez, P.A. An Optimized Impedance Model for the Estimation of the State-of-Charge of a Li-Ion Cell: The Case of a LiFePO4 (ANR26650). Energies 2019, 12, 681. [Google Scholar] [CrossRef] [Green Version]
- He, H.; Xiong, R.; Fan, J. Evaluation of lithium-ion battery equivalent circuit models for state of charge estimation by an experimental approach. Energies 2011, 4, 582–598. [Google Scholar] [CrossRef]
- Hossain, E.; Murtaugh, D.; Mody, J.; Faruque, H.; Sunny, S.; Mohammad, N. A Comprehensive Review on Second-Life Batteries: Current State, Manufacturing Considerations, Applications, Impacts, Barriers & Potential Solutions, Business Strategies, and Policies. IEEE Access 2019, 7, 73215–73252. [Google Scholar]
- Wang, Q.; Jiang, B.; Li, B.; Yan, Y. A critical review of thermal management models and solutions of lithium-ion batteries for the development of pure electric vehicles. Renew. Sustain. Energy Rev. 2016, 64, 106–128. [Google Scholar] [CrossRef]
- Seaman, A.; Dao, T.-S.; McPhee, J. A survey of mathematics-based equivalent-circuit and electrochemical battery models for hybrid and electric vehicle simulation. J. Power Sources 2014, 256, 410–423. [Google Scholar] [CrossRef] [Green Version]
- Lee, K.-J.; Smith, K.; Pesaran, A.; Kim, G.-H. Three dimensional thermal-, electrical-, and electrochemical-coupled model for cylindrical wound large format lithium-ion batteries. J. Power Sources 2013, 241, 20–32. [Google Scholar] [CrossRef]
- Randles, J.E.B. Kinetics of rapid electrode reactions. Discuss. Faraday Soc. 1947, 1, 11–19. [Google Scholar] [CrossRef]
- Shepherd, C.M. Design of primary and secondary cells: II. An equation describing battery discharge. J. Electrochem. Soc. 1965, 112, 657–664. [Google Scholar] [CrossRef]
- Bernardi, D.; Pawlikowski, E.; Newman, J. A general energy balance for battery systems. J. Electrochem. Soc. 1985, 132, 5–12. [Google Scholar] [CrossRef] [Green Version]
- Shen, P.; Ouyang, M.; Lu, L.; Li, J.; Feng, X. The co-estimation of state of charge, state of health, and state of function for lithium-ion batteries in electric vehicles. IEEE Trans. Veh. Technol. 2018, 67, 92–103. [Google Scholar] [CrossRef]
- Lai, X.; Gao, W.; Zheng, Y.; Ouyang, M.; Li, J.; Han, X.; Zhou, L. A comparative study of global optimization methods for parameter identification of different equivalent circuit models for Li-ion batteries. Electrochim. Acta 2019, 295, 1057–1066. [Google Scholar] [CrossRef]
- Yang, J.; Xia, B.; Huang, W.; Fu, Y.; Mi, C. Online state-of-health estimation for lithium-ion batteries using constant-voltage charging current analysis. Appl. Energy 2018, 212, 1589–1600. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Liu, C.; Chen, Z. A novel approach of battery pack state of health estimation using artificial intelligence optimization algorithm. J. Power Sources 2018, 376, 191–199. [Google Scholar] [CrossRef]
- Shen, P.; Ouyang, M.; Lu, L.; Li, K.; Feng, X. State of Charge, State of Health and State of Function Co-Estimation of Lithium-Ion Batteries for Electric Vehicles. In Proceedings of the IEEE Vehicle Power and Propulsion Conference (VPPC), Hangzhou, China, 17–20 October 2016; pp. 1–5. [Google Scholar]
- Gholizadeh, M.; Salmasi, F.R. Estimation of state of charge, unknown nonlinearities, and state of health of a lithium-ion battery based on a comprehensive unobservable model. IEEE Trans. Ind. Electron. 2014, 61, 1335–1344. [Google Scholar] [CrossRef]
- Zou, C.; Klintberg, A.; Wei, Z.; Fridholm, B.; Wik, T.; Egardt, B. Power capability prediction for lithium-ion batteries using economic nonlinear model predictive control. J. Power Sources 2018, 396, 580–589. [Google Scholar] [CrossRef]
- Karlsen, H.; Dong, T.; Yang, Z.; Carvalho, R. Temperature-Dependence in Battery Management Systems for Electric Vehicles: Challenges, Criteria, and Solutions. IEEE Access 2019, 7, 142203–142213. [Google Scholar] [CrossRef]
- You, H.W.; Bae, J.I.; Cho, S.J.; Lee, J.M.; Kim, S.-H. Analysis of equivalent circuit models in lithium-ion batteries. AIP Adv. 2018, 8, 125101. [Google Scholar] [CrossRef] [Green Version]
- How, D.; Hannan, M.; Lipu, M.S.H.; Ker, P.J. State of Charge Estimation for Lithium-Ion Batteries Using Model-Based and Data-Driven Methods: A Review. IEEE Access 2019, 7, 136116–136136. [Google Scholar] [CrossRef]
- Hentunen, A.; Lehmuspelto, T.; Suomela, J. Time-Domain Parameter Extraction Method for Thévenin-Equivalent Circuit Battery Models. IEEE Trans. Energy Convers. 2014, 29, 558–566. [Google Scholar] [CrossRef]
- Li, Y.; Abdel-Monem, M.; Gopalakrishnan, R.; Berecibar, M.; Maury, E.N.; Omar, N.; Bossche, P.; Mierlo, J.V. A quick on-line state of health estimation method for Li-ion battery with incremental capacity curves processed by Gaussian filter. J. Power Sources 2018, 373, 40–53. [Google Scholar] [CrossRef]
- Wang, W.; Gaillard, A.; Hissel, D. Online electrochemical impedance spectroscopy detection integrated with step-up converter for fuel cell electric vehicle. Int. J. Hydrogen Energy 2019, 44, 1110–1121. [Google Scholar] [CrossRef]
- Xing, J.; Wu, P. State of Charge Estimation of Lithium-Ion Battery Based on Improved Adaptive Unscented Kalman Filter. Sustainability 2021, 13, 5046. [Google Scholar] [CrossRef]
- Morello, R.; Di Rienzo, R.; Roncella, R.; Saletti, R.; Baronti, F. Hardware-in-the-loop platform for assessing battery state estimators in electric vehicles. IEEE Access 2018, 6, 68210–68220. [Google Scholar] [CrossRef]
- Wang, W.; Wang, X.; Xiang, C.; Wei, C.; Zhao, Y. Unscented Kalman filter-based battery SoC estimation and peak power prediction method for power distribution of hybrid electric vehicles. IEEE Access 2018, 6, 35957–35965. [Google Scholar] [CrossRef]
- Lipu, M.S.H.; Hussain, A.; Saad, M.H.M.; Ayob, A.; Hannan, M.A. Improved Recurrent NARX Neural Network Model for State of Charge Estimation of Lithium-ion Battery Using PSO Algorithm. In Proceedings of the IEEE Symposium on Computer Applications & Industrial Electronics (ISCAIE), Penang, Malaysia, 28–29 April 2018; pp. 354–359. [Google Scholar]
- Wu, X.; Li, X.; Du, J. State of charge estimation of lithium-ion batteries over wide temperature range using unscented Kalman filter. IEEE Access 2018, 6, 41993–42003. [Google Scholar] [CrossRef]
- Xu, G.; Du, X.; Li, Z.; Zhang, X.; Zheng, M.; Miao, Y.; Gao, Y.; Liu, Q. Reliability design of battery management system for power battery. Microelectron. Reliab. 2018, 88–90, 1286–1292. [Google Scholar] [CrossRef]
- Hu, X.; Zhang, K.; Liu, K.; Lin, X.; Dey, S.; Onori, S. Advanced Fault Diagnosis for Lithium-Ion Battery Systems: A Review of Fault Mechanisms, Fault Features, and Diagnosis Procedures. IEEE Ind. Electron. Mag. 2020, 14, 65–91. [Google Scholar] [CrossRef]
- Momma, T.; Matsunaga, M.; Mukoyama, D.; Osaka, T. Ac impedance analysis of lithium ion battery under temperature control. J. Power Sources 2012, 216, 304–307. [Google Scholar] [CrossRef]
- Marongiu, A.; Nußbaum, F.H.W.; Waag, W.; Garmendia, M.; Sauer, D.U. Comprehensive study of the influence of aging on the hysteresis behavior of a lithium iron phosphate cathode-based lithium ion battery–An experimental investigation of the hysteresis. Appl. Energy 2016, 171, 629–645. [Google Scholar] [CrossRef]
- Han, X.; Ouyang, M.; Lu, L.; Li, J.; Zheng, Y.; Li, Z. A comparative study of commercial lithium ion battery cycle life in electrical vehicle: Aging mechanism identification. J. Power Sources 2014, 251, 38–54. [Google Scholar] [CrossRef]
- Zheng, Y.; Ouyang, M.; Lu, L.; Li, J.; Han, X.; Xu, L.; Ma, H.; Dollmeyer, T.A.; Freyermuth, V. Cell state-of-charge inconsistency estimation for LiFePO4 battery pack in hybrid electric vehicles using mean-difference model. Appl. Energy 2013, 111, 571–580. [Google Scholar] [CrossRef]
- Ezemobi, E.; Tonoli, A.; Silvagni, M. Battery State of Health Estimation with Improved Generalization Using Parallel Layer Extreme Learning Machine. Energies 2021, 14, 2243. [Google Scholar] [CrossRef]
- Lavigne, L.; Sabatier, J.; Francisco, J.M.; Guillemard, F.; Noury, A. Lithium-ion Open Circuit Voltage (OCV) curve modelling and its ageing adjustment. J. Power Sources 2016, 324, 694–703. [Google Scholar] [CrossRef]
- Xing, Y.; He, W.; Pecht, M.; Tsui, K.L. State of charge estimation of lithium-ion batteries using the open-circuit voltage at various ambient temperatures. Appl. Energy 2014, 113, 106–115. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, W.; Lin, S.; Feng, Z. A novel model of the initial state of charge estimation for LiFePO4 batteries. J. Power Sources 2014, 248, 1028–1033. [Google Scholar] [CrossRef]
- Roscher, M.A.; Sauer, D.U. Dynamic electric behavior and open-circuit-voltage modeling of LiFePO4-based lithium ion secondary batteries. J. Power Sources 2011, 196, 331–336. [Google Scholar] [CrossRef]
- Zhu, L.; Sun, Z.; Dai, H.; Wei, X. A novel modeling methodology of open circuit voltage hysteresis for LiFePO4 batteries based on an adaptive discrete Preisach model. Appl. Energy 2015, 155, 91–109. [Google Scholar] [CrossRef]
- Unterrieder, C.; Zhang, C.; Lunglmayr, M.; Priewasser, R.; Marsili, S.; Huemer, M. Battery state-of-charge estimation using approximate least squares. J. Power Sources 2015, 278, 274–286. [Google Scholar] [CrossRef] [Green Version]
- Petzl, M.; Danzer, M.A. Advancements in OCV Measurement and Analysis for Lithium- Ion Batteries. IEEE Trans. Energy Conver. 2013, 28, 675–681. [Google Scholar] [CrossRef]
- Pei, L.; Wang, T.; Lu, R.; Zhu, C. Development of a voltage relaxation model for rapid open-circuit voltage prediction in lithium-ion batteries. J. Power Sources 2014, 253, 412–418. [Google Scholar] [CrossRef]
- Pei, L.; Lu, R.; Zhu, C. Relaxation model of the open-circuit voltage for state-of-charge estimation in lithium-ion batteries. IET Electr. Syst. Transp. 2013, 3, 112–117. [Google Scholar] [CrossRef]
- Waag, W.; Sauer, D.U. Adaptive estimation of the electromotive force of the lithium-ion battery after current interruption for an accurate state-of-charge and capacity determination. Appl. Energy 2013, 111, 416–427. [Google Scholar] [CrossRef]
- Hu, Y.; Yurkovich, S. Battery cell state-of-charge estimation using linear parameter varying system techniques. J. Power Sources 2012, 198, 338–350. [Google Scholar] [CrossRef]
- Wenzl, H. Batteries and fuel cells; Efficiency. In Encyclopedia of Electrochemical Power Sources; Elsevier: Amsterdam, The Netherlands, 2009; pp. 544–551. [Google Scholar]
- Truchot, C.; Dubarry, M.; Liaw, B.Y. State-of-charge estimation and uncertainty for lithium-ion battery strings. Appl. Energy 2014, 119, 2018–2227. [Google Scholar] [CrossRef]
- Tang, X.; Wang, Y.; Chen, Z. A method for state-of-charge estimation of LiFePO4 batteries based on a dual-circuit state observer. J. Power Sources 2015, 296, 23–29. [Google Scholar] [CrossRef]
- Duong, V.-H.; Bastawrous, H.A.; Lim, K.; See, K.W.; Zhang, P.; Dou, S.X. Online state of charge and model parameters estimation of the LiFePO4 battery in electric vehicles using multiple adaptive forgetting factors recursive least-squares. J. Power Sources 2015, 296, 215–224. [Google Scholar] [CrossRef]
- Chiang, Y.-H.; Sean, W.-Y.; Ke, J.-C. Online estimation of internal resistance and open-circuit voltage of lithium-ion batteries in electric vehicles. J. Power Sources 2011, 196, 3921–3932. [Google Scholar] [CrossRef]
- Dai, H.; Xu, T.; Zhu, L.; Wei, X.; Sun, Z. Adaptive model parameter identification for large capacity Li-ion batteries on separated time scales. Appl. Energy 2016, 184, 119–131. [Google Scholar] [CrossRef]
- Wei, Z.; Meng, S.; Xiong, B.; Ji, D.; Tseng, K.J. Enhanced online model identification and state of charge estimation for lithium-ion battery with a FBCRLS based observer. Appl. Energy 2016, 181, 232–241. [Google Scholar] [CrossRef]
- Fuyuan, S.; Zhenglin, L.; Long, X.; Jiang, F.; Hua, W. Research on Estimation of Battery State of Electric Vehicle Battery Management System. In Proceedings of the IEEE 5th Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 12–14 June 2020; pp. 465–469. [Google Scholar]
- Sepasi, S.; Ghorbani, R.; Liaw, B.Y. Improved extended Kalman filter for state of charge estimation of battery pack. J. Power Sources 2014, 255, 368–376. [Google Scholar] [CrossRef]
- Balasingam, B.; Avvari, G.V.; Pattipati, B.; Pattipati, K.R.; Bar-Shalom, Y. A robust approach to battery fuel gauging, part I: Real time model identification. J. Power Sources 2014, 272, 1142–1153. [Google Scholar] [CrossRef]
- Ouyang, M.; Liu, G.; Lu, L.; Li, J.; Han, X. Enhancing the estimation accuracy in low state-of-charge area: A novel onboard battery model through surface state of charge determination. J. Power Sources 2014, 270, 221–237. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Peng, J. Real-time estimation of battery state-of-charge with unscented Kalman filter and RTOS μCOS-II platform. Appl. Energy 2016, 162, 1410–1418. [Google Scholar] [CrossRef]
- Yang, F.; Xing, Y.; Wang, D.; Tsui, K.-L. A comparative study of three model-based algorithms for estimating state-of-charge of lithium-ion batteries under a new combined dynamic loading profile. Appl. Energy 2016, 164, 387–399. [Google Scholar] [CrossRef]
- Sun, F.; Xiong, R.; He, H.; Li, W.; Aussems, J.E.E. Model-based dynamic multi-parameter method for peak power estimation of lithium-ion batteries. Appl. Energy 2012, 96, 378–386. [Google Scholar] [CrossRef]
- Verma, M.K.S.; Basu, S.; Patil, R.S.; Hariharan, K.S.; Adiga, S.P.; Kolake, S.M.; Oh, D.; Song, T.; Sung, Y. On-Board State Estimation in Electrical Vehicles: Achieving Accuracy and Computational Efficiency Through an Electrochemical Model. IEEE Trans. Veh. Technol. 2020, 69, 2563–2575. [Google Scholar] [CrossRef]
- Li, J.; Lai, Q.; Wang, L.; Lyu, C.; Wang, H. A method for SOC estimation based on simplified mechanistic model for LiFePO4 battery. Energy 2016, 114, 1266–1276. [Google Scholar] [CrossRef]
- Li, J.; Wang, L.; Lyu, C.; Pecht, M. State of charge estimation based on a simplified electrochemical model for a single LiCoO2 battery and battery pack. Energy 2017, 133, 572–583. [Google Scholar] [CrossRef]
- Zhang, T.; Guo, N.; Sun, X.; Fan, J.; Yang, N.; Song, J.; Zou, Y. A Systematic Framework for State of Charge, State of Health and State of Power Co-Estimation of Lithium-Ion Battery in Electric Vehicles. Sustainability 2021, 13, 5166. [Google Scholar] [CrossRef]
- Han, X.; Ouyang, M.; Lu, L.; Li, J. Simplification of physics-based electrochemical model for lithium ion battery on electric vehicle. Part II: Pseudo-two-dimensional model simplification and state of charge estimation. J. Power Sources 2015, 278, 814–825. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, H.; Sahinoglu, Z.; Wada, T.; Hara, S. Adaptive Estimation of the State of Charge for Lithium-Ion Batteries: Nonlinear Geometric Observer Approach. IEEE Trans. Contr. Syst. Trans. 2015, 23, 948–962. [Google Scholar] [CrossRef] [Green Version]
- Crocioni, G.; Pau, D.; Delorme, J.-M.; Gruosso, G. Li-Ion Batteries Parameter Estimation with Tiny Neural Networks Embedded on Intelligent IoT Microcontrollers. IEEE Access 2020, 8, 122135–122146. [Google Scholar] [CrossRef]
- Turksoy, A.; Teke, A.; Alkaya, A. A comprehensive overview of the dc-dc converter-based battery charge balancing methods in electric vehicles. Renew. Sustain. Energy Rev. 2020, 133, 1–20. [Google Scholar] [CrossRef]
- Vidal, C.; Hauÿmann, M.; Barroso, D.; Shamsabadi, P.M.; Biswas, A.; Chemali, E.; Ahmed, R.; Emadi, A. Hybrid Energy Storage System State-of-Charge Estimation Using Artificial Neural Network for Micro-Hybrid Applications. In Proceedings of the IEEE Transportation Electrification Conference and Expo (ITEC), Long Beach, CA, USA, 13–15 June 2018; pp. 1075–1081. [Google Scholar]
- Liu, H.; Gegov, A.; Cocea, M. Rule Based Systems for Big Data; Springer: Cham, Switzerland, 2016; Volume 13. [Google Scholar]
- Chemali, E.; Kollmeyer, P.J.; Preindl, M.; Emadi, A. State-of-charge estimation of Li-ion batteries using deep neural networks: A machine learning approach. J. Power Sour. 2018, 400, 242–255. [Google Scholar] [CrossRef]
- Hannan, M.A.; Lipu, M.S.H.; Hussain, A.; Mohamed, A. A review of lithium-ion battery state of charge estimation and management system in electric vehicle applications: Challenges and recommendations. Renew. Sustain. Energy Rev. 2017, 78, 834–854. [Google Scholar] [CrossRef]
- Emadi, A. Advanced Electric Drive Vehicles; CRC Press: New York, NY, USA, 2015. [Google Scholar]
- Hu, Y.; Wang, Z. Study on SOC Estimation of Lithium Battery Based on Improved BP Neural Network. In Proceedings of the 8th International Symposium on Next Generation Electronics (ISNE), Zhengzhou, China, 9–10 October 2019; pp. 1–3. [Google Scholar]
- Hannan, M.A.; Lipu, M.S.H.; Hussain, A.; Saad, M.H.; Ayob, A. Neural Network Approach for Estimating State of Charge of Lithium-Ion Battery Using Backtracking Search Algorithm. IEEE Access 2018, 6, 10069–10079. [Google Scholar] [CrossRef]
- Roscher, M.A.; Bohlen, O.S.; Sauer, D.U. Reliable State Estimation of Multicell Lithium-Ion Battery Systems. IEEE Trans. Energy Conver. 2011, 26, 737–743. [Google Scholar] [CrossRef]
- Wang, S.; Verbrugge, M.; Wang, J.S.; Liu, P. Multi-parameter battery state estimator based on the adaptive and direct solution of the governing differential equations. J. Power Sources 2011, 196, 8735–8741. [Google Scholar] [CrossRef]
- Nejad, S.; Gladwin, D.T. Online Battery State of Power Prediction Using PRBS and Extended Kalman Filter. IEEE Trans. Ind. Electron. 2020, 67, 3747–3755. [Google Scholar] [CrossRef]
- Thenaisie, G.; Park, C.; Lee, S. A Real-Time Entropy Estimation Algorithm for Lithium Batteries Based on a Combination of Kalman Filter and Nonlinear Observer. IEEE Trans. Ind. Electron. 2020, 67, 8034–8043. [Google Scholar] [CrossRef]
- Li, D.; Ouyang, J.; Li, H.; Wan, J. State of charge estimation for LiMn2O4 power battery based on strong tracking sigma point Kalman filter. J. Power Sources 2015, 279, 439–449. [Google Scholar] [CrossRef]
- Partovibakhsh, M.; Liu, G. An Adaptive Unscented Kalman Filtering Approach for Online Estimation of Model Parameters and State-of-Charge of Lithium-Ion Batteries for Autonomous Mobile Robots. IEEE Trans. Contr. Syst. 2015, 23, 357–363. [Google Scholar] [CrossRef]
- Tian, Y.; Xia, B.; Sun, W.; Xu, Z.; Zheng, W. A modified model based state of charge estimation of power lithium-ion batteries using unscented Kalman filter. J. Power Sources 2014, 270, 619–626. [Google Scholar] [CrossRef]
- Li, Y.; Wang, C.; Gong, J. A combination Kalman filter approach for State of Charge estimation of lithium-ion battery considering model uncertainty. Energy 2016, 109, 933–946. [Google Scholar] [CrossRef]
- Zou, Y.; Hu, X.; Ma, H.; Li, S.E. Combined State of Charge and State of Health estimation over lithium-ion battery cell cycle lifespan for electric vehicles. J. Power Sources 2015, 273, 793–803. [Google Scholar] [CrossRef]
- Sepasi, S.; Ghorbani, R.; Liaw, B.Y. A novel on-board state-of-charge estimation method for aged Li-ion batteries based on model adaptive extended Kalman filter. J. Power Sources 2014, 245, 337–344. [Google Scholar] [CrossRef]
- Xiong, R.; Sun, F.; Chen, Z.; He, H. A data-driven multi-scale extended Kalman filtering based parameter and state estimation approach of lithium-ion polymer battery in electric vehicles. Appl. Energy 2014, 113, 463–476. [Google Scholar] [CrossRef]
- Waag, W.; Käbitz, S.; Sauer, D.U. Experimental investigation of the lithium-ion battery impedance characteristic at various conditions and aging states and its influence on the application. Appl. Energy 2013, 2, 885–897. [Google Scholar] [CrossRef]
- Eddahech, A.; Briat, O.; Woirgard, E.; Vinassa, J.M. Remaining useful life prediction of lithium batteries in calendar ageing for automotive applications. Microelectron. Reliab. 2012, 52, 2438–2442. [Google Scholar] [CrossRef]
- Zhu, J.G.; Sun, Z.C.; Wei, X.Z.; Dai, H.F. A new lithium-ion battery internal temperature on-line estimate method based on electrochemical impedance spectroscopy measurement. J. Power Sources 2015, 274, 990–1004. [Google Scholar] [CrossRef]
- Kim, I.-S. Nonlinear state of charge estimator for hybrid electric vehicle battery. IEEE Trans. Power Electron. 2008, 23, 2027–2034. [Google Scholar]
- Zuboff, S. The Age of Surveillance Capitalism: The Fight for a Human Future at the New Frontier of Power, 1st ed.; PublicAffairs: New York, NY, USA, 2019. [Google Scholar]
- Baumhöfer, T.; Brühl, M.; Rothgang, S.; Sauer, D.U. Production caused variation in capacity aging trend and correlation to initial cell performance. J. Power Sources 2014, 247, 332–338. [Google Scholar] [CrossRef]
- Li, S.E.; Wang, B.; Peng, H.; Hu, X. An electrochemistry-based impedance model for lithium-ion batteries. J. Power Sources 2014, 258, 9–18. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs Part 1. Background. J. Power Sources 2004, 134, 252–261. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 2. Modeling and identification. J. Power Sources 2004, 134, 262–276. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 3. State and parameter estimation. J. Power Sources 2004, 134, 277–292. [Google Scholar] [CrossRef]
- Xu, J.; Mi, C.C.; Cao, B.; Deng, J.; Chen, Z.; Li, S. The state of charge estimation of lithium-ion batteries based on a proportional-integral observer. IEEE Trans. Veh. Technol. 2014, 63, 1614–1621. [Google Scholar]
- Zhang, F.; Liu, G.; Fang, L.; Wang, H. Estimation of battery state of charge with H1 observer: Applied to a robot for inspecting power transmission lines. IEEE Trans. Ind. Electron. 2012, 59, 1086–1095. [Google Scholar] [CrossRef]
- Xiong, R.; Cao, J.; Yu, Q.; He, H.; Sun, F. Critical Review on the Battery State of Charge Estimation Methods for Electric Vehicles. IEEE Access 2019, 6, 1832–1843. [Google Scholar] [CrossRef]
- Yatsui, M.W.; Bai, H. Kalman Filter Based State-of-Charge Estimation for Lithium-ion Batteries in Hybrid Electric Vehicles Using Pulse Charging. In Proceedings of the Vehicle Power and Propulsion Conference, Chicago, IL, USA, 6–9 September 2011; pp. 1–5. [Google Scholar]
- Wei, J.; Dong, G.; Chen, Z. On-board adaptive model for state of charge estimation of lithium-ion batteries based on Kalman filter with proportional integral-based error adjustment. J. Power Sources 2017, 365, 308–319. [Google Scholar] [CrossRef]
- He, H.; Liu, Z.; Hua, Y. Adaptive extended Kalman filter based fault detection and isolation for a lithium-ion battery pack. Energy Procedia 2015, 75, 1950–1955. [Google Scholar] [CrossRef] [Green Version]
- Xia, B.; Sun, Z.; Zhang, R.; Lao, Z. A Cubature Particle Filter Algorithm to Estimate the State of the Charge of Lithium-Ion Batteries Based on a Second-Order Equivalent Circuit Model. Energies 2017, 10, 457. [Google Scholar] [CrossRef] [Green Version]
- Ye, M.; Guo, H.; Xiong, R.; Yu, Q. A double-scale and adaptive particle filter-based online parameter and state of charge estimation method for lithium-ion batteries. Energy 2018, 144, 789–799. [Google Scholar] [CrossRef]
- Ting, T.O.; Man, K.L.; Lim, E.G.; Leach, M. Tuning of Kalman Filter Parameters via Genetic Algorithm for State-of-Charge Estimation in Battery Management System. Sci. World J. 2014, 2014, 176052. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, R.; Cao, L.; Bao, S.; Tan, J. A method for connected vehicle trajectory prediction and collision warning algorithm based on V2V communication. Int. J. Crashworth. 2017, 22, 15–25. [Google Scholar] [CrossRef]
- Oyarbide, M.; Arrinda, M.; Sánchez, D.; Macicior, H.; McGahan, P.; Hoedemaekers, E.; Cendoya, I. Capacity and Impedance Estimation by Analysing and Modeling in Real Time Incremental Capacity Curves. Energies 2020, 13, 4855. [Google Scholar] [CrossRef]
- Xiong, B.; Zhao, J.; Wei, Z.; Skyllas-Kazacos, M. Extended Kalman filter method for state of charge estimation of vanadium redox flow battery using thermal-dependent electrical model. J. Power Sources 2014, 262, 50–61. [Google Scholar] [CrossRef]
- Xiong, R.; Gong, X.; Mi, C.C.; Sun, F. A robust state-of-charge estimator for multiple types of lithium-ion batteries using adaptive extended Kalman filter. J. Power Sources 2013, 243, 805–816. [Google Scholar] [CrossRef]
- Xiong, R.; He, H.; Sun, F.; Zhao, K. Evaluation on State of Charge Estimation of Batteries with Adaptive Extended Kalman Filter by Experiment Approach. IEEE Trans. Veh. Technol. 2013, 62, 108–117. [Google Scholar] [CrossRef]
- Zheng, F.; Xing, Y.; Jiang, J.; Sun, B.; Kim, J.; Pecht, M. Influence of different open circuit voltage tests on state of charge online estimation for lithium-ion batteries. Appl. Energy 2016, 182, 513–525. [Google Scholar] [CrossRef]
- Plett, G.L. Sigma-point Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 1: Introduction and state estimation. J. Power Sources 2006, 161, 1356–1368. [Google Scholar] [CrossRef]
- Plett, G.L. Sigma-point Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 2: Simultaneous state and parameter estimation. J. Power Sources 2006, 161, 1369–1384. [Google Scholar] [CrossRef]
- He, Z.; Liu, Y.; Gao, M.; Wang, C. A Joint Model and SOC Estimation Method for Lithium Battery Based on the Sigma Point KF. In Proceedings of the Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 18–20 June 2012; pp. 1–5. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Xia, B.; Cui, D.; Sun, Z.; Lao, Z.; Zhang, R.; Wang, W.; Sun, W.; Lai, Y.; Wang, M. State of charge estimation of lithium-ion batteries using optimized Levenberg-Marquardt wavelet neural network. Energy 2018, 153, 694–705. [Google Scholar] [CrossRef]
- Dang, X.; Yan, L.; Xu, K.; Wu, X.; Jiang, H.; Sun, H. Open-Circuit Voltage-Based State of Charge Estimation of Lithium-ion Battery Using Dual Neural Network Fusion Battery Model. Electrochim. Acta 2016, 188, 356–366. [Google Scholar] [CrossRef]
- Tong, S.; Lacap, J.H.; Park, J.W. Battery state of charge estimation using a load-classifying neural network. J. Energy Storage 2016, 7, 236–243. [Google Scholar] [CrossRef]
- Chaoui, H.; Ibe-Ekeocha, C.C.; Gualous, H. Aging prediction and state of charge estimation of a LiFePO4 battery using input time-delayed neural networks. Electr. Power Syst. Res. 2017, 146, 189–197. [Google Scholar] [CrossRef]
- Hu, J.N.; Hu, J.J.; Lin, H.B.; Li, X.P.; Jiang, C.L.; Qiu, X.H.; Li, W.S. State-of-charge estimation for battery management system using optimized support vector machine for regression. J. Power Sources 2014, 269, 682–693. [Google Scholar] [CrossRef]
- Sheng, H.; Xiao, J. Electric vehicle state of charge estimation: Nonlinear correlation and fuzzy support vector machine. J. Power Sources 2015, 281, 131–137. [Google Scholar] [CrossRef]
- Blaifi, S.; Moulahoum, S.; Colak, I.; Merrouche, W. An enhanced dynamic model of battery using genetic algorithm suitable for photovoltaic applications. Appl. Energy 2016, 169, 888–898. [Google Scholar] [CrossRef]
- Xu, J.; Cao, B.; Chen, Z.; Zou, Z. An online state of charge estimation method with reduced prior battery testing information. Int. J. Electr. Power Energy Syst. 2014, 63, 178–184. [Google Scholar] [CrossRef]
- Gao, Z.; Cing, C.S.; Woo, W.L.; Jia, J.; Toh, W.D. Genetic Algorithm Based Back-Propagation Neural Network Approach for Fault Diagnosis in Lithium-ion Battery System. In Proceedings of the International Conference on Power Electronics Systems and Applications (PESA), Hong Kong, China, 15–17 December 2015; pp. 1–6. [Google Scholar]
- Awadallah, M.A.; Venkatesh, B. Accuracy improvement of SOC estimation in lithium-ion batteries. J. Energy Storage 2016, 6, 95–104. [Google Scholar] [CrossRef]
- Dai, H.; Guo, P.; Wei, X.; Sun, Z.; Wang, J. ANFIS (Adaptive Neuro-Fuzzy Inference System) based online SOC (State of Charge) correction considering cell divergence for the EV (Electric Vehicle) traction batteries. Energy 2015, 80, 350–360. [Google Scholar] [CrossRef]
- Wang, Q.-K.; He, Y.-J.; Shen, J.-N.; Hu, X.; Ma, Z.-F. State of Charge Dependent Polynomial Equivalent Circuit Modeling for Electrochemical Impedance Spectroscopy of Lithium-Ion Batteries. IEEE Trans. Power Electron. 2018, 33, 8449–8460. [Google Scholar] [CrossRef]
- Yu, Z.; Xiao, L.; Li, H.; Zhu, X.; Huai, R. Model Parameter Identification for Lithium Batteries Using the Coevolutionary Particle Swarm Optimization Method. IEEE Trans. Ind. Electron. 2017, 64, 5690–5700. [Google Scholar] [CrossRef]
- Wang, Z.; Ma, J.; Zhang, L. State-of-Health Estimation for Lithium-Ion Batteries Based on the Multi-Island Genetic Algorithm and the Gaussian Process Regression. IEEE Access 2017, 5, 21286–21295. [Google Scholar] [CrossRef]
- Rahimi-Eichi, H.; Baronti, F.; Chow, M.-Y. Online Adaptive Parameter Identification and State-of-Charge Coestimation for Lithium-Polymer Battery Cells. IEEE Trans. Ind. Electron. 2014, 61, 2053–2061. [Google Scholar] [CrossRef]
- Fan, G.; Li, X.; Canova, M. A Reduced-Order Electrochemical Model of Li-Ion Batteries for Control and Estimation Applications. IEEE Trans. Veh. Technol. 2018, 67, 76–91. [Google Scholar] [CrossRef]
- Li, Y.; Liu, K.; Foley, A.M.; Zülke, A.; Berecibar, M.; Nanini-Maury, E.; Mierlo, J.V.; Hoster, H.E. Data-driven health estimation and lifetime prediction of lithium-ion batteries: A review. Renew. Sustain. Energy Rev. 2019, 113, 109254. [Google Scholar] [CrossRef]
- Tan, X.; Tan, Y.; Zhan, D.; Yu, Z.; Fan, Y.; Qiu, J.; Li, J. Real-Time State-of-Health Estimation of Lithium-Ion Batteries Based on the Equivalent Internal Resistance. IEEE Access 2020, 8, 56811–56822. [Google Scholar] [CrossRef]
- Stroe, D.; Schaltz, E. Lithium-Ion Battery State-of-Health Estimation Using the Incremental Capacity Analysis Technique. IEEE Trans. Ind. Appl. 2020, 56, 678–685. [Google Scholar] [CrossRef]
- Sarrafan, K.; Muttaqi, K.; Sutanto, D. Real-time estimation of model parameters and state-of-charge of lithium-ion batteries in electric vehicles using recursive least-square with forgetting factor. In Proceedings of the IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Chennai, China, 18–21 December 2018; pp. 1–6. [Google Scholar]
- Kim, J.; Cho, B.H. State-of-Charge Estimation and State-of-Health Prediction of a Li-Ion Degraded Battery Based on an EKF Combined with a Per-Unit System. IEEE Trans. Veh. Technol. 2011, 60, 4249–4260. [Google Scholar] [CrossRef]
- Kim, I. A Technique for Estimating the State of Health of Lithium Batteries Through a Dual-Sliding-Mode Observer. IEEE Trans. Power Electron. 2010, 25, 1013–1022. [Google Scholar]
- Kim, K.; Lee, S.; Cho, B. Discrimination of Battery Characteristics Using Discharging/Charging Voltage Pattern Recognition. In Proceedings of the IEEE Energy Conversion Congress and Exposition, San Jose, CA, USA, 24–27 September 2009; pp. 1799–1805. [Google Scholar]
- Lievre, A.; Sari, A.; Venet, P.; Hijazi, A.; Ouattara-Brigaudet, M.; Pelissier, S. Practical Online Estimation of Lithium-Ion Battery Apparent Series Resistance for Mild Hybrid Vehicles. IEEE Trans. Veh. Technol. 2016, 65, 4505–4511. [Google Scholar] [CrossRef] [Green Version]
- Zhao, S.; Wu, F.; Yang, L.; Gao, L.; Burke, A.F. A measurement method for determination of dc internal resistance of batteries and supercapacitors. Electrochem. Commun. 2010, 12, 242–245. [Google Scholar] [CrossRef]
- Zenati, A.; Desprez, P.; Razik, H.; Rael, S. A Methodology to Assess the State of Health of Lithium-ion Batteries Based on the Battery’s Parameters and a Fuzzy Logic System. In Proceedings of the IEEE International Electric Vehicle Conference, Greenville, SC, USA, 4–8 March 2012; pp. 1–6. [Google Scholar]
- Chen, Y.; Liu, X.; Yang, G. An Internal Resistance Estimation Method of Lithium-ion Batteries with Constant Current Tests Considering Thermal Effect. In Proceedings of the 43rd Annual Conference of the IEEE Industrial Electronics Society (IECON), Beijing, China, 29 October–1 November 2017; pp. 7629–7635. [Google Scholar]
- Gou, B.; Xu, Y.; Feng, X. State-of-Health Estimation and Remaining-Useful-Life Prediction for Lithium-Ion Battery Using a Hybrid Data-Driven Method. IEEE Trans. Veh. Technol. 2020, 69, 10854–10867. [Google Scholar] [CrossRef]
- Islam, S.; Park, S. Precise Online Electrochemical Impedance Spectroscopy Strategies for Li-Ion Batteries. IEEE Trans. Ind. Appl. 2020, 56, 1161–1169. [Google Scholar] [CrossRef]
- Legrand, N.; Raël, S.; Knosp, B.; Hinaje, M.; Desprez, P.; Lapicque, F. Including double-layer capacitance in lithium-ion battery mathematical models. J. Power Sources 2014, 251, 370–378. [Google Scholar] [CrossRef]
- Gamry Instruments. Introduction to Electrochemical Impedance Spectroscopy. 2015. Available online: https://www.gamry.com/assets/Uploads/Basics-of-Electrochemical-Impedance-Spectroscopy.pdf (accessed on 31 May 2021).
- Hossain, M.K.; Islam, S.M.R.; Park, S. Performance analysis of filter sensing board for measuring the battery online impedance. In Proceedings of the Asian Conference Energy, Power and Transportation Electrification (ACEPT), Singapore, 25–27 October 2016; pp. 1–6. [Google Scholar]
- Kurzweil, P.; Scheuerpflug, W. State-of-Charge Monitoring and Battery Diagnosis of Different Lithium Ion Chemistries Using Impedance Spectroscopy. Batteries 2021, 7, 17. [Google Scholar] [CrossRef]
- Qahouq, J.A.A. Online Battery Impedance Spectrum Measurement Method. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 20–24 March 2016; pp. 3611–3615. [Google Scholar]
- Din, E.; Schaef, C.; Moffat, K.; Stauth, J.T. A Scalable Active Battery Management System with Embedded Real-Time Electrochemical Impedance Spectroscopy. IEEE Trans. Power Electron. 2017, 32, 5688–5698. [Google Scholar] [CrossRef]
- Xia, Z.; Qahouq, J.A.A. An Online Battery Impedance Spectrum Measurement Method with Increased Frequency Resolution. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; pp. 1930–1933. [Google Scholar]
- Li, W.; Huang, Q.; Yang, C.; Chen, J.; Tang, Z.; Zhang, F.; Li, A.; Zhang, L.; Zhang, J. A fast measurement of Warburg-like impedance spectra with Morlet wavelet transform for electrochemical energy devices. Electrochim. Acta 2019, 322, 134760. [Google Scholar] [CrossRef]
- Okazaki, S.; Higuchi, S.; Kubota, N.; Takahashi, S. Predicted and observed initial short circuit current for lead-acid batteries. J. Appl. Electrochem. 1986, 16, 631–635. [Google Scholar] [CrossRef]
- Mao, L.; Jackson, L.; Davies, B. Effectiveness of a Novel Sensor Selection Algorithm in PEM Fuel Cell On-Line Diagnosis. IEEE Trans. Ind. Electron. 2018, 65, 7301–7311. [Google Scholar] [CrossRef] [Green Version]
- Yang, R.; Xiong, R.; He, H.; Chen, Z. A fractional-order model-based battery external short circuit fault diagnosis approach for all-climate electric vehicles application. J. Cleaner Prod. 2018, 187, 950–959. [Google Scholar] [CrossRef]
- Chen, Z.; Xiong, R.; Lu, J.; Li, X. Temperature rise prediction of lithium-ion battery suffering external short circuit for all-climate electric vehicles application. Appl. Energy 2016, 213, 375–383. [Google Scholar] [CrossRef]
- Spotnitz, R.; Franklin, J. Abuse behavior of high-power, lithium-ion cells. J. Power Sources 2003, 113, 81–100. [Google Scholar] [CrossRef]
- Zhang, D.; Dey, S.; Perez, H.E.; Moura, S.J. Real-Time Capacity Estimation of Lithium-Ion Batteries Utilizing Thermal Dynamics. IEEE Trans. Control. Syst. Technol. 2020, 28, 992–1000. [Google Scholar] [CrossRef]
- Hunt, I.A.; Patel, Y.; Szczygielski, M.; Kabacik, L.; Offer, G.J. Lithium sulfur battery nail penetration test under load. J. Energy Storage 2015, 2, 25–29. [Google Scholar] [CrossRef]
- Leising, R.A.; Palazzo, M.J.; Takeuchi, E.S.; Takeuchi, K.J. Abuse Testing of Lithium-Ion Batteries: Characterization of the Overcharge Reaction of LiCoO2/Graphite Cells. J. Electrochem. Soc. 2001, 148, 838–844. [Google Scholar] [CrossRef]
- Mevawalla, A.; Panchal, S.; Tran, M.-K.; Fowler, M.; Fraser, R. Mathematical Heat Transfer Modeling and Experimental Validation of Lithium-Ion Battery Considering: Tab and Surface Temperature, Separator, Electrolyte Resistance, Anode-Cathode Irreversible and Reversible Heat. Batteries 2020, 6, 61. [Google Scholar] [CrossRef]
- El Mejdoubi, A.; Oukaour, A.; Chaoui, H.; Gualous, H.; Sabor, J.; Slamani, Y. State-of-Charge and State-of-Health Lithium-Ion Batteries’ Diagnosis According to Surface Temperature Variation. IEEE Trans. Ind. Electron. 2016, 63, 2391–2402. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Z.; Zhang, C. On-line remaining energy prediction: A case study in embedded battery management system. Appl. Energy 2017, 194, 688–695. [Google Scholar] [CrossRef]
- Wang, Q.-K.; He, Y.-J.; Shen, J.-N.; Ma, Z.-F.; Zhong, G.-B. A unified modeling framework for lithium-ion batteries: An artificial neural network based thermal coupled equivalent circuit model approach. Energy 2017, 138, 118–132. [Google Scholar] [CrossRef]
- Altaf, F.; Egardt, B.; Mårdh, L.J. Load Management of Modular Battery Using Model Predictive Control: Thermal and State-of-Charge Balancing. IEEE Trans. Control Syst. Technol. 2017, 25, 47–62. [Google Scholar] [CrossRef] [Green Version]
- Farag, M.; Sweity, H.; Fleckenstein, M.; Habibi, S. Combined electrochemical, heat generation, and thermal model for large prismatic lithium-ion batteries in real-time applications. J. Power Sources 2017, 360, 618–633. [Google Scholar] [CrossRef]
- You, G.-W.; Park, S.; Oh, D. Real-time state-of-health estimation for electric vehicle batteries: A data-driven approach. Appl. Energy 2016, 176, 92–103. [Google Scholar] [CrossRef]
- Chemali, E.; Kollmeyer, P.J.; Preindl, M.; Ahmed, R.; Emadi, A. Long Short-Term Memory Networks for Accurate State-of-Charge Estimation of Li-ion Batteries. IEEE Trans. Ind. Electron. 2018, 65, 6730–6739. [Google Scholar] [CrossRef]
- Salaken, S.M.; Khosravi, A.; Nguyen, T.; Nahavandi, S. Seeded transfer learning for regression problems with deep learning. Expert Syst. Appl. 2019, 115, 565–577. [Google Scholar] [CrossRef]
- He, Y.; Tian, Y.; Liu, D. Multi-view transfer learning with privileged learning framework. Neurocomputing 2019, 335, 131–142. [Google Scholar] [CrossRef]
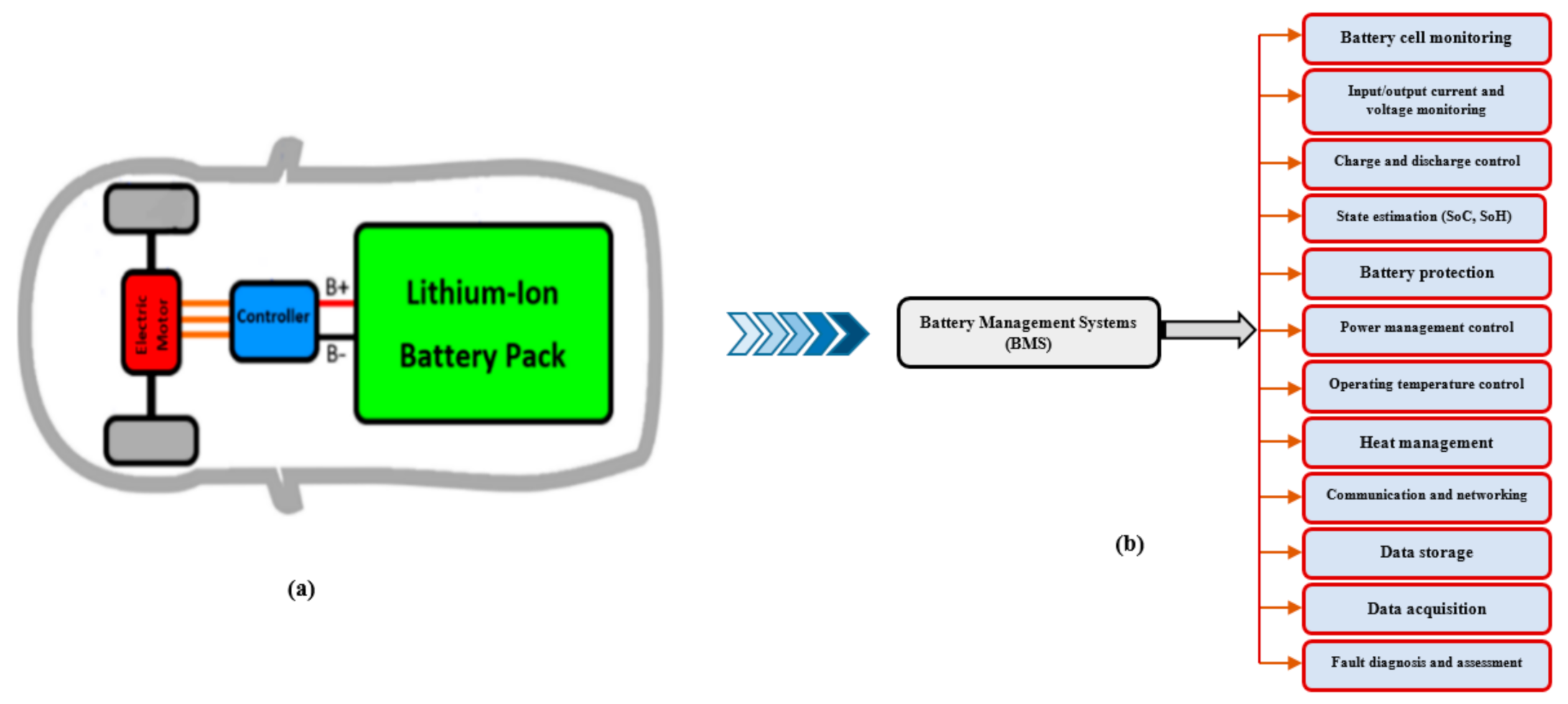


| Lithium-Ion Battery | |
|---|---|
| Advantages | Disadvantages |
| Has a high energy density | Involves the risk of bursting |
| The rate of charge loss is low | Costly, compared to other batteries |
| Has a greater number of charge and discharge cycles | Complete discharge damages the battery |
| Need not be discharged completely | Extremely sensitive to high temperature (degrades very quickly if exposed to heat) |
| Operates at high voltage | Short lifespan |
| Battery Name | Abbrev. | Year | Nominal Voltage (V) | Specific Energy (Wh/Kg) | Charge (C) | Discharge (C) | Lifespan | Thermal Runaway (°C) |
|---|---|---|---|---|---|---|---|---|
| Lithium cobalt oxide | LCO | Since 1991 | 3.7–3.9 | 150–200 | 0.7–1 | 1 | 500–1000 | 150 |
| Lithium nickel oxide | LNO | Since 1996 | 3.6–3.7 | 150–200 | 0.7–1 | 1 | >300 | 150 |
| Lithium manganese oxide | LMO | Since 1996 | 3.7–4.0 | 100–150 | 0.7–1 | 1 | 300–700 | 250 |
| Lithium nickel manganese cobalt oxide | NMC | Since 2008 | 3.8–4.0 | 150–220 | 0.7–1 | 1 | 1000–2000 | 210 |
| Lithium iron phosphate | LFP | Since 1993 | 3.2–3.3 | 90–130 | 1 | 1 | 1000–2000 | 270 |
| Lithium nickel cobalt aluminum oxide | NCA | Since 1999 | 3.6–3.65 | 200–260 | 0.7 | 1 | 500 | 150 |
| Lithium titanate | LTO | Since 2008 | 2.3–2.5 | 70–85 | 1 | 10 | 3000–7000 | . |
| Equivalent Model | Schematic Diagram | Characteristics | |
| The Rint model | 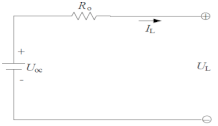 | Ro and open-circuit voltage Uoc are functions of SoC, SoH, and temperature. | |
| IL: load current | |||
| UL: is the terminal voltage. | |||
| … | |||
| (1) | |||
| The RC model |  | Cc: a small capacitance represents the surface effects of a battery, and it is named surface capacitor. | |
| Cb: a very large capacitance represents bulk capacitor. | |||
| Rt, Re, Rc: are terminal resistor, end resistor and capacitor resistor. Ub and Uc are the voltages across Cb and Cc, respectively. | |||
| (2) | |||
| The Thevenin model | 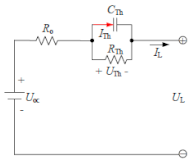 | Uoc: Open-circuit voltage, | |
| Ro: Internal resistances and equivalent capacitances. | |||
| RTh: The polarization resistance. | |||
| CTh: The equivalent capacitance used to describe the transient response during charging and discharging. | |||
| UTh is the voltages across CTh. | |||
| ITh is the outflow current of CTh. | |||
| (3) | |||
| The PNGV model | 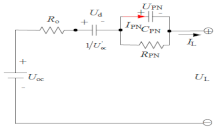 | Adding a capacitor 1/Uoc in series, based on the Thevenin model, to describe the changing of open circuit voltage generated in the time accumulation of load current. | |
| (4) | |||
| The DP model | 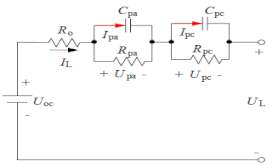 | Uoc: Open-circuit voltage. | |
| Ro: Internal resistances, such as the ohmic resistance. | |||
| Rpa: The polarization resistances, and electrochemical polarization. | |||
| Rpc: The effective resistance characterizing concentration polarization. | |||
| Cpa and Cpc: Used to characterize the transient response during transfer of power to/from the battery, and to describe the electrochemical polarization and the concentration polarization separately. | |||
| (5) | |||
| Authors | Description | Applications | Advantages | Disadvantages | |
|---|---|---|---|---|---|
| OCV based estimation | [83,84,85,86] | The SoC-OCV curve is reliable and the OCV curve is very accurate. While this SoC-OCV curve is relatively stable for LiB, it modifies with the life cycle. | Lead Acid, Lithium, Za/Br. |
|
|
| [87,88,89] | A reliable SoC-OCV curve and a precise OCV. But it changes also with life cycle and temperature. | ||||
| [90,91] | The estimate, largely dependent on the OCV, is only used for a sufficiently long rest time in a particular operating condition, i.e., 3 h can be an appropriate rest time for most working conditions. | ||||
| [92,93] | Some empiric models may be used to estimate the OCV or may be combined with a theoretical analysis. | ||||
| [94,95] | Models via an OCV estimate are not very well suited to SoH or changes in temperature. | ||||
| [96] | An adaptive method for estimating OCVs for online applications. | ||||
| [97] | When the LiFePO4 cathode is used in the LiB. The SoC estimate based on the OCV within the SoC range of the flat SoC-OCV curve is not accurate. | ||||
| Ampere-hour counting estimation (AHC) | [98,99] | AHC evaluation has very limited computation costs and hence it is frequently used for online SoC estimation. | All battery systems, most applications. |
|
|
| [100] | For the AHC methods, the precision may be fair, such as daily adjustment of the initial SoC and capacity and modifying the current drifting sensor. | ||||
| Equivalent Circuit Model (ECM) based estimation | [101,102,103,104] | Estimate SoC directly by identifying the parameters of the ECM. | All battery systems, most applications. |
|
|
| [105,106] | The use of an adaptive model will improve the precision of the system, but also increases the sophistication of the model. | ||||
| [107] | The identification in real time of the parameters needs an additional central processing unit (CPU) load and even more storage space. | ||||
| [108,109,110,111] | Precision of conventional ECM voltage in the low range of SoCs. | ||||
| Electrochemical model based estimation | [112] | Reduced-order on-board thermal electrochemical model (ROTM). On-board ROTM estimates the voltage and SoC of the single cells and the pack level, using a simpler, high-speed module system with greater accuracy than the commonly used ECM. | All battery systems, most applications. |
|
|
| [113,114] | The calculation of SoC can be made directly by identifying the amount of LiB in the negative or positive electrodes of the electrochemical model. | ||||
| [115,116,117] | A new SOC is updated by using a predefined SoC to obtain model voltage and used an electrochemical model and to evaluate it to the measured voltage. | ||||
| [86] | Partial differential equations, for considering secondary reactions, must also be integrated to the electrochemical model, which will again improve the model complexity. | ||||
| Machine learning based estimation | [118,119] | Battery state estimates using data learning techniques have been associated with new advancements in artificial intelligence (AI) such as computer vision and autonomous vehicles. E.g. the Adaptive Neuro-Fuzzy Inferential Method (ANFIM). | All battery systems, most applications. |
|
|
| [120,121] | A vast quantity of data is recorded and processed in a partly or entirely automatic manner in order to meet the nature and usage of the battery. This volume of data has made it possible to boost BMS output through Big Data, the Internet of Things (IoT), data storage, and the ML methodologies being analyzed. | ||||
| [122] | Based on ML methodologies, SoC and SoH are estimated. The main computational load required by these techniques happens mostly during offline training process, which enables the implementation of typical BMS hardware. | ||||
| [82,123,124] | Full review of the use of machine learning techniques for estimating SoC, SoH, SoP and other battery states. | ||||
| [122] | It is shown that FNN is suitable for estimating the SoC battery at various temperatures, such as low temperatures like 20 °C. | ||||
| [125] | The internal resistance data obtained from the laboratory tester was used, as well as the voltage, current and temperature of the battery, to form and test the SoC estimation by the FNN. | ||||
| [126] | Introduction of a procedure to methodically modify the FNN structure using offline optimization technique to identify the optimum FNN structure. SoC is estimated using the general structure selected for the calculation of the initial cost (mean square error) to be used in the next step. | ||||
| Modern control theory based estimation | [32,126,127,128] | With an acceptable input gain by comparing the voltage model with the observed, the actual SoC could be changed. The algorithm calculates the gain. Luenberger is one of the easiest observers. | All battery systems, Photovoltaic, Hybrid Electric Vehicles. |
|
|
| [129,130] | KF family algorithms are a better choice for more appropriate feedback gain. | ||||
| [10,130,131,132] | EKF is a commonly used and studied SoC estimation algorithm. The main theory of the EKF algorithm is to identify the correct efficiency of the filter by assessing the model and quantifying the noise. However, the literature suggests that EKF may lack robustness and cannot guarantee an optimal feedback gain due to the linearization of non-linear LiB systems. | ||||
| [95,132,133,134] | Unscented Kalman Filter (UKF); the calculation complexity is increased. | ||||
| [135,136,137] | The precision of the SoC estimation, based on modern control systems, is directly associated to the precision of the battery voltage model. Battery voltage model parameters change with aging and LiB temperature. For the KF family, and due to changes in model parameters over the life of the battery, joint or dual KF family algorithms may be used. | ||||
| [136] | Used an update method for an on-board parameter, but not based on a joint or double KF method. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laadjal, K.; Cardoso, A.J.M. Estimation of Lithium-Ion Batteries State-Condition in Electric Vehicle Applications: Issues and State of the Art. Electronics 2021, 10, 1588. https://doi.org/10.3390/electronics10131588
Laadjal K, Cardoso AJM. Estimation of Lithium-Ion Batteries State-Condition in Electric Vehicle Applications: Issues and State of the Art. Electronics. 2021; 10(13):1588. https://doi.org/10.3390/electronics10131588
Chicago/Turabian StyleLaadjal, Khaled, and Antonio J. Marques Cardoso. 2021. "Estimation of Lithium-Ion Batteries State-Condition in Electric Vehicle Applications: Issues and State of the Art" Electronics 10, no. 13: 1588. https://doi.org/10.3390/electronics10131588
APA StyleLaadjal, K., & Cardoso, A. J. M. (2021). Estimation of Lithium-Ion Batteries State-Condition in Electric Vehicle Applications: Issues and State of the Art. Electronics, 10(13), 1588. https://doi.org/10.3390/electronics10131588








