Optimal Distribution Coefficients of Energy Resources in Frequency Stability of Hybrid Microgrids Connected to the Power System
Abstract
:1. Introduction
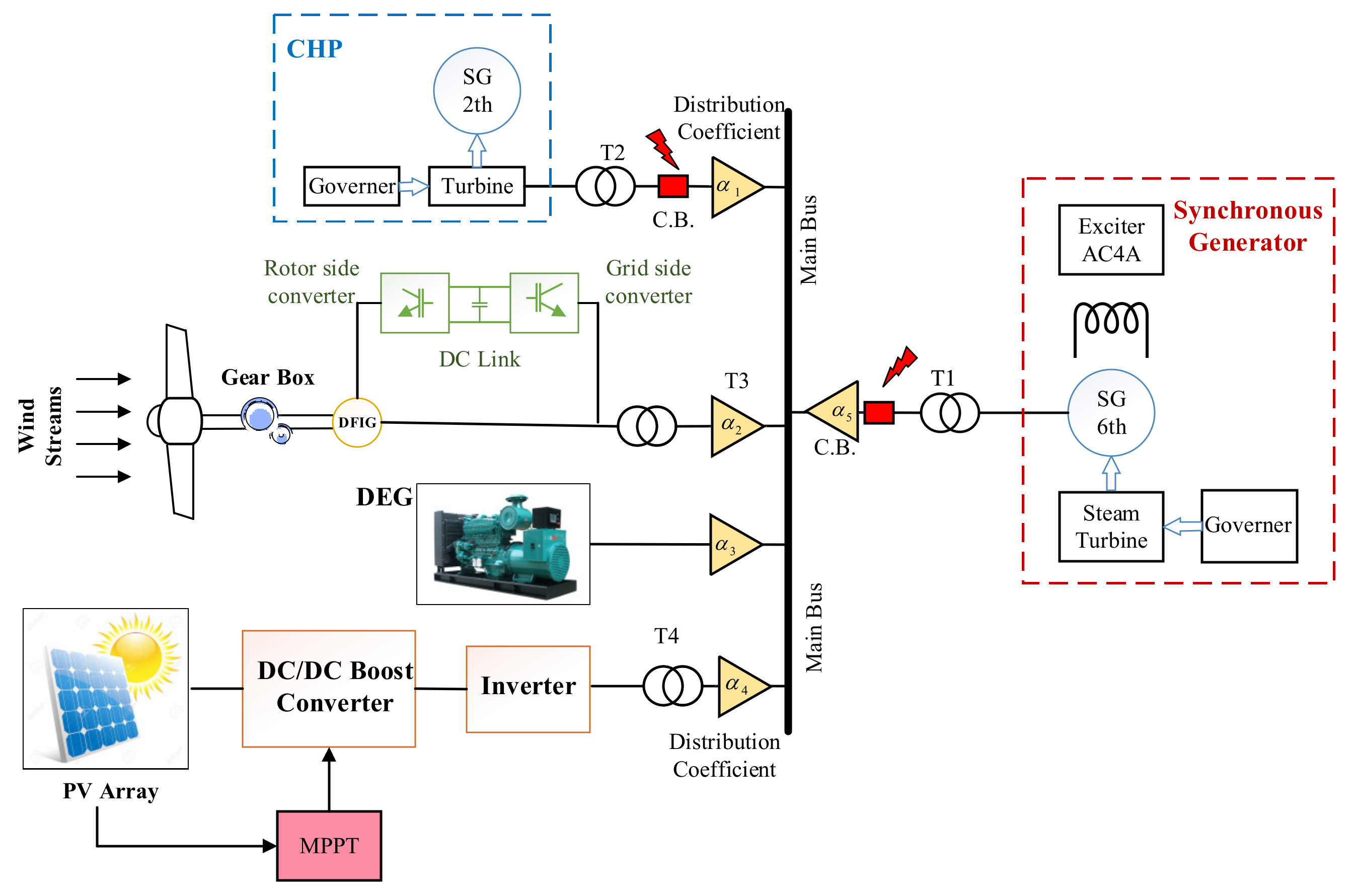
2. System Modeling and Configuration
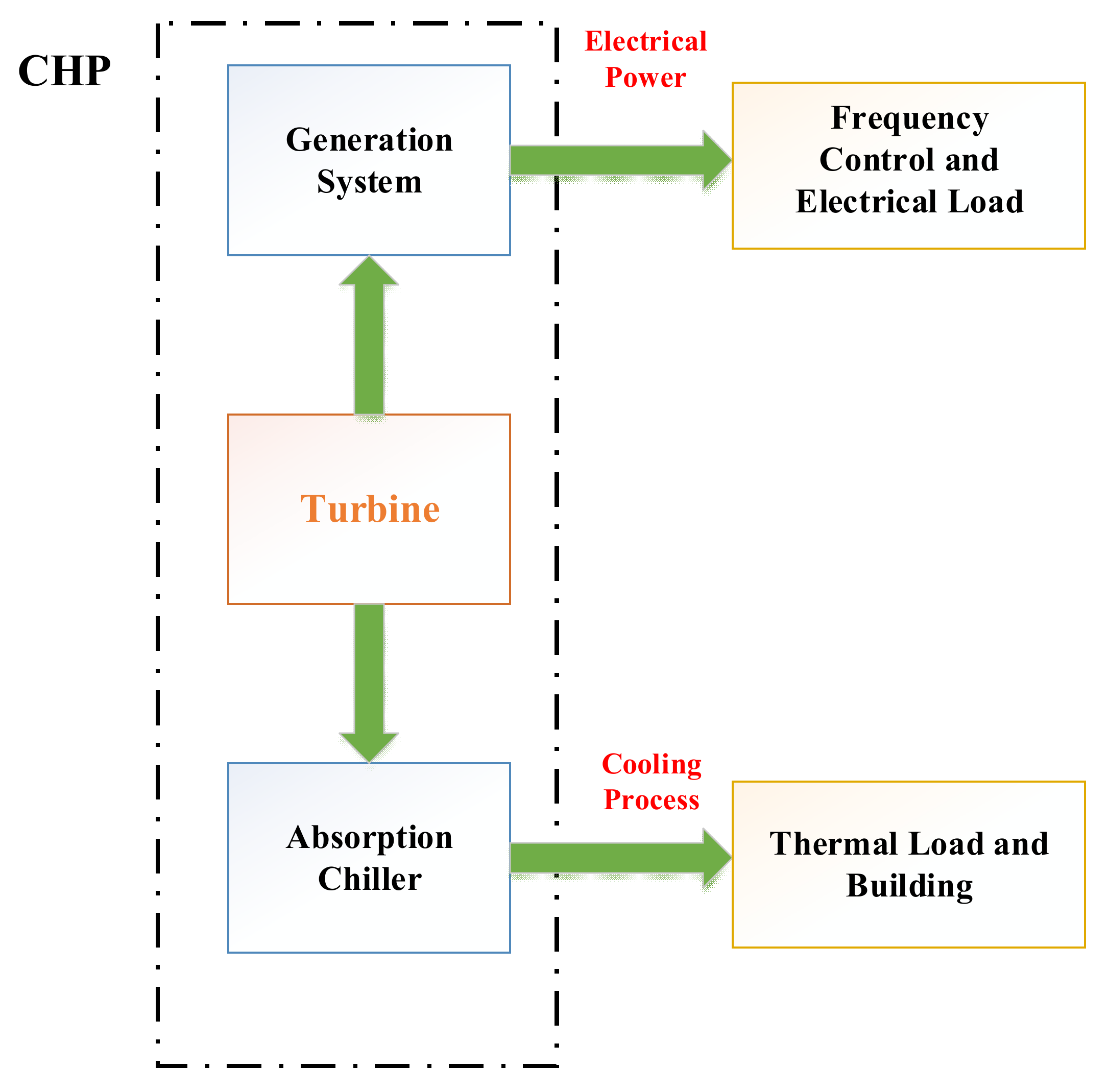
2.1. Combined Heat and Power (CHP)
2.2. Synchronous Generator Model
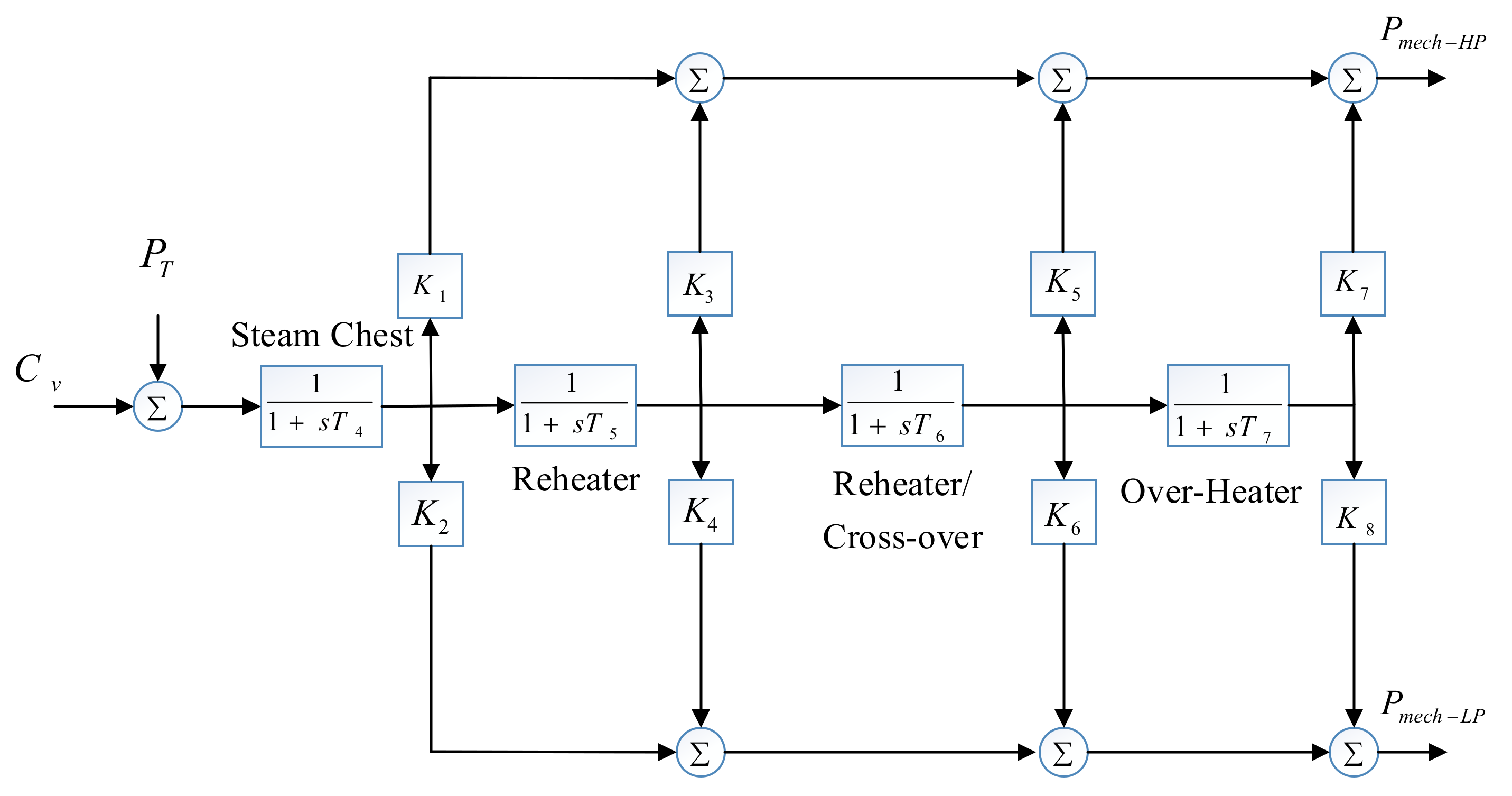
2.2.1. Steam Turbine Model
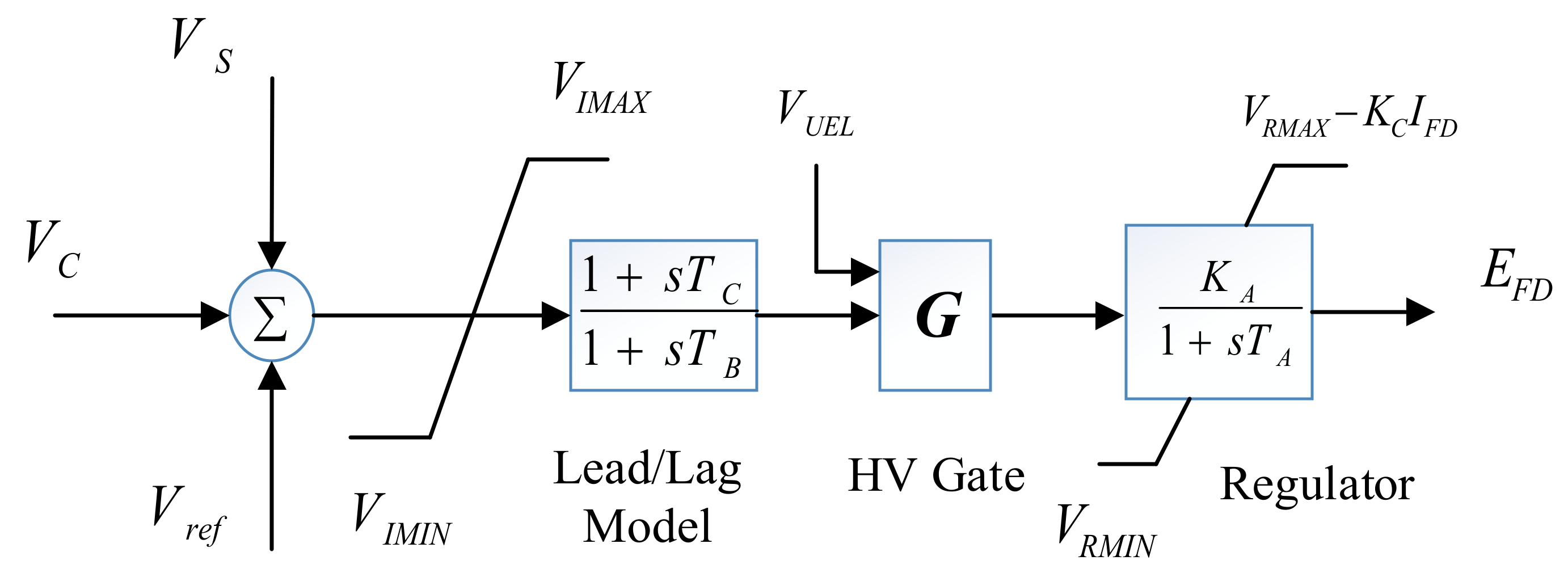
2.2.2. Excitation System
2.3. Wind Turbine Generator
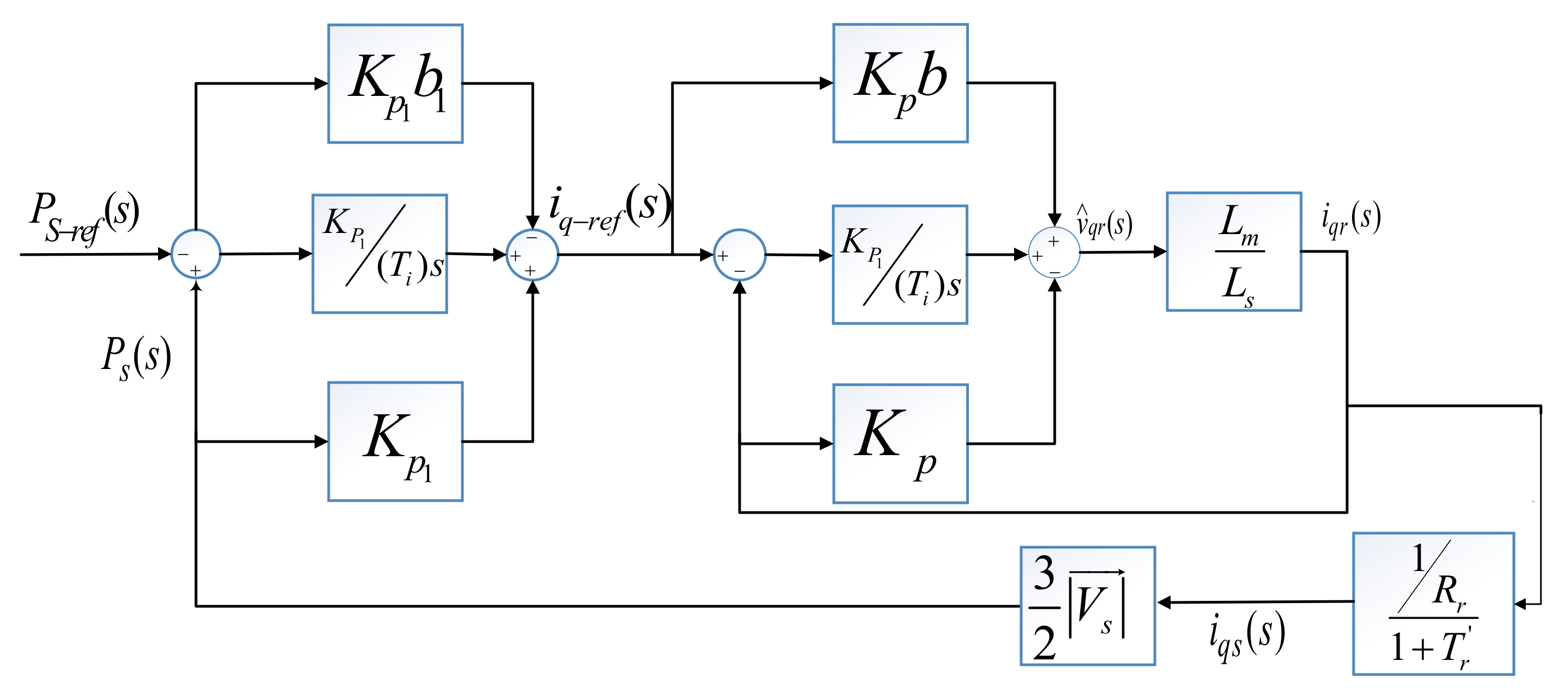
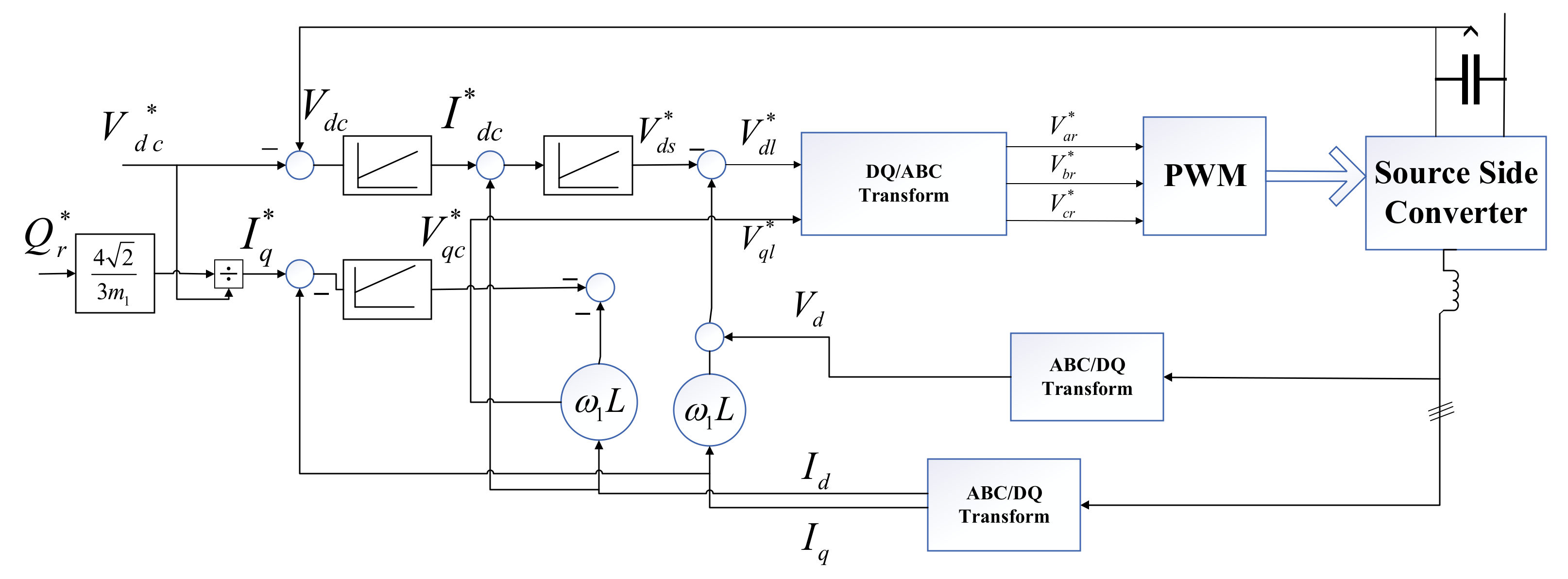
2.3.1. Rotor Side Converter Vector Control
2.3.2. Grid Side Converter Vector Control
3. Optimum Contribution of DERs in Frequency Improvement Scheme
3.1. Multi-Objective Function
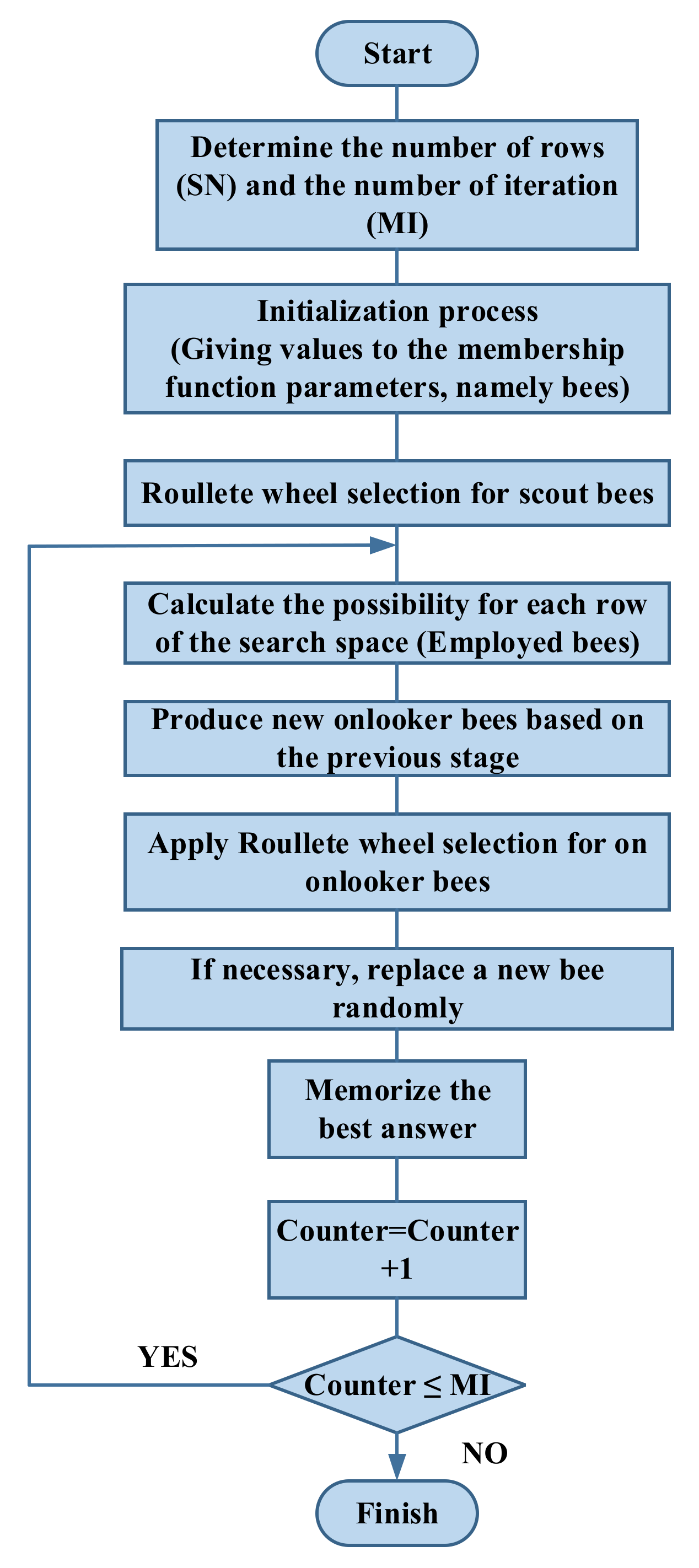
3.2. Artificial Bee Colony (ABC) Algorithm
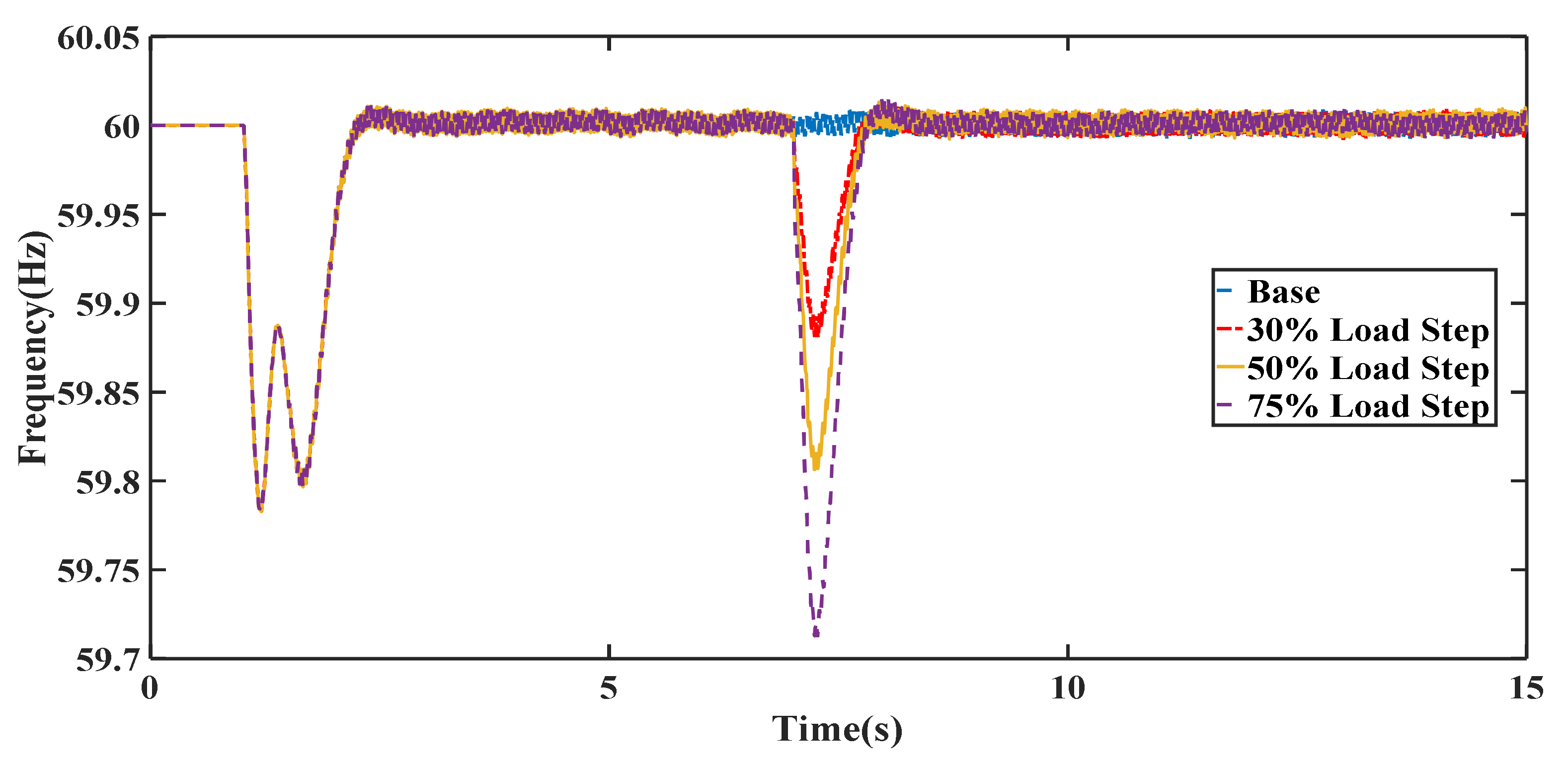
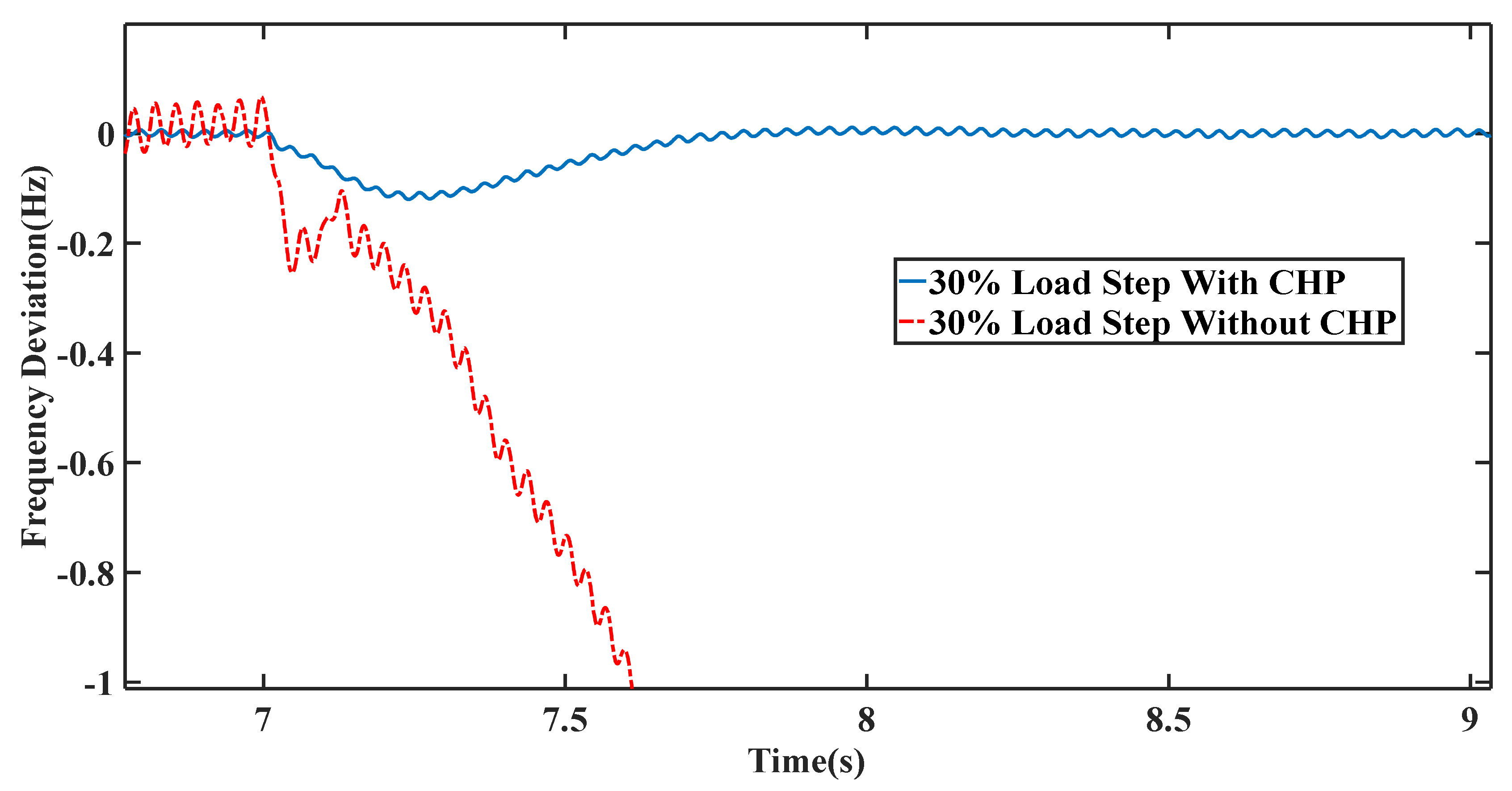
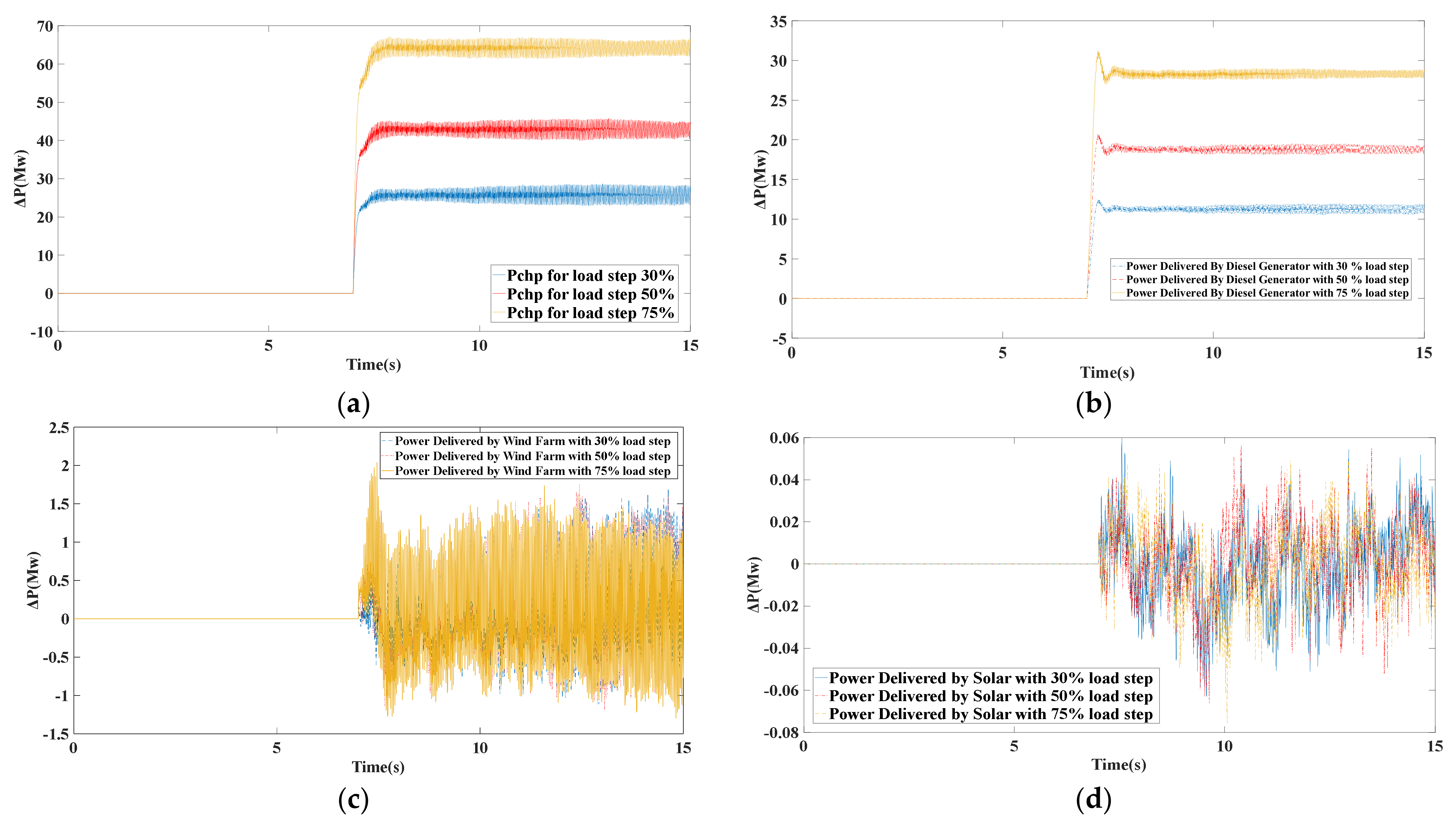
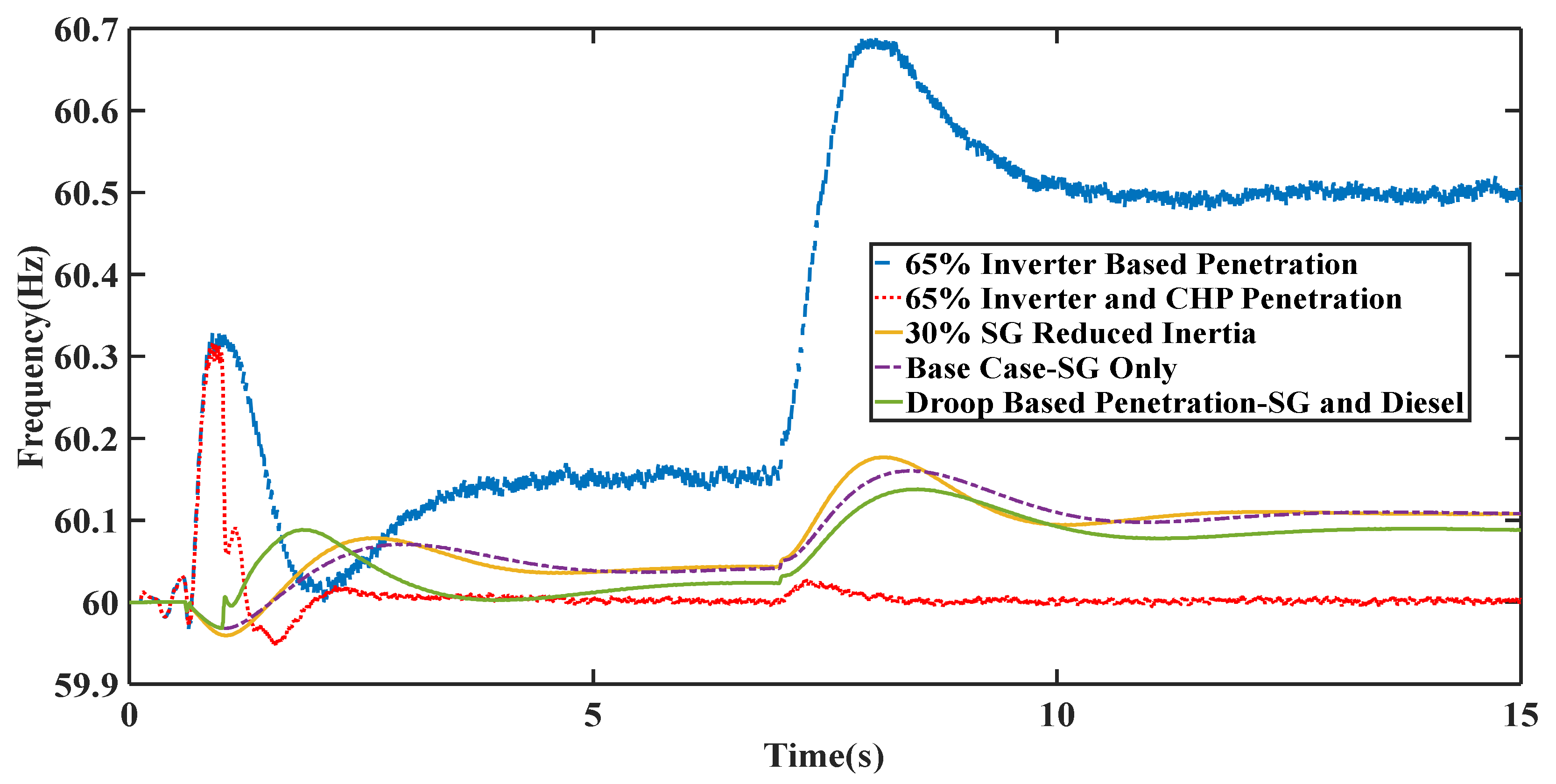
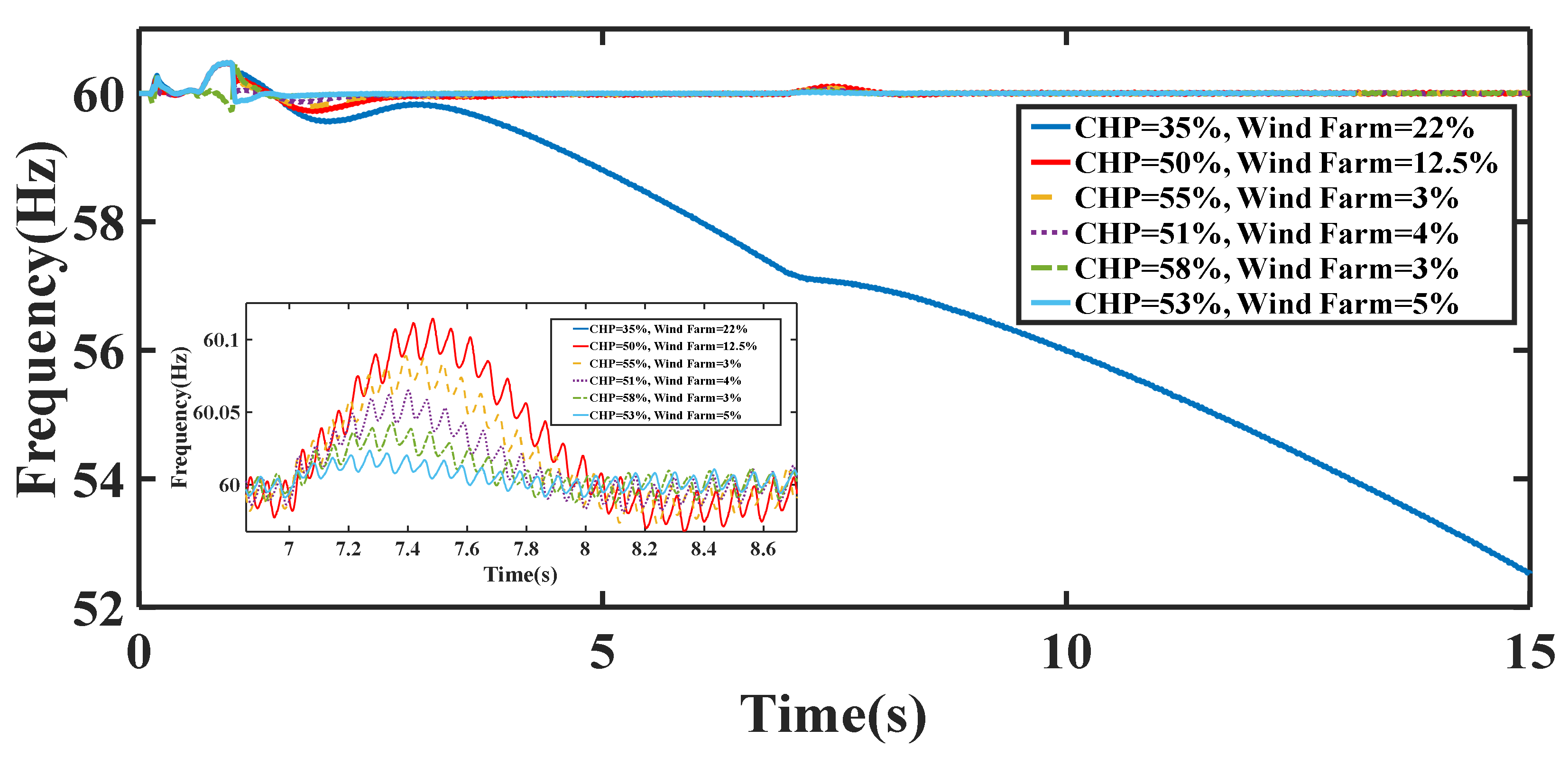
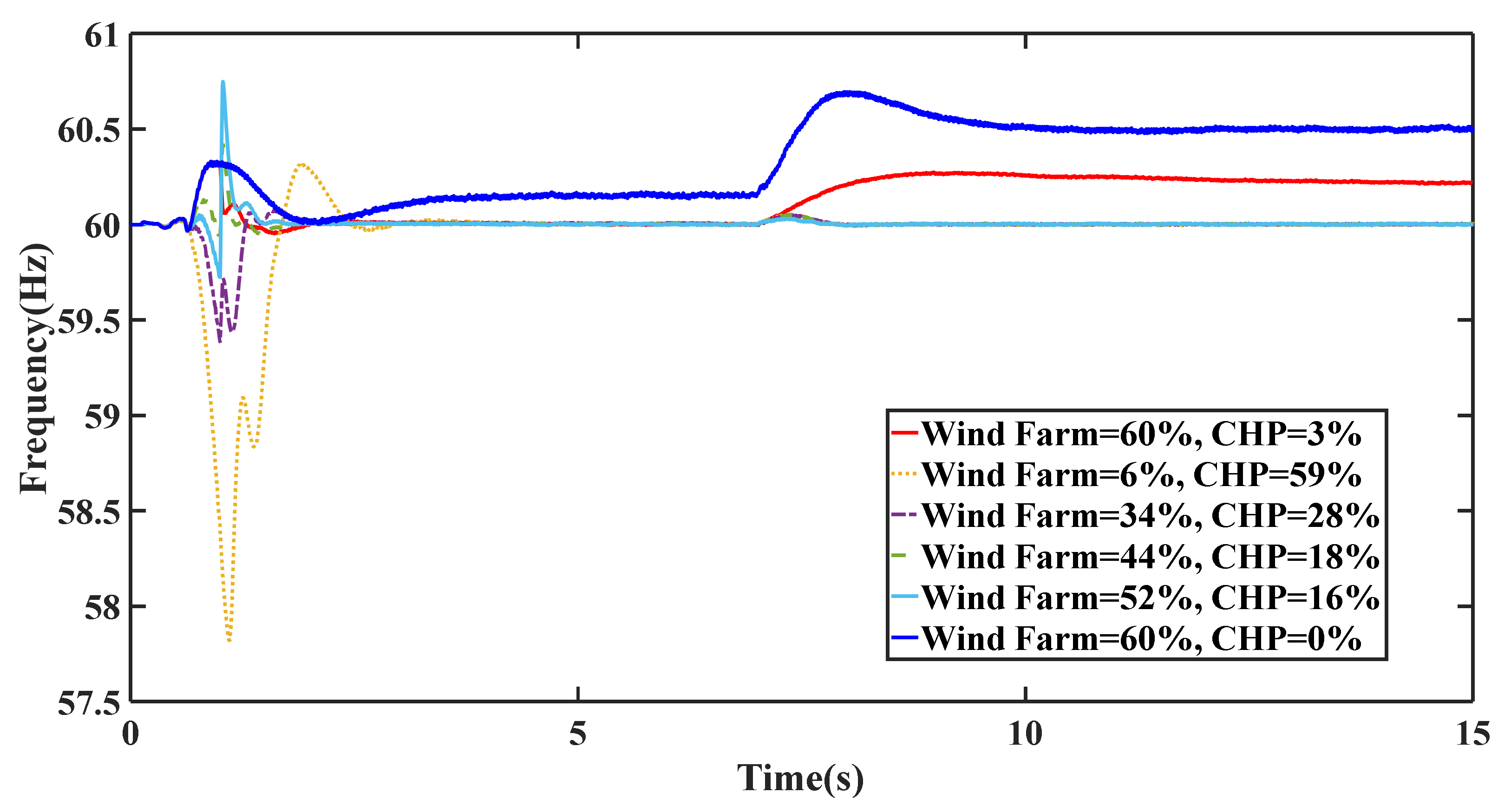
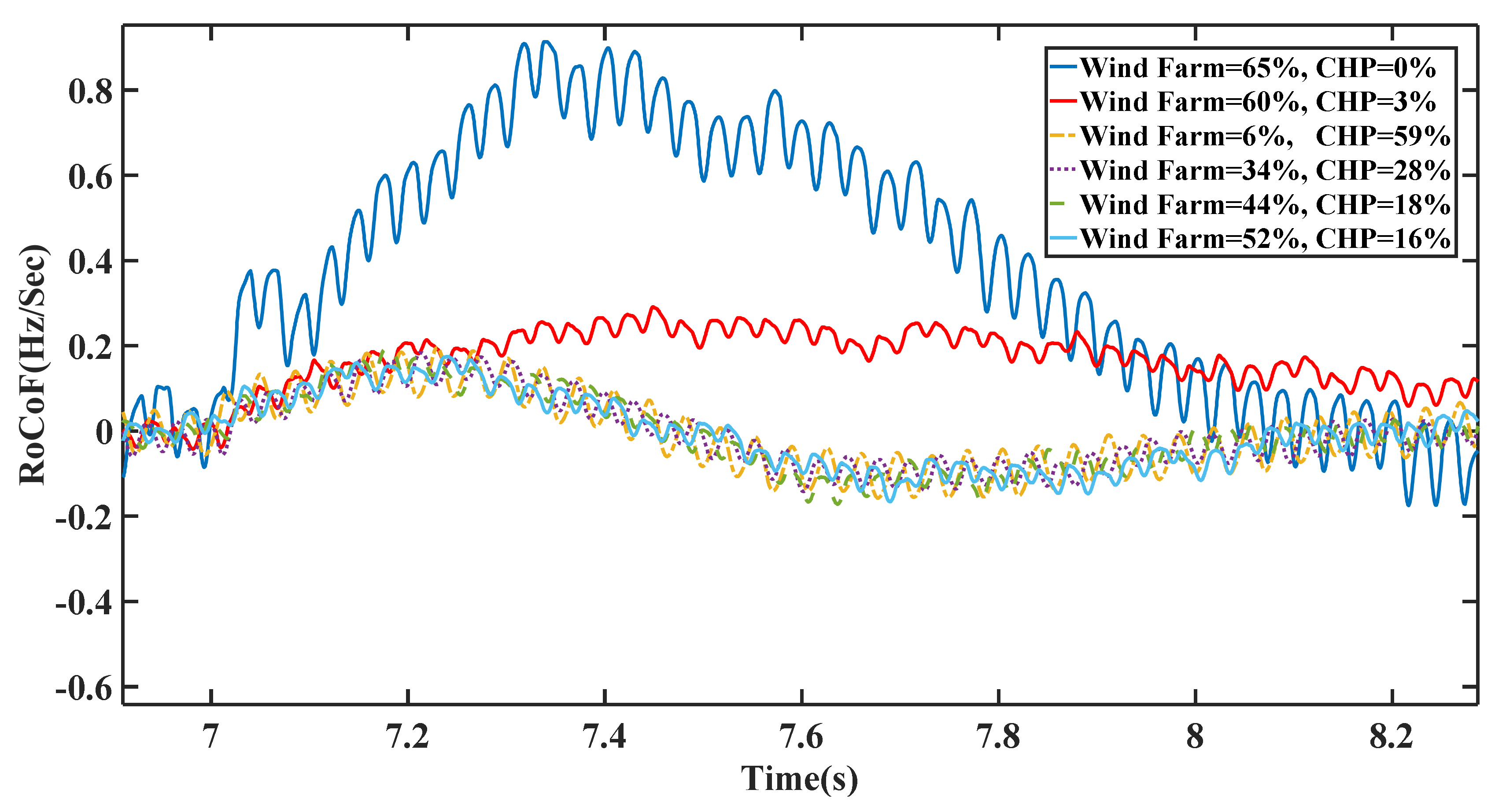
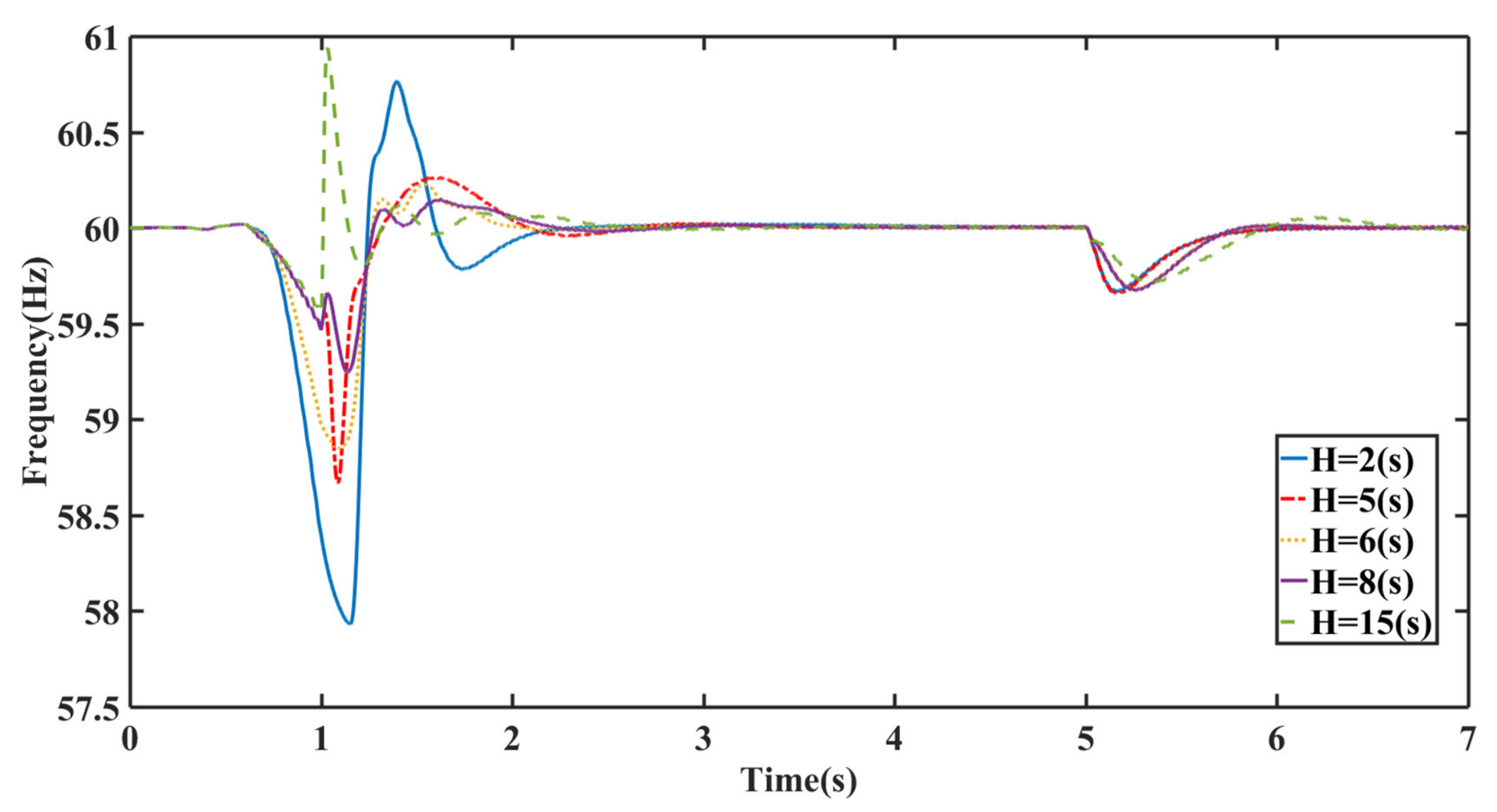
4. Simulation Results and Discussion
4.1. Scenario I
4.2. Scenario II
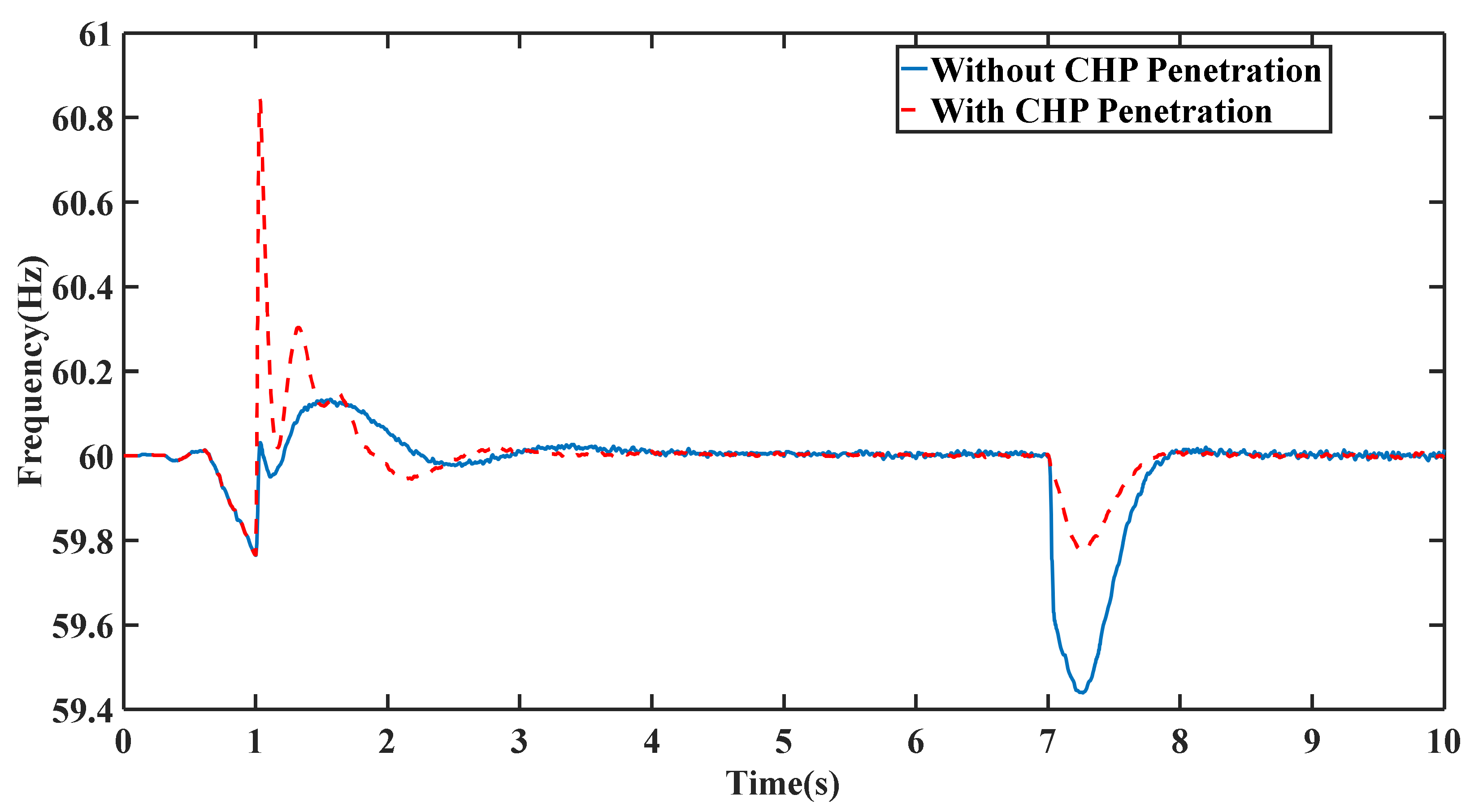
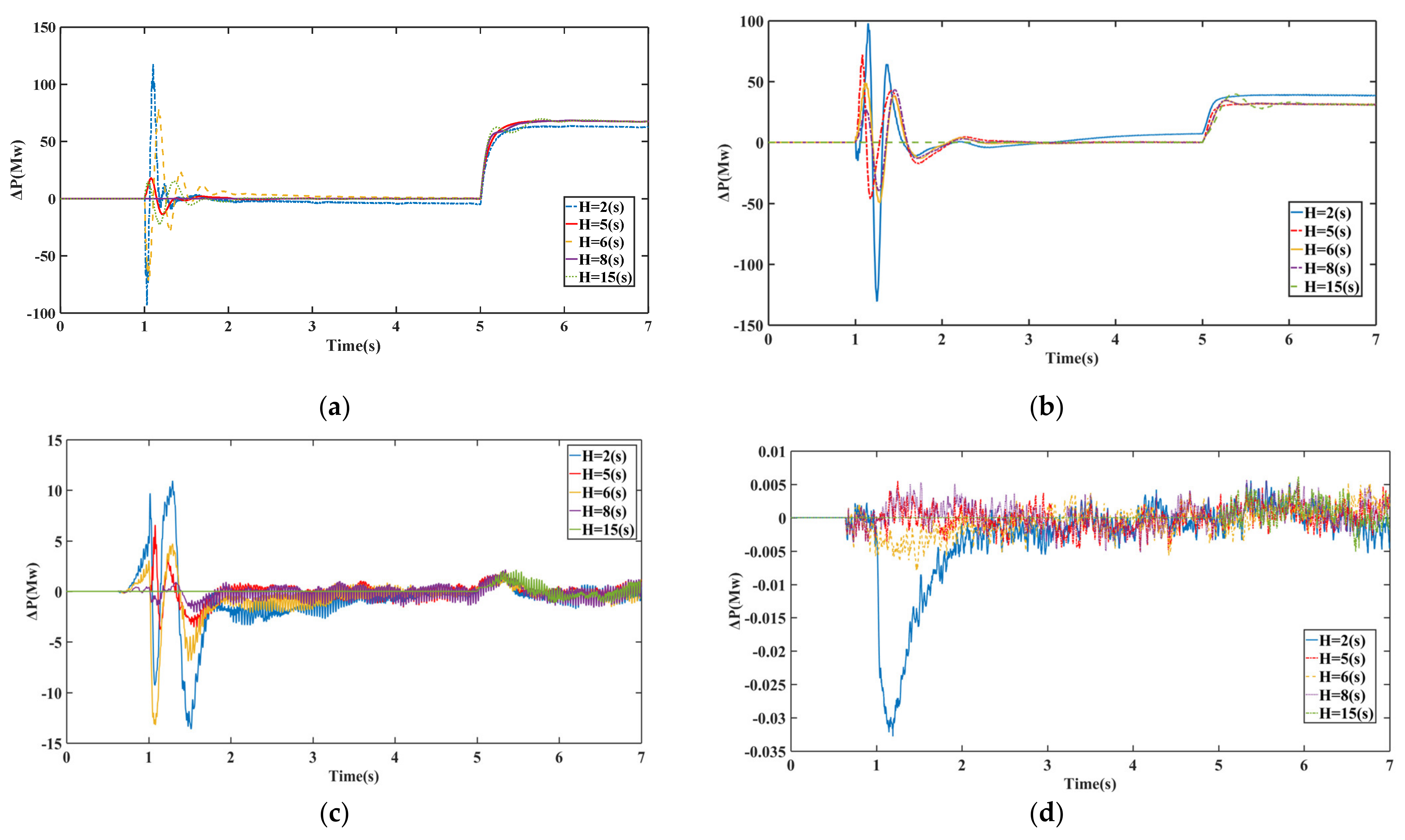
4.3. Scenario III
4.4. Scenario IV
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| MG | Microgrid |
| RES | Renewable Energy Sources |
| FCAS | Frequency Control Ancillary Services |
| DER | Distributed Energy Resources |
| PEIG | Power Electronic Interferences Generation |
| RoCoF | Rate of Change of Frequency |
| ABC | Artificial Bee Colony |
| DG | Distributed Generation |
| CHP | Combined Heat and Power |
| WTG | Wind turbine Generator |
| WECS | Wind Energy Conversion System |
| MPPT | Maximum Power Point Tracking |
| PV | Photovoltaic Panles |
| LFC | Load Frequency Control |
| MOF | Multi-Objective Function |
| SG | Synchronous Generator |
| DEG | Diesel Engine Generator |
| DFIG | Doubly Fed Induction Generator |
| GSC | Grid Side Converter |
| RSC | Rotor Side Converter |
| ISE | Integral Square Error |
| KPI | Key Performance Indicator |
| GFL | Grid Following |
| GFM | Grid Forming |
| CIG | Converter Interface Generator |
| PCC | Point of Common Coupling |
| IGB | Inverter-based Generation Resources |
| NSG | Non-synchronous Based Generation |
References
- Nejabatkhah, F. Overview of control, integration and energy management of microgrids. J. Mod. Power Syst. Clean Energy 2014, 2, 212–222. [Google Scholar]
- Tayyebi, A.; Groß, D.; Anta, A.; Kupzog, F.; Dörfler, F. Frequency Stability of Synchronous Machines and Grid-Forming Power Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1004–1018. [Google Scholar] [CrossRef] [Green Version]
- Ortiz-Villalba, D.; Rahmann, C.; Alvarez, R.; Canizares, C.A.; Strunck, C. Practical Framework for Frequency Stability Studies in Power Systems with Renewable Energy Sources. IEEE Access 2020, 8, 202286–202297. [Google Scholar] [CrossRef]
- Milano, F.; Dörfler, F.; Hug, G.; Hill, D.J.; Verbič, G. Foundations and Challenges of Low-Inertia Systems (Invited Paper). In Proceedings of the 2018 Power Systems Computation Conference (PSCC), Dublin, Ireland, 11–15 June 2018. [Google Scholar]
- Kenyon, R.W.; Hoke, A.; Tan, J.; Hodge, B. Grid-Following Inverters and Synchronous Condensers: A Grid-Forming Pair. In Proceedings of the 2020 Clemson University Power Systems Conference (PSC), Clemson, SC, USA, 10–13 March 2020; pp. 1–7. [Google Scholar]
- Fernández-Guillamón, A.; Gómez-Lázaro, E.; Muljadi, E.; Molina-García, Á. Power systems with high renewable energy sources: A review of inertia and frequency control strategies over time. Renew. Sustain. Energy Rev. 2019, 115, 109369. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, H.T.; Yang, G.; Nielsen, A.H.; Jensen, P.H.; Pal, B. Applying Synchronous Condenser for Damping Provision in Converter-Dominated Power System. J. Mod. Power Syst. Clean Energy 2020, 9, 639–647. [Google Scholar] [CrossRef]
- Ademola-Idowu, A.; Zhang, B. Frequency Stability Using MPC-Based Inverter Power Control in Low-Inertia Power Systems. IEEE Trans. Power Syst. 2021, 36, 1628–1637. [Google Scholar] [CrossRef]
- Unruh, P.; Nuschke, M.; Strauß, P.; Welck, F. Overview on Grid-Forming Inverter Control Methods. Energies 2020, 13, 2589. [Google Scholar] [CrossRef]
- Schneider, K.P.; Radhakrishnan, N.; Tang, Y.; Tuffner, F.K.; Liu, C.-C.; Xie, J.; Ton, D. Improving Primary Frequency Response to Support Networked Microgrid Operations. IEEE Trans. Power Syst. 2019, 34, 659–667. [Google Scholar] [CrossRef]
- Abazari, A.; Dozein, M.G.; Monsef, H. A New Load Frequency Control Strategy for an AC Micro-grid: PSO-based Fuzzy Logic Controlling Approach. In Proceedings of the 2018 Smart Grid Conference (SGC), Sanandaj, Iran, 28–29 November 2018; pp. 1–7. [Google Scholar]
- Abazari, A.; Dozein, M.G.; Monsef, H.; Wu, B. Wind turbine participation in micro-grid frequency control through self-tuning, adaptive fuzzy droop in de-loaded area. IET Smart Grid 2019, 2, 301–308. [Google Scholar] [CrossRef]
- Abazari, A.; Soleymani, M.M.; Babaei, M.; Ghafouri, M.; Monsef, H. High penetrated renewable energy sources-based AOMPC for microgrid’s frequency regulation during weather changes, time-varying parameters and generation unit collapse. IET Gener. Transm. Distrib. 2020, 14, 5164–5182. [Google Scholar] [CrossRef]
- Rakhshani, E.; Rodriguez, P. Active power and frequency control considering large scale RES. In Large Scale Renewable Power Generation: Advances in Technologies for Generation Transmission and Storage; Springer: Singapore, 2013. [Google Scholar]
- Gu, H.; Yan, R.; Saha, T.K. Minimum Synchronous Inertia Requirement of Renewable Power Systems. IEEE Trans. Power Syst. 2018, 33, 1533–1543. [Google Scholar] [CrossRef] [Green Version]
- Alaboudy, A.H.K.; Zeineldin, H.H.; Kirtley, J.L. Microgrid stability characterization subsequent to fault-triggered islanding incidents. IEEE Trans. Power Del. 2012, 27, 658–669. [Google Scholar] [CrossRef]
- Oshnoei, A.; Kheradmandi, M.; Muyeen, S.M. Robust control scheme for distributed battery energy storage systems in load frequency control. IEEE Trans. Power Syst. 2020, 35, 4781–4791. [Google Scholar] [CrossRef]
- Meegahapola, L.; Flynn, D. Impact on transient and frequency stability for a power system at very high wind penetration. In Proceedings of the IEEE PES General Meeting, Minneapolis, MN, USA, 24–28 June 2010; pp. 1–8. [Google Scholar]
- Oshnoei, A.; Kheradmandi, M.; Muyeen, S.M.; Hatziargyriou, N. Disturbance Observer and Tube-based Model Predictive Controlled Electric Vehicles for Frequency Regulation of an Isolated Power Grid. IEEE Trans. Smart Grid. 2021, 10, 1. [Google Scholar] [CrossRef]
- Lal, D.K.; Barisal, A.K. Load frequency control of AC microgrid interconnected thermal power system. IOP Conf. Ser. Mater. Sci. Eng. 2017, 225, 012090. [Google Scholar] [CrossRef]
- Cam, E.; Kocaarslan, I. Load frequency control in two area power systems using fuzzy logic controller. Energy Convers. Manag. 2005, 46, 233–243. [Google Scholar] [CrossRef]
- Schonbergerschonberger, J.; Duke, R.; Round, S.D. DC-bus signaling: A distributed control strategy for ahybrid. IEEE Trans. Ind. Electron. 2006, 53, 1453–1460. [Google Scholar] [CrossRef]
- Khooban, M.H.; Niknam, T.; Blaabjerg, F.; Davari, P. A robust adaptive load frequency control for micro-grids. ISA Trans. 2016, 65, 220–229. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Zhili, Z.; Yufei, T.; Jun, Y.; Haibo, H.; Yunliang, W. Load frequency control in isolated micro-grids with electrical vehicles based on multivariable generalized predictive theory. Energies 2015, 8, 2145–2164. [Google Scholar] [CrossRef]
- Zhang, S.; Tang, T.; Song, B.; Lu, S.; Ye, B. Stable adaptive PI control for permanent magnet synchronous motor drive based on improved JITL technique. ISA Trans. 2013, 54, 539–549. [Google Scholar] [CrossRef] [PubMed]
- Yaseli:, E. Interval type-2 fuzzy PID load frequency controller using big bang-big crunch optimization. App. Soft. Comp. 2014, 15, 100–112. [Google Scholar]
- Massucco, S.; Pitto, A.; Silvestro, F. A gas turbine model for studies on distributed generation penetration into distribution networks. IEEE Trans. Power Syst. 2011, 26, 992–999. [Google Scholar] [CrossRef]
- Sun, T.; Lu, J.; Li, Z.; Lubkeman, D.L.; Lu, N. Modeling Combined Heat and Power Systems for Microgrid Applications. IEEE Trans. Smart Grid 2018, 9, 4172–4180. [Google Scholar] [CrossRef]
- Hossein, J.M.; Pota, H.R.; Mahmud, M.A.; Aldeen, M. Robust control for power sharing in microgrids with low-inertia wind and PV generators. IEEE Trans. Sustain. Energy 2015, 6, 1067–1077. [Google Scholar] [CrossRef]
- Abazari, A.; Dozein, M.G.; Monsef, H. An optimal fuzzy-logic based frequency control strategy in a high wind penetrated power system. J. Frankl. Inst. 2018, 355, 6262–6285. [Google Scholar] [CrossRef]
- Abazari, A.; Monsef, H.; Wu, B. Load frequency control by de-loaded wind farm using the fuzzy-based PID droop controller. IET Renew. Power Generat. 2018, 13, 180–190. [Google Scholar] [CrossRef]
- Vidyanandan, K.V.; Senroy, N. Primary frequency regulation by deloaded wind turbines using variable droop. IEEE Trans. Power Syst. 2013, 28, 837–846. [Google Scholar] [CrossRef]
- Datta, M.; Senju, T. Fuzzy control of distributed PV inverters/energy storage systems/ electric vehicles for frequency regulation in a large power system. IEEE Trans. Smart Grid 2013, 1, 479–488. [Google Scholar] [CrossRef]
- Taghizadeh, M.; Mardaneh, M.; Sadeghi, M.S. Frequency control of a new topology in proton exchange membrane fuel cell/wind turbine/photovoltaic/ultra capacitor/ battery energy storage system based isolated networks by a novel intelligent controller. J. Renew. Sustain. Energy 2014, 6, 53121. [Google Scholar] [CrossRef]
- Oshnoei, A.; Kheradmandi, M.; Oshnoei, S. Optimal model predictive control of photovoltaic plants for frequency regulation in an interconnected power system. In Proceedings of the 34th International Power System Conference (PSC), Tehran, Iran, 9–11 December 2019; pp. 428–433. [Google Scholar]
- Machowski, J.; Lubosny, Z.; Bialek, J.; Bumby, J.R. Power System Dynamics: Stability and Control; Wiley: Hoboken, NJ, USA, 2020. [Google Scholar]
- Kundur, P.; Balu, N.J.; Lauby, M.G. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Task Force on Turbine Governor Modeling; Power System Dynamic Performance Committee; Power System Stability Subgroup. Dynamic Models for Turbine-Governors in Power System Studies. Available online: https://resourcecenter.ieee-pes.org/publications/technical-reports/PESTR1.html (accessed on 2 June 2021).
- IEEE Recommended Practice for Excitation System Models for Power System Stability Studies. Available online: https://www.semanticscholar.org/paper/IEEE-recommended-practice-for-excitation-system-for-Board/05bc9ef274285d8be39c5aa0ff9fe0611a6c7874 (accessed on 5 June 2021).
- Tapia, G.; Tapia, A.; Ostolaza, J.X. Two alternative modeling approaches for the evaluation of wind farm active and reactive power performance. IEEE Trans. Energy Convers. 2006, 21, 909–920. [Google Scholar] [CrossRef]
- Boldea, I. Variable Speed Generator; Taylor & Francis Group: New York, NY, USA, 2006. [Google Scholar]
- Xing, P.; Fu, L.; Wang, G.; Wang, Y.; Zhang, Y. A compositive control method of low-voltage ride through for PMSG-based wind turbine generator system. Gener. Transm. Distrib. IET 2018, 12, 117–125. [Google Scholar] [CrossRef]
- Pena, R.; Clare, J.C.; Asher, G.M. Doubly fed induction generator using back-to-back PWM converters and its application to variable-speed wind-energy generation. Proc. Inst. Elect. Eng. 1996, 143, 231–241. [Google Scholar] [CrossRef] [Green Version]
- Qiao, W.; Zhou, W.; Aller, J.M.; Harley, R.G. Wind speed estimation based sensorless output maximization control for a wind turbine driving a DFIG. IEEE Trans. Power Electron. 2008, 23, 1156–1169. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical optimization: Artificial bee colony (ABC). J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]



| Description | Symbol | Value |
|---|---|---|
| Proportional gain | 40 | |
| Integral time constant | 0.2 | |
| Lead–Lag time constant | 0.2 | |
| Turbine time constant | 0.1 |
| Description | Symbol | Value |
|---|---|---|
| Rated RMS line-neutral voltage | 66.47 [kV] | |
| Rated RMS line current | 0.7 [kA] | |
| Inertia constant | 3.85 [s] | |
| Mechanical friction | 0.01 [pu] | |
| Armature resistance | 0.003 [pu] | |
| Poitier reactance | 0.11 [pu] | |
| Unsaturated reactance | 1.79 [pu] | |
| Unsaturated transient reactance | 0.24 [pu] | |
| Unsaturated transient time (Open) | 5.9 [s] | |
| Unsaturated sub-transient reactance | 0.185 [pu] | |
| Unsaturated sub-transient time (Open) | 0.033 [s] | |
| Unsaturated reactance | 1.64 [pu] | |
| Unsaturated transient reactance | 0.38 [pu] | |
| Unsaturated transient time (Open) | 0.54 [s] | |
| Unsaturated sub-transient reactance | 0.185 [pu] | |
| Unsaturated sub-transient time (Open) | 0.076 [s] |
| Description | Symbol | Value |
|---|---|---|
| Steam chest time constant | 0.2 | |
| Reheater time constant | 0.2 | |
| Reheater/cross-over time constant | 1.0 | |
| Over-heater time constant | 1.0 | |
| Turbine (HP + LP) initial output power | 1.0 | |
| Different fraction for LP and HP stages(p.u.) | 0.125 |
| Description. | Symbol | Value |
|---|---|---|
| Lead time constant | 1.0 s | |
| Lag time constant | 10 s | |
| Regulator integral gain | 200 p.u. | |
| Regulator time constant | 0.015 | |
| Rectifier loading factor | 0.2 p.u. | |
| Transducer time constant | 0.1 s | |
| Upper limit on error signal | 10 | |
| Lower limit on error signal | −10 | |
| Maximum regulator output | 5.64 | |
| Minimum regulator output | −4.53 |
| WTG Parameters. | Symbol | Values |
| Rated power | 15 MW | |
| LL Voltage | 0.69 kV | |
| Base Angular Frequency | 60 Hz | |
| Stator/Rotor turns ratio | 0.85 | |
| Angular moment of inertia(j = 2 h) | 0.6 | |
| Mechanical Damping | 0.0001 p.u | |
| Stator Resistance | R1 | 0.0054 p.u |
| Wound rotor resistance | R2 | 0.00607 p.u |
| First Squirrel cage resistance | R3 | 0.298 p.u |
| Magnetizing Inductance | 4.5 | |
| Stator leakage inductance | 0.10 | |
| Wound rotor Leakage inductance | 0.11 | |
| First Cage Leakage Inductance | 0.05 | |
| Converter Parameters | Symbol | Values |
| Convertor reactor | 0.00134 H | |
| Capacitance | 50,000 μF | |
| Machine terminal Voltage | 0.69 KV | |
| Stator resistance | 0.0054 p.u |
| Total System Inertia | Reduced Inertia | ΔP(MW) Response Requirement | ||||
|---|---|---|---|---|---|---|
| Based on the Second | Utility Grid | Droop-Based DERs | 50 MW SG Loss (42% of Total Capacity) | 100 MW SG Loss (55% of Total Capacity) | 300 MW SG Loss (59% of Total Capacity) | 100 MW Load Step (83% of Total Load) |
| 15 | ✓ | ✓ | 59 MW | 100 MW | 215 MW | 98 MW |
| 8-Normal | 54 MW | 99 MW | 214 MW | 103 MW | ||
| 6 | ✓ | 55 MW | 99 MW | 216 MW | 103.5 MW | |
| 5 | ✓ | 54 MW | 100 MW | 203 MW | 104 MW | |
| 2 | ✓ | ✓ | 54 MW | 102 MW | 206 MW | 104 MW |
| H(s) | SG | Diesel Generator | CHP |
|---|---|---|---|
| 15 | 4.96 | 4.96 | 4.96 |
| 8 | 3.96 | 1.96 | 2.31 |
| 6 | 1.73 | 1.96 | 2.31 |
| 5 | 3.96 | 0.5 | 0.5 |
| 2 | 1.0 | 0.5 | 0.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arzani, M.; Abazari, A.; Oshnoei, A.; Ghafouri, M.; Muyeen, S.M. Optimal Distribution Coefficients of Energy Resources in Frequency Stability of Hybrid Microgrids Connected to the Power System. Electronics 2021, 10, 1591. https://doi.org/10.3390/electronics10131591
Arzani M, Abazari A, Oshnoei A, Ghafouri M, Muyeen SM. Optimal Distribution Coefficients of Energy Resources in Frequency Stability of Hybrid Microgrids Connected to the Power System. Electronics. 2021; 10(13):1591. https://doi.org/10.3390/electronics10131591
Chicago/Turabian StyleArzani, Mohsen, Ahmadreza Abazari, Arman Oshnoei, Mohsen Ghafouri, and S. M. Muyeen. 2021. "Optimal Distribution Coefficients of Energy Resources in Frequency Stability of Hybrid Microgrids Connected to the Power System" Electronics 10, no. 13: 1591. https://doi.org/10.3390/electronics10131591
APA StyleArzani, M., Abazari, A., Oshnoei, A., Ghafouri, M., & Muyeen, S. M. (2021). Optimal Distribution Coefficients of Energy Resources in Frequency Stability of Hybrid Microgrids Connected to the Power System. Electronics, 10(13), 1591. https://doi.org/10.3390/electronics10131591









