Unity-Gain Zero-Offset CMOS Buffer with Improved Feedforward Path

Abstract

A voltage unity-gain zero-offset CMOS amplifier with reduced gain error and increased PSRR (power supply rejection ratio) is proposed. The amplifier uses two feed mechanisms, negative feedback and supporting positive feedforward, to achieve low deviation from unit gain over the entire input range. The circuit, designed in a standard 180-nanometer 1.8-voltage CMOS process, is compared with two known buffers of similar topology, also designed in the same process. Simulations show that, with the same supply (1.8 V), power (1.2 mW), load (12 pF), bandwidth (50 MHz), and similar area (600 µm²), the proposed buffer achieves the lowest gain error (0.3%) and the highest PSRR (72 dB).

1. Introduction

A unity-gain buffer is an analogue amplifier with a voltage gain equal to 1 V/V. Among these amplifiers there are unity-gain zero-offset buffers characterized by zero offset between input and output voltages [1,2,3,4,5,6,7,8]. Unity-gain zero-offset buffers have found application in the testing of analogue chips [8], in analogue filtering [9,10,11], oscillators [12], voltage regulators [13,14], and in LCD panels [15,16]. Most of these buffer solutions use the classic approach based on a high-gain differential amplifier and a negative feedback to obtain unity gain and zero offset. 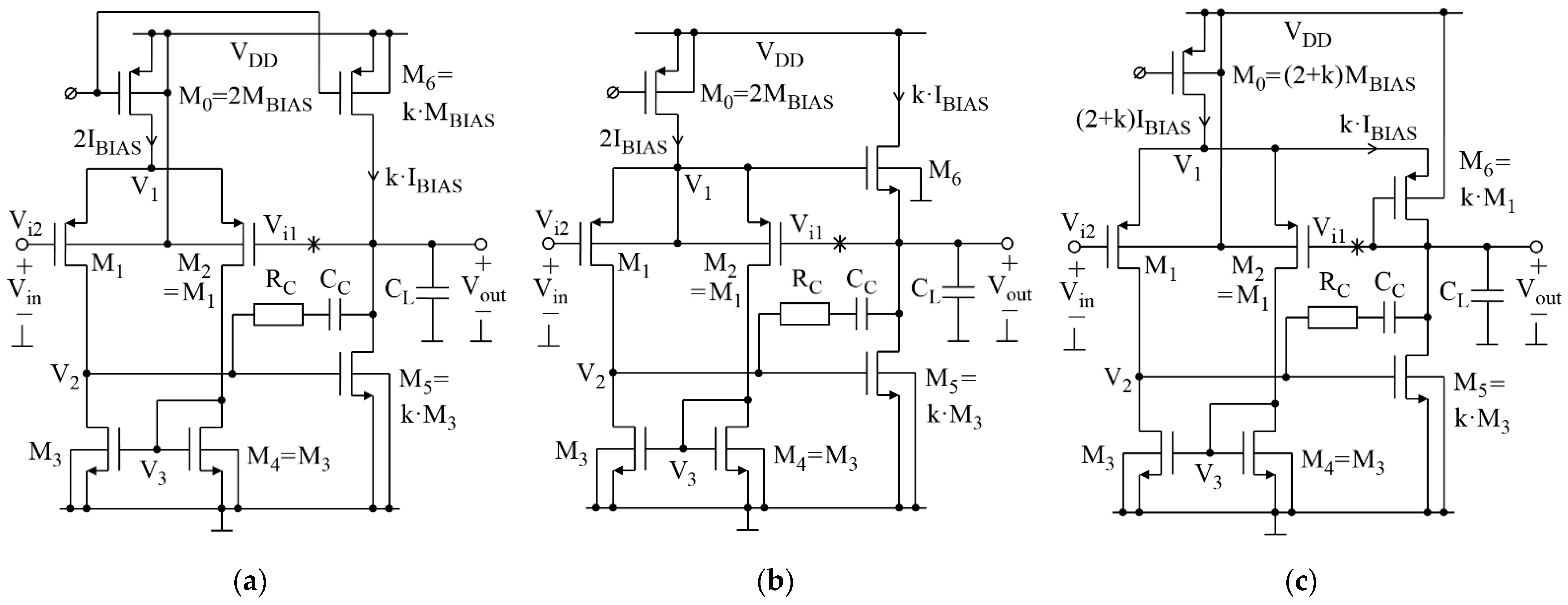A representative example of the classic approach is the Miller opamp (operational amplifier) with an output connected to an inverting input (Figure 1a). The advantages of this buffer solution are its relatively simple design, wide input voltage range, and its full compatibility with standard CMOS technologies. Furthermore, since the Miller OpAmp has a high open-loop gain for differential-mode signals, a buffer gain can be very close to 1 V/V. To further reduce the gain error, it was proposed in [1] to use also a common-mode signal. In this case, a common-mode signal component is forwarded from the input to the output along an additional path. Such a feedforward path for a common-mode signal can be relatively simple to implement by using only one n-channel transistor (M₆ in Figure 1b). A limitation of such a solution is the need for using an n-channel transistor without the body effect, which is not available in standard CMOS processes. In this paper, an improvement of the solution of [1] is proposed (Figure 1c), which gives substantially reduced gain error, improved PSRR, and full applicability in standard CMOS technologies.

The circuits in Figure 1a–c are studied and the impact on circuit performance from introducing a common-mode feedforward path is examined. To make this study meaningful, key parameters, such as power consumption, load capacitance, bandwidth, and layout area, are assumed to be similar in all three circuits. The results of theoretical analyses and simulations, followed by discussion assuming the circuits realization in 180-nm 1.8-V process of austriamicrosystems AG (ams AG), are presented in the following sections.

2. Theoretical Analysis

The circuits in Figure 1a–c are closed-loop differential amplifiers with two stages. The first stage is exactly the same in all cases and is composed of the transistors M₁-M₄. The second stage in Figure 1a,b consists of M₅ loaded by M₆. In Figure 1c, the second stage can be identified as M₅ loaded by the series connection of M₆ and M₁-M₂. The transistors are sized so that the first and second stages are biased at 2I_BIAS and kI_BIAS, respectively.

Each circuit has a traditional negative feedback loop (the loop breaking point is marked by the symbol *) operating on a differential-mode component of the input signal (V_i1 − V_i2). The circuits in Figure 1b,c also have a positive feedforward loop operating with the common-mode component, (V_i1 + V_i2)/2. The common-mode component is generated at node V₁ by the differential pair and is transferred to the output by M₆.

In the following analysis, the common-mode signal at node V₂ is omitted because it is suppressed by the first stage due to its symmetry (owing to CMRR).

When the negative feedback loop is opened (broken in the point *), the output small-signal voltage can be determined using the superposition principle [1]

$$V_{out}=A_D\cdot \left(V_{i1}-V_{i2}\right)+A_C\cdot \frac{V_{i1}+V_{i2}}{2}$$

(1)

where A_D and A_C are the small-signal gains for the differential- and common-mode components, respectively.

$$A_D={\frac{V_{out}}{V_{i1}-V_{i2}}|}_{V_{i1}+V_{i2}=0}$$

(2)

$$A_C={\frac{V_{out}}{\left(V_{i1}+V_{i2}\right)/2}|}_{V_{i1}-V_{i2}=0}$$

(3)

After closing the loop (V_i1 = V_out, V_i2 = V_in) the voltage gain becomes

$$\frac{V_{out}}{V_{in}}=1-\frac{1-A_C}{1-A_D-A_C/2}\cong 1-\frac{1-A_C}{-A_D}$$

(4)

Equation (4) indicates that, as A_C is close to 1, the gain error is significantly reduced even though A_D is reduced.

The result of applying the superposition principle (1) to each of the circuits in Figure 1a–c is shown in the corresponding diagrams in Figure 2a–c.

2.1. Gain Error in the Classic Buffer

The circuit in Figure 1a processes only the differential-mode component due to the CMRR effect, as mentioned earlier. This means that A_C = 0 and A_D = A_1D·A₂, where A_1D and A₂ are the gains of the first and the second stage, respectively,

$$A_{1D}={\frac{V_2}{V_{i1}-V_{i2}}|}_{V_{i1}+V_{i2}=0}=\frac{g_{m1,2}}{g_{ds1,2}+g_{ds3,4}}$$

(5)

where g_m1,2 = g_m1 = g_m2, g_ds1,2 = g_ds1 = g_ds2, g_ds3,4 = g_ds3 = g_ds4, and

$$A_2=\frac{V_{out}}{V_2}=-\frac{g_{m5}}{g_{ds5}+g_{ds6}}$$

(6)

Thus

$$\frac{V_{out}}{V_{in}}=1-\frac{1}{-A_{1D}{A}_2}=1-\frac{g_{ds5}+g_{ds6}}{A_{1D}{g}_{m5}}$$

(7)

The gain error in (7) can be relatively small because the product |A_1D·A₂| ranges from 10² to 10³, depending on I_BIAS and transistor sizes.

2.2. Gain Error in the Buffer of Figure 1b

The circuit in Figure 1b processes differential- and common-mode components, as shown in Figure 2b. The differential signal path (A_1D followed by A_2D) is the same as in the classic circuit, but the gain of the second stage (A_2D) is lower and is close to −1.

$$A_{2D}={\frac{V_{out}}{V_2}|}_{V_{i1}+V_{i2}=0}=-\frac{g_{m5}}{g_{m6}+g_{mb6}+g_{ds6}+g_{ds5}}\underset{\begin{array}{l}{g}_m>>g_{ds}\\ g_{mb}>>g_{ds}\end{array}}{\cong }-\frac{g_{m5}}{g_{m6}+g_{mb6}}$$

(8)

The common-mode signal passes, firstly, through the differential pair to node V₁ and, next, through the source follower M₆ to the buffer output. The particular gains of the common-mode feedforward path are

$$A_{1C}={\frac{V_1}{\left(V_{i1}+V_{i2}\right)/2}|}_{V_{i1}-V_{i2}=0}=\frac{g_{m1,2}}{g_{m1,2}+g_{ds1,2}+g_{ds0}}\underset{g_m>>g_{ds}}{\cong }1$$

(9)

and

$$A_{2C}={\frac{V_{out}}{V_1}|}_{V_{i1}-V_{i2}=0}=\frac{g_{m6}}{g_{m6}+g_{mb6}+g_{ds6}+g_{ds5}}\underset{\begin{array}{l}{g}_m>>g_{ds}\\ g_{mb}>>g_{ds}\end{array}}{\cong }\frac{g_{m6}}{g_{m6}+g_{mb6}}\cong 0.8$$

(10)

where A_2C is the gain of the follower M₆. Note that in a typical CMOS process, A_2C is about 0.8 V/V, because the transconductance ratio in M₆ (g_mb6/g_m6) is close to 0.2. Therefore, the common-mode signal is forwarded to the buffer output with a gain less than 1 (A_C = A_1C·A_2C < 1).

Hence, the buffer gain is

$$\frac{V_{out}}{V_{in}}=1-\frac{1-A_{1C}{A}_{2C}}{-A_{1D}{A}_{2D}}=1-\frac{g_{mb6}}{A_{1D}{g}_{m5}}$$

(11)

As A_1D and g_m5 in (11) are the same as in (7), the gain error is larger than in the classic solution because of the body effect of M₆ (because g_mb6 is larger than g_ds6 + g_ds5).

2.3. Gain Error in the Proposed Buffer

In the proposed buffer (Figure 1c), the NMOS source follower (M₆) is replaced by a PMOS voltage shifter, i.e., the diode-connected PMOS FET. Thus, the body effect of M₁-M₂ and M₆ cancels each other out, and the common-mode component is transferred to the output with a gain theoretically equal to 1,

$$A_{1C}={\frac{V_{out}}{\left(V_{i1}+V_{i2}\right)/2}|}_{V_{i1}-V_{i2}=0}\underset{\begin{array}{l}{g}_m>>g_{ds}\\ g_{mb}>>g_{ds}\end{array}}{\cong }\frac{1+g_{mb6}/g_{m6}}{1+g_{mb1,2}/g_{m1,2}}=\frac{1+\left(k\cdot g_{mb1,2}\right)/\left(k\cdot g_{m1,2}\right)}{1+g_{mb1,2}/g_{m1,2}}=1$$

(12)

Furthermore, the gain of the differential path is higher than that of the circuit in Figure 1b, as M₅ is loaded by a higher resistance resulting from the series connection of M₆ and M₁-M₂.

$$A_{2D}\underset{\begin{array}{l}{g}_m>>g_{ds}\\ g_{mb}>>g_{ds}\end{array}}{\cong }-\frac{g_{m5}}{g_{m6}}\left(1+\frac{g_{m6}+g_{mb6}}{g_{m1,2}+g_{mb1,2}}\right)=-\frac{g_{m5}}{g_{m6}}\left(1+k\right)$$

(13)

Thus

$$\frac{V_{out}}{V_{in}}=1-\frac{1-A_{1C}}{-A_{1D}{A}_{2D}}=1-\frac{\frac{g_{m6}}{1+k}}{A_{1D}{g}_{m5}}\left(1-A_{1C}\right)=1$$

(14)

Comparing (14) and (7), it can be seen that the gain error of the proposed solution can be lower than the classic one due to the fact that A_1C is 1.

2.4. Output Resistance

The output resistances (R_out) of the considered buffers are practically the same as it is determined mainly by g_m5 and A_1D. In detail, the output resistance of the classic buffer is

$$R_{out}=\frac{1}{g_{ds5}+g_{ds6}}\cdot \frac{1}{1-A_{1D}{A}_2}=\frac{1}{g_{m5}{A}_{1D}+g_{ds5}+g_{ds6}}\cong \frac{1}{g_{m5}{A}_{1D}}$$

(15)

For the buffer of [1] it is

$$R_{out}\cong \frac{1}{g_{m5}{A}_{1D}+\left(g_{m6}+g_{mb6}\right)/2}\cong \frac{1}{g_{m5}{A}_{1D}}$$

(16)

And, for the proposed one the output resistance is

$$R_{out}\cong \frac{1}{g_{m5}{A}_{1D}+g_x/2}\cong \frac{1}{g_{m5}{A}_{1D}}$$

(17)

where 1/g_x ≅ 1/(g_m6 + g_mb6) + 0.5/(g_m1,2 + g_mb1,2).

2.5. Power Supply Rejection Ratio

Supply interference paths, from V_DD to V_out, are different in each of the buffers. In the buffer in Figure 1a, V_DD interference passes to V_out in three ways: through M₀ (g_ds0), M_1,2 (bulk), and M₆ (g_ds6). The output conductance of M₆ (g_ds6) together with R_out form a resistive divider. Since 1/g_ds6 >> R_out, interference passing through g_ds6 to V_out is suppressed. V_DD interference passing through M₀ and M_1,2 is attenuated in the first stage, owing to CMRR.

In the circuit in Figure 1b, as M_1,2 bulk is not connected to V_DD, the supply interference passes in two ways: through M₀ (g_ds0) and M₆ (g_ds6). Interference that passes through g_ds6 is suppressed, similar to Figure 1a. Nevertheless, the interference that passes through g_ds0 is not suppressed at all because the follower M₆ transfers it from node V₁ directly to V_out. Since V₁ interference is at a comparable level to that in the circuit of Figure 1a, the feedforward path formed by M₆ causes PSRR degradation.

In the buffer in Figure 1c, V_DD interference goes in one way only, through g_ds0, because transfer through M_1,2 and M₆ bulks is suppressed due to the body effect compensation, as mentioned earlier. Interference from V_DD passes through g_ds0 to V₁ and, next, this interference is transferred by the shifter M₆ directly to V_out. However, in opposite to Figure 1b, M₆ is a diode-connected transistor and, thereby, its conductance (g_m6), together with g_ds0, g_m1,2 and R_out, compose a divider that substantially attenuates V₁ interference. As a result, the level of V₁ interference in the circuit in Figure 1c is much lower than in Figure 1a. Since there is no another path of interference, a higher PSRR than in the circuit in Figure 1a can be obtained. Above conclusions are confirmed by simulation results in the next section where detailed values of PSRR of each of the buffers are presented in a performance summary.

3. Simulations

The example designs of the buffers in Figure 1a–c were made for testing analogue chips (for buffering and monitoring internal analogue nodes). Therefore, a C_L of 12 pF is assumed as it is a capacitance of a typical oscilloscope probe (also such value of C_L was used in [1]). The transistor scaling factor k is set to five due to Miller compensation requirements. In a practical two-stage opamp, proper compensation is possible when the transconductance of a second stage is at least five times larger than in a first stage. I_BIAS is set to 100 µA, which results from limiting the power supply to 1 mW at a supply voltage of 1.8 V. The sizes of the transistors are given in

Table 1. Transistors sizes (W/L in µm/µm) and values of R_C and C_C.

	Figure 1a	Figure 1b	Figure 1c
M0	2 × 20/0.25	2 × 20/0.25	(5+2) × 20/0.25
M1, M2	10/0.25	10/0.25	10/0.25
M3, M4	10/0.25	10/0.25	10/0.25
M5	5 × 10/0.25	5 × 10/0.25	5 × 10/0.25
M6	5 × 20/0.25	5 × 10/0.25	5 × 10/0.25
RC/CC/CL	2.8 kΩ/2.5 pF/12 pF	2.4 kΩ/1.4 pF/12 pF	2.6 kΩ/1.9 pF/12 pF

. The 1.8-voltage standard-V_TH transistors with V_THP ≈ −0.4 V and V_THN ≈ 0.45 V were used.

The buffers were compensated to obtain similar −3-dB frequencies in small-signal characteristics (Figure 3a) as well as minimal overshoots under pulse excitation (Figure 3b). The applied values of the compensating elements, R_C and C_C, are given in Table 1. Some small overshoot still exists in the classical buffer impulse response, and of course this can be suppressed, but then the −3-dB frequency will be lower. The circuit of [1] features the best positive slew rate (SR+), but it results from the fact that the increase in gain error causes an increase in I_DS6 (the larger the difference in V_in − V_out, the larger V_GS6 becomes).

The detailed characteristic of the gain error can be determined directly from a derivative of the static responses in Figure 4a. The gain error is the deviation of the derivative from 1, i.e., gain error = dV_out/dV_in − 1. The plots of derivatives presented in Figure 4b show that, for low V_in, the classic solution has the smallest gain error. However, the gain error integrated across the entire available input range is the smallest in the proposed circuit (the available ranges are marked in Figure 4b and are determined by the boundaries beyond which the derivatives sharply change their value). The integrated gain errors are 1.2%, 2.3%, and 0.3% for the classic, from [1], and proposed circuits, respectively.

The influence of the process spread and mismatch on the gain is depicted in Figure 5a,b, respectively. All the buffers show a relatively small sensitivity to process spread. However, the mismatch increases the gain error near the upper boundaries of the input ranges.

The process spread and the mismatch also cause an offset between V_out and V_in. Figure 6a,b show the difference (V_out − V_in) under conditions of process spread and mismatch, respectively. Note that (V_out − V_in) contains both the offset and gain errors. However, (V_out − V_in) is dominated by the offset error. The process-induced offset (Figure 6a) is the highest in the topology of [1] because M₁-M₂ and M₆ are opposite-type. On the other side, the mismatch-induced offset (Figure 6b) is similar in all of the topologies because it is determined mainly by the matching of transistors in the first stage. An aggregated (process + mismatch induced) offset is comparable in all the topologies, and is 6.58 mV, 6.29 mV, and 6.48 mV (1 sigma) for the circuits in Figure 1a–c, respectively.

The buffers parameters are summarized in

Table 2. Simulated buffer performance ¹ using 180-nm CMOS process of ams AG.

	Classic (Figure 1a)	Based on [1] (Figure 1b)	Proposed (Figure 1c)
Supply (VDD)	1.8 V	1.8 V	1.8 V
Power	1.25 mW	1.19 mW	1.18 mW
−3-dB small-signal bandwidth	45.2 MHz	51.5 MHz	49.8 MHz
Area (active and passive devices)	763 µm2	506 µm2	611 µm2
DC input range 2	0.2–1.6 V	0.4–1.2 V	0.2–1.4 V
Gain error 3	1.2%	2.3%	0.3%
1-sigma offset 4 (mismatch+process)	6.58 mV	6.29 mV	6.48 mV
Input sine 5 amplitude @ THDout = 1%	462 mV	290 mV	370 mV
SR+/SR− (for 10–90% transition)	32.7/32.9 V/µs	42.8/51.7 V/µs	33.8/46.8 V/µs
Settling time (for 1% accuracy)	36 ns	25 ns	19 ns
Overshoot	3.76%	0.06%	0.63%
Output resistance (Rout)	13.13 Ω	13.12 Ω	13.94 Ω
Input noise (for 100 Hz–50 MHz)	176 µVRMS	165 µVRMS	171 µVRMS
PSRR (in band)	57 dB	51 dB	72 dB

¹ At T = 25 °C, C_L = 12 pF, I_BIAS = 100 µA, k = 5. ² Determined in Figure 4b. ³ RMS error integrated over the DC input range. ⁴ At DC V_in = 0.7 V. ⁵ Frequency 5 MHz, DC component 0.7 V.

. In accordance with the design goal, similar power consumption, bandwidth, and occupied area were achieved. Furthermore, the output resistance and noise are practically the same. In these conditions, the classic buffer has the widest DC input range (0.2–1.6 V) and a moderate gain error (1.2%). The proposed solution features an input range (0.2–1.4 V) that is narrower by 200 mV, but the gain error (0.3%) is four times smaller. Moreover, the PSRR (72 dB) is about 20 dB better.

4. Discussion (Circuit Design Principle and Trade-Off)

In this paper, an improved version of a unity-gain zero-offset buffer, which uses an additional feedforward path for a common-mode signal component, is proposed. This modification results in an improvement of some parameters while maintaining circuit complexity similar to the classic Miller OpAmp. The principles of optimization of power consumption, bandwidth, and stability are still the same as in the classical solution. This fact greatly facilitates design of the proposed circuit. Selection of circuit component parameters, depending on design requirements, is carried out in the traditional way. For example, in order to achieve a small offset between V_out and V_in, it is necessary to reduce mismatch of threshold voltages in the input differential-pair transistors M_1,2 (due to the fact that V_out = V_in +V_sg1 − V_sg2). Reduction in offset involves using large transistors in the differential pair. Noise optimization requires the reduction in noise from dominant sources, i.e., from the current mirror (M_3,4) and from M_1,2. In all three buffers designed in this work, contributions from M_3,4 and M_1,2 to the total buffer noise are 80% and 10%, respectively. The contribution from the current mirror is highest because gates of M_3,4 (i.e., noise sources at M_3,4 gates) are at a node (V₃) of highest gain to V_out (i.e., V_out/V₃ is higher than V_out/V₂, V_out/V₁, and V_out/V_in).

The proposed common-mode feedforward, when applied to the classic buffer, reduces its input voltage range, but improves its gain error and PSRR. Thus, the choice of an appropriate buffer variant depends on the trade-off between input range, gain error, and PSRR. From the point of view of speed performance (slew rate, settling time, overshoot, etc.), it is worth considering the solution from Figure 1b. In this circuit, the n-channel output stage gives a higher slew rate than achievable using the mixed p-n-channel stages in the classic and proposed buffers. Note that the solution in Figure 1b would also allow for low gain error if implemented in a triple-well or silicon-on-insulator process, where there is no body effect in the n-channel M₆ transistor. On the other hand, stage arrangements in the classic and proposed buffers are less sensitive to process variations because the first and second stages are better matched, as M_1,2 and M₆, and M_3,4 and M₅, have the same channel type.

5. Conclusions

The proposed improved feedforward common-mode path ensures full compatibility with standard CMOS processes, lower gain error, and higher PSRR. Improvement in PSRR makes the proposed buffer solution particularly useful in biomedical sensors and filters, since immunity to power interference is one of the key requirements in biomedical applications.