Gaussian Belief Propagation on a Field-Programmable Gate Array for Solving Linear Equation Systems
Abstract
:1. Introduction
2. Gaussian Belief Propagation
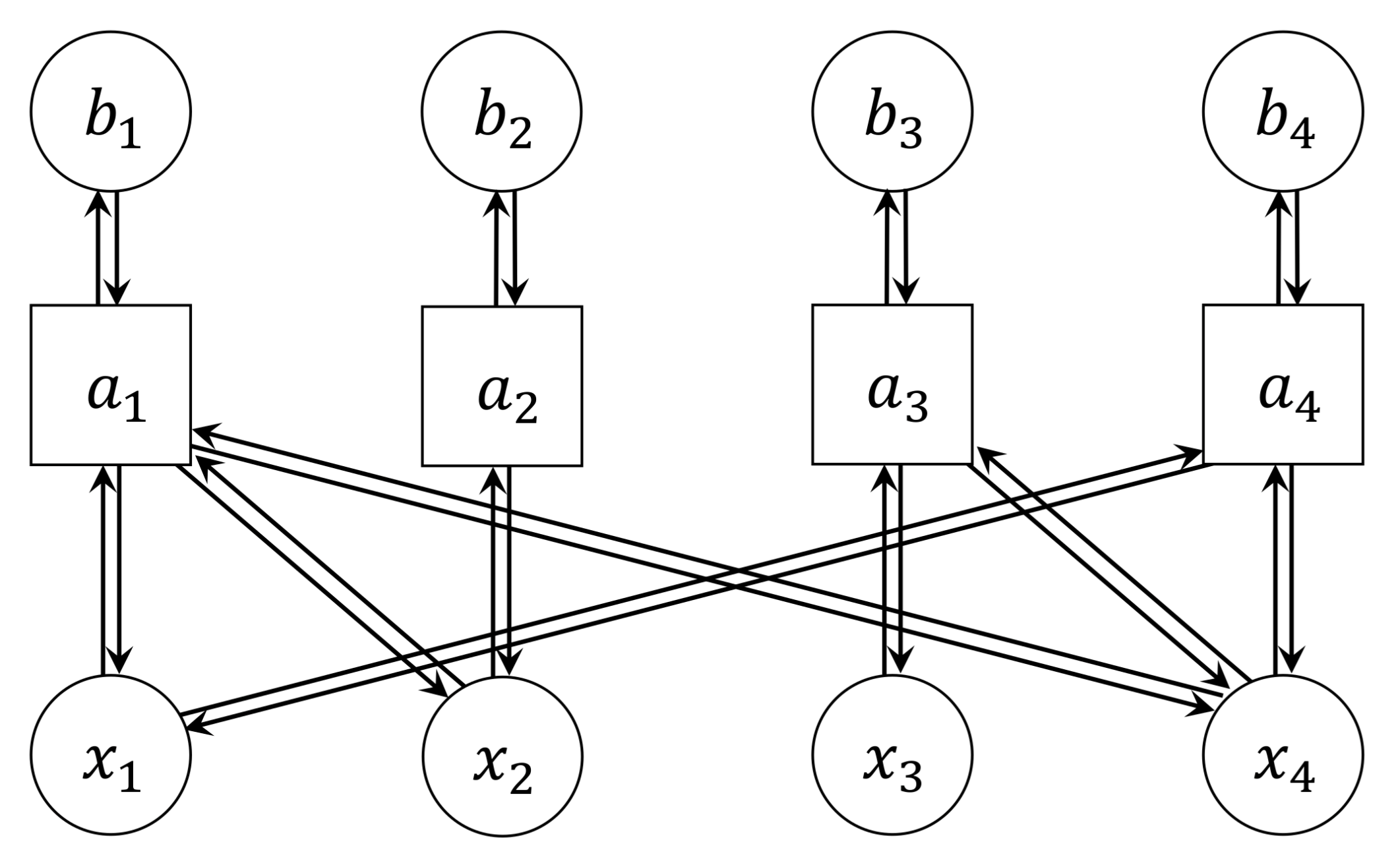
2.1. Factor Graph Representation of a Linear Equation System
2.2. Message Passing Algorithm
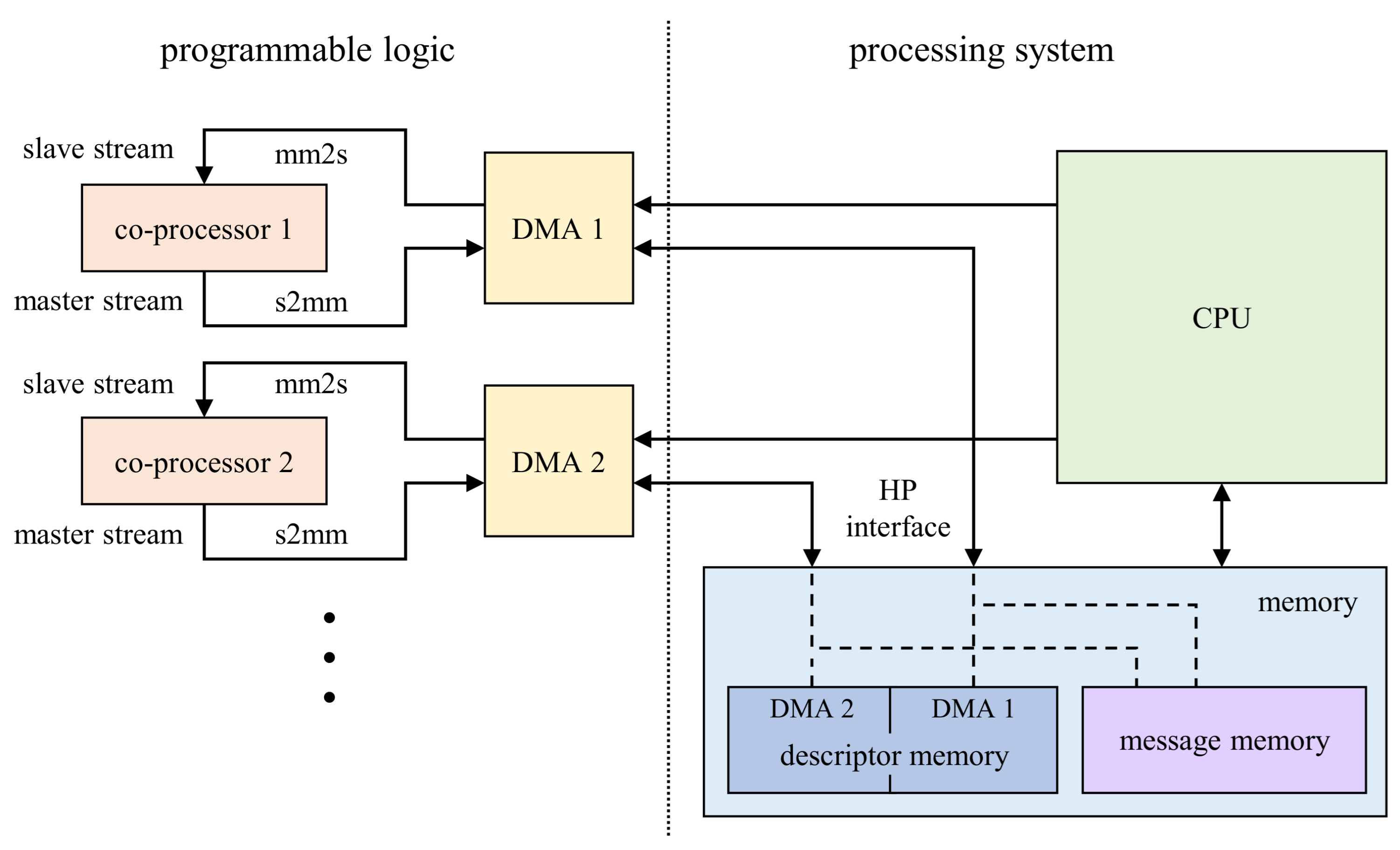
3. Hardware Implementation in a FPGA
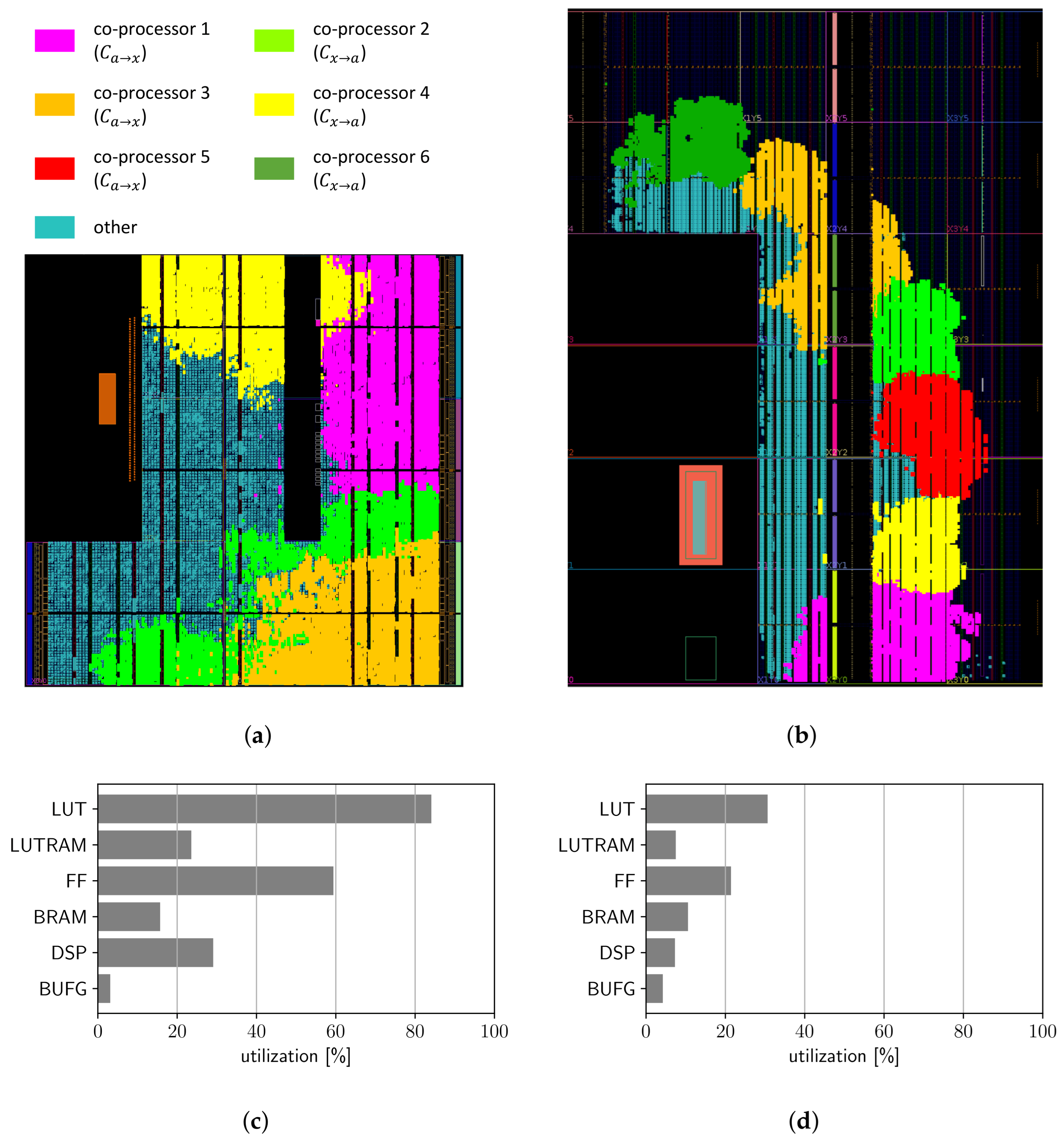
3.1. Dedicated Co-Processors for Message Passing
3.1.1. Co-Processor
3.1.2. Co-Processor
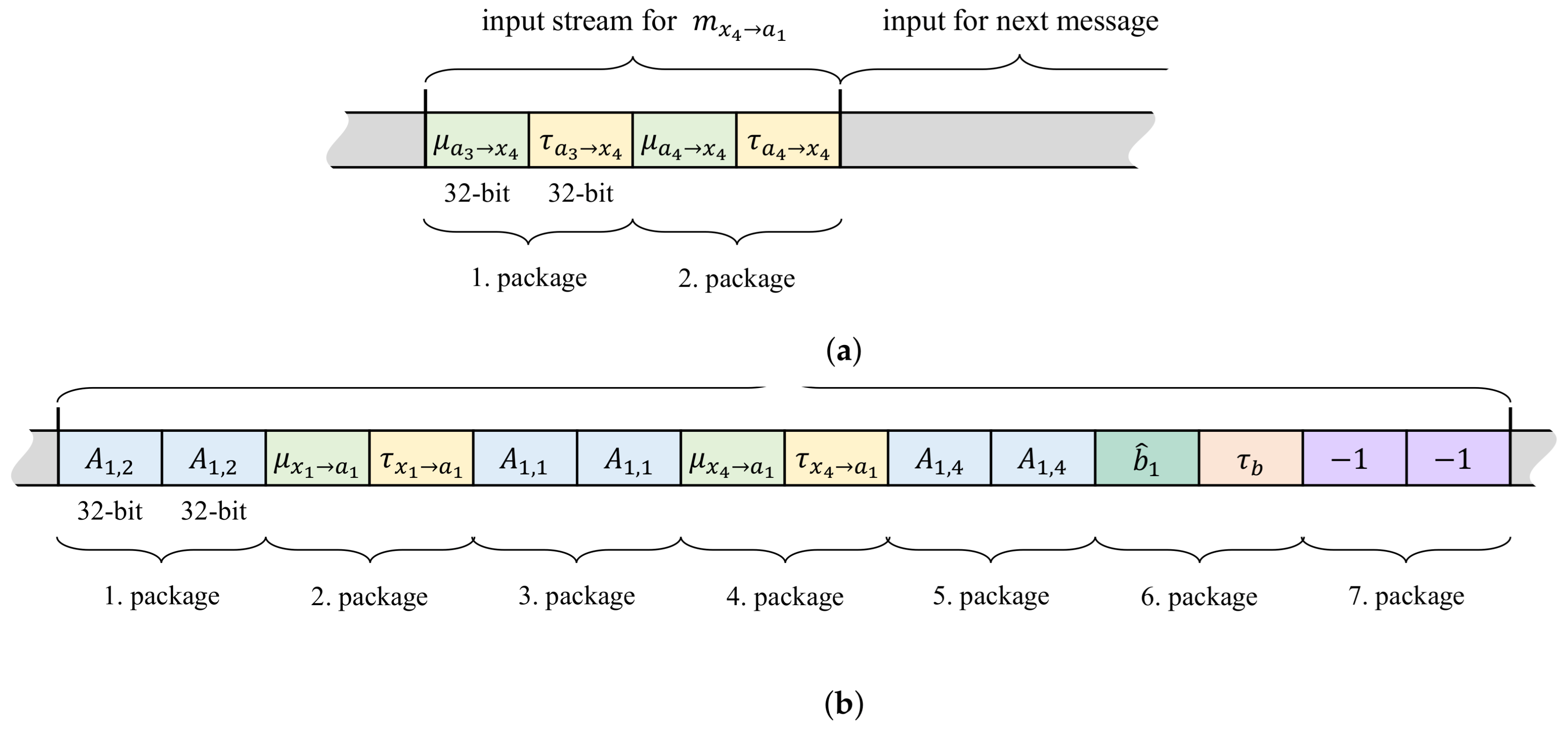
3.2. Interfaces and Memory Access of the Co-Processors
- Memory Mapped to Stream (mm2s) descriptors contain the addresses in memory where to fetch data from as well as the number of bytes to fetch. The fetched data is streamed to the hardware co-processor connected with an AXI4-Stream interface to the DMA.
- Stream to Memory Mapped (s2mm) descriptors on the other hand contain the addresses in memory where to write data to and the data length. The data is coming to the DMA also via an AXI4-Stream interface.
4. Evaluation
4.1. Deployed SoPC Boards
4.2. Evaluation Data Sets
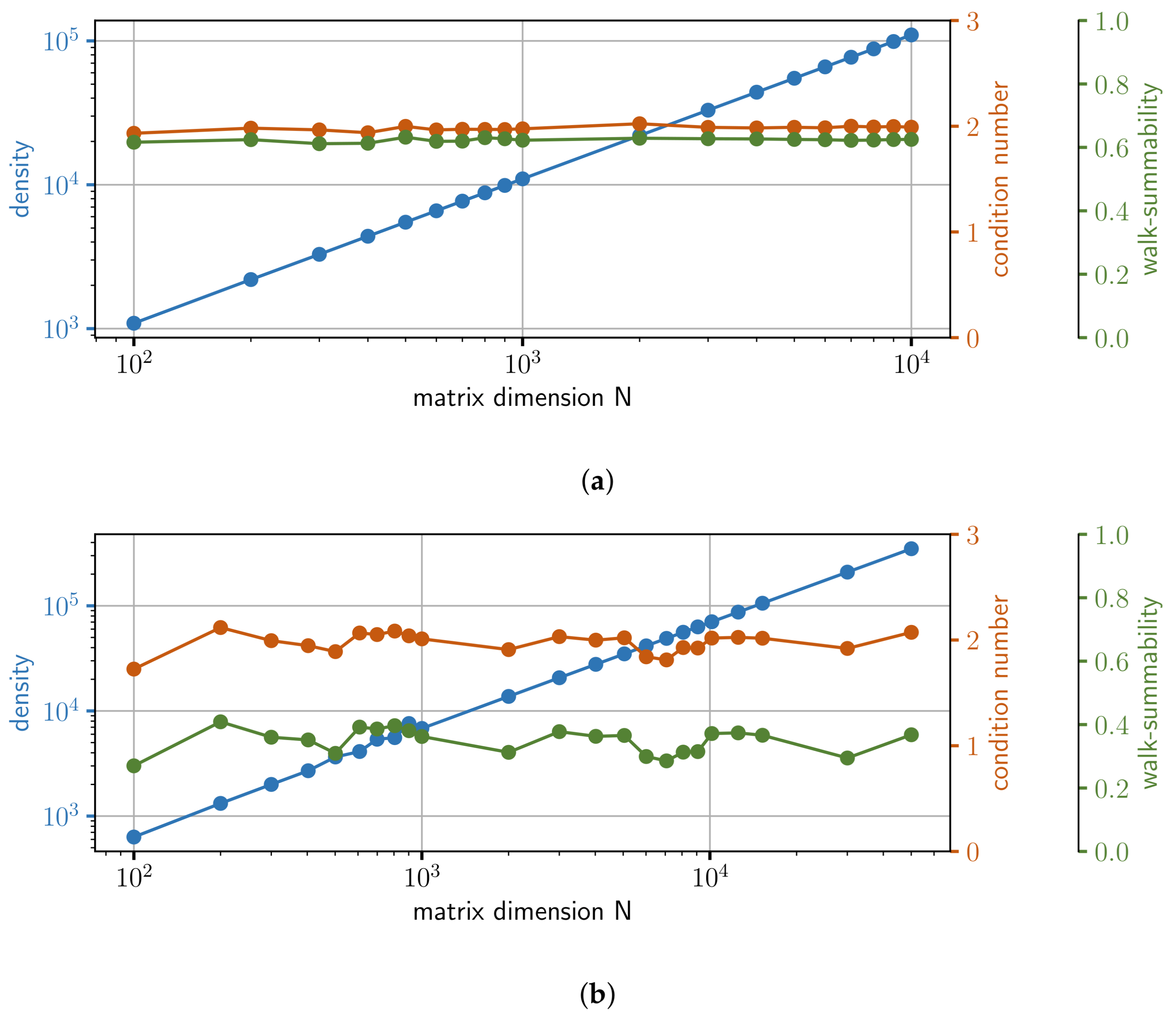
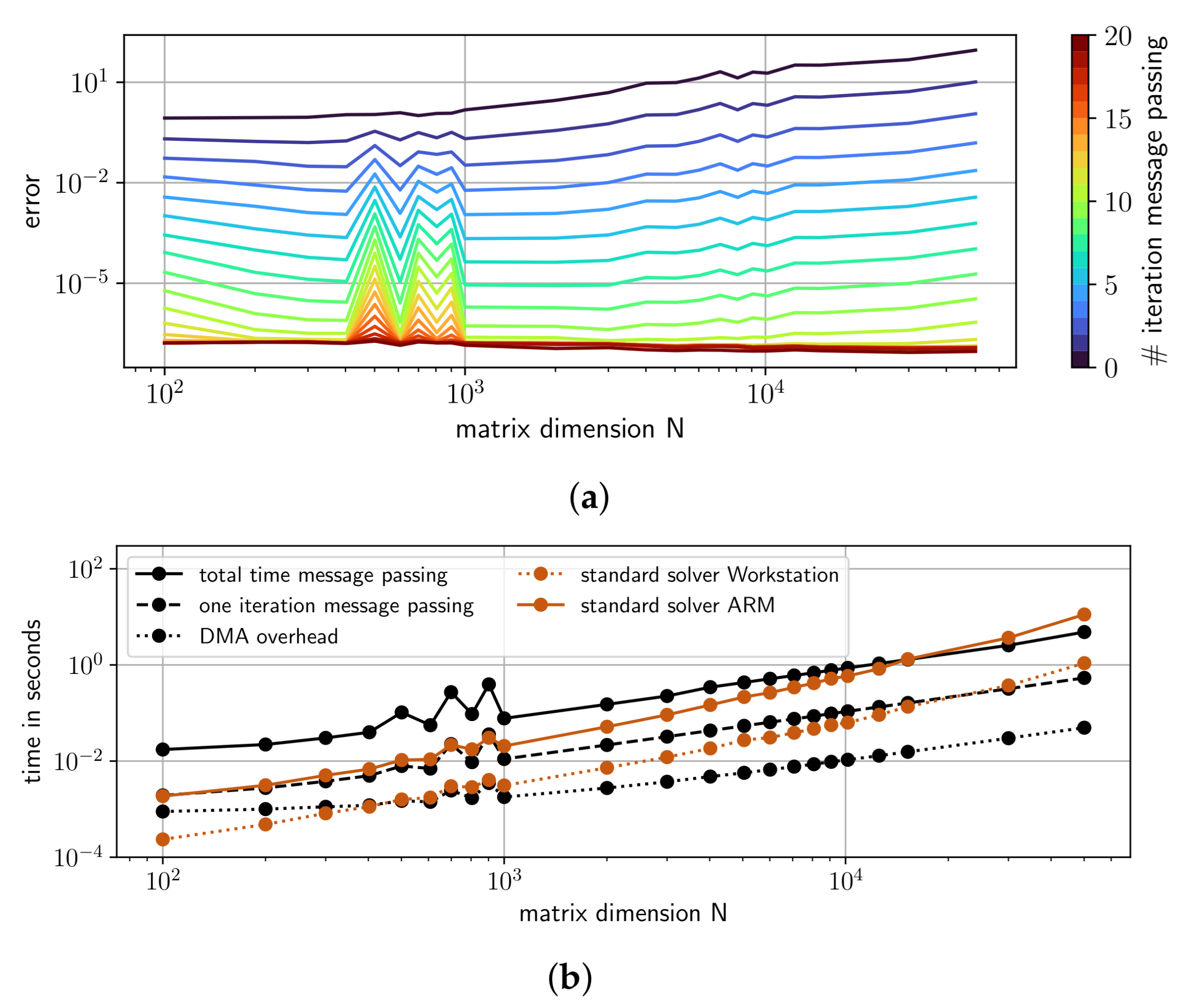
- Random LESs: We generate and for different dimensions N, i.e., number of equations. Here N covers the whole list [100, 200, 300, 400, 500, 600, 700, 800, 900, 1000, 2000, 3000, 4000, 5000, 6000, 7000, 8000, 9000, 10,000]. The entries in the vector are sampled from a random uniform distribution between and 1. Matrix is designed in a way so that it is sparse and diagonal dominant. The density, i.e., the number of elements that are not zeros, is chosen to be , where the location of non-zero elements is random (Here we make use of the scipy library [25], namely the function “scipy.sparse.random”). The non-zero entries are also sampled from a random uniform distribution between and 1. In addition, we add the value 8 to all diagonal elements of the random sparse matrix to get our final matrix . The main properties of the matrices in this set of LESs are depicted in Figure 8a, where each dot on a line represents one matrix. As can be seen, the condition number, as well as the walk-summability is roughly constant, while the density increases linearly with dimension N. This set contains in total 19 LESs.
- Finite Element Method (FEM) LESs: For the second set, we consider the Poisson PDE with and the domain with boundary condition on border of domain . We numerically approximate this variational problem by FEM and Lagrange elements of order one. FEM turns our problem into a LES . However, this approach requires discretizing the domain by a finite number of elements spanning a mesh. The number of nodes of this mesh defines dimension N of our LES. A higher number of nodes and thus a better resolution of the numerical approximation results in a higher dimension N. Before we solve the LES on our hardware, we use an incomplete LU preconditioner [26]. The preconditioner is parameterized in a sub-optimal way. This is on purpose to challenge our solver and to make sure that we do not accidentally solve a linear system where the matrix is the identity matrix, or very close to it. (This would be a trivial problem.) Preconditioning is also a common approach for standard numerical solvers of LES [26]. The main properties of the matrices in this set are depicted in Figure 8b. We parametrize the preconditioner so that the condition number and walk-summability are roughly constant. Nevertheless, there is some variation. We used different meshes in the FEM with different resolutions. Thus, the set contains in total 23 LESs with different dimensions N. All entries in vector are set to zero, except the one entry corresponding to the point in the middle of the domain. This entry is set to 1.
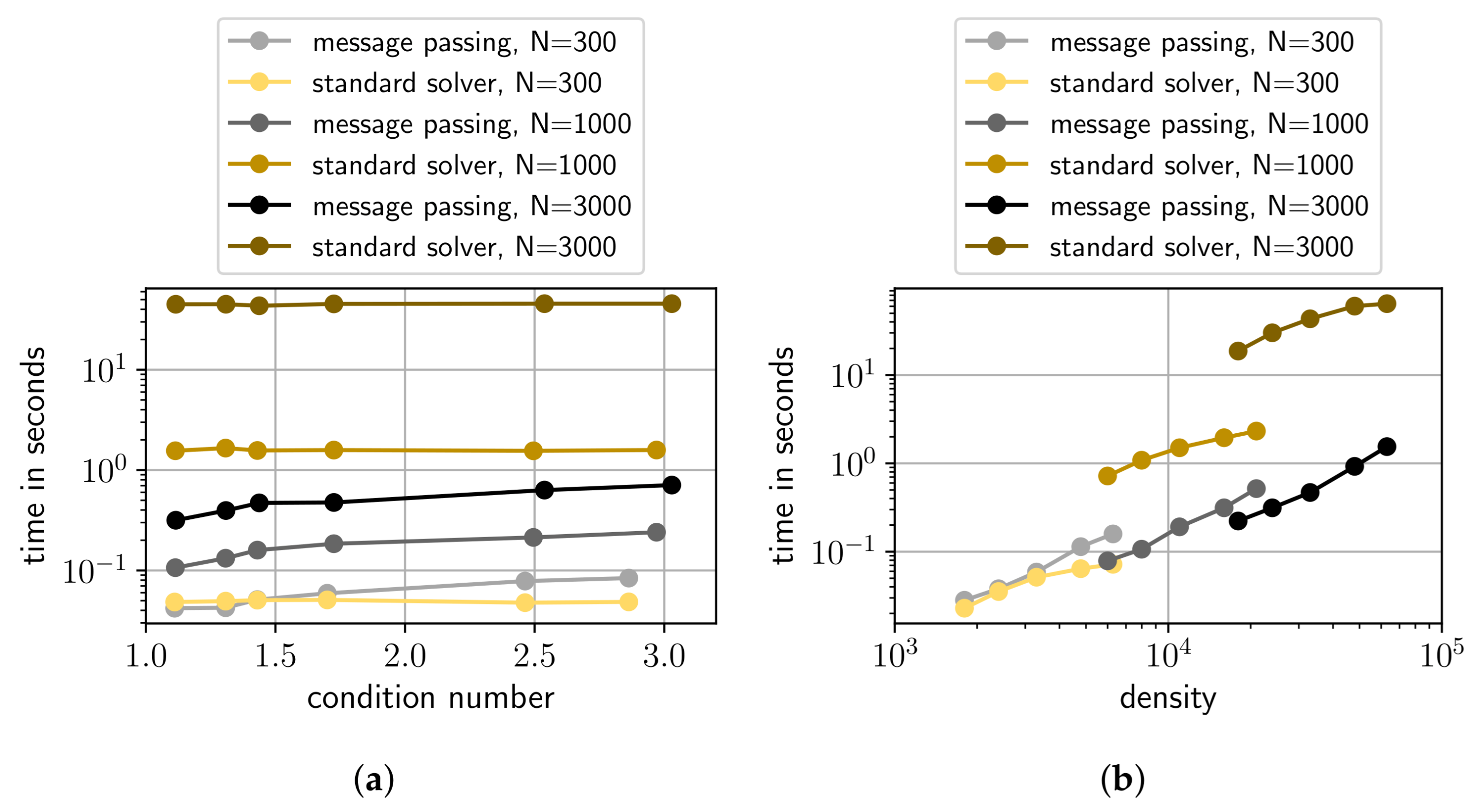
- Constant density LESs: This set of LESs is generated in a similar way as the Random LESs, however, only for dimensions {300, 1000, 3000}. The density of matrix is again . In contrast to the Random LESs, we add different values to the diagonal elements of the randomly generated sparse matrices (5.1, 6, 10, 15, 20, 50). The properties of matrices are shown in Figure 9a. As can be seen, in this set, for a given dimension N, the density is constant for different condition numbers. Entries in vector are again sampled from a random uniform distribution between and 1.
- Constant condition number LESs: Again this set is generated similar to the Random LESs, but only for dimensions 300, 1000, 3000}. This time, we generate matrices with different densities, namely , with 6, 10, 15, 20, 50}. We also add to the diagonal elements of resulting in approximately constant condition numbers for different densities. This dependency is also depicted in Figure 9b. Entries in vector are again sampled from a random uniform distribution between and 1.
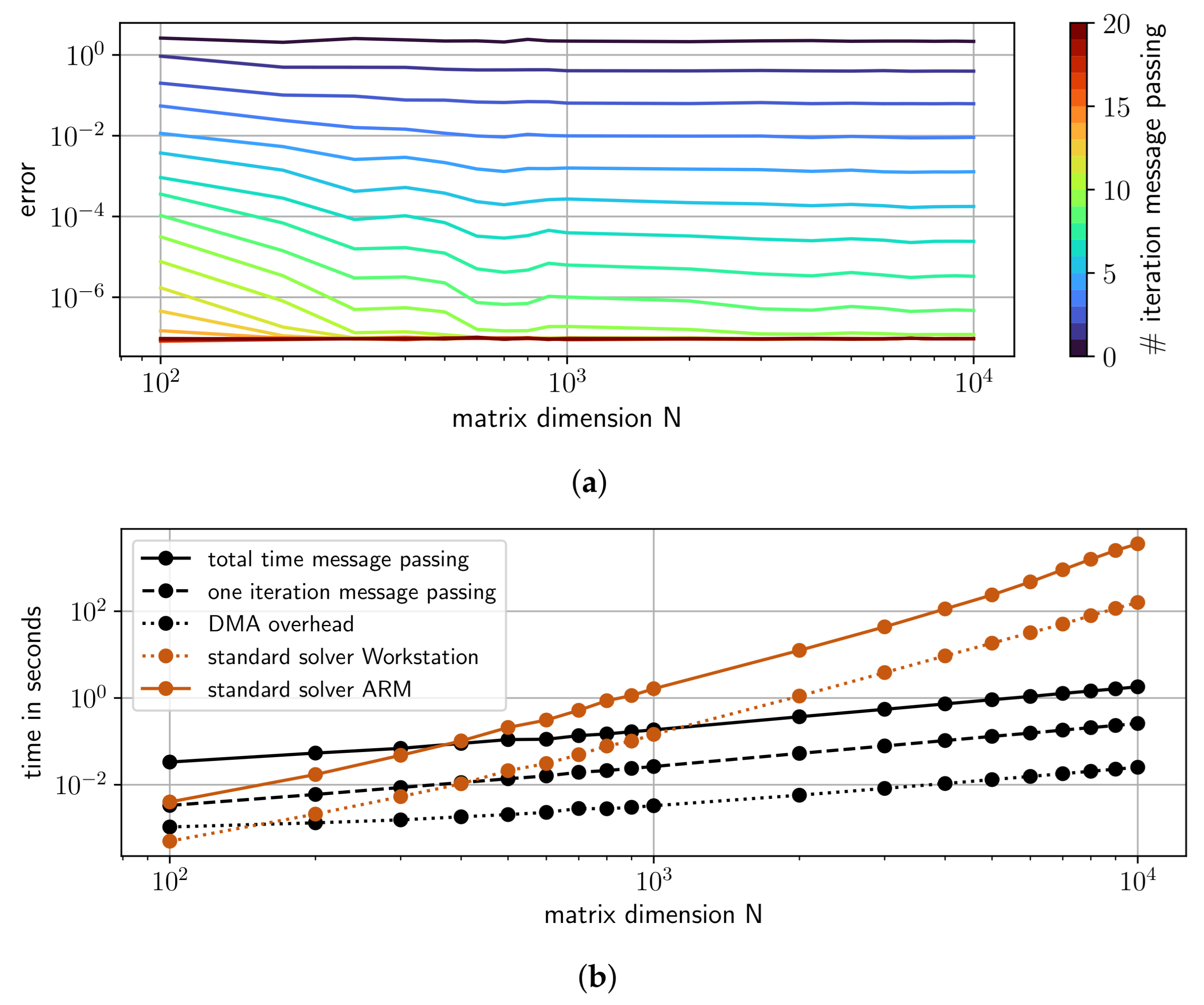
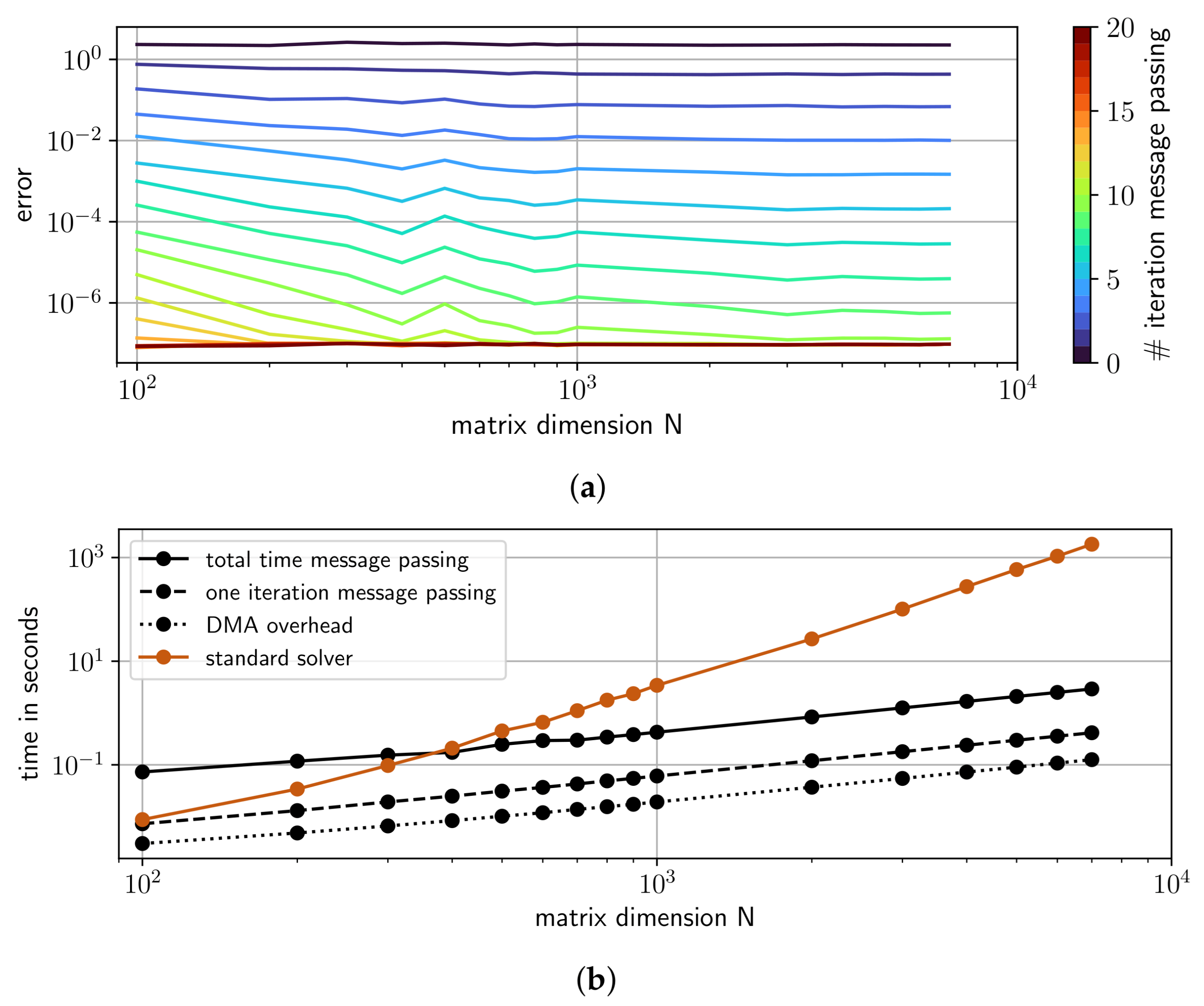
4.3. Performance of GaBP on a SoPC
5. Conclusions and Remarks
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| PDE | Partial Differential Equation |
| FPGA | Field-Programmable Gate Array |
| LES | Linear Equation System |
| GaBP | Gaussian Belief Propagation |
| SoPC | System on a Programmable Chip |
| DMA | Direct Memory Access |
| FEM | Finite Element Method |
| FDM | Finite Difference Method |
| Probability Density Function | |
| FG | Factor Graph |
| CPU | Central Processing Unit |
| IP | Intellectual Property |
References
- Wiedemann, T.; Manss, C.; Shutin, D.; Lilienthal, A.J.; Karolj, V.; Viseras, A. Probabilistic modeling of gas diffusion with partial differential equations for multi-robot exploration and gas source localization. In Proceedings of the European Conference on Mobile Robots (ECMR), Paris, France, 6–8 September 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Pearl, J. Probabilistic Reasoning in Intelligent Systems; Morgan Kaufmann Publishers: San Francisco, CA, USA, 1988. [Google Scholar]
- Frey, B.J.; Kschischang, F.R. Probability Propagation and Iterative Decoding. In Proceedings of the 34th Allerton Conference on Communications, Control and Computing, Champaign-Urbana, IL, USA, 2–4 October 1996. [Google Scholar]
- Loeliger, H.A. An Introduction to Factor Graphs. IEEE Signal Process. Mag. 2004, 21, 28–41. [Google Scholar] [CrossRef] [Green Version]
- Oommen, M.S.; Ravishankar, S. FPGA implementation of an advanced encoding and decoding architecture of polar codes. In Proceedings of the 2015 International Conference on VLSI Systems, Architecture, Technology and Applications, VLSI-SATA 2015, Bengaluru, India, 8–10 January 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Yang, Q.; Wang, L.; Yang, R.; Stewénius, H.; Nistér, D. Stereo matching with color-weighted correlation, hierarchical belief propagation, and occlusion handling. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 492–504. [Google Scholar] [CrossRef] [PubMed]
- Pérez, J.M.; Sánchez, P.; Martínez, M. High memory throughput FPGA architecture for high-definition belief-propagation stereo matching. In Proceedings of the 3rd International Conference on Signals, Circuits and Systems, SCS 2009, Medenine, Tunisia, 6–8 November 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Maechler, P.; Studer, C.; Bellasi, D.E.; Maleki, A.; Burg, A.; Felber, N.; Kaeslin, H.; Baraniuk, R.G. VLSI design of approximate message passing for signal restoration and compressive sensing. IEEE J. Emerg. Sel. Top. Circuits Syst. 2012, 2, 579–590. [Google Scholar] [CrossRef] [Green Version]
- Bai, L.; Maechler, P.; Muehlberghuber, M.; Kaeslin, H. High-speed compressed sensing reconstruction on FPGA using OMP and AMP. In Proceedings of the 2012 19th IEEE International Conference on Electronics, Circuits, and Systems, ICECS 2012, Seville, Spain, 9–12 December 2012; pp. 53–56. [Google Scholar] [CrossRef]
- Weiss, Y.; Freeman, W.T. Correctness of belief propagation in Gaussian graphical models of arbitrary topology. Neural Comput. 2001, 13, 673–679. [Google Scholar] [CrossRef] [PubMed]
- Shental, O.; Siegel, P.H.; Wolf, J.K.; Bickson, D.; Dolev, D. Gaussian belief propagation solver for systems of linear equations. In Proceedings of the 2008 IEEE International Symposium on Information Theory, Toronto, ON, Canada, 6–11 July 2008; pp. 1863–1867. [Google Scholar] [CrossRef] [Green Version]
- El-Kurdi, Y.; Gross, W.J.; Giannacopoulos, D. Efficient Implementation of Gaussian Belief Propagation Solver for Large Sparse Diagonally Dominant Linear Systems. IEEE Trans. Magn. 2012, 48, 471–474. [Google Scholar] [CrossRef] [Green Version]
- Bickson, D.; Dolev, D.; Shenta, O.; Siegel, P.H.; Wolf, J.K. Linear detection via belief propagation. In Proceedings of the 45th Annual Allerton Conference on Communication, Control, and Computing 2007, Monticello, IL, USA, 26–28 September 2007; Volume 2, pp. 1207–1213. [Google Scholar]
- Malioutov, D.M.; Johnson, J.K.; Willsky, A.S. Walk-Sums and Belief Propagation in Gaussian Graphical Models. J. Mach. Learn. Res. 2006, 7, 2031–2064. [Google Scholar]
- Johnson, J.K.; Malioutov, D.M.; Willsky, A.S. Walk-sum interpretation and analysis of Gaussian belief propagation. In Proceedings of the 18th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 5–8 December 2005; pp. 579–586. [Google Scholar]
- Kschischang, F.R.; Frey, B.J.; Loeliger, H.A. Factor graphs and the sum-product algorithm. IEEE Trans. Inf. Theory 2001, 47, 498–519. [Google Scholar] [CrossRef] [Green Version]
- Frey, B.; MacKay, D. A Revolution: Belief Propagation in Graphs with Cycles. Adv. Neural Inf. Process. Syst. 1998, 10, 479–485. [Google Scholar]
- Murphy, K.P.; Weiss, Y.; Jordan, M.I. Loopy belief propagation for approximate inference: An empirical study. Proc. Fifteenth Conf. Uncertain. Artif. Intell. 1999, 9, 467–475. [Google Scholar]
- Elidan, G.; McGraw, I.; Koller, D. Residual belief propagation: Informed scheduling for asynchronous message passing. In Proceedings of the 22nd Conference on Uncertainty in Artificial Intelligence, UAI 2006, Cambridge, MA, USA, 13–16 July 2006; pp. 165–173. [Google Scholar]
- Crockett, L.H.; Elliot, R.A.; Enderwitz, M.A.; Stewart, R.W. The Zynq Book: Embedded Processing with the Arm Cortex-A9 on the Xilinx Zynq-7000 All Programmable Soc; Strathclyde Academic Media: Glasgow, Scotland, 2014. [Google Scholar]
- Xilinx Inc. ZCU104 Evaluation Board User Guide. 2018. Available online: https://www.xilinx.com/support/documentation/boards_and_kits/zcu104/ug1267-zcu104-eval-bd.pdf (accessed on 1 July 2021).
- Xilinx Inc. Floating-Point Operator V7. 1, LogicCore IP Product Guide, Vivado Design Suite. 2020. Available online: https://www.xilinx.com/support/documentation/ip_documentation/floating_point/v7_1/pg060-floating-point.pdf (accessed on 1 July 2021).
- Xilinx Inc. AXI DMA v7. 1, LogicCore IP Product Guide, Vivado Design Suite. 2019. Available online: https://www.xilinx.com/support/documentation/ip_documentation/axi_dma/v7_1/pg021_axi_dma.pdf (accessed on 1 July 2021).
- Digilent Inc. PYNQ-Z1 Board Reference Manual. 2017. Available online: https://reference.digilentinc.com/_media/reference/programmable-logic/pynq-z1/pynq-rm.pdf (accessed on 1 July 2021).
- SciPy Library. Available online: https://www.scipy.org/version1.4.1 (accessed on 1 July 2021).
- Saad, Y. Iterative Methods for Sparse Linear Systems, 2nd ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2003. [Google Scholar] [CrossRef]
- Kamper, F.; Steel, S.J.; du Preez, J.A. Regularized Gaussian belief propagation with nodes of arbitrary size. J. Mach. Learn. Res. 2019, 20, 1–37. [Google Scholar]
- Su, Q.; Wu, Y.C. On convergence conditions of Gaussian belief propagation. IEEE Trans. Signal Process. 2015, 63, 1144–1155. [Google Scholar] [CrossRef] [Green Version]
- Manss, C.; Shutin, D.; Wiedemann, T.; Viseras, A.; Mueller, J. Decentralized multi-agent entropy-driven exploration under sparsity constraints. In Proceedings of the 2016 4th International Workshop on Compressed Sensing Theory and its Applications to Radar, Sonar and Remote Sensing (CoSeRa), Aachen, Germany, 19–22 September 2016; pp. 143–147. [Google Scholar] [CrossRef]
- Wiedemann, T.; Manss, C.; Shutin, D. Multi-agent exploration of spatial dynamical processes under sparsity constraints. Auton. Agents Multi-Agent Syst. 2018, 32, 134–162. [Google Scholar] [CrossRef] [Green Version]
- Tipping, M.E. Sparse Bayesian Learning and the Relevance Vector Machine. J. Mach. Learn. Res. 2001, 1, 211–244. [Google Scholar]
- Xilinx Inc. Zynq-7000 AP SoC Technical Reference Manual. 2021. Available online: https://www.xilinx.com/support/documentation/user_guides/ug585-Zynq-7000-TRM.pdf (accessed on 1 July 2021).
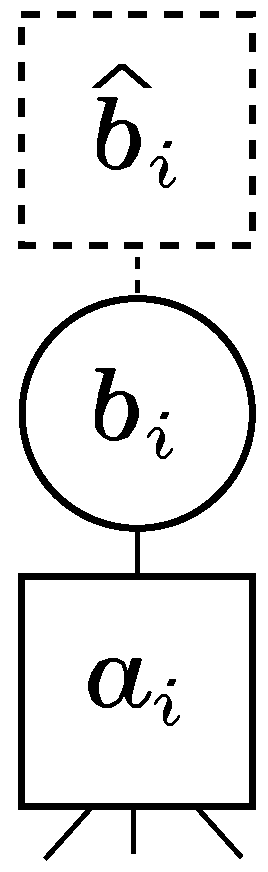





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wiedemann, T.; Spengler, J. Gaussian Belief Propagation on a Field-Programmable Gate Array for Solving Linear Equation Systems. Electronics 2021, 10, 1695. https://doi.org/10.3390/electronics10141695
Wiedemann T, Spengler J. Gaussian Belief Propagation on a Field-Programmable Gate Array for Solving Linear Equation Systems. Electronics. 2021; 10(14):1695. https://doi.org/10.3390/electronics10141695
Chicago/Turabian StyleWiedemann, Thomas, and Julian Spengler. 2021. "Gaussian Belief Propagation on a Field-Programmable Gate Array for Solving Linear Equation Systems" Electronics 10, no. 14: 1695. https://doi.org/10.3390/electronics10141695
APA StyleWiedemann, T., & Spengler, J. (2021). Gaussian Belief Propagation on a Field-Programmable Gate Array for Solving Linear Equation Systems. Electronics, 10(14), 1695. https://doi.org/10.3390/electronics10141695





