1. Introduction
With an increase in the proliferation of clean energy, several promising power generation candidates have been receiving increased attention. Proton-exchange membrane fuel cells (PEMFC), also known as polymer electrolyte membrane fuel cells, are increasing in their adoption as they offer several advantages: being emissions-free, efficient, quiet operation, relatively low-temperature operation, quick start-up, etc. One of the most important components of a fuel cell is the flow distributor or the flow field, accounting for 60–80% of the weight and about 30–50% of the cost [
1,
2]. These flow fields have been extensively researched over the last few decades and a variety of geometries have emerged has leading candidates, each with its own strengths.
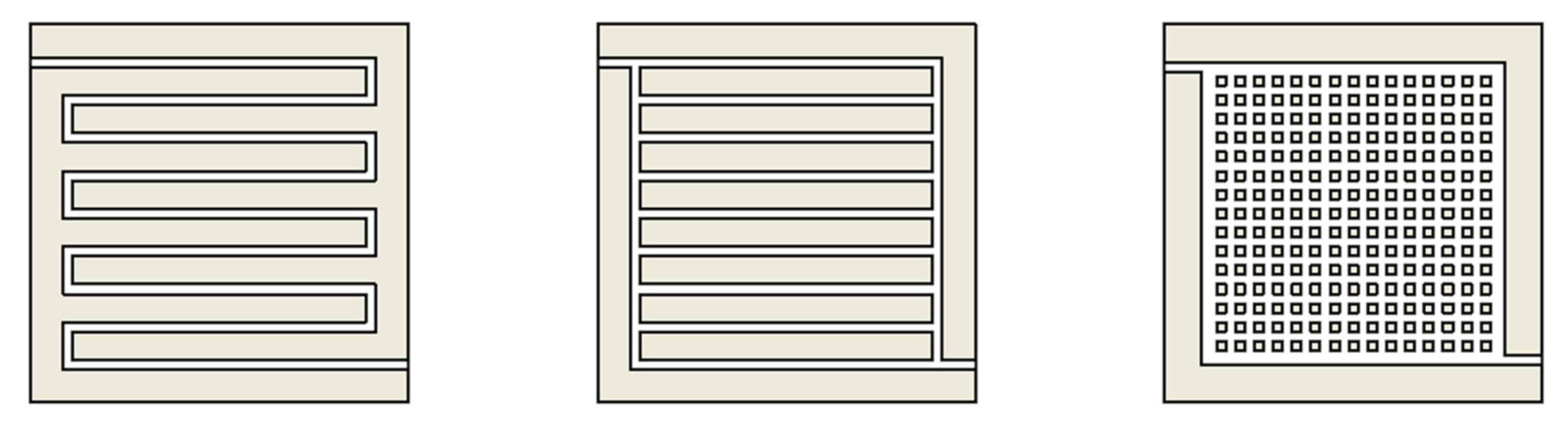
Figure 1 shows three such geometries, the serpentine, columnar, and pin-type.
Several design approaches have been used to improve the weaknesses of flow fields to improve overall fuel cell performance. Biomimetic principles have been extensively studied and applied to the design of flow fields. The review paper in [
3] summarizes the state of the art in the application of biomimetics to flow field design. Inspiration is derived from bionics, fractals, honeycombs, leaves, lungs, sponges, etc. The study in [
4] compared a leaf design and a lung design to common designs. Both designs outperformed conventional designs, but the leaf was found to be the best. The study in [
5] explored several nature-inspired designs as well. A significant finding that was common to such designs was that performance improvements attributed to flow fields came from uniform reactant distribution and reduced pressure drop. Wang et al. [
6] explored a novel biometric design that demonstrated superior water removal ability when compared to conventional designs.
One explanation that has been proffered to explain the efficacy of leaf-type or lung-type designs is Murray’s Law [
7]. This law states that when biological systems pumping fluids in a vessel need to branch, the sum of the cubes of the radii of the daughter vessels should be the cube of the parent vessel to minimize the amount of pumping power necessary for the entire system. This phenomenon has been studied extensively in natural fluid systems carrying air (lungs), blood (blood vessels), sap (leaves), etc. The study reported in [
8] is an example of using this law to design flow fields for PEMFCs. Here, the hydraulic diameter was used instead of radius as the channels were rectangular in cross-section. Several design variations based on Murray’s Law can be found in the literature.
The study in [
9] is a graduate thesis that specifically explored how Murray’s Law is transposed from biological systems to engineered ones. It pointed out that past studies focused on the geometric and physical aspects of Murray’s Law without taking a closer look at the performance implications. The main finding in a related study by the same author [
10] found that about 30% of the overall improvement in performance of a flow field design compared to another could be explained by the increased pressure drop across that flow field. In other words, by forcing the reactants through the flow channels at higher pressures, more of it passed through the gas diffusion layer out of the channel to participate in the electrochemical reaction that produces power. As expected, this increased pressure needs to be constantly maintained and increases the overall operating costs, thereby negating some of the gains.
This study takes a critical look at the basis for the application of Murray’s Law to flow structures in flow fields, specifically the implications of pumping work and metabolic work. There is a dearth of optimization studies pertaining to flow field design, because such geometric optimization tends to be labor-intensive and requires prohibitive computational effort. The few existing studies only look at performance from a flow standpoint, without considering electrical condition or manufacturability. The following section attempts to cast Murray’s Law in a manner more suitable to flow field design and then proposes a multiobjective optimization framework that can implement it efficiently.
2. Examination of Murray’s Law
The primary purpose of the flow field in a fuel cell or similar device is to distribute reactants uniformly to the catalyst layer via the gas diffusion layer and to remove products such as water. Excess reactants are also removed [
11]. It must be pointed out that flow fields are not limited to fuel cells. In this study, that is the primary focus: distribution of fluids. Flow fields are integral parts of the design of several other complex engineered structures such as flow batteries, heat exchanges, nuclear reactors, etc. Flow fields are also referred to as flow channels, flow distributors, flow separators, etc.
Typically, there is one inlet into the fuel cell and one outlet. Thus, the flow field must be designed such that the reactants entering from a single point get distributed as uniformly across the entire area of the fuel cell. Any unused reactant that exits is recirculated. Several geometries, such as those in
Figure 1, have been studied. The most effective flow fields slow down the inlet gas, allowing sufficient time for diffusion out of the channels and into the gas diffusion layer. The pins in the pin-type design act like obstacles to the flow. This increases diffusion, but also causes a large pressure drop between the inlet and the outlet. The inlet pressure must be high enough to overcome this differential and also to force out any water that would otherwise clog the channels. This is a parasitic loss that designers try to minimize by striking a balance between low pressure drop and performance.
It is thought that by mimicking designs from nature, fuel cells can benefit from the greatest strengths of such designs: uniform reactant distribution and waste product removal while requiring the least pumping effort. For a biological system, minimizing pumping effort is critical to reduce the metabolic burden on the organism. This can be accomplished by evolving large diameter vessels. Further, increasing the number of such vessels will make it easier to reach all parts of the organism to ensure proper distribution of nutrients and removal of waste. However, building and maintaining such large and numerous vessels also exerts a metabolic cost on the organism. Thus, over millions of years, across numerous species, nature has evolved an optimal relationship between the size of vessels, the size of branching vessels, their branching angles, their overall number, etc. [
12,
13]. In this study, the branching angles and the frequency of branching were not considered. Only the diameter relationship between parent and daughter vessels was considered. Other considerations can be explored in future studies.
Sherman [
13] explains the mathematical optimization behind Murray’s Law. It is summarized here in brief. Equation (1) is the Hagen–Poiseuille relationship:
where
pi is the pressure drop across the
ith channel or vessel,
μ is the fluid viscosity,
Li is the channel length,
qi is the volumetric flow rate, and
ri is the channel radius (hydraulic diameter,
Di, for rectangular flow field channels). The pumping power,
Pf, is:
where
a = 128
μL/
π and
L can be taken to be 1 or some arbitrary value. The metabolic power required to maintain a vessel is:
where
m is a metabolic coefficient and
b =
mπL. The total power required is:
Differentiating with respect to
r to find the minimum and rearranging terms produces:
where
k is a constant. In general, for successive branching generations:
Equation (6) can be written for hydraulic diameters and by eliminating flow by assuming mass continuity.
where
D(
i) is the hydraulic diameter of the parent branch and
D(
i + 1) is the hydraulic diameter of the daughter branch. Thus, by balancing the need for larger vessels to reduce pumping work with the need for smaller vessels to reduce metabolic work, the cubic relation is reached.
2.1. Challenges to the Cubic Relation
Studies to validate the cubic relation have pointed out how, for a number of reasons related to the complexity of natural biological systems and preparation of samples, this relation is not perfectly encapsulated in all organisms. Both [
13,
14] cited studies that found that the expected cubic relation can vary from 2.33 to 3.006. This depends on the generation, i.e., how far down the branching network the measurements are made, the organ, the organism, etc. Sciubba [
15] conducted an entropy analysis to point out weaknesses in Murray’s Law applied to biological systems. In Murray’s Law, a symmetric split in the first generation leads to a radius ratio of 1:2
1/3 or 1:0.7937. Sciubba [
15] pointed out alternative optimal ratios ranging from 1:0.198 (turbulent flow) to 1:0.8. Equation (4) can be modified to obtain something other than a cubic relation. Either the pumping work or the metabolic work terms can be modified. Assuming the pumping work is accurately described by the Hagen–Poiseuille equation, the metabolic work term’s exponent can be modified:
where
n is taken to be between 1.5 and 3 as an example. Then, the exponent in Equation (7) would be (
n + 4)/2. If
n = 1.5, then the exponent is 2.75. For 3, it becomes 3.5. Physically, this means that the metabolic cost is not necessarily proportionate to the volume of the vessel as implied in Equation (3).
2.2. Challenges to Applicability to Non-Biological Flow Fields
Both [
8,
9] caution the designer on improperly applying Murray’s Law, or any biomimetic design, to non-biological flow fields. They point out the high degree of interconnectedness in biological systems, which provides redundancy in the case of damage to a particular vessel. This is usually absent from non-biological flow fields. Biological flow fields also typically transport different types of fluids and their flow rates can vary due to diffusion in and out of the vessels. The directions are also often reversed, with nutrients in one direction and waste in the opposite direction. They postulate that the key strengths of biological designs are to distribute nutrients and remove wastes efficiently, meaning uniformly and with minimum pressure losses. It is further suggested in this study that the entire system’s design and performance must be considered, not just the flow aspect. This is because biological evolution, from which biomimetics draws inspiration, happens on whole organisms and not just individual aspects of organisms.
2.3. Analogy to Metabolic Work
The balance in Murray’s Law and biological systems that emulate it to any extent is between pumping effort and metabolic effort. However, in non-biological flow fields, there is no cost to maintain the structures once the part has been manufactured. Rather, it is argued here that the cost comes from the manufacturability of the design: how much does it cost to design, test, and manufacture a complex branching network as opposed to any simple design like the ones in
Figure 1. Thus, the efficacy of Murray’s Law becomes limited if applied improperly. This study considers different metrics that should be considered besides minimization of pressure loss. As mentioned above, a design that is overly complicated will exact a steep manufacturing cost. In the current era dominated by prototypes, a large number of flow fields are still manufactured using rapid prototyping techniques as opposed to mass production techniques. Thus, complex designs portend complex design changes and it becomes prohibitively expensive to make even small changes, analyze them, build, test, and operate them. In this study, manufacturability is proposed as an objective to be minimized. Its exact function would depend on a variety of factors, but, for demonstration purposes, its form is taken to be the same as the metabolic cost,
brn. Note that when
n = 2,
brn =
m·
V, where
V is the volume. The argument here is that the more volume of material that has to be removed in a machining process, the more expensive the manufacturing would be. To account for additional expense due to design, the exponent can be increased to 2.5 or 3. Along with this, it is argued that having a large number of disparate channel widths makes the design and manufacturing process more complex, so minimizing the standard deviation of the channel widths would be desirable. More studies on the manufacturability of flow fields are certainly required. Some comments are provided later in this paper on variations of this function.
Another consideration is conduction. In Reference [
16], a pin-type flow field’s channel widths were optimized to make the flow as uniform as possible. The standard deviation of the flow velocity in every channel was minimized. The authors recognized that channels closer to the inlet and outlet would be larger than channels in the middle. However, they also identified that simply making channels large reduces the total amount of “land” or “rib” area, the material around the channels that makes direct contact with the electrolyte and is responsible for current collection. If this area is too small, ohmic losses will overcome any gains in transport losses. They tackled this issue by make the rib area a constraint, at least 40% of total area. In this study, the conduction area is treated as another objective. By minimizing the total channel area, the conduction area is maximized. This also increases the overall strength of the flow field plate. Note that it is a structural component as well and must bear the stress of being bolted to the opposite side flow field plate and holding the fuel cell together.
2.4. Multiobjective Optimization Approach to Flow Field Design
It is clear that existing studies have applied Murray’s Law to design flow fields in a limited sense and without optimization. In this study, flow field optimization is carried out using multiobjective optimization. Rather than programming Murray’s Law, a genetic algorithm, which mimics the principles of natural selection leading to a global optimal solution, was used to find the best channel widths. The objectives of interest were minimization of the pressure drop, the area of the channels (maximizing the area of conduction), the design effort or manufacturability, and the standard deviation of the flow velocities in each channel.
The input to the problem was the widths of all the channel. This means the problem was a multivariable problem—having several decision variables. Some of the objectives mentioned are in direct conflict with one another: improving the pressure drop with wider channels directly leads to reduced area available for conduction and a wide range of flow velocities. Channels with uniform width may be easy to manufacture, but the flow velocities would be non-uniform. Such problems are classified as multiobjective optimization problems (MOOP). It is not possible to simultaneously optimize each objective. Rather, in a MOOP, the designer obtains a Pareto-front of solutions, which includes the extreme values for each objective. Then, some higher-level information is applied to select one solution with the best tradeoff to implement. Such an approach gives the designer flexibility as a wide range of solutions is available.
In this study, a genetic algorithm was used to solve the problem. A genetic algorithm (GA) is an optimization tool that mimics the principles of genetics and natural selection. They operate by applying the principle of “survival of the fittest” on a population of candidate solutions to successively produce better solutions through each generation. Multiobjective Gas (MOGA) area a class of tools based on Gas that are used find a set of solutions based on the principle of non-domination. The closer this set of solutions is to the true Pareto-optimal front, the better the algorithm. A MOGA was used in this study as it produces a solution set that is a good approximation of the Pareto-front thereby effectively solving the MOOP. Local minima are also avoided. Furthermore, it gives solutions that are distributed throughout the front, leading to a wide choice from which the designer can pick a solution that best fits their need. To do this, a non-dominated sorting genetic algorithm, NSGA-II [
17], one of the most widely used GA, was adopted.
Figure 2 shows a step-by-step procedure for NSGA-II for a problem with two objective functions and one decision variable, which can be easily adopted for an arbitrary number of objectives and decision variables. A detailed description with a practical example can be found in Reference [
18].
Optimization of fuel cell flow fields is not well studied in the literature and there are even fewer studies involving multiobjective optimization. Kizilova et al. [
19] used the principle of minimum entropy generation to optimize fractal-like flow channel designs for PEMFCs. A simplified 1D model was found to give results of comparable accuracy to a 3D model. Zhang et al. [
20] looked at the serpentine flow field with three different flow rates and four different land widths. The highest flow rate gave the best performance. Similarly, the larger the land width, the better the performance. Pumping power was found to significantly affect all these results. Similarly, Luo et al. [
21] looked at adding rib grooves to the serpentine flow field channels. A diminishing rate of return was found with increasing rate of rib grooves. Li et al. [
22] was a study that used a GA coupled with a CFD (computational fluid dynamics) package to optimize a blocked channel design. The block heights in the channels were the decision variables. Only 20 generations were needed to achieve convergence, most likely because only one channel was analyzed. Liu et al. [
23] used a genetic algorithm to solve a MOOP whose objectives were maximizing energy efficiency and output power of the fuel cell. The operating conditions and channel dimensions were the decision variables. Sohani et al. [
24] also optimized the operating conditions, i.e., pressure, temperature, stoichiometry, etc., to find the best efficiency, economics, size, and environmental impact. The results were presented for various applications. Xie et al. [
25] also optimized channel geometry to improve output power and reduce power consumption. None of the studies in the literature considered the objective functions mentioned here simultaneously while optimizing the geometry of an entire flow field.
The following section presents the flow field model used for optimization. A pin-type flow field was used as an example. The section after that presents optimization results.
5. Fuel Cell Performance
CFD software packages have been used extensively in the literature to test the performance of various flow field designs used in PEMFCs. Several studies have derived inspiration from Murray’s law and compared CFD simulations to experimental results [
8,
9,
10,
16]. This section uses a similar approach to provide a quick, cost-effective way to compare the performance of the proposed design in a fuel cell. The same CFD settings in
Table 3 were used. The additional FC-specific parameters were from [
16] and are summarized in
Table 5. Note the GDL refers to the gas diffusion layer of the fuel cell.
Figure 15 shows flow results. The mass fraction of water is shown because the aim of this study is to investigate the performance of nature-inspired designs using Murray’s Law. Water is a byproduct in PEMFC operation and has been shown to be a significant limiting factor at high current densities [
10]. Thus, removal of water is a critical determining factor in selecting effective designs. Note that in
Figure 15, the upper limit is set to 0.3 in order to glean greater details in the results; mass fraction of water is not expected to be significantly close to 1.0 as most of the fluid in the channel is the reactant gas. As can be seen, the non-optimized design has a higher mass fraction in several regions, particularly in the corners opposite the inlet/outlet. Comparatively, the MOGA design does a better job at removing water. These results are generally consistent with previous studies on pin-type designs. Guo et al. [
16] found a similar issue with water saturation in the corners.
It is difficult to quantify the difference. If the mass fraction at every computational node in the flow channels is averaged, the value for the unoptimized design is 0.1712 and for the MOGA design it is 0.1564, about 9% lower. Heck et al. [
10] came to similar conclusions on nature-inspired designs being better at water management. These results are also consistent with the flow simulation results in
Figure 12. The peak current density in the unoptimized design was 0.76 A/cm
2 and for the MOGA design it was 1.35 A/cm
2. This further confirms the efficacy of the MOGA design and matches results found in [
16].
6. Conclusions
The present work examines the applicability of Murray’s Law to flow fields for fuel cells and other flow devices. To design effective flow fields, the problem was cast as a multiobjective optimization problem with conflicting objectives. Four objectives were considered and applied to the pin-type flow field. Two geometric scales were analyzed, the 3 × 3 and the 11 × 11 design. Pareto-fronts were obtained. One solution from these fronts was picked for illustrative purposes. Then, using the channel widths produced by NSGA-II, the flow fields were modeled in SolidWorks and CFD simulations were performed. The optimized designs were compared with their unoptimized counterparts, those with constant channel widths. In both cases, the optimized designs had a lower maximum flow velocity and the standard deviation of the flow velocities in the channels was lower, 94% and 57% lower for the 3 × 3 and the 11 × 11 designs, respectively. These were found to be similar to existing studies. The nearest point method was used to demonstrate how one solution from a front of non-dominated solutions may be selected. Finally, CFD fuel cell simulations further confirmed the performance benefits of the MOGA design. Future studies can consider other geometries and consider reactant consumption. Branching ratios and frequency can also be studied.