Adaptive Chaotic Image Encryption Algorithm Based on RNA and Pixel Depth
Abstract
:1. Introduction
2. Related Works
3. Materials and Methods
3.1. 2D-ILASM Chaotic System
3.2. Chen-4D Hyperchaotic System
3.3. RNA Encoding Rules and Operations
3.4. Pixel Depth
3.5. 3D Adaptive Arnold Transform
4. Results
4.1. Proposed Algorithm
4.1.1. Key Generation
4.1.2. Encryption Process
4.1.3. Decryption Process
4.2. Experiments
4.3. Algorithm Analyses
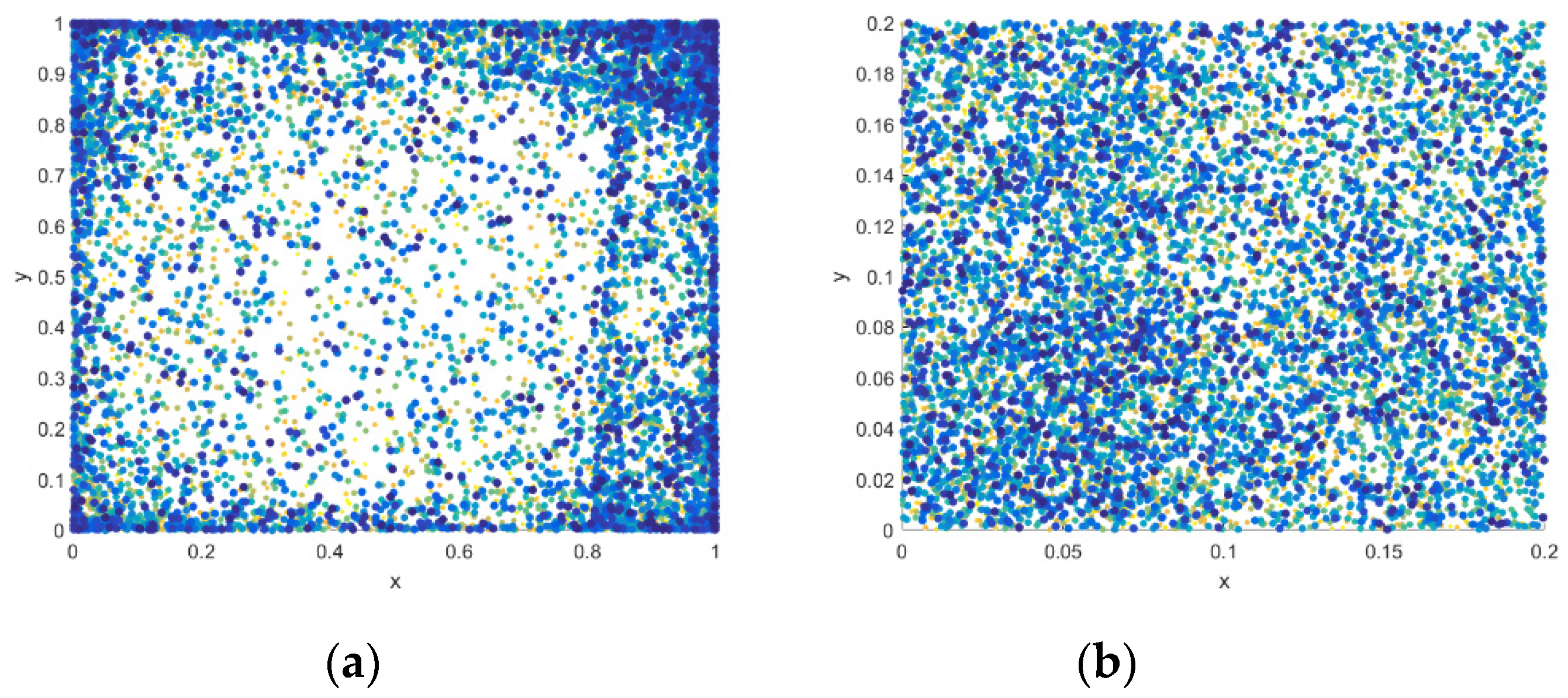
4.3.1. Key Space Analysis
4.3.2. Key Sensitivity Analysis
4.3.3. Histogram Analysis
4.3.4. Chi-Squared Test
4.3.5. Information Entropy Analysis
4.3.6. Differential Attack Analysis
4.3.7. Encryption Quality Analysis
4.3.8. Correlation Analysis
4.3.9. Robustness Analysis
4.3.10. Time Complexity Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhang, Y.; Tang, Y. A plaintext-related image encryption algorithm based on chaos. Multimed. Tools Appl. 2018, 77, 6647–6669. [Google Scholar] [CrossRef]
- Zhu, S.; Zhu, C.; Wang, W. A New Image Encryption Algorithm Based on Chaos and Secure Hash SHA-256. Entropy 2018, 20, 716. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, L.; Li, Z.; Li, J.; Hua, W. A novel bit-level image encryption algorithm based on chaotic maps. Opt. Lasers Eng. 2016, 78, 17–25. [Google Scholar] [CrossRef]
- Wang, X.; Feng, L.; Zhao, H. Fast image encryption algorithm based on parallel computing system. Inform. Sci. 2019, 486, 340–358. [Google Scholar] [CrossRef]
- Matthews, R. On the derivation of a chaotic encryption algorithm. Cryptologia 1989, 13, 29–42. [Google Scholar] [CrossRef]
- Herbadji, D.; Belmeguenai, A.; Derouiche, N.; Liu, H. Colour image encryption scheme based on enhanced quadratic chaotic map. IET Image Process. 2020, 14, 40–52. [Google Scholar] [CrossRef]
- Wu, J.; Shi, J.; Li, T. A Novel Image Encryption Approach Based on a Hyperchaotic System, Pixel-Level Filtering with Variable Kernels, and DNA-Level Diffusion. Entropy 2020, 22, 5. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Han, J.; Ye, Y. Image encryption algorithm based on image hashing, improved chaotic mapping and DNA coding. IET Image Process. 2019, 13, 2905–2915. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, X. Multiple-Image Encryption Algorithm Based on the 3D Permutation Model and Chaotic System. Symmetry 2018, 10, 660. [Google Scholar] [CrossRef] [Green Version]
- Anwar, S.; Meghana, S. A pixel permutation based image encryption technique using chaotic map. Multimed. Tools Appl. 2019, 78, 27569–27590. [Google Scholar] [CrossRef]
- El-Latif, A.A.A.; Abd-El-Atty, B.; Belazi, A.; Iliyasu, A.M. Efficient Chaos-Based Substitution-Box and Its Application to Image Encryption. Electronics 2021, 10, 1392. [Google Scholar] [CrossRef]
- Musanna, F.; Dangwal, D.; Kumar, S. Novel image encryption algorithm using fractional chaos and cellular neural network. J. Ambient Intell. Humaniz. Comput. 2021, 1–22, (prepublish). [Google Scholar] [CrossRef]
- Pourasad, Y.; Ranjbarzadeh, R.; Mardani, A. A New Algorithm for Digital Image Encryption Based on Chaos Theory. Entropy 2021, 23, 341. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhang, J. A Multidimensional Chaotic Image Encryption Algorithm based on DNA Coding. Multimed. Tools Appl. 2020, 79, 21579–21601. [Google Scholar] [CrossRef]
- Zhou, S.; Wang, X.; Wang, M.; Zhang, Y. Simple colour image cryptosystem with very high level of security. Chaos Solitons Fractals 2020, 141, 110225. [Google Scholar] [CrossRef]
- Gan, Z.; Chai, X.; Han, D.; Chen, Y. A chaotic image encryption algorithm based on 3-D bit-plane permutation. Neural Comput. Appl. 2019, 31, 7111–7130. [Google Scholar] [CrossRef]
- Arab, A.; Rostami, M.J.; Ghavami, B. An image encryption method based on chaos system and AES algorithm. J. Supercomput. 2019, 75, 6663–6682. [Google Scholar] [CrossRef] [Green Version]
- Xu, Q.; Sun, K.; Cao, C.; Zhu, C. A fast image encryption algorithm based on compressive sensing and hyperchaotic map. Opt. Lasers Eng. 2019, 121, 203–214. [Google Scholar] [CrossRef]
- Wang, X.; Ren, Q.; Jiang, D. An adjustable visual image cryptosystem based on 6D hyperchaotic system and compressive sensing. Nonlinear Dynam. 2021, 104, 4543–4567. [Google Scholar] [CrossRef]
- Zhang, Q.; Han, J. A novel color image encryption algorithm based on image hashing, 6D hyperchaotic and DNA coding. Multimed. Tools Appl. 2021, 80, 13841–13864. [Google Scholar] [CrossRef]
- Batool, S.I.; Waseem, H.M. A novel image encryption scheme based on Arnold scrambling and Lucas series. Multimed. Tools Appl. 2019, 78, 27611–27637. [Google Scholar] [CrossRef]
- Li, X.; Li, T.; Wu, J.; Xie, Z.; Shi, J. Joint image compression and encryption based on sparse Bayesian learning and bit-level 3D Arnold cat maps. PLoS ONE 2019, 14, e224382. [Google Scholar] [CrossRef]
- Jithin, K.C.; Sankar, S. Colour image encryption algorithm combining Arnold map, DNA sequence operation, and a Mandelbrot set. J. Inf. Secur. Appl. 2020, 50, 102428. [Google Scholar] [CrossRef]
- Jiao, K.; Ye, G.; Dong, Y.; Huang, X.; He, J. Image Encryption Scheme Based on a Generalized Arnold Map and RSA Algorithm. Secur. Commun. Netw. 2020, 2020, 1–14. [Google Scholar] [CrossRef]
- Wang, T.; Wang, M. Hyperchaotic image encryption algorithm based on bit-level permutation and DNA encoding. Opt. Laser Technol. 2020, 132, 106355–106367. [Google Scholar] [CrossRef]
- Kumar, A.; Raghava, N.S. An efficient image encryption scheme using elementary cellular automata with novel permutation box. Multimed. Tools Appl. 2021, 80, 21727–21750. [Google Scholar] [CrossRef]
- Patro, K.A.K.; Acharya, B. An efficient dual-layer cross-coupled chaotic map security-based multi-image encryption system. Nonlinear Dynam. 2021, 104, 2759–2805. [Google Scholar] [CrossRef]
- Li, Z.; Peng, C.; Tan, W.; Li, L. An Efficient Plaintext-Related Chaotic Image Encryption Scheme Based on Compressive Sensing. Sensors 2021, 21, 758. [Google Scholar] [CrossRef]
- El-Khamy, S.E.; Mohamed, A.G. An efficient DNA-inspired image encryption algorithm based on hyper-chaotic maps and wavelet fusion. Multimed. Tools Appl. 2021, 80, 23319–23335. [Google Scholar] [CrossRef]
- Xian, Y.; Wang, X.; Yan, X.; Li, Q.; Wang, X. Image Encryption Based on Chaotic Sub-Block Scrambling and Chaotic Digit Selection Diffusion. Opt. Laser. Eng. 2020, 134, 106202–106223. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, X. Multiple-image encryption algorithm based on bit planes and chaos. Multimed. Tools Appl. 2020, 79, 20753–20771. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, J.; Han, D.; Wu, P.; Sun, Y.; Moon, Y.S. A multidimensional chaotic image encryption algorithm based on the region of interest. Multimed. Tools Appl. 2020, 79, 17669–17705. [Google Scholar] [CrossRef]
- Zarebnia, M.; Pakmanesh, H.; Parvaz, R. A fast multiple-image encryption algorithm based on hybrid chaotic systems for gray scale images. Optik 2019, 179, 761–773. [Google Scholar] [CrossRef]
- Yadollahi, M.; Enayatifar, R.; Nematzadeh, H.; Lee, M.; Choi, J. A novel image security technique based on nucleic acid concepts. J. Inf. Secur. Appl. 2020, 53, 102505–102515. [Google Scholar] [CrossRef]
- Abbasi, A.A.; Mazinani, M.; Hosseini, R. Chaotic evolutionary-based image encryption using RNA codons and amino acid truth table. Opt. Laser Technol. 2020, 132, 106465–106477. [Google Scholar] [CrossRef]
- JarJar, A. Two Feistel rounds in image cryptography acting at the nucleotide level exploiting dna and rna property. SN Appl. Sci. 2019, 1, 1411–1427. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.; Chen, L.; Li, T. Hyper-Chaotic Color Image Encryption Based on Transformed Zigzag Diffusion and RNA Operation. Entropy 2021, 23, 361. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, Y. Image encryption using 2D Logistic-adjusted-Sine map. Inform. Sci. 2016, 339, 237–253. [Google Scholar] [CrossRef]
- Zhao, H.; Xie, S.; Zhang, J.; Wu, T. Efficient image encryption using two-dimensional enhanced hyperchaotic Henon map. J. Electron. Imaging 2021, 29, 23007–23033. [Google Scholar] [CrossRef]
- Rukhin, A.; Soto, J.; Nechvatal, J.; Smid, M.; Barker, E. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications. NIST Spec. Publ. 2010. 22–800 Revision 1a. [Google Scholar]
- Chai, X.; Fu, X.; Gan, Z.; Lu, Y.; Chen, Y. A color image cryptosystem based on dynamic DNA encryption and chaos. Signal Process. 2019, 155, 44–62. [Google Scholar] [CrossRef]
- Zhang, J.; Hou, D.; Ren, H. Image Encryption Algorithm Based on Dynamic DNA Coding and Chen’s Hyperchaotic System. Math. Probl. Eng. 2016, 2016, 1–11. [Google Scholar] [CrossRef]
- Wang, X.; Guan, N. A novel chaotic image encryption algorithm based on extended Zigzag confusion and RNA operation. Opt. Laser Technol. 2020, 131, 106366–106382. [Google Scholar] [CrossRef]
- Pan, T.G.; Li, D.Y. A New Algorithm of Image Encryption Based on 3D Arnold Cat. Adv. Eng. Forum. 2011, 1, 183–187. [Google Scholar] [CrossRef] [Green Version]
- Murillo-Escobar, M.A.; Meranza-Castillón, M.O.; López-Gutiérrez, R.M.; Cruz-Hernández, C. Suggested Integral Analysis for Chaos-Based Image Cryptosystems. Entropy 2019, 21, 815. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, X.; Liu, L. Application of chaotic Josephus scrambling and RNA computing in image encryption. Multimed. Tools Appl. 2021, 80, 1–22. [Google Scholar] [CrossRef]
- Zhu, H.; Zhao, Y.; Song, Y. 2D Logistic-Modulated-Sine-Coupling-Logistic Chaotic Map for Image Encryption. IEEE Access 2019, 7, 14081–14098. [Google Scholar] [CrossRef]
- Amina, S.; Mohamed, F.K. An efficient and secure chaotic cipher algorithm for image content preservation. Commun. Nonlinear Sci. 2018, 60, 12–32. [Google Scholar] [CrossRef]
- Chai, X.; Chen, Y.; Broyde, L. A novel chaos-based image encryption algorithm using DNA sequence operations. Opt. Lasers Eng. 2017, 88, 197–213. [Google Scholar] [CrossRef]
- Rushdi, M.H.A.A.; Nehary, E.A. Image encryption via discrete fractional Fourier-type transforms generated by random matrices. Signal Process. Image Commun. 2016, 49, 25–46. [Google Scholar] [CrossRef]
- Liao, X.; Kulsoom, A.; Ullah, S. A modified (Dual) fusion technique for image encryption using SHA-256 hash and multiple chaotic maps. Multimed. Tools Appl. 2016, 75, 11241–11266. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, L.; Zhou, Z.; Niu, Y. A Chaos-Based Image Encryption Technique Utilizing Hilbert Curves and H-Fractals. IEEE Access 2019, 7, 74734–74746. [Google Scholar] [CrossRef]
- Song, Y.; Zhu, Z.; Zhang, W.; Yu, H.; Zhao, Y. Efficient and Secure Image Encryption Algorithm Using a Novel Key-Substitution Architecture. IEEE Access 2019, 7, 84386–84400. [Google Scholar] [CrossRef]
























| Test Items | p-Value | Results | |
|---|---|---|---|
| X | Y | ||
| Frequency test | 0.898977 | 0.596600 | Pass |
| Frequency test within a block | 0.758731 | 0.291061 | Pass |
| Runs test | 0.632272 | 0.963952 | Pass |
| Test for longest run of ones in a block | 0.931298 | 0.408512 | Pass |
| Binary matrix rank test | 0.424943 | 0.434479 | Pass |
| Discrete Fourier transform test | 0.657982 | 0.349486 | Pass |
| Non-overlapping template matching test | 0.342668 | 0.962718 | Pass |
| Overlapping template matching test | 0.144245 | 0.174696 | Pass |
| Maurer’s “Universal Statistical” test | 0.138558 | 0.148293 | Pass |
| Linear complexity test | 0.876999 | 0.988846 | Pass |
| Serial test * | 0.989594 | 0.263659 | Pass |
| Approximate entropy test | 0.825184 | 0.091003 | Pass |
| Cumulative sums test * | 0.976507 | 0.439422 | Pass |
| Random excursions test * | 0.641919 | 0.553448 | Pass |
| Random excursions variant test * | 0.757583 | 0.467278 | Pass |
| Rule | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 00 | A | A | U | U | C | C | G | G |
| 01 | C | G | C | G | A | U | A | U |
| 10 | G | C | G | C | U | A | U | A |
| 11 | U | U | A | A | G | G | C | C |
| + | A | G | C | U |
|---|---|---|---|---|
| A | A | G | C | U |
| G | G | C | U | A |
| C | C | U | A | G |
| U | U | A | G | C |
| − | A | G | C | U |
|---|---|---|---|---|
| A | A | U | C | G |
| G | G | A | U | C |
| C | C | G | A | U |
| U | U | C | G | A |
| +’ | A | G | C | U |
|---|---|---|---|---|
| A | U | C | G | A |
| G | C | G | A | U |
| C | G | A | U | C |
| U | A | U | C | G |
| −’ | A | G | C | U |
|---|---|---|---|---|
| A | U | A | G | C |
| G | C | U | A | G |
| C | G | C | U | A |
| U | A | G | C | U |
| XOR⊕ | A | G | C | U |
|---|---|---|---|---|
| A | A | G | C | U |
| G | G | A | U | C |
| C | C | U | A | G |
| U | U | C | G | A |
| XNOR⊙ | A | G | C | U |
|---|---|---|---|---|
| A | U | C | G | A |
| G | C | U | A | G |
| C | G | A | U | C |
| U | A | U | C | U |
| Category of Amino Acids | Operator |
|---|---|
| Aliphatic hydrophobic amino acid | |
| Aliphatic hydrophilic amino acid | |
| Aromatic amino acids | |
| Stop codon | |
| Heterocyclic amino acid | |
| Start codon |
| BPP | N | Period of 2D-AT | Period of 3D-AAT |
|---|---|---|---|
| 8 | 102 | 36 | 27,937 |
| 16 | 128 | 96 | 224 |
| 24 | 146 | 222 | 12,607 |
| 32 | 162 | 108 | 2457 |
| Component | Values |
|---|---|
| External parameters | = 0.9865, = 1.4335, = 1.4977, = 0.5501, = 2.5159, = 1.3714, = 1.6686, = 0.2759, = 2.5568 |
| Algorithms | Time (Unit: Seconds) |
|---|---|
| Proposed algorithm | 0.9274 |
| Ref. [46] | 0.6840 |
| Ref. [47] | 2.7113 |
| Ref. [48] | 16.2561 |
| Images | Component | Average | Results | ||
|---|---|---|---|---|---|
| Lena (8BPP) | - | 236.56 | 236.56 | Pass | |
| Lena (16BPP) | - | 258.36 | 258.36 | Pass | |
| R | 278.47 | 293.25 | Pass | ||
| Baboon (24BPP) | G | 232.33 | 249.16 | Pass | |
| B | 236.69 | Pass |
| Images | Plain Image | Proposed Algorithm | Ref. [51] | Ref. [46] | Ref. [47] |
|---|---|---|---|---|---|
| Lena (8BPP) | 7.44557 | 7.99935 | 7.9979 | 7.9979 | 7.99934 |
| Lena (16BPP) | 7.46533 | 7.99932 | - | - | - |
| Baboon (24BPP) | 7.36642 | 7.99934 | 7.9976 | 7.99911 | 7.99932 |
| Images | NPCR | UACI | ||||||
|---|---|---|---|---|---|---|---|---|
| Proposed | Ref. [48] | Ref. [52] | Ref. [53] | Proposed | Ref. [48] | Ref. [52] | Ref. [53] | |
| Lena (8BPP) | 99.6132 | 99.57 | 99.5636 | 99.6101 | 33.4236 | 33.33 | 33.4417 | 33.4745 |
| Lena (16BPP) | 99.6145 | - | - | - | 33.4572 | - | - | - |
| Baboon (24BPP) | 99.6021 | 99.57 | 99.6293 | 99.6113 | 33.4768 | 33.47 | 33.3796 | 33.4928 |
| Encrypted Image | MSE | PSNR (dB) | SSIM |
|---|---|---|---|
| Lena (8BPP) | 7757 | 9.2338 | 0.0106 |
| Lena (16BPP) | 65,535 | 7.9416 | 0.0103 |
| Baboon (24BPP) | 8562 | 8.8047 | 0.0089 |
| Algorithms | Images | Components | Plain Images | Cipher Images | ||||
|---|---|---|---|---|---|---|---|---|
| H | V | D | H | V | D | |||
| Lena (8BPP) | - | 0.9719 | 0.9849 | 0.9591 | 0.0024 | −0.0017 | 0.0011 | |
| Lena (16BPP) | - | 0.9726 | 0.9839 | 0.9604 | 0.0056 | 0.0012 | 0.0054 | |
| Proposed | R | 0.9427 | 0.8758 | 0.8503 | 0.0012 | −0.0030 | −0.0012 | |
| Baboon (24BPP) | G | 0.9139 | 0.8170 | 0.7770 | 0.0017 | 0.0011 | 0.0008 | |
| B | 0.9489 | 0.8936 | 0.8691 | 0.0043 | −0.0006 | −0.0018 | ||
| Ref. [51] | Lena (8BPP) | - | 0.9276 | 0.9574 | 0.9231 | 0.0009 | −0.0028 | −0.0027 |
| Ref. [46] | Lena (8BPP) | - | 0.9329 | 0.9650 | 0.9066 | 0.0017 | 0.0019 | 0.0008 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Yan, X. Adaptive Chaotic Image Encryption Algorithm Based on RNA and Pixel Depth. Electronics 2021, 10, 1770. https://doi.org/10.3390/electronics10151770
Zhang X, Yan X. Adaptive Chaotic Image Encryption Algorithm Based on RNA and Pixel Depth. Electronics. 2021; 10(15):1770. https://doi.org/10.3390/electronics10151770
Chicago/Turabian StyleZhang, Xiaoqiang, and Xuangang Yan. 2021. "Adaptive Chaotic Image Encryption Algorithm Based on RNA and Pixel Depth" Electronics 10, no. 15: 1770. https://doi.org/10.3390/electronics10151770
APA StyleZhang, X., & Yan, X. (2021). Adaptive Chaotic Image Encryption Algorithm Based on RNA and Pixel Depth. Electronics, 10(15), 1770. https://doi.org/10.3390/electronics10151770







