Next Article in Journal
Terahertz High-Q Absorber Based on Holes Array Perforated into a Metallic Slab
Next Article in Special Issue
An Ultra-Low-Power CMOS Supercapacitor Storage Unit for Energy Harvesting Applications
Previous Article in Journal
Quadrature Demodulator-Assisted Estimation of Load Voltage and Resistance Based on Primary-Side Information of a Wireless Power Transfer Link
Previous Article in Special Issue
Design of a Charge Pump Circuit and System with Input Impedance Modulation for a Flexible-Type Thermoelectric Generator with High-Output Impedance
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Electronics
Volume 10
Issue 15
10.3390/electronics10151859
electronics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Battery Management System Algorithm for Energy Storage Systems Considering Battery Efficiency

by
Jeong Lee
1,
Jun-Mo Kim
2,
Junsin Yi
1 and
Chung-Yuen Won
1,*
1
Department of Electrical and Computer Engineering, Sungkyunkwan University, Suwon 16419, Korea
2
Interdisciplinary Program in Photovoltaic System Engineering, Sungkyunkwan University, Suwon 16419, Korea
*
Author to whom correspondence should be addressed.
Electronics 2021, 10(15), 1859; https://doi.org/10.3390/electronics10151859
Submission received: 7 July 2021 / Revised: 25 July 2021 / Accepted: 30 July 2021 / Published: 2 August 2021
(This article belongs to the Special Issue Energy Harvesting and Energy Storage Systems)
Browse Figures
Versions Notes

Abstract

:
Aging increases the internal resistance of a battery and reduces its capacity; therefore, energy storage systems (ESSs) require a battery management system (BMS) algorithm that can manage the state of the battery. This paper proposes a battery efficiency calculation formula to manage the battery state. The proposed battery efficiency calculation formula uses the charging time, charging current, and battery capacity. An algorithm that can accurately determine the battery state is proposed by applying the proposed state of charge (SoC) and state of health (SoH) calculations. To reduce the initial error of the Coulomb counting method (CCM), the SoC can be calculated accurately by applying the battery efficiency to the open circuit voltage (OCV). During the charging and discharging process, the internal resistance of a battery increase and the constant current (CC) charging time decrease. The SoH can be predicted from the CC charging time of the battery and the battery efficiency, as proposed in this paper. Furthermore, a safe system is implemented during charging and discharging by applying a fault diagnosis algorithm to reduce the battery efficiency. The validity of the proposed BMS algorithm is demonstrated by applying it in a 3-kW ESS.

1. Introduction

Energy storage systems (ESSs) store electricity when surplus electricity is generated or electricity rates are low and supply the stored electricity to the unit when electricity is in high demand or prices are high; therefore, for the efficient operation of power facilities, the development of an energy management system (EMS) algorithm is imperative.
Battery characteristics [1,2,3] and the sizing of ESSs have been extensively investigated [4,5,6] because the battery accounts for most of the budget when designing ESSs; therefore, battery selection and management are important, as the aging problems caused by inappropriate battery management costs account for a large part of the replacement budget.
Many ESSs use lithium-ion batteries, since they offer a high energy density and high efficiency [7,8]; however, it is crucial to identify the charging state of batteries because there is a risk of fire during charge-discharge cycles and because there is a need to predict the state of health (SoH) and state of charge (SoC) for battery state management [9]. The ESS consists of cells in series-parallel [10,11] with a large capacity. To solve the safety problems related to fires and explosions [12], a system that manages the battery status is required [13].
The purpose of a battery management system (BMS) is to manage the battery [14,15]. To improve the reliability and safety of the battery [16,17], many BMS functions are being developed [18]. The functions of BMS can be classified as real-time monitoring, calculation and prediction, protection, and optimization. The battery voltage, current, temperature, SoC, SoH, and other factors can be confirmed via monitoring [19,20,21]. In addition, the SoC, SoH, and internal impedance can be calculated and predicted [19,22,23,24,25]. The protection process limits overcurrent, overvoltage, and overheating and performs fault diagnosis [26,27,28,29]. The optimization process maintains the optimal state of charge of a battery by considering the amount of charge between cells [30,31,32]. As the cycle of a battery increases, the battery ages and its state changes [33]; therefore, to manage a battery, it is necessary to improve the performance of BMSs. The performance of a BMS varies according to the estimation accuracy of the SoC and SoH, indicators of the battery state [10,34,35].
Charge-discharge cycles, temperature, overcharge and overdischarge, and increased internal resistance cause batteries to age, which reduces their capacity. The calculation of battery efficiency can be performed based on the current and SoC [36], via aging analysis based on charge-discharge capacities [37], or via charging-discharging power differences [38,39]; however, it is difficult to accurately estimate the battery state using this approach, as it does not consider the internal resistance changes arising from the aging phenomenon.
Since the internal resistance increases along with the aging phenomenon of the battery, it should be estimated during the operation, therefore, a battery efficiency estimation method is proposed in this paper. The efficiency of the battery is obtained based on the charging and discharging power losses. Since the internal resistance varies according to the battery efficiency, the battery states can be identified using this variation of internal resistance.
A battery efficiency calculation formula is used to predict the SoC and SoH of the battery. The conventional methods used for estimating battery SoC for BMS performance improvements include deep neural network-based methods for error rating reduction [40], extended Kalman filter (EKF)-based methods with the Thevenin model [41], particle swarm optimization (PSO) [42], and hysteresis voltage of the open circuit voltage (OCV) [43]. Additionally, SoC and internal resistance estimation methods based on an unscented Kalman filter (UKF) with analysis of model parameters [44] and estimation based on the adaptive cubature Kalman filter (ACKF) with neural networks are proposed in [45]. In addition, there are other related studies on SoC estimation, such as equivalent circuit model (ECM)-based estimation with noise compensation [46], OCV error compensation based on DNN [47], the open circuit voltage–charge amount (OCV-Q) curve fitting method using a convolutional neural network (CNN) [48], the event-driven Coulomb counting method (CCM) algorithm for unbalanced SoCs [49], and CCM based on modified parameters [50]; however, DNN- and KF-based methods require high computational power and an additional learning process. The OCV and CCM are primarily used to indicate the charging state of a battery [51,52]; however, because OCV is used when the internal battery state is stabilized, it is not sufficiently stable for a nonlinear battery [9]. Furthermore, because another CCM calculates the SoC by accumulating the charge current, the CCM has the disadvantage of increasing the SoC if an error occurs in the initial current measurement value [53].
In this paper, an SoC estimation method combining OCV with CCM is proposed to improve upon the drawbacks of both OCV and CCM. This estimation algorithm does not require excessive computational power and can improve the estimation accuracy. The proposed algorithm uses the OCV equation with the internal resistance and efficiency of the battery. Additionally, the equation can calculate the charge-discharge of the battery by accurately considering the initial value of the CCM by applying OCV while considering the state of the battery.
Based on the battery efficiency formula, a formula that predicts the SoH of a battery based on the charging time required to safely operate the battery is also applied to the BMS algorithm to improve the reliability.
Research related to SoH estimation to improve BMS performance includes the multilayer perceptron (MLP)-based method [54], the self-adaptive weight particle swarm optimization (SWPSO)-based estimation method using a dynamic recurrent neural network (DRNN) with the ability to conduct dynamic mapping [55], and the XGBoost-based estimation method [56]. Additionally, a state estimation method combining the battery model with a data-based method [57] and a voltage–power-curve-based estimation method [58] has been researched. In [59], a more accurate SoH estimation method was proposed by considering the charging time of the battery, although it did not consider the internal resistance variation and showed estimation error; however, as the SoH estimated without considering the internal resistance is incorrect, some researchers have considered it a constant value [60,61]. Although the SoH is also predicted based on its constant current (CC) charging time [62,63,64], the internal resistance and temperature [65] of a battery are considered when a system is operated for a long time, while the accurate characteristics of a battery cannot be numerically represented; however, this research used the battery efficiency equation, allowing for a more accurate estimation of the battery state by numerically defining the capacity reduction and the internal resistance of a battery.
The BMS measures the battery’s initial SoH and stores the value. The BMS stores the current SoH by comparing the current values with the initial SoH based on the changing values as the battery is used. According to the battery status, the temperature of the battery arises and internal resistance increases along with it. Because of the increase in the internal resistance, the SoH of a battery decreases and it takes less time to charge-discharge the battery; therefore, the CC time period decreases. Based on this time period difference among the charge-discharge cycles, the SoH estimation method is proposed in this paper. The proposed SoH estimation method uses the integral value of the CC time period difference among the charge-discharge cycles for more accurate SoH estimation. In this paper, the battery efficiency equation is used to predict the SoH of a battery considering the decrease in the CC charging time of the SoH due to the increase in the internal resistance of the battery and the fact that the capacity of a battery decreases when it heats up.
An algorithm for predicting battery-related system safety and accurate SoC and SoH by determining a battery fault using the battery efficiency equation is proposed.
The literature on the fault diagnosis of batteries shows that the estimated SoH method is typically used. Many studies on battery fault diagnosis have focused on SoH estimation, since it is a major part of fault diagnosis. For example, in [66], the fault diagnosis method is based on the estimated SoH using the surface temperature of the battery, while fault detection is performed using the SoH estimated based on a multilayer neural network (MNN) in [67].
In this paper, a novel fault diagnosis algorithm that detects the fault state based on the SoH and the efficiency of the battery is proposed for more accurate fault detection. With the proposed method, the battery can be managed more safely because battery faults can be detected beforehand, since the battery efficiency plummets in the fault state before the SoH reaches its fault range.
In this study, we implement the SoC calculation combined with the OCV and CCM, SoH based on the charging time, as well as a fault diagnosis algorithm in a 3 kW ESS. Furthermore, the validity of the proposed BMS algorithm is investigated.

2. Battery Efficiency for Predicting Battery State

Figure 1 illustrates the factors affecting the performance of a battery.
As the number of charge-discharge cycles increases, a chemical reaction occurs in the battery, causing aging, which reduces the SoH of the battery. Aging increases the internal resistance of a battery and decreases its charge-discharge capacity. As the capacity of a battery decreases, its charge voltage reaches the maximum value.
Identifying the occurrence of aging during the charge-discharge operation of a battery requires determination of the magnitude by which its capacity decreases by calculating its internal resistance or efficiency.
Although accurate modeling of a battery is required to understand its state, it is difficult to perform accurate modeling because of the nonlinear characteristics. Furthermore, given the various factors for batteries, the system costs increase because the roles of the BMS managing the battery vary and the number of computations increases. This paper proposes a battery efficiency calculation formula that considers the internal resistance, which significantly affects the performance of a battery, as well as a system that considers the nonlinear characteristics.
Figure 2 shows an ESS system, in which the proposed algorithm was implemented. The ESS consisted of a battery system and a power conversion system (PCS). The battery system consisted of a battery and a BMS. The ac-dc of the PCS comprised a two-level converter that was easy to control with high efficiency, while the dc-dc comprised a full-bridge converter [68].
Figure 3 illustrates the BMS configuration of the battery system. The BMS received data regarding the battery voltage, current, and temperature and predicted the SoC and SoH. Furthermore, the data were transmitted using controller area network (CAN) communication. When any abnormalities occurred in the battery voltage, current, or state, the charge-discharge state of the battery was cut off to protect it. Furthermore, the BMS provided a protection function to secure the battery safety when an abnormality in the battery temperature occurred [69]. By applying the proposed algorithm, the BMS sensed the battery voltage, current, and temperature; accumulated data; calculated the battery efficiency; and predicted the SoC and SoH. In addition, battery’s efficiency protected it in from faults.

3. ESS Considering Battery Efficiency

Figure 4 illustrates the proposed EMS algorithm and shows a day-ahead EMS algorithm based on the proposed battery management algorithm.
The ESS supported the grid by discharging during the daytime (when there are many power users) and charging at night. During the charge-discharge process, the proposed algorithm could sense the battery state through CAN communication using the BMS algorithm and proceeded with charging. If the SoC of the ESS battery was below 80%, the battery was charged, while if it was above 80%, charging was terminated. The minimum and maximum values of the battery SoC could be redefined by the user, and this paper defines the operational SoC as that defined between 20% and 80%. After charging, if the power required by the grid increased, the ESS proceeded with discharging. Furthermore, the ESS used an algorithm that terminated the discharging of the battery when the SoC dropped below 20%.
The EMS algorithm is an algorithm for the charge-discharge process of a battery, which ensures high safety when connected with the BMS. The paper did not separately consider the system fault diagnosis performed by the EMS because the EMS algorithm was proposed considering the battery state; however, further studies are necessary to investigate the fault diagnosis and response in EMS, which are critical factors affecting the charge-discharge process required for the grid.

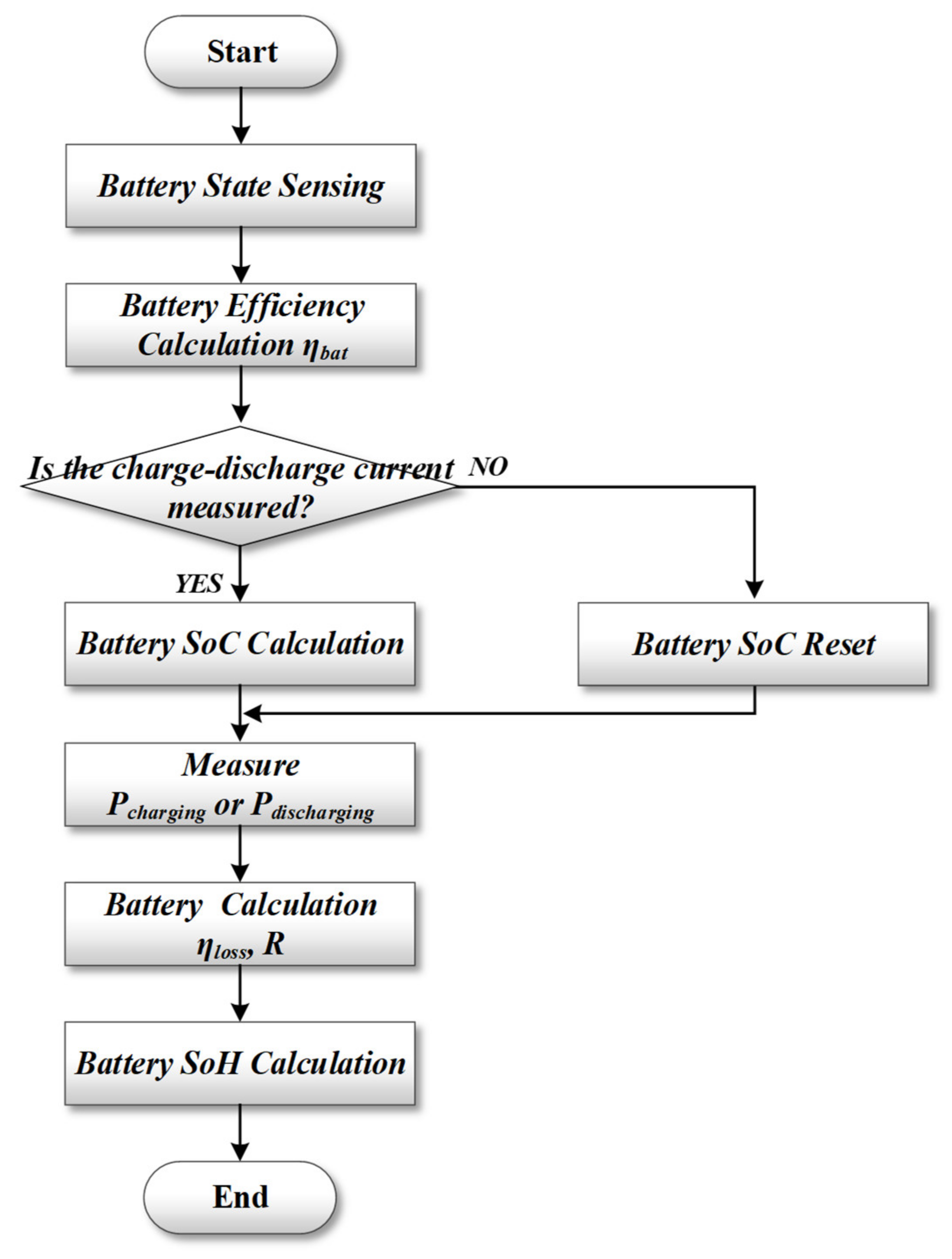
3.1. Proposed BMS Algorithm

The ESS, which charges and discharges energy from a battery, is directly affected by battery performance; thus, a BMS that manages and protects the battery and communicates with the outside is critical.
One of the problems in nonlinear batteries is that their internal characteristics change based on the number of charge-discharge cycles; thus, the primary goal of a BMS is to accurately follow these changes.
This paper proposes a method to improve battery safety and performance based on the reduction in its efficiency (which occurs during battery use), derive a battery efficiency equation, and apply it to calculate and predict the SoC and SoH of the battery. Furthermore, based on the battery efficiency calculation, this paper proposes an algorithm for terminating the use of the battery and diagnosing faults.
Figure 5 illustrates the proposed BMS algorithm. The proposed BMS algorithm can sense the battery voltage, current, and temperature and calculate its efficiency. When the efficiency of a battery is calculated, its charge-discharge current is measured to determine whether the ESS is in the charge-discharge state. When the ESS is charged or discharged, the SoC is calculated using the combination of the OCV and CCM.
When the ESS is not in the charge-discharge state, the SoC of the battery is reset to increase the accuracy of the initial value of the SoC.
At the end of the charging and discharging operation of the battery, the charging power Pcharging or discharging power Pdischarging is measured to estimate battery loss and internal resistance for the next cycle. As a day-ahead EMS was used in this paper, one cycle represents a day of operation; therefore, the internal resistance of the battery was estimated based on the difference between the charging and discharging energies for a day.
After the charge-discharge process, the SoH, to which the battery efficiency was applied, was calculated and predicted to improve the battery safety and performance.

Battery Efficiency

Battery efficiency can be used as an indicator of the current usage time compared to the initial time. A battery efficiency equation was proposed to express the relationship between the capacity and voltage of the battery model. Because the internal resistance of a battery affects the battery output, the battery’s internal resistance must be accurately calculated.
The internal resistance of a battery is the key indicator of its state. The internal resistance of a battery increases with an increase in the heat generated during the charge-discharge of the battery.
Figure 6 illustrates the current capacity of the ESS with aging.
As the battery aged, its internal resistance increased and the current capacity decreased, which significantly affected the performance of the ESS when the capacity was large. Furthermore, the use of a battery with reduced performance causes overcharging and overdischarging, which limits battery safety.
The current battery capacity is the amount of current that a fully charged battery can discharge for one hour. Compared to a battery in the birth of life (BOL) state, an aging battery, upon discharge, reaches the terminal voltage limit faster because of its reduced current capacity.
The efficiency of a battery decreases when it is used. As a battery shows the maximum efficiency at the initial state, its efficiency can only decrease when it is in operation.
Equation (1) defines the efficiency of a battery. The efficiency of a battery ηbat can be expressed by subtracting the battery loss ηloss from the initial battery efficiency, 100%.
As the decrease in the efficiency can be expressed as the increase in the internal resistance, ηloss can be calculated based on the charging and discharging powers, as shown in Equation (2).
Ibat is the charge-discharge current, R is the battery’s internal resistance, and Vbat is the battery voltage.
η b a t = 100 − η l o s s
η l o s s = I b a t 2 × R V b a t × I b a t
In this case, the charge-discharge current of the battery can be represented by Equation (3).
During the charge-discharge of a battery, the current can be calculated as the amount of charge (battery capacity) and the C-rates at which the battery has been charged or discharged over time. Qbat is the battery capacity, while t is the charge-discharge time of the battery. Equation (3) uses the electric charge equation.
Equations (2) and (3) give the total loss in battery efficiency, as represented in Equation (4). Using Equation (4), the battery loss equation, as well as Equation (1), the battery efficiency can be calculated. Equation (4) can be used to determine the internal resistance of a battery. Equation (5) gives the internal resistance of the battery. In this paper, as the charge-discharge process progressed, the battery efficiency decreased.
I b a t = Q b a t t
η l o s s = Q b a t t × R V b a t
R = η l o s s × V b a t × t Q b a t

3.2. Improved SoC and SoH Prediction Method

A battery protection system monitors the battery state and prevents it from overcharging and overdischarging, improving its safety and performance. The performance of a BMS is evaluated based on how accurately it predicts the SoC and SoH of the battery [34].
CCM is used to track the SoC with the value calculated by integrating the current during the charge-discharge of the battery to the initial value of the SoC; however, because the current is accumulated to the initial value of the CCM, errors are accumulated if the precise initial value is unknown [70,71]. Because errors gradually increase, the paper propose following the SoC with an improved method combining the OCV and CCM to improve the initial value.
Equation (6) expresses the voltage calculated using the open circuit voltage formula of the battery through Equation (5). The battery state can be more accurately predicted using the internal resistance obtained through Equation (5) and the OCV of the battery.
The final CCM is depicted in Equation (7). The accuracy of the prediction of the battery state can be improved by applying the internal resistance value derived from the battery efficiency equation to the conventional CCM. SoC(t) is the SoC at time t, SoC(t−1) is the initial SoC, Cn is the battery capacity, and Vocv is the battery voltage in the open state [72,73].
S o C ( t − 1 ) = V o c v + I b a t × η l o s s × V b a t × t Q b a t
S o C ( t ) = S o C ( t − 1 ) + ∫ 0 t I ( t ) C n d t
SoH, which is an indicator of the battery life time, is essential for managing the battery charge-discharge process. Various models for predicting SoH have been proposed to improve the battery safety and performance. The standard method predicts the life time of a battery by analyzing it according to the chemical principle of the battery and through mathematical or physical modeling [74,75,76]; however, these methods do not consider the internal resistance of a battery, which significantly affects its life time.
Figure 7 illustrates the constant current–constant voltage (CC–CV) charging curve of a battery.
A battery is typically charged through the CC–CV [77]. Whenever the battery is charged, its CC charging time decreases, while the CV charging time increases. As the battery charging proceeds, the battery temperature increases and internal resistance increases, resulting in a decrease in its SoH.
Figure 8 shows the discharge characteristics of a battery.
As in the charging cycle, the time to reach the cut-off voltage is also reduced during charging because the SoH decreases as the temperature and internal resistance of the battery increase, as shown in the charging curve.
This paper considered the internal resistance of a battery, which significantly affects the SoH, to propose a method for predicting the battery SoH based on the charging time after the charge-discharge process. Although previous studies [62,64] did not accurately predict the internal resistance value, they numerically derived and applied the internal resistance value based on the battery efficiency.
To calculate a battery’s SoH, the equation should be rearranged by t using the SoC derived from Equations (6) and (7) after the SoC charge-discharge process, resulting in Equation (8). By applying the internal resistance equation derived from the battery efficiency equation, the charge-discharge time is compared based on the charge-discharge cycle of the battery. Here, tafter is the time after the charge-discharge process, which can be used to predict the battery SoH using the battery characteristics by comparing the values after the charge-discharge process (Equations (8) and (9)). SoHafter is the SoH of the battery compared to the time after charging and discharging. The SoH of the battery can be predicted using the charge-discharge time of the battery. Here, tbefore is the battery charge-discharge time before tafter.
t a f t e r = C n × ( S o C ( t ) − V o c v − η l o s s × V b a t ) I b a t
S o H a f t e r = t a f t e r t b e f o r e × 100 %

3.3. Method Used to Diagnose Battery Fault

Figure 9 illustrates the proposed battery fault diagnosis algorithm.
The fault diagnosis algorithm considers two situations. After the battery information is sensed through the BMS and the battery efficiency is evaluated regarding whether the value corresponds to the over range, charging proceeds. If the battery efficiency is not higher than the over range, the charge-discharge process is performed; however, if the battery efficiency is higher than the over range and the battery SoH is 40% or less, the charge-discharge process is terminated.
This over range value changes depending on the battery state, battery type, and other factors, and this value should be set before the operation. In this paper, the fault state was set when the efficiency was below 80% and the SoH was below 40%.
Although the battery’s charge-discharge SoC is used correctly at 0–100% for the ESS, in this paper, the SoC was charged at 20–80%, the optimal operation region for lithium-ion batteries from a safety viewpoint. Furthermore, the SoH was subjected to charge-discharge cycles up to the maximum region of the battery. Charging was terminated based on the experimental requirements and safety considerations—when the SoH reached 40% or less—to confirm the disposal of the battery through a signal.
The BMS senses the final output values of Equations (1) and (9), then a charge-discharge termination signal is transmitted through CAN communication if the value is within the over range. The paper predicted the correct battery state through BMS and diagnosed the fault using the proposed method during the charge-discharge process to propose a BMS algorithm for an ESS that uses a large battery capacity.

4. Experiments to Verify the Proposed Algorithm

A 3-kW ESS was implemented to verify the BMS algorithm of the ESS considering the battery efficiency.
The BMS algorithm proposed in this paper was applied to the ESS and the battery efficiency was tested during the charge-discharge process by charging several battery modules.
The internal resistance calculated from the battery efficiency was applied to the SoC. Then, the OCV, CCM, and proposed algorithm were compared and the SoC was confirmed in the case of a battery fault. The charge-discharge cycle was performed by converting the SoC calculated from the internal resistance of the battery into the charging-discharging time. Furthermore, the termination of the charge-discharge cycle was confirmed through the connection between the ESS and BMS in the case of a fault. In the additional part of the algorithm, the total efficiency of the ESS was further confirmed to verify its validity.
Figure 10 illustrates the ESS experiment hardware used in this paper, while Table 1 lists the experiment parameters. The PCS of the ESS consists of a two-level inverter, a full bridge converter, and a master controller. The output side comprised three lithium-ion battery modules (1 module: 24 cells × 4.2 V) and a BMS. The experiment was conducted using an oscilloscope and a laptop computer to confirm the operation.
For the battery efficiency experiment, battery efficiency was confirmed by the charge-discharge of a faulty battery module and a normal battery module.
The profiling of the battery was carried out in four steps. The data were confirmed in the order of (1) securing the charge-discharge data, (2) deriving an equation through curve fitting, (3) performing the charge-discharge cycle, and (4) extracting the target data from the implemented correlation equation.
An experiment battery was proposed to verify the battery efficiency by configuring the battery with three modules and assigning modules 1 and 2 as the normal batteries and module 3 as the battery subjected to repeated charge-discharge cycles.
Figure 11 illustrates the efficiency graph of the battery module.
During battery charging, the difference in the final internal resistance values of the battery was confirmed, as depicted in Figure 11. If a specific range was set during the charge-discharge cycle for testing, the change in the state of the battery caused by aging was detected.
The battery efficiency test revealed a significant change in the efficiency of the battery after investigating the changes in the efficiency of the faulty or abnormal batteries that occurred during the charge-discharge cycle of the ESS and those of the normal battery. The difference between the efficiencies of the faulty (aged) and normal batteries was 38.4%. The results suggest that the battery efficiency of the proposed algorithm could be applied for predicting the SoC and SoH, which requires improved accuracy, while the change in the internal resistance (which has the greatest impact on the battery state) could also be applied to increase the accuracy of the battery state prediction.
Figure 12 and Table 2 illustrate the SoC profile of the battery to which the proposed battery efficiency equation was applied.
All three normal battery modules were discharged up to 20% and charged up to 80% of the maximum SoC.
By applying the battery efficiency, the OCV, CCM, and proposed SoC algorithm could be compared.
The SoC profile was confirmed using the proposed algorithm.
To confirm the SoC calculation, the OCV and CCM were compared with the proposed SoC calculation algorithm. The CCM was charged after accurately determining the initial value. The OCV could not accurately determine the SoC during charging. The CCM and proposed SoC operation seemed to accurately calculate the SoC; however, when using the actual CCM, the user could not directly and accurately set the initial value. As such, using the algorithm proposed in this paper, the SoC can be determined more accurately.
Figure 13 illustrates the SoH profile to which the proposed algorithm was applied, while Table 3 presents the CC termination time based on the battery state.
50 cycles were charged and discharged at 0.3 C-rate, and CC charging time was compared in the 51st cycle.
The battery was charged by applying the internal resistance to which the battery efficiency was applied. The results demonstrated that the CC charging time of the module decreased when the battery failed or had other problems.
Equation (10), which compared the SoH profiles obtained using the three methods investigated, confirmed that the SoH prediction was possible based on the CC termination time of the battery. The ΔSoH is the amount of change between SoHbefore and SoHafter, while SoHbefore is the SOH before SoHafter.
Δ S o H = 1 − S o H a f t e r S o H b e f o r e × 100
It is difficult to accurately diagnose faulty batteries based on environmental changes, such as battery aging. Because the characteristics of the battery vary when a cell comprises modules, the internal resistance and capacity deviation occurs, causing overdischarge; thus, because the safety and energy efficiency of the battery system is significantly reduced, in this paper we diagnosed the battery state using two methods, whereby faulty batteries were diagnosed based on when the (1) battery efficiency and (2) SoH battery efficiency were reached.
Figure 14a shows the charging voltage and current waveform at the time of a fault signal, while Figure 14b is the discharge voltage and current waveform at the time of a fault signal. Figure 14 illustrates the fault signals when the battery efficiency is reduced and the SoH is 40% or less. If a fault is detected, the charge–discharge cycle of the battery is terminated with the general purpose input output (GPIO) signal, which cuts off the battery MC through the BMS. The main controller then terminates the pulse width modulation signal, causing the ESS to enter into a stop state.
Figure 15 illustrates the efficiency waveform of the ESS when the system was implemented by applying the proposed algorithms.
The efficiency of ESS is caused by the decrease in the difference between the power consumed by charging and the power generated by discharging; therefore, the operating cost for using the battery increases. Efficiency was measured when applying the proposed EMS and BMS algorithms. When the algorithm proposed in this paper was applied, the maximum efficiency was 97.57%.
This paper proposes a BMS algorithm for an ESS. To apply the BMS algorithm to the ESS, the experiment was conducted by deriving the internal resistance of the battery from its efficiency. Moreover, the increase in battery state accuracy was verified through experiments by applying the battery efficiency to the SoC with the OCV and CCM and the SoH considering the charging time. Furthermore, increased safety through the diagnosis of faulty batteries was verified through experiments.

5. Conclusions

In this paper we proposed a BMS algorithm that considers battery efficiency. The algorithm was applied to an ESS to improve the battery safety and performance. The algorithm proposed in this paper was divided into three parts.
First, the efficiency of the battery was used to estimate the state of the battery. The internal resistance of the battery was estimated based on the difference between the charging and discharging power to obtain the value of the variable internal resistance. The variation in the internal resistance was confirmed by the experimental results, which showed the increase in the charging-discharging power difference during the battery’s operation.
Second, the SoC and SoH estimation methods were proposed. For SoC estimation, the method of combining OCV and CCM with the estimated battery states was proposed to compensate for both low initial estimation accuracies of CCM and incorrect estimation of OCV. An SoH estimation algorithm based on the charging time was also proposed. This proposal was based on the fact that an increase in the temperature of a battery results in an increase in its internal resistance and a decrease in the CC charging time. This charging time decrement according to the internal resistance variation was confirmed in the experiment. Based on the estimated SoH, the battery lifespan estimation method, which observes the charging-discharging SoH difference for a long period of time, was proposed. Additionally, the proposed method is more flexible than conventional methods, since it does not require any additional analysis of different kinds of battery cells for SoH estimation.
Third, this paper proposed a battery fault diagnosis algorithm that aims to improve battery safety. Using this method, faults are diagnosed through efficiency and SoH, and this fault diagnosis algorithm was validated through experiments.
In conclusion, accurate SoC and SoH estimations were proposed by applying battery efficiency to the estimation process. The estimated SoC and SoH were used to improve not only the performance of BMS but also the battery safety via a fault diagnosis algorithm with accurate SoH estimation.

Author Contributions

Conceptualization, J.L.; software, J.L. and J.-M.K.; formal analysis, J.L.; investigation, J.L. and J.-M.K.; writing—original draft preparation, J.L.; writing—review and editing, J.Y. and C.-Y.W. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Acknowledgments

This work was supported by the Korea Institute of Energy Technology Evaluation and Planning (KETEP) and the Ministry of Trade, Industry, and Energy (MOTIE) of the Republic of Korea (No. 2019381010001B).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Diouf, B.; Pode, R. Potential of lithium-ion batteries in renewable energy. Renew. Energy 2015, 76, 375–380. [Google Scholar] [CrossRef]
  2. Zubi, G.; Dufo-López, R.; Carvalho, M.; Pasaoglu, G. The lithium-ion battery: State of the art and future perspectives. Renew. Sustain. Energy Rev. 2018, 89, 292–308. [Google Scholar] [CrossRef]
  3. Raijmakers, L.; Danilov, D.; Eichel, A.; Notten, P. A review on various temperature-indication methods for Li-ion batteries. Appl. Energy 2019, 240, 918–945. [Google Scholar] [CrossRef]
  4. Fossati, J.P.; Galarza, A.; Martín-Villate, A.; Fontan, L. A method for optimal sizing energy storage systems for microgrids. Renew. Energy 2015, 77, 539–549. [Google Scholar] [CrossRef]
  5. Xia, S.; Chan, K.W.; Luo, X.; Bu, S.; Ding, Z.; Zhou, B. Optimal sizing of energy storage system and its cost-benefit analysis for power grid planning with intermittent wind generation. Renew. Energy 2018, 122, 472–486. [Google Scholar] [CrossRef]
  6. Yang, Y.; Bremner, S.; Menictas, C.; Kay, M. Battery Energy Storage System Size Determination in Renewable Energy Systems: A review. Renew. Sustain. Energy Rev. 2018, 91, 109–125. [Google Scholar] [CrossRef]
  7. Nadeem, F.; Hussain, S.M.S.; Tiwari, P.K.; Goswami, A.K.; Ustun, T.S. Comparative Review of Energy Storage Systems, Their Roles, and Impacts on Future Power Systems. IEEE Access 2019, 7, 4555–4585. [Google Scholar] [CrossRef]
  8. Santos-Pereira, K.; Pereira, J.D.; Veras, L.S.; Cosme, D.L.; Oliveira, D.Q.; Saavedra, O.R. The requirements and constraints of storage technology in isolated microgrids: A comparative analysis of lithium-ion vs. lead-acid batteries. Energy Syst. 2021, 1–24. [Google Scholar] [CrossRef]
  9. Shahriari, M.; Farrokhi, M. On-line state of health estimation of VRLA batteries using state of charge. IEEE Trans. Ind. Electron. 2013, 1, 191–202. [Google Scholar] [CrossRef]
  10. Lim, N.G.; Kim, J.Y.; Lee, S. Estimation of the Hot Swap Circulation Current of a Multiple Parallel Lithium Battery System with an Artificial Neural Network Model. Electronics 2021, 10, 1448. [Google Scholar] [CrossRef]
  11. Lee, H.; Park, J.; Kim, J. Incremental Capacity Curve Peak Points—Based Regression Analysis for the State-of-Health Prediction of a Retired LiNiCoAlO2 Series/Parallel Configured Battery Pack. Electronics 2019, 8, 1118. [Google Scholar] [CrossRef] [Green Version]
  12. Wang, Q.; Mao, B.; Stoliarov, S.I.; Sun, J. A review of lithium ion battery failure mechanisms and fire prevention strategies. Prog. Energy Combust. Sci. 2019, 73, 95–131. [Google Scholar] [CrossRef]
  13. Gabar, H.A.; Othman, A.M.; Abdussami, M.R. Review of Battery Management Systems(BMS) Development and Industrial Standards. Technologies 2021, 9, 28. [Google Scholar] [CrossRef]
  14. Wei, Z.; Zhao, J.; He, H.; Ding, G.; Cui, H.; Liu, L. Future smart battery and management: Advanced sensing from external to embedded multi-dimensional measurement. J. Power Sources 2021, 489, 229462. [Google Scholar] [CrossRef]
  15. Xiong, R.; Ma, S.; Li, H.; Sun, F.; Li, J. Toward a safer battery management system: A critical review on diagnosis and prognosis of battery short circuit. Iscience 2020, 23, 101010. [Google Scholar] [CrossRef] [PubMed]
  16. Hemavathi, S. Li-ion Battery Health Estimation Based on Battery Internal Impedance Measurement. In Innovations in Sustainable Energy and Technology; Springer: Singapore, 2021; pp. 183–193. [Google Scholar]
  17. Aiello, O. Electromagnetic Susceptibility of Battery Management Systems’ ICs for Electric Vehicles: Experimental Study. Electronics 2020, 9, 510. [Google Scholar] [CrossRef] [Green Version]
  18. Nordmann, H.; Frisch, M.; Sauer, D.U. Thermal Fault-Detection Method and Analysis of Peripheral Systems for Large Battery Packs. EES J. Meas. 2017, 114, 484–491. [Google Scholar] [CrossRef]
  19. Lee, C.-J.; Kim, B.-K.; Kwon, M.-K.; Nam, K.; Kang, S.-W. Real-Time Prediction of Capacity Fade and Remaining Useful Life of Lithium-Ion Batteries Based on Charge/Discharge Characteristics. Electronics 2021, 10, 846. [Google Scholar] [CrossRef]
  20. Samanta, A.; Chowdhuri, S.; Williamson, S.S. Machine Learning-Based Data-Driven Fault Detection/Diagnosis of Lithium-Ion Battery: A Critical Review. Electronics 2021, 10, 1309. [Google Scholar] [CrossRef]
  21. Lelie, M.; Braun, T.; Knips, M.; Nordmann, H.; Ringbeck, F.; Zappen, H.; Sauer, D.U. Battery management system hardware concepts: An overview. Appl. Sci. 2018, 8, 534. [Google Scholar] [CrossRef] [Green Version]
  22. Kurzweil, P.; Scheuerpflug, W. State-of-charge monitoring and battery diagnosis of NiCd cells using impedance spectroscopy. Batteries 2020, 6, 4. [Google Scholar] [CrossRef] [Green Version]
  23. Ko, Y.; Choi, W. A New SOC Estimation for LFP Batteries: Application in a 10 Ah Cell (HW 38120 L/S) as a Hysteresis Case Study. Electronics 2021, 10, 705. [Google Scholar] [CrossRef]
  24. Meddings, N. Application of electrochemical impedance spectroscopy to commercial Li ion cells: A review. J. Power Sources 2020, 480, 228742. [Google Scholar] [CrossRef]
  25. Laadjal, K.; Cardoso, A.J.M. Estimation of Lithium-Ion Batteries State-Condition in Electric Vehicle Applications: Issues and State of the Art. Electronics 2021, 10, 1588. [Google Scholar] [CrossRef]
  26. Raj, A.; Rodrigues, M.T.F.; Abraham, D.P. Rate-dependent aging resulting from fast charging of Li-ion cells. J. Electrochem. Soc. 2020, 167, 120517. [Google Scholar] [CrossRef]
  27. Juarez-Robles, D.; Vyas, A.A.; Fear, C.; Jeevarajan, J.A.; Mukherjee, P.P. Overcharge and Aging Analytics of Li-Ion Cells. J. Electrochem. Soc. 2020, 167, 090547. [Google Scholar] [CrossRef]
  28. Bhattacharjee, A.; Mohanty, R.K.; Ghosh, A. Design of an Optimized Thermal Management System for Li-Ion Batteries under Different Discharging Conditions. Energies 2020, 13, 5695. [Google Scholar] [CrossRef]
  29. Werner, D.; Paarmann, S.; Wiebelt, A.; Wetzel, T. Inhomogeneous temperature distribution affecting cyclic aging of Li-ion cells. Part ii: Analysis and correlation. Batteries 2020, 6, 12. [Google Scholar] [CrossRef] [Green Version]
  30. Luo, X.; Kang, L.; Lu, C.; Linghu, J.; Lin, H.; Hu, B. An Enhanced Multicell-to-Multicell Battery Equalizer Based on Bipolar-Resonant LC Converter. Electronics 2021, 10, 293. [Google Scholar] [CrossRef]
  31. Pham, V.L.; Duong, V.T.; Choi, W.J. A Low Cost and Fast Cell-to-Cell Balancing Circuit for Lithium-Ion Battery Strings. Electronics 2020, 9, 248. [Google Scholar] [CrossRef] [Green Version]
  32. Van, C.N.; Vinh, T.N.; Ngo, M.D.; Ahn, S.J. Optimal SoC Balancing Control for Lithium-Ion Battery Cells Connected in Series. Energies 2021, 14, 2875. [Google Scholar] [CrossRef]
  33. Venet, P.; Redondo-Iglesias, E. Batteries and Supercapacitors Aging. Batteries 2020, 6, 18. [Google Scholar] [CrossRef] [Green Version]
  34. Xiong, R.; Li, L.; Tian, J. Towards a smarter battery management system: A critical review on battery state of health monitoring methods. J. Power Sour. 2018, 405, 18–29. [Google Scholar] [CrossRef]
  35. Wei, Z.; Zhao, D.; He, H.; Cao, W.; Dong, G. A noise-tolerant model parameterization method for lithium-ion battery management system. Appl. Energy 2020, 268, 114932. [Google Scholar] [CrossRef]
  36. Kang, J.; Yan, F.; Zhang, P.; Du, C. Comparison of comprehensive properties of Ni-MH (nickel-metal hydride) and Li-ion(lithium-ion) batteries in terms of energy efficiency. Energy 2014, 70, 618–625. [Google Scholar] [CrossRef]
  37. Eddahech, A.; Briat, O.; Vinassa, J.M. Performance comparison of four lithium-ion battery technologies under calendar aging. Energy 2015, 84, 542–550. [Google Scholar] [CrossRef]
  38. Ahmadi, L.; Fowler, M.; Young, S.; Fraser, R.; Gaffney, B.; Walker, S. Energy efficiency of Li-ion battery packs re-used in stationary power applications. Sustain. Energy Technol. Assess. 2014, 8, 9–17. [Google Scholar] [CrossRef]
  39. Meister, P.; Jia, H.; Li, J.; Kloepsch, R.; Winter, M.; Placke, T. Best Practice: Performance and Cost Evaluation of Lithium Ion Battery Active Materials with Special Emphasis on Energy Efficiency. Chem. Mater. 2016, 28, 7203–7217. [Google Scholar] [CrossRef]
  40. How, D.N.; Hannan, M.A.; Lipu, M.S.H.; Sahari, K.S.; Ker, P.J.; Muttaqi, K.M. State-of-Charge Estimation of Li-Ion Battery in Electric Vehicles: A Deep Neural Network Approach. IEEE Trans. Ind. Appl. 2020, 56, 5565–5574. [Google Scholar] [CrossRef]
  41. Zhi, L.; Peng, Z.; Zhifu, W.; Qiang, S.; Yinan, R. State of Charge Estimation for Li-ion Battery Based on Extended Kalman Filter. Energy Procedia 2017, 105, 3515–3520. [Google Scholar] [CrossRef]
  42. Bian, X.; Wei, Z.; He, J.; Yan, F.; Liu, L. A two-step parameter optimization method for low-order model-based state of charge estimation. IEEE Trans. Transp. Electrif. 2020, 7, 399–409. [Google Scholar] [CrossRef]
  43. Baccouche, I.; Jemmali, S.; Manai, B.; Omar, N.; Essoukri Ben Amara, N. Improved OCV model of a Li-ion NMC battery for online SOC estimation using the extended Kalman filter. Energies 2017, 10, 764. [Google Scholar] [CrossRef] [Green Version]
  44. Chen, Z.; Yang, L.; Zhao, X.; Wang, Y.; He, Z. Online state of charge estimation of Li-ion battery based on an improved unscented Kalman filter approach. Appl. Math. Modell. 2019, 70, 532–544. [Google Scholar] [CrossRef]
  45. Tian, Y.; Lai, R.; Li, X.; Xiang, L.; Tian, J. A combined method for state-of-charge estimation for lithium-ion batteries using a long short-term memory network and an adaptive cubature Kalman filter. Appl. Energy 2020, 337–339. [Google Scholar] [CrossRef]
  46. Wei, Z.; He, H.; Pou, J.; Tsui, K.L.; Quan, Z.; Li, Y. Signal-Disturbance Interfacing Elimination for Unbiased Model Parameter Identification of Lithium-Ion Battery. IEEE Trans. Ind. Inform. 2020, 17, 5887–5897. [Google Scholar] [CrossRef]
  47. Kamrueng, C.; Kittiratsatcha, S.; Polmai, S. Fast Approach of Open Circuit Voltage Estimation for Li-ion Battery Based on OCV Error Compensation. In Proceedings of the 2020 23rd International Conference on Electrical Machines and Systems (ICEMS), IEEE, Hamamatsu, Japan, 24–27 November 2020; pp. 1583–1586. [Google Scholar]
  48. Tian, J.; Xiong, R.; Shen, W.; Sun, F. Electrode ageing estimation and open circuit voltage reconstruction for lithium ion batteries. Energy Storage Mater. 2021, 37, 283–295. [Google Scholar] [CrossRef]
  49. Qaisar, S.M. Event-Driven Approach for an Efficient Coulomb Counting Based Li-Ion Battery State of Charge Estimation. Procedia Comput. Sci. 2020, 168, 202–209. [Google Scholar] [CrossRef]
  50. Zhang, S.; Guo, X.; Dou, X.; Zhang, X. A data-driven coulomb counting method for state of charge calibration and estimation of lithium-ion battery. Sustain. Energy Technol. Assess. 2020, 40, 100752. [Google Scholar]
  51. Ouyang, T.; Xu, P.; Lu, J.; Hu, X.; Liu, B.; Chen, N. Co-estimation of state-of-charge and state-of-health for power batteries based on multi-thread dynamic optimization method. IEEE Trans. Ind. Electron. 2021. [Google Scholar] [CrossRef]
  52. Swarup, S.; Tan, S.X.D.; Liu, Z.; Wang, H.; Hao, Z.; Shi, G. Battery state of charge estimation using adaptive subspace identification method. In Proceedings of the 2011 9th IEEE International Conference on ASIC, IEEE, Xiamen, China, 25–28 October 2011; pp. 91–94. [Google Scholar]
  53. Yang, K.; Tang, Y.; Zhang, Z. Parameter Identification and State-of-Charge Estimation for Lithium-Ion Batteries Using Separated Time Scales and Extended Kalman Filter. Energies 2021, 14, 1054. [Google Scholar] [CrossRef]
  54. Jungsoo, K.; Jungwook, Y. Estimation of Li-ion Battery State of Health based on Multilayer Perceptron: As an EV Application. IFAC-Pap. Line 2018, 51, 392–397. [Google Scholar]
  55. Che, Y.; Liu, Y.; Cheng, Z.; Zhang, J. SOC and SOH Identification Method of Li-ion Battery Based on SWPSO-DRNN. IEEE Journal of Emerging and Selected Topics in Power Electronics 2020, 9, 4050–4061. [Google Scholar] [CrossRef]
  56. Shuxiang, S.; Chen, F.; Haiying, X. Lithium-Ion Battery SOH Estimation Based on XG Boost Algorithm with Accuracy Correction. Energies 2020, 13, 812. [Google Scholar]
  57. Bian, X.; Wei, Z.; He, J.; Yan, F.; Liu, L. A Novel Model-based Voltage Construction Method for Robust State-of-health Estimation of Lithium-ion Batteries. IEEE Trans. Ind. Electron. 2020, 1. [Google Scholar] [CrossRef]
  58. He, J.; Wei, Z.; Bian, X.; Yan, F. State-of-Health Estimation of Lithium-Ion Batteries Using Incremental Capacity Analysis Based on Voltage–Capacity Model. IEEE Trans. Transp. Electrif. 2020, 6, 417–426. [Google Scholar] [CrossRef]
  59. Zhang, S.; Guo, X.; Dou, X.; Zhang, X. A Rapid Online Calculation Method for State of Health of Lithium-Ion Battery based on Coulomb Counting Method and Differential Voltage Analysis. J. Power Sources 2020, 479, 228740. [Google Scholar] [CrossRef]
  60. Li, N.; Gao, F.; Hao, T.; Ma, Z.; Zhang, C. SOH Balancing Control Method for the MMC Battery Energy Storage System. IEEE Trans. Ind. Electron. 2018, 65, 6581–6591. [Google Scholar] [CrossRef]
  61. Yang, Y.; Wen, J.; Shi, Y.; Zeng, J. State of Health Prediction of Lithium-Ion Batteries Based on the Discharge Voltage and Temperature. Electronics 2020, 10, 1497. [Google Scholar] [CrossRef]
  62. Lee, J.; Kim, J.; Ryu, K.; Won, C. An Energy Storage System’s Operational Management and Control Method Considering a Battery System. Electronics 2020, 9, 356. [Google Scholar] [CrossRef] [Green Version]
  63. Huang, W.X.; Abu Qahouq, J.A. An Online Battery Impedance Measurement Method Using DC-DC Power Converter Control. IEEE Trans. Ind. Electron. 2014, 61, 5987–5995. [Google Scholar] [CrossRef]
  64. Kim, J. A Study on SOH Estimation Method for Lithium Ion Battery Using Charging Time. Master’s Thesis, Korea University, Seoul, Korea, 2015; pp. 1–94. [Google Scholar]
  65. Yang, R.; Xiong, R.; Shen, W.; Lin, X. Extreme Learning Machine Based Thermal Model for Lithium-ion Batteries of Electric Vehicles under External Short Circuit. Engineering 2020, 7, 395–405. [Google Scholar] [CrossRef]
  66. Tian, J.; Xiong, R.; Shen, W. State-of-Health estimation based on differential temperature for lithium ion batteries. IEEE Trans. Power Electron. 2020, 35, 10363–10373. [Google Scholar] [CrossRef]
  67. Lee, J.H.; Kim, H.S.; Lee, I.S. Multilayer Neural Network-Based Battery Module SOH Diagnosis. Int. J. Eng. Res. Technol. 2020, 13, 316–319. [Google Scholar] [CrossRef]
  68. Copper Development Association. Market Evaluation for Energy Storage in the United States; KEMA, Inc.: Burlington, MA, USA, 2012. [Google Scholar]
  69. Andrea, D. Battery Management Systems for Large Lithium-Ion Battery Packs; Artech House: Norwood, MA, USA, 2010. [Google Scholar]
  70. Shin, D.; Yoon, B.; Yoo, S. Compensation Method for Estimating the State of Charge of Li-Polymer Batteries Using Multiple Long Short-Term Memory Networks Based on the Extended Kalman Filter. Energies 2020, 14, 349. [Google Scholar] [CrossRef]
  71. Meng, J.; Ricco, M.; Luo, G.; Swierczynski, M.; Stroe, D.I.; Stroe, A.I.; Teodorescu, R. An overview and comparison of online implementable soc estimation methods for lithium-ion battery. IEEE Trans. Ind. Appl. 2018, 54, 1583–1591. [Google Scholar] [CrossRef]
  72. Movassagh, K.; Raihan, A.; Balasingam, B.; Pattipati, K. A Critical Look at Coulomb Counting Approach for State of Charge Estimation in Batteries. Energies 2021, 14, 4074. [Google Scholar] [CrossRef]
  73. Lu, L.; Han, X.; Li, J.; Hua, J.; Ouyang, M. A review on the key issues for lithium-ion battery management in electric vehicles. J. Power Sources 2013, 226, 272–288. [Google Scholar] [CrossRef]
  74. Topan, P.A.; Ramadan, M.N.; Fathoni, G.; Cahyadi, A.I.; Wahyunggoro, O. State of charge (SOC) and state of health (SOH) estimation on lithium polymer battery via Kalman filter. In Proceedings of the 2nd International Conference on Science and Technology-Computer (ICST), Yogyakarta, Indonesia, 27–28 October 2016; pp. 93–96. [Google Scholar]
  75. Mo, B.; Yu, J.; Tang, D.; Liu, H. A remaining useful life prediction approach for lithium-ion batteries using Kalman filter and an improved particle filter. In Proceedings of the 2016 IEEE International Conference on Prognostics and Health Management (ICPHM), Ottawa, ON, Canada, 20–22 June 2016; pp. 1–5. [Google Scholar]
  76. Pola, D.; Navarrete, H.F.; Orchard, M.E.; Rabie, R.S.; Cerda, M.A.; Olivares, B.E.; Silva, J.F.; Espinoza, P.A.; Perez, A. Particle-Filtering-Based Discharge Time Prognosis for Lithium-Ion Batteries With a Statistical Characterization of Use Profiles. IEEE Trans. Reliab. 2015, 64, 1–11. [Google Scholar] [CrossRef]
  77. Zun, C.Y.; Park, S.U.; Mok, H.S. New Cell Balancing Charging System Research for Lithium-ion Batteries. Energies 2020, 13, 1393. [Google Scholar] [CrossRef] [Green Version]
Electronics 10 01859 g001 550
Figure 1. Factors affecting the state of a battery.
Figure 1. Factors affecting the state of a battery.
Electronics 10 01859 g001
Electronics 10 01859 g002 550
Figure 2. Proposed ESS configuration diagram.
Figure 2. Proposed ESS configuration diagram.
Electronics 10 01859 g002
Electronics 10 01859 g003 550
Figure 3. Proposed BMS configuration diagram.
Figure 3. Proposed BMS configuration diagram.
Electronics 10 01859 g003
Electronics 10 01859 g004 550
Figure 4. EMS charge-discharge algorithm according to time.
Figure 4. EMS charge-discharge algorithm according to time.
Electronics 10 01859 g004
Electronics 10 01859 g005 550
Figure 5. BMS algorithm that considers the battery efficiency.
Figure 5. BMS algorithm that considers the battery efficiency.
Electronics 10 01859 g005
Electronics 10 01859 g006 550
Figure 6. The current capacity of a battery during aging.
Figure 6. The current capacity of a battery during aging.
Electronics 10 01859 g006
Electronics 10 01859 g007 550
Figure 7. Voltage and SoH of a battery during charging.
Figure 7. Voltage and SoH of a battery during charging.
Electronics 10 01859 g007
Electronics 10 01859 g008 550
Figure 8. Voltage and SoH of a battery during discharging.
Figure 8. Voltage and SoH of a battery during discharging.
Electronics 10 01859 g008
Electronics 10 01859 g009 550
Figure 9. Proposed fault diagnosis algorithm.
Figure 9. Proposed fault diagnosis algorithm.
Electronics 10 01859 g009
Electronics 10 01859 g010 550
Figure 10. ESS hardware configuration for the application of the proposed algorithm.
Figure 10. ESS hardware configuration for the application of the proposed algorithm.
Electronics 10 01859 g010
Electronics 10 01859 g011 550
Figure 11. Battery efficiency difference profile graph according to battery power.
Figure 11. Battery efficiency difference profile graph according to battery power.
Electronics 10 01859 g011
Electronics 10 01859 g012 550
Figure 12. SoC comparison profile graph.
Figure 12. SoC comparison profile graph.
Electronics 10 01859 g012
Electronics 10 01859 g013 550
Figure 13. SoH profile with CC charging time, to which the battery efficiency was applied.
Figure 13. SoH profile with CC charging time, to which the battery efficiency was applied.
Electronics 10 01859 g013
Electronics 10 01859 g014 550
Figure 14. Waveforms for battery fault diagnosis: (a) charging voltage and charging current waveform; (b) discharging voltage and discharging current waveform.
Figure 14. Waveforms for battery fault diagnosis: (a) charging voltage and charging current waveform; (b) discharging voltage and discharging current waveform.
Electronics 10 01859 g014
Electronics 10 01859 g015 550
Figure 15. ESS efficiency waveform when the proposed algorithm was implemented.
Figure 15. ESS efficiency waveform when the proposed algorithm was implemented.
Electronics 10 01859 g015
Table
Table 1. ESS experimental parameters for the application of the proposed algorithm.
Table 1. ESS experimental parameters for the application of the proposed algorithm.
ParameterSymbolsValuesUnits
Rated powerPESS3kW
Input voltageVac_in220Vac
DC link voltageVdc_link400V
Output voltageVdc_out96V
Output CurrentIdc_out30A
Switching frequencyfacdc40kHz
Switching frequencyfdcdc100kHz
Table
Table 2. SoC profile of the batteries according to the algorithm.
Table 2. SoC profile of the batteries according to the algorithm.
Algorithm0 s1080 s2160 s3240 s4320 s5400 s6480 s7560 s8460 s9720 s10,800 s
OCV20.3%30.1%32.1%31.5%43.5%49.1%54.1%60.8%77.3%72.1%80%
CCM20.3%25.3%30.1%35.8%40.3%46.3%57.2%64.2%70.8%78.2%80%
Proposed20.2%25.1%30.6%36.1%40.7%46.8%58.2%65.1%70.9%80.3%80%
Table
Table 3. SoH table for three battery modules to which the battery efficiency was applied.
Table 3. SoH table for three battery modules to which the battery efficiency was applied.
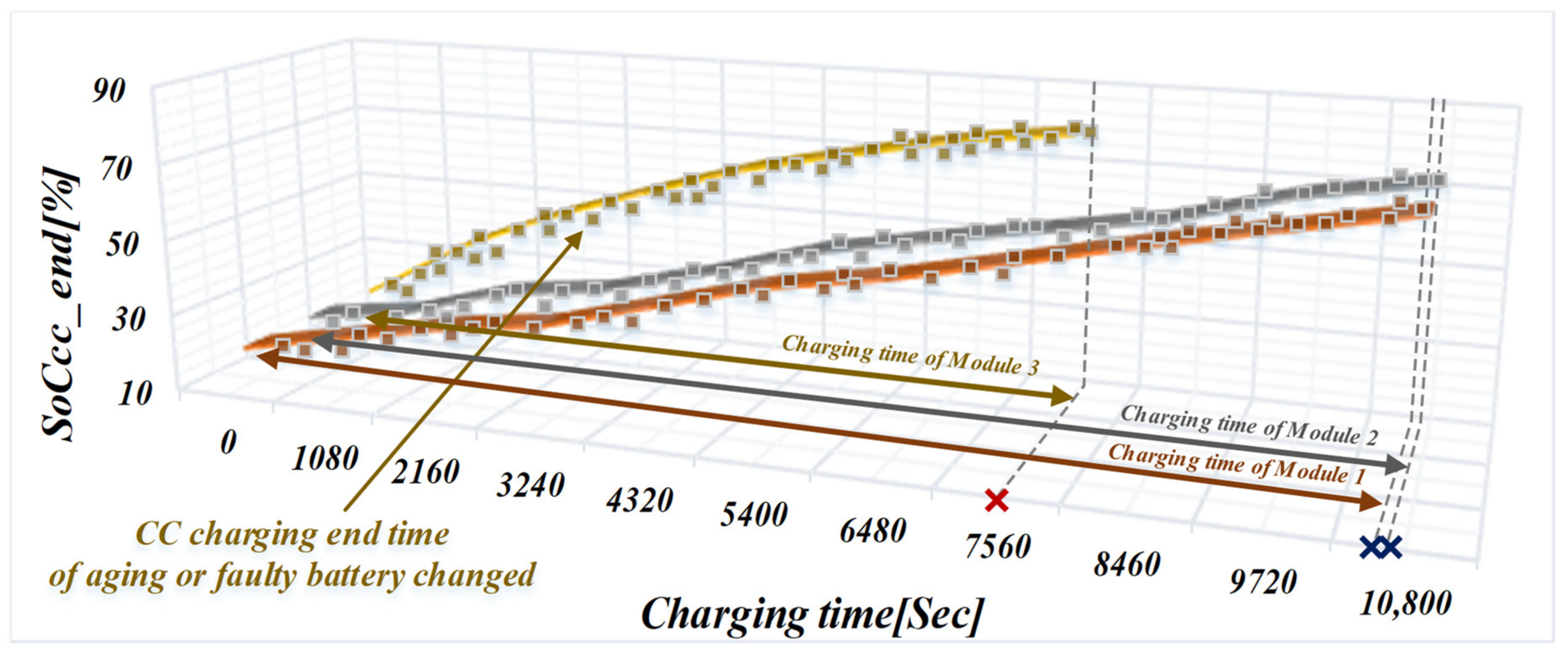
ParameterCharging Time (Before)Charging Time (After)ΔSoC
Module 110,740 s10,610 s0.02%
Module 210,760 s10,700 s0.01%
Module 310,740 s7430 s31%
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Lee, J.; Kim, J.-M.; Yi, J.; Won, C.-Y. Battery Management System Algorithm for Energy Storage Systems Considering Battery Efficiency. Electronics 2021, 10, 1859. https://doi.org/10.3390/electronics10151859

AMA Style

Lee J, Kim J-M, Yi J, Won C-Y. Battery Management System Algorithm for Energy Storage Systems Considering Battery Efficiency. Electronics. 2021; 10(15):1859. https://doi.org/10.3390/electronics10151859

Chicago/Turabian Style

Lee, Jeong, Jun-Mo Kim, Junsin Yi, and Chung-Yuen Won. 2021. "Battery Management System Algorithm for Energy Storage Systems Considering Battery Efficiency" Electronics 10, no. 15: 1859. https://doi.org/10.3390/electronics10151859

APA Style

Lee, J., Kim, J. -M., Yi, J., & Won, C. -Y. (2021). Battery Management System Algorithm for Energy Storage Systems Considering Battery Efficiency. Electronics, 10(15), 1859. https://doi.org/10.3390/electronics10151859

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop