Wideband Frequency Invariant Array Synthesis Based on Matrix Singular Value Decomposition
Abstract
:1. Introduction
2. Materials and Methods
3. Results
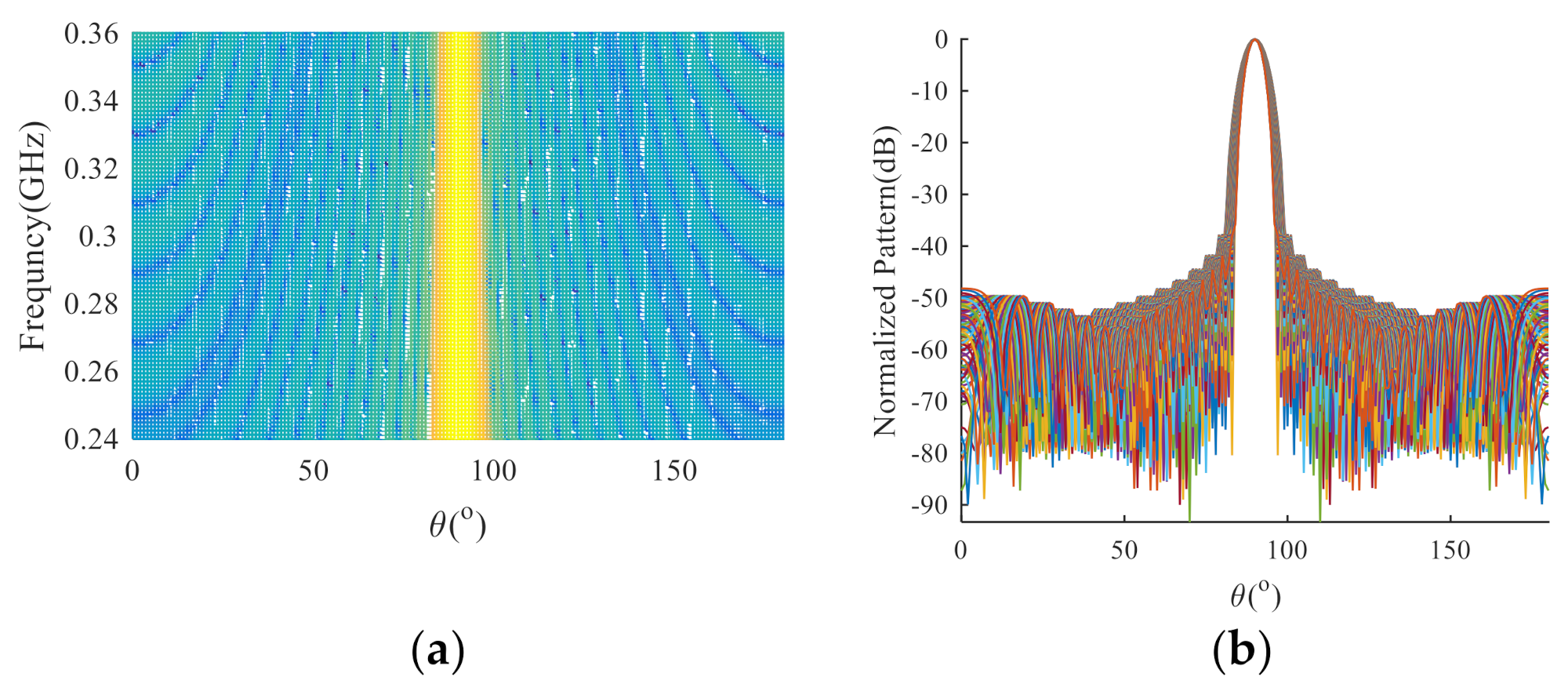
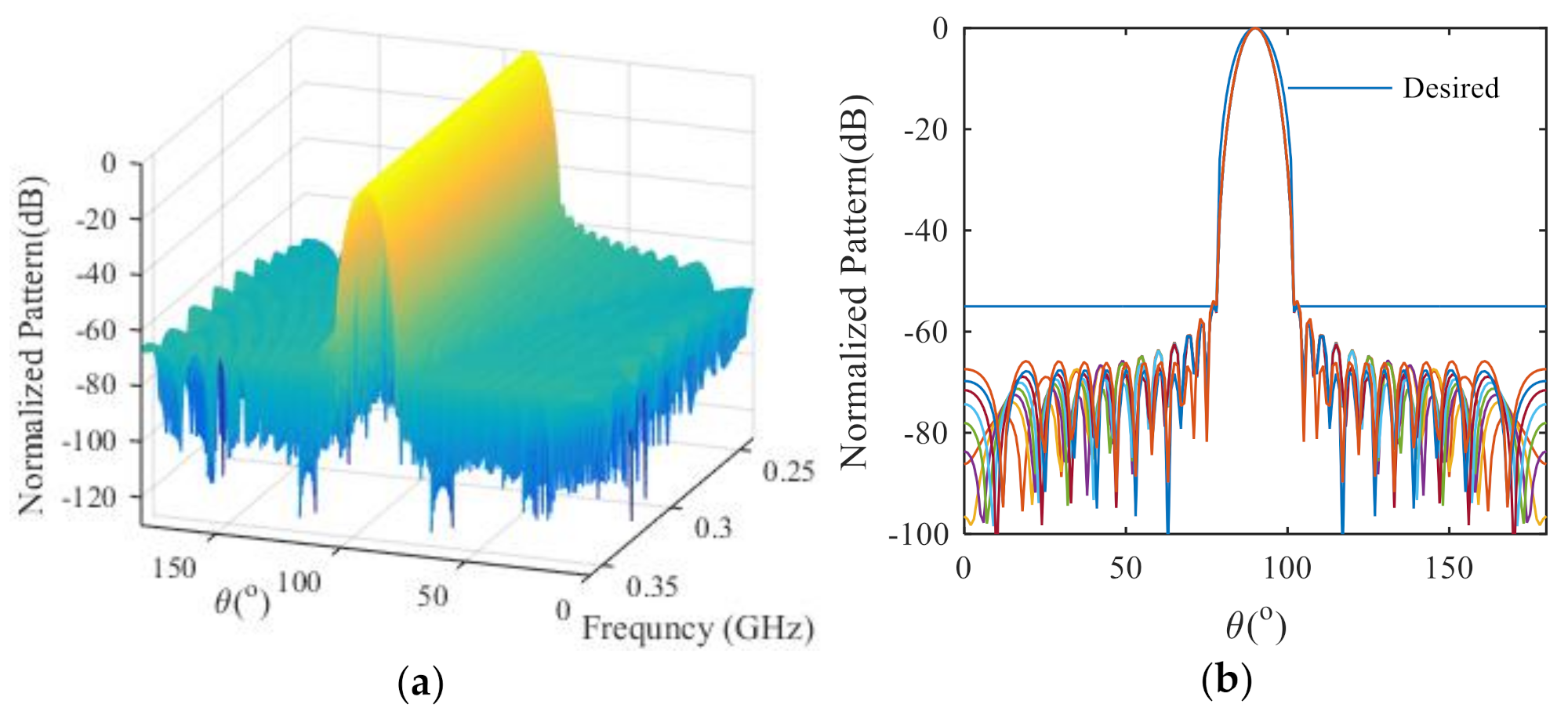
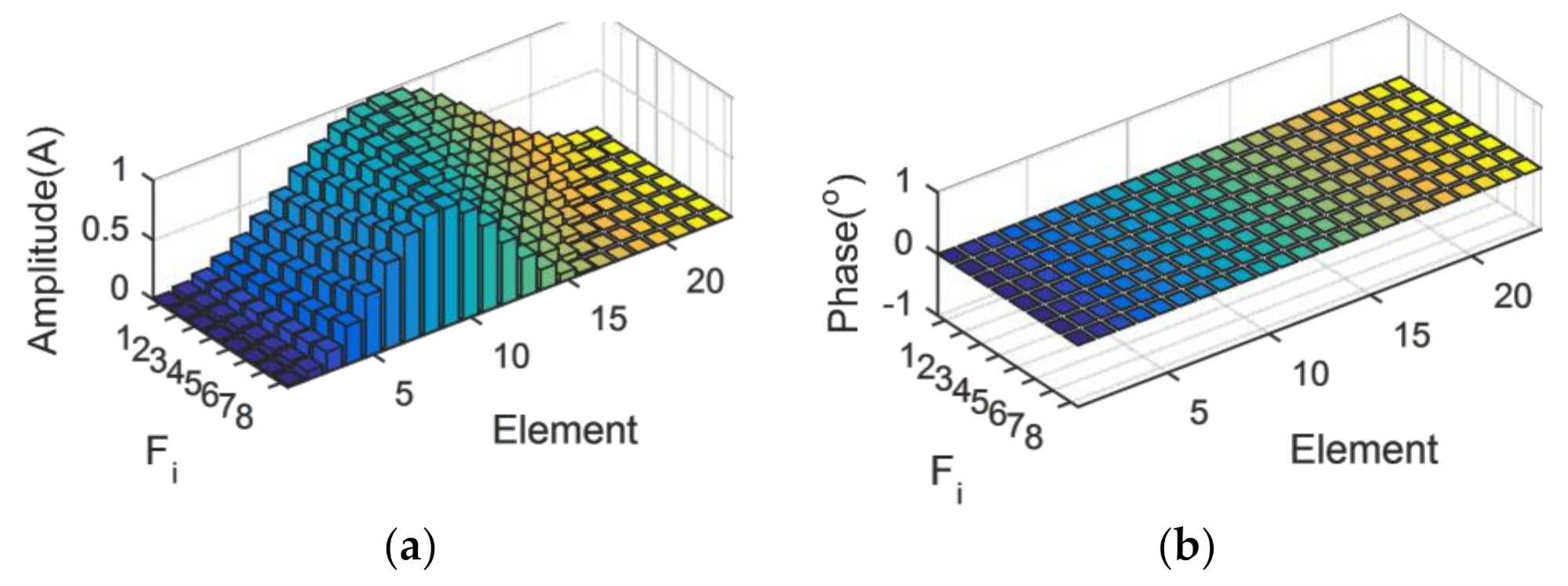
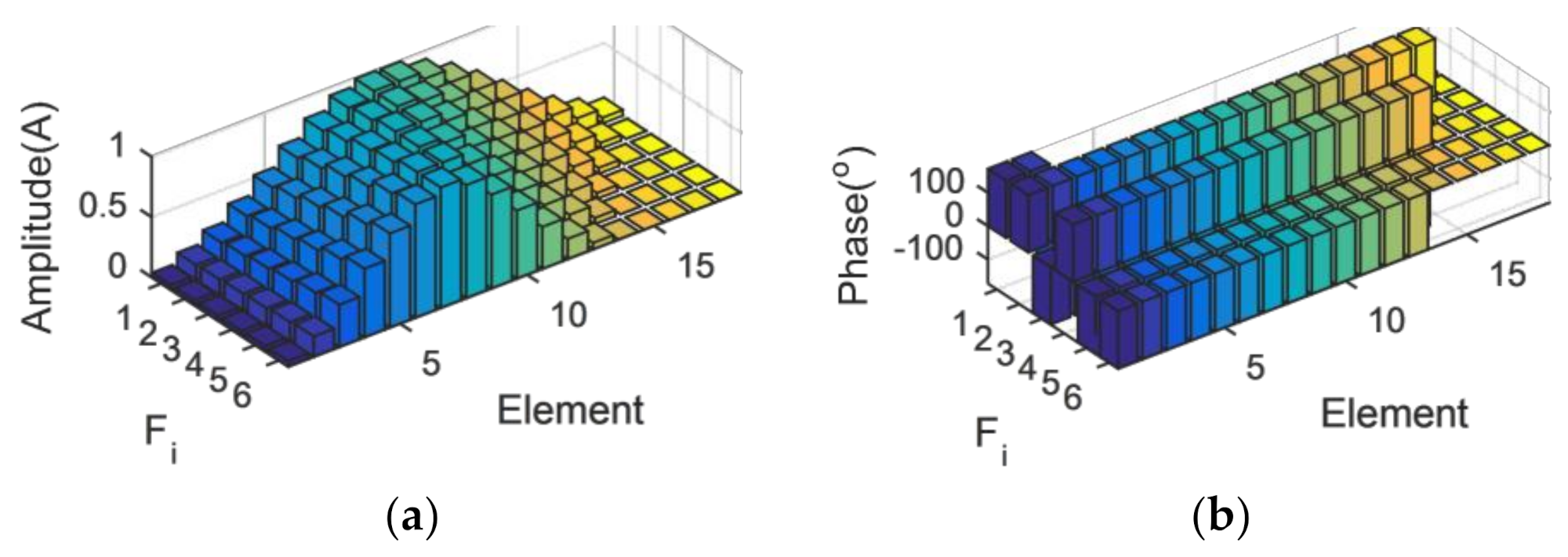
3.1. Uniform Linear Array of 23 Isotropic Ideal Point Elements
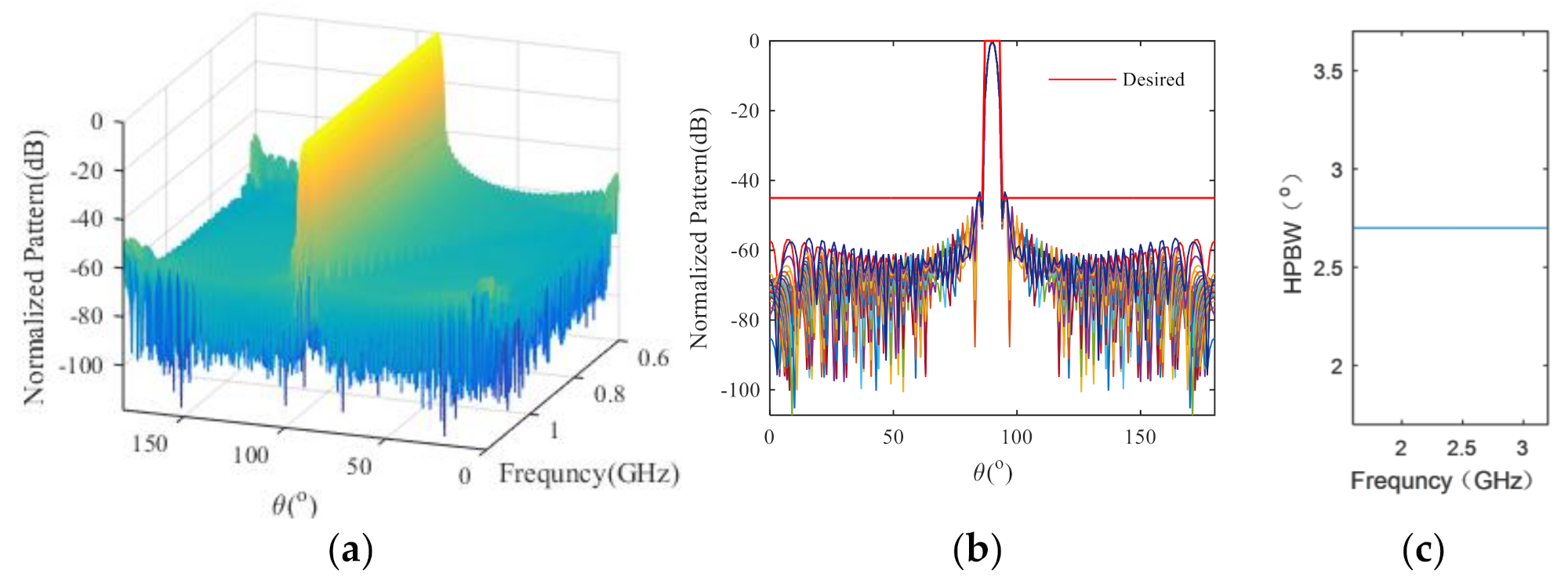
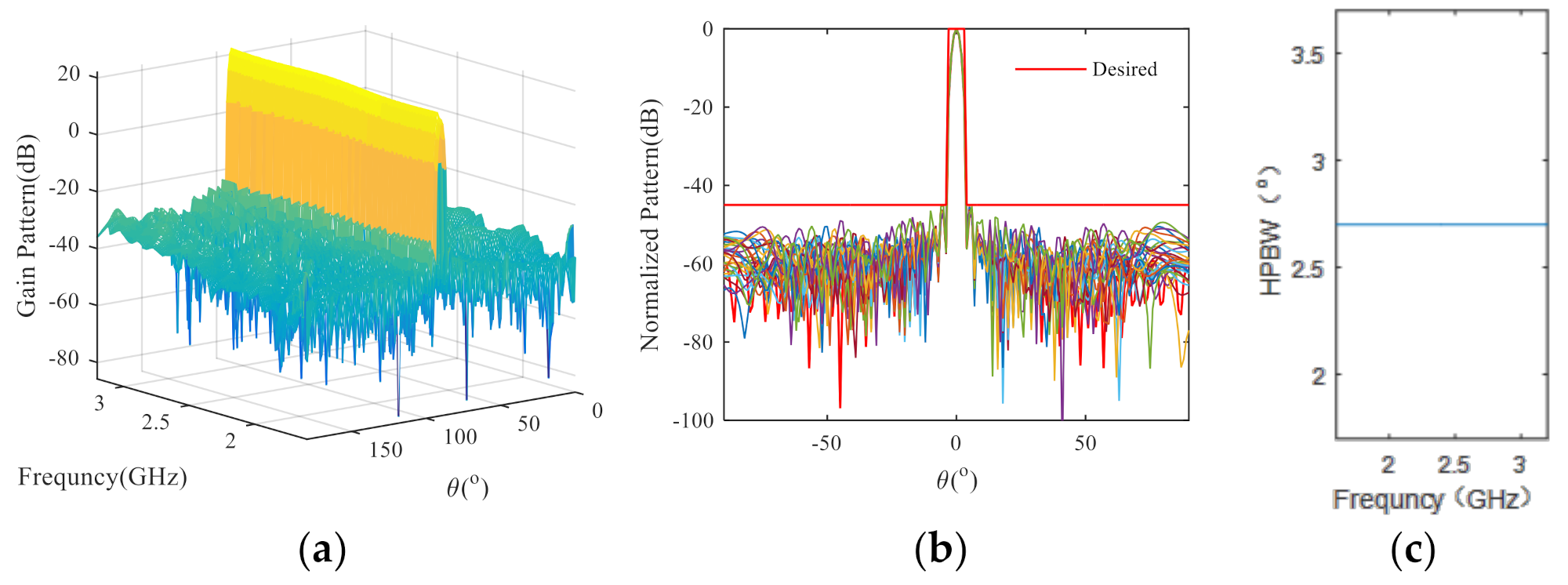
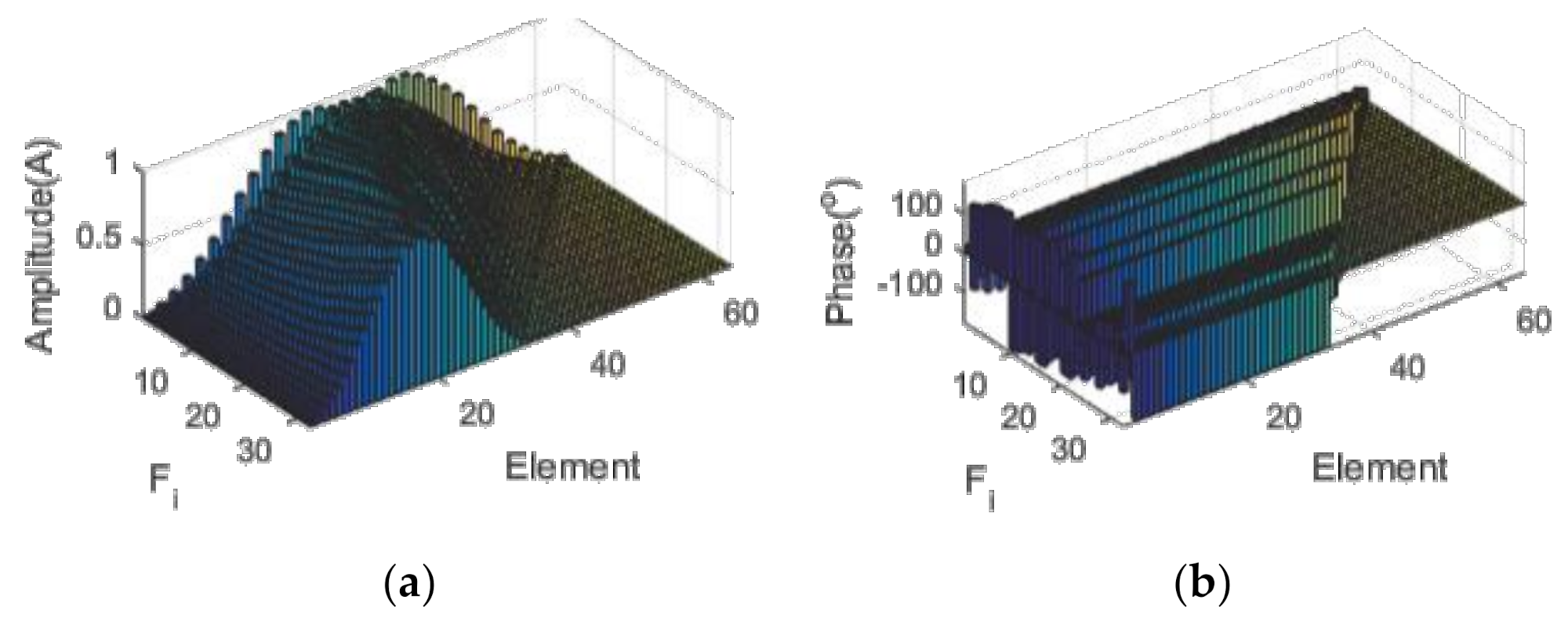
3.2. Uniform Linear Array of 64 Isotropic Ideal Point Elements
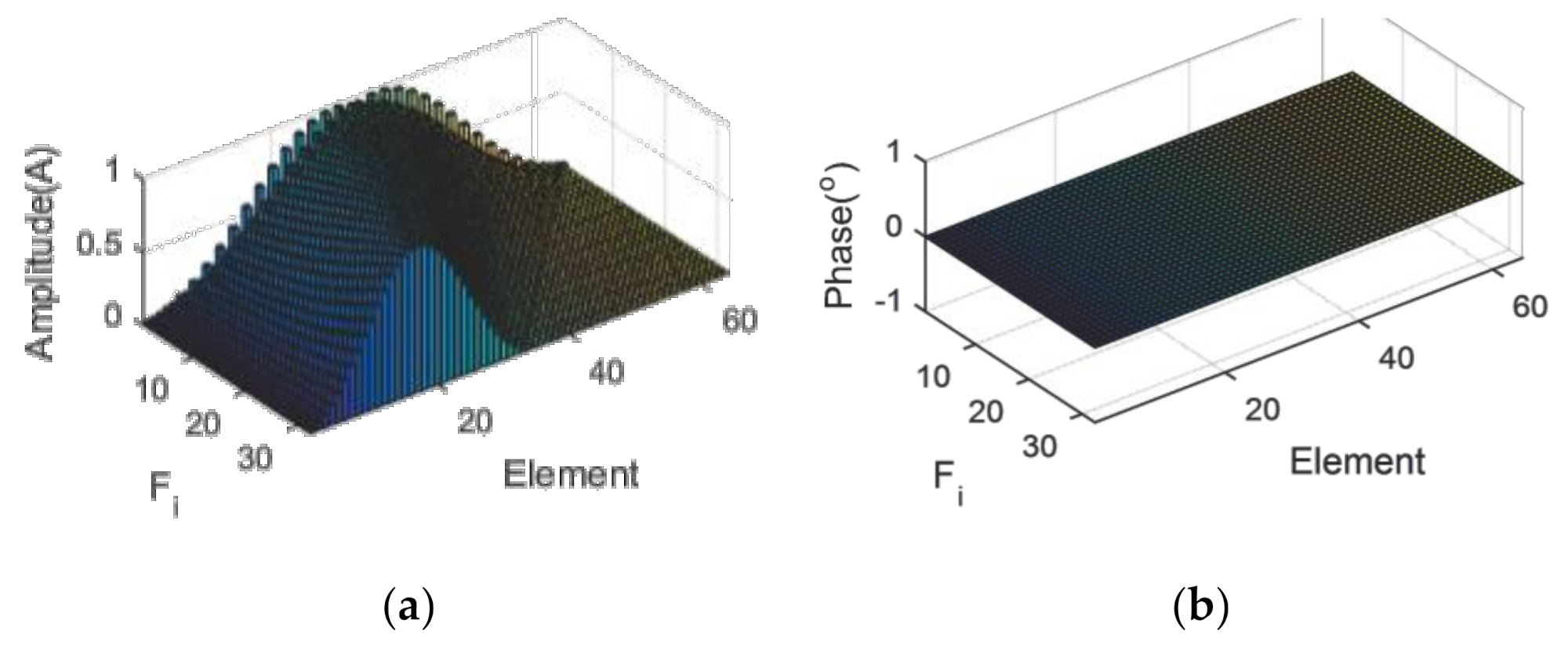
3.3. Uniform Linear Array of 44 Isotropic Ideal Point Elements
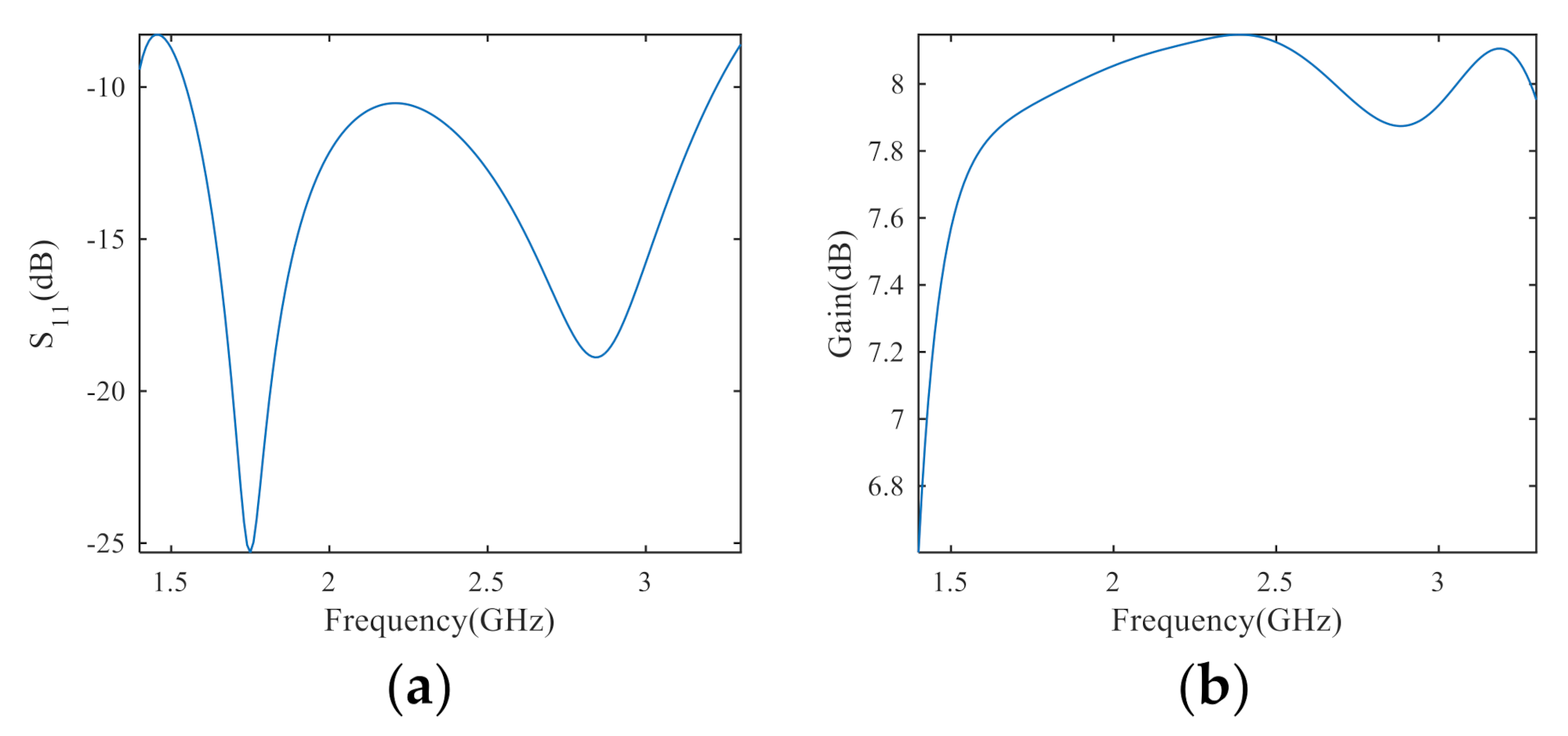
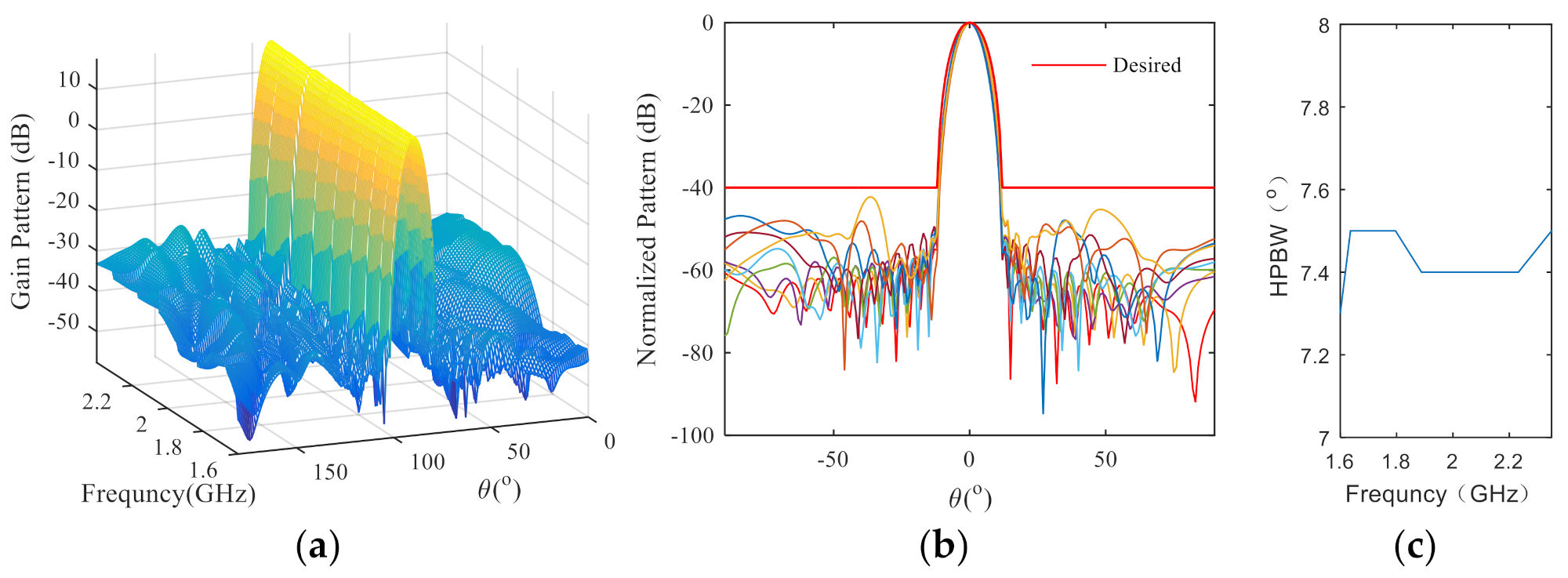
3.4. Uniform Linear Array with Isotropic Antennas
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jacob, B.; Israel, C.; Jingdong, C. Fundamentals of Signal Enhancement and Array Signal Processing, 1st ed.; Wiley-IEEE: Hoboken, NJ, USA, 2018; pp. 371–375. [Google Scholar]
- Pei, C.; Yongjun, Z.; Chengcheng, L. A novel adaptive wideband frequency invariant beamforming algorithm for conformal arrays. In Proceedings of the 2017 18th International Radar Symposium (IRS), Prague, Czech Republic, 28–30 June 2017; pp. 1–10. [Google Scholar]
- Li, S.; Yang, X.; Ning, L.; Long, T.; Sarkar, T.K. Broadband constant beamwidth beamforming for suppressing mainlobe and sidelobe interferences. In Proceedings of the 2017 IEEE Radar Conference (RadarConf), Seattle, WA, USA, 8–12 May 2017; pp. 1041–1045. [Google Scholar]
- Frost, O.L. An algorithm for linearly constrained adaptive array processing. Proc. IEEE 1972, 60, 926–935. [Google Scholar] [CrossRef]
- Smith, R.P. Constant Beamwidth Receiving Arrays for Broad Band Sonar Systems. Acta Acust. United Acust. 1970, 23, 21–26. [Google Scholar]
- Hixson, E.L.; Au, K.T. Widebandwidth constant beamwidth acoustic array. J. Acoust. Soc. Am. 1970, 48, 117. [Google Scholar] [CrossRef]
- Ward, D.B.; Kennedy, R.A.; Williamson, R.C. Theory and design of broadband sensor arrays with frequency invariant far-field beam patterns. J. Acoust. Soc. Amer. 1996, 97, 1023–1034. [Google Scholar] [CrossRef]
- Ward, D.B.; Kennedy, R.A.; Williamson, R.C. FIR filter design for frequency invariant beamformers. IEEE Signal Process. Lett. 1996, 3, 69–71. [Google Scholar] [CrossRef] [Green Version]
- Lebret, H.; Boyd, S. Antenna array pattern synthesis via convex optimization. IEEE Trans. Signal Process. 1997, 45, 526–532. [Google Scholar] [CrossRef] [Green Version]
- Yan, S.F.; Ma, Y.L.; Hou, C.H. Optimal array pattern synthesis for broadband arrays. J. Acoust. Soc. Am. 2007, 122, 2686–2696. [Google Scholar] [CrossRef] [PubMed]
- Duan, H.; Ng, B.P.; See, C.M.S.; Fang, J. Applications of the SRV constraint in broadband pattern synthesis. Signal Process. 2008, 88, 1035–1045. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, W.; Langley, R. Application of the least squares approach to flxed beam former design with frequency-invariant constraints. IET Signal Process. 2011, 5, 281–291. [Google Scholar] [CrossRef]
- Crocco, M.; Trucco, A. Design of Robust Superdirective Arrays with a Tunable Tradeoff Between Directivity and Frequency-Invariance. IEEE Trans. Signal Process. 2011, 59, 2169–2181. [Google Scholar] [CrossRef]
- Crocco, M.; Trucco, A. Stochastic and Analytic Optimization of Sparse Aperiodic Arrays and Broadband Beamformers With Robust Superdirective Patterns. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 2433–2447. [Google Scholar] [CrossRef]
- Sekiguchi, T.; Karasawa, Y. Wideband beamspace adaptive array utilizing FIR fan filters for multibeam forming. IEEE Trans. Signal Process. 2000, 48, 277–284. [Google Scholar] [CrossRef]
- Ghavami, M. Wideband smart antenna theory using rectangular array structures. IEEE Trans. Signal Process. 2002, 50, 2143–2151. [Google Scholar] [CrossRef]
- Liu, W.; Weiss, S. Frequency invariant beamforming for two-dimensional and three-dimensional arrays. Signal Process. 2007, 87, 2535–2543. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.; Weiss, S. Design of Frequency Invariant Beamformers for Broadband Arrays. IEEE Trans. Signal Process. 2008, 56, 855–860. [Google Scholar] [CrossRef]
- Liu, W.; McLernon, D.C.; Ghogho, M. Design of Frequency Invariant Beamformer Without Temporal Filtering. IEEE Trans. Signal Process. 2009, 57, 798–802. [Google Scholar] [CrossRef]
- Liu, W. Design and implementation of a rectangular frequency invariant beamformer with a full azimuth angle converage. J. Frankl. Inst. 2011, 348, 2556–2569. [Google Scholar] [CrossRef]
- Zhu, C.; Li, X.; Liu, Y.; Liu, L.; Liu, Q.H. An Extended Generalized Matrix Pencil Method to Synthesize Multiple-Pattern Frequency-Invariant Linear Arrays. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 2311–2315. [Google Scholar] [CrossRef]
- Liu, Y.; Cheng, J.; Xu, K.D.; Yang, S.; Liu, Q.H.; Guo, Y.J. Reducing the Number of Elements in the Synthesis of a Broadband Linear Array With Multiple Simultaneous Frequency-Invariant Beam Patterns. IEEE Trans. Antennas Propag. 2018, 66, 5838–5848. [Google Scholar] [CrossRef]
- Tang, W.; Zhou, Y. Frequency invariant power pattern synthesis for arbitrary arrays via simulated annealing. Electron. Lett. 2010, 46, 1647–1648. [Google Scholar] [CrossRef]
- Liu, Y.; Nie, Z.; Liu, Q.H. Reducing the Number of Elements in a Linear Antenna Array by the Matrix Pencil Method. IEEE Trans. Antennas Propag. 2008, 56, 2955–2962. [Google Scholar] [CrossRef]
- Cheng, Q.; Fusco, V.; Zhu, J.; Wang, S.; Gu, C. SVD-Aided Multi-Beam Directional Modulation Scheme Based on Frequency Diverse Array. IEEE Wirel. Commun. Lett. 2020, 9, 420–423. [Google Scholar] [CrossRef]
- Xu, L.; Yang, Y.; Li, R. Fast arrays synthesis by the matrix method with embedded patterns of standard cell. Prog. Electromagn. Res. C 2019, 93, 237–251. [Google Scholar] [CrossRef] [Green Version]
- Luk, K.M.; Wong, H. A New Wideband Unidirectional Antenna Element. Int. J. Microw. Opt. Technol. 2006, 1, 35–44. [Google Scholar]











| Subarray | Active Elements | BW | |||||||
|---|---|---|---|---|---|---|---|---|---|
| F1 | 1 | 2 | … | … | … | … | N − 1 | N | [fb, f2) |
| F2 | 1 | 2 | … | … | … | … | N − 1 | [f2, f3) | |
| . | . | . | … | … | … | … | . | ||
| Fl | 1 | 2 | … | … | Nl | [fl, fl+1) | |||
| . | . | . | … | … | . | ||||
| FL | 1 | 2 | … | NL | [fL, fu] | ||||
| Element Number | Maximum(°) | Minimum(°) | Mean(°) |
|---|---|---|---|
| 18 | 8.7 | 8.1 | 8.3 |
| 23 | 7.5 | 7.1 | 7.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, L.; Li, R.; Chen, X.; Wei, F.; Shi, X. Wideband Frequency Invariant Array Synthesis Based on Matrix Singular Value Decomposition. Electronics 2021, 10, 2039. https://doi.org/10.3390/electronics10162039
Xu L, Li R, Chen X, Wei F, Shi X. Wideband Frequency Invariant Array Synthesis Based on Matrix Singular Value Decomposition. Electronics. 2021; 10(16):2039. https://doi.org/10.3390/electronics10162039
Chicago/Turabian StyleXu, Le, Rui Li, Xiaoqun Chen, Feng Wei, and Xiaowei Shi. 2021. "Wideband Frequency Invariant Array Synthesis Based on Matrix Singular Value Decomposition" Electronics 10, no. 16: 2039. https://doi.org/10.3390/electronics10162039
APA StyleXu, L., Li, R., Chen, X., Wei, F., & Shi, X. (2021). Wideband Frequency Invariant Array Synthesis Based on Matrix Singular Value Decomposition. Electronics, 10(16), 2039. https://doi.org/10.3390/electronics10162039










